九年级数学PPT课件24.1.2-垂径定理》课件
合集下载
垂径定理 初中九年级数学教学课件PPT 人教版

●O
侧的两个半圆重合,点A与点B
AM
B C 重合,AM与BM重合,
D
线段:AM=BM
·O
⌒ AC和B⌒C重合, ⌒AD和B⌒D重合.
M A
B 等弧: A⌒C=B⌒C, A⌒D =B⌒D.
D
证明:
C
连接OA、 则OA=OB. ∵CODB⊥, AB ∴∠OMA=∠OMB
在Rt△OAM和Rt△OBM中,
即CD所在直线是AA'的垂直平分线 ∴对于圆上任意一点A,在圆上都有关于直 A 线CD的对称点A',即:
'
圆是轴对称图形,任何一条直径所在直 线都是圆的对称轴.
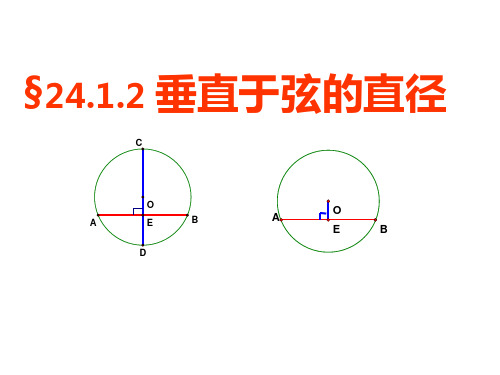
AB是⊙O的一条弦.
作直径CD,使CD⊥AB,垂足为M.
C
你能发现图中有那些相等的线 段和弧?为什么?理由.
把圆沿着直径CD折叠时,CD两
} { 题设
(1)直径 (2)垂直于弦
直径
结论
(3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧
垂径定理:
定理: 垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
C
题设
A
●O
M
由 ① CD是直径 B ② CD⊥AB
可推得
D
结论
①AM=BM,
②A⌒C=B⌒C, ③A⌒D=B⌒D.
定理辨析
CD ⊥AB,垂足为M,OM=3,
则CD= 8 .
A
●O
CM
D
B
3、在⊙O中,CD ⊥AB于M,AB为 直径,若CD=10,AM=1,则⊙O的半
径是 13 .
注意:解决有关弦的问题时,半径是常用的一种 辅助线的添法.往往结合勾股定理计算。
垂径定理优秀课件
C
推论:平分弦(不是直径)的直径垂
直于弦,并且平分弦所对的两条弧。
(2)垂直于弦 (1)过圆心 (4)平分弦所对的一条弧 (3)平分弦 (5)平分弦所对的另一条弧
O
A C O B D E D B
不是直径
CD是直径 CD AB AE BE ( AB不是直径)
OE AC OD AB AB AC
B
3.已知⊙O的直径是50 cm,⊙O的两条平行弦 AB=40 cm ,CD=48cm, 求弦AB与CD之间的距离。
过点O作直线OE⊥AB,交CD于F。
A
C
20 E
25 25 24
F
15 . O 7
B D
A
C
E
F . O
B
D
AB、CD在点O两侧 EF=OE+OF=15+7=22 AB、CD在点O同侧 EF=OE-OF=15-7=8
⌒ ⌒ AD=BD.
下列图形是否具备垂径定理的条件?
C
c
C
C
A
O A D E B
D O
B
O
O A E B
A E D B
是
不是
是
不是
直径垂直弦,才能平分弦,平分弦所对的弧.
适用垂径定理的几个基本图形:
C
A E
O A D E B
B
A
O E D B
O
A
O
E B
D
CD过圆心
CD⊥AB于E
AE=BE AC=BC AD=BD
§24.1.2 垂直于弦的直径
C O A D E B
A
O E B
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的 弦的长)为37.4米,拱高(弧的中点到弦的距离) 为7.2米,你能求出赵州桥主桥拱的半径吗?
24.垂径定理的应用PPT课件(人教版)

经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根
据垂径定理,D是AB的中点,C是 由题设得
AB 7.2,CD
AB 的中点,CD就是拱高.
2.4, HN 1 MN 1.5.
AD
1
AB
1 7.2
2 3.6,
2
2
OD OC DC R 2.4.
在Rt△OAD中,由勾股定理,得
①④ ②③⑤ 平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的 ①⑤ ②③④ 另一条弧.
②③ ①④⑤ 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
②④ ②⑤ ③④ ③⑤
①③⑤ 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且
①③④ 平分弦和所对的另一条弧.
①②⑤ 平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于 ①②④ 弦,并且平分弦所对的另一条弧.
O
A
B
P
2、如图,⊙O的直径AB和弦CD相交于点E,
AE=1厘米,EB=5厘米,∠BED=30°,
求CD的长。
D
No 在Rt△OEF中,OE=3-1=2,
∠BED=30°则OF=1
B
Image 又在Rt△DOF中
F OE
A C
DF= OD2 OF2 32 12 2 2
∴CD=2DF= 4 2
2、通过作出弦心距后,可构造直角三角形,然 后用直角三角形的边角关系或勾股定理来求解.
B
AD AB 37.4 18.7,
2
2
R
R-7.2
OD OC DC R 7.2.
在Rt⊿AOD中,由勾股定理,得
O
OA2 AD2 OD 2 ,
即R2 18.72 (R 7.2)2.
24.1.2 垂直于弦的直径 课件(共23张PPT) 人教版数学九年级上册

【解析】如图所示:连接OD ∵直径AB=15 ∴BO=7.5 ∵OC:OB=3:5 ∴CO=4.5 ∴ DC DO2 CO2 6 ∴DE=2DC=12.
3.(2021•杭州期末)如图,已知MN是⊙O的直径,AB是⊙O的弦, AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
ABC ACB BAC
A⌒B ⌒BC
⌒ A⌒CB BAC
B O●
C
判断:半圆是弧,但弧不一定是半圆.( )
1.进一步认识圆,了解圆是轴对称图形. 2.理解垂直于弦的直径的性质和推论,并能应用它解 决一些简单的计算、证明和作图问题.(重点) 3.灵活运用垂径定理解决有关圆的问题.(难点)
圆是轴对称图形吗?如果是,它的对称轴是什么?
③ AE=BE
④ A⌒C=B⌒C ⑤ A⌒D=⌒BD C
举例证明其中一种组合方法 已知:
求证:
O
E
A
B
D
【证明举例】
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2) A⌒C与B⌒C相等吗? A⌒D与B⌒D相等吗?为什么?
C
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
A
E
B
O
【跟踪训练】
如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= 16cm.
解析:连接OA, ∵ OE⊥AB,
AE OAc2m OE2
102 62
8
∴ AB=16cm.
A
E
B
O·
垂径定理
内容
推论
辅助线
基本图形及 变式图形
人教版九年级数学上册《24.1.2 垂直于弦的直径》 PPT课件

A.4 2 B.8 2
C.2 5
D.4 5
练习巩固,综合应用
2.如图,将半径为2 cm 的圆形纸片折叠后,圆弧恰好 经过圆心O,则折痕AB的长为 __2__3__cm.
3.⊙O的直径为10,弦AB的长为8,P是弦AB 上的一个动点,则OP长的取值范围为 3≤OP≤5.
练习巩固,综合应用
4.已知⊙O中,若弦AB的长为
8 cm,圆心O到AB的距离为3 cm, A 求⊙O的半径.
解:连结OA,过O作OE⊥AB,
E
B
.
O
垂足为E,则OE=3 cm,AE=BE.
∵AB=8 cm,∴AE=4 cm.
在Rt△AOE中,根据勾股定理可得OA=5 cm.
∴⊙O的半径为5 cm.
练习巩固,综合应用
5.如图,AB是⊙O的直径,作半径OA的垂直平分 线,交⊙O于C,D两点,垂足为H,连接BC,BD.
——过圆心作垂直于弦的线段; ——连接半径.
再见
2
∴r=2 3.
故⊙O的半径长是2 3 .
练习巩固,综合应用
6.银川市某居民区一处圆形下水管道破裂,修 理人员准备更换一段新管道.如下图所示,污水水 面宽度为60 cm,水面至管道顶部距离为10 cm,问 修理人员应准备内径多大的管道?
练习巩固,综合应用
解:如图所示,连接OA,过点O作OE⊥AB,垂足为E,交圆于
2
2
在Rt△OAD中,由勾股定理,得
C
OA2=AD2+OD2,即R2=18.52+(R-7.23)2. 解得R≈27.3(m). 因此,赵州桥的主桥拱半径约为27.3 m.
D
A
B
R
O
练习巩固,综合应用
九年级上数学《24.1.2 垂直于弦的直径》课件
M
C A O 证明:作直径MN垂直于弦AB D ∵ AB∥CD B ∴ 直径MN也垂直于弦CD ⌒ ⌒ ∴AM=BM, ⌒ ⌒ CM=DM ⌒ ⌒ ⌒ ⌒ ∴AM-CM =BM-DM ⌒ ⌒ 即 AC=BD
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况: O A C D A O C D B B
E
O
题设
③平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧 结论
垂径定理的推论1
① 直径过圆心 ③ 平分弦 C ② 垂直于弦 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
A
E
O B
已知:CD是直径,AB是弦,CD平分AB 求证:CD⊥AB,AD=BD,AC=BC
⌒ ⌒ ⌒ ⌒
D
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
① 直径过圆心 ③ 平分弦 ⑤ 平分弦所对的劣弧
② 垂直于弦 ⑤ 平分弦所对的劣弧
① 直径过圆心 ③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心 ② 垂直于弦 ⑤ 平分弦所对的劣弧
③ 平分弦 ⑤ 平分弦所对的劣弧
B
在 a , d , r, h中,已知其中任 意两个量,可以 求出其它两个量 .
B
⌒ 点O就是AB的圆心.
O
你 能 破 镜 重
m
n
A
C
圆
吗?
B O
作法: 作弦AB、AC及它们的垂直平分线m、n, 交于O点;以O为圆心,OA为半径作圆. 依据: 弦的垂直平分线经过圆心,并且平分弦 所对的两条弧.
垂径定理三角形
C A O 证明:作直径MN垂直于弦AB D ∵ AB∥CD B ∴ 直径MN也垂直于弦CD ⌒ ⌒ ∴AM=BM, ⌒ ⌒ CM=DM ⌒ ⌒ ⌒ ⌒ ∴AM-CM =BM-DM ⌒ ⌒ 即 AC=BD
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况: O A C D A O C D B B
E
O
题设
③平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧 结论
垂径定理的推论1
① 直径过圆心 ③ 平分弦 C ② 垂直于弦 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
A
E
O B
已知:CD是直径,AB是弦,CD平分AB 求证:CD⊥AB,AD=BD,AC=BC
⌒ ⌒ ⌒ ⌒
D
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
① 直径过圆心 ③ 平分弦 ⑤ 平分弦所对的劣弧
② 垂直于弦 ⑤ 平分弦所对的劣弧
① 直径过圆心 ③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心 ② 垂直于弦 ⑤ 平分弦所对的劣弧
③ 平分弦 ⑤ 平分弦所对的劣弧
B
在 a , d , r, h中,已知其中任 意两个量,可以 求出其它两个量 .
B
⌒ 点O就是AB的圆心.
O
你 能 破 镜 重
m
n
A
C
圆
吗?
B O
作法: 作弦AB、AC及它们的垂直平分线m、n, 交于O点;以O为圆心,OA为半径作圆. 依据: 弦的垂直平分线经过圆心,并且平分弦 所对的两条弧.
垂径定理三角形
人教版九年级数学上册课件:24.1.2垂径定理(共15张PPT)
船能过拱桥吗
AB 7.2,CD 2.4, HN 1 MN 1.5.
AD 1 AB 1 7.2 3.6,
2
2
2
OD OC DC R 2.4.
在Rt△OAD中,由勾股定理,得
OA2 AD2 OD 2 ,
即R2 3.62 (R 2.4)2.
A
D
E C
O
B
自学指导(二)
认真阅读课本8 2页赵州桥问题,并思考:
1、解决赵州桥求半径问题做了什么辅助过线圆?心作弦的垂线 2、由图24.1-8知主桥拱是__A_B____, 跨度是__弦_A_B__,拱 高是__C_D__,弦心距是__O_D___,半径是__O_A_,_O_B___ , AD= _B_D___.
任意知道两个量,可根据垂径定理求出第三个量:
必做题:课本P83练习1、2题。 选做题:课本P89第2题。 思考题:课本P89第8题。
判断下列说法的正误
①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥弦的垂直平分线一定经过圆心
2、如图,直径为10cm的圆中,圆心到弦 AB的距离OM为4cm,求弦AB的长。
O
A
M
B
相信自己,我能行
破镜重圆
自学指导(一)
认真阅读课本81页—82页“赵州桥问 题” 上面的内容: 1、圆是______图形, __________都是它 的对称轴,对称轴有____条.
2、垂径定理的内容是_________________.
3、对照24.1-6用符号语言表示垂径定理 ? 4、垂径定理的推论是什么?
24.1.2垂径定理_课件ppt(新人教版九年级上)
判断下列说法的正误
①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦, 必平分此弦所对的弧
解决求赵州桥拱半径的问题 ⌒ 表示主桥拱,设 AB所在圆的圆心为O, ⌒ 如图,用 AB
直径垂直于弦=>
=>
直径平分弦
直径平分弧
=>
直径平分弧所对的弦
直径垂直于弧所对的弦
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的 货船要经过拱桥,此货船能否顺利通过这座拱桥?
B A
半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC 与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是 ⌒ AB 的中点,CD 就是拱高. 在图中 AB=37.4,CD=7.2, 1 1 AD AB 37.4 18.7, 2 2
OD=OC-CD=R-7.2 在Rt△OAD中,由勾股定理,得 OA2=AD2+OD2 A 即 R2=18.72+(R-7.2)2 解得:R≈27.9(m)
∴ AE=AD ∴ 四边形ADOE为正方形.
E
·
O D B
A
在直径为650mm的圆柱形油槽内装入一些油后,截面 的油面宽AB = 600mm,求油的最大深度.
D
A
O ┌ E
A
B
600
B
O ø650
D
D
600
人教版九年级数学上册 24.1.2垂径定理(共21张PPT)
下课!
课堂作业:课本 家庭作业:练习册
O
A
B
E
D
∴ CD⊥弦AB ,A⌒D=
⌒
BD
,A⌒C=B⌒C
1.判断下列图形,能否满足垂径定理?
B
B
B
O
O
O
C A
(×)
DC A
DC E
(×)
(√)
注意:定理中的两个条件
(直径,垂直于弦)缺一不可!
DC
O D
A
(√)
2.如图,在圆O中,直径MN⊥AB,垂足
是C,则下列结论中错误的D是( )
A.A⌒N=⌒BN B. AC=BC
2
2
OD=OC-CD=R-7.2
在Rt△OAD中,由勾股定理,得A
C D B
OA2=AD2+OD2
R
即 R2=18.72+(R-7.2)2
O
解得:R≈27.9(m)
因此,赵州桥的主桥拱半径约为27.9m.
图一:AC、BD有什么关系? A C O D B
变式:图二AC=BD依然成立吗? (1)
AC
O
将圆心到弦的距离、半径、 弦长构成直角三角形,把问题 转化为直角三角形的问题。
B
A P
O
如图,A⌒B 所在圆的圆心是点O, 过O作OC⊥AB于点D,若CD=4 m, 弦AB=16 m,求此圆的半径.
课本例题
如图,1 400 多年前,我国隋代建造的赵州石拱桥 主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m, 拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥 拱的半径(精确到 0.1 m).
M
C.A⌒M=⌒BM D.OC=CN
24.1.2垂直于弦的直径 课件人教版数学九年级上册
(1)证明:∵PG平分∠EPF,
∴∠DPO=∠APO. ∵AOIIPE,∴∠DPO=∠AOP, ∴∠APO=∠AOP,.∴AP=AO.
【综合拓展类作业】
(2)解:如图,过点O作OH⊥AB 于点H,
在Rt△AOH中, ∵AO=5,AH=4, ∴OH=√52-42=3. ∵AP=AO=5, ∴PH=AP+AH=9,
探究:剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了 什么?由此你能得出什么结论?
猜想:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
你能证明上述结论吗?
证明:如图,设CD是○O的任意一条直径, A为 0O上点C,D 以外的任意一点. 过点A作AA'⊥CD, 交00于点A', 垂足为M, 连接OA,OA'.
构造Rt△利用勾股定理计算或建立方程.
垂直于圆的直径 1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧 2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
【知识技能类作业】必做题:
1.往直径为52cm 的圆柱形容器内装入一些水以后,截面如图所示,若水面 宽AB=48cm, 则水的最大深度为( C )
A.4cm
B.3cm
C.2cm
D.1cm
【知识技能类作业】必做题: 3.已知○ O 中,弦AB=8cm, 圆 心 到AB 的距离为3cm, 则此圆的半径为_5 cm.
4.如图,OE⊥AB 于E, 若○ O 的半径为10cm,OE=6cm, 则AB=16 .cm.
【知识技能类作业】选做题:
5.如图,在00中,弦AB的长为8cm, 圆心O到AB的距离为3cm.求 0 0 的半径.
∵OA=OB∴△OAB是等腰三角形
∴∠DPO=∠APO. ∵AOIIPE,∴∠DPO=∠AOP, ∴∠APO=∠AOP,.∴AP=AO.
【综合拓展类作业】
(2)解:如图,过点O作OH⊥AB 于点H,
在Rt△AOH中, ∵AO=5,AH=4, ∴OH=√52-42=3. ∵AP=AO=5, ∴PH=AP+AH=9,
探究:剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了 什么?由此你能得出什么结论?
猜想:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
你能证明上述结论吗?
证明:如图,设CD是○O的任意一条直径, A为 0O上点C,D 以外的任意一点. 过点A作AA'⊥CD, 交00于点A', 垂足为M, 连接OA,OA'.
构造Rt△利用勾股定理计算或建立方程.
垂直于圆的直径 1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧 2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
【知识技能类作业】必做题:
1.往直径为52cm 的圆柱形容器内装入一些水以后,截面如图所示,若水面 宽AB=48cm, 则水的最大深度为( C )
A.4cm
B.3cm
C.2cm
D.1cm
【知识技能类作业】必做题: 3.已知○ O 中,弦AB=8cm, 圆 心 到AB 的距离为3cm, 则此圆的半径为_5 cm.
4.如图,OE⊥AB 于E, 若○ O 的半径为10cm,OE=6cm, 则AB=16 .cm.
【知识技能类作业】选做题:
5.如图,在00中,弦AB的长为8cm, 圆心O到AB的距离为3cm.求 0 0 的半径.
∵OA=OB∴△OAB是等腰三角形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平分弦(不是直径)的直径垂直于 弦,并且平分弦所对的两条弧。
(2)“不是直径”这个条件能去掉吗?如 果不能,请举出反例。
C
A ·O B
D
C
① CD是直径, ② CD⊥AB, ③ AM=BM
A M└
B
●O
④A⌒C=B⌒C,
⑤A⌒D=B⌒D.
D
如果具备上面五个条件中的任何两个,那
么一定可以得到其他三个结论吗?
温故而知新
1.垂径定理的内容是什么?画出适合题意的 图形,用符号语言表示出来.
垂直于弦的直径平分弦,且平分弦所对的两条弧.
图形语言
C
●O
A E└
B
D
符号语言
∵ CD是直径, CD⊥AB,
∴AE=BE,
A⌒C =B⌒C, A⌒D=B⌒D.
垂径定理推论
平分弦(不是直径)的直径垂直 于弦,并且平分弦所对的两条弧。
OP=3cm, 则过P点的弦中,
(1)最长的弦=
cm
(2)最短的弦=
cm
(3)弦的长度为整数的共有( )
A、2条 b、3条 C、4条 D、5条 C
5 3 OO
A
4 PP B
D
4、如图,点A、B是⊙O上两点,AB=8,点P 是⊙O上的动点(P与A、B不重合),连接AP、 BP,过点O分别作OE⊥AP于E,OF⊥BP于
F,EF= 4 。
O
AE
F
B
P
船能过拱桥吗?
例3.如图,某地有一圆弧形拱桥,桥下水面宽为 7.2米,拱顶高出水面2.4米.现有一艘宽3米、 船舱顶部为长方形并高出水面2米的货船要经 过这里,此货船能顺利通过这座拱桥吗?
船能过拱桥吗
解:如图,用 AB 表示桥拱, AB所在圆的圆心为O,半径为Rm,
一条直线满足:(1)过圆心;(2)垂直于弦;(3)
平分弦(不是直径); (4)平分弦所对优弧;(5进行推导: ②
③ ④ ⑤
①过圆心 ②垂直于弦 ③平分弦
① ③
② ④ ⑤
① ④
③ ② ⑤
④平分弦所对优弧 ① ⑤平分弦所对劣弧 ⑤
③② ④③ ②
① ④ ⑤
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所
短的弦等于 2 5cm .
2.过⊙O内一点M的最长弦长为4厘米,最短 弦长为2厘米,则OM的长是多少?
B
O
D
P E
C
A
A OM
某圆直径是10,内有两条平行弦, 长度分别为6和8
求这两条平行弦间的距离.
回顾与思考 •这节课你有什么收获? •还有哪些疑问?
1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8 ㎝,那么⊙o的半径是 5㎝ 2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD,那 么C到AB的距离等于 1㎝或9㎝
.
(2)若AM=MB, CD是直径,
D
则 CD⊥AB 、 A⌒D=B⌒D 、A⌒C=B⌒C .
(3)若CD⊥AB, AM=MB, 则 CD是直径 、 A⌒D=B⌒D 、A⌒C=B⌒C . (4)若A⌒C=B⌒C ,CD是直径, 则 CD⊥AB 、 AM=BM 、 A⌒D=B⌒D .
试一试
2.判断:
对的两条弧。
(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分
弦所对的另一条弧。
(3)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
只要具备上述五个条件中任两个,就可以推出其余三个.
练习 1.如图所示:
C
A M└
B
(1)若CD⊥AB, CD是直径,
●O
则 AM=BM 、A⌒D=B⌒D
⌒⌒ 、 AC=BC
经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根
据 由垂题径设定 得理A,DB是A7B.的2,中CD点,C2是.4,AHBN的中1点M,CND就 1是.5拱. 高.
AD 1 AB 1 7.2 3.6, 2
2
2
OD OC DC R 2.4.
在Rt△OAD中,由勾股定理,得
试一试
已知A、B、C是⊙O上三点,且AB=AC, 圆心O到BC的距离为3厘米,圆的半径为5厘 米,求AB长。
A
O
B
D
C
A
D
B
C
O
练习
已知⊙O的半径为5厘米,弦AB的长为8厘米, 求此弦的中点到这条弦所对的弧的中点的距 离。
E
O
D
A
B
E
O
A
DB
1.已知P为⊙O内一点,且OP=2cm, 如果⊙O的半径是3cm,那么过P点的最
C
∵ CD是直径, AE=BE
·O
∴
CD⊥AB,A⌒C
=⌒BC,
A⌒ D
⌒
=BD.
AE
B
D
C
(1)如何证明?
已知:如图,CD是⊙O的直径,
·O
AB为弦,且AE=BE.
求证:CD⊥AB,且A⌒D=⌒BD, A⌒C
A
=B⌒C
E D
B
证明:连接OA,OB,则OA=OB
∵ AE=BE ∴ CD⊥AB ∴ A⌒D=B⌒D, A⌒C =B⌒C
OA2 AD2 OD 2 ,
即R2 3.62 (R 2.4)2.
解得 R≈3.9(m). 在Rt△ONH中,由勾股定理,得
OH ON2 HN2 , 即OH 3.92 1.52 3.6. DH 3.6 1.5 2.1 2. ∴此货船能顺利通过这座拱桥.
3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1㎝,
那么⊙O的半径为
5 Cm
4.如图,在⊙O中弦AB⊥AC,
B
OM⊥AB,ON⊥AC,垂足分别为M,
M
A
N,且OM=2,0N=3,则AB= 6 , AC= 4 ,OA= 13
ON C
()(1)垂直于弦的直线平分这条弦, 并且平分
弦所对的两条弧.
√( )(2)平分弦所对的一条弧的直径一定平分 这条弦所对的另一条弧.
( )(3)经过弦的中点的直径一定垂直于弦. ( )(4)圆的两条弦所夹的弧相等,则这两条弦平行.
√( )(5)弦的垂直平分线一定平分这条弦所对的弧.
3、如图,点P是半径为5cm的⊙O内一点,且
