【浙教版】八年级数学下册：5.1《矩形的性质(第1课时)》ppt课件

浙教版数学八年级下册 5.1 矩形说课课件(共35张PPT)

教学问题诊断分析
教学技术支持条件
【设计意图】数学的学习不应该是单方面的教师授课制度，应该是学生在自己的操作、实验、合作中完成的更有意义，因此这部分更加强调的是对一个新的性质探索的路径，学生于此充分的感受活动，独立思考和小组配合以诞生猜想和结论。
05
教学内容
教学目标
教学问题
教学技术
及其解析
教学问题诊断分析
教学技术支持条件
【设计意图】首先让学生描述一下生活中能够抽象到的矩形，注重对学生用数学眼光观察现实世界的培养。再类比已学的几何图形研究视角，归纳几何图形探究的视角可以从边，角，特殊的线和对称性进行研究，从而让矩形学习的发生更加自然。
05
教学内容
及其解析
架构体系，启航
教学目标及其解析
03
教学内容
教学目标
及其解析
及其解析
教学技术支持条件
教学过程及其设计
（1）具备的基础（知识、能力）在知识层面上，八年级的下册学生已经经历第四章平行四边形的推理过程，也感受过从普通四边形特殊化到平行四边形的过程，本章作为特殊平行四边形的起始课，学生初步能用特殊化角的视角进行展开；从情感角度看，作为此阶段的学生，基本的推理能力已经具备，也懂得一定自我探索和总结的方法，因此需要将过程更多的交给学生.
05
教学内容
及其解析
概念生成，源起
教学目标及其解析
教学问题诊断分析
教学技术支持条件
【设计意图】架设平行四边形的一种特殊化视角，介绍概念，通过定义强调出矩形和平行四边形的包含关系，作为新概念课程，书写方式的规范性和几何语言的表达也需要一定强调。
05
教学内容

矩形的判定(课件)八年级数学下册(浙教版)

学以致用
4.如图，在△AEC、△BED中，∠AEC=∠BED=90°，AC、BD相交于点 O，且O是AC、BD的中点．求证：四边形ABCD是矩形．
学以致用
5.如图，在平行四边形ABCD中，角线AC、BD相交于点O，动点E以1个单位每秒的速度从点A出发沿AC向运动，点F同时以1个单位每秒的速度从点C发沿 CA方向运动，若AC=12，BD=8，求出经过几秒后，四边形BPDQ是矩形？
矩形的判定1
矩形的定义：
D
C
有一个角是直角的平行四边形是矩形.
A
B
∠A=90° 平行四边形ABCD
四边形ABCD是矩形。
“矩形的对角线相等”，反过来，猜想对角线相等的四边形是矩形，你觉得对吗？
不对，矩形是特殊的平行四边形，所以它的对角线不仅相等且平分.
不对，等腰梯形的对角线也相等.
我猜想：对角线相等的平行四边形是矩形.
∴四边形EFGHBCD形状如图，它的两条对角线相互垂直.若要从这张纸中剪
出一个矩形，并使它的四个顶点分别落在四边形ABCD的四条边上，可怎样剪？
D
C
D
GC
O
H
OF
A
B
A
E
B
解：如图，在AB、BC、CD、AD上取中点E、F、G、H，连接EF、FG、GH、HE,
∵ EF是△ABC的中位线， ∴ EF∥AC, ∵ AC⊥BD. ∴ EF⊥BD.
∵ EH是△ABD的中位线， ∴ EH∥BD, ∵ EF⊥EH,即∠HEF=90° 同理，∠EHG=90°，∠HGF=90°
∴四边形EFGH是矩形.
学以致用
1.如图，BD是平行四边形ABCD的一条对角线，E是CD的中点，连接AE并延长交BC的延长线于F. (1)求证：BC=CF. (2)当DB=DF时,求证：四边形ABCD是矩形．

浙教初中数学八下《5.1 矩形》PPT课件 (9)

图 28－7
·浙教版
第28课时 │ 当堂检测
6．[2011·广安] 如图 28－8 所示，在菱形 ABCD 中，∠ABC＝60°， DE∥AC 交 BC 的延长线于点 E.
求证：DE＝12BE.
图 28－8
·浙教版
第28课时 │ 当堂检测
证明：证法一：连结 BD. ∵四边形 ABCD 是菱形，∠ABC＝60°， ∴BD⊥AC，∠DBC＝30°， ∵DE∥AC， ∴DE⊥BD，即∠BDE＝90°， ∴DE＝12BE.
·浙教版
第28课时 │ 浙考探究
·浙教版
第28课时 │ 浙考探究
(2)∵AG∥BD， ∴∠G＝∠DBC＝90°， ∴△DBC 为直角三角形．又∵F 为边 CD 的中点． ∴BF＝12DC＝DF，又∵四边形 DEBF 为平行四边形， ∴四边形 DEBF 是菱形．
·浙教版
第28课时 │ 浙考探究
又∵∠1＝∠2，∠4＝∠5， ∴∠1＋∠5＝∠2＋∠4. 又∵∠1＋∠5＋∠2＋∠4＝180°， ∴∠2＋∠4＝90°，
∴四边形 AECF 是矩形．
·浙教版
矩形是特殊的平行四边形，它具有平行四边形的所有性质，同时也具有特殊的性质．所以，判定矩形的方法也是多样的，可以先判定这个四边形是平行四边形，然后再判定其是矩形．
·浙教版
第28课时 │ 浙考探究
► 类型之二菱形的性质及判定的应用
命题角度： 1．菱形的性质 2．菱形的判定
[2011·宁波] 如图 28－3，在▱ ABCD 中，E，F 分别为边 AB， CD 的中点，BD 是对角线，过 A 点作 AG∥DB 交 CB 的延长线于点 G.
(1)求证：DE∥BF； (2)若∠G＝90°，求证：四边形 DEBF 是菱形．

浙教版八年级数学下《5.1.2矩形》课件共19页

谢谢！
51、天下之事常成于困约，而败于奢靡。——陆游 52、生命不等于是呼吸，生命是活动。——卢梭
53、伟大的事业，需要决心，能力，组织和责任感。 ——易卜生 54、唯书籍不朽。——乔特55、为中 ຫໍສະໝຸດ 之崛起而读书。 ——周恩来
浙教版八年级数学下《5.1.2矩形》课
件
21、没有人陪你走一辈子，所以你要适应孤独，没有人会帮你一辈子，所以你要奋斗一生。 22、当眼泪流尽的时候，留下的应该是坚强。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之首，因为这种德性保证了所有其余的德性。--温斯顿．丘吉尔。 25、梯子的梯阶从来不是用来搁脚的，它只是让人们的脚放上一段时间，以便让别一只脚能够再往上登。

浙教八年级下册数学第五章第1节《矩形的性质与判定》复习课件(浙教版)

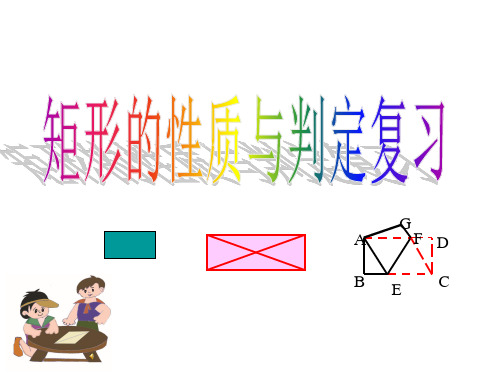
4、如图，矩形ABCD中，O是对角线的交点，若AE⊥BD于E，且 OE∶OD＝1∶2， AE＝ cm，则∠AOD = ， DE＝ cm。
（1）求证：DE＝BF；
（2）若四边形 BEDF是菱形，则四边形 AGBD是什么特殊四边形？并证明你的结论．
A
2.如图，利用一面墙（墙的长度不超过45m），用80m长的篱笆围一个矩形场地．⑴怎样围才能使矩形场地的面积为750m2?⑵能否使所围矩形场地的面积为810m2，为什么?
墙
3.2008年爆发的世界金融危机，是自上世纪三十年代以来世界最严重的一场金融危机。受金融危机的影响，某商品原价为200元，连续两次降价a％后售价为148元，下面所列方程正确的是( )A.200(1+a％)2=148; B.200(1-a％)2=148; C.200(1-2a％)=148; D.200(1+a2％)=148;
当a=3,则PA+PB=____
拓展题:
①则AD=____ BC=____
1
2
②
当a=1 时，则PA+PB=____,
③
2、如图，P是矩形ABCD内一点， PA＝3，PD＝4，PC＝5，则PB＝。
E
F
提示：过点P作其中一边的垂线，利用勾股定理来解。
1.如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米2，则修建的路宽应为（）A．1米 B．1.5米 C．2米 D．2.5米
A
D
B
C
P
Q
分类讨论思想
A
B
P
D
C
已知△ABP的一边AB=
（1）在如图所示的4×4的方格中画出格点△ABP，使三角形的三边为

2020年新浙教版八年级数学下册同步导学课件5.1 第1课时矩形的性质

谢谢观看！
第1课时矩形的性质
2.如图5-1-2,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,
则∠AOB的大小为 ( B ) A.30° B.60° C.90°
D.120°
图5-1-2
第1课时矩形的性质
筑方法
类型一利用矩形的性质求角度
例1 [教材补充例题] 如图5-1-3,在矩形ABCD中,AC,BD相交于点 O,AE平分∠BAD,交BC于点E.若∠CAE=15°,求∠BOE的度数.
在矩形ABCD中,∠ABC的平分线分矩形的一边AD为1 cm和3 cm的两部分,则这个矩形的面积为 4 cm2 . (1)错因分析: (2)纠错:
第1课时矩形的性质
解: (1)没有仔细审题,题中没有具体指出分得的两部分分别长多少,应分类讨论. (2)如图.
∵四边形 ABCD 是矩形, ∴AB=CD,AD=BC,AD∥BC, ∴∠AEB=∠CBE. ∵BE 平分∠ABC, ∴∠ABE=∠CBE, ∴∠AEB=∠ABE,∴AB=AE.
第1课时矩形的性质
∴△AOB 是等边三角形, ∴OB=AB,∠ABO=60°, ∴∠OBE=∠ABC-∠ABO=90°-60°=30°. ∵∠BEA=90°-∠BAE=45°=∠BAE, ∴AB=BE,∴OB=BE, ∴∠BOE=��°-��∠�� =��°��-��°=75°.
即重叠部分△DEF
的面积为��
��
cm2.
第1课时矩形的性质
【归纳总结】解决矩形中折叠问题的基本思路折叠就是以折痕所在直线为对称轴的轴对称变换,因此中垂线的性质、全等图形的性质是解决折叠问题的常用知识点,最后数形结合, 利用勾股定理建立方程求解.

2015春浙教版数学八下5.1《矩形》课件

B
做一做
3、在直角坐标系中有点A（a，b），B（a，c），C
（-a，-b），D（-a，-c）（a≠0，b≠c）。若要使
四边形ABCD是矩形，b，c应满足什么条件？说明你的
理由。
下课了!
证法二
A D O
已知：如图，在□ABCD中，AC=BD 求证： □ABCD是矩形证明：在□ABCD中，AO=OC，BO=DO，又∵AC=BD ∴AO=BO=CO ∴∠OAB=∠OBA，∠OBC=∠OCB ∵∠OAB+∠OBA+∠OBC+∠OCB=180° ∴∠OBA+∠OBC=90°即∠ABC=90° ∴□ABCD是矩形
5.1 矩形(2)
想一想：
一位很有名望的木工师傅，招收了两名徒弟。一天，师傅有事外出，两徒弟就自己练习。他们各用一块四边形的废料做了一扇矩形式的门，做成之后，两人都说对方做的门不是矩形，而自己做的是矩形。甲说：“我用角尺量我做的门的任意三个角，发现他们都是直角，所以我做的这个门一定是矩形。” 乙说：“我用直尺量我做的门的两条对角线，发现它们的长度相等，所以我做的门一定是矩形” 根据它们的对话，你能肯定谁做的门一定是矩形吗？
矩形定义判定一：矩形的定义有一个角是直角的平行四边形叫做矩形 ∵四边形ABCD是□，∠A=90° C 四边形ABCD为矩形 A
D
B
探究新知：
除了利用定义来判定一个四边形是否为矩形外，还可以用以下判定定理来证明:
定理1：有三个角是直角的四边形是矩形。定理2：对角线相等的平行四边形是矩形。
B B A
A
D
A
D
B
C
C
矩形的判定定理2：对角线相等的平行四边形是矩形；