春季第九讲:简单的数阵图
学而思三年级奥数第9讲.数阵图进阶
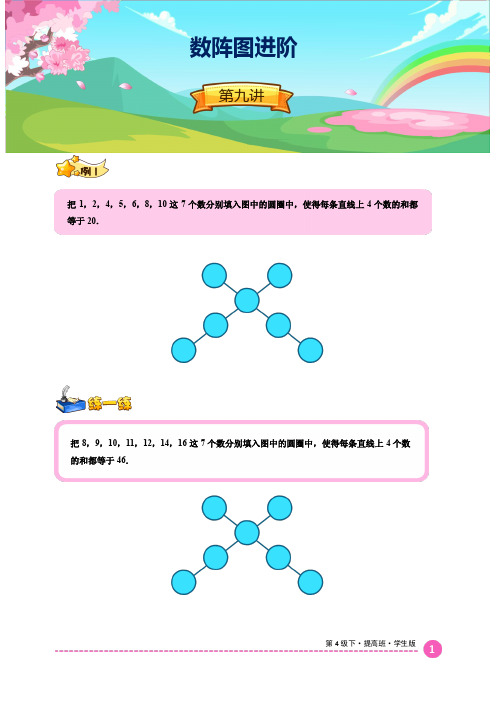
把8,9,10,11,12,14,16这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于46.把1,2,4,5,6,8,10这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于20.数阵图进阶第九讲第4级下·提高班·学生版第4级下·提高班·学生版把2,3,4,5,6,7,8这七个数分别填入图中的圆圈中,使两个正方形中四个数之和都等于19. 将5,9,13,14,17,21,25这7个数分别填入图中的圆圈中,使得每条直线上3个数的和都等于44.第4级下·提高班·学生版将5,6,9,11,14,15这6个数分别填入图中的圆圈里,使两个大圆上4个数的和都等于40.把1,5,9,10,16,21这6个数分别填入图中的○里,使每一个大圆上的四个数之和都等于36.第4级下·提高班·学生版1. 把5,6,7,8,9这5个数分别填在下图的内,使横行、竖列3个数的和都等于( )中的数.把1,3,4,5,6,8,11,15这8个数分别填入图中的圆圈里,使得每个大圆上5个数的和都等于33.第4级下·提高班·学生版2. 把3,5,7,9,11,13,15这7个数分别填入图中的圆圈内,使每条直线上的3个数的和都等于27.3. 把2,4,6,8,10,12,14,16,18这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都等于24.4.把2,3,4,5,6,7,8这七个数分别填入图中的圆圈内,使两个正方形中四个数之和都等于21.5.把1,2,4,5,6,11这6个数分别填入图中的○里,使每个圆圈上的四个数之和都等于22.第4级下·提高班·学生版第4级下·提高班·学生版6. 把2,5,6,8,10,12,14,22这8个数分别填入下图中,使得每个大圆上的5个数的和都等于49.思维跳板——剪指甲小华的爸爸1分钟可以剪好5个自己的指甲.那么,他在5分钟内可以剪好几个自己的指甲呢?。
三年级春季班常规内容
4、市供热厂采用新技术后,在一周内的前3 天共节约用煤12.6吨,后4天平均每天节约 用煤3.5吨。这一周平均每天节约用煤多少 吨?
5、朝阳小学五年级有两个班,一班有51人 ,二班有49人,期中考试两个班全体同学 的平均成绩是81分,已知二班的平均成绩 比一班的平均成绩高7分,那么二班的平均 成绩是多少分?
热身挑战
阶梯闯关
例1:今天是9日星期三,本月26日是星期 几?
例2:2000年1月5日是星期三,那么, 2000年2月3日是星期几?
例3:2019年的元旦是星期二,那么, 2019年元旦是星期几?
例4:今天是25日星期四,本月3日是星期 几?
快乐练兵
练习一:2019年7月1日是星期五,那么, 2019年7月25日是星期几?
6、某农场前3天共收稻谷450公顷,后3天平 均每天比前3天多收稻谷60公顷,这个农场 这6天里平均每天收稻谷多少公顷?
7、三年级一班和二班的平均人数48人,二 班和三班平均人数46人,一班比三班人数多 几人?
第六讲:年月日
热身 挑战
阶梯 闯关
快乐 练兵
思维 导图 PK 大赛
生活大闯关:
1、今天是星期几? 2、今天是几月几日? 3、5天后是几月几日,星期几? 4、7天过后是几月几日,星期几? 5、14天过后是星期几? 6、你的生日是星期几? 7、每一个月的日期,最多有几排?最少有 几排?
快乐练兵
练习一: 886×5= 25×36= 64×125= 13×5×125×4×8=
练习二:
13×13= 18×19= 15×18= 14×19=
练习三:
51×41= 31×71= 81×51= 41×81=
练习四:
11×1543= 76822×11= 11×892= 94267×11=
数阵图PPtPPT课件
2021
1
例1. 把1--- 7这七个数填入下图,使每条 线段上三个○内的数的和相等.
2021
2
和都等于己于14,且数字1出现在四边形 的一个顶点上.
2021
3
2021
4
例3.把1---7这七个数填入下图中的7个○内, 使每条线段上三个数的和两个圆上的数的和 都相等 .
2021
5
2021
2021
13
例8. 如下左图有5个圆,它们相交后相互分 成几个区域,现在两个区域里已分别填上数 字10、6,请在另外七个区域里分别填进2、 3、4、5、6、7、9七个数字,使每个圈内 的数的和都是15.
2021
14
2021
15
6
例4. 将1~16分别填入下图(1)中圆圈 内,要求每个扇形上四个数之和及中间正方 形的四个数之和都为34,图中已填好八个数, 请将其余的数填完.
2021
7
2021
8
例5. 10个连续的自然数中从小到大的第三 大的数是9,把这10个数填入图中的10个方 格内,每格填一个数,要求图中3个2×2的正 方形中4个数之和相等,那么这个和最小值是
______.
2021
9
例6. 将1~8填入左下图的○内,要求按照 自然数顺序相邻的两个数不能填入有直线连 接的相邻的两个○内
2021
在下左图的七个圆圈内各填上一个数, 要求每条线上的三个数中,当中的数是两边 两个数的平均数,现在已填好两个数,求x 是多少?
2021
12
简单数阵图

简单数阵图一、知识点:一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为“数阵图”,数阵图的种类繁多,绚丽多彩,这里只向大家介绍三种数阵图,即辐射型数阵图、封闭型数阵图和复合型数阵图。
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字:要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力,思维的灵活性和严密性。
二、典例剖析:1.辐射型数阵:辐射型数阵图只有一个重叠数,重叠次数是“直线条数”-1,即m-1。
对于辐射型数阵图,有已知各数之和+重叠数×重叠次数=直线上各数之和×直线条数。
由此得到:(1)若已知每条直线上各数之和,则重叠数等于(直线上各数之和×直线条数-已知各数之和)÷重叠次数。
(2)若已知重叠数,则直线上各数之和等于(已知各数之和+重叠数×重叠次数)÷直线条数。
(3)若重叠数与每条直线上的各数之和都不知道,则要从重叠数的可能取值分析讨论。
例1:把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了,其余各数就好填了(见上图)。
随堂练习:1、将2~8这7个数分别填在下图中的圆圈内,使每条线段上三个圆圈内数的和相等.2、把1~9这9个数字,分别填入下图的各圆圈内,使每条线上5个数的和相等.2、封闭型数阵:例2:将1~6分别填在图中,使每条边上的三个○内的数的和都等于9.分析:因为 1+2+3+4+5+6 = 21 ,而每条边上的三个数的和为9,则三条边上的和为 9×3 = 27 , 27-21 = 6 ,这个 6 就是由于三个顶点都被重复算了一次。
数阵图

数阵图
一、数阵图定义及分类:
定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.
数阵:是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.
二、解题方法:
解决数阵类问题可以采取从局部到整体再到局部的方法入手:
第一步:区分数阵图中的普通点(或方格)和关键点(或方格);
第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;
第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.
简单数阵图
一、辐射型数阵图
从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中心数,多算的次数,公共的和
数和+中心数×重复次数=公共的和×线数
数和:指所有要填的数字加起来的和
中心数:指中间那数字,即重复计算那数字
重复次数:中心数多算的次数,一般比线数少1
公共的和:指每条直线上几个数的和
线数:指算公共和的线条数
二、封闭型数阵图
多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
突破关键:确定顶点上的数字,公共的和
数和+重叠数的和=公共的和×边数
数和、公共的和跟辐射型数阵图一样的意思
重叠数的和:指数阵图顶角重复算的数全加起来的和
边数:指封闭图形的边数。
二年级第九讲简单的数阵图
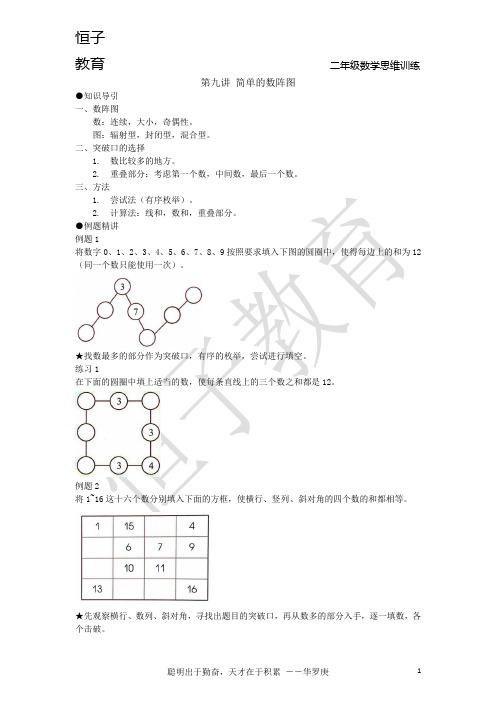
第九讲简单的数阵图●知识导引一、数阵图数:连续,大小,奇偶性。
图:辐射型,封闭型,混合型。
二、突破口的选择1.数比较多的地方。
2.重叠部分:考虑第一个数,中间数,最后一个数。
三、方法1.尝试法(有序枚举)。
2.计算法:线和,数和,重叠部分。
●例题精讲例题1将数字0、1、2、3、4、5、6、7、8、9按照要求填入下图的圆圈中,使得每边上的和为12(同一个数只能使用一次)。
★找数最多的部分作为突破口,有序的枚举,尝试进行填空。
练习1在下面的圆圈中填上适当的数,使每条直线上的三个数之和都是12。
例题2将1~16这十六个数分别填入下面的方框,使横行、竖列、斜对角的四个数的和都相等。
★先观察横行、数列、斜对角,寻找出题目的突破口,再从数多的部分入手,逐一填数,各个击破。
练习2将数字0、1、2、3、4、5、6、7、8、9分别填入下面的圆圈中,使得每边上的和为10,同一个数只能使用一次。
例题3把2,3,4,5,6这五个数分别填入空格中,使每行、每列上三个数相加的和都等于11,每个数只能是一次。
★找突破口(重叠部分),条件中要填的数是连续的,选择第一个、中间的、最后一个数进行重叠数的尝试,最后小数配大数。
练习3把5,6,7,8,9这五个数分别填入空格中,使每行、每列上三个数相加的和都等于22,每个数只能使用一次。
例题4将1~9这九个数分别填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数相加之和等于12,每个数只能使用一次。
★找突破口(重叠部分),条件给出的数是连续的,选择第一个、中间的、最后一个进行尝试。
练习4将1,2,3,4,5,6,7这7个数分别填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数相加之和等于14,每个数只能使用一次。
例题5把1,2,3,5,7,9,11这七个数分别填入圆圈里,使每条直线上的三个数相加的和都为14,每个数只能使用一次。
★找突破口(重叠部分),条件给出的数不是连续的,奇偶性尝试或者计算的方法。
一年级春季第九讲有趣的数阵图

第九讲有趣的数阵图
本讲主要通过学两种类型的数阵图,即辐射型和封闭型的,认识数阵图并找到解答数阵图的方法
一、一般数阵图
方法:由数多的入手想
例将1-16这十六个数分别填入下面的方框中,使横行、竖行、斜行的和都相等。
1 15 14 4
12 6 7 9
8 10 11 5
13 3 2 16
分析:先由数多的入手,即从对角线上的已知数求出和为34,然后按顺序求解就可以了。
二、辐射型数阵图
方法:(1)先填中间数(重叠数)
(2)尝试法:如果所填数是连续数,那么可以:
留头、留尾、留中间
剩下的数:小手拉大手
如果不是连续数,从小到大去尝试中间数即可
例把1,2,3,4,5,6,7这七个数分别填入里,使每条
直线上的三个数相加的和都相等,你能做出几种答案,让我们一起试试吧!
分析:(1)先填重叠数,留头1,剩下的数小手拉大手分组,2和7,3和6,4和5.对应填入即可
(2)留尾7,1和6,2和5,3和4
(3)留中间4,1和7,2和6,3和5
三、封闭型数阵图
方法:(1)先填重叠数,封闭型往往有多个重叠数
(2)拆数法然后再观察
例上填上1-6,使每条线上的和为9
分析:可以看出有3个重叠数,是三角形三个角上的数,如果尝试,就不太好想,所以要拆数了,即把9拆成三个数的和,再拆的时候注意要按从小到大的顺序。
9=1+2+6=1+3+5=2+3+4
然后再去观察出现2次得数,即1,2,3.重叠数要填1、2、3即可,其它的数对应的填入即可。
拓展训练
把1-11这11个数填入图中的圆圈中,使每条直线上的三个数的
和是18
答案:中间填6。
第9讲-封闭型数阵图

第九讲:观察与发现(十)——封闭型数阵图一、训练目标知识传递:填写封闭性数阵图的方法。
能力强化:观察能力、分析能力、计算能力。
思想方法:观察思想、分析思想。
二、知识与方法归纳数阵图就是将一些数,按照一定要求排列而成的某种图形,有时简称数阵。
它的类型一般分为三种:辐射型数阵图;封闭型数阵图;复合型数阵图。
辐射型数阵图:从一个中心出发,向外作了一些射线,我们把这种数阵图叫做辐射型数阵图。
一般地,有M条射线,每条射线有N个数的图形称为M—N图。
辐射型数阵图只有一个重叠数,重叠次数是“射线条数”-1,即M-1.对于辐射型数阵图,有:已知各数之和+重叠数×重叠次数=射线上各数之和×射线条数。
封闭型数阵图:一个数阵图,如果它的各边之间相互连接,形成封闭图形,我们称它们为封闭型数阵图。
封闭型M—N图有M个重叠数,重叠次数都是1次。
对于封闭型数阵图因为重叠数只重叠一次,所以:已知各数之和+重叠数之和=每边各数之和×边数。
(主要是顶点数字,抓住条件提供的关系式,进行分析,用试验的方法确定顶点数以及各边上的数字只和,最后填出数阵图。
)解答数阵图问题的关键在于找到重叠数和每条线上和。
三、经典例题例1、把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
解:例2、把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
解:例3、把1~5这五个数填入右图中的○里,使每条直线上的三个数之和相等。
解:例4、将1~8这八个数分别填入右图的○中,使两个大圆上的五个数之和都等于21。
解:例5、将1~6这六个自然数分别填入下图的六个○内,使得三角形每条边上的三个数之和都等于11。
解:例6、将1~6这六个自然数分别填入右图的六个○中,使得三角形每条边上的三个数之和都相等。
解:例7、将2~9这八个数分别填入下图的○里,使每条边上的三个数之和都等于18。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10 9 3 1
0 88
7 04 7
1 9 10
( 1)+(9 )=10( 0)+( 8)=8
4
6
2
6
( 0)+( 7 )=7(1 )+(9 )=10
2
5
2
8
例
2(★★★) ⑴填0~9的数且不能出现数字重复,使横行、
竖行的三个数相加都+ ( 9 ) +5=18 ( 6 ) + ( 7 ) +5=18
例 2(★★★)
⑴填0~9的数且不能出现数字重复,使横行、 竖行的三个数相加都得18。
4+5+( 9 )=18
98
4+6+( 8 )=18 5+6+( 7 )=18
7
例 3(★★★)
小朋友试一试,在每个方格中填入适当的数,使每一横行、竖行 的和以及两斜行的三个数之和都是19。
98
0
13
10
4
5+6+(8 )=19 8+2+( 9 )=19 9+6+( 4 )=19 4+5+(10)=19 10+9+( 0)=19
2+4+(13)=19
例
4(★★★★)
把7,8,9这三个数分别填入圆圈中,使每条线上三个数相加的 和都等于19。
9
解题过程
应该使用大小配原则,最
小的2周围应该是最大的
8
7
两个数:8和9,9在3和4 中应该选择更小的3。
例
5(★★★★)
你能把1,3,5,7,9这五个数分别填入下面的空格里,使横行 、竖行的三个数相加都得15?
2
3
4
例6(★★★★★)
⑵将1,3,4,5,6,7,9这七个数分别填入○里,使每条直 线上的三个数相加的和都为15。
1
解思题路过引程导
9
5 76
掐头、去尾、取中间,首尾 配对组相等。
3
4
例1(★★)
使用数字0,1,2,3,4,5,6,7,8,9做加法。在每一道题 中,同一个数字不能重复出现。
12
1
9
12
4
1 9
10
2 8 10
9
( 1 )+( 9 )=10
3
7
( 1 )+( 9 )=10
2
8
3
7
4
6
例1(★★)
使用数字0,1,2,3,4,5,6,7,8,9做加法。在每一道题 中,同一个数字不能重复出现。
3 159
7
解思题路过引程导
掐头、去尾、取中间,首尾 配对组相等。
例6(★★★★★)
⑴将0,2,3,4,6,7分别填入○里,使每一个大椭圆上的四 个数之和等于16。
0
3
2
解题过程
7+( 0 )+(3 )+( 6)=16
6
4 7+( 2 )+(3 )+( 4 )=16
∴( 0)+( 3)+( 6)=9
