《离散数学》第2次作业

合集下载

华工离散数学第二次作业

A．F ={<1，b>，<2，a>，<3，c>，<1，d>，<5，e>}
B．F={<1，c>，<2，a>，<3，b>，<4，e>，<5，d>}
C．F ={<1，b>，<2，a>，<3，d>，<4，a>}
D．F={<1，e>，<2，a>，<3，b>，<4，c>，<5，e>}
答题： A. B. C. D.
参考答案：B
13.运算“＋”是整数集I上的普通加法，则群<I,＋>的么元是( )
A．1 B．0 C．2 D．3
答题： A. B. C. D.
参考答案：B
14.下列说法不对的是（）
A．简单图不含平行边和环
B．每个图中，度数为奇数的节点数为偶数
C．有向图中节点的入度等于出度
D．完全图的边数为
答题： A. B. C. D.
C．f ={<1，7>，<2，6>，<3，5>，<4，6>}
D．f ={<1，10>，<2，6>，<3，7>，<4，8>，<5，10>}
答题： A. B. C. D.
参考答案：B
9.设A={1，2，3，4，5, 6}，B={a，b，c，d，e}，以下哪个函数是从A到B的满射函数( )
A．F ={<1，b>，<2，a>，<3，c>，<1，d>，<5，e>, <6，e>}

离散数学课后习题答案二

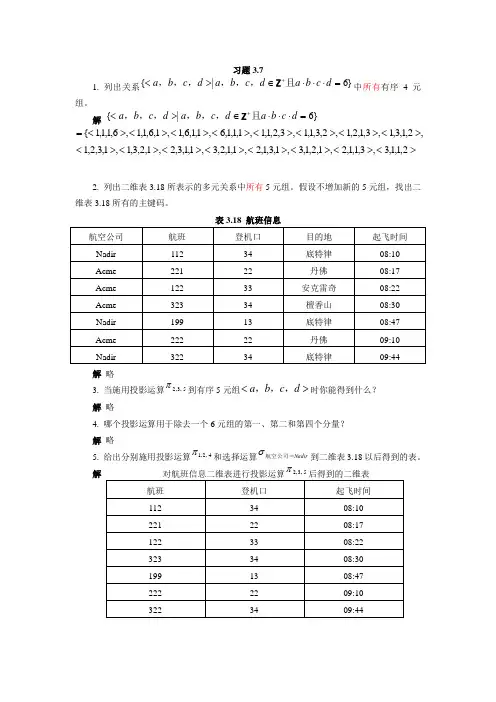
习题3.71. 列出关系}6|{=⋅⋅⋅∈><+d c b a d c b a d c b a 且，，，，，，Z 中所有有序4元组。

解 }6|{=⋅⋅⋅∈><+d c b a d c b a d c b a 且，，，，，，Z,2,1,3,1,3,1,2,1,2,3,1,1,3,2,1,1,1,1,1,6,1,1,6,1,1,6,1,1,6,1,1,1{><><><><><><><><=><><><><><><><><2,1,1,3,3,1,1,2,1,2,1,3,1,3,1,2,1,1,2,3,1,1,3,2,1,2,3,1,1,3,2,12. 列出二维表3.18所表示的多元关系中所有5元组。

假设不增加新的5元组，找出二维表3.18所有的主键码。

表3.18 航班信息航空公司航班登机口目的地起飞时间 Nadir 112 34 底特律 08:10 Acme 221 22 丹佛 08:17 Acme 122 33 安克雷奇 08:22 Acme 323 34 檀香山 08:30 Nadir 199 13 底特律 08:47 Acme 222 22 丹佛 09:10 Nadir 32234底特律09:44解略3. 当施用投影运算5,3,2π到有序5元组><d c b a ，，，时你能得到什么？解略4. 哪个投影运算用于除去一个6元组的第一、第二和第四个分量？解略5. 给出分别施用投影运算4,2,1π和选择运算Nadir 航空公司＝σ到二维表3.18以后得到的表。

解对航班信息二维表进行投影运算5,3,2π后得到的二维表航班登机口起飞时间 112 34 08:10 221 22 08:17 122 33 08:22 323 34 08:30 199 13 08:47 222 22 09:10 3223409:44对航班信息二维表进行选择运算Nadir 航空公司＝后得到的二维表航空公司航班登机口目的地起飞时间 Nadir 112 34 底特律 08:10 Nadir 199 13 底特律 08:47 Nadir 32234底特律09:446. 把连接运算3J 用到5元组二维表和8元组二维表后所得二维表中有序多元组有多少个分量？解略7. 构造把连接运算2J 用到二维表3.19和二维表3.20所得到的二维表。

离散数学第二次作业题及答案.doc

第2次作业一、单项选择题(本大题共40分，共20小题，每小题2分)1.假设A={a, b, c, d},考虑子集S= {{a, b}, {b, c}, {d}},则下列选项正确的是()oA.S是A的覆盖B.S是A的划分C.s既不是划分也不是覆盖D.以上选项都不正确2.设h是群G上的一个同态，|G|二12,山(G)|二3,则|K| (K是h的核)二_________________ ()A.1B.2C.D.3.L23 ), 设G是连通(n,m)的平面图，有r个面，且每个面的次数至少为L( 则A.m>3n-6B.Hl <c.m+n-r=2D.m+r-n二24.如果小王和小张都不去，则小李去。

设P：小王去。

Q：小张去。

R：小李去。

则命题符号化为_________ oA.-I QA-i PVRB.(Q->P)ARC.(n PAn QLRD.(PAQ)-R5.没有不犯错误的人。

M(x)： x为人。

F (x) : x犯错误。

则命题可表示为()OA.(Vx) (M(x) F (x)B.(3x) (M(x) AF(x)C.(Vx) (M(x)AF(x))D.(3x) (M(x)-F(x)6.(1)燕子北冋，春天来了。

设P:燕了北回。

Q：春天來了。

则(1)可以表示为___________ oP->QQ-PC.UQD.P VQ7.命题公式(P->QA-i P)的类型是___________ 。

A.重言式B.矛盾式C.可满足式D.永真式6.一阶逻辑公式Vx(F(x, y)AG(y, z) )—VzF(z, y)是()前束范式封闭公式C.永真式D.永假式7.谓词公式(3x)P(x, y) A (Vx) (Q(x, z)-> Gx) (Vy)R(x, y, z)中的量词Vx 的辖域是()。

A.(Vx)(Q(x,z)->(3 x)( Vy)R(x,y ,z)B.Q(x, z)-> (Vy)R(x, y, z)C.Q (x, z) —(3x) (Vy) R (x, y, z)D.Q(x, z)8.关于半群的性质，下面说法不正确的是()A.若〈S,*>S且*在8上是封闭的，那么匸是一个半群，B<B, *>也是一个半群。

离散数学第2次作业参考答案

1
1
0
0
1
1
1
0
0
1
1
1
1
1
1
0
1
0
1
(3-2)主析取范式：
(4)由真值表和主析取范式分别可以验证该推理正确。
6、(每题12分，共24分)
(1)如果今天是星期六，我们就要到颐和园或圆明园去玩。如果颐和园游人太多，我们就不去颐和园。今天是星期六。颐和园游人太多。所以我们去圆明园玩。
解：
(1)令p:今天是星期六; q:我们要到颐和园玩; r:我们要到圆明园玩; s:颐和园游人太多.
5、(20分)用2种方法(真值表法、主析取范式法)判断下面推理是否正确。
若是奇数，则不能被2整除。若是偶数，则能被2整除。因此，如果是偶数，则不是奇数。
解：(1)简单命题符号化：
p: 是奇数，q: 能被2整除，r: 是偶数。
(2)前提和结论分别符号化为：
若是奇数，则不能被2整除: p→ q。
2018级离散数学第二次作业参考答案
学号：姓名：班级：总分：
1、(每空5分，共30分)
(1)已知公式A含有3个命题变项p,q,r,并且它的成真赋值为000，011，110，那么命题公式A的成假赋值为001,010,100,101,111,主析取范式为 ,主合取范式为M1∧M2∧M4∧M5∧M7。
(2)已知公式A含有3个命题变项，并且公式A的主合取范式为，那么公式A的成真赋值为000, 010,101,110,111，成假赋值为001, 011, 100，公式A的主析取范式为。
解：
令p:小王是理科生, q:小王是文科生, r:小王的数学成绩很好.
前提: p→r, ¬q→p, ¬r

离散数学第一第二次作业

第1部分命题逻辑一、单项选择题1. 下列哪个语句是真命题( )。

(A)我正在说谎(B)如果1+2 = 3,则雪是黑色的(C)如果1+2 = 5,则雪是黑色的(D)上网了吗2 .命题公式为P > (Q > P)( )。

(A)重言式(B)可满足式(C)矛盾式(D)等值式3. 设命题公式P (Q厂P),记作G,则使G的真值指派为1的P, Q 的取值是( )。

(A) (0,0) (B) (0,1) (C) (1,0) (D) (1,1)4. 与命题公式P > (Q > R)等值的公式是( )。

(A) (P Q) > R (B)(P Qp R (C)(P > Q) > R (D)P》(Q R)5 .命题公式(P Q) > P是( )。

(A)永真式(B)永假式(C)可满足式(D)合取范式二、填空题1. ____________________________________________ P, Q为两个命题，当且仅当 _________________________________________ 时，P Q的真值为1,当且仅当_______________________ 时，P Q的真值为0。

2. 给定两个命题公式A, B,若 ________________________________ 时，则称A和B是等值的，记为A= B。

3. ________________________________ 任意两个不同极小项的合取为_______ 式。

4 .设P:天下雨，Q:我们去郊游。

贝S⑴命题如果天不下雨，我们就去郊游”可符号化为_______ 。

第1页(共16页)⑵命题只有天不下雨，我们才去郊游”可符号化为_______ 。

⑶命题我们去郊游，仅当天不下雨”可符号化为_________ 。

5 .设命题公式G = P (-Q R),则使G取真值为1的指派6. 已知命题公式为G = (-P Q) > R,则命题公式G的析取范式是三、计算题1.将下列命题符号化：⑴ 李强不是不聪明，而是不用功；⑵ 如果天不下雨，我们就去郊游；⑶ 只有不下雨，我们才去郊游。

离散数学作业（2）分解

离散数学作业（2）分解离散数学作业布置第1次作业（P15）1.16 设p、q的真值为0；r、s的真值为1，求下列各命题公式的真值。

解：（1）p∨(q∧r)=0∨(0∧1)=0（2）（p?r）∧(﹁q∨s)=（0?1）∧(1∨1)=0∧1 =0（3）（﹁p∧﹁q∧r）?(p∧q∧﹁r)=（1∧1∧1）?(0∧0∧0)=0(4)（r∧s）→(p∧q)=（0∧1）→(1∧0)=0→0=11.17 判断下面一段论述是否为真：“π是无理数。

并且，如果3是无理数，则2也是无理数。

另外只有6能被2整除，6才能被4整除。

”解：p: π是无理数 1q: 3是无理数0r: 2是无理数 1s: 6能被2整除 1t: 6能被4整除0命题符号化为：p∧(q→r)∧(t→s)的真值为1，所以这一段的论述为真。

1.19 用真值表判断下列公式的类型：（4）(p→q) →(﹁q→﹁p)（5）(p∧r) ?(﹁p∧﹁q)（6）((p→q) ∧(q→r)) →(p→r)解：（4）p q p→q q p q→p (p→q)→( q→p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式，最后一列全为1（5）公式类型为可满足式（方法如上例），最后一列至少有一个1（6）公式类型为永真式（方法如上例，最后一列全为1）。

第2次作业（P38）2.3 用等值演算法判断下列公式的类型，对不是重言式的可满足式，再用真值表法求出成真赋值.(1) ﹁(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)解：(1) ﹁(p∧q→q) ?﹁(﹁(p∧q) ∨q) ?(p∧q) ∧﹁q?p∧(q ∧﹁q) ? p∧0 ?0所以公式类型为矛盾式(2)（p→(p∨q)）∨(p→r) ? (﹁p∨(p∨q))∨(﹁p∨r) ?﹁p∨p∨q∨r?1所以公式类型为永真式(3) (p∨q) →(p∧r) ?￢(p∨q) ∨(p∧r) ? (￢p∧￢q) ∨(p∧r)易见, 是可满足式, 但不是重言式. 成真赋值为: 000,001, 101, 111 P q r ￢p∧￢q p∧r (￢p∧￢q) ∨(p∧r)0 0 0 1 0 10 0 1 1 0 10 1 0 0 0 00 1 1 0 0 01 0 0 0 0 01 0 1 0 1 11 1 0 0 0 01 1 1 0 1 1所以公式类型为可满足式2.4 用等值演算法证明下面等值式：(2) ( (p→q)∧(p→r) ) ? (p→(q∧r))(4)(p∧﹁q)∨(﹁p∧q) ? (p∨q)∧﹁(p∧q)证明（2）(p→q)∧(p→r)( ﹁p∨q)∧(﹁p∨r)﹁p∨(q∧r))p→(q∧r)（4）(p∧﹁q)∨(﹁p∧q) ?(p∨(﹁p∧q)) ∧(﹁q∨(﹁p∧q) ) (p∨﹁p)∧(p∨q)∧(﹁q∨﹁p) ∧(﹁q∨q)1∧(p∨q)∧(﹁p∨﹁q)∧1(p∨q)∧﹁(p∧q)第3次作业（P38）2.5 求下列公式的主析取范式, 并求成真赋值:(1)( ￢p→q) →(￢q∨p)(2) (￢p→q) ∧q∧r(3)(p∨(q∧r)) →(p∨q∨r)(4) ￢(p→q) ∧q∧r解：(1)(￢p→q) →(￢q∨p)￢(p∨q) ∨(￢q∨p)￢p∧￢q ∨￢q ∨p￢q ∨p (吸收律)(￢p∨p)∧￢q ∨p∧(￢q∨q)￢p∧￢q∨p∧￢q ∨p∧￢q ∨p∧q ?m0∨m2∨m2∨m3 m0∨m2∨m3成真赋值为00, 10, 11.(2) (￢p→q) ∧q∧r(p∨q) ∧q∧r(p∧q∧r) ∨q∧r(p∧q∧r) ∨(￢p ∨p) ∧q∧rp∧q∧r∨￢p ∧q∧r∨p∧q∧rm3∨m7成真赋值为011，111.(3) (p∨(q∧r)) →(p∨q∨r)￢(p∨(q∧r)) ∨(p∨q∨r)￢p∧￢(q∧r) ∨(p∨q∨r)￢p∧(￢q∨￢r)∨(p∨q∨r)￢p∧￢q∨￢p∧￢r∨p∨q∨r￢p∧￢q∧(r∨￢r)∨￢p∧(q∨￢q)∧￢r∨p∧(q∨￢q) ∧(r∨￢r) ∨(p∨￢p) ∧q∧(r∨￢r)∨(p∨￢p) ∧(q∨￢q) ∧rm0∨m1∨m2∨m3∨m4∨m5∨m6∨m7, 为重言式.(4) ￢(p→q) ∧q∧r￢(￢p∨q) ∧q∧r(p∧￢q) ∧q∧rp∧(￢q ∧q)∧r主析取范式为0, 无成真赋值, 为矛盾式.第4次作业（P38）2.6 求下列公式的主合取范式, 并求成假赋值:(1) ￢(q→￢p) ∧￢p(2)(p∧q) ∨(￢p∨r)(3)(p→(p∨q)) ∨r解：(1) ￢(q→￢p) ∧￢p￢(￢q∨￢p) ∧￢pq∧p ∧￢pq∧0M0∧M1∧M2∧M3这是矛盾式. 成假赋值为00, 01, 10, 11.(2)(p∧q) ∨(￢p∨r)(p∧q) ∨￢p∨r(p∨￢p)∧(￢p ∨q)∨r(￢p ∨q)∨r￢p ∨q∨rM4, 成假赋值为100.(3)(p→(p∨q)) ∨r(￢p∨(p∨q)) ∨r(￢p∨p)∨q ∨r1主合取范式为1, 为重言式.第5次作业（P41）2.32 用消解原理证明下述公式是矛盾式:(1) (￢p∨q) ∧(￢p∨r) ∧(￢q∨￢r) ∧(p∨￢r) ∧r(2) ￢((p∨q) ∧￢p→q)解：(1) (￢p∨q) ∧(￢p∨r) ∧(￢q∨￢r) ∧(p∨￢r) ∧r第一次循环S0=Φ, S1=｛￢p∨q,￢p∨r,￢q∨￢r,p∨￢r,r｝, S2=Φ由￢p∨r, p∨￢r消解得到λ输出“no”，计算结束(2) ￢((p∨q) ∧￢p→q)￢(￢((p∨q) ∧￢p) ∨q)((p∨q) ∧￢p) ∧￢q(p∨q) ∧￢p ∧￢q第一次循环S0=Φ, S1=｛p∨q,￢p, ￢q｝, S2=Φ由p∨q,￢p消解得到q,由q, ￢q消解得到λ,输出“no”，计算结束2.33 用消解法判断下述公式是否可满足的:(1) p∧(￢p∨￢q) ∧q(2) (p∨q) ∧(p∨￢q) ∧(￢p∨r)解：(1) p∧(￢p∨￢q) ∧q第一次循环S0=Φ, S1=｛p, ￢p∨￢q, q｝, S2=Φ由p, ￢p∨￢q消解得到￢q,由q, ￢q消解得到λ,输出“no”，计算结束(2) (p∨q) ∧(p∨￢q) ∧(￢p∨r)第一次循环S0=Φ, S1=｛p∨q, p∨￢q, ￢p∨r｝, S2=Φ由p∨q, p∨￢q消解得到p,由p∨q, ￢p∨r消解得到q ∨r,由p∨￢q, ￢p∨r消解得到￢q ∨r,由p, ￢p∨r消解得到r,S2=｛p, q ∨r, ￢q ∨r, r｝第二次循环S0=｛p∨q, p∨￢q, ￢p∨r｝, S1=｛p, q ∨r, ￢q ∨r, r｝, S2=Φ由p∨q, ￢q ∨r消解得到p∨r,由p∨￢q, q ∨r消解得到p∨r,由p∨￢q, q ∨r消解得到p∨r,由￢p∨r, p 消解得到r,S2=｛p∨r｝第三次循环S0=｛p, q ∨r, ￢q ∨r, r｝, S1=｛p∨r｝, S2=ΦS2=Φ输出“yes”，计算结束第6次作业（P52）3.6 判断下面推理是否正确. 先将简单命题符号化, 再写出前提, 结论, 推理的形式结构(以蕴涵式的形式给出)和判断过程(至少给出两种判断方法):(1)若今天是星期一, 则明天是星期三；今天是星期一. 所以明天是星期三.(2)若今天是星期一, 则明天是星期二；明天是星期二. 所以今天是星期一.(3)若今天是星期一, 则明天是星期三；明天不是星期三. 所以今天不是星期一.(4)若今天是星期一, 则明天是星期二；今天不是星期一. 所以明天不是星期二.(5)若今天是星期一, 则明天是星期二或星期三. 今天是星期一. 所以明天是星期二.(6)今天是星期一当且仅当明天是星期三；今天不是星期一. 所以明天不是星期三. 设p: 今天是星期一, q: 明天是星期二, r: 明天是星期三.(1)推理的形式结构为(p→r) ∧p→r此形式结构为重言式, 即(p→r) ∧p?r所以推理正确.(2)推理的形式结构为(p→q) ∧q→p此形式结构不是重言式, 故推理不正确.(3)推理形式结构为(p→r) ∧￢r→￢p此形式结构为重言式, 即(p→r) ∧￢r?￢p故推理正确.(4)推理形式结构为(p→q) ∧￢p→￢q此形式结构不是重言式, 故推理不正确.(5)推理形式结构为(p→(q∨r) )∧p →q它不是重言式, 故推理不正确.(6)推理形式结构为(p?r) ∧￢p→￢r此形式结构为重言式, 即(p?r) ∧￢p?￢r故推理正确.推理是否正确, 可用多种方法证明. 证明的方法有真值表法, 等值演算法. 证明推理正确还可用构造证明法.下面用等值演算法和构造证明法证明(6)推理正确.1. 等值演算法(p?r) ∧￢p→￢r(p→r) ∧(r→p)∧￢p→￢r￢((￢p∨r) ∧(￢r∨p)∧￢p) ∨￢r￢(￢p∨r) ∨￢(￢r∨p) ∨p ∨￢r(p∧￢r)∨(r∧￢p)∨p ∨￢r(r∧￢p)∨p ∨￢r 吸收律(r∧￢p)∨￢（￢p ∨r）德摩根律1即(p?r) ∧￢p?￢r故推理正确2.构造证明法前提: (p?r), ￢p结论: ￢r证明:①p?r 前提引入②(p→r) ∧(r→p) ①置换③r→p ②化简律④￢p 前提引入⑤￢r ③④拒取式所以, 推理正确.第7次作业（P53-54）3.15 在自然推理系统P中用附加前提法证明下面各推理: (1)前提: p→(q→r), s→p, q结论: s→r(2)前提: (p∨q) →(r∧s), (s∨t) →u结论: p→u(1)证明:①s 附加前提引入②s→p 前提引入③p①②假言推理④p→(q→r) 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理(2)证明:①P 附加前提引入②p∨q ①附加③(p∨q) →(r∧s) 前提引入④r∧s ②③假言推理⑤S ④化简⑥s∨t ⑤附加⑦(s∨t) →u 前提引入⑧u ⑥⑦假言推理3.16 在自然推理系统P中用归谬法证明下面推理: (1)前提: p→￢q, ￢r∨q, r∧￢s结论: ￢p(2)前提: p∨q, p→r, q→s结论: r∨s(1)证明:①P 结论否定引入②p→￢q 前提引入③￢q ①②假言推理④￢r∨q 前提引入⑤￢r ③④析取三段论⑥r∧￢s 前提引入⑦r ⑥化简规则⑧￢r∧r ⑤⑦合取引入规则⑧为矛盾式, 由归谬法可知, 推理正确.(2)证明:①￢(r∨s) 结论否定引入②p∨q 前提引入③p→r 前提引入④q→s 前提引入⑤(p→r) ∧(q→s) ∧(p∨q) ②③④合取引入规则⑥r∨s ⑤构造性二难⑦(r∨s) ∧￢(r∨s) ④⑤合取引入规则⑦为矛盾式, 所以推理正确.第8次作业（P65-66）4.5 在一阶逻辑中将下列命题符号化:(1)火车都比轮船快.(2)有的火车比有的汽车快.(3)不存在比所有火车都快的汽车.(4)“凡是汽车就比火车慢”是不对的.解：因为没指明个体域, 因而使用全总个体域(1) ?x?y(F(x) ∧G(y) →H(x,y))其中, F(x): x 是火车, G(y): y 是轮船, H(x,y):x 比y 快. (2) ?x?y(F(x) ∧G(y) ∧H(x,y))其中, F(x): x 是火车, G(y): y 是汽车, H(x,y):x 比y 快. (3) ￢?x(F(x) ∧?y(G(y) →H(x,y)))或?x(F(x) →?y(G(y) ∧￢H(x,y)))其中, F(x): x 是汽车, G(y): y 是火车, H(x,y):x 比y 快.(4) ￢?x?y(F(x) ∧G(y) →H(x,y))或x?y(F(x) ∧G(y) ∧￢H(x,y) )其中, F(x): x 是汽车, G(y): y 是火车, H(x,y):x 比y 慢.4.9 给定解释I 如下:(a)个体域为实数集合R.(b)特定元素a=0.(c)特定函数-f(x,y)=x y, x,y∈R.(d)谓词-F(x,y): x=y,-G(x,y): x<="">给出下列公式在I 下的解释, 并指出它们的真值:(1) ??x?y(G(x,y) →￢F(x,y))(2) ??x?y(F(f(x,y),a)→G(x,y))(3) ??x?y(G(x,y) →￢F(f(x,y),a))(4) ??x?y(G(f(x,y),a) →F(x,y))解：(1) ??x?y(x<="">(2) ??x?y((x-y=0) →x<="">(3) ??x?y((x<="">(4) ??x?y((x y<0) → (x=y)), 真值为0.第9次作业（P79-80）5.5 给定解释I如下:(a) 个体域D={3,4}；(b)-f(x)：-f(3)=4,-f(4)=3；(c)-F(x,y)：-F(3,3)=-F(4,4)=0,-F(3,4)=-F(4,3)=1. 试求下列公式在I下的真值:(1) ?x?yF(x,y)(2) ?x?yF(x,y)(3) ?x?y(F(x,y)→F(f(x),f(y)))解：(1) ?x?yF(x,y)(F(3,3)∨F(3,4))∧(F(4,3)∨F(4,4))(0∨1)∧(1∨0) ? 1(2) ?x?yF(x,y)(F(3,3)∧F(3,4))∨(F(4,3)∧F(4,4))(0∧1)∨(1∧0) ? 0(3) ?x?y(F(x,y)→F(f(x),f(y)))(F(3,3)→F(f(3),f(3)))∧(F(4,3)→F(f(4),f(3)))∧(F(3,4)→F(f(3),f(4)))∧(F(4,4)→F(f(4),f(4)))(0→0)∧(1→1)∧(1→1)∧(0→0) ?15.12 求下列各式的前束范式.(1)?xF(x)→?yG(x, y)(3)?xF(x, y) ??xG(x, y)(5) ?x1F(x1, x2)→(F(x1)→￢?x2G(x1, x2)).解：前束范式不是唯一的.(1) ?xF(x)→?yG(x, y)x (F(x)→?yG(t, y))x?y(F(x)→G(t, y)).(3) ?xF(x, y) ??xG(x, y)(?xF(x, y)→?xG(x, y))∧(?xG(x, y)→?xF(x, y)) ? (?xF(x, y)→?uG(u, y))∧(?xG(x, y)→?vF(v, y))x?u(F(x, y)→G(u, y))∧?x?v(G(x, y)→F(v, y))x?u(F(x, y)→G(u, y))∧?w?v(G(w, y)→F(v, y))x?u?w?v ((F(x, y)→G(u, y))∧(G(w, y)→F(v, y))) (5)?x1F(x1, x2)→(F(x1)→￢?x2G(x1, x2))x1F(x1, x2)→(F(x1)→?x2￢G(x1, x2))x1F(x1, x2)→?x2(F(x1)→￢G(x1, x2))x1F(x1, x3)→?x2(F(x4)→￢G(x4, x2))x1(F(x1, x3)→?x2(F(x4)→￢G(x4, x2)))x1?x2 (F(x1, x3)→(F(x4)→￢G(x4, x2)))第10次作业（P79-80）5.15 在自然推理系统F L中,构造下面推理的证明:(1) 前提: ?xF(x) →?y((F(y)∨G(y))→R(y)),?xF(x)结论:?xR(x).(2) 前提:?x(F(x)→(G(a)∧R(x))),?xF(x)结论:?x(F(x)∧R(x))(3) 前提:?x(F(x)∨G(x)),￢?xG(x)结论:?xF(x)(4) 前提:?x(F(x)∨G(x)),?x(￢G(x)∨￢R(x)),?xR(x) 结论: ?xF(x)(1)证明:①?xF(x) →?y((F(y)∨G(y))→R(y)) 前提引入②?xF(x) 前提引入③?y((F(y)∨G(y))→R(y)) ①②假言推理④(F(c)∨G(c))→R(c) ③全称量词消去规则⑤F(c) ①存在量词消去规则⑥F(c) ∨G(c) ⑤附加⑦R(c) ④⑥假言推理⑧?xR(x) ⑦存在量词引入规则(2) 证明:①?xF(x) 前提引入②F(c) ①存在量词消去规则③?x(F(x)→(G(a)∧R(x))) 前提引入④F(c)→(G(a)∧R(c)) ④全称量词消去规则⑤G(a)∧R(c) ②④假言推理⑥R(c) ⑤化简⑦F(c)∧R(c) ②⑥合取引入⑧?x(F(x)∧R(x)) ⑦存在量词引入规则(3) 证明:①￢?xG(x) 前提引入②?x￢G(x) ①置换③￢G(c) ②全称量词消去规则④?x(F(x)∨G(x)) 前提引入⑤F(c)∨G(c) ④全称量词消去规则⑥F(c) ③⑤析取三段论⑦?xF(x) ⑥存在量词引入规则(4) 证明:①?x(F(x)∨G(x)) 前提引入②F(y)∨G(y) ①全称量词消去规则③?x(￢G(x)∨￢R(x)) 前提引入④￢G(y) ∨￢R(y) ③全称量词消去规则⑤?xR(x) 前提引入⑥R(y) ⑤全称量词消去规则⑦￢G(y) ④⑥析取三段论⑧F(y) ②⑦析取三段论⑥?xF(x) ⑧存在量词引入规则第11次作业（P96）6.4. 设F 表示一年级大学生的集合, S 表示二年级大学生的集合, M 表示数学专业学生的集合, R 表示计算机专业学生的集合, T表示听离散数学课学生的集合, G 表示星期一晚上参加音乐会的学生的集合, H 表示星期一晚上很迟才睡觉的学生的集合. 问下列各句子所对应的集合表达式分别是什么? 请从备选的答案中挑出来.(1)所有计算机专业二年级的学生在学离散数学课.(2)这些且只有这些学离散数学课的学生或者星期一晚上去听音乐会的学生在星。

国家开放大学电大本科《离散数学》网络课形考任务2作业及答案

国家开放大学电大本科《离散数学》网络课形考任务2作业及答案此任务2 g选择题题目1 无向完全图K4是()、选择一项：A、树 B、欧拉图 C、汉密尔顿图 D、非平面图题目2 已知一棵无向树T中有8个顶点，4度、3度、2度的分支点各一个，T 的树叶数为()、选择一项： A、4 B、8 C、3 D、5 题目3 设无向图G的邻接矩阵为 011111 0 0111 0 0 0 011 0 011 01 0 则G 的边数为( 选择一项： A、7 B、14 C、6 D、1 题目4 如图一所示，以下说法正确的是()、选择一项： A、 ((a, e), (b, c)｝是边割集 B、｛(a, e)｝是边割集 C、｛（d, e）｝是边割集 D、（（a, e）｝是割边题目5 以下结论正确的是（）、选择一项： A、有n个结点n-l条边的无向图都是树B、无向完全图都是平面图 C、树的每条边都是割边 D、无向完全图都是欧拉图题目6 若G是一个欧拉图，则G一定是（）、选择一项： A、汉密尔顿图 B、连通图 C、平面图 D、对偶图题目7 设图G=, vGV,则下列结论成立的是（）、选择一项：A、云 d做、）=2|% B、2>“ = |司 w C、 deg（v）=2|S| D、deg（v）=|E| 题目8 图G如图三所示，以下说法正确的是（）、选择一项： A、（b, d｝是点割集 B、｛c｝是点割集 C、｛b, c｝是点割集 D、 a是割点题目9 设有向图（a）、（b）、（c）与（d）如图五所示，则下列结论成立的是（）、选择一项： (a)是费连通的 B、 (d)是强连通的 C、 (c)是强连通的D、 (b)是强连通的题目10 设有向图(a)、(b)、(c)与(d)如图六所示，则下列结论成立的是()、选择一项： A、 (b)只是弱连通的 B、 (c)只是弱连通的 C、 (a)只是弱连通的 D、 (d)只是弱连通的判断逝题目11 设图G是有6个结点的连通图，结点的总度数为18,则可从G中删去4条边后使之变成树、()选择一项：对错题目12 汉密尔顿图一定是欧拉图、()选择一项：对错题目13 设连通平面图G的结点数为5,边数为6,则面数为4、()选择一项：对错题目14 设G是一个有7个结点16条边的连通图，则G为平面图、()选择一项：对错题目15 如图八所示的图G存在一条欧拉回路、()选择一项：对错题目16 设图G如图七所示，则图G的点割集是{f}、()选择一项：对错题目172>瞒)=2圜设G是一个图，结点集合为V,边集合为E,则代衫()选择一项：对错题目18 设图G是有5个结点的连通图，结点度数总和为10,则可从G中删去6条边后使之变成树、()选择一项：对错题目19 如图九所示的图G不是欧拉图而是汉密尔顿图、()选择一项：对错题目20 若图 G=,其中 V=( a, b, c, d }, E={ (a, b), (a, d), (b, c), (b, d)},则该图中的割边为(b, c)、()选择一项：对。

离散数学第二次作业

班级姓名学号成绩一、图的概念、连通性与矩阵表示选择/填空题1、任何n个节点m条边的图G = (V,E) , 边数与顶点度数的关系是。

2、任一有向图中，度数为奇数的结点有( )个。

3、n阶完全图K n的边数为。

4、n个结点的有向完全图边数是( )，每个结点的度数是( )。

5、已知图G中有1个1度结点，2个2度结点，3个3度结点，4个4度结点，则G的边数是．6、下面四组数能构成无向图的度数列的有( )。

A、 2,3,4,5,6,7；B、 1,2,2,3,4；C、 2,1,1,1,2；D、 3,3,5,6,0。

7、设无向图G有16条边且每个顶点的度数都是2，则图G有( )个顶点。

(1) 10 (2) 4 (3) 8 (4) 168、在有n个顶点的连通图中，其边数（）。

(1) 最多有n-1条 (2) 至少有n-1 条(3) 最多有n条 (4) 至少有n 条9、如右图相对于完全图K5的补图为（）。

10、给定无向图G如下图所示，下面给出的结点集子集中，不是点割集的为（）．A．{b, d} B．{d}C．{a, c} D．{b, e}11、图G 如右图所示，以下说法正确的是 ( ) ．A ．{(a , c )}是割边B ．{(a , c )}是边割集C ．{(b , c )}是边割集D ．{(a, c ) ,(b, c )}是边割集 12、给定无向图G=<V, E>如下图所示，下面哪个边集不是其边割集（）。

A 、；B 、{<v1,v4>,<v4,v6>};C 、；D 、。

13、设有向图（a ）、（b ）、（c ）与（d ）如下图所示，则下列结论成立的是( )．A ．（a ）是强连通的B ．（b ）是强连通的C ．（c ）是强连通的D ．（d ）是强连通的14、下图的邻接矩阵A=15、设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100000100，则G 的边数为( )．A ．5B ．6C ．3D ．416、图的邻接矩阵为( )。

国家开放大学电大本科《离散数学》网络课形考任务2作业及答案

选择一项：
A. 有n个结点n－1条边的无向图都是树
B. 无向完全图都是平面图
C. 树的每条边都是割边
D. 无向完全图都是欧拉图
题目6
若G是一个欧拉图，则G一定是( )．
选择一项：
A. 汉密尔顿图
B. 连通图
C. 平面图
D. 对偶图
题目7
设图G＝<V, E>，v∈V，则下列结论成立的是 ( ) ．
选择一项：
选择一项：
对
错
题目17
设G是一个图，结点集合为V，边集合为E，则 ( )
选择一项：
对
错
题目18
设图G是有5个结点的连通图，结点度数总和为10，则可从G中删去6条边后使之变成树．( )
选择一项：
对
错
题目19
如图九所示的图G不是欧拉图而是汉密尔顿图．( )
选择一项：
对
错
题目20
若图G=<V, E>，其中V={ a, b, c, d }，E={ (a, b), (a, d),(b, c), (b, d)}，则该图中的割边为(b, c)．( )
题目8
图G如图三所示，以下说法正确的是 ( )．
选择一项：
A. {b, d}是点割集
B. {c}是点割集
C. {b, c}是点割集
D. a是割点
题目9
设有向图（a）、（b）、（c）与（d）如图五所示，则下列结论成立的是( )．
选择一项：
A. （a）是强连通的
B. （d）是强连通的
C. （c）是强连通的
选择一项：
对
错
题目12
汉密尔顿图一定是欧拉图．( )
选择一项：
对

离散数学第2次作业参考答案

离散数学第二次作业参考答案学号：姓名：班级：总分：1、 (每空5分，共30分)(1) 已知公式A 含有3个命题变项p , q , r ,并且它的成真赋值为000，011，110，那么命题公式A 的成假赋值为 001,010,100,101,111 ,主析取范式为 , 主合取范式为 M 1∧M 2∧M 4∧M 5∧M 7 。

(2) 已知公式A 含有3个命题变项，并且公式A 的主合取范式为134M M M ∧∧，那么公式A 的成真赋值为 000, 010,101,110,111 ，成假赋值为 001, 011, 100 ，公式A 的主析取范式为。

2、(12分)用真值表法计算公式()p q r ⌝∨∧的主析取范式和主合取范式解：真值表为p q r p q ⌝∨ ()p q r ⌝∨∧0 0 0 1 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 0 0 1 0 1 0 0 1 1 0 1 0 1 1 111主析取范式：137m m m ∨∨主合取范式：02456M M M M M ∧∧∧∧3、(14分)甲、乙、丙、丁4人中有且仅有2个人参加围棋比赛。

关于谁参加了比赛，下列判断都是正确的：(1) 甲和乙只有一人参加。

(2) 若丙参加，则丁必参加。

(3) 乙或者丁至多参加一人。

(4) 丁不参加，则甲也不会参加。

问：哪两个人参加了比赛。

解：其它解题方法，只要解释清楚，答案正确就给分① 设p : 甲参加，q :乙参加，r :丙参加，s :丁参加。

② 4个条件分别符号化为()()p q p q ⌝∧∨∧⌝，()r s →，()q s ⌝∨⌝，()s p ⌝→⌝ 根据题意可得公式[()()]()()()p q p q r s q s s p ⌝∧∨∧⌝∧→∧⌝∨⌝∧⌝→⌝ 该公式的成真赋值为可能可行的方案。

③经过演算可得[()()]()()()()()()()()p q p q r s q s s p p q p q r s q s p s ⌝∧∨∧⌝∧→∧⌝∨⌝∧⌝→⌝⇔⌝∨⌝∧∨∧⌝∨∧⌝∨⌝∧⌝∨④由于p 和q 有且仅有一个为1，因此公式的成真赋值只能是10XX 或者01XX 。

离散数学(专升本)阶段性作业2

离散数学(专升本)阶段性作业2总分: 100分考试时间:分钟单选题1. 永假式的否定是_____。

(6分)(A) 永真式(B) 永假式(C) 可满足式(D) (1)--(3)均有可能参考答案：C2. 设谓词P(x)：x是奇数，Q(x)：x是偶数，谓词公式$x(P(x)ÚQ(x))在个体域中___ __为真。

(6分)(A) 自然数(B) 实数(C) 复数(D) (1)--(3)均成立参考答案：A3. 合式公式是_____。

（称作P与Q的“与非” 当且仅当P与Q的真值都是真时，的真值为假，否则的真值为真。

）(6分)(A) 重言式(B) 可满足式(C) 矛盾式(D) 等价式参考答案：B4. 下列命题公式不是重言式的是_____。

(6分)(A) Q→(P∨Q)(B) (P∧Q)→P(C) （P∧Q）(D) （P∧0）参考答案：C5. 下列命题公式中为永真式的是_____。

(5分)(A) Q∨1(B) Q→P(C) Q∧P(D) Q∨P．参考答案：A6. 下面命题公式中不等价的是_____。

(6分)(A)(B)(C)(D)参考答案：C多选题7. 令p：今天下雪了，q：路滑，则命题“虽然今天下雪了，但是路不滑”可符号化为____ _(5分)(A) p→┐q(B) p∨┐q(C) ┐(┐p∨q)(D) p∧┐q参考答案：C,D8. 下列不是两个命题变元p，q的小项是_____(5分)(A) p∧┐p∧q(B) ┐p∨q(C) ┐p∧q(D) ┐p∨p∨q参考答案：A,B,D9. 设命题公式G＝Ø(P®Q)，H＝P®(Q®ØP)，则G与H的关系是_____。

(5分)(A) GÞH(B) HÞG(C) G＝H(D) 以上都不是.参考答案：A,B10. 下列公式中是永真式为_______。

(5分)(A) (┐P Q)→(Q→R)(B) P→(Q→Q)(C) (P Q)→P(D) P→(P Q)判断题11. 设P：我生病，Q：我去学校，则下列命题“只有在生病时，我才不去学校”可符号化为。

计算机科学专业离散数学平时作业二

一、判断(共计50分,每题2.5分)1、“5是2的倍数。

”不是命题。

A. 正确B. 错误正确：【B】2、两图同构，则每个顶点的度相同。

A. 正确B. 错误正确：【A】3、若关系R是自反的，则其关系图的每个结点都没有环。

A. 正确B. 错误正确：【B】4、如果a是集合A中的元素，则称a属于A，记作a∉A。

A. 正确B. 错误正确：【B】5、设，，则A. 正确B. 错误正确：【A】6、一个从A到B的二元关系是有序偶的集合R，在每一个有序偶中，第一个元素取自A，第二个元素取自B。

A. 正确B. 错误正确：【A】7、“如果1+1≠3，则2+2≠4”是真命题。

A. 正确B. 错误正确：【B】8、自然数集合N上的加法、乘法是N上的二元运算，但减法、除法不是。

A. 正确B. 错误正确：【A】9、在有补分配格〈L，∨，∧〉中，任一元素a∈L的补元素是唯一的。

A. 正确B. 错误正确：【A】10、对于任何（n，m）—图。

A. 正确B. 错误正确：【A】11、大于100的整数集合可以表示为{101,102,103，…}。

A. 正确B. 错误正确：【A】12、设n阶无向连通图G有m条边，则m<n－1。

A. 正确B. 错误正确：【B】13、只由一个孤立结点构成的图称为平凡图。

A. 正确B. 错误正确：【A】14、简单图不含平行边。

A. 正确B. 错误正确：【A】15、一个代数系统的单位元、零元、逆元如存在，则必唯一。

A. 正确B. 错误正确：【A】16、半群满足交换律。

A. 正确B. 错误正确：【B】17、具有条边的连通图最多具有个结点。

A. 正确B. 错误正确：【A】18、设R是集合A上的关系，若对于任意a，b∈A，当(a，b)∈R时，必有(b，a)∈R，则称R为对称的。

A. 正确B. 错误正确：【A】19、连通且不含圈的图称为树。

A. 正确B. 错误正确：【A】20、无向图G为欧拉图，则G是连通的。

A. 正确B. 错误正确：【A】二、单选(共计50分,每题2.5分)21、下列不一定是树的是（）A. 无回路的连通图B. 有n个结点，n-1条边的连通图C. 每对结点之间都有通路的图D. 连通但删去一条边则不连通的图正确：【C】22、设论域为整数集，下列真值为真的公式是（）A.B.C.D.正确：【A】23、在公式中变元y是（）A. 自由变元B. 约束变元C. 既是自由变元，又是约束变元D. 既不是自由变元，又不是约束变元正确：【B】24、欧拉回路是（）A. 路径B. 迹C. 既是初级回路也是迹D. 既非初级回路也非迹正确：【B】25、设A=，B=P（P（A）），以下不正确的式子是（）A. 包含于BB. 包含于BC. 包括于BD. 包含于B正确：【D】26、设个体域是整数集，则下列命题的真值为真的是（）A. yx(x·y=1)B. xy (x·y≠0)C.D.正确：【C】27、设有代数系统G=〈A，*〉，其中A是所有命题公式的集合，*为命题公式的合取运算，则G的幺元是（）A. 矛盾式B. 重言式C. 可满足D. 公式p∧q正确：【B】28、下列命题联结词集合中，是最小联结词组的是（）A. {┐，}B. {┐，∨，∧}C. {┐，∧}D. {∧，→}正确：【C】29、下列命题公式中不是重言式的是（）A. p→(q→r)B. p→(q→p)C. p→(p→p)D. (p→(q→r))(q→(p→r))正确：【A】30、设A是正整数集，R={(x，y)|x，y∈A∧x+3y=12}，则R∩({2，3，4，6}×{2，3，4，6})=（）A.B. {<3，3>}C. {<3，3>，<6，2>}D. {<3，3>，<6，2>，<9，1>}正确：【C】31、下列各图是无向完全图的是（）A.B.C.D.正确：【C】32、下列集合对所给的二元运算封闭的是（）A. 正整数集上的减法运算B. 在正实数的集R+上规定为ab=ab-a-b a,b∈R+C. 正整数集Z+上的二元运算为xy=min(x,y) x,y∈Z+D. 全体n×n实可逆矩阵集合Rn×n上的矩阵加法正确：【C】33、下列语句中不是命题的只有（）A. 鸡毛也能飞上天？B. 或重于泰山，或轻于鸿毛。

离散第二次作业

13、(1) x( A( x) yB( y))
解： x( A( x) yB( y)) x(A( x) yB( y)) xy(A( x) B( y)) xy( A( x) B( y))
13、(3)
xP( x) xQ( x) x(P( x) Q( x))
US (3) T (2)(4) I US (5) T (1)(6)
17、(1)证明下列推理的正确性。所有的有理数都是实数。某些有理数是整数。因此某些实数是整数。解首先将命题符号化。设个体域是全总个体域。令P(x)：x是实数。 Q(x)：x是有理数。 R(x)：x是整数。 x(Q( x ) P ( x )), x(Q( x ) R( x )) 则有前提：结论：x( P ( x ) R( x ))
2、(1)所有的整数是实数.
解：设 Z ( x) : x是整数； R( x) : x是实数。该命题符号化为 x(Z ( x) R( x)).
2、(3) 某些运动员是大学生.
解：设 P( x) : x是运动员 ; L( x） : x是大学生; 该命题符号化为 x( P( x) L( x).
y是自由变元。 6、(4) xyP( x, y) Q( z ) 解： x的辖域是 P( x, y), 在P( x, y)中， x是约束变元 y是自由变元 . y的辖域是 P( x, y ), 在P( x, y )中， y是约束变元 x是自由变元 .
Q(z)不在量词的辖域中， z是自由变元
1、(4)有一些数是素数.
解：设 P( x) : x是数； Q( x) : x是素数。该命题符号化为 x( P( x) Q( x)).

西南大学《离散数学》网上作业题及答案

[0004]《离散数学》网上作业题答案第1次作业[论述题]第1次作业一、填空题1. 设|A | = 5, |B | = 2, 则可定义A 到B 的函数( )个，其中有( )单射，( )个满射.2. 令G (x ): x 是金子，F (x ): x 是闪光的，则命题“金子都是闪光的，但闪光的未必是金子”符号化为( ).3. 设X 是非空集合，则X 的幂集P (X )关于集合的⋃运算的单位元是( )，零元是( )，P (X )关于集合的⋂运算的单位元是( ).4. 6阶非Abel 群的2阶子群共有( )个，3阶子群共有( )个，4阶子群共有( )个.5. 对于n 阶完全无向图K n , 当n 为( )时是Euler 图，当n ≥ ( )时是Hamilton 图，当n ( )时是平面图.二、单选题1. 幂集P (P (P (∅))) 为( )(A){{∅}, {∅, {∅}}}. (B){∅, {∅, {∅}}, {∅}}. (C){ ∅, {∅, {∅}}, {{∅}}, {∅}} (D){ ∅, {∅, {∅}}}. 2. 设R 是集合A 上的偏序关系，则1-⋃R R 是( ).(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上答案都不对 3. 下列( )组命题公式是不等值的.(A))(B A →⌝与B A ⌝∧. (B) )(B A ↔⌝与)()(B A B A ∧⌝∨⌝∧. (C))(C B A ∨→与C B A →⌝∧)(. (D))(C B A ∨→与)(C B A ∨∧⌝. 4.下列代数结构(G , *)中，( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法. 5.4阶完全无向图4K 中含3条边的不同构的生成子图有 (A)3 (B)4 (C)5 (D)2三、设A 和B 是集合，使B B A =-成立的充要条件是什么，并给出理由. 四、设R 和S 是集合A 上的对称关系，证明S R 对称的充要条件是R S S R =. 五、分别利用(1)等值演算法和(2)真值表求命题公式))(())((r q p p q r A ∨→→→∨⌝=的主析取范式和主合取范式.六、设G 是(n , m )无向图，若n m ≥，证明G 中必存在圈.参考答案：第1次作业答案一、1. 32，0，30.2.))()(())()((x G x F x x F x G x ⌝∧∃∧→∀.3.∅，X ，X .4. 3，1，0.5.n 为奇数，3，4≤n .二、1(C); 2(B); 3(D); 4(D); 5(A). 三、证 ==⇔=-B A B B A ∅. (⇐)显然.(⇒)因为B A B A ⋂=-，根据B B A =-得B B B B A ⋂=⋂⋂)(，于是B = ∅，进而A = ∅.四、解由于R 和S 是对称的，所以S S R R==--11,.(⇐)因为R S S R =，两边取逆得11)()(--=R S S R ，而S R S R R S ==---111)(.所以S R S R =-1)(，因此S R 是对称关系.(⇒)由于S R 对称，所以S R S R =-1)(. 而R S R S S R ==---111)(，因而R S S R =.五、解 (1)等值演算法 A 的主合取范式:))(())((r q p p q r A ∨→→→∨⌝== ))(())((r q p p q r ∨∨⌝→∨⌝∨⌝ = )())((r q p p q r ∨∨⌝∨∨⌝∨⌝⌝= )()(r q p p q r ∨∨⌝∨⌝∧∧ = r q p ∨∨⌝(由吸收律得到). 于是，A 的主析取范式为))(())((r q p p q r A ∨→→→∨⌝== ∨⌝∧⌝∧∨⌝∧∧⌝∨∧⌝∧⌝∨⌝∧⌝∧⌝)()()()(r q p r q p r q p r q p)()()(r q p r q p r q p ∧∧∨⌝∧∧∨∧⌝∧.(2)真值表法命题公式))(())((r q p p q r A ∨→→→∨⌝=的真值表如下:由表可知，))(())((r q p p q r A ∨→→→∨⌝=的主合取范式为r q p A ∨∨⌝=.A 的主析取范式为A = ∨⌝∧⌝∧∨⌝∧∧⌝∨∧⌝∧⌝∨⌝∧⌝∧⌝)()()()(r q p r q p r q p r q p)()()(r q p r q p r q p ∧∧∨⌝∧∧∨∧⌝∧.七、证(反证)假设G 中不含圈. 设G 有k (k ≥ 1)个连通分支k G G G ,...,,21，其节点个数分别为k n n n ,...,,21，其边数分别为k m m m ,...,,21. 这时，i G 为树，根据树的基本性质有1-=i i n m )1(k i i ≤≤. 进而n k n n m m ki i k i i <-=-==∑∑==)1(11，与已知n m ≥矛盾. 证毕.第2次作业[论述题]第2次作业一、填空题1.设A = {2, {3}, 4, a }, B = {1, 3, 4, {a }}, 则{3}( )A ，{a }( )B ，{{a }}( )B .2. 设A = {1, 2, 3, 4, 5}上的关系R = {(1, 2), (3, 4), (2, 2)}, S = {(4, 2), (2, 5), (3, 1), (1, 3)}, 则=S R { }, =R S { },=R R { }.3. 在同构意义下，3阶群有( )个，4阶群有( )个，5阶群有( )个.4.任意有限布尔代数)1,0,,,,(⋅+B 均与集合代数( )同构，其元素个数为( ), 其中( )是B 的所有原子组成的集合.5. 不同构的5阶无向树有( )棵，不同构的5阶根树有( )棵.二、单选题1. 在有理数集合Q 上定义运算“*”如下：对于任意x , y ∈ Q ，y x * = x + y – xy ，则Q 关于*的单位元是( ).(A)x . (B)y . (C)1. (D)0.2. 设A = {1, 2, 3}, 下图分别给出了A 上的两个关系R 和S ，则S R 是( )关系.(A)自反. (B)对称. (C)传递. (D)等价.3.令T (x ): x 是火车，B (x ): x 是汽车，F (x , y ): x 比y 快，则“某些汽车比所有的火车慢”符号化为( ).(A)()()),()()(y x H x T x y B y →∀∧∃. (B)()()),()()(y x H x T x y B y ∧∀→∃. (C)()()),()()(y x H x T y B y x ∧→∃∀.G SG R(D)()()),()()(y x H x T x y B y →∀→∃.4. 整数集合Z 关于数的加法“+”和数的乘法“⋅”构成的代数结构(Z, +, ⋅)是( ). (A)域 (B)域和整环 (C)整环 (D) 有零因子环5.设G 是简单图，G 是G 的补图，若G G ≅，则称G 为自补图. 5阶不同构的自补图个数为( ).(A)0. (B)1. (C)2. (D)3.三、设C B g B A f →→:,:, 若g f 是单射，证明f 是单射，并举例说明g 不一定是单射.四、设A = {a , b , c , d }上的关系R = {(a , b ), (b , d ), (c , c ), (a , c )}, 画出R 的关系图，并求出R的自反闭包r (R )、对称闭包s (R )和传递闭包t (R ).五、设G 是(6，12) 的简单连通平面图，则G 的面由多少条边围成，为什么？六、任意6个人中，一定有3个人彼此认识或有3个人彼此不认识.参考答案：第2次作业答案一、1. ∈，∈，⊆.2.{(1,5), (3, 2), (2, 5)}, {(4, 2), (3, 2), (1, 4)}, {(1, 2), (2, 2)}.3. 1, 2, 1.4. ,,,),((⋂⋃X P ∅, X ), 2n , n .5. 3, 9.二、1(D); 2(B); 3(A); 4(C); 5(C).三、证对于任意A x x ∈21,，若)()(21x f x f =，则))(())((21x f g x f g =，于是))(())((21x f g x g f =. 由于g f 是单射，所以21x x =，因此f 是单射.例如，A = {a , b }, B = {1, 2, 3}, C = {α, β, γ}, f = {(a , 1), (b , 2)}, g = {(a , α), (b , β), (c , β)}, 这时)},2(),,1{(βα=g f ，它是A 到C 的单射，但g 不是单射. 四、解 R 的关系图如下：}),(),,(),,(),,(),,(),,(),,{()(d d b b a a c a c c d b b a R r =, }),(),,(),,(),,(),,(),,(),,{()(a c b d a b c a c c d b b a R s =. }),(),,(),,(),,(),,{()(d a c a c c d b b a R t =.五、证根据Euler 公式，G 的面数为r = 12 – 6 +2 = 8. 由握手定理知，∑=⋅=vv 24122)deg(，而简单连通平面图的每个面至少由3条边围成，所以G 的每个面恰由3条边围成.六、证用6个节点分别表示这6个人，可得6阶完全无向图6K . 若两个人认识，则在相应的两个节点所在的边上涂上红色，若两个人不认识，则在相应的两个节点所在的边上涂上蓝色.对于任意的6K 的节点v ，因为5)deg(=v ，与v 邻接的边有5条，当用红、蓝颜色去涂时，至少3条边涂的是同一种颜色，不妨设321,,vv vv vv 是红色. 若3条边21v v ，32v v ，31v v 是红色，则存在红色3K ，这意味着有3个人相互认识; 若21v v ，32v v ，31v v 都是蓝色，则存在蓝色3K ，这意味着有3个人相互不认识. 结论成立.第3次作业[论述题]第3次作业参考答案：第3次作业一、1.{1, 3, {1, 2}, {3}}；{{2, 3}, {1}}；{1, 3, {1, 2}, {3}, {2, 3}, {1}}.2.0，1，0.3. ))()((x O x Z x →⌝∀.4. p n , p 为素数，n 为正整数.abd5. 是，3，10.二、1(B); 2(C); 3(D); 4(C); 5(A).三、证对于任意C z ∈，由于g f 是满射，必存在A x ∈，使得z x f g x g f ==))(())(( . 令B x f y ∈=)(，有z y g =)(，因此，g 是满射.设},,{c b a A =，}3,2,1{=B ，},{βα=C ，令B A f →:，,:C B g →3)(,3)(,2)(===c f b f a f ,βαβ===)3(,)2(,)1(g g g .这时，α==))(())((a f g a g f ，β==))(())((b f g b g f ，显然有},{)(ran βα=g f ，g f 是满射. 而ran f = {2, 3}，f 不是满射.四、证 (1)对于任意x ∈ Z , 由于x x x x +=+22, 所以(x , x ) ∈ R , 即R 是自反的. (2)因为(0, 0) ∈ R , 因此R 不是反自反的.(3)对于任意x , y ∈ Z , 若(x , y ) ∈ R , 则y y x x +=+22, 于是x x y y +=+22, 进而(y , x ) ∈ R , 即R 是对称的.(4)因为(2, -3) ∈ R 且(-3, 2) ∈ R ，因此R 不是反对称的.(5)对于任意x , y , z ∈ Z , 若(x , y ) ∈ R 且(y , z ) ∈ R , 则y y x x +=+22且z z y y +=+22，于是z z x x +=+22，所以(x , z ) ∈ R , 即R 是传递的. 综上所述，知R 是自反的、对称的和传递的.五、解命题公式)())(q p q p A ⌝→↔→⌝=的真值表如下：A 的主析取范式为：)()(q p q p A ⌝∧∨∧=.A 的主合取范式为：)()(q p q p A ∨∧⌝∨=.六、证对于任意的6K 的节点v ，因为5)deg(=v ，与v 邻接的边有5条，当用红、蓝颜色去涂时，至少3条边涂的是同一种颜色，不妨设321,,vv vv vv 是红色. 若3条边21v v ，32v v ，31v v 是红色，则存在红色3K ; 若21v v ，32v v ，31v v 都是蓝色，则存在蓝色.第4次作业[论述题]第4次作业参考答案：第4次作业答案一、1.自反性、对称性和传递性.2. Abel.3. 6.4. 封闭性和结合性.5. 不含圈的连通.二、1(A); 2(C); 3(B); 4(D); 5(C).三、证对于任意A b a ∈,，假定)()(b f a f =. 由于≤是偏序，于是a a ≤，所以)(a f a ∈，进而)(b f a ∈，根据定义知b a ≤. 同理可证，a b ≤. 根据偏序的反对称性有b a =，因此f 是单射.当b a ≤时，对于任意)(a f x ∈，于是a x ≤. 根据偏序的传递性有b x ≤，即)(b f x ∈，故)()(b f a f ⊆.四、证 (1) 与非联结词“↑”的运算表如下：(2)p p p p p ↑=∧⌝=⌝)(.)()()())((q p q p q p q p q p ↑↑↑=↑⌝=∧⌝⌝=∧. )()()()()(q q p p q p q p q p ↑↑↑=⌝↑⌝=⌝∧⌝⌝=∨.五、解 ))),(),((),,((v y vQ u x uQ z y x zP y x ∃→∃∧∃∀∀=))),(),((),,((v y vQ u x uQ z y x zP y x ∃∨⌝∃∧∃∀∀ =))),(),((),,((v y vQ u x Q u z y x zP y x ∃∨⌝∀∧∃∀∀=))),(),((),,((v y Q u x Q v u z y x zP y x ∨⌝∃∀∧∃∀∀ =))),(),((),,((v y Q u x Q z y x P v u z y x ∨⌝∧∃∀∃∀∀ 六、证 (1)根据Euler 公式，有2+-=n m r . (2)31052)2(5-≤⇒≤+-n m m n m . (3) 若Petersen 图是平面图，由于其每个面至少5条边围成，于是由(2)知3105-≤n m . 因为在Petersen 图中，m = 15, n = 10, 于是31010515-⋅≤，矛盾.第5次作业[论述题]第5次作业参考答案：第5次作业答案一、1. 2n .2. 反自反、反对称、传递.3. 是.4. 独异点.5. 上确界和下确界. 二、1(C); 2(A); 3(B); 4 (D); 5(B).三、(1)证对于任意∈),(),,(2211y x y x R ⨯ R ，若)),(()),((2211y x f y x f =，于是),(),(22221111y x y x y x y x -+=-+，进而2211y x y x +=+且2211y x y x -=-. 由此可得，2121,y y x x ==，因而),(),(2211y x y x =，故f 是单射.对于任意∈),(q p R ⨯ R ，取2,2qp y q p x -=+=，容易得知),(),()),((q p y x y x y x f =-+=.由上可知，f 是双射. (2)解由上的证明过程知，⎪⎭⎫⎝⎛-+=-2,2)),((1y x y x y x f.(3)解很显然If f =- 1R ⨯R ，即),()),)(((1y x y x f f=- .)2,2())()(),()(()),(()),)(((y x y x y x y x y x y x y x f y x f f =--+-++=-+= .四、解 }),(),,(),,(),,(),,{()(c c b b c b b a a a I R R r A =⋃=. }),(),,(),,(),,(),,{()(1b c a b c b b a a a RR R s =⋃=-.}),(),,(),,(),,{()(c a c b b a a a R t =. 五、证(1))(x xP ∀ P (2)P (c ) US(1) (3))))()(()((x R y Q x P x ∧→∀ P (4)))()(()(c R y Q c P ∧→ US(3) (5))()(c R y Q ∧ T(2)(4)I (6)Q (y ) T(5)I (7)R (c ) T(5)I (8))()(c R c P ∧ T(2)(7)I (9)))()((x R x P x ∧∀ UG(8) (10)))()(()(x R x P x y Q ∧∀∧ T(6)(9)I六、证设G 是一棵阶数2≥的无向树，k k v v v v L 121...:-是G 中的最长路径. `若1v 和k v 至少有一个不是树叶，不妨设k v 不是树叶，即2)deg(≥k v ，则k v 除与1-k v 邻接外，还存在1+k v 与k v 邻接.若1+k v 在L 上，则G 中存在圈，不可能. 若1+k v 不在L 上，则G 中存在一条比L 长1的路径1121...+-k k k v v v v v ，与L 是G 中最长路径矛盾.第6次作业[论述题]第6次作业参考答案：第6次作业答案一、1. 1,3,5,7,11,13,17,19.2. 平行.3. 010, 100, 101, 110, 111.4. 2.5. 3.二、1(B); 2(A); 3(D); 4(C); 5(A).三、(1)证任意∈),(),,(2211y x y x R ×R , 若),(),(2211y x f y x f =，则),(),(22221111y x y x y x y x -+=-+，进而2211y x y x +=+且2211y x y x -=-，于是21x x =且21y y =，从而f 是单射.任意∈),(q p R ×R , 取⎪⎩⎪⎨⎧-=+=22q p y q p x , 通过计算易知),(),(q p y x f =，因此f 是满射. 故f 是双射.(2) 解由上面的证明知，f 存在逆函数且⎪⎭⎫⎝⎛-+=-2,2),(1y x y x y x f.又()()),(2,2,1y x y x y x f y x f f=⎪⎭⎫⎝⎛-+=- ，即I f f=- 1R ×R ,而()()())2,2())()(),()((,,y x y x y x y x y x y x y x f y x f f =--+-++=++= .四、解 R 的传递闭包t (R )的关系图如下：于是，有t (R ) = {(1, 3), (3, 1), (2, 3), (4, 3), (4, 5), (6, 5), (1, 1), (3, 3)，(2,1)，(4,1)}. 五、解首先写出命题公式()())()(p q r r q p A →→↔→→=的真值表如下：从真值表可得命题公式A 的主析取范式为：∨⌝∧⌝∧∨∧⌝∧∨∧∧=)()()(r q p r q p r q p A)()()(r q p r q p r q p ⌝∧⌝∧⌝∨∧⌝∧⌝∨⌝∧∧⌝.命题公式A 的主合取范式为：)()(r q p r q p A ∨⌝∨⌝∧⌝∨⌝∨=.七、解对于2, 3, 5, 7, 8，先组合两个最小的权2+3 = 5, 得5, 5, 7, 8；在所得到的序列中再组合5+5 = 10, 重新排列后为7, 8, 10；再组合7+8 =15, 得10, 15；最后组合10+15 = 25.2515108710875587532 所求的最优2叉树树如下：。

吉林大学离散数学II试题A及答案

吉林大学离散数学II试题A及答案2004级《离散数学II 》期末考试试题（A 卷）满分80分，考试时间：2个小时一、[20分] 判断题（正确的在括号内打√号，错误的打?号）1、设（G ，?）是有限半群，而且有壹，如果关于运算?满足消去律，则（G ，?）是群。

（）2、任意置换σ恰有一法写成轮换的乘积。

（）3、设H 是G 的子群，则H 中的壹与G 的壹一致。

（）4、设环R 是一个含壹环，则R 的子环R ’也一定是含壹环。

（）5、设（R ,+, ?）是一个环，则 ? 运算一定满足交换律。

（）6、按照剩余类的加法与乘法，环R 对于其理想N 的所有剩余类的集合R/N 是一个剩余环，则从R 到R/N 有一个同态映射存在。

（）7、设F 是 q 元有限域，则 F 的q-1个非零元素在乘法下一定作成一个循环群。

（） 8、下列部分序集都是格。

( )A B C D9、格的同态映射是保序的，反之，保序映射也是同态映射。

（）10、下列4个格所对应的哈斯图不都是分配格。

( )A B C D二、[20分] （20分）（G,*）为群，其中运算*定义如表所示。

1. 写出子群(a)；2. 设H=(a)，证明(a)*c=c*(a)；3. 找出所有2个元素的子群；4. 求出G 的元数除以(f)的元数的商；5. 求(f)的所有右陪集。

三、[10分] 设(R,+,?) 为一代数系统，其中R 为实数集合，+为实数加法，任取a,b ∈R ，a ?b=|a |b ，试判断(R,+,?)是否为环。

如果是，请证明你的结论；如果不是请说明理由。

四[10分] 下面给出的多项式是R 0上的质式吗？请给出证明。

（1）x 3-5x+5；（2）x 5+7x 2-3。

五、[14分] (1) 计算Φ24(x);(2) 构造元数为9的有限域(不要求写出加法与乘法运算表)。

六、[6分]设(G ,*)为循环群，生成元素为a 。

设（A,*）和(B,*)均为(G ,*)的子群，而a i 和a j 分别为（A,*）和(B,*)的生成元。

交大网络学院离散数学第二次作业

1. 令f和g分别为从{1，2，3，4}到｛a,b,c，d｝和从{a，b,c,d｝到{1,2，3，4｝的两个函数，且满足f（1)=d, f(2)=c，f(3)=a, f（4)=b和g（a)=2，g（b）=1, g（c)=3，g（d)=2.则：（1）f 是一对一的函数吗？g呢？（2）f是映上函数吗? g呢?（3）f或g是否有逆函数？若有，求出逆函数。

解:(1）∵f=｛（1，d),（2,c),（3，a），（4，b)} ∴f是一对一函数∵g=｛(a，2）,（b，1），(c,3)，（d,2)} 又∵g(a）=2=g(d) ∴g不是一对一函数(2) f是映上函数,因为Y= {a，b,c，d｝中的每个元素至少被X={1，2，3，4｝的一个元素所指向。

g不是映上函数,因为Y={1，2，3，4}中的元素4没有被X=｛a，b,c,d｝的元素所指向.（3）∵f是一对一的映上函数∴f有逆函数，f—1=｛（d,1）,（c，2），（a，3）,(b，4）｝∵g不是一对一且映上的函数∴g没有逆函数2。

以8,14，32,86，248开头的序列之项推测一个表达式,并据此求出该序列的后续三项。

解:3。

方程x1+x2+x3+x4+x5=21有多少个解？其中xi≥2 （i=1，2，3,4,5)是非负整数.解：可将题目转化为把21个相同的球放入5个不同的盒子,每个盒子至少放2个球有多少种方法的问题.使用隔板法可得C（21-5x2+5—1，21—5x2）=C（15，11）= = 1365个解.4. 把6个相同的球放到9个不同的箱子，有多少种方法？解：C（9+6—1, 6）= C(14，6) ==3003 种方法5。

使用ABRACADABRA 中的所有字母可以构造多少个不同的串？解:C(11，5）C(6，2）C（4，2)C(2，1）===41580。