勾股定理之最短路径(填空选择)中考题
中考数学复习《勾股定理求最短路径》专项检测卷-附带答案

中考数学复习《勾股定理求最短路径》专项检测卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.如图,一牧童在A处牧马,牧童家在B处,A、B处距河岸的距离AC、BD的长分别为500m和700m,且C、D两地的距离为500m,天黑前牧童从A点将马牵引到河边去饮水后,再赶回家,那么牧童至少要走()A.2900m B.1200m C.1300m D.1700m2.如图,圆柱体盒子放在水平地面上,该圆柱体的高为9cm,点M离盒底的距离为3cm,cm,一只蚂蚁沿着该圆柱体盒子的表面从点M爬行到点N,则该蚂蚁爬行的最底面半径为8π短路程为()cm.A.6B.10C.2√73D.6+16π3.如图是一个三级台阶,它的每一级的长,宽,高分别是20dm,3dm,2dm,A和B是这个台阶相对的端点,点A处有一只蚂蚁,想到B处去吃食物,则这只蚂蚁爬行的最短距离为()A.25dm B.26dm C.24dm D.27dm4.如图是放在地面上的一个长方体盒子,其中AB=7,BC=4,BF=6点M在棱AB上,且AM=1,点N是FG的中点,一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为()A.10B.4√5C.6√2D.2√135.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为()m.(π取3)A.30B.28C.25D.226.如图,在等腰直角△ABC中AB=BC=4,点D在边BC上且CD=1,点E,F分别为边AB,AC上的动点,连接DE,EF,DF得到△DEF,则△DEF周长的最小值为()A.5√2B.2√13C.3√7D.√6+2√27.如图,在RtΔABC中∠ACB=90°,AC=10,BC=12点D是ΔABC内的一点,连接AD,CD,BD满足∠ADC=90°,则BD的最小值是()A.5B.6C.8D.13S矩形ABCD则点P 8.如图,在矩形ABCD中AB=5 AD=3.动点P满足S△PAB=13到A B两点的距离之和P A+PB的最小值为()A.√29B.√34C.√41D.√529.已知圆锥底面半径为1 母线长为4 地面圆周上有一点A一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线P A中点B则蚂蚁爬行的最短路程为()A.πB.√5πC.2√5D.2π10.如图△ABC为边长3的等边三角形AD△BC于点D点E在AB边上且AE=1 P为线段AD上的一个动点则PB+PE的最小值是()√3 A.3B.√7C.√3D.3211.如图在一个长为9m宽为6m的长方形草地上放着一根长方体木块它较长的边和草地的宽AD平行且长大于AD木块从正面看是边长为1m的正方形一只蚂蚁从点A出发到达点C处需要走的最短路程为()A.12m B.√157m C.6√5m D.13m12.如图矩形ABCD中AB=4BC=6以A为圆心2为半径画圆A E是圆A 上一动点P是BC上一动点则PE+PD最小值是()A.4√2B.2√10C.8D.1213.如图正方形ABCD中AB=4点E F分别在边AB BC上点P在对角线AC上EF∥AC PE+PF=m.下列结论错误..的是()A.若BE=2则m的最小值为4B.若m的最小值为4 则BE=2C.若BE=0.5则m的最小值为5D.若m的最小值为5 则BE=0.5 14.数形结合是数学的重要思想和解题方法如:“当0<x<12时求代数式√x2+4+√(12−x)2+9的最小值” 其中√x2+4可看作两直角边分别为x和2的Rt△ACP的斜边长√(12−x)2+9可看作两直角边分别是12−x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值如图所示当AP与BP共线时AP+BP为最小.请你解决问题:当0<x<4时则代数式√x2+1+√(4−x)2+4的最小值是()A.4B.5C.6D.715.如图有一条直角弯道河流河宽为2 A B两地到河岸边的距离均为1 AH= BF=1AD=7BE=9现欲在河道上架两座桥MN PQ使AM+MN+NP+PQ+QB最小则最小值为()A.√130B.√145+2C.14D.1216.如图平行四边形ABCD中AB=12AD=10∠A=60°E是边AD上一点且AE=6F是边AB上的一个动点将线段EF绕点E顺时针旋转60°得到EN连接BN CN则BN+CN的最小值是()A.3√21B.4√14C.14D.4√1317.如图在平面直角坐标系xoy中点A C分别在坐标轴上且四边形OABC是边长(x>0)的图像与BC,AB边分别交于E,D两点△DOE 为3的正方形反比例函数y=kx的面积为4 点P为y轴上一点则PD+PE的最小值为()A.3B.2√5C.3√2D.518.如图在平面直角坐标系中点A(3,a)是直线y=2x与直线y=x+b的交点点B 是直线y=x+b与y轴的交点点P是x轴上的一个动点连接P A PB则PA+PB 的最小值是()A.6B.3√5C.9D.3√1019.如图已知正方形ABCD的边长是4 点E是AB边上一动点连接CE过点B 作BG△CE于点G点P是AB边上另一动点则PD+PG的最小值是()A.2√10−2B.4√3−2C.2√13−2D.2√14−220.如图① 在正方形ABCD中点E是AB的中点点P是对角线AC上一动点设PC=x PE+PB=y图②是y关于x的函数图象且图象上最低点Q的坐标为(m,2√5)则正方形ABCD的边长为()A .2√2B .2√5C .4D .5参考答案1.解:如图 由题意得:DB ⊥CD AC ⊥CD A ′C =AC =500m BD =700m CD =500m作A 点关于河岸的对称点A ′ 连接BA ′交河岸与P 则PB +P A =PB +P A ′=BA ′时最短 过点A ′ 作A ′B ′⊥BD 交BD 延长线于点B ′△四边形A ′B ′DC 是矩形△A ′B ′=CD =500m DB ′=A ′C =500m△BB ′=BD +DB ′=1200m在Rt △A ′B ′B 中 BA ′=√BB ′2+A ′B ′2=√12002+500=1300m .故选:C2.解:把圆柱侧面展开 展开图如图所示 点M N 的最短距离为线段MN 的长 △AM =9﹣3=6(cm ) AN 为底面半圆弧长 AN =2×12•8π•π=8(cm )在Rt△AMN 中MN =√AM 2+AN 2=√62+82=10(cm ).故选:B .3.解:三级台阶平面展开图为长方形长为20dm 宽为(2+3)×3dm则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B点最短路程为x dm由勾股定理得:x2=202+[(2+3)×3]2=252解得x=25.故选:A.4.解:如图1中把面ABFE与面EFGH沿EF展开∵AM=1,AB=7,BC=4,BF=6,点N是FG的中点∴MB=6,FN=2,BN=BF+FN=8,∴MN=√MB2+BN2=10,如图2 把面ABFE与面BCGF沿BF展开同理可得:MP=8,PN=BF=6,∴MN=√MP2+PN2=10,如图3 把面ABCD与面BCGF沿BC展开同理:MF=MB+BF=12,FN=2,∴MN=√122+22=√148=2√37,∵10=√100<√148=2√37,所以一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N它需要爬行的最短路程为10.故选:A.5.解:其侧面展开图如图:作点C关于AB的对称点F连接DF△中间可供滑行的部分的截面是半径为2.5cm的半圆△BC=πR=2.5π=7.5cm AB=CD=20cm△CF=2BC=15cm在R t△CDF中DF=√CF2+CD2=√152+202=25cm故他滑行的最短距离约为25cm.故选C.6.解:如图作点D关于AB的对称点G作点D关于AC的对称点H连接BG CH DH FH GH∵∠ABC=90°点D与点G关于AB对称∴∠GBE=∠ABC=90°∴G B D C在同一条直线上△在等腰直角△ABC中AB=BC△∠A=∠ACB=45°△BC=4CD=1△由对称性可知:GB=DB=3CH=CD=1∠FCH=∠FCD=45°FH=FD EG=ED∴∠HCG=90°GC=GB+BD+DC=3+3+1=7∴GH=√GC2+CH2=√72+12=5√2∴DE+EF+FD=GE+EF+FH⩾GH=5√2∴△DEF的周长的最小值5√2.故选:A.7.解:如图取AC中点O连接DO.∵∠ADC=90°∴点D在以点O为圆心AC长为直径的圆周上运动且DO=12AC=12×10=5当O D B在同一直线上时OB最短此时BD=OB−OD=OB−5为最短.在RtΔOCB中OC=5BC=12则OB=√122+52=13∴BD=OB−OD=OB−5=13−5=8即BD的最小值是8.故选:C.8.解:设ΔABP中AB边上的高是ℎ.∵SΔPAB=13S矩形ABCD∴12AB⋅ℎ=13AB⋅AD∴ℎ=23AD=2∴动点P在与AB平行且与AB的距离是2的直线l上如图作A关于直线l的对称点E连接AE连接BE则BE的长就是所求的最短距离.在RtΔABE中∵AB=5AE=2+2=4∴BE=√AB2+AE2=√52+42=√41即PA+PB的最小值为√41.故选:C.9.解:根据题意将该圆锥展开如下图所示的扇形则线段AB就是蚂蚁爬行的最短距离.△点B是母线P A的中点PA=4△PB=2△圆锥的底面圆的周长=扇形的弧长又△圆锥底面半径为1△扇形的弧长=圆锥底面周长即l=2πr=2π扇形的半径=圆锥的母线=P A=4由弧长公式可得:l=nπR180=nπ×4180=2π△扇形的圆心角n=90°在Rt△APB中由勾股定理可得:AB=√PA2+PB2=√42+22=2√5所以蚂蚁爬行的最短路程为2√5故选:C.10.解:作E关于AD的对称点E′连接BE′交AD于P则此时PE + PB有最小值PE+ PB的最小值=BE′△AE′= AE= 1△ CE'=3-1=2作E'F△BC于F△△ABC为等边三角形△C= 60°△∠CE′F=30°△CF=12CE′=1 E′F=√CE′2−CF2=√22−12=√3△AC= BC= 3△BF=3-1= 2BE′=√BF2+E′F2=√22+(√3)2=√7△PE+ PB的最小值=√7故选:B11.解:由题意可知将木块展开如图长相当于是AB+2个正方形的宽△长为9+2×1=11(m);宽为6 m.于是最短路径为:√62+112=√157(m).故选B.12.解:如图作点D关于直线BC的对称点F连接AF交BC于点P交⊙A于点E此时PE+PD最小等于AF−AE△四边形ABCD是矩形AB=4BC=6△AB=CD=4AD=BC=6△DF=8∠ADF=90°△AF=√AD2+DF2=√62+82=10△AE+EF=10△EF=10−2=8△PE+PD的最小值为8故选C.13.解:如图根据正方形的对称性在AD上取点E关于AC的对称点G连接FG交AC 于点P则PE=PG△PE+PF=PG+PF=FG为m的最小值△AG=AE=4−BE∠BAD=90°△EG2=AE2+AG2=2AE2=2(4−BE)2△EF∥AC△∠BEF=∠BAC=45°∠BFE=∠BCA=45°△BF=BE△EF2=BE2+BF2=2BE2△FG⊥AC△EG⊥EF△∠FEG=90°△FG=√EF2+EG2=2√(BE−2)2+4当BE=2时FG=2√(2−2)2+4=4△A正确;当FG=4时2√(BE−2)2+4=4△√(BE−2)2+4=2△(BE−2)2+4=4△(BE−2)2=0△BE=2△B正确;当BE=0.5时FG=2√(0.5−2)2+4=5△C正确;当FG=2√(BE−2)2+4=5时(BE−2)2+4=254△(BE−2)2=94△BE−2=±32△BE=0.5,或BE=3.5△D不正确.故选:D.14.解:如图所示√x2+1可看作两直角边分别为x和1的Rt△ACP的斜边长√(4−x)2+4可看作两直角边分别是4−x和2的Rt△BDP的斜边长.△求√x2+1+√(4−x)2+4的最小值即求AP+BP的最小值当AP与BP共线时AP+BP为最小即AB的长.连接AB△∠E=90°AE=AC+CE=AC+DB=3△AB=√AC2+BE2=5△代数式√x2+1+√(4−x)2+4的最小值是5.故选:B.15.解:延长AH到J使得AJ=MN=2延长BF到K使得BK=PQ=2连接JK交河道于点N′P′得到两座桥N′M′P′Q′此时AM′+M′N′+N′P′+P′Q′+BQ′的值最小.△四边形AJN′M′是平行四边形△AM′=JN′同理:BQ′=P′K延长AH交BK的延长线于点W.△WH=BE=9WF=AD=7△WJ=WH+AH−AJ=9+1−2=8WK=AD+BF−BK=7+1−2=6在Rt△JWK中JK=√KW2+WJ2=√62+82=10∴AM′+M′N′+N′P′+P′Q′+BQ′=HN′+2+N′P′+2+P′K=4+JK=14∴AM+MN+NP+PQ+QB的最小值为14.故选:C.16.解:取AB的中点G连接CE EG.由已知得AG=AE=6∠A=60°△△AEG是等边三角形△∠AGE=∠AEG=60°.△∠AEF+∠GEF=∠GEF+NEG=60°△∠AEF=∠NEG.△AE=EG NE=FE△△AEF△△GEN△∠A=∠NGE=60°△∠BGN=60°.△BG=EG∠BGN=∠NGE NG=NG△△BNG△△ENG△BN=EN.要求BN+CN最小就是求CN+NE最小即BN+CN=NE+CN≥CE.作EH⊥CD交延长线于点H△AB∥CD△∠EDH=∠A=60°.在Rt△DEH中DE=4∠DEH=30°△DH=2EH=2√3△CH=CD+DH=12+2=14.在Rt△CEH中CE=√CH2+EH2=√142+(2√3)2=4√13.所以BN+CN的最小值是4√13.故选:D.17.解:∵正方形OABC的边长是3∴点D的横坐标和点E的纵坐标为3∴D(3,k3)E(k33)∴BE=3−k3BD=3−k3∵△ODE的面积为4∴3×3−12×3×k3−12×3×k3−12×(3−k3)2=4∴k=3或−3(舍去)∴D(3,1)E(1,3)作E关于y轴的对称点E′连接DE′交y轴于P则DE′的长=PD+PE的最小值∵CE=CE′=1=AD∴BE′=4BD=2∴DE′=√BE′2+BD2=√42+22=2√5即PD+PE的最小值为2√5故选:B.18.解:作点A关于x轴的对称点A′连接A′B如图所示:则P A+PB的最小值即为A′B的长将点A(3 a)代入y=2x得a=2×3=6△点A坐标为(3 6)将点A(3 6)代入y=x+b得3+b=6解得b=3△点B坐标为(0 3)根据轴对称的性质可得点A'坐标为(3 -6)△A′B=√32+(−6−3)2=3√10△P A+PB的最小值为3√10.故选:D.19.解:如图:取点D关于直线AB的对称点D′.以BC中点O为圆心OB为半径画半圆.连接OD′交AB于点P交半圆O于点G连BG.连CG并延长交AB于点E.由以上作图可知BG△EC于G.PD+PG=PD′+PG=D′G由两点之间线段最短可知当点D′ G O三点共线时PD+PG最小.△D′C′=4 OC′=6△D′O=√42+62=2√13△D′G=2√13−2△PD+PG的最小值为2√13−2故选C.20.解:如图点D是点B关于直线AC的对称点连接DE交AC于点P根据点的对称性PB=PD则y=PE+PB=PD+PE=DE为最小故ED=2√5设正方形的边长为a则AE=12a在Rt△ADE中由勾股定理得:DE2=AD2+AE2即a2+(12a)2=(2√5)2解得:a=4(负值已舍去)故选:C.。
专题18勾股定理最短路径问题(专项培优训练)(学生版)

专题18 勾股定理—最短路径问题(专项培优训练)试卷满分:100分考试时间:120分钟难度系数:0.39试卷说明:本套试卷结合沪教新版版数学八年级上册同步章节知识点,精选易错,常考,压轴类问题进行专题汇编!题目经典,题型全面,解题模型主要选取热点难点类型!同步复习,考前强化必备!适合成绩中等及偏上的学生拔高冲刺。
一、选择题:本大题共10小题,每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2分)如图,在一个长为20m,宽为16m的长方形草地上放着一根长方体木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2m的正方形,若点A处有一只蚂蚁,它从点A处爬过木块到达点C 处去吃面包碎,则它需要走的最短路程是()A.24m B.C.D.16m2.(2分)如图,圆柱底面半径为,高为18cm,点A、B分别是圆柱两底面圆周上的点,且点B在点A的正上方,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为()A.21cm B.24cm C.30cm D.32cm3.(2分)如图,有一棱长为3dm的正方体盒子,现要按图中箭头所指方向从点A到点D拉一条捆绑线绳,使线绳经过ABFE、BCGF、EFGH、CDHG四个面,则所需捆绑线绳的长至少为()dm.A.15 B.9 C.D.4.(2分)如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点,一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径长是()A.12cm B.C.D.9cm5.(2分)如图,一圆柱体的底面周长为10cm,高AB为12cm,BC是直径,一只蚂蚁从点A出发沿着圆柱的表面爬行到点C的最短路程为()A.17cm B.13cm C.12cm D.14cm6.(2分)如图,有一个圆柱,底面圆的直径,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短路程为()A.11cm B.12cm C.9cm D.10cm7.(2分)固定在地面上的一个正方体木块(如图①),其棱长为4cm,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为()A.B.C.D.8.(2分)如图,四边形ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m,一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走()A.13m B.m C.5m D.12m9.(2分)有一个如图所示的上底面是敞口的长方体透明玻璃鱼缸,其长AD=80cm,高AB=60cm,宽DF =40cm.在顶点E处有一块面包屑,一只蚂蚁想从鱼缸外的A点沿鱼缸侧面吃面包屑,蚂蚁爬行的最短路线长是()cm.A.B.C.D.10.(2分)如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为()A.4dm B.2dm C.2dm D.4dm二、填空题:本大题共10小题,每小题2分,共20分.11.(2分)如图,在一个长方形草坪ABCD上,放着一根长方体的木块.已知AD=6米,AB=4米,该木块的较长边与AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是米.12.(2分)如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是cm.13.(2分)在一个长2.5米,宽为1米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽AD,木块的主视图是边长0.5米的等边三角形,一只蚂蚁从点A处到C处需要走的最短路程是米.14.(2分)在底面直径为2cm,高为4cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为(π取3)15.(2分)如图,长方体的长为6,宽为5,高为8,棱上一点C到顶点B的距离为2,一只蚂蚁若要沿着长方体的表面从顶点A爬到点C,则爬行的最短路程为.16.(2分)在一个长为2米,宽为1米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽AD,木块的主视图是边长为0.4米的正三角形,一只蚂蚁从点A处到C处需要走的最短路程是米.17.(2分)如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短距离是cm.18.(2分)如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为cm(假设蜂蜜不会下滑).19.(2分)如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为5cm.一只蚂蚁如果要沿着该盒子的表面从点A爬到点B,那么需要爬行的最短路程为cm.20.(2分)如图,有一个长宽高分别为2cm,1cm,3cm的长方体,有一只小蚂蚁想从点A2爬到点C1处,则它爬行的最短路程为cm.三、解答题:本大题共8小题,共60分.21.(6分)如图,一只蚂蚁在底面半径为10cm,高为20πcm的圆柱下底面的点A处,它想吃到上底面上与点A相对的点B处的食物,求蚂蚁沿圆柱侧面爬行的最短路程是多少?22.(6分)如图,后面靠墙,底面着地放置一个长、宽、高分别为15,10,20的长方体,已知BC=5,一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?(不经过靠墙的面;画出示意图再解答)23.(8分)如图a,圆柱的底面半径为4cm,圆柱高AB为2cm,BC是底面直径,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:路线1:高线AB+底面直径BC,如图a所示,设长度为l1.路线2:侧面展开图中的线段AC,如图b所示,设长度为l2.(1)你认为小明设计的哪条路线较短?请说明理由;(2)小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为2cm,高AB为4cm”继续按前面的路线进行计算.(结果保留π)①此时,路线1的长度l1=,路线2的长度l2=;②所以选择哪条路线较短?试说明理由.24.(8分)如图,机器人利用吸盘爬大楼玻璃幕墙,要用8分钟的时间先垂直向上,再水平横行,最后垂直下行,完成如图矩形三边A→B→C→D的行程,若上、下行速度都是3米/分钟,横行速度是4米/分钟,问如何安排上、下行和横行的时间,才能使矩形ABCD的面积为72m2,而且机器人走的路线较短?25.(8分)(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程;(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?26.(8分)如图,圆柱形无盖玻璃容器,高18cm,底面圆的直径为cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.(结果保留根号)27.(8分)吴老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.(1)如图(1)正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处;(2)如图(2)长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从长方体底面上的点A沿长方体表面爬到点C1处;(3)如图(3)是底面周长为10cm,高为5cm的圆柱体,一只蚂蚁欲从圆柱体底面上的点A沿圆柱体表面爬到点C处.28.(8分)请阅读下列材料:问题:如图(1),圆柱的底面半径为4cm,圆柱高AB为2cm,BC是底面直径,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:路线1:高线AB+底面直径BC,如图(1)所示.路线2:侧面展开图中的线段AC,如图(2)所示.设路线1的长度为l1,则l1=AB+BC=2+8=10;设路线2的长度为l2,则l2===;∵=102﹣(4+16π2)=96﹣16π2=16(6﹣π2)<0∴即l1<l2所以选择路线1较短.(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为2cm,高AB为4cm”继续按前面的路线进行计算.(结果保留π)①此时,路线1:l1=.路线2:l2=.②所以选择哪条路线较短?试说明理由.(2)请你帮小明继续研究:当圆柱的底面半径为2cm,高为hcm时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.。
勾股定理最短路径问题-解析版--初中数学专题训练

利用勾股定理求最短路径问题【考法导图】解题技巧:把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
1◎类型1台阶中的最值问题1(2017秋·山东济南·八年级济南外国语学校校考期中)如图,是一个三级台阶,它的每一级的长,宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是()A.12B.13C.14D.15【答案】B【分析】将台阶展开,根据勾股定理即可求解.【详解】将台阶展开,如下图,因为AC=3×3+1×3=12,BC=5,所以AB2=AC2+BC2=169,所以AB=13(cm),所以蚂蚁爬行的最短线路为13cm.故选B.【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.2(2023·全国·九年级专题练习)一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程为()A.481B.25C.30D.35【答案】B【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【详解】如图所示,∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3,∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长AB.由勾股定理得:AB2=202+2+3×32=252,解得:AB=25.故选:B.【点睛】本题考查了平面展开-最短路径问题以及勾股定理的应用,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.3(2020·山东淄博·统考一模)地面上铺设了长为20cm,宽为10cm的地砖,长方形地毯的位置如图所示.那么地毯的长度最接近多少?()A.50cmB.100cmC.150cmD.200cm【答案】C【分析】根据等腰直角三角形的性质即可得到结论.【详解】解:观察图像可知,地毯长可以看做是10个等腰直角三角形的斜边长度之和,则斜边=102+102=102,∴长方形地毯的长为:10×102=1002≈141.4cm,故选C.【点睛】本题考查了生活中的平移现象,等腰直角三角形的性质,正确的识别图形是解题的关键.4(2023春·八年级课时练习)如图是楼梯的一部分,若AD=2,BE=1,AE=3,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为()A.5B.3C.13D.25【答案】D【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.【详解】解:将台阶展开,如图,因为DC=AE+BE=3+1=4,AD=2,所以AC2=DC2+AD2=20,所以AC=25,故选:D.【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.2◎类型2正方体中的最值问题1(2023·江苏常州·校考一模)如图,是一个棱长为1的正方体纸盒,若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是()A.3B.2C.5D.3【答案】C【分析】根据正方体展开图的特点,将正方体展开,然后利用勾股定理求解即可.【详解】解:如图所示,将正方体展开,则AC=2,BC=1,∠ACB=90°,∴由勾股定理得AB=AC2+BC2=5,∴需要爬行的最短路程是5,故选C.【点睛】本题主要考查了勾股定理的实际应用,正确将正方体展开,利用勾股定理进行求解是解题的关键.2(2023秋·陕西西安·八年级统考期末)如图,正方体盒子的棱长为2,M为EH的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为()A.10B.213C.13D.25【答案】C【详解】先把图中展开,根据两点间线段距离最短,再根据勾股定理求出BM的长即可;【解答】解:如图,连接BM,则线段BM的长就是蚂蚁需爬行的最短路程,∵正方体的棱长为2,M是EH的中点,∴∠Q=90°,MQ=2,BQ=1+2=3,由勾股定理得BM=22+32=13,故选:C.【点睛】本题考查两点间线段距离最短及勾股定理,解题的关键是理解最短路线.3(2022秋·广东佛山·八年级校考阶段练习)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是()A.10cmB.4cmC.17cmD.5cm【答案】C【分析】正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短,根据勾股定理可求出路径长,【详解】解:如图,它运动的最短路程AB=(2+2)2+222=17(cm),故选:C.【点睛】本题考查平面展开最短路径问题,掌握两点之间线段最短,找到起点终点,根据勾股定理求出是解题的关键.4(2023春·北京大兴·八年级北京市第八中学大兴分校校考阶段练习)如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从A点沿盒子的表面爬行到M点的最短距离为()A.23B.13C.14D.17【答案】B【分析】先利用展开图确定最短路线,再利用勾股定理求解即可.【详解】解:如图,蚂蚁沿路线AM爬行时距离最短;∵正方体盒子棱长为2,M为BC的中点,∴AD=2,MD=3,∴AM=22+32=13,故选:B.【点睛】本题考查了蚂蚁爬行的最短路径为题,涉及到了正方形的性质、正方体的展开图、勾股定理、两点之间线段最短等知识,解题关键是牢记相关概念与灵活应用.3◎类型3长方体中的最值问题1(2023春·全国·八年级专题练习)如图所示,有一个长、宽各2米,高为3米的无盖长方体纸盒放在桌面上,一只昆虫从顶点A要爬到顶点B,那么这只昆虫爬行的最短路程为()A.3米B.4米C.5米D.6米【答案】C【分析】分别画出三个路径的示意图,利用勾股定理求出路程,再从中找出最短路程即可.【详解】解:由题意,有以下三个路径:①如图,路径一:则这只昆虫爬行的路程为22+(2+3)2=29(米);②如图,路径二:则这只昆虫爬行的路程为32+(2+2)2=5(米);③如图,路径三:则这只昆虫爬行的路程为22+(3+2)2=29(米);因为29>5,所以这只昆虫爬行的最短路程为5米,故选:C.【点睛】本题考查了勾股定理的应用,正确画出三个路径的示意图是解题关键.2(2022秋·陕西西安·八年级校考阶段练习)如图,一只蚂蚁从长为4cm,宽为3cm,高为5cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是()A.12cmB.74cmC.80cmD.90cm【答案】B【分析】先将图形展开,再根据两点之间线段最短,再由勾股定理求解即可.【详解】解:将长方体展开,如图1所示,连接A、B,根据两点之间线段最短,AB=(3+4)2+52=74 cm;如图2所示,(3+5)2+42=45cm,如图3所示,32+(5+4)2=310cm,∵74<45<310,∴蚂蚁所行的最短路线为74cm.【点睛】本题考查最短路径问题,将长方体展开,根据两点之间线段最短,运用勾股定理是解题.3(2023春·全国·八年级专题练习)如图,正四棱柱的底面边长为4cm,侧棱长为6cm,一只蚂蚁从点A 出发,沿棱柱外表面到C′点处吃食物,那么它需要爬行的最短路径的长是()A.229cmB.14cmC.(213+4)cmD.10cm【答案】D【分析】把正四棱柱展开为平面图形,分两种情形求出路径,比较即可解答.【详解】解:把正四棱柱展开为平面图形,分两种情形:如图1中,AC =AB2+BC 2=42+102=116=229,如图2中,AC =AC2+CC 2=82+62=10,∵10<229,∴爬行的最短路径是10cm.故选:D【点睛】本题考查平面展开-最短路径问题,涉及了勾股定理的应用,解题的关键是将问题进行转化,然后根据勾股定理求解.4(2022秋·江苏·八年级专题练习)如图,长方体的长、宽、高分别是6、3、5,一只蚂蚁要从点A爬行到点B,则爬行的最短距离是()A.130B.126C.10D.86【答案】C【分析】做此题要把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.【详解】解:第一种情况:把我们所看到的前面和上面组成一个平面,则这个长方形的长和宽分别是8和6,则所走的最短线段是82+62=10;第二种情况:把我们看到的左面与上面组成一个长方形,则这个长方形的长和宽分别是11和3,所以走的最短线段是112+32=130;第三种情况:把我们所看到的前面和右面组成一个长方形,则这个长方形的长和宽分别是9和5,所以走的最短线段是92+52=106;∵10<106<130,三种情况比较而言,第一种情况最短,最短路程=10,故选:C .【点睛】本题考查了平面展开---最短路径问题,解题的关键是将图形展开,转化为直角三角形利用勾股定理解答.4◎类型4圆柱(锥)中的最值问题1(2023春·全国·八年级专题练习)如图,圆柱的底面半径为6πcm ,AC 是底面圆的直径,点P 是BC 上一点,且PC =4cm ,一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是()A.45cmB.213cmC.56cmD.10cm【答案】B【分析】把圆柱侧面展开后,连接AP .由已知可求得圆柱底面圆的周长,从而可求得周长的一半,由勾股定理即可计算出AP 的长.【详解】侧面展开图如图所示:∵圆柱的底面半径为6cm,π∴圆柱的底面周长为12cm,∴AC′=6cm.在Rt△ACP中,AP=42+62=213(cm).故选:B.【点睛】本题考查了勾股定理的应用,关键是把圆柱展开,即把空间问题转化为平面问题来解决,体现了转化思想.2(2022春·全国·八年级假期作业)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B.20C.18D.30【答案】A【分析】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,则BC就是蚂蚁到达蜂蜜的最短距离,根据勾股定理即可求得BC的长.【详解】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,如图所示:则DB=AD=4cm,由题意及辅助线作法知,M与N分别为GH与DF的中点,且四边形CMHE为长方形,∴CE=MH=9cm,EH=CM=4cm,∴DE=DH-EH=12-4=8cm,∴BE=DE+DB=8+4=12cm,在Rt△BEC中,由勾股定理得:BC=BE2+CE2=122+92=15cm,即蚂蚁到达蜂蜜的最短距离为15cm,故选;:A.【点睛】本题考查了勾股定理,两点间线段最短,关键是把空间问题转化为平面问题解决,这是数学上一种重要的转化思想.3(2022秋·全国·八年级专题练习)如图,有一个圆柱形玻璃杯,高为10cm,底而周长为12cm,在圆柱的下底面的内壁A处有一只蚂蚁,它想吃到在杯内离杯上沿2cm的点E处的一滴蜂蜜,求蚂蚁到达蜂蜜的最短距离()A.261cmB.234cmC.413cmD.10cm【答案】D【分析】根据题意画出图形,然后根据勾股定理,即可求解.【详解】解:如图,根据题意得:BC=10cm,AB=12×12=6cm,CE=2cm,∴BE=BC-CE=8cm,在Rt△ABE中,由勾股定理得:AC=AB2+BE2=62+82=10cm,即蚂蚁到达蜂蜜的最短距离10cm.故选:D.【点睛】本题主要考查了勾股定理的应用,明确题意,画出图形是解题的关键.4(2019·全国·八年级专题练习)如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要()A.12mB.13mC.17mD.20m【答案】B【分析】先把圆柱的侧面展开得到一个长方形,利用勾股定理求出AB的长即可得到答案.【详解】解:将圆柱形油罐的侧面展开如图所示,由题意可知,在△ABC中,∠C=90°,BC=5m,AC=12m,∴由勾股定理可得:AB=AC2+BC2=52+122=169=13m,∴梯子最短需要13m.故选B.【点睛】本题主要考查了勾股定理的应用,本题的解题要点是:将圆柱的侧面展开,结合题意就可将问题转化到Rt△ABC中,这样就可利用“勾股定理”求出AB的长度,从而得到梯子的最短长度.。
1.3 勾股定理的应用-勾股定理与最短路径问题 同步练习(含答案)

1.3勾股定理的应用-勾股定理与最短路径问题一、选择题1.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁沿侧面爬行,想吃到B点的食物,需要爬行的最短路径是( )A.9B.13C.14D.252.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为( )A.12cm B.14cm C.20cm D.24cm3.如图所示的圆柱体中底面圆的半径是4,高为3,若一只小虫从A点出发沿着圆柱体的侧面π爬行到C点,则小虫爬行的最短路程是( )A.5B.5C.73D.44.今年9月22日是第三个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为10cm的圆柱粮仓模型,如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )A.20πcm B.40πcm C.102cm D.202cm5.已知长方体的长2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是( )A.29cm B.5cm C.37cm D.4.5cm6.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )A.8cm B.10cm C.12cm D.15cm7.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为( )米.A.16B.82C.146D.1788.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为( )A.229B.45C.10D.3149.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )A.1089B.505C.120D.13010.如图,圆柱的高为4cm,底面半径为3πcm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是( )cm.A.5B.5πC.3+4πD.3+8π二、填空题11.如图,一个长方体盒子的长、宽、高分别为5cm、4cm、3cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是 cm.12.如图所示,一圆柱高AB为2cm,底面直径BC为4cm,一只蚂蚁从点A出发沿圆柱表面爬行到点C,则蚂蚁爬行的最短路程是 cm(π取3).13.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是 cm.14.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为 .15.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 cm.16.如图所示,有一个正方体盒子,其棱长为2dm,一只虫子在顶点A处,一只蜘蛛在顶点B 处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,它所走的最短路程是 dm.(结果保留根号)17.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24cm.则蚂蚁爬行的最短距离为 cm.18.如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C'处,若长方体的长AB=4cm,宽BC=2cm,高BB'=1cm,则蚂蚁爬行的最短路径长是 .三、解答题19.如图,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)20.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?21.如图所示,有一个圆柱,底面圆的直径AB=16,高BC=12cm,在BC的中点P处有一块π蜂蜜,聪明的蚂蚁总能找到距离食物的最短路径,求蚂蚁从A点爬到P点的最短距离.22.如图,长方体的长为20cm,宽为10cm,高为15cm,点B与点C之间的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖.(1)求出点A到点B的距离;(2)求蚂蚁从点A爬到点B的最短路程是多少?23.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上底面距离为4cm 的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为多少?24.如图所示,一个无盖四棱柱容器,其底面是一个边长为3cm的正方形,高为20cm.现有一根彩带,从底面A点开始缠绕四棱柱,刚好缠绕4周到达B点(假设彩带完美贴合四棱柱).(1)请问彩带的长度是多少?(2)如图所示,一只蚂蚁在容器外A点发现容器的内部距离顶部2cm处有一滴蜂蜜,它想以最短的路程到达C处.请问蚂蚁走的最短路程是多少呢?(注:以上两问均要画出平面展开示意图,再解答)答案一、选择题B.D.A.D.B.D.B.C.B.A.二、填空题11.74.12.6.13.285.14.20cm.15.30.16.25.17.65.18.5cm.三、解答题19.如图所示,将圆柱体侧面展开,连接AB,则AB的长即为蜘蛛爬行的最短路程.根据题意得AC=20cm,BC=πR=5π=5×3=15cm,在Rt△ABC中,由勾股定理得AB2=BC2+AC2=152+202=625,所以AB=25cm,即最短路程是25cm.20.如图1,∵AB=18cm,BC=GF=12cm,BF=10cm,∴BM=18﹣6=12,BN=10+6=16,∴MN=122+162=20(cm);如图2,∵AB=18cm,BC=GF=12cm,BF=10cm,∴PM=18﹣6+6=18,NP=10,∴MN=182+102=2106(cm).如图3中,MN =222+62=2130(cm ),∵20<2106<2130,∴蚂蚁沿长方体表面爬到米粒处的最短距离为20cm .21.将圆柱体的侧面展开,如图所示:AB =12底面周长=12×π×16π=8(cm ),AP =12BC =6(cm ),所以AP =82+62=10(cm ),故蚂蚁从A 点爬到P 点的最短距离为10cm .22.(1)将长方体沿CF 、FG 、GH 剪开,向右翻折,使面FCHG 和面ADCH 在同一个平面内,连接AB ,如图1,由题意可得:BD=BC+CD=5+10=15cm,AD=CH=15cm,在Rt△ABD中,根据勾股定理得:AB=BD2+AD2=152+152=152cm;将长方体沿DE、EF、FC剪开,向上翻折,使面DEFC和面ADCH在同一个平面内,连接AB,如图2,由题意得:BH=BC+CH=5+15=20cm,AH=10cm,在Rt△ABH中,根据勾股定理得:AB=BH2+AH2=202+102=105cm,则需要爬行的最短距离是152cm.连接AB,如图3,由题意可得:BB′=B′E+BE=15+10=25cm,AB′=BC=5cm,在Rt△AB′B中,根据勾股定理得:AB=BB′2+AB′2=252+52=526cm,综上所述,点A到点B的距离为:152cm,105cm,526cm;(2)由(1)知,∵点A到点B的距离为:152cm,105cm,526cm;∴152<105<526,∴则需要爬行的最短距离是152cm.23.如图:将圆柱展开,EG为上底面圆周长的一半,作A关于E的对称点A',连接A'B交EG于F,则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF 的长,即AF+BF=A'B=20cm,延长BG,过A'作A'D⊥BG于D,∵AE=A'E=DG=4cm,∴BD=16cm,Rt△A'DB中,由勾股定理得:A'D=202―162=12(cm),则该圆柱底面周长为24cm.24.(1)如图,将长方体的侧面沿AB展开,取A′B′的四等分点C、D、E,取AB的四等分点C′、D′、E′,连接B′E′,D′E,C′D,AC,则AC+C′D+D′E+E′B′=4AC为所求的最短细线长,∵AC2=AA′2+A′C2,AC=122+52=13,∴AC+C′D+D′E+E′B′=4AC=52,答:彩带的长度是52cm;(2)如图,将四棱柱展开,找到C的对称点C′,连接AC′,则AC′即为蚂蚁走的最段路程,在直角△AMC中,AM=6cm,MC′=20+(20﹣18)=22cm,由勾股定理得:AC′2=AM2+MC′2=62+222=520,则AC′=2130cm,答:蚂蚁走的最短路程是2130cm.。
勾股定理之最短路径(填空选择)中考题

实用文案一、选择题(共17小题)1、(2011•广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A、B、5cmC、D、7cm2、(2009•乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为()A、B、2C、3D、33、(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A、5B、25C、10+5D、354、(2005•山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是()A、40cmB、20cmC、20cmD、10cm5、(2005•贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A、6cmB、12cmC、13cmD、16cm6、(2004•淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是()A、(3+2)cmB、cmC、cmD、cm7、(2004•梅州)如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为()A、 aB、(1+)aC、3aD、 a8、(2004•济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是()A、B、3C、5D、9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是()A、12cmB、10cmC、14cmD、无法确定10、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约()A、10cmB、12cmC、19cmD、20cm11、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是()A、8B、2C、2D、2+212、如图所示,是一个圆柱体,ABCD是它的一个横截面,AB=,BC=3,一只蚂蚁,要从A点爬行到C点,那么,最近的路程长为()A、7B、C、D、513、如图是一个长4m,宽3m,高2m的有盖仓库,在其内壁的A处(长的四等分)有一只壁虎,B处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为()A、4.8B、C、5D、14、有一长、宽、高分别是5cm,4cm,3cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为()A、5cmB、cmC、4cmD、3cm15、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是()A、3B、C、D、116、如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为()A、3米B、4米C、5米D、6米17、如图,在棱长为20cm的正方体盒子上有一只蚂蚁欲从A点出发向B爬去吃食,则蚂蚁所走最短路程是()A、40cmB、20cmC、20cmD、20cm二、填空题(共13小题)18、(2007•呼伦贝尔)如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是_________ m.(结果不取近似值)19、(2007•怀化)如图所示的圆柱体中底面圆的半径是,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是_________ .(结果保留根号)20、(2007•金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC 的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为_________ .21、(2007•梅州)如图,有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至A1(A,A1在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是_________ .22、(2008•昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是_________ cm.(π取3)23、(2008•青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是_________ cm(结果用带根号和π的式子表示).24、(2009•青岛)如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要_________ cm;如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要_________ cm.25、(2011•荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为_________ cm.26、(2006•茂名)如图,点A、B分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A沿其表面爬到点B 的最短路程是_________ .27、(2005•青海)如图,已知正方体的棱长为2,则正方体表面上从A点到C1点的最短距离为_________ .28、(2003•泸州)如图,一只昆虫要从边长为acm的正方体盒子的一个顶点爬到相距最远的另一个顶点,沿盒子表面爬行的最短路程是_________ cm.29、如图,有一圆柱,其高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为_________ cm.(π取3)30、一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是_________ .答案与评分标准一、选择题(共17小题)1、(2011•广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A、B、5cmC、D、7cm考点:平面展开-最短路径问题。
(完整版)勾股定理--最短距离问题
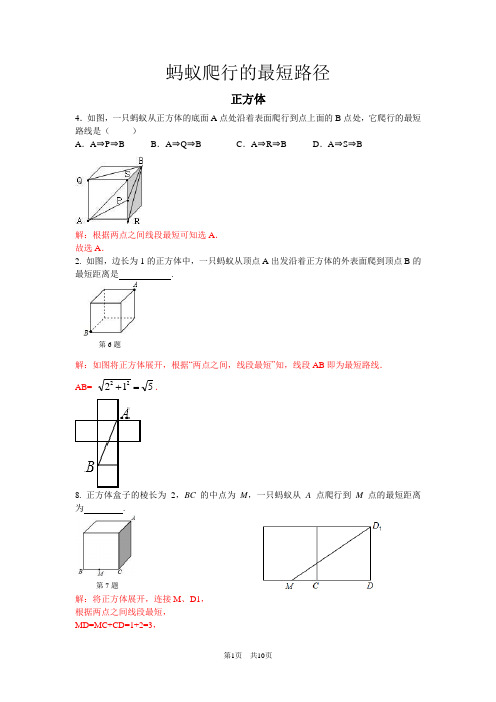
蚂蚁爬行的最短路径正方体4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒ B解:根据两点之间线段最短可知选A . 故选A .2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线. AB=51222=+.8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D1, 根据两点之间线段最短, MD=MC+CD=1+2=3,第6题第7题AB121MD 1=132322212=+=+DD MD .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB= ()1012122=++.故选C .9.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB= = cm ;(2)展开底面右面由勾股定理得AB==5cm ;所以最短路径长为5cm ,用时最少:5÷2=2.5秒.长方体10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
解:将长方体展开,连接A 、B ,根据两点之间线段最短,AB==25.A B A 1B 1D CD 1C 121411. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为 .解:正面和上面沿A 1B 1展开如图,连接AC 1,△ABC 1是直角三角形, ∴AC 1=()5342142222212=+=++=+BC AB18.(2011•荆州)如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂奴爬行的最短路径长为 cm .解:∵PA=2×(4+2)=12,QA=5 ∴PQ=13.故答案为:13.19.如图,一块长方体砖宽AN=5cm ,长ND=10cm ,CD 上的点B 距地面的高BD=8cm ,地面上A 处的一只蚂蚁到B 处吃食,需要爬行的最短路径是多少?解:如图1,在砖的侧面展开图2上,连接AB , 则AB 的长即为A 处到B 处的最短路程.解:在Rt △ABD 中,因为AD=AN+ND=5+10=15,BD=8, 所以AB 2=AD 2+BD 2=152+82=289=172. 所以AB=17cm .故蚂蚁爬行的最短路径为17cm .49、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?12.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
最新中考专题研究用勾股定理解决最短路线问题
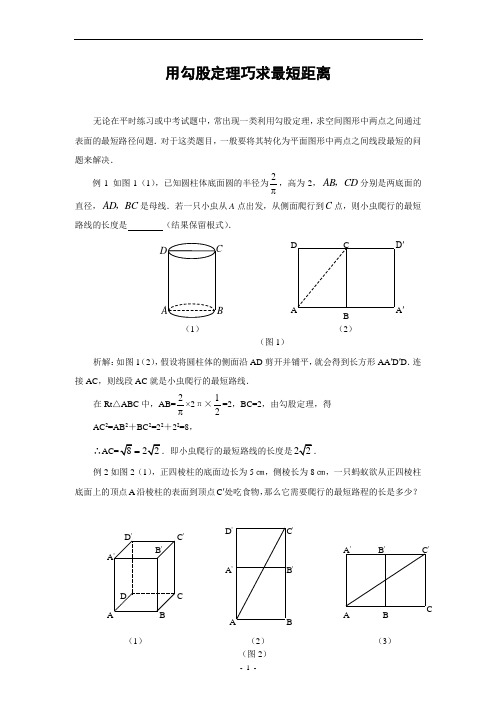
用勾股定理巧求最短距离无论在平时练习或中考试题中,常出现一类利用勾股定理,求空间图形中两点之间通过表面的最短路径问题.对于这类题目,一般要将其转化为平面图形中两点之间线段最短的问题来解决.例1 如图1(1),已知圆柱体底面圆的半径为2π,高为2,AB CD ,分别是两底面的直径,AD BC ,是母线.若一只小虫从A 点出发,从侧面爬行到C 点,则小虫爬行的最短路线的长度是 (结果保留根式).析解:如图1(2),假设将圆柱体的侧面沿AD 剪开并铺平,就会得到长方形AA ′D ′D .连接AC ,则线段AC 就是小虫爬行的最短路线.在Rt △ABC 中,AB=2π×2π×21=2,BC=2,由勾股定理,得 AC 2=AB 2+BC 2=22+22=8,∴=例2如图2(1),正四棱柱的底面边长为5㎝,侧棱长为8㎝,一只蚂蚁欲从正四棱柱底面上的顶点A 沿棱柱的表面到顶点C ′处吃食物,那么它需要爬行的最短路程的长是多少?B(1) (2) (图1)D′A ′D C BA DCBAD 'C 'B 'A 'CBAC 'B 'A '(1) (2) (3)(图2)BAD ' C 'B 'A '分析:由题可知,沿正四棱柱的表面从A到C′的走法有两大类:过底面或过侧面.由对称性知只需考虑两种情况:(1)沿面A′AB到面A′B′C′;(2)沿面A′AB到面B′BC.将立体图形转化为平面图形后,由两点之间线段最短确定最短路线。
解:(1)沿底边A′B′,将底面A′B′C′和侧面A′AB展开如图2(2),连接AC′,则AC′就是蚂蚁走的最短路线.在Rt△ABC′中,AB=5,BC′=BB′+B′C′=8+5=13,由勾股定理,得AC′ 2=AB2+B′C′ 2=52+132=194,∴AC′(2)沿侧棱BB′,将侧面A′AB和侧面B′BC展开如图2(3),连接AC′,则AC′就是蚂蚁走的最短路线.在Rt△ACC′中,AC=AB+BC=5+5=10,CC′=8,由勾股定理,得AC′ 2=AC2+CC′ 2=102+82=164,∴AC′==∴蚂蚁需要爬行的最短路程的长是点评:在将空间图形中最短路径问题转化为平面图形问题来解决的同时,还必须全方位考虑各种可能性,只有这样才能得到正确的答案.用勾股定理解决最短路线问题行程最短问题是日常生活中常见的问题之一,其解法一般要用到勾股定理,现举几例如下:例1 如图1,学校有一块长方形花铺,有极少数人从A 走到B ,为了避开拐角C 走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.分析:由图可见,走出来的“路”是直角边分别为3m和4m的直角三角形的斜边,由勾股定理,得该“路”的长为5m,因此,行人仅仅少走了2米(即10步)路.【点评】爱护花草人人有责,仅仅因为少走10步而不惜踩伤花草,破坏环境的确是大不应该的。
勾股定理--最短距离问题蚂蚁爬行的最短路径

1A B A 1B 1DCD 1C 124勾股定理--最短距离问题蚂蚁爬行的最短路径正方体1.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .3. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .4.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
10题 11 12 1311. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),蚂蚁到B 处吃食,需要爬行的最短路径是多少?14、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?15.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
1514 16 17 第2题 第3题 ABCD.1283016.如图,直四棱柱侧棱长为4cm ,底面是长为5cm 宽为3cm 的长方形.一只蚂蚁从顶点A 出发沿棱柱的表面爬到顶点B .求:(1)蚂蚁经过的最短路程;(2)蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.17.如图,长方体的长、宽、高分别为6cm ,8cm ,4cm .一只蚂蚁沿着长方体的表面从点A 爬到点B .则蚂蚁爬行的最短路径的长是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理之最短路径(填空选择)中考题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、选择题(共17小题)1、(2011•广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC 上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A、B、5cmC、D、7cm2、(2009•乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为()A、B、2C、3D、33、(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A、5B、25C、10+5D、354、(2005•山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是()A、40cmB、20cmC、20cmD、10cm5、(2005•贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A、6cmB、12cmC、13cmD、16cm6、(2004•淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是()A、(3+2)cmB、cmC、cmD、cm7、(2004•梅州)如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为()A、 aB、(1+)aC、3aD、 a8、(2004•济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是()A、B、3C、5D、9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是()A、12cmB、10cmC、14cmD、无法确定10、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约()A、10cmB、12cmC、19cmD、20cm11、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是()A、8B、2C、2D、2+212、如图所示,是一个圆柱体,ABCD是它的一个横截面,AB=,BC=3,一只蚂蚁,要从A点爬行到C点,那么,最近的路程长为()A、7B、C、D、513、如图是一个长4m,宽3m,高2m的有盖仓库,在其内壁的A处(长的四等分)有一只壁虎,B处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为()A、4.8B、C、5D、14、有一长、宽、高分别是5cm,4cm,3cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为()A、5cmB、cmC、4cmD、3cm15、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是()A、3B、C、D、116、如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为()A、3米B、4米C、5米D、6米17、如图,在棱长为20cm的正方体盒子上有一只蚂蚁欲从A点出发向B爬去吃食,则蚂蚁所走最短路程是()A、40cmB、20cmC、20cmD、20cm二、填空题(共13小题)18、(2007•呼伦贝尔)如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是_________m.(结果不取近似值)19、(2007•怀化)如图所示的圆柱体中底面圆的半径是,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是_________.(结果保留根号)20、(2007•金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A 处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为_________.21、(2007•梅州)如图,有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A 至A1(A,A1在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是_________.22、(2008•昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A 点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是_________cm.(π取3)23、(2008•青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是_________ cm(结果用带根号和π的式子表示).24、(2009•青岛)如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要_________cm;如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要_________cm.25、(2011•荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为_________cm.26、(2006•茂名)如图,点A、B分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A沿其表面爬到点B的最短路程是_________.27、(2005•青海)如图,已知正方体的棱长为2,则正方体表面上从A点到C1点的最短距离为_________.28、(2003•泸州)如图,一只昆虫要从边长为acm的正方体盒子的一个顶点爬到相距最远的另一个顶点,沿盒子表面爬行的最短路程是_________cm.29、如图,有一圆柱,其高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为_________cm.(π取3)30、一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是_________.24.(本小题10分)问题探究:(1)如图①所示是一个半径为32π,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形ABB A′′,则蚂蚁爬行的最短路程即为线段AB′的长)(2)如图②所示是一个底面半径为23,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.(3)如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.答案与评分标准一、选择题(共17小题)1、(2011•广安)如图,圆柱的底面周长为6cm ,AC 是底面圆的直径,高BC=6cm ,点P 是母线BC 上一点,且PC=BC .一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是( )A 、B 、5cmC 、D 、7cm考点:平面展开-最短路径问题。
分析:首先画出圆柱的侧面展开图,根据高BC′=6cm ,PC=BC ,求出PC′=×6=4cm ,在Rt △AC′P 中,根据勾股定理求出AP 的长.解答:解:侧面展开图如图所示,∵圆柱的底面周长为6cm ,∴AC′=3cm ,∵PC′=BC′,∴PC′=×6=4cm ,B A A ' B ′ 图① A ' P A 图② P A 图③(第24在Rt△ACP中,AP2=AC′2+CP2,∴AP==5.故选B.点评:此题主要考查了平面展开图,以及勾股定理的应用,做题的关键是画出圆柱的侧面展开图.2、(2009•乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为()A、B、2C、3D、3考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.解答:解:由题意知,底面圆的直径AB=4,故底面周长等于4π.设圆锥的侧面展开后的扇形圆心角为n°,根据底面周长等于展开后扇形的弧长得4π=,解得n=120°,所以展开图中∠APD=120°÷2=60°,因为半径PA=PA′,故三角形PAA′为等腰三角形,又∵D为AA′的中点,所以PD⊥AA′,在直角三角形PAD中,PA=6,PD=3,根据勾股定理求得AD=3,所以蚂蚁爬行的最短距离为3.故选C.点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.3、(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A、5B、25C、10+5D、35考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.解答:解:将长方体展开,连接A、B,根据两点之间线段最短,BD=10+5=15,AD=20,由勾股定理得:AB====25.故选B.点评:本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.4、(2005•山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是()A、40cmB、20cmC、20cmD、10cm考点:平面展开-最短路径问题。
分析:由平面图形的折叠及立体图形的表面展开图的特点解题.解答:解:根据两点之间线段最短,把正方体展开,可知由A处向B处爬行,所走的最短路程是20cm.故选C.点评:熟练掌握两点之间线段最短这一性质.5、(2005•贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A、6cmB、12cmC、13cmD、16cm考点:平面展开-最短路径问题。
