PID电动机转速控制与显示
基于单神经元PID的异步电动机转速的自适应控制
Ａｄ ａ ｐ ｔ ｉ ｖ ｅ Ｓｐ ｅ ｅ ｄ Ｃｏ ｎ ｔ ｒ ｏ ｌ ｏ ｆ Ａｓ ｙ ｎ ｃ ｈ ｒ ｏ ｎ ｏ ｕ ｓ Ｍｏ ｔ ｏ ｒ Ｂａ ｓ ｅ ｄ ｏ ｎ Ｓｉ ｎ ｇ ｌ ｅ Ｎｅ ｕ ｒ ｏ ｎ ＰＩ Ｄ
Ｙ Ａ Ｎ Ｇ Ｙ ｏ ｕ — ｌ ｉ ｎ ． ｗｕ Ｑ ｉ ｎ ｇ — ｈ ｕ ｉ （ Ｃ ｏ ｌ ｌ ｅ ｇ ｅ ｏ ｆＥ ｎ ｇ ｉ ｎ ｅ ｅ ｒ ｉ ｎ ｇ ， Ｂ ｏ ｈ ａ ｉ Ｕ ｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ ， Ｊ ｉ ｎ ｚ ｈ ｏ ｕ Ｌ ｉ ａ ｏ ｎ ｉ ｎ ｇ １ ２ １ ０ １ ３ ， Ｃ ｈ ｉ ｎ ａ ）
Ｋｅ ｙ ｗｏ ｒ ｄ ｓ ： ａ ｓ ｙ ｎ ｃ ｈ ｒ ｏ ｎ ｏ ｕ ｓ ｍｏ ｔ ｏ ｒ ；ｍｏ ｔ ｏ ｒ ｓ ｐ ｅ ｅ ｄ；ｖ ｅ ｃ ｔ ｏ ｒ ｃ ｏ ｎ ｔ ｒ ｏ ｌ ；ｓ ｉ ｎ ｇ ｌ ｅ ｎ ｅ ｕ ｒ ｏ ｎ；ｌ ｅ ａ ｒ ｎ ｉ ｎ ｇ ａ ｌ ｇ ｏ ｒ ｉ ｔ ｈ ｍ；ａ ｄ ａ ｐ ｔ ｉ ｖ ｅ ｃ ｏ ｎ ｔ ｒ ｏ ｌ
电机控制系统中的电机速度PID控制
电机控制系统中的电机速度PID控制电机控制系统中的电机速度PID控制在工业自动化领域中扮演着重要的角色。
PID控制器是指比例积分微分控制器，通过调整这三个参数来实现对电机速度的精准控制。
本文将分析电机控制系统中电机速度PID控制的原理、优势以及应用。
1. 原理PID控制器是通过测量电机转速与期望转速之间的误差，根据比例、积分、微分这三个参数计算出控制电机所需的输出信号。
比例项（P）是误差的比例增益，积分项（I）是误差的积分增益，而微分项（D）是误差的微分增益。
通过这三个参数的调节，电机的运行速度可以得到准确控制，实现闭环反馈。
2. 优势使用PID控制器进行电机速度控制具有以下优势：- 精准度高：PID控制系统具有快速响应速度和稳定性，能够精确控制电机速度。
- 调节方便：PID控制器的三个参数可以根据实际情况进行调节，适用于不同的电机控制需求。
- 适用性广：PID控制器在工业自动化控制中广泛应用，适用于各种类型的电机控制系统。
3. 应用电机控制系统中的电机速度PID控制被广泛应用于各种场景，包括但不限于以下几个方面：- 电动汽车：在电动汽车中，PID控制器可以用于控制电动机的转速，提高电动汽车的驾驶性能和节能性。
- 工业机械：在工业机械中，PID控制器可以用于控制各种类型的电机，实现生产线自动化运行。
- 机器人：在机器人领域，PID控制器可以用于控制机器人臂的运动速度，实现精准操作和抓取。
综上所述，电机控制系统中的电机速度PID控制是一种高效、精准的控制方法，具有广泛的应用前景。
随着工业自动化技术的不断发展，PID控制器将继续发挥重要作用，推动工业生产的进步与优化。
用PID调节优化电机驱动系统的效率和精度
用PID调节优化电机驱动系统的效率和精度PID调节是一种常用的控制策略，可用于优化电机驱动系统的效率和精度。
本文将介绍PID调节的原理和应用，并探讨其在电机驱动系统中的具体应用案例。
一、PID调节的原理PID调节是一种基于反馈控制的方法，通过不断调整输出信号，使系统的实际输出与期望输出之间达到最优的差距。
PID控制器由比例（P）、积分（I）和微分（D）三个部分组成。
1. 比例（Proportional）部分：根据误差的大小决定输出信号的变化幅度。
比例控制主要用于快速响应系统变化，并减小稳态误差。
2. 积分（Integral）部分：根据误差的累积值决定输出信号的变化幅度。
积分控制主要用于消除系统的静态误差。
3. 微分（Derivative）部分：通过计算误差变化率来调整输出信号的变化速度。
微分控制主要用于抑制系统的震荡和提高系统的稳定性。
通过合理地调节PID控制器的参数，可以使系统达到期望的效果，并提高系统的响应速度、稳定性和精度。
二、PID调节在电机驱动系统中的应用电机驱动系统是一种常见的控制系统，PID调节在其中被广泛应用。
下面将以直流电机驱动系统为例，介绍PID调节在电机驱动中的应用。
1. 速度控制直流电机的转速控制是电机驱动系统的重要任务之一。
PID调节可用于实时调整电机的驱动信号，使电机达到期望的转速。
控制器根据电机实际转速与期望转速之间的差异，不断调整输出信号，实现电机转速的精确控制。
2. 位置控制除了速度控制，PID调节还可用于电机的位置控制。
通过控制电机的驱动信号，使电机在给定的位置上停止或定位到指定位置。
控制器根据电机实际位置与期望位置之间的差异，调整输出信号，实现电机位置的精确控制。
3. 力矩控制在某些应用中，需要通过控制电机的力矩来实现特定的任务。
PID 调节可用于调整电机的驱动信号，使电机输出期望的力矩。
控制器根据电机实际输出力矩与期望输出力矩之间的差异，调整输出信号，实现电机力矩的精确控制。
pid算法控制电机转速原理
pid算法控制电机转速原理英文回答：Proportional-integral-derivative (PID) control is a widely used control algorithm in industrial automation and robotics. It is used to control the speed of electric motors by adjusting the motor's input voltage or current based on the difference between the desired speed and the actual speed.The PID controller consists of three terms:Proportional (P) term: This term is proportional to the error between the desired speed and the actual speed. It provides a quick response to changes in the error.Integral (I) term: This term is proportional to the integral of the error over time. It helps to eliminate steady-state error, which is the difference between the desired speed and the actual speed when the error is zero.Derivative (D) term: This term is proportional to the derivative of the error with respect to time. It helps to predict future changes in the error and provides a faster response.The PID controller gains (Kp, Ki, and Kd) are tuned to optimize the control performance. The tuning process involves finding the values of the gains that provide the desired response, such as fast settling time, minimal overshoot, and good stability.Here is a block diagram of a PID controller used to control the speed of an electric motor:[Block diagram of a PID controller]The reference input is the desired speed, and the feedback input is the actual speed. The error is the difference between the reference and feedback inputs. The PID controller calculates the output voltage or current based on the error and the gains. The output is thenapplied to the motor to control its speed.中文回答：PID算法控制电机转速原理。
电机控制进阶2——PID位置控制
电机控制进阶2——PID位置控制描述上篇文章讲解了电机的速度环控制，可以控制电机快速准确地到达指定速度。
本篇来介绍电机的位置环控制，实现电机快速准确地转动到指定位置。
1 位置控制与速度控制的区别回顾上篇，电机速度PID控制的结构图如下，目标值是设定的速度，通过编码器获取电机的转速作为反馈，实现电机转速的控制。
再来看电机位置PID控制，其结构图如下，目标值是设定的位置，通过编码器获取电机累计转动的脉冲数作为反馈，实现电机位置的控制。
所以：对比两张图，速度控制与位置控制的主要区别，就是控制量的不同。
2 核心程序了解了速度控制与位置控制的区别后，下面就可以修改程序。
2.1 编码器相关2.1.1 电机与编码器参数编码器部分，需要根据自己电机的实际参数进行设定，比如我用到的电机：编码器一圈的物理脉冲数为11定时器编码器模式通过设置倍频来实现4倍频电机的减速齿轮的减速比为1：34所以，电机转一圈总的脉冲数，即定时器能读到的脉冲数为11*4*34= 1496。
#define ENCODER_RESOLUTION 11 /*编码器一圈的物理脉冲数*/ #define ENCODER_MULTIPLE 4 /*编码器倍频，通过定时器的编码器模式设置*/ #define MOTOR_REDUCTION_RATIO 34 /*电机的减速比*/ /*电机转一圈总的脉冲数(定时器能读到的脉冲数) = 编码器物理脉冲数*编码器倍频*电机减速比*/ /* 11*4*34= 1496*/ #define TOTAL_RESOLUTION ( ENCODER_RESOLUTION*ENCODER_MULTIPLE*MOTOR_REDUC TION_RATIO )想要了解更多关于编码器的使用，可参照之前的文章: ( /d/1639052.html )2.1.2 定时器编码器模式配置用于编码器捕获的定时器的一些宏定义。
#define ENCODER_TIM_PSC 0/*计数器分频*/#define ENCODER_TIM_PERIOD 65535/*计数器最大值*/#define CNT_INIT 0/*计数器初值*/配置主要关注重装载值，倍频，溢出中断设置。
直流无刷电机转速控制
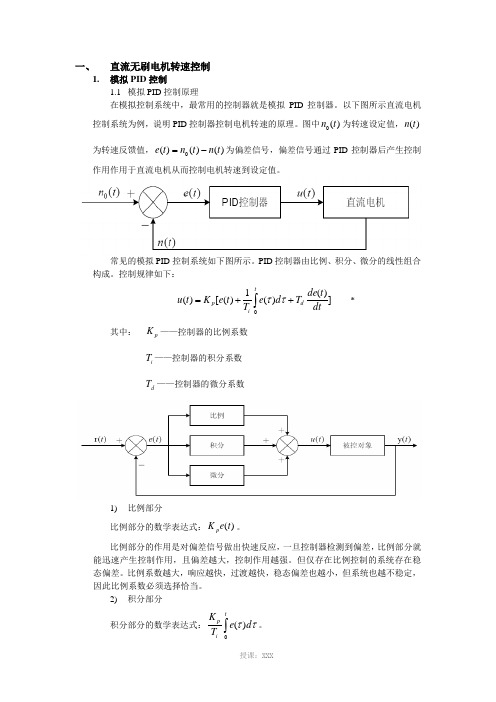
一、 直流无刷电机转速控制1. 模拟PID 控制1.1 模拟PID 控制原理在模拟控制系统中，最常用的控制器就是模拟PID 控制器。
以下图所示直流电机控制系统为例，说明PID 控制器控制电机转速的原理。
图中)(0t n 为转速设定值，)(t n 为转速反馈值，)()()(0t n t n t e -=为偏差信号，偏差信号通过PID 控制器后产生控制作用作用于直流电机从而控制电机转速到设定值。
常见的模拟PID 控制系统如下图所示。
PID 控制器由比例、积分、微分的线性组合构成。
控制规律如下：])()(1)([)(0⎰++=td i p dtt de T d e T t e K t u ττ *其中： p K ——控制器的比例系数 i T ——控制器的积分系数d T ——控制器的微分系数1) 比例部分比例部分的数学表达式：)(t e K p 。
比例部分的作用是对偏差信号做出快速反应，一旦控制器检测到偏差，比例部分就能迅速产生控制作用，且偏差越大，控制作用越强。
但仅存在比例控制的系统存在稳态偏差。
比例系数越大，响应越快，过渡越快，稳态偏差也越小，但系统也越不稳定，因此比例系数必须选择恰当。
2) 积分部分积分部分的数学表达式：⎰tip d e T K 0)(ττ。
从积分部分表达式可以看出，只要系统输出与设定值存在偏差，积分作用就会不断增加，知道偏差为零，因此积分部分可以消除稳态偏差。
但积分作用会降低系统的响应速度，增加系统的超调量。
积分常数越小，积分作用越强，过渡过程容易产生震荡，但回复时间减小；积分常数越大，积分作用越弱，过渡过程不产生震荡，但回复时间增长。
因此应根据具体情况选取积分常数。
3) 微分部分微分部分的数学表达式： dtt de T K dp )(。
微分作用能阻值偏差的变化。
它根据偏差的变化趋势进行控制。
偏差变化越快，微分作用越强，能在偏差变化之前就行控制。
微分作用的引入有助于减小超调量，克服振荡；但微分作用对噪声很敏感，导致系统的错误响应，使系统不稳定。
变频器的PID控制运行操作
变频器的PID控制运行操作一、背景介绍变频器是一种能够控制电机转速的调节装置，通过改变电源的频率来改变电机的转速。
PID控制是一种常用的自动控制方法，可以对变频器进行精确的转速控制。
PID控制器由比例（P）、积分（I）和微分（D）三个控制参数组成，通过对这些参数的调整可以实现准确的速度控制。
二、PID控制的原理PID控制器通过测量物理过程的输出（变频器的转速）与期望的输入（设定的转速）之间的误差来调整输出信号，从而使物理过程的输出尽可能地接近期望的输入。
具体来说，PID控制器实时计算输出信号，其计算公式为：输出信号=Kp×误差+Ki×积分（误差）+Kd×微分（误差）其中，Kp、Ki和Kd分别为比例、积分和微分参数，需要根据具体的应用进行调整。
三、PID控制在变频器中的实现1.设定转速：首先需要通过变频器的控制面板或者计算机软件设定期望的转速，将该值作为PID控制的目标输入。
2.传感器测量：使用传感器实时测量变频器的转速，将测量值作为PID控制的实际输出。
3.计算误差：将目标输入与实际输出进行比较，计算出PID控制需要的误差值。
4.控制器计算输出信号：根据PID控制的公式，通过调整参数Kp、Ki和Kd计算出控制器的输出信号。
5.输出信号传递：将控制器的输出信号传递给变频器，用于调节电源的频率，从而实现转速的控制。
6.参数调整：根据实际应用的需要，对PID控制器的参数进行调整，以提高控制的稳定性和精度。
7.循环控制：PID控制器会根据实时的误差值进行不断的计算和调整，以实现持续的转速控制。
四、PID控制在变频器中的优势1.高精度稳定性：PID控制器能够根据实时的误差值进行精确的调整，从而实现高精度的转速控制，提高了系统的稳定性。
2.快速响应：PID控制器能够快速地根据实时的误差值进行调整，从而具有快速的控制响应能力，适用于需要实时控制的场景。
3.鲁棒性：PID控制器具有较强的鲁棒性，对系统参数的变化和外部扰动具有一定的适应能力，能够保持较好的控制效果。
发动机传动电机的转速控制BPPID
文档从互联网中收集，已重新修正排版，word格式支持编辑，如有帮助欢迎下载支持。
目录一、设计题目······································································································错误!未定义书签。
二、系统的工作原理 ··························································································错误!未定义书签。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
PID 电动机转速控制与显示摘要：在运动控制系统中，电机转速控制占有至关重要的作用。
本文以A T89S51单片机为控制核心，产生占空比受数字PID 算法控制的PWM 脉冲实现对直流电机转速的控制。
同时利用光电传感器将电机速度转换成脉冲频率反馈到单片机中，实现转速闭环控制，达到转速无静差调节的目的。
在系统中采128×64LCD 显示器作为显示部件，通过4×4键盘设置P 、I 、D 、V 四个参数和正反转控制，启动后可以通过显示部件了解电机当前的转速和运行时间。
该系统控制精度高，具有很强的抗干扰能力。
关键词：数字PID ；PWM 脉冲；占空比；无静差调节1．PID 控制技术简介1.1 PID 算法控制算法是微机化控制系统的一个重要组成部分，整个系统的控制功能主要由控制算法来实现。
目前提出的控制算法有很多。
根据偏差的比例（P ）、积分（I ）、微分（D ）进行的控制，称为PID 控制。
实际经验和理论分析都表明，PID 控制能够满足相当多工业对象的控制要求，至今仍是一种应用最为广泛的控制算法之一。
下面分别介绍模拟PID 、数字PID 及其参数整定方法。
1.1.1 模拟PID在模拟控制系统中，调节器最常用的控制规律是PID 控制，常规PID 控制系统原理框图如图1.1所示，系统由模拟PID 调节器、执行机构及控制对象组成。
图1.1 模拟PID 控制系统原理框图PID 调节器是一种线性调节器，它根据给定值)(t r 与实际输出值)(t c 构成的控制偏差： )(t e =)(t r －)(t c （1.1）将偏差的比例、积分、微分通过线性组合构成控制量，对控制对象进行控制，故称为PID 调节器。
在实际应用中，常根据对象的特征和控制要求，将P 、I 、D 基本控制规律进行适当组合，以达到对被控对象进行有效控制的目的。
例如，P 调节器，PI 调节器，PID 调节器等。
模拟PID 调节器的控制规律为])()(1)([)(0dtt de T dt t e T t e K t u D t I p ++=⎰ （1.2）式中，P K 为比例系数，I T 为积分时间常数，D T 为微分时间常数。
简单的说，PID 调节器各校正环节的作用是：（1）比例环节：即时成比例地反应控制系统的偏差信号)(t e ,偏差一旦产生，调节器立即产生控制作用以减少偏差；（2）积分环节：主要用于消除静差，提高系统的无差度。
积分作用的强弱取决于积分时间常数I T ，I T 越大，积分作用越弱，反之则越强；（3）微分环节：能反映偏差信号的变化趋势（变化速率），并能在偏差信号的值变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。
由式1.2可得，模拟PID 调节器的传递函数为)11()()()(S T ST K S E S U S D D I P ++== （1.3） 由于本设计主要采用数字PID 算法，所以对于模拟PID 只做此简要介绍。
1.1.2 数字PID在DDC 系统中，用计算机取代了模拟器件，控制规律的实现是由计算机软件来完成的。
因此，系统中数字控制的设计，实际上是计算机算法的设计。
由于计算机只能识别数字量，不能对连续的控制算式直接进行运算，故在计算机控制系统中，首先必须对控制规律进行离散化的算法设计。
为将模拟PID 控制规律按式（1.2）离散化，我们把图1.1中)(t r 、)(t e 、)(t u 、)(t c 在第n 次采样的数据分别用)(n r 、)(n e 、)(n u 、)(n c 表示，于是式（1.1）变为 ：)(n e =)(n r －)(n c （1.4）当采样周期T 很小时dt 可以用T 近似代替，)(t de 可用)1()(--n e n e 近似代替，“积分”用“求和”近似代替，即可作如下近似T n e n e dt t de )1()()(--≈ （1.5） ⎰∑=≈t n i T i e dt t e 01)()( （1.6） 这样，式（1.2）便可离散化以下差分方程01})]1()([)()({)(u n e n e T T n e T T n e K n u n i D IP +--++=∑= （1.7） 上式中0u 是偏差为零时的初值,上式中的第一项起比例控制作用,称为比例（P ）项)(n u P ,即 )()(n e K n u P p = （1.8）第二项起积分控制作用,称为积分（I ）项)(n u I 即∑==n i IP I i e T T K n u 1)()( （1.9） 第三项起微分控制作用,称为微分（D ）项)(n u D 即 )]1()([)(--=n e n e TT K n u D P D （1.10） 这三种作用可单独使用(微分作用一般不单独使用)或合并使用,常用的组合有:P 控制: 0)()(u n u n u P += （1.11）PI 控制: 0)()()(u n u n u n u I P ++= （1.12）PD 控制: 0)()()(u n u n u n u D P ++= （1.13）PID 控制: 0)()()()(u n u n u n u n u D I P +++= （1.14）式（1.7）的输出量)(n u 为全量输出,它对于被控对象的执行机构每次采样时刻应达到的位置。
因此,式（1.7）又称为位置型PID 算式。
由（1.7）可看出，位置型控制算式不够方便，这是因为要累加偏差)(i e ,不仅要占用较多的存储单元，而且不便于编写程序，为此对式（1.7）进行改进。
根据式（1.7）不难看出u (n -1)的表达式，即011})]2()1([)()1({)1(u n e n e TT n e T T n e K n u n i D I P +---++-=-∑-= （1.15） 将式（1.7）和式（1.15）相减，即得数字PID 增量型控制算式为)1()()(--=∆n u n u n u)]2()1(2)([)()]1()([-+--++--=n e n e n e K n e K n e n e K D I P （1.16）从上式可得数字PID 位置型控制算式为)(n u 0)]2()1(2)([)()]1()([u n e n e n e K n e K n e n e K D I P +-+--++--= （1.17） 式中： P K 称为比例增益；IPI T T K K =称为积分系数； T T K K D P D =称为微分系数[1]。
数字PID 位置型示意图和数字PID 增量型示意图分别如图1.2和1.3所示：图1.2 数字PID 位置型控制示意图图1.3 数字PID 增量型控制示意图1.1.3 数字PID 参数整定方法如何选择控制算法的参数，要根据具体过程的要求来考虑。
一般来说，要求被控过程是稳定的，能迅速和准确地跟踪给定值的变化，超调量小，在不同干扰下系统输出应能保持在给定值，操作变量不宜过大，在系统和环境参数发生变化时控制应保持稳定。
显然，要同时满足上述各项要求是很困难的，必须根据具体过程的要求，满足主要方面，并兼顾其它方面。
PID 调节器的参数整定方法有很多，但可归结为理论计算法和工程整定法两种。
用理论计算法设计调节器的前提是能获得被控对象准确的数学模型，这在工业过程中一般较难做到。
因此，实际用得较多的还是工程整定法。
这种方法最大优点就是整定参数时不依赖对象的数学模型，简单易行。
当然，这是一种近似的方法，有时可能略嫌粗糙，但相当适用，可解决一般实际问题。
下面介绍两种常用的简易工程整定法。
（1）扩充临界比例度法这种方法适用于有自平衡特性的被控对象。
使用这种方法整定数字调节器参数的步骤是：①选择一个足够小的采样周期，具体地说就是选择采样周期为被控对象纯滞后时间的十分之一以下。
②用选定的采样周期使系统工作：工作时，去掉积分作用和微分作用，使调节器成为纯比例调节器，逐渐减小比例度δ（P K /1=δ）直至系统对阶跃输入的响应达到临界振荡状态，记下此时的临界比例度K δ及系统的临界振荡周期k T 。
③选择控制度：所谓控制度就是以模拟调节器为基准，将DDC 的控制效果与模拟调节器的控制效果相比较。
控制效果的评价函数通常用误差平方面积⎰∞02)(t e 表示。
控制度＝模拟])([])([0202⎰⎰∞∞dt t e dt t e DDC（1.18）实际应用中并不需要计算出两个误差平方面积，控制度仅表示控制效果的物理概念。
通常，当控制度为1.05时，就可以认为DDC 与模拟控制效果相当；当控制度为2.0时，DDC 比模拟控制效果差。
④根据选定的控制度，查表1.1求得T 、P K 、I T 、D T 的值[1]。
表1.1 扩充临界比例度法整定参数（2）经验法经验法是靠工作人员的经验及对工艺的熟悉程度，参考测量值跟踪与设定值曲线，来调整P 、I 、D 三者参数的大小的，具体操作可按以下口诀进行：参数整定找最佳，从小到大顺序查；先是比例后积分，最后再把微分加；曲线振荡很频繁，比例度盘要放大；曲线漂浮绕大湾，比例度盘往小扳；曲线偏离回复慢，积分时间往下降；曲线波动周期长，积分时间再加长；曲线振荡频率快，先把微分降下来；动差大来波动慢，微分时间应加长。
下面以PID 调节器为例，具体说明经验法的整定步骤：①让调节器参数积分系数I K =0，实际微分系数D K =0，控制系统投入闭环运行，由小到大改变比例系数P K ，让扰动信号作阶跃变化，观察控制过程，直到获得满意的控制过程为止。
②取比例系数P K 为当前的值乘以0.83，由小到大增加积分系数I K ，同样让扰动信号作阶跃变化，直至求得满意的控制过程。
③积分系数I K 保持不变，改变比例系数P K ，观察控制过程有无改善，如有改善则继续调整，直到满意为止。
否则，将原比例系数P K 增大一些，再调整积分系数I K ，力求改善控制过程。
如此反复试凑，直到找到满意的比例系数P K 和积分系数I K 为止。
④引入适当的实际微分系数D K 和实际微分时间D T ，此时可适当增大比例系数P K 和积分系数I K 。
和前述步骤相同，微分时间的整定也需反复调整，直到控制过程满意为止。
PID 参数是根据控制对象的惯量来确定的。
大惯量如：大烘房的温度控制，一般P 可在10以上,I 在（3、10）之间,D 在1左右。
小惯量如：一个小电机闭环控制，一般P 在（1、10）之间,I 在（0、5）之间,D 在（0.1、1）之间,具体参数要在现场调试时进行修正。
1.2 PWM 脉冲控制技术PWM (Pulse Width Modulation )控制就是对脉冲的宽度进行调制的技术。