分类讨论思想在等腰三角形中的应用
分类讨论思想在确定等腰(直角)三角形顶点位置中的应用
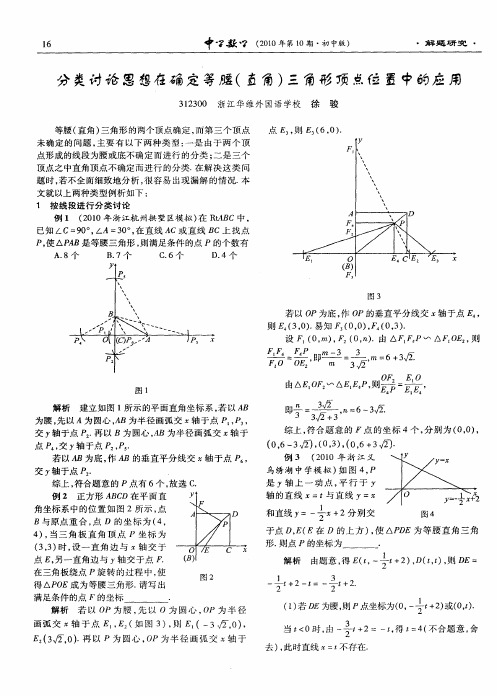
徐
骏
点 E , E ( ,) ,则 , 6 0
F l 、 、
、 、
点形成 的线段为腰或底不确定而进 行的分类 ; 二是三个 顶点之 中直角顶点不确定而进行 的分类. 在解决 这类 问 题时 , 若不全面细致 地分析 , 很容易 出现漏解 的情况. 本
在 三角板绕点 P旋转 的过程 中 , 使
得 AP E成 为等 腰 三 角 形 . 写 出 O 请
图2
一
满 足条件的点 F的坐标
.
— — 一
( ) 舾 为腰 , 尸点 坐标 为 ( , + ) ( 1若 则 0 ~ 1 2或 0
,
解析
若以O P为腰 , 以 0为 圆 心 , P为半 径 先 O
当 <0时 , 一 3z 由 +2
f. )
画弧交 轴于点 E , 如 图 3 , E ( 3 ,) 。E ( )则 。 一 0 ,
= 一 , f 4 不合题意 , z得 = ( 舍
E ( 4 ,)再以 P为圆心 , P为半径 画弧交 轴 于 :3 Y 0 . O
去 ) 此 时 直 线 =t 存 在 . , 不
A8 .个 B 7个 .
y
_ 一
C6 .个
D4 .个
I E
/
爱
D
F
I 璺Ij
E Ct E2
, \
,
j
()
、 、 、 、 、
、 、 、 、
,
若以 D P为底 , O 作 尸的垂直平分线交 轴 于点 E , 4
~ .
/ J
《等腰三角形中分类思想》论文

《等腰三角形中的分类思想》一、教材分析:等腰三角形是九年制义务教育课程标准实验教科书(人教版)八年级上册第十二章“轴对称”第三节的内容。
它是一个特殊的三角形,两腰相等且两底角相等。
它的性质可以用来解决很多几何问题,但也正是因为它有这样的特性,与它相关的问题会因为条件的不确定而出现多解。
因此,在解等腰三角形边、角问题时,常常要运用分类思想。
在等腰三角形复习课中,将分类讨论作为一个专题复习很有必要。
二、学情分析:八年级的学生已经有了一些几何知识的积累,在本节课以前,学生已经学习了有关等腰三角形的一些知识,如等腰三角形的定义,等腰三角形的性质,等腰三角形的判定等。
对于等腰三角形中的分类讨论,有时学生感到似乎比较简单,但要真正完整解答,却并非容易。
学生遇到的最常见问题是漏解,有些同学甚至从初学阶段到最后的复习阶段都反复出现同样的错误。
要解决这一问题,除了认真仔细,更重要的是要学会运用分类思想解等腰三角形边、角问题。
三、教学目标:(一)知识与技能目标:1、培养分类讨论的思想;2、会运用分类讨论的思想来解决等腰三角形有关问题。
(二)过程与方法目标:1、让学生在知识点复习、归纳以及充分的变式训练过程中,体会分类思想;2、在上述过程中,发展学生归纳、概括和有条理表达活动的过程和结论的能力。
(三)情感态度与价值观:1、培养学生积极参与、合作交流的意识;2、在分类讨论的过程中,体验获得结论的快乐,锻炼克服困难的勇气。
四、教学重点:1、了解等腰三角形边、角分类讨论的情况;2、会运用分类思想解等腰三角形边、角问题。
五、教学难点:会运用分类思想解等腰三角形综合题六、教学思路:首先,通过知识点流程图复习等腰三角形边、角有关知识点,让学生明白因为等腰三角形边、角的特殊性,所以在解与它相关问题时常常要分类讨论。
接着,通过变式训练让学生了解等腰三角形边、角分类讨论情况。
最后,让学生学会运用分类思想解等腰三角形边、角综合题。
七、教具准备:内角为110°、20°、50°的三角形纸板、三角板、ppt课件、电脑、投影仪等。
等腰三角形中的分类讨论思想

等腰三角形中的分类讨论思想作者:李贵生来源:《初中生之友·中旬刊》2012年第09期在解决等腰三角形问题时,由于等腰三角形的特殊性,为了解题方便,可以将问题分为不同种类,然后逐类解决,从而达到解决问题的目的,这一思想方法称为分类讨论的思想方法。
下面结合例题介绍分类讨论思想在等腰三角形中的应用,供同学们参考。
一、三角形的形状不确定等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为()A.60°B.120°C.60°或150°D.60°或120°分析根据题意满足条件的三角形可能是锐角三角形,也有可能是钝角三角形。
解(1)当等腰三角形为锐角三角形时,一腰上的高在三角形内部,它与另一腰的夹角为30°,则顶角∠C为60°,如图1—1。
(2)当等腰三角形为钝角三角形时,一腰上的高在腰的延长线上,它与另一腰的夹角为30°,则顶角的补角是60°,顶角的度数为120°,如图1—2。
综上所述,顶角的度数为60°或120°。
故答案选D。
点评因为三角形的形状不确定,因此,所对应的三角形的顶角的度数也就不一样。
二、线段未确定在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有()A.1个B.2个C.3个D.4个分析线段OA可以是底边,也可以是腰。
解如图2所示,若OA为底,则P1(1,0);点评以上解答是按OA为边时的情况讨论,当然也可以按A为顶角的顶点和O为顶角的顶点的情况讨论。
三、角未确定已知等腰三角形的一个角为80°,则它的另外两个角是_______。
分析题目中没有指出80°角是等腰三角形的底角还是顶角,因此,需要分两种情况求解。
四、边未确定已知AD为等腰△ABC的腰BC上的高,∠DAB=60°,求这个三角形内角的度数。
“分类讨论”在等腰三角形中的应用

“分类讨论”在等腰三角形中的应用在最近几年的全国各地中考试卷中,出现了以等腰三角形为背景,考查学生分类讨论能力的试题,为帮助同学们提高对此类问题的解题能力,现列举几例:一、要讨论谁是底边或腰长例1、已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长()A. 12 B 17 C 19 D 17或19分析:题中并未说明5或7是底边,还是腰,应分情况讨论.解:当等腰三角形的一腰长为5时,此时7为底边,满足任意两边之和大于第三边,所以满足题意的三角形的周长为5+5+7=17;当等腰三角形的一腰长为7时,此时5为底边,也满足任意两边之和大于第三边,故满足题意的三角形的周长为7+7+5=19.综上知选D.例2、有一个等腰三角形,三边分别是3x-2,4x-3,6-2x,求等腰三角形的周长.分析:已知等腰三角形三边长,说明有两边相等,但不知谁是腰,必须分三种情况分析.解:(1)当3x-2=4x-3时,即x=1,则三边为1,1,4,由于1+1<4,所以不成立;(2)当3x-2=6-2x时,即85x=,则三边长为141714555、、,由于141417555+>,所以成立;(3)当4x-3=6-2x时,即x=1.5,则三边为2.5,3,3,由于2.5+3>3,所以成立.由上可知等腰三角形周长为9或8.5.说明:如果等腰三角形的腰长为A,底边长为B,则有222b b aa+<<.二、要讨论腰与底谁较大例3、一等腰三角形的周长为20cm,从底边上的一个顶点引腰的中线,分三角形周长为两部分,其中一部分比另一部分长2cm,求腰长.分析:题目中的条件是一部分比另一部分长2cm,这里可能是腰比底长,也可能是底比腰长,应分两种情况讨论,因为是中线,周长分成的两部分之差就是腰长与底边长之差.解:不妨设腰长为x cm,底边长为y cm ,根据题意有(1)当腰长大于底边时,有2220x yx y-=⎧⎨+=⎩,解得221633x y==、;(2)当腰长小于底边时,有2220y xx y-=⎧⎨+=⎩,解得68x y==、;因为两种情形都符合三角形的三边关系定理,故腰长为223cm或6cm.说明:分类讨论后,要用三角形三边关系定理来判断所给三边能否构成三角形,从而避免造成错解.三、要讨论谁是底角或顶角例4、(1)等腰三角形的一个角是30°,求底角.(2)等腰三角形的一个角是100°,求底角.分析:等腰三角形的一个角可能指底角,也可能指顶角,须分情况讨论,但顶角可以是锐有、直角、钝角,而底角只能是锐角.解:(1)当30°是底角时,底角即为30°;当30°是顶角时,底角为180302︒-︒,即为75°;(2)因100°只能是顶角,所以底角是1801002︒-︒,即为40°.说明:等腰三角形的底角只能为锐角,不能为直角、钝角,但顶角可以为锐角、直角、钝角.四、要讨论高在三角形内部或外部例5、已知等腰三角形ABC中,BC边上的高12AD BC=,求∠BAC的度数.分析:题中未交代哪条边是底边,哪条边是腰,所以必须分三种情况讨论.解:(1)当BC为底边时,则D是BC中点,△ABC为等腰直角三角形∠BAC=90°;(2)当BC为腰,且高AD在△ABC内部时,1122AD BC AB==,∠B=30°,所以∠BAC=75°;(3)当BC为腰,且高AD在△ABC的外部时,1122AD BC AB==,∠DBA=30°;所以∠BAC=15°.综上所述∠BAC的度数可以为15°、75°、90°.说明:由于题目的图形未画出,因此考虑情况时要周全,不要出现漏解.试一试:1、在活动课上,小红已有两根长为4cm、8cm的小木棒,现打算拼一个等腰三角形,则小红应取的第三根小木棒长是_____Cm.2、在平面直角坐标系中,已知点为A(-2,0),B(2,0)画出等腰三角形ABC(画出一个即可),并写出你画出的ABC的顶点C的坐标.3、下面是数学课堂的一个学习片段,,阅读后, 请回答下面的问题:学习等腰三角形有关内容后,张老师请同学们交流讨论这样一个问题:“已知等腰三角形ABC的角A等于30°,请你求出其余两角”.同学们经片刻的思考与交流后,李明同学举手说:“其余两角是30°和120°”;王华同学说:“其余两角是75°和75°” ,还有一些同学也提出了不同的看法……(1)假如你也在课堂中,你的意见如何? 为什么?(2)通过上面数学问题的讨论, 你有什么感受? (用一句话表示)“分类讨论”在等腰三角形中的应用当面临的问题不宜用一种方法处理或同一种形式叙述时,我们就要想到“分类讨论”——“分而治之,各个击破”.下面就让“分类讨论”思想在等腰三角形中“大放光彩”吧!例1 等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为()A、60°B、120°C、60°或150°D、60°或120°分析:分两种情况,①当顶角是锐角时,如图1,∵∠ABD=30°,∠ADB=90°,∴∠A=60°;②当顶角是钝角时,如图2,∵∠ABD=30°,∠ADB=90°,∴∠BAD=60°,∴∠BAC =120°.所以顶角度数为60°或120°,所以选D .例2 等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为( ) A 、7 B 、3 C 、5或3 D 、5分析:长为3的边可能是底边,也可能是腰,因此有两种情况,①若长为3的边为底边,则该等腰三角形的底边长为3; ②若长为3的边为腰,则该等腰三角形的底边长为(13-3)÷2=5.故选C .说明:边长为3的边、可能是底边,不要只认为它是腰.例3 已知点A 和点B ,以点A 和点B 为其中两个点作位置不同的等腰直角三角形,一共可以作出( )A 、2个B 、4个C 、6个D 、8个分析:如图3,以线段AB 为底边可作出两个等腰直角三角形,以AB 为腰可作出4个等腰直角三角形,因此,共可作出6个等腰直角三角形,故选C . 说明:解题时容易忽视为腰长的情况,因此,分析问题一定要用心,充分考虑各种情形. 例4 如图4,在等边△ABC 所在的平面内求一点P ,使△P AB 、△PBC 、△P AC 都是的等腰三角形,你能找到几个这样的点?画图描述它们的位置.分析:如图4,△ABC 三条边的垂直平分线的交点1p 满足条件,分别以点A 、点B 为圆心,AB 为半径画圆弧,交AC 的垂直平分线于2p 、3p 两点,则△、、、AC P BC P AB P 222∆∆、、、AC P BC P AB P 333∆∆也是等腰三角形,同样可以在AB 、BC 的垂直平分线上再找到4个点P ,使△P AB 、△PBC 、△P AC 是等腰三角形.所以共有7个点.画出的图形如图4.说明:此题乍一看只能确定在△ABC 内一点,关键要注意三个等腰三角形的腰是哪两条边.分类讨论探究题既是中考热点又是考生易错点,克服方法是解题时常提醒自己:“还有其它情况吗?”切记!…图1B 图2 图3B。
分类思想在等腰三角形中的应用

考 ; 问 过 少 过 疏 , 使 整 个 课 堂 缺 少 师 生 间 的交 流 和 提 则
互 动 , 目不 利 于 教 师 了解 和 调 控 学 生 的 状 态 。 以 , 并 所 课 堂 提 问 要 适 度 适 时 , 不 要 太 多 , 不 要 太 少 , 把 握 好 既 也 要
法 。 要 求 学 生 能 把 某 个 较 为 复 杂 的 问 题 经 过 严 谨 周 密 它
的 思 考 , 定 一 个 分 类 标 准 , 按 同 一 个 标 准 把 它 分 别 确 并
为若 干 类 较 为 简 单 的情 况 ,然 后 逐 一 讨 论 研 究 解 决 , 使 研 究 的结 果 不 重 复 , 遗 漏 , 等 腰 三 角 形 中 由 于 边 。 不 而 角
张 , 易 造 成 学 生 的 疲 劳 和 不 耐 烦 , 利 于 学 生 深 入 思 容 不
位 学 生 的 微 妙 变 化 , 过 信 息 反 馈 , 捉 那 些 容 易 被 通 捕
ቤተ መጻሕፍቲ ባይዱ
忽 视 的 思 想 浪 花 , 过 不 同 层 次 的 问题 , 动 起 全 体 学 通 调 生的学 习兴趣 , 每个 学 生都能得 到提 高 。 使
等 角 对 等 边 。“ 线 合 一 ” 。 三 等 师 : 好 。 了进 一 步 认 识 和 研 究 它 , 想 请 一 名 同 很 为 我 学 上黑板来 画一个 等腰 三角形 。
( 中 一 名 学 生 自告 奋 勇 上 黑 板 , 画 了 一 个 顶 角 其 他 为 锐角 的等腰 三角形 ) 师 : 其 他 同学 想 一 想 , 还 有 什 么 要 补 充 的 吗 ? 请 你 生 3 他 画 的 不 全 面 , 们 所 碰 到 的 等 腰 三 角 形 其 实 : 我 还应该有 等腰直角三 角形和顶角为钝 角的等腰三角形 。
分类讨论在等腰三角形的应用

分类讨论在等腰三角形的应用
等腰三角形在很多方面都有应用,下面是其中一些主要应用:
一、在建筑中:等腰三角形可以用于在建筑中制作梁弓楼梯,它能起到稳定结构,从而使结构更加坚固。
二、在机械工程中:等腰三角型可以用于机械设备,如拓扑分析机,它可以提高传动效率和节能效果。
三、在电子工程中:等腰三角形可以用于各种电路,其中一个常用的就是三角互补电路,可以很好地抑制外界电磁干扰。
四、在布局中应用:等腰三角形可以用于室内外布局,如装饰、安装设备等,它可以使空间变得更加实用和美观。
五、在数学上:等腰三角形可以用于求解平面几何相关问题,并且可以为绘制多边形提供一些参考。
怎样运用分类讨论思想解答几何中的动点问题

数学篇几何动点问题一直是初中几何中的一个难点,因为点运动的位置不同,形成的图形就不同,符合结论的情况可能就不止一种.同学们在求解此类问题时常常因为考虑不周导致漏解而出错.因此,解答动点问题尤其要注意分类讨论.下面就如何运用分类讨论思想解答两类几何图形中的动点问题进行分析,以供参考.一、运用分类讨论思想解答等腰三角形中的动点问题等腰三角形具有两条边相等、底角相等的特点,在求解涉及等腰三角形的动点问题时,由于边的不确定性或角的不确定,需要运用分类讨论思想,从动态的角度逐一讨论三角形的三边两两相等的三种情况,或三角形的三个角为其顶角的三种可能性,然后综合所有分类的结果确定最终答案.例1如图1,在直角坐标系中,已知点P (-2,-1),点T (t ,0)是x 轴上的一个动点.(1)求点P 关于原点的对称点P ′的坐标;(2)当[t ]取何值时,△P ′TO是等腰三角形?图1图1-1分析:第(1)问求P 点的对称点P ′比较简单,利用对称性即可解答.第(2)问,T 是x 轴上的动点,它在运动的过程中△P ′TO 可能是等腰三角形但顶点未确定,需要分情况讨论.解:(1)∵P (-2,-1),∴P 关于原点的对称点P ′坐标为(2,-1),(2)由(1)知P ′(2,-1),作图如图1-1所示,①当△P ′TO 中,点P ′为顶点时,T 点为图1-1中T 4点,此时P ′T =P ′O ,T 坐标为T 4(4,0),②当△P ′TO 中,点T 为顶点时,T 点为图1-1中T 2点,此时TO =TP ′,又∵T (t ,0)且P ′(2,-1),∴(0-t )2+(0-0)2=(2-t )2+(-1-0)2解得,t =54,此时点T 坐标为T 2(54,0),③当△P ′TO 中,点O 为顶点时,T 点为图1-1中T 1和T 3点,此时TO =P ′O ,∵T (t ,0)且P ′(2,-1),∴(0-t )2+(0-0)2=(0-2)2+[0-(-1)]2,解得,t =±5,此时T 点坐标为T 1(-5,0)和T 3(5,0),综合①②③可知,当t 取-5、54、5、4时,△P ′TO 是等腰三角形.评注:本题看似简单,实则非常复杂.由于题目中没有明确等腰三角形的顶点,且T 为坐标轴上的一个动点,所以点T 、O 、P 均有可能为等腰三角形顶角的顶点,需要对此进怎样运用分类讨论思想解答几何中盐城市新洋初级中学吉华丽解法荟萃32数学篇行分类讨论.二、运用分类讨论思想解答圆中的动点问题圆既是轴对称图形,又是中心对称图形,还具有旋转不变性.圆的这些特性决定了与圆有关的动点问题可能存在多解.在解题时,我们可以根据题目要求初步绘制“圆”可能存在的位置,然后依据分类标准(比如x 轴、y 轴等)逐一分类讨论,做到不重不漏,最后综合所有情况得到完整答案.例2如图2,直线y =-43x +4与x 轴、y 轴分别交于点M ,N .(1)求M ,N 两点的坐标;(2)如果点P 在坐标轴上,以点P 为圆心,125为半径的圆与直线y=-43x +4相切,求点P 的坐标.图2图2-1分析:这是一个直线与圆相结合的题目.第(1)问,我们借助直线方程y=-43x +4可以直接求出M 、N 的坐标.第(2)问P 点在坐标轴上,到底在x 轴还是y 轴不确定,所以以P 点为圆心,半径为125的圆也具有不确定性,需要借助分类讨论思想加以讨论.解:(1)∵直线y =-43x +4与x 轴、y 轴分别交于点M ,N ,∴令x =0,y =4,即N (0,4).同理可得M (3,0).(2)经过分析发现P 点可能在x 轴上或y 轴上,通过作图发现可能有4种情况,如图2-1所示.①当P 在x 轴上时,设P (x 0,0),则圆P可能是图2-1中的两个虚线圆.125=43x ,解得x 0=0或6,此情况下P 点坐标为P 1(0,0)P 2(6,0);②当P 在y 轴上时,设P (0,y 0),则圆P可能是图2-1中的两个实线圆.125=|-43×0-y 0+4|4,解得y 0=0或8,此情况下P 坐标为P 3(0,0)和P 4(0,8),由此可见P 1和P 3重合,是同一个点.综合①②,符合条件的P 点一共有3个,分表为(0,0)、(6,0)、(0,8).评注:审题时一定要充分挖掘隐含条件,“点P 在坐标轴上”就是一个不确定的表述,可能存在多种情况.另外作图要准确,可以通过作图的方式大致确定点的位置,预估答案.此外,该题还有一个关键之处,即“点到直线的距离公式”.考试中常用的有两种公式,分别为:①设直线方程为一般式Ax +By +C =0,点P 的坐标为(x 0,y 0),则点P 到直线L 的距离为:d =|Ax 0+By 0+C |A 2+B2;②当P (x 0,y 0),直线L 的方程为截距式y =kx +b ,则P 点到直线的距离为d =|kx 0-y 0+b |1+k2.总之,动点问题常常要借助分类讨论思想辅助解题.一般涉及到与“直角三角形”“等腰三角形”“相似三角形”“圆”等相关的动点问题,往往具有不确定性,存在多解的情况.解法荟萃。
分类讨论思想在等腰三角形中的应用

如图等腰三角形△ABC中 边:腰和底边 角:顶角和底角
方法与应用一 遇角需考虑讨论顶角和底角
已知等腰三角形的一个 底内 角是 13000°° , 则它的顶角是 1210100或200°3000 .
方法与应用二 遇边需考虑讨论腰和底边
1、已知等腰三角形的两边长分别是 31 和 2 , 则它的周长是 7或5 8
以10为底边
以10为腰
课堂小结 1、遇边需考虑分类讨论腰和底边 2、遇角需考虑分类讨论顶角和底角 3、遇高线需考虑分类讨论三角形的类别
作业布置
收集用分类讨论思想解决的,与等腰三角 形有关的问题,并按一定的标准对收集的问 题进行归类。
2、若等腰三角形一腰上的中线分周长为9cm和 12cm两部分,求这个等腰三角形的底和腰的长。
方法与应用三 遇高线需考虑讨论三角形的类别
等腰三角形一腰上的高。
RJ DJ
综合应用
为了美化环境,计划在某小区内用草皮铺设一 块面积为30,一边长为10的等腰三角形绿地, 请你求出这个等腰三角形绿地的另两边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分类讨论思想
在解等腰三角形问题应用
等腰三角形是一种特殊的三角形,它的两腰相等,两底角相等。
正是由于其特殊性,在解有关等腰三角形的问题时,必须全面思考,分情况讨论,以防漏解。
有关等腰三角形的题目,很多情况下会有两解甚至更多解,因此能充分体现出分类讨论思想的应用。
一、当腰和底边不能确定时
例1.
(1)如果一个等腰三角形的两边长分别为4cm和6cm,那么这个等腰三角形的周长是。
(2)如果一个等腰三角形的两边长分别为4cm和9cm,那么这个等腰三角形的周长是。
(3) 已知一个等腰三角形的周长为13,其中一边长为4,那么它的底边长为。
二、有腰上的中线引起的讨论
例2.
(1)等腰三角形一腰上的中线将它的周长分为15cm和18cm 两部分,求它的腰长和底边长。
(2) 已知一个等腰三角形的周长是15cm,一腰上的中线将它
分成的两个三角形的周长的差为3cm,则它的腰长和底边长分别是。
三、当底角和顶角不能确定时
例3.
(1)已知等腰三角形的一个外角是100°,那么这个等腰三角形的顶角的度数是。
(2)已知等腰三角形的一个外角是80°,那么这个等腰三角形的底角的度数是。
四、当高的位置不确定时
由于锐角三角形的高都在三角形内部,钝角三角形中钝角的两条边上的高都在三角形外部,直角三角形的两直角边上的高分别是另一条直角边,因此,当已知等腰三角形一腰上的高的情况时,应分锐角三角形、钝角三角形和直角三角形等情况讨论。
例4.如果等腰三角形一腰上的高与另一腰的夹角为50°,那么它的底角为。
五、由腰的垂直平分线引起的讨论
例5.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线所成的锐角为50°,则∠B= 。
