光栅衍射光栅方程
光的衍射2
棱镜光谱是零级光谱。只有 一个级次，没有重级现象。
定义恰能分辨的两条谱线的平均波长 与 R 它们的波长差 之比为光栅的分辨本领 R
由光栅方程
P
( a b) sin k ( k 0,1,2) 加强
kf x a b
( k 0,1,2)
明纹
播放动画
播放动画
例：分光计作光栅实验，用波长 = 632.8 nm的激光照射光栅常数 d = 1/300 mm的光栅上，问最多能看到几条谱线。
解：在分光计上观 察谱线，最大衍射 角为 90°,
d
( a b) sin k
kmax ( a b) sin 90
o x
f
P
kmax
( a b) sin 90
3 . 5
3 1 10 9 300 632.8 10
-8
单缝衍射 轮廓线
4 8
-4
0
a b k m a k'
(m 1，3) 2，
m为整数时，光栅谱线中m、2m、3m等 处缺级。
I单
当 m=4 时 谱线中的第 –8、 – 4、4、 8级条纹缺级。
-2 -1
0 I 光栅衍射 光强曲线 1 2
单缝衍射 轮廓线
4 8
-8
-4
0
第五节 光栅光谱
X 射线的应用不仅开创了研究晶体结构的新领域， 而且用它可以作光谱分析，在科学研究和工程技 术上有着广泛的应用。 在医学和分子生物学领域也不断有新的突破。 1953年英国的威尔金斯、沃森和克里克利用 X 射线的结构分析得到了遗传基因脱氧核糖 核酸（DNA) 的双螺旋结构，荣获了1962 年 度诺贝尔生物和医学奖。
光栅衍射
k
-12
-8
-4
4
8
12
谱线中第±４、±8、 ±12… 级条纹缺级。
k
22
-12
-8
-4
o
4
8
12
三、衍射光谱
(a b)sin k
( k 0,1, 2, )
※ 对同级明纹，波长较长的光波衍射角较大。
入射光为白光时， k不同，按波长分开形成光谱。 不同，
I
sin
0 一级光谱 三级光谱 ab 二级光谱
在单缝衍射光强大的地方，光栅衍射明纹的光强也大； 在单缝衍射光强小的地方，光栅衍射明纹的光强也小； 在单缝衍射光强为0的地方，光栅衍射明纹的光强也为0。
20
缺级现象：
当多缝干涉的主极大位置，恰好与单缝衍射暗 纹位置重合时，本应出现主极大的明纹就不出现， 该处成了暗纹。这种现象称为缺级现象。
a sin k' ab 所缺级次为： k k k 1, 2 a
×
多缝干涉光强
2
sin sin N I p I 0单 sin
2
I 0单
单缝中央主极大光强
2
sin 单缝衍射因子
sin N 多光束干涉因子 sin
2
18
I I0
23
I
sin
0 一级光谱 三级光谱 ab 二级光谱
例如：二级光谱重叠部分光谱范围
(a b)sin 3紫
(a b)sin 2 白光 400 ~ 760nm
3 紫 600nm 2
二级光谱重叠部分:
600 ~ 760nm
光栅频率公式
光栅频率公式光栅频率公式是描述光栅衍射现象的一个重要公式，它被广泛应用于光栅衍射实验和光学仪器的设计中。
光栅是一种具有周期性结构的光学元件，通过光栅衍射可以实现光的分光、波长测量等应用。
光栅频率公式的一般形式为：nλ = d sinθ其中，n表示衍射级次，λ表示入射光的波长，d表示光栅的周期，θ表示衍射角。
这个公式可以用来计算出特定级次的衍射光的波长，或者根据已知波长来确定衍射角。
在光栅频率公式中，d是一个重要的参数，它表示光栅的周期，也称为光栅的间隔。
光栅的间隔决定了衍射光的方向和强度分布。
当入射光垂直照射到光栅上时，根据衍射理论可知，光栅衍射光的主极大和次极大分布在不同的衍射角上。
光栅的间隔越小，衍射角越大，衍射主极大和次极大的角度差也越大。
光栅频率公式中的sinθ项表示衍射角的正弦值，它与衍射光的角度有关。
当衍射角较小时，sinθ可以近似等于θ，因此可以用θ来代替sinθ进行计算。
这样，光栅频率公式可以简化为：nλ = dθ在实际应用中，光栅频率公式通常用于光栅衍射实验和光学仪器的设计中。
通过测量特定级次的衍射光的角度和入射光的波长，可以计算出光栅的间隔。
反过来，如果已知光栅的间隔和入射光的波长，可以根据光栅频率公式来确定衍射角。
光栅频率公式的应用不仅限于光栅衍射实验，还可以用于其他光学领域。
例如，在光谱仪中，通过使用具有不同光栅间隔的光栅，可以实现对不同波长的光进行分光和波长测量。
光栅频率公式可以帮助我们确定光栅的间隔，从而实现对不同波长光的精确测量。
光栅频率公式还可以应用于光栅衍射仪器的设计和优化。
通过调整光栅的间隔和入射光的波长，可以实现对特定波长的光的衍射效果的优化。
光栅频率公式可以作为设计光栅衍射仪器的重要依据，帮助我们选择合适的光栅参数，以获得理想的衍射效果。
光栅频率公式是描述光栅衍射现象的重要工具，它可以帮助我们计算出特定级次的衍射光的波长，或者根据已知波长来确定衍射角。
光栅频率公式在光栅衍射实验和光学仪器的设计中具有广泛的应用价值，它为我们研究和应用光栅衍射提供了重要的理论基础。
光栅常数的实验报告
一、实验目的1. 了解光栅的分光特性；2. 掌握什么是光栅常数以及求光栅常数的基本原理与公式；3. 掌握一种测量光栅常数的方法。
二、实验原理光栅是一种重要的分光元件，它可以将不同波长的光分开并形成明亮细窄的谱线。
光栅常数是指光栅上相邻两条狭缝（或刻痕）之间的距离，用d表示。
光栅常数是光栅基本常数之一，其倒数为光栅密度，即光栅的单位长度上的条纹数。
光栅衍射原理：当一束平行光垂直照射到光栅平面上时，透过每一狭缝的光都会发生单缝衍射，同时透过所有狭缝的光又会彼此产生干涉，从而形成光栅衍射光谱。
光栅衍射光谱的强度由单缝衍射和缝间干涉两因素共同决定。
光栅方程：d sinθ = k λ，其中d为光栅常数，θ为衍射角，k为衍射级数，λ为光波波长。
三、实验仪器1. 分光计；2. 透射光栅；3. 汞灯；4. 光栅常数测量装置（如：标尺、游标卡尺等）；5. 计算器。
四、实验步骤1. 将分光计调整至水平状态，并确保分光计的光源与光栅平行；2. 将光栅放置在分光计的物镜焦平面上，确保光栅与光束垂直；3. 打开汞灯，调整光栅与光源的距离，使光束通过光栅后形成衍射光谱；4. 使用分光计观察衍射光谱，记录第k级明纹的衍射角θ；5. 使用光栅常数测量装置测量光栅常数d；6. 根据光栅方程计算光波波长λ。
五、实验数据及结果1. 光栅常数d：通过光栅常数测量装置测得光栅常数d为1.0000mm；2. 第k级明纹的衍射角θ：通过分光计测得第k级明纹的衍射角θ为10.5000°；3. 光波波长λ：根据光栅方程计算得到光波波长λ为546.1nm。
六、实验结果分析1. 光栅常数d的测量结果与光栅常数测量装置的精度相符，说明实验装置可靠；2. 第k级明纹的衍射角θ的测量结果与光栅方程的计算结果相符，说明实验原理正确；3. 光波波长λ的测量结果与汞灯的波长相符，说明实验结果准确。
七、实验总结通过本次实验，我们成功地测量了光栅常数，并掌握了用分光计和光栅常数测量装置测量光栅常数的方法。
光栅衍射
光栅衍射衍射光栅是利用单缝衍射和多缝干涉原理使光发生色散的元件。
它是在一块透明板上刻有大量等宽度等间距的平行刻痕，每条刻痕不透光，光只能从刻痕间的狭缝通过。
因此，可把衍射光栅(简称为光栅)看成由大量相互平行等宽等间距的狭缝所组成。
由于光栅具有较大的色散率和较高的分辨本领，故它已被广泛地应用于各种光谱仪器中。
光栅一般分为两类：一类是利用透射光衍射的光栅称为透射光栅；另一类是利用两刻痕间的反射光进行衍射的光栅称为反射光栅。
本实验选用的是透射光栅。
一. 实验目的1. 进一步熟悉分光计的调整和使用。
2. 观察光栅衍射的现象，测量汞灯谱线的波长。
二. 实验仪器分光计、光栅、汞灯、平面镜等。
三. 实验原理当一束平行单色光垂直入射到光栅上，透过光栅的每条狭缝的光都产生有衍射，而通过光栅不同狭缝的光还要发生干涉，因此光栅的衍射条纹实质应是衍射和干涉的总效果。
设光栅的刻痕宽度为a ，透明狭缝宽度为b ，相邻两缝间的距离d=a+b ，称为光栅常数，它是光栅的重要参数之一。
如图3-15-1所示，光栅常数为d 的光栅，当单色平行光束与光栅法线成角度i 入射于光栅平面上，光栅出射的衍射光束经过透镜会聚于焦平面上，就产生一组明暗相间的衍射条纹。
设衍射光线AD 与光栅法线所成的夹角（即衍射角）为φ，从B 点作BC 垂直入射线CA ，作BD 垂直于衍射线AD ，则相邻透光狭缝对应位置两光线的光程差为：)sin (sin i d AD AC +=+ϕ （3-15-1）当此光程差等于入射光波长的整数倍时，多光束干涉使光振动加强而在F 处产生一个明条纹。
因而，光栅衍射明条纹的条件为：λϕK i d K =+)sin (sin K=0，±1，±2， （3-15-2）式中λ为单色光波长，K 是亮条纹级次，K ϕ为K 级谱线的衍射角，ｉ为光线的入射角。
此式称为光栅方程，它是研究光栅衍射的重要公式。
本实验研究的是光线垂直入射时所形成的衍射，此时，入射角i=0图3-15-1 光栅衍射原理示意图则光栅方程变为：λϕK d K =sin K=0，±1，±2，··· （3-15-3）由（3-15-3）可以看出，如果入射光为复色光，K=0时，有：00=φ，不同波长的零级亮纹重叠在一起，则零级条纹仍为复色光。
12-4 衍射光栅及光栅光谱解析
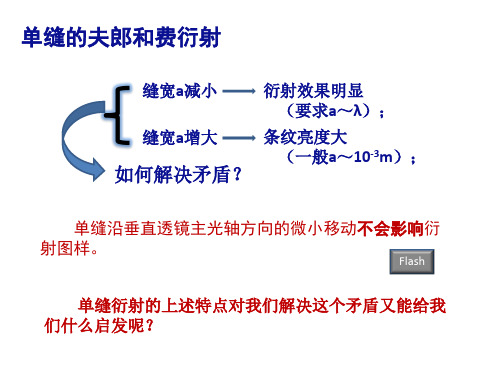
光栅衍射 光强曲线 单缝衍射 轮廓线
0
sin
Hale Waihona Puke 单缝衍射对缝间干涉调制的特例：缺级
若衍射角θ同时满足条件
1， 2，（缝间干涉主极大） d sin k ， k 0， 2， 3，（单缝衍射暗纹） a sin k ， k 1，
则每缝出射的光线因各缝自身的单缝衍射而相消， 因而尽管各缝间的干涉是加强，但仍为暗纹。 ——这一现象叫缺级
7
6
l
二. 光栅衍射图样的形成
光栅平面 透镜L S 观察屏 透镜L p · 0 f f
*
那么光栅的衍射条纹是不是把N个缝的衍射 条纹直接叠加就可以了呢？下面我们看一些在 实验室拍的单缝和光栅衍射的照片。
单缝和不同缝数光栅的衍射条纹
N 1
N 5
N 2
N 6
N 3
N 20
单缝衍射与光栅衍射条纹光强分布的比较
d km a
N、a、d和λ对条纹的影响 光栅方程
Flash
d sin k , (k 0,1,2,)
主极大半角宽度
半
主极大间隔
Nd
d
k 1, sin k 1 sin k
三 衍射光谱
入射光为白光时， k不同，按波长分开形成光谱. 不同，
缺级满足的关系 从
d sin k 和 a sin k
得
d k a k
d k k (k 1,2,3) a
则 2,4,6 缺级
缺级满足关系
如果
d 2 a
问：缺级是否一定从存在？ 光栅条纹的特点四：可能缺级
例：双缝衍射的结果讨论
大学物理第十八讲 光栅衍射、晶体的X射线衍射
● 实际中纯干涉难于实现，通常都与衍射同时存在.
12
例：一光栅透光部分宽度为 0.035mm，用波长700nm的单 色光垂直照射。在距光栅1m的屏上测得相邻条纹间距y =0.5cm。求：①在单缝衍射的中央明纹宽度内，最多可以 看到几级、共几条明纹？ ②光栅不透光部分宽度为多少？
2
2
4级明纹 3级明纹 2级明纹 1级明纹
d sin k
k 0,1,2,3...
光栅方程
决定各级主极大方向的方程.
或 用 图 解 法 求
d
中央明纹 -1级明纹
a
b
B
C
-2级明纹 -3级明纹 -4级明纹
BC d sin k
6
3.缺级现象 ●在某些方向，同时满足光栅衍射的明纹条件和单缝衍 射的暗纹条件，则该方向上的光栅衍射明纹将不会出现， 称这种现象为“缺级”。 第k级光栅衍射主极大：
a
a b 3a 3 10 cm
② kmax
4
ab
sin
2
k a 1 N 3333 / cm ab
kmax 5.5 5 (向前取整数)
14
共呈现5级，共9条谱线： k 0, 1, 2, 4, 5.
③ k 2, v 400nm, r 760nm
§11-6
光栅衍射
一、光栅 在透光或反光性能上具有周期性空间结构的光学元件.
平面光栅—在透明平面玻璃上刻成若干等间距的刻痕, 或在镀铬板上用光刻的办法刻出若干条刻痕做成的器 件。 透射光栅
反射光栅
大学物理下册衍射光栅
衍射角 L
P
Q
o
f
1、光栅方程
任意相邻两缝对应点在衍射角为 方向的两衍射光
到达P点的光程差为
dsin
衍射角
由双缝干涉可知，当满足
dsink
d
k 0 , 1 , 2 ,
干涉相长，在方向形成明条纹。
（1）主极大
光栅方程
dsin k (k0 ,1 ,2.....)
2
1
（2）由 sin1，可求得最高明纹级次为
2
ka b4 .8 1 6级 0 9 .6 级 9 级
m
5 1 70
例3 以氢放电管发出的光垂直照射在某光栅上,在
衍射角 410方向上看到165.62nm和241.10nm
的谱线重合，求光栅常数的最小值。
满足上面条件时出现明纹。
k=0称为中央明纹，k=1，2分别称为第一级，
第二级主极大。
（2）极小 可以证明：在两个相邻主极大之间有N-1个暗纹。
（3）次极大 相邻两极小之间有一个次极大，相邻两主极大间 有N - 2个次极大；次极大的亮度很小，实验中观 察不到。
五、衍射条纹在屏上的分布
1、主极大明纹在屏幕上的位置
§14-8 衍射光栅
一、光栅 1、定义 许多等宽度、等距离的狭缝排列起来形成
的光学元件.广义讲，任何具有空间周期性的衍 射屏都可叫作光栅。
2、种类 透射光栅 ，反射光栅，平面光栅，凹面光栅
透
反
射
射
光
光
栅
栅
3.光栅常量 a是透光部分的宽度，
b是不透光部分的宽度，
光栅常量d = a + b，是光
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
λ
d
P ·
sin α E E m α
sin α I I m α
2
f
π a sin φ α λ
单缝衍射振幅曲线
相邻两缝发出的光在 P 点引起的光振动相位差为
2π δ d sin φ λ δ π d sin φ 取 β 由几何关系可得: 2 λ E φ 2 R s in β E P 2 R s in N β
(2) 主极大光强是相应位置处单缝引起光强的 52 倍。
6
2. N 缝干涉 对N 缝干涉两主极大间 有N - 1个极小， N - 2 个次极大。 衍射屏上总能量
m 1
4I 强度分布
25 I 0
I
EN
m 1
主极大的强度 I N 2 由能量守恒，主极大的
π π ( ) 最多明条纹数 2 2
B
k max
d π (sin sin ) 2
k max
d π (sin - sin ) 2
18
N k m ax k m ax 1
d cos φ1,k Δφ1,2, k kΔλ
其中 Δφ1,2,k φ2, k
kΔλ φ1,k = d cos φ1,k
...(1)
λ 波长 1 第 k 级 Δφ1,k 主极大半角宽度 Nd cos φ1,k
根据瑞利判据： 当 1, 2 , k 1, k 时刚好能分辨 由(1) 、(2) 得 讨论
N δ 2m π
2π d sin 为相邻缝光振动矢量夹角 其中 δ
N d sin m
m 1, 2 , , N 2 , N 1, N 1, N 2
9
暗纹条件 ( a b ) sin m N m 1, 2 , 3 , N 1, N 1, N 2 , 2 N 1, 2 N 1,
d (sin sin ) k a (sin sin ) k '
d k k k 1, 2 ,3 , a
20
10 5 3 7 6 4.8 10
k m ax d
o d (sin sin 3 0 ) k (2)
当 = 90o 时
k m ax 5
19
当 = -90o 时 k m ax 1
说明 (1) 斜入射级次分布不对称
13
例如：a b 4a
4a sin φ kλ
sin I p I m单
2
sin N sin
2
各级主极大光强不同， 特别是刚好遇上单缝衍射 因子零点的那几级主极大 消失了——missing order (单缝衍射) 强度分布
2. 缺级条件分析
k 0 ,1, 2 ,3 ,
— 光栅方程
多缝干涉主极大光强受单缝衍射光强调制，使得主极大光 强大小不同，在单缝衍射光强极小处的光栅主极大缺矢。
d sin k a sin k
缺级条件
sin k a k d
如
d k 1, 2 ,3 , k k a d a2 k 2, 4, 6 k 3, 6 , 9 d a3 2
例 一束波长为 480 nm 的单色平行光，照射在每毫米内有600 条刻痕的平面透射光栅上。 求 (1) 光线垂直入射时，最多能看到第几级光谱？
(2) 光线以 30o入射角入射时，最多能看到第几级光谱？
解 (1) d sin k
1 1 5 d 10 m 3 600 10 6
暗纹条件 5 δ 2mπ 5 d sin m m 1, 2 , , 4 ,6 , ,9 ,11,
I/I
暗纹条件
A4
A3
A2
A5
A1
-6
-5
-4
-3
-2
-1
0 +1 +2 +3 +4 +5 +6 k
结论
(1) 对五缝干涉，相邻两主极大间有4个极小，3个次极大。
-3级 白光的光栅光谱 3级
-2级 2. 光栅的色分辨本领
-1级
0级
1级
2级
( 将波长相差很小的两个波长 和 + 分开的能力 ) 色谱仪的色分辨率
R
16
光栅的色分辨率
设两波长 1 和 2 = 1+ 在第 k 级能被光栅分辨，则有
d sin 1, k k 1 d sin 2 , k k 2
R
N
EP
δ δ
δ
E E δ
11
sin N β E P Eφ sin β 讨论
sin α sin N β I0 Im α sin β
2
2
2
sin α 单缝衍射因子 α 主极大位置及光强
若 δ 2 β 2kπ
(1)
同时
sin N sin
N
2 kπ
2π d sin
(2)
即 d sin k (1)、 (2)联立得 k
k 0 ,1, 2 , 3
d k ' (k 取 非 零 整 数 ) a
k 4, 8, 12
出现缺级
缺级
缺级
8
3. 暗纹条件 光栅衍射中，两主极大条纹之间分布着一些暗纹，这是 缝间干涉相消而成。 设光栅总缝数为 N，各缝在观察屏上某点 P 引起的光振动矢 量为
A1 , A2 , , Ai , , A N
当这些振动矢量组成的多边形封闭时，合矢量为零，对应点 为暗纹，则 暗纹条件
o
f
ab
d sin
相邻两缝在 P 点引起的光振动相位差为
d sin δ 2π 2 kπ
主极大强度 A
5 A A
A 为主极大条件下每个单缝在
P 点引起光振动矢量的振幅
2 I A 5 2 I
5
各缝光振幅矢量: A1 , A2 , A3 ..., A5 2π d sin 相邻矢量相位差: δ
Eo
Ep
δ
sin α I p I Io α
2
2
光学仪器的分辨本领 - 圆孔的夫琅禾费衍射
衍射屏
L
0
相对光强曲线
经圆孔衍射后, 一个点光源对 应一个艾里斑
中央亮斑 (艾里斑)
孔径为D
f
瑞利判据 对于两个等光强的 非相干物点：如果一个像 斑中心恰好落在另一像斑的边缘(第一暗纹处 )，则此两像被认为是刚好能分辨。此时两像 斑中心角距离为最小分辨角
大学物理
1
单缝衍射强度 (振幅矢量法)
x
N
B
·
C
P
0
2π β a sin φ λ N
A
f
0
β 0
E o E m ax
δ
E0
N E0 Eo
Ep
E0
δ
β
E0
Eo
2
sin
2
δ
Eo β sin α E p 2 sin Eo β 2 α
Nd cos k
主极大的半角宽度与
k 越小， 越大， 这意味着主 极大的锐度越大（条纹越细）
Nd
成反比，
Nd
在给定光栅常数之后，主极大的位置就被确定 单缝衍射因子不改变主极大的位置和半角宽度
其作用仅在于影响强度在各级主极大间的分配
15
光栅光谱及分辨本领
1. 光栅光谱
(2) 斜入射时，可得到更高级次的光谱，提高分辨率。
(3) 垂直入射和斜入射相比，完整级次数不变。 上题中垂直入射级数 k 3 , 2 , 1, 0 , 1, 2 , 3 斜入射级数 k 1, 0 , 1, 2 , 3 , 4 , 5 (4) 垂直入射和斜入射相比，缺级级次相同。
两个明纹之间有N - 1条暗纹， 相邻暗纹之间有 1 条次级明纹， 两个明纹之间共有N - 2条次级明纹。
结果：缝数 N 增大
明纹变细， 暗纹增多
暗区扩大
强调： m 的取值及与主极大级次 k 的关系
k级主极大
kN 1
k N 1 级极小
k 1 级主极大
10
4. 光栅衍射光强分布公式 单缝衍射的振幅分布 和强度分布为
...(2)
R kN
( 光栅的色分辨本领 )
增大主极大级次 k 和总缝数 N ，可提高光栅的分辨率。
17
斜入射的光栅方程
主极大条件
d (sin sin ) k
k = 0, 1, 2, 3… 缺级条件
N
A
p
a (sin sin ) k ' d (sin sin ) k
δ 0 1 .22 D
3
光栅的夫琅禾费衍射
L
P
a
透光 宽度
o
b
d ab
不透光 宽度
ab
d sin
L
d
a
I f 总强度的分布？
4
光栅衍射 - 缝间干涉
1. 五缝干涉例子
L
P