第十章 统计指数(答案)
第十章统计指数
费氏公式（理想公式）
K p
p1q0 p0q0
p1q1 p0q1
Kq
q1 p0 q0 p0
q1 p1 q0 p1
一般编制原则
⒈数量指标综合指数旳编制：
—采用基期旳质量指标作为同度量原因
K q
q1 p0 q0 p0
⒉质量指标综合指数旳编制：
—采用报告期旳数量指标作为同度量原因
K p
将两个不同步期旳总量指标对比，以测定指数化指 标旳数量变动程度。
指数化原因
K q
q1 p0 q0 p0
K p
p1 q1 p0 q1
同度量原因
1、数量指标旳综合指数（例：销售量总指数）
销售量指数
q P 10
q 1
P 0
q P q P
00
00
以基期价格计算 旳报告期销售额
报告期和基期旳销售 基期价格作为 量，为指数化原因 同度量原因
[例]商品价格平均数指数计算表
商品 计量 名称 单位
甲件
价格
p0 p1
50 52
个体指数
Kp
p1 p0
1.0400
报告期销售 额（元）
假定Ⅱ
p1q0
30680 57200 15000
— — 106900 104200 108000 102880
拉氏物量指数：
相对数分析：K q
p0 q1 108000 1.0103或101.03% p0 q0 106900
绝对数分析： p0 q1 p0 q0 108000 106900 110（ 0 元）
63200 106.99% 59070
绝对数分析：
绝对数分析：
p1q1 p0q1
第10章 对比分析与指数分析
计算结果表明，报告期与基期相比，该公司三种商品的销售 量平均增长12.42％。 该指数同时也可以反映销售量变动对销售总额的影响，即：
按基期价格来计算，销售量变动使销售总额增加12.42％; 由于销售量变动而使销售总额增加的数额为：
【例10-3】解：
（2）拉氏价格指数：
计算结果表明，报告期与基期相比，该公司三种商品的价格 平均上升了3.45％。 同时，这一结果也反映了价格变动对销售总额的影响，即:
ip p1 p0
商品价格（元） 商品 类别 计量单位 报告期p1
iq
销售量
q1 q0
指数（%）
基期p0
百公斤(吨)
基期q0
报告期q1
p1/p0
q1/q0
大米 猪肉 食盐 服装 电视机 合计 改变单位 后合计
公斤 500克 件 台
300(3000) 18 1 100 4500 4919 7519
商品 类别 大米 猪肉 食盐 服装 电视机 合计 改变单位 后合计 商品价格（元） 计量单位 销售量 指数（%）
基期p0
百公斤(吨)
报告期p1
360(3600)
基期q0
2400(240)
报告期q1
2600(260)
p1/p0
120 111.11 80 130 95.56 536.67
q1/q0
108.33 113.10 150 95.83 120 587.26
【例10-4】(续 )
（2）帕氏价格指数：
计算结果表明：报告期与基期相比，
该公司三种商品的价格平均上升了3.1％。； 按报告期销售量来计算，由于价格变动使销售总 额增加 3.1％，亦即由于价格变动而使销售总额增 加的数额为：
第十章 统计指数分析
指数法既古老、又新颖，既令人困惑、 指数法既古老 、 又新颖 ， 既令人困惑 、 又引STAT 人入胜。 人入胜。 数百年来曾经吸引了众多经济学家和统计学 家悉心研究。 家悉心研究。 其理论传统和实践积累都非常丰厚。 其理论传统和实践积累都非常丰厚。 在种类繁多的经济数量分析方法中， 在种类繁多的经济数量分析方法中 ， 很难找 到一种方法比指数法的应用更为广泛。 到一种方法比指数法的应用更为广泛。 指数法的研究和应用水平是经济统计学发展 程度的重要标志之一。 程度的重要标志之一。
第十章 统计指数分析
第十章 统计指数分析
STAT
§10.1 统计指数概述 §10.2 综合指数 §10.3 平均指数 §10.4 指数体系及因素分析法
第十章 统计指数分析
§10.1 统计指数概述 ★ 一、问题的提出
二、指数的概念及性质 三、指数的分类
STAT
问题的提出
第十章 统计指数分析
指数起源于人们对 价格动态的关注。 价格动态的关注。
⒈相对性 ⒉综合性 ⒊平均性
第十章 统计指数分析
指数的作用 综合反映复杂现象总体变动的方向 和程度； 和程度； 根据现象之间的联系，利用指数体 根据现象之间的联系， 系对现象的总变动进行因素分析； 系对现象的总变动进行因素分析； 编制指数数列，反映现象变化的长 编制指数数列， 期趋势。 期趋势。
统计指数的作用
指数的定义
指由于各个部分的不同性质 而在研究其数量时， 而在研究其数量时，不能直 接进行加总或对比的总体 数量变动的相对数； 数量变动的相对数；
从广义上讲，指数是指反映社会经济现象总体 从广义上讲， 从狭义上讲，指数是指反映复杂社会经济现象 从狭义上讲， 的相对数。 总体数量综合变动 的相对数。
统计指数习题及答案
统计指数习题及答案统计学是一门研究数据收集、分析和解释的学科，具有广泛的应用领域。
在统计学学习过程中，习题是非常重要的一部分，通过解答习题可以帮助我们巩固知识，提高应用能力。
本文将介绍一些常见的统计指数习题，并给出相应的答案。
1. 平均数习题a) 某班级有10名学生，他们的身高分别为160、165、170、155、175、180、170、165、160、175（单位：厘米），求班级学生的平均身高。
答案：将所有身高相加得到：160+165+170+155+175+180+170+165+160+175=1695，然后除以学生人数10，得到平均身高为169.5厘米。
b) 一家电商公司在过去一周的每天销售额分别为5000、6000、7000、8000、9000、10000、11000元，求这一周的平均销售额。
答案：将每天销售额相加得到：5000+6000+7000+8000+9000+10000+11000=57000，然后除以7天，得到平均销售额为8142.86元。
2. 中位数习题a) 某班级有30名学生，他们的考试成绩从低到高排列如下：60、65、70、75、80、85、90、95、100、105、110、115、120、125、130、135、140、145、150、155、160、165、170、175、180、185、190、195、200、205。
求班级学生的中位数。
答案：由于学生人数为偶数，中位数为第15和第16个成绩的平均值，即(135+140)/2=137.5。
b) 一家公司的员工薪资从低到高排列如下：3000、3500、4000、4500、5000、5500、6000、6500、7000、7500、8000、8500、9000、9500、10000元。
求公司员工的中位数。
答案：由于员工人数为奇数，中位数为第8个薪资，即6000元。
3. 众数习题a) 某班级有40名学生，他们的考试成绩如下：60、70、80、80、90、90、90、100、100、100、100、110、110、110、110、120、120、120、120、120、130、130、130、130、130、130、140、140、140、150、150、150、150、150、150、150、150、150、160、160。
统计学知到章节答案智慧树2023年中国石油大学(华东)
统计学知到章节测试答案智慧树2023年最新中国石油大学（华东）第一章测试1.对某城市工业企业未安装设备的价值进行调查，总体是（）参考答案:该城市所有的工业企业的未安装设备2.某企业员工平均工资为7800元，则（）参考答案:平均工资7800是指标3.调查某市职工家庭的生活状况，则总体是（）参考答案:该市全部职工家庭4.几位学生的身高分别是1.68米，1.75米，1.78米元，这几个数字是（）。
变量值5.某学校的所有学生为一总体时，则学生的平均年龄就是（）参考答案:质量指标6.要了解某班50个学生的学习情况，则总体单位是（）参考答案:每一个学生7.构成统计总体的总体单位( )参考答案:可以有多个标志8.下列标志中属品质标志的是（）性别9.下列指标属于质量指标的是（）。
参考答案:资金产值率10.统计一词的三种涵义是（）。
参考答案:统计工作、统计资料、统计学第二章测试1.根据统计表的编制要求，下列说法不正确的是（）参考答案:统计表中相同的数据可以用“同上”填写2.为直观反映近10年来公司收益状况，收集了2008-2017年公司年利润的数据，，用（）图形展示最为合适。
参考答案:折线图3.决定统计图形式的不是数据，也不是尺寸，而是你想说明的主题和你想指出的内容要点。
参考答案:对4.企业产品按产品等级分组、按产品销售区域分组、按产品销量分组和按生产车间分组四种统计分组中属于按品质标志分组的有3个。
参考答案:对5.对统计数据进行分组整理时的基本原则是组间差异尽可能大，组内差异尽可能小。
参考答案:对第三章测试1.对于具有对称分布的数据而言，大约有（）的数据值与平均数的距离在3个标准差之内。
参考答案:100%2.两组数据的平均数不等，但标准差相等，则（）参考答案:平均数小的，离散程度大3.一组数据的算术平均数是50，标准差系数系数为0.6，则该组数据的方差是（）参考答案:9004.一组数据存在极端值时，不能计算的指标是（）算术平均数5.箱线图不仅可以反映一组数据的分布是否对称，是否存在离群点，还可以对多组数据的分布特征进行比较。
统计学习题答案 第10章 统计指数
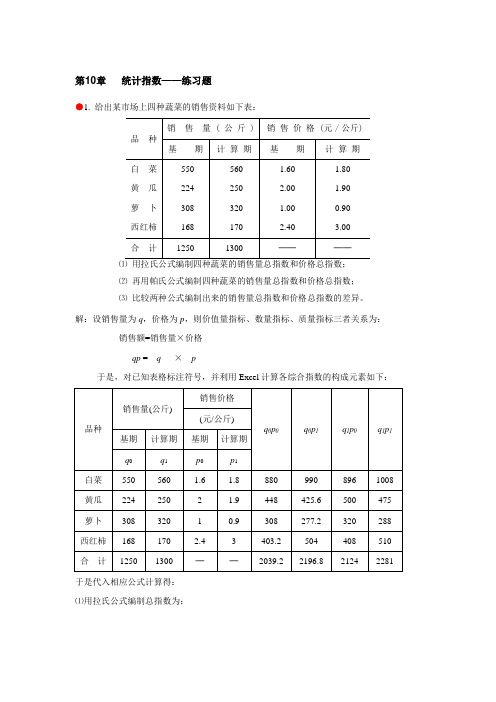
第10章统计指数——练习题●1. 给出某市场上四种蔬菜的销售资料如下表：⑵再用帕氏公式编制四种蔬菜的销售量总指数和价格总指数；⑶比较两种公式编制出来的销售量总指数和价格总指数的差异。
解：设销售量为q，价格为p，则价值量指标、数量指标、质量指标三者关系为：销售额=销售量×价格qp = q×p于是，对已知表格标注符号，并利用Excel计算各综合指数的构成元素如下：于是代入相应公式计算得：⑴用拉氏公式编制总指数为：四种蔬菜的销售量总指数 10002124104.16% , 2039.2q q p L q p===∑∑四种蔬菜的价格总指数 0102196.8107.73%2039.2p q p L q p===∑∑⑵ 用帕氏公式编制总指数：四种蔬菜的销售量总指数为 11012281103.83% 2196.8q q p P q p===∑∑四种蔬菜的价格总指数为 1112281107.39%2124p q p P q p===∑∑ ⑶ 比较两种公式编制出来的销售量总指数和价格总指数，可见：拉氏指数＞帕氏指数 在经济意义上，拉氏指数将同度量因素固定在基期。
销售量总指数说明消费者为保持与基期相同的消费价格，因调整增减的实际购买量而导致实际开支增减的百分比；价格总指数说明消费者为购买与基期相同数量的四种蔬菜，因价格的变化而导致实际开支增减的百分比。
帕氏指数将同度量因素固定在计算期。
销售量总指数说明消费者在计算期购买的四种蔬菜，因销售量的变化而导致实际开支增减的百分比；价格总指数说明消费者在计算期实际购买的四种蔬菜，因价格的变化而导致实际开支增减的百分比。
●2.依据上题的资料，试分别采用埃奇沃斯公式、理想公式和鲍莱公式编制销售量指数；然后，与拉氏指数和帕氏指数的结果进行比较，看看它们之间有什么关系。
解：采用埃奇沃斯公式编制销售量指数为：1011011101()()212422814405103.9896%2039.22196.84236q q pp q p q p E q pp q p q p++==+++===+∑∑∑∑∑∑采用理想公式编制销售量指数为：103.994869%q F ===采用鲍莱公式编制销售量指数为：1011000111()()22104.16%103.83%104.00%2q q q q p q p B L P q p q p =+=++==∑∑∑∑与拉氏销售量指数和帕氏销售量指数的结果进行比较，它们之间的关系是： q q q q q L B F E P >>>>即拉氏销售量指数最大，鲍莱销售量指数次大，理想销售量指数居中，埃奇沃斯销售量指数较小，帕氏销售量指数最小。
第十章指数
第十章指数内容提要：1．指数概述2．综合指数3．平均指数近期应用4．指数体系与因素分析目的要求：1．指数的含义和种类2．综合指数和平均指数的编制方法和编制特点3．综合指数与平均指数的因素分析方法4．统计指数在社会经济问题中的应用重点、难点：1．拉氏指数、帕氏指数2．综合指数和平均指数的编制方法3．综合指数与平均指数的因素分析方法讲授内容：第一节指数的概念和种类1．概念（1）广义指数：广义指数是指用来测定社会经济现象中一个变量值对另一个特定的变量值大小的相对数.（2）狭义指数：狭义指数是一种特殊的相对数，是表明不能直接相加和对比的复杂现象总体综合变动程度的相对数.2．种类个体指数（1）按对象的范围分总指数数量指标指数（2）按指标的性质分质量指标指数动态指数（3）按反映的时态分静态指数综合指数（4）按编制的方法分平均指数平均指标指数3．作用（1）综合反映复杂现象总体数量上的变动状况；（2）分析复杂现象中的各内在因素变动的方向与变动程度以及对总体变动影响程度；（3）说明在总平均指标变动中，变量水平和总体结构变动的作用；（4）分析研究社会经济现象在长时间内的发展变化趋势.第二节综合指数一、综合指数编制的基本原理综合指数用类似对比的总量指标中包含两个或两个以上的因素，只观察其中一个因素的变动，将其他因素的变动固定下来，这样编制的总指数，称为综合指数.编制综合指数首先要明白两个概念：一是“指数化指标”，所谓指数化指标就是编制综合指数所要测定因素;二是“同度量因素”，所谓“同度量因素”是指媒介因素，借助媒介因素，把不同度量单位的现象总体转化为数量上可以加总，并客观上体现出它在实际经济现象或过程中的份额或比重. 综合指数的基本公式如下：p k =10i i p q p q ∑∑； q = 10i iq p q p ∑∑. 公式中，k 表示综合指数，p 表示质量指标，q 表示数量指标；小标1和0分别表示报告期和基期，i 为同度量因素固定的时期.编制综合指数的基本方法是“先综合，后对比”，即首先把指数化因素乘以同度量因素加以综合，然后再进行对比. 二、拉氏指数p k =1000p q p q ∑∑； q k =100q p q p∑∑.拉氏指数由于以基期变量值为权数，可以消除权数变动对指数的影响，从而使不动时期的指数具有可比性.例 假定某市场3中商品的销售价格和销售量资料如表10-1所示.计算拉氏价格指数和销售量指数.解 q k =10q p q p ∑∑=1926018440=104.4% ， p k =1000p q p q∑∑=1790018440=97.1% . 综合指数不仅可以反映现象的相对变动程度.还可以进行绝对数分析，即用于测定指数化指标变动所引起的相应总值的绝对变动额.对于上面的资料，我们有10p q ∑-00p q ∑= 17900 - 18440 = -540（元）； 1q p ∑-0q p∑= 19260 – 18440 = 820（元）.即由于价格下降2.9%，使销售额减少了540元；又由于销售量增长4.4%，使销售额增加了820元. 三、帕氏指数p =1101p q p q ∑∑； q k =111q p qp ∑∑.帕氏指数因以报告期变量值为权数，不能消除权数变动对指数的影响，因而不同时期的指数缺乏可比性；但帕氏指数可以同时反映出价格和消费结构的变化，具有比较明确的经济意义. 例 以表10-1的资料，计算帕氏价格指数和销售量指数. 解 p =1101p q p q∑∑ =1850019260= 96.1% , q k =111q p q p∑∑ = 1850017900 = 103.4% .类似地，依据帕氏指数也可以就价格和销售量的变化进行绝对数分析.对于上面的资料，计算得到11p q ∑- 01p q ∑ = 18500 - 19260 = - 760（元），11q p ∑- 01q p ∑ = 18500 - 17900 = - 600（元）.即由于价格下降了3.9%，使销售额减少了760元；又由于销售量增长3.4%，使销售额增加了600元. 四、拉氏指数与帕氏指数的比较首先，由于拉氏指数和帕氏指数各自选取的同度量因素不同，即使利用同样的资料编制指数，两者给出的计算结果一般也会存在差异.其次，拉氏指数和帕氏指数的同度量因素水平和计算结果的不同，表明它们具有不完全相同的经济分析意义.通常人们认为，帕氏价格指数的分子与分母之差，即11p q ∑- 01p q ∑ = 101()p p q -∑能够表明报告期实际销售的商品由于价格变化而增减了多少的销售额，因而较之拉氏价格指数具有更强的显示经济意义.不过，从另一个角度看，拉氏价格指数的分子与分母之差，即10p q ∑- 00p q ∑ = 100()p p q -∑ 仍然是有意义的.它至少能够说明，消费者为了维持基期的消费水平或购买同基期一样多的商品，由于价格的变化将会增减多少实际开支.由此可见，从经济分析意义的角度看，拉氏指数和帕氏指数孰优孰劣，其实并无绝对的特别判断标准.关键在于能够辨别两者的细微差异，并明确我们利用有关指数具体是要说明什么样的问题. 五、综合指数的其他类型 1.马埃指数p k =011010()2()2q q p q q p ++∑∑=101001()()p q q p q q ++∑∑=10110001p q p q p q p q ++∑∑∑∑， q k =101100()2()2p p q p p q ++∑∑=101001()()q p p q p p ++∑∑=11100100q p q p q p q p ++∑∑∑∑.上述公式实质上使，分子分别为拉氏公式分子和帕氏公式分子之和，分母分别为拉氏公式分母与帕氏公式分母之和. 2.固定权数综合指数p k =10n n p qp q ∑∑， q k =10n nq p q p∑∑.式中：n q 和n p 分别表示特定的数量和价格水平.由于固定权数综合指数的同度量因素不因比较时期（报告期和基期）的改变而改变，因此采用固定权数综合指数.它不但方便指数的编制，而且便于观察现象长期发展变化的趋势. 3.理想指数p FqF第三节 平均数指数及其应用一、平均数指数的编制原理与总指数恰好相反，编制平均指数的基本方式是“先对比，后平均”，也即首先通过对比计算个别现象的个体指数，然后将个体指数加以平均得到总指数.根据经济分析的一般要求，平均指数的权数应该是与所要编制的指数密切关联的价值总量，即pq .但权数的水平却可以考虑不同的情况，分别有以下四种：对于质量指标指数 p k 对于数量指标指数q k权数Ⅰ 00p q 权数Ⅰ 00q p 权数Ⅱ 01p q 权数Ⅱ 01q p 权数Ⅲ 10p q 权数Ⅲ 10q p 权数Ⅳ 11p q 权数Ⅳ 11q p但从实用的角度看，权数Ⅱ和权数Ⅲ的资料一般不易获得，故通常应用较多的还是权数Ⅰ和权数Ⅳ.即基期的总值资料（00p q ）和报告期的总值资料（11q p ）.平均指数的形式一般有三种，即算术平均指数、调和平均指数以及几何平均指数.平均指数的各种形式在分析上没有绝对的优劣之分.但从实用的角度上看，算术平均指数计算较为简便，含义比较直观，故应用的最为普通，其次就是调和平均指数，几何平均指数计算比较复杂，故应用的较少一些. 二、平均数指数的类型 （一）算术平均指数算术平均指数一般用00p q 加权，基本公式如下pk =100000p p q p p q ∑∑，q=10000q p q q p q∑∑. 例10.3 以表10-1的资料，分别计算价格和销售量的算术平均指数.解 p k =100000p p q p p q ∑∑=558007550008000544050100068500080005440⨯+⨯+⨯++=1790018440=97.1%；qk =100000q p qq p q∑∑=110970500080005440100880500080005440⨯+⨯+⨯++=1926018440=104.4%. 这两式的计算结果与前面综合指数中的拉氏指数的计算结果完全相同.不难发现，这是因为当个体指数与总值权数之间存在严格的一一对应关系时，采用基期总值加权的平均指数，实际上式拉氏综合指数的变形.但当复杂总体所包括的变量比较多时，用综合指数计算是很繁杂的，一是资料收集困难；二是需要全部商品治疗.而平均指数完全可以克服这些困难，使计算更简单、方便.因此，平均指数是一种相对对立的总指数编制方法，具有比综合指数更广泛的适用性. 以价格指数为例，其计算公式可变形为p k =10000p p q p p q ∑∑=001000p q p p p q ⨯∑∑=100p w p ∑. 为了简化指数编制工作，实践中常常将相对权数固定起来，连续使用若干个指数编制时期.仍以价格指数为例，其公式就成为p k =10c p W p ∑或 p k =1100cp W p ∑. 其中c W 为固定起来的相对权数，它可以用小数表示（此时权数之和等于1），也可以用百分点表示（此时权数之和等于100），这称作“固定加权算术平均指数”. （二）调和平均指数调和平均指数一般用11p q 加权，基本计算形式如下p =111111p q p qp p ∑∑，q k =111111p q p qq q ∑∑.例10.4 以表10-1的资料，分别计算价格和销售量的调和平均指数. 解 p k =111111p q p qp p ∑∑=605072005250111605072005250558007550100068++⨯+⨯+⨯=1850019260=96.1%；q k =11111p qp qq q ∑∑=605072005250111605072005250100880++⨯+⨯+⨯=1850017900=103.4%.这两式的计算结果和前面综合指数中帕氏指数的计算结果完全相同.不难发现，这也是因为当个体指数与总值权数之间存在严格的一一对应关系时，采用报告期总值加权的平均指数实际上是帕氏综合指数的变形.第四节 指数体系与因素分析一、指数体系指数体系的基本含义是：若干因素指数的乘积应等于总变动指数，若干因素影响差额的总和应等于实际发生的总差额.指数体系在指数分析中具有重要的作用.第一，利用指数体系可以对现象的总变动进行因素分析.在利用指数体系分析现象的总变动中各个因素变动的影响程度时，可以从相对数和绝对数两个方面进行说明.从相对数方面分析时，各因素指数乘积应等于总变动指数.从绝对数方面分析时，各因素影响差额之和应等于实际发生的总差额.第二，利用指数体系可以进行指数之间的相互推算.在三个指数（一个总变动数和两个因素指数）形成的指数体系之中，只要已知其中任何两个指数，就可以推算出剩余的另一个指数来.二、因素分析1.因素分析的意义因素分析是借助于指数体系来分析社会经济现象变动中各种因素变动发生作用的影响程度.社会经济现象的变动分两种情况：一种是社会经济现象的总变动，另一种是社会经济现象的平均变动，因素分析均可以解决这两方面的问题.第一，分析社会经济现象总体总量指标的变动受各种因素变动的影响程度.它是利用综合指数体系，从数量指标指数和质量指标指数的相互联系中，分析这种现象因素的变动影响关系.第二，分析社会经济现象总体平均指标变动受各种因素变动的影响程度.它是利用综合指数编制的方法原理，通过平均指标指数体系来进行分析.进行因素分析，一方面要从数量上使指数之间形成等式关系，另一方面还要具有一定的经济意义，明确数据所代表的经济内容.按非全面资料所编制的各种平均指数，并不具有承担因素分析的条件. 2.因素分析的种类按照分析现象包含因素的多少，可分为两因素分析和多因素分析.两因素分析之现象只包含两个因素，分别分析两个因素对现象变动的影响.多因素分析是指分析的现象由多个因素构成，分别分析各因素对现象变动的影响.按照分析指标的种类不同，可分为总量指标的因素分析和平均指标的因素分析.总量指标的因素分析又分总量指标的两因素分析和多因素平均指标的因素分析也包括两因素分析和多因素分析.3.因素分析的基本方法因素分析的基本方法是连锁替代法.连锁替代法时实际工作中经常应用的因素分析方法.这种方法是在被分析的指标所包含的因素结合式中，将各因素的基期数字顺次以报告期数字替代，有多少因素就有多少次替代；每次替代所得结果与替代前所得结果进行对比，就是该因素的影响程度，二者的差额就是被替代因素的变动对被分析指标影响的绝对额. 4.因素分析的步骤（1）计算被分析指标的总变动程度和绝对额； （2）计算各因素变动影响程度和绝对额；（3）对影响因素进行综合分析，即总变动程度等于各因素变动程度之连乘积，总变动绝对额等于各因素变动影响绝对额之总和. 三、两因素分析下面结合例子说明，用连锁替代法进行两因素分析的计算过程和实际分析意义.例 某个体服装摊位某月两周销售资料，如表10-2所示.表10-2 某个体服装摊位销售资料进行销售额变动的因素分析.解 销售额变动分析销售额变动指数=110q p q p ∑∑=54402600≈2.092，销售额变动的绝对额=11q p ∑-00q p ∑=5440-2600=2840（元）.销售量变动影响分析销售额变动影响程度=10q p q p∑∑=62002600≈2.385， 销售额变动影响绝对额=10q p ∑-00q p ∑=6200-2600=3600（元）.销售价格变动影响分析销售价格变动影响程度=111q p q p ∑∑=54406200=0.877， 销售价格变动影响绝对额=11q p ∑-10q p ∑=5440-6200= -760（元）.影响因素综合分析110q p q p∑∑=101101q p q p qp q p⨯∑∑∑∑，即2.092≈0.877⨯2.385.11q p ∑-00q p ∑=（10q p ∑-00q p ∑）+（11q p ∑-10q p ∑）， 即2840 = -760 + 3600.分析结果表明：从相对数方面看，该个体服装摊位的销售额第二周比第一周增加了1.092倍，是由于销售量提高了1.385倍和价格下降了12.3%，这两个因素共同作用的结果；从绝对数方面看，该个体服装摊位销售额第二周比第一周增加了2840元，是由于销售量上升使销售额增加了3600元，销售价格下降使销售额减少760元共同作用的结果. 四、多因素分析指数体系因素分析法，可以推广到三个、四个甚至更多因素分析.假如要对企业的产品产量进行因素分析，可将产品产量按下述方式分解产品产量=生产工人数（f ）⨯平均每工人工作天数（a ）⨯平均每天工作小时数（b ）⨯平均每工时产量（c ）.按照连锁替代法，可以得到多因素分析体系1111100011001110111100000000100011001110f a b c f a b c f a b c f a b c f a b cf a b c f a b c f a b c f a b c f a b c =⨯⨯⨯∑∑∑∑∑∑∑∑∑∑，1111f a b c ∑-0000f a b c ∑=（1000f a b c ∑-0000f a b c ∑） +（1100f a b c ∑-1000f a b c ∑） +（1110f a b c ∑-1100f a b c ∑） +（1111f a b c ∑-1110f a b c ∑）.例 某企业生产及劳动的部分资料，如表10-3所示.试分析生产工人数、工人工作天数、每天工作小时数、每小时产量对产量的影响.解（1）产量总指数=11110000f a b c f a b c∑∑=388.572374.5=1.0376. 产量报告期比基期增加了3.76%，绝对额为1111f a b c ∑-0000f a b c ∑= 3885720-3745000 = 140720（件）.（2）工人人数指数=10000000f a b c f a b c∑∑=338.1374.5= 90.28%. 工人人数报告期比基期减少了9.72%，由此而减少的产量为 1000f a b c ∑-0000f a b c ∑= 3381000-3745000 = - 364000（件）. （3）工作日指数=11001000f a b c f a b c∑∑=318.276338.1= 94.14%. 工作日报告期比基期减少了5.86%，由此而减少的产量为1100f a b c ∑-1000f a b c ∑= 3182760-3381000 = -198240（件）.（4）工作时指数=11101100f a b c f a b c∑∑=328.626318.276=118.24%. 工时数报告期比基期提高3.25%，由此而增加的产量为1110f a b c ∑-1100f a b c ∑=3286260-3182760=103500（件）. （5）小时劳动生产率指数=11111110f a b c f a b c∑∑=388.572328.626=118.24%. 小时劳动生产率报告期比基期提高18.24%，由此而增加的产量为1111f a b c ∑-1110f a b c ∑=3885720-3286260=599460（件）.上列计算结果的综合分析130.76%=90.28%⨯94.14%⨯103.25%⨯118.24%， 140720=（-364000）+（-198240）+103500+599460. 分析结果说明，报告期由于小时劳动生产率提高18.24%，工时数提高3.25%和工人人数减少9.72%，工作日减少5.86%，四方面因素综合作用的结果使产量增长3.76%；产量总额增加140720件，主要是由于小时劳动生产率的提高使产量增加599460件，工时数延长，使产量增加103500件.但由于工人人数的精简及劳动日的减少，分别使产量减少364000件和198240件.因此，得出的结论是：企业应该实行减员增效.五、总平均数指数与平均指标变动的因素分析总平均指数也称平均指标指数，它是对总体平均指标变动的测定，如平均工资指数、劳动生产率指数都属于平均指标指数.平均指标指数有两个特点：首先，它是利用分组资料计算的指数.他所测定的总平均数是对组平均数的加权平均，其权数是各组的单位数.总平均数即加权算术平均数，其表示形式为x=/i iix f f ∑∑.式中被平均标志i x 位各组平均水平，权数i f 为各组单位数.它所综合的变量并非不可同度量，而是不同地区、不同单位或不同部门的同一指标，无需采用同度量因素.其次，从作用看，总平均数指数除了测定总平均指标的变动程度外，还测定了总体内部各组平均数变动和各组权数（结构变动）对总平均指标变动的影响.分析平均指标的变动，需要计算以下三种指数 （1）可变构成指数.分析总平均数的变动，计算形式为1001i x f x ff f÷∑∑∑∑.（2）固定构成指数.分析总体内部各组平均水平变动对总平均数的影响，计算形式为10111i x f x ff f÷∑∑∑∑.（3）结构变动影响指数.分析总体内部各组权数（结构变动）对总平均指标变动的影响，计算形式为01001x f x f f f÷∑∑∑∑.可变构成指数、固定构成指数和结构变动指数都是反映复杂现象变动的指数，因此都是总指数.这三个指数存在内在的联系（1）可变构成指数=结构变动指数⨯固定结构指数1100010011011111()()x f x f x f x f x f x f f ff ff f÷=÷⨯÷∑∑∑∑∑∑∑∑∑∑∑∑. （2）总平均数变动绝对额=结构变动影响额+各组平均变动影响额1100010011011111()()x f x fx f x f x f x f f ff ff f -=-+-∑∑∑∑∑∑∑∑∑∑∑∑.下面结合例子说明总平均数指数的计算与应用. 例 某企业职工有关工资资料，见表10-4.从表10-4中的数据可以看出，该企业两类职工的工资水平和人数在基期和报告期都不同，并且变动的幅度也不同，这必然导致该企业报告期和基期的总平均工资水平的变动.解 （1）计算总平均工资变动指数可变构成指数=110010x f x f f f÷∑∑∑∑=883.8828.6=106.67%，变动绝对额=11001x f x f f f-∑∑∑∑=883.8-828.6=55.2（元）.（2）计算各组工资变动影响指数固定构成指数=110111x f x f f f ÷∑∑∑∑=883.8833.8=106.00%， 各组变量水平变动绝对额=110111x f x ff f-∑∑∑∑=883.8-833.8=50（元）. （3）计算结构变动影响指数结构影响指数=01001x f x f f f ÷∑∑∑∑=883.8828.6=100.63%， 结构影响变动绝对额=01001x f x ff f-∑∑∑∑=883.8-828.6=5.2（元）. 所以总平均工资指数=结构变动影响指数⨯各组平均工资变动影响指数 即106.67%=100.63%⨯106.00%；总平均工资变动绝对额=结构变动影响额+各组工资变动影响额 即111x f f ∑∑-00x f f∑∑=（011x f f ∑∑-00x f f∑∑）+（111x f f ∑∑-011x f f∑∑），亦即883.8-828.6=（833.8-828.6）+（883.8-833.8），则55.2=5.2+50.分析结果表明，从相对数方面看，该企业总平均工资报告期比基期上涨了6.67%，这是因为各组职工工资水平变动使总平均工资上涨6.00%，职工结构变动影响使总平均工资上涨0.63%，二者共同作用的结果；从绝对数方面看，该企业总平均工资报告期比基期增加55.2元，这是因为各组职工工资水平变动使总平均工资增加50元，职工结构变动影响使总平均工资增加5.2元的共同结果.第五节 指数的应用一、居民消费价格指数居民消费价格指数在国外也被称为消费者价格指数（Consumer Price Index ，简记为CPI ），是反映一定时期居民支付所购买的生活消费品价格和获得服务项目趋势和程度的一种相对数，它可以观察居民生活消费品及服务项目价格的变动对居民生活的影响，为各级政府掌握居民消费价格政策、工资政策以及为新国民经济核算体系中消除价格变动因素的核算提供科学依据.居民消费价格指数还是反映通货膨胀的重要指标.居民消费价格指数上升，意味着货币购买力下降，货币贬值；反之，居民消费价格指数下降，意味着货币购买了上升，货币增值.居民消费价格指数的倒数，就是货币购买力指数. 二、股票价格指数 （一）股票与股票价格指数股票是股份公司发行给股东的，证明持股人对公司部分资产拥有所有权的证明.股份作为公司的构成成分，它是一种价值的反映，可以用货币加以度量.股票是股份的表现形式，因此它是一种有价证券股票价格指数（Stock price index ）是反映某一股票市场上多种股票价格变动趋势的一种相对数，简称股价指数.其单位一般用“点”（point ）表示，即将基期指数作为100，没上升或下降一个单位称为“一点”.股票价格指数的编制方法有多种，综合指数公司是其中的一种重要方法.我国的上证指数、美国标准普尔指数、香港恒生股票指数等，都是采用综合指数公式编制.其计算公式为00r p p q k p q =∑∑. （10.26）式（10.26）是以基期的股票发行量（或流通量）为同度量因素的拉式综合指数.式中0q 代表基期股票发行量（活流通量）. （二）几种主要的股票指数 1.道 琼斯股票价格平均指数 2.标准普尔指数3.伦敦《金融时报》股票价格指数4.日经指数5.我国几种股价指数本章小结：1．指数是用来分析社会经济现象数量变动的对比性指标.广义指数是用来测定社会经济现象中一个变量值对另一个特定的变量值大小的相对数.狭义指数是一种特殊的相对数，是表明不能直接相加和对比的复杂现象总体综合变动程度的相对数.2．综合指数的编制特点是先综合后对比.编制综合指数必须明确指数化指标和同度量因素，指数化指标是被测定的因素，同度量因素也即权数，作为同度量因素的指标固定在哪个时期上，不是固定不变的。
统计学 指数习题及答案
第十章统计指数一、填空题1．狭义指数是反映复杂现象总体变动的2.指数按其所反映的对象范围的不同，分为指数和指数。
3.指数按其所标明的指标性质的不同，分为指数和指数。
4.指数按其采用基期的不同，分为指数和指数。
5. 指数是在简单现象总体条件下存在的，指数是在复杂现象总体的条件下进行编制的。
6.总指数的计算形式有两种，一种是指数，一种是指数。
7.按照一般原则，编制数量指标指数时，同度量因素固定在，编制质量指标指数时，同度量因素固定在。
8.在编制质量指标指数时，指数化指标是指标，同度量因素是与之相联系的指标。
9.综合指数编制的特点，一是选择与指标相联系的同度量因素，二是把同度量因素的时期。
10.拉氏指数对于任何指数化指标的同度量因素都固定在，派氏指数对于任何指数化指标的同度量因素都固定在。
11.编制指数的一般方法是：指数是按拉氏指数公式编制的；指数是按派氏指数公式编制的。
12．综合指数的编制方法是先后。
13．编制综合指数时，与指数化指标相联系的因素称，还可以称为。
14.平均指数的计算形式为指数和指数。
15.平均指数是先计算出数量指标或质量指标的指数，然后再进行计算，来测定现象的总变动程度。
16.在编制平均指数时，算术平均数指数多用为权数，调和平均数指数多用为权数。
17.数量指标的算术平均数指数，在采用为权数的特定条件下，和一般综合指数的计算结论相同；而质量指标的调和平均数指数，在采用为权数的特定条件下，计算结果和综合指数一致。
18.编制数量指标平均指数，一是掌握，二是掌握。
19.编制质量指标平均指数，一是掌握，二是掌握。
20.在零售物价指数中，K表示，W表示。
21.平均指数既可依据资料编制，也可依据资料编制，同时还可用估算的权数比重进行编制计算。
22.因素分析包括数和数分析。
23.总量指标二因素分析是借助于来进行，即当总量指标是两个原因指标的时，才可据此进行因素分析。
24指数体系中，指数之间的数量对等关系表现在两个方面：一是结果指数等于因素指数的，二是结果指数的分子分母之差等于各因素指数的。