对流和辐射计算公式
传热效率计算公式
传热效率计算公式传热效率是指在传热过程中所消耗的能量与所传递的能量之间的比值。
计算传热效率的公式可以通过不同传热方式来确定。
下面将分别介绍对流传热、辐射传热和传导传热的传热效率计算公式。
一、对流传热的传热效率计算公式：对流传热是指通过传热介质（如气体或液体）进行传热的方式。
对流传热效率通常由Nu数（Nusselt数）来表示，可以通过以下公式进行计算：Nu=h*L/λ其中，Nu为Nusselt数，h为对流传热系数（W/(m^2·K)），L为待传热表面的特征长度（m），λ为传热介质的导热系数（W/(m·K)）。
传热效率η可以通过Nusselt数（Nu）和表面积比（A^*）来计算，公式如下：η=Nu*A^*/A其中，A^*为受热表面积，A为总表面积。
二、辐射传热的传热效率计算公式：辐射传热是指通过电磁波辐射进行传热的方式。
辐射传热效率可以通过以下公式计算：η=q/(σ*A*(T1^4-T2^4))其中，q为辐射传热速率（W），σ为斯特藩-玻尔兹曼常数（5.67×10^(-8)W/(m^2·K^4)），A为辐射表面积（m^2），T1和T2为被辐射表面和周围环境的温度（K）。
三、传导传热的传热效率计算公式：传导传热是指通过物质内部原子、分子之间的振动或传递方式进行传热的方式。
传导传热效率可以通过以下公式计算：η=(T1-T2)/(T1-T∞)其中，T1为热源温度（K），T2为待传热物体的温度（K），T∞为周围环境温度（K）。
综上所述，传热效率的计算公式取决于传热方式的不同。
通过对流传热、辐射传热和传导传热的计算公式的运用，可以有效地评估和分析传热系统的传热效率。
传热温差计算公式
传热温差计算公式
1.热传导传热温差计算公式：
热传导是指由于物体内部的温度差异而发生的传热现象。
热传导传热温差计算公式如下：
ΔT=Q/(k·A·L)
其中，ΔT为传热温差，Q为传热量，k为物体的热导率，A为传热面积，L为传热距离。
2.对流传热温差计算公式：
对流是指由流体的流动而引起的传热现象，常用公式如下：
ΔT=Q/(h·A)
其中，ΔT为传热温差，Q为传热量，h为对流换热系数，A为传热面积。
3.辐射传热温差计算公式：
辐射是指由于物体的热辐射而引起的传热现象。
辐射传热温差计算公式如下：
ΔT=(Σε·A·σ·T^4-Σε·A·σ·T^4)/(ε·A·σ)
其中，ΔT为传热温差，Σε为发射率乘以表面积的总和，σ为斯特藩-玻尔兹曼常数，T为物体的温度，ε为物体的发射率。
需要注意的是，传热温差的计算公式可能会根据具体的传热方式以及实际情况进行修正。
例如，在对流传热中，对流换热系数h的计算可能需要考虑流体的传热特性以及流动方式。
传热温差是传热计算中一个重要的参数，它的大小直接影响传热量的大小。
传热温差越大，传热量也越大。
因此，准确计算传热温差对于正确估计传热过程中的热量交换是非常重要的。
需要说明的是，以上仅是常见的传热温差计算公式，实际应用中可能还会有其他因素进行修正和考虑。
具体的计算公式应根据实际情况和具体问题进行选择。
传热学计算总结
《传热学》计算题总结一、 题型导热换热、对流换热、辐射换热、换热器 二、 公式小结1、 平壁稳态导热 第一类边界条件： 1） 单层：xt t t t w w w δ121--=221/)(m W t t q w w -=δλ多层∑∑=+=+-=-=ni in n i i in R t t t t q 1,11111λλδ第三类边界条件：传热问题2112111h h t t q n i i f f ++-=∑=λδ单位W/m 22、 圆筒壁稳态导热第一类边界条件 单层：121121r r n r r nt t t t w w w =--()12212112212r r n l t t t t r r n lw w w w πλπλ-=-=Φ多层：∑=++-=Φn i ii i n w w r r n l t t 111,1121 λπ第三类边界条件：1211112121ln 2121+=+++-=∑n n i i if f l r h ri r r h t t q ππλπ单位：W/m3、 对流换热 牛顿冷却公式：[]W )(f w t t hA Φ-=吸放热热量（热对流）：tvc t t mc p f f p ∆=-=Φρ)(21平板对流换热表面换热系数h管内对流换热表面换热系数h ：n Nu Pr Re023.08.0=（紊流，流体被加热n=0.4,流体被冷却 n=0.3）对流换热解题步骤1）定性温度→查物性，下标f 由t f 确定，下标w 由t w 确定； 2）由Re 判断流态；3）据Re 选择准则关联式计算Nu f ； 4）计算h 。
注意：1）外掠平板定性温度tm=1/2(tw+tf);管内定性温度tf 2）外掠平板临界Re=5×105；管内临界Re=104 3）换热量据牛顿冷却公式计算。
4、辐射换热斯蒂芬－玻尔兹曼定律（四次方定律）: （黑体）两表面封闭体系的辐射换热量：（实际表面）几种特殊情况的简化式： （a ） X 1-2=1时：（其中一个表面为平面或凸表面）（b ）A 1=A 2 时：（两无限大平壁之间）(c) A 1/A 2≈0 时 （空腔与内包壁）遮热板：111)T T (21214241b 2,1-+-=εεσq5、换热器设计计算传热过程方程式m t kA ∆=Φ；minmax minmax t lnt t t t m ∆∆∆-∆=∆热平衡式)()(22221111t t c M t t c M '-''=''-'=Φ， 其中M 为质量流量kg/s,c 为定压比热，由对应算术平均温度确定。
空气散热计算公式
空气散热计算公式空气散热是指通过空气传递热量，以降低物体的温度。
在实际应用中，我们常常需要计算空气散热的量，以确定适当的散热方式和散热设备。
本文将介绍一些常见的空气散热计算公式。
一、传热功率传热功率指的是单位时间内传递给或从物体中流动的热量，通常用单位时间内传热量的绝对值表示，单位为瓦特（W）。
对于空气散热，传热功率可以通过以下公式计算：Q=h*A*ΔT其中，Q表示传热功率，h表示传热系数，A表示热交换面积，ΔT表示物体温度与环境温度之间的温差。
传热系数h是一个物质特性，取决于流体的性质、流动方式、流速等因素。
对于空气散热而言，传热系数一般需要通过实验测定或参考经验值。
热交换面积A是指热量传递的表面积。
对于平板形式的热交换器，热交换面积等于散热片的表面积。
温差ΔT是指物体温度与环境温度之间的差值。
在实际计算中，可以使用摄氏度或开尔文温标进行表示。
二、对流传热在空气散热中，传热主要是通过对流传热实现的。
对流传热是由于流体动力学引起的热量传递，可以通过以下公式计算：Q=h*A*ΔT其中，Q表示传热功率，h表示对流传热系数，A表示传热面积，ΔT 表示物体温度与环境温度之间的温差。
对流传热系数h是一个关于流动速度、气体性质和传热面积的函数。
对于自然对流（即无外力作用的对流），传热系数一般较低；而对于强制对流（即外力作用下的对流），传热系数一般较高。
传热面积A是传热的表面积，可以视具体情况选择合适的计算方法。
温差ΔT是物体温度与环境温度之间的差值，可以使用摄氏度或开尔文温标进行表示。
三、辐射传热辐射传热是指通过电磁辐射（主要是红外辐射）进行的热量传递。
辐射传热是一个复杂的过程，一般需要通过辐射传热系数来描述。
辐射传热可以通过以下公式计算：Q=ε*σ*A*(T1^4-T2^4)其中，Q表示传热功率，ε表示辐射率，σ表示史蒂芬-波尔兹曼常数，A表示辐射传热面积，T1和T2分别表示物体表面温度和环境温度。
辐射率ε是一个描述物体辐射特性的参数，取决于物体表面材料、几何形状和表面状况等因素。
自然散热情况下辐射和对流哪个占主导作用
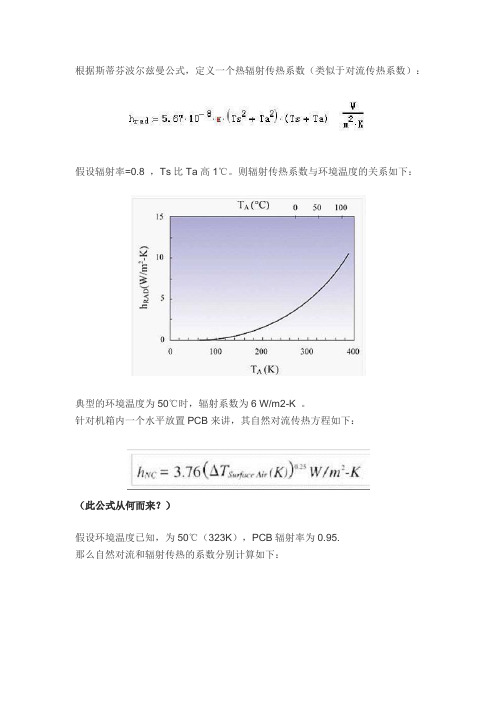
根据斯蒂芬波尔兹曼公式，定义一个热辐射传热系数（类似于对流传热系数）：假设辐射率=0.8 ，Ts比Ta高1℃。
则辐射传热系数与环境温度的关系如下：典型的环境温度为50℃时，辐射系数为6 W/m2-K 。
针对机箱内一个水平放置PCB来讲，其自然对流传热方程如下：（此公式从何而来？）假设环境温度已知，为50℃（323K），PCB辐射率为0.95.那么自然对流和辐射传热的系数分别计算如下：从图中可以看出，在温差<20℃（K）时，辐射传热系数大于自然对流系数。
温差超过20℃时，两种传热系数几乎相等。
所以在温差较小时，辐射传热一定不能被忽略。
当然，实际情况千差万别，但这个简单的例子可以帮助建立一些基本的概念。
Don't underestimate radiation in electronic coolingFebruary 1, 2001 Bruce GueninCalculation Corner, Design, Number 1, Volume 7Heat Transfer Coefficient, Stephan-Boltzmann Constant, Thermal Radiationdon’t underestimate radiation in elec tronics coolingBruce M. Guenin, Ph.D., Associate Editor, Amkor Technology, Inc.It is easy to underestimate the role of thermal radiation as a significant contributor to electronics cooling in environments without forced air flow. By its very nature it is invisible. The propertreatment of it can be intimidating due to the complicated nature of thephenomenon in environments in which localized hot regions are in the view of other localized hot regions.However, it is possible to get a basic understanding of radiation without even worrying about such complications as view factors.The first thing to do is to respond to the basic engineering urge tolinearize anything possible. Hence, Equation 1 is a recasting of the familiar Stephan-Boltzman equation, dividing it by the temperature difference between a surface (assumed isothermal) and the facing surface(assumed to be at the air temperature). The result is a heat transfer coefficient, which represents the effect of radiation at a given temperature.The numerical factor is the Stephan-Boltzmann constant and is the emissivity. The emissivity is inthe range 0.8 – 0.9 for dielectrics and 0.1 – 0.2 for commercial metals. The temperatures are expressed in absolute temperature Kelvin units.Figure 1. Temperature dependence.Even though we have linearized the S-B equation, the resultant heat transfer coefficient is still highlytemperature-dependent. In fact, it is proportional to the third power of the absolute temperature. Figure 1 illustrates this temperature dependence, where we have assumed an emissivity of 0.8 and atemperature difference between the surface and the air of 1°C.The lower x axis indicates absolute temperature.The upper x axis indicates degrees centigrade in therange of interest to electronics cooling. At a typical ambient temperature range, say around 50°C, h RAD is approximately 6 W/m2-K.It is useful to compare the radiation heat transfer coefficient to the heat transfer coefficient applicableto a horizontal printed circuit board in a large enclosure. This expression represents an average for heat transfer from the top and bottom surfaces of the board [1].The following graph, Figure 2, compares the magnitude of the radiation and natural convection heat transfer coefficients as a function of the temperature difference between the surface and airtemperature, where the air temperature is assumed to be 50°C.Figure 2. Magnitude of radiation and natural convection heat transfer coefficients.One sees that the h RAD is actually greater than h NC up to a temperature difference of about 25°C. For temperature differences exceeding this, they are nearly equal.In more realistic situations, the details of radiation heat transfer can be very complicated. The relativeheat transfer by radiation and natural convection can differ significantly from that demonstrated in this comparatively simple example. However, the fact remains that radiation heat transfer is significant inmany natural convection cooling situations and must not be overlooked.Reference1 B. S. Lall, B. M. Guenin, R. C. Marrs, and R. J. Molnar, “Parametric FEA Thermal Model forQFP Packages,” Proceedings, SEMI-THERM XII Conference, March, 1996, pp. 105-110.。
热量传递的三种基本方式导热(热传导)、对流(热对流)和热辐射。
一. 大空间自然对流换热的实验关联式 工程中广泛使用的是下面的关联式：
l / d 60
层流
湍流
二. 横掠管束换热实验关联式
• 外掠管束在换热器 中最为常见。 • 通常管子有叉排和 顺排两种排列方式。 顺叉排换热的比较： 叉排换热强、阻力 损失大并难于清洗。 影响管束换热的因 Pr 素除 Re 、 数外，还 有：叉排或顺排； 管间距；管束排数 等。
后排管受前排管尾流的扰动作用对平均表面传热系数的影 响直到10排以上的管子才能消失。 这种情况下，先给出不考虑排数影响的关联式，再采用管 束排数的因素作为修正系数。 气体横掠10排以上管束的实验关联式为
(5) 流体的热物理性质：
3 密度 [kg m ] 热导率 [ W (m C) ] 2 比热容 c [J (kg C) ] 动力粘度 [ N s m ] 运动粘度 [m 2 s] 体胀系数 [1 K ]
1 v 1 v T p T p
Nu c Re n Nu c Re n Pr m Nu c(Gr Pr)n
式中，c、n、m 等需由实验数据确定，通常由图解法和 最小二乘法确定
④常见准则数的定义、物理意义和表达式，及其各量的 物理意义
⑤模化试验应遵循的准则数方程 强制对流:
Nu f (Re, Pr)； Nu x f ( x ' , Re, Pr)
导热热阻：平壁，圆筒壁
q
t w1 t w 2 t w1 t w 2
t r t R
t
t w1
dt
dx
Φ
A
Q
0
tw2
R A
r
热量损失计算公式物理解释
热量损失计算公式物理解释热量损失是指物体在与外界环境接触时，由于温度差异而导致的热量流失。
热量损失的计算对于建筑物的保温设计、工业生产过程中的能量消耗等都具有重要意义。
在物理学中，热量损失可以通过热传导、对流和辐射等方式发生，而热量损失的计算公式可以通过这些热传导方式的物理原理来解释。
热传导是物体内部分子间的热量传递过程，当物体与外界环境温度存在差异时，热传导会导致热量从高温区向低温区传递，从而导致热量损失。
热传导的计算公式可以通过热传导方程来表示，即热传导率乘以温度差异除以物体的厚度。
这个公式的物理意义是描述了热传导过程中热量损失的速率，热传导率越大、温度差异越大、物体厚度越小，热量损失也就越大。
对流是指物体表面与流体（空气或液体）之间的热量传递过程，当流体与物体表面温度存在差异时，对流会导致热量从物体表面向流体传递，从而导致热量损失。
对流的计算公式可以通过牛顿冷却定律来表示，即对流换热系数乘以温度差异。
这个公式的物理意义是描述了对流过程中热量损失的速率，对流换热系数越大、温度差异越大，热量损失也就越大。
辐射是指物体表面向外界环境发射或吸收电磁波的过程，当物体表面温度高于外界环境时，辐射会导致物体向外界环境发射热量，从而导致热量损失。
辐射的计算公式可以通过斯特藩-玻尔兹曼定律来表示，即辐射率乘以温度的四次方。
这个公式的物理意义是描述了辐射过程中热量损失的速率，辐射率越大、温度的四次方越大，热量损失也就越大。
综合以上三种热传导方式，热量损失的总计算公式可以表示为：Q = U A (T1 T2)。
其中，Q表示热量损失，U表示总的传热系数，A表示传热面积，T1表示内部温度，T2表示外部温度。
这个公式的物理意义是描述了物体与外界环境之间热量损失的速率，传热系数、传热面积、温度差异都会影响热量损失的大小。
在建筑保温设计中，热量损失的计算公式可以帮助工程师评估建筑物保温效果，选择合适的保温材料和保温结构。
化工原理 传热 习题课公式
ln A 1
d1
二、对流给热 1.对流传热基本方程式---------牛顿冷却定律 t t t T TW tW t
Q At
1 A
R
T、t 平均温度
2.与对流传热有关的准数
l Nu
努塞尔数
lu Re
雷诺数
cp
对平壁或薄圆壁：
1 1 1 R1 R2 K 1 2
4、热量衡算式
热流体：无相变时 ，Q = ms1cp1( T1-T2 ) 有相变时， Q = ms1[r1+cp1( T1-T2 )] 冷流体：无相变时 ，Q = ms2cp2( t2-t1 ) 有相变时， Q = ms2[r2+cp2(t2-t1 )] 根据不同的情况计算传热量，如
2
3
1/ 3
Re 0.4 M
r g 0.725 dt
2
3
1/ 4
三、热辐射
斯蒂芬-波尔茨曼定律（四次方定律）
E0 T
4
斯蒂芬 波尔兹曼常数: 5.67 10 8W / m2 K 4
黑体发射系数：C0 5.67W / m 2 K 4
Pr
gtl 3 2 Gr 2
格拉斯霍夫数
普朗特数
3.流体在圆形直管中作强制对流
（1）强制湍流时：
对气体或低粘度的液体：
Nu 0.023Re Pr
0.8
b=
b
或
du 0.8 cp b 0.023 ( ) ( ) d
=0.4被加热 =0.3被冷却
对粘度高或温差较大的液体：
du 0.8 c p 0.33 0.14 0.027 ( ) ( ) ( ) d w
传热公式
定性温度 定性 准则数
关联式
换热温差
传热量
尺寸
外掠平 板
tm=
t∞
+ 2
tw
管内流 动
t
m
=
t
' f
+
t
" f
2
横掠圆 管
tm=
t∞
+ 2
tw
l
Re = ul γ
Nux
=
hl λ
=
0.332Re1 2
Pr1 3
Δt = tw − t∞ Q = hA(tw − t∞ )
Nu = hl Nu = hl = 0.664Re1 2 Pr1 3
Lambert 定律，Wien 位移定律， Kirchhoff 定律； 3. 两个近似：灰表面，漫射面 4. 发射辐射概念：辐射力，光谱辐射力，定向辐射力，辐射强
度，投射辐射 5. 几个系数：发射率，光谱发射率，定向发射率，
吸收比，光谱吸收比，穿透比，反射比； 6. 其它重要概念：立体角，选择性吸收
Φ
tw1
tw2
δ
t f2，h2
传热过程的剖析
( ) Φ
=
A 1
tf1 −tf2
+δ + 1
h1 λ h2
( ) Φ = kA t f 1 − t f 2 = kAΔt
传热系数，[W m 2K ]
传热方程式
一维稳态传热过程中的热量传递
传热系数：
是指用来表征传热过程强烈程度的指标，不 是物性参数，与过程有关。
(3) 可加性
如图所示，表面2可分为2a和2b两个面，当然 也可以分为n个面，则角系数的可加性为
n
传热热负荷的计算公式
传热热负荷的计算公式
传热热负荷是指单位时间内通过物体的热量，通常用单位功
率（W）表示。
计算传热热负荷的公式根据具体情况而定，常
用的计算公式如下：
1.对流传热热负荷计算公式：
传热热负荷=对流换热系数×整体传热面积×温度差
其中，对流换热系数表示物体表面与流体之间的传热能力，
单位为W/(m^2·K)；整体传热面积表示物体的传热面积的总和，单位为m^2；温度差表示物体表面温度和流体温度之间的差值，单位为K。
2.辐射传热热负荷计算公式：
传热热负荷=辐射系数×表面发射率×整体传热面积×(表面温度^4环境温度^4)
其中，辐射系数为StefanBoltzmann常数，值约为
5.67×10^(8)W/(m^2·K^4)；表面发射率表示物体表面的辐
射能力，取值范围为0到1；表面温度为物体表面的温度，单
位为K；环境温度为物体周围环境的温度，单位为K。
3.导热传热热负荷计算公式：
传热热负荷=热传导系数×整体传热面积×温度差/物体厚度
其中，热传导系数表示物体对热传导的能力，单位为
W/(m·K)；整体传热面积表示物体的传热面积的总和，单位为m^2；温度差表示物体的两侧温度差值，单位为K；物体厚度表示传热的距离，单位为m。
需要注意的是，以上计算公式仅适用于特定情况下的传热热负荷计算，具体的计算公式还需要针对具体的应用场景和热传导方式进行选择和修正。
在实际应用中，可以根据具体需求和实际情况选择适合的计算公式进行计算。
辐射传热计算公式
辐射传热计算公式辐射传热是物体表面和另一物体间传热机制中最重要的类型，它涉及传热过程中表面物体间的能量交换。
传热公式是用来描述表面物体及其交换质量之间能量交换关系的公式，通常被用于辐射对流复合传热中计算传热量的公式。
辐射传热计算公式的基本原理是表面物体之间的能量交换。
它的计算公式可以分为两部分：一部分是用来计算物体表面辐射热传递系数，指出从物体表面向外传递的热量；另一部分是用来计算对流热传递系数，指出物体表面周围的气体和其它物体的热量交换情况。
辐射传热计算公式的具体表达式是：Q=εσAT(T1^4-T2^4)式中：Q表示物体表面之间散热量，单位为W；ε表示物体表面辐射热传递系数；σ表示摩尔辐射常数，单位是W/m^2K^4；A表示物体表面面积；T1和T2分别表示表面物体两端温度，单位是K。
由于物体表面辐射热传递系数ε和对流热传递系数α之间比例关系的存在，因此在辐射对流复合传热过程中，计算传热量的公式为： Q=αAT（T1-T2）式中：Q表示物体表面之间散热量，单位为W；α表示物体表面对流热传递系数；A表示物体表面面积；T1和T2分别表示表面物体两端温度，单位是K。
从上面所介绍的两个传热公式可以看出，计算传热量时，要根据传热的机制，准确的计算物体表面的辐射热传递系数ε和对流热传递系数α以及物体表面面积A，物体表面两端温度T1和T2之间的差值，才能准确的计算出传热量。
计算传热量公式的正确应用可以用于提高物体表面的温度，降低物体表面的温度，改善传热效率，提高设备性能，确定加热器或冷却器的设计参数等。
因此，辐射传热计算公式对于机械工程、热能工程等领域有着重要的意义。
因此，在实际应用中，要根据不同情况，选择合适的传热公式来计算，以确保传热仿真的准确性和可靠性。
此外，还要注意表面物体的性质，如比热容、热导率等，只有正确的参数，才能确保仿真计算结果。
综上所述，辐射传热计算公式对于物体表面间的能量交换机制的研究具有重要的意义，它涉及表面物体间的辐射热传递系数、对流热传递系数、物体表面面积、温度等重要参数，这些参数的准确计算才能保证传热仿真的准确性与可靠性，从而可以实现物体表面的温度控制，提高物体表面的温度控制效果，为机械工程、热能工程的发展做出贡献。
热传导三种方式公式
热传导三种方式公式热传导是指热量通过材料的传递，通常有三种方式：传导、对流和辐射。
1. 传导（Conduction）：传导是通过材料的直接接触而传递热量的方式。
它是由分子之间的碰撞和振动所引起的能量传递。
传导的热传递率由 Fourier 定律来描述，其公式为：Q=k*A*(ΔT/d)其中，Q是传导热流量，单位为瓦特（W），k是材料的热导率，单位为瓦特/（米·开尔文），A是传热的横截面积，单位为平方米（m²），ΔT是温度差，单位为开尔文（K），d是传热路径的长度，单位为米（m）。
传导的热传递率与材料的导热性能、温度差和传热距离有关。
热导率越大，热传导速率越快。
当温度差增大或传热距离减小时，热传导速率也会增加。
2. 对流（Convection）：对流是指通过材料内部的流体运动而传递热量的方式。
对流一般包括自然对流和强迫对流两种形式。
自然对流是通过流体本身的密度和温度的差异产生的传热方式。
自然对流的热传递率可以由 Nuussult 数来计算，其公式为：Nu=h*L/λ其中，Nu 为 Nuussult 数，L 为流体流动路径的特征长度，单位为米（m），h 是传热系数，单位为瓦特/（平方米·开尔文）（W/（m²·K）），λ 为流体的导热系数，单位为瓦特/（米·开尔文）（W/（m·K））。
强迫对流是通过外部施加的压力或机械力引起的传热方式。
对流的热传递率与流体的性质、流速、温度差和流动路径有关。
3. 辐射（Radiation）：辐射是通过电磁波的辐射来传递热量的方式。
辐射传热不需要物质的存在，可以在真空中传播。
辐射的热传递率可以由Stefan-Boltzmann 定律来计算，其公式为：Q=ε*σ*A*(T₁⁴-T₂⁴)其中，Q 是辐射热流量，单位为瓦特（W），ε 是表面的辐射发射率，σ 是 Stefan-Boltzmann 常数，约为5.67 × 10⁻⁸瓦特/（平方米·开尔文的四次方）（W/（m²·K⁴）），A 是辐射传热的表面积，单位为平方米（m²），T₁和 T₂分别是两个表面的温度，单位为开尔文（K）。
对流和辐射计算公式
对流和辐射计算公式流和辐射计算公式是在热力学和辐射传热学中广泛应用的公式，用于计算热量和热能的传递。
一、流计算公式1.线热流密度（q）计算公式：线热流密度是单位时间内通过单位长度的传热量，通常以瓦特/米表示。
q=λ*ΔT/Δx其中，q表示线热流密度，λ表示热导率，ΔT表示温度差，Δx表示传热距离。
这个公式适用于常导热系数情况下的传热。
2.对流热传导公式（q）：对流热传导是通过流体（气体或液体）传递热量的过程，可以通过以下公式计算：q=h*A*ΔT其中，q表示热量传递速率，h表示对流传热系数，A表示传热面积，ΔT表示温差。
3.对流传热系数（h）计算：对流传热系数是对流热传导中的一个参数，它表示单位面积传递的热量。
对于强制对流和自然对流，其计算公式分别为：对于强制对流：h=Nu*λ/L对于自然对流：h=Nu*λ/Lf其中，h表示传热系数，Nu表示努塞尔数，λ表示热导率，L表示流动方向的特征长度，Lf表示特征长度。
4.热传导效应（Bi）：热传导效应是描述对流与热传导相对重要性的参数，可以用如下公式计算：Bi=h*L/λ其中，Bi表示热传导效应，h表示对流传热系数，L表示特征长度，λ表示热导率。
当Bi<0.1时，热传导可以忽略不计；当Bi>0.1时，热传导效应非常重要。
1.斯特藩-玻尔兹曼定律：根据斯特藩-玻尔兹曼定律，一个黑体单位时间内发射的辐射功率（P）与其绝对温度（T）的四次方成正比，可以用以下公式表示：P=σ*ε*A*T^4其中，P表示辐射功率，σ为斯特藩-玻尔兹曼常数（5.67*10^-8W/(m^2·K^4)），ε表示发射率，A表示表面积，T表示绝对温度。
2.斯特藩-玻尔兹曼定律（应用于非黑体）：对于非黑体，通过引入一个修正因子，斯特藩-玻尔兹曼定律可以表示为：P=σ*ε*A*T^4*F其中，P表示辐射功率，σ为斯特藩-玻尔兹曼常数，ε表示发射率，A表示表面积，T表示绝对温度，F表示修正因子。
物理热量计算公式全部
物理热量计算公式全部热量的定义和基本概念。
热量是物体内部的能量，是由于分子、原子和离子的运动而产生的一种能量。
在物理学中，热量是热力学系统中的一种能量形式，通常用符号Q表示。
热量的单位是焦耳（J）或卡路里（cal）。
热量的传递方式。
热量可以通过传导、对流和辐射等方式传递。
传导是指热量通过物质内部的分子振动和碰撞传递的过程。
对流是指热量通过流体的运动传递的过程，如空气和水的对流。
辐射是指热量通过电磁波辐射传递的过程，如太阳光的辐射。
热量的计算公式。
热量的计算公式可以根据热力学定律和热传导定律来推导。
以下是一些常见的热量计算公式：1. 热量的传导计算公式。
热量的传导计算公式可以用热传导定律来表示，即：Q = k A (T2 T1) / d。
其中，Q表示传导热量，k表示热导率，A表示传热面积，T2和T1表示两个温度，d表示两个温度之间的距离。
2. 热量的对流计算公式。
热量的对流计算公式可以用牛顿冷却定律来表示，即：Q = h A (T2 T1)。
其中，Q表示对流热量，h表示对流换热系数，A表示传热面积，T2和T1表示两个温度。
3. 热量的辐射计算公式。
热量的辐射计算公式可以用斯特藩-玻尔兹曼定律来表示，即：Q = εσ A (T2^4 T1^4)。
其中，Q表示辐射热量，ε表示发射率，σ表示斯特藩-玻尔兹曼常数，A表示辐射面积，T2和T1表示两个温度。
热量的单位换算。
热量的单位换算是物理学中常见的计量问题。
常见的热量单位有焦耳（J）和卡路里（cal）。
1焦耳等于4.184卡路里，1千焦等于1000焦耳，1千卡等于1000卡路里。
热量的应用。
热量在生活和工业中有着广泛的应用。
在生活中，人们常常使用热量来烹饪食物、取暖、制冷等。
在工业中，热量被用来发电、生产化工产品、加工金属等。
总结。
热量是物体内部的能量，是热力学系统中的一种能量形式。
热量可以通过传导、对流和辐射等方式传递。
热量的计算公式可以根据热传导定律、牛顿冷却定律和斯特藩-玻尔兹曼定律来推导。
水冷散热理论计算公式
水冷散热理论计算公式水冷散热是一种通过水来散热的技术，广泛应用于计算机、工业设备等领域。
水冷散热的原理是利用水的高热传导性和大比热容来传递热量，从而实现散热的目的。
水冷散热的理论计算公式涉及热传导、热对流和热辐射等方面的知识，下面将详细介绍。
一、热传导方面的计算公式：热传导是指热量通过固体物体内部的传导方式传递的现象。
对于水冷散热而言，热传导是水冷散热的基本机制之一、下面是几个常用的热传导计算公式：1.热传导率公式：热传导率是指单位厚度和单位温度梯度下的热传递率。
对于固体物体而言，热传导率是一个常量。
在水冷散热中，热传导率可以通过测量得到或者查表获得。
2.热传导公式：根据热传导定律，热流量（Q）等于热传导率（λ）乘以传热面积（A），再乘以温度梯度（ΔT）。
即Q=λ*A*ΔT。
这个公式可以用来计算热量在固体物体中的传导情况。
3.热阻计算公式：热阻是指单位面积和单位温度差下，热量通过材料时所遇到的阻力。
对于水冷散热器来说，热阻是指冷却水流过散热设备时所遇到的阻力。
热阻的计算公式是:R=ΔT/Q，其中ΔT代表温度差，Q代表热流量。
二、热对流方面的计算公式：热对流是指热量通过流体以对流方式传递的现象。
对于水冷散热器而言，冷却水通过设备表面形成的薄膜进行传热，这涉及到了热对流的问题。
热对流的计算公式如下：1.弗劳德数计算公式：弗劳德数是用来描述流体对流传热和热传导传热的相对大小的一个参数。
计算弗劳德数的公式是：Fr=ρ*v^2/(g*L)，其中Fr代表弗劳德数，ρ代表流体密度，v代表流体速度，g代表重力加速度，L代表特征长度。
2.努塞尔数计算公式：努塞尔数是用来描述热对流的强弱程度的一个参数。
计算努塞尔数的公式是：Nu=α*L/λ，其中Nu代表努塞尔数，α代表对流传热系数，L代表特征长度，λ代表热传导率。
3.对流传热计算公式：根据努塞尔数，可以计算出对流传热系数。
对流传热系数是指单位面积上的热流量与温度差之比。
热传导三种方式公式
热传导三种方式公式热传导是指物体内部或不同物体之间因温度差异而产生热量传递的现象。
热传导过程可以通过三种方式进行：热对流、热辐射和热传导。
本文将分别介绍三种热传导方式及其公式。
1.热对流热对流是指流体（气体或液体）在物体表面或内部通过对流方式进行热传递。
在流体中，热量传递是通过流体分子间的碰撞实现的。
热对流的公式如下所示：Q=hAΔT其中，Q为热量，h为热传递系数，A为传热面积，ΔT为温度差异。
热传递系数h是由流体的性质、流速、传热面积等因素决定的，通过实验得到的。
例如，一个半径为10cm的球体，其表面与气体接触，气体温度为30℃，球体内部温度为100℃，求其表面每秒钟传递多少热量？解：首先计算出表面积，A=4πr²=4π某10²=1256.64cm²。
然后选择恰当的热传递系数，假设为h=10W/(m²·K)，将其转换为cm单位，得h=0.1W/(cm²·K)。
最后代入公式得到：Q=hAΔT=0.1某1256.64某(100-30)=940.98W。
2.热辐射热辐射是指物体通过辐射方式进行热传递，而不需要介质来传递热量。
所有物体都可以辐射热量，其公式如下所示：Q=σεA(T₁⁴-T₂⁴)其中，Q为热量，σ为斯特腾-玻尔兹曼常数，ε为辐射率，A为表面积，T₁和T₂分别为两侧物体的绝对温度。
斯特腾-玻尔兹曼常数σ是一个物理常数，其数值为5.67某10⁻⁸W/(m²·K⁴)，可以通过实验测定得到物体的辐射率ε。
例如，一个黑色矩形板，长50cm、宽30cm、温度为100℃，悬空悬浮在25℃的房间内，求每秒钟它向房间内传递多少热量？解：首先计算出表面积，A=2(50某30+30某100+50某100)cm²=27,000cm²。
然后计算出物体的辐射率，或参考已知黑色物体的典型值，假设为ε=1、最后代入公式得到：Q=σεA(T₁⁴-T₂⁴)=5.67某10⁻⁸某1某27,000某(373⁴-298⁴)=648.43W。
化工原理传热计算题
化工原理传热计算题
在化工工艺中，传热是一个重要的计算问题。
传热计算常根据热传导、对流传热和辐射传热三种不同的机制进行分析。
热传导是物质内部热量传递的机制，其计算可以根据傅立叶定律进行。
傅立叶定律表明，传导热流密度与温度梯度成正比。
传热的计算公式可以表示为:
q = -k * A * (dT/dx)
其中，q表示单位时间传导热量，k是物质的热导率，A是传热面积，(dT/dx)是单位长度温度梯度。
对流传热是指通过流体的对流传递热量的机制。
其计算需要考虑流体的流动动力学特性和换热系数。
一般情况下，对流传热可以使用努塞尔数（Nu）来描述。
根据对流传热公式，传热率可以表示为:
q = h * A * (ΔT)
其中，q表示传导热量，h是换热系数，A是传热面积，ΔT是流体之间的温度差。
辐射传热是通过电磁波辐射传递热量的机制。
辐射传热的计算涉及辐射热通量、辐射发射率和辐射吸收系数等参量。
根据斯特藩-玻尔兹曼定律，辐射传热的计算公式可以表示为:
q = ε * σ * A * (T^4-T_s^4)
其中，q表示单位时间辐射传导热量，ε是辐射发射率，σ是斯特藩-玻尔兹曼常数，A是传热面积，T是物体表面温度，T_s是周围介质温度。
在实际的传热计算中，常常需要结合以上各种传热机制并考虑物料的特性和实际条件，综合分析并得出准确的结果。
这些传热计算可以应用于各种化工工艺中，例如换热器设计、反应器的冷却等。
热传递与热量的计算
热传递与热量的计算热传递是指热量从一个物体传递到另一个物体的过程。
在热传递过程中，热量会通过传导、传热和传辐射等途径传递。
在实际生活中，我们经常需要计算热量的大小，以便更好地理解和应用热传递的原理。
本文将介绍热传递的基本原理和常见的热量计算方法。
一、传导热传递传导热传递是指固体或液体内部热量的传递过程。
在传导热传递中，热量从高温区域传递到低温区域，其传热速率与传导物质的热导率、温度差以及传热长度有关。
计算传导热传递时，可以使用以下公式：Q = k * A * ΔT / d其中，Q表示传导热量，k表示传导物质的热导率，A表示传热截面积，ΔT表示温度差，d表示传热长度。
例如，我们有一个铝杆，热导率为200 W/(m·K)，传热截面积为0.01 m²，温度差为30 K，传热长度为0.1 m，那么我们可以通过上述公式计算出传导热量为：Q = 200 * 0.01 * 30 / 0.1 = 600 W二、对流热传递对流热传递是指通过液体或气体的流动来传递热量的过程。
在对流热传递中，热量主要通过流体的传送来实现，其传热速率与流体的流速、温度差以及传热面积有关。
对于强迫对流（即通过外力驱动流动）情况下的对流热传递，可以使用以下公式进行计算：Q = h * A * ΔT其中，Q表示对流热量，h表示对流换热系数，A表示传热面积，ΔT表示温度差。
例如，我们有一个水管，对流换热系数为1000 W/(m²·K)，传热面积为0.05 m²，温度差为10 K，那么我们可以通过上述公式计算出对流热量为：Q = 1000 * 0.05 * 10 = 500 W三、辐射热传递辐射热传递是指通过热辐射来传递热量的过程。
在辐射热传递中，物体表面发射的热辐射能量与物体的发射率、绝对温度以及表面积有关。
计算辐射热传递时，可以使用以下公式：Q = ε * σ * A * (T₁⁴ - T₂⁴)其中，Q表示辐射热量，ε表示物体的发射率，σ表示玻尔兹曼常数（约为5.67×10^(-8) W/(m²·K⁴))，A表示物体表面积，T₁和T₂分别表示物体表面和外界的绝对温度。
热传导三种方式公式
热传导三种方式公式
热传导是热力学中的一种重要现象，它是热能在物体中传递的过程。
根据传导的方式，热传导可以分为三种类型：导热、对流和辐射。
导热是指热量通过物体内部分子之间的碰撞传递。
导热的热流密
度可以用下列公式来计算：
q = -kA(dT/dx)
其中，q是热流密度，单位为瓦特每米方，k是物质的热导率，A
是热传导的面积，dT是热量的温度差，dx是热传导的路径长度。
对流是指热量通过流体的运动传递。
导致流体运动的原因可以是
温度差、密度差、压力差等。
对流的热流密度可以用下列公式来计算：q = hA(Ts - T∞)
其中，q是热流密度，h是流体的对流热传递系数，A是热传导的
面积，Ts是表面的温度，T∞是环境温度。
辐射是指热量通过电磁波辐射传递。
辐射的热流密度可以用下列
公式来计算：
q = εσA(Ts4 - Tsur4)
其中，q是热流密度，ε是表面的辐射率，σ是斯特藩-玻尔兹曼常数，A是热传导的面积，Ts是表面的温度，Tsur是环境温度。
总的来说，这三种热传导方式在日常生活和工业生产中都有广泛的应用。
对于热力学工程师、光学工程师、建筑师等科技从业人员来说，对于热传导的理解从而采取对应的工艺措施可以更有效的保护生产设备和提升室内环境。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.热对流
热对流：是指由于流体的宏观运动使物体不同的流体相对位移而产生的热量传递现象。
特点：只能发生在流体中；必然伴随有微观粒子热运动产生的导热。
对流换热：流体与固体表面之间的热量传递。
对流换热公式如下：
()F t t Q f w -=α
式中，Q 为对流换热量，单位为W ；
w t 、f t 为壁面和流体的平均温度，单位为℃；
F 为对流换热面积，单位为m 2；
α为对流换热系数，单位为C m W ︒⋅2/。
2.热辐射
辐射：是指物体受到某种因素的激发而向外发射辐射能的现象。
热辐射：由于物体内部微观粒子的热运动（或者说由于物体自身的温度）而使物体向外发射辐射能的现象。
辐射换热：当物体之间存在温差时，以热辐射的方式进行能量交换的结果使高温物体失去热量，低温物体获得热量，这种热量传递称为辐射换热。
两物体辐射换热的公式如下：
44121100100n T T Q C F ⎡⎤⎛⎫⎛⎫=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦
式中，n C 为辐射系数；
1T 、2T 为两物体的温度；
1F 为辐射体的辐射表面积。
（注：文档可能无法思考全面，请浏览后下载，供参考。
可复制、编制，期待你的好评与关注！）。