DTB DTC类比输入输出转换(配合PID设定)
PID算法控制 三个参数的重点解释

PID算法控制从网上找的PID讲解,感觉还不错,是基于电机的PID控制讲的:PID算法原理及调整规律一、PID算法简介首先必须明确PID算法是基于反馈的。
一般情况下,这个反馈就是速度传感器返回给单片机当前电机的转速。
简单的说,就是用这个反馈跟预设值进行比较,如果转速偏大,就减小电机两端的电压;相反,则增加电机两端的电压。
顾名思义,P指是比例(Proportion),I指是积分(Integral),D指微分(Differential)。
在电机调速系统中,输入信号为正,要求电机正转时,反馈信号也为正(PID算法时,误差=输入-反馈),同时电机转速越高,反馈信号越大。
要想搞懂PID算法的原理,首先必须先明白P,I,D各自的含义及控制规律:²比例P:比例项部分其实就是对预设值和反馈值差值的发大倍数。
举个例子,假如原来电机两端的电压为U0,比例P为0.2,输入值是800,而反馈值是1000,那么输出到电机两端的电压应变为U0+0.2*(800-1000)。
从而达到了调节速度的目的。
显然比例P越大时,电机转速回归到输入值的速度将更快,及调节灵敏度就越高。
从而,加大P值,可以减少从非稳态到稳态的时间。
但是同时也可能造成电机转速在预设值附近振荡的情形,所以又引入积分I解决此问题。
²积分I:顾名思义,积分项部分其实就是对预设值和反馈值之间的差值在时间上进行累加。
当差值不是很大时,为了不引起振荡。
可以先让电机按原转速继续运行。
当时要将这个差值用积分项累加。
当这个和累加到一定值时,再一次性进行处理。
从而避免了振荡现象的发生。
可见,积分项的调节存在明显的滞后。
而且I值越大,滞后效果越明显。
²微分D:微分项部分其实就是求电机转速的变化率。
也就是前后两次差值的差而已。
也就是说,微分项是根据差值变化的速率,提前给出一个相应的调节动作。
可见微分项的调节是超前的。
并且D值越大,超前作用越明显。
可以在一定程度上缓冲振荡。
PID算法的理解及实现

PID算法的理解及实现关于理解PID控制算法最典型的一个例子就是一个漏水的水缸的问题。
网上有很多讲解PID的帖子会讲到这个例子。
这里我也把我自己对于PID的理解用这个例子阐述一遍。
有个漏水的水缸,而且漏水的速度还不是恒定的。
然后我们还有个水桶,我们可以控制往水缸里面加水或者从水缸里面舀水出来。
另外我们可以检测水平面。
现在我们的目的就是要控制水平面稳定在我们想要的任何一个平面上。
注意我们使用PID需要在一个闭环系统里面。
什么叫闭环系统,就是有输入有反馈,输入就是能输入一个量去影响和控制我们的系统,反馈就是我们要能知道我们最终控制的东西的状态。
在这个漏水的水缸系统中,输入就是这个水桶,我们能通过水桶往水缸里面加水或者从水缸里面舀水出来来影响我们水缸的水平面,反馈的话也就是说我们要能测量水平面,知道水平面是多少。
控制系统原理图如下:我们来看看公式:其中Kp为比例系数,Ti为积分时间常量,Td为积分时间常量。
比例控制理解首先是比例控制。
比例控制就好比是通过水桶往水缸加水或者从水缸舀水。
假设我们需要把水平面稳定在A平面,而实际水平面在B平面,那么水平面差值Err=A-B,那这个时候我们需要往里面加水的量就是Kp*Err,Kp就是我们的比例控制系数。
如果A>B,Err为正,就往水缸里面加水;如果A<> 这里也许有人会有疑问,如果这里把比例控制系数Kp直接设置成1,然后加水的量直接为Err=A-B不就可以了。
然而实际上很多系统是做不到这点的。
比如温度控制系统,实际温度为10度,我要通过加热把温度提升到40度,这里难道我们能一次性准确的给系统加30度?显然这是做不到的。
那么比例控制的最终结果是Err的值趋向于0。
比例控制部分公式如下图:微分控制理解然后我们先看看微分控制。
在我们的比例控制的作用下,Err是开始减小的(假设一开始预期水平面A大于实际水平面B,也就是说Err是一个正值),那么也就是说Err 随时间是一条斜率小于0的曲线,那么在周期时间内,Err 越大,微分的绝对值越大,那么也就对Err的减小速度是起到抑制的作用的,直到最后斜率为0微分才会停止作用。
PID控制改进算法—变结构PID控制原理

U umax
NO
U umax
YES
U u min
YES
NO
U umin
输出控制量U
4.2 比例环节的作用
比例控制器所产生的原理性稳态误差和结构性稳态误差可以通过引入位置记忆环节来消除, 代 替积分环节的作用。 即令 u (n) Ke(n) u(n 1 ) , 其中 u(n 1) 为上一个控制周期 PID 控制器输出 到执行器的控制变量, 它与本次控制周期输出控制变量之前的阀门位置相对应。 这样只要有误差存 在,就可以使调节阀在当前位置的基础上继续动作,从而消除稳态误差, K P 0 。 比例环节贯穿调节全程, 发挥主导作用, 第 n 次信号采样之后, 比例控制器输出的控制变量为:
(2)当被控变量处于调节阶段时,微分环节将抑制偏差值的减小,可以起到抑制过大超调的作用, 但过强的微分作用必然会使调节速度受到影响甚至使系统提前制动,延长调节时间
如上图所示,在箭头所指位置,虽然被控变量还没有达到给定值,但由于微分环节抑制偏差变化的特性, 使得偏差绝对值减小受阻,从而延长了系统的调节时间,使控制系统动态性能下降。
(2)当目标值与被控变量初始值跨度较大时,由于偏差的初始值较大,使得比例项所输出的控制 作用也较强,调节速度较快;当目标值与被控变量初始值跨度较小时,由于偏差的初始值较小,使 得比例项所输出的控制作用也较弱,调节速度较慢。
可见, 采用固定的比例系数很难同时满足调节过程的不同阶段、 目标值与被控变量初始值不同 跨度时的控制要求。 最理想的情况是:当目标值与被控变量初始值的跨度较大时,使用较小的比例系数,当目标值 与被控变量初始值的跨度较小时,使用较大的比例系数;在调节过程当中,比例系数可以随着偏差 值的变化而进行自动调整,从而既可提高响应速度, 又可防止产生过大的超调量,保证稳定性。
pid算法的原理和算法

pid算法的原理和算法一、pid算法简介PID(Proportional-Integral-Derivative,比例-积分-微分)算法是一种广泛应用于工业控制领域的调节算法。
它通过计算系统误差与期望值的比值(比例控制)、误差积分和误差变化率(微分控制)来调节控制器的输出,从而使被控对象达到期望状态。
二、pid算法原理1.比例(P)控制:比例控制是根据系统误差与期望值的比值来调节控制器输出。
当误差较大时,比例控制输出较大,有利于快速消除误差;当误差较小时,比例控制输出较小,有利于提高系统的稳定性。
2.积分(I)控制:积分控制是根据系统误差的积分来调节控制器输出。
当误差持续存在时,积分控制输出逐渐增大,有助于消除误差。
但过大的积分控制会导致系统响应过慢,甚至产生振荡。
3.微分(D)控制:微分控制是根据系统误差的变化速度来调节控制器输出。
它能预测系统的变化趋势,从而减小超调量和调整时间,提高系统稳定性。
三、pid算法应用1.控制器设计:PID算法可以用于设计各类控制器,如PID控制器、模糊PID控制器、自适应PID控制器等。
2.参数调节:PID算法的三个参数(Kp、Ki、Kd)需要根据被控对象的特性进行调节。
合理的参数设置可以使系统在稳定性和响应速度之间达到平衡。
四、pid算法优化与改进1.抗积分饱和:当系统误差持续存在时,积分控制输出可能超过控制器最大输出,导致积分饱和。
通过引入抗积分饱和算法,可以限制积分控制的输出,提高系统稳定性。
2.抗积分粘滞:为避免积分控制输出在零附近震荡,可以采用抗积分粘滞算法,使积分控制输出在零附近呈现出非线性特性。
3.抗积分震荡:在积分控制中引入微分项,可以减小积分震荡,提高系统稳定性。
五、pid算法在实际工程中的应用案例PID算法在我国工业控制领域得到了广泛应用,如电力系统、温度控制系统、流量控制系统等。
通过合理设计PID控制器及其参数,可以实现对被控对象的稳定控制。
PID控制算法介绍与实现知识讲解
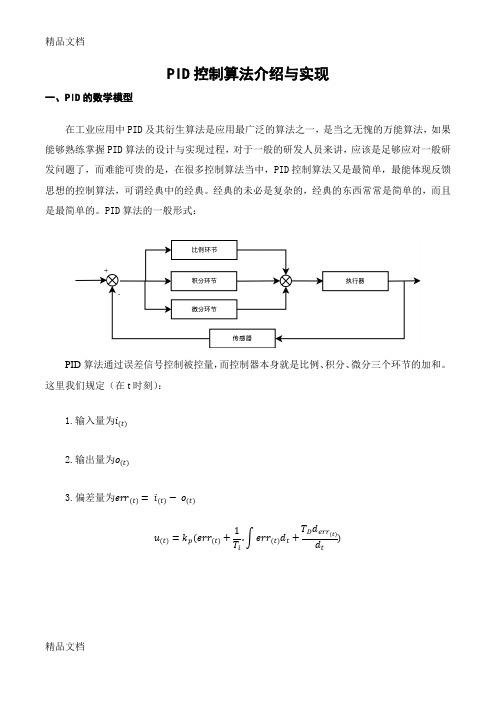
PID控制算法介绍与实现一、PID的数学模型在工业应用中PID及其衍生算法是应用最广泛的算法之一,是当之无愧的万能算法,如果能够熟练掌握PID算法的设计与实现过程,对于一般的研发人员来讲,应该是足够应对一般研发问题了,而难能可贵的是,在很多控制算法当中,PID控制算法又是最简单,最能体现反馈思想的控制算法,可谓经典中的经典。
经典的未必是复杂的,经典的东西常常是简单的,而且是最简单的。
PID算法的一般形式:PID算法通过误差信号控制被控量,而控制器本身就是比例、积分、微分三个环节的加和。
这里我们规定(在t时刻):1.输入量为i(t)2.输出量为o(t)3.偏差量为err(t)=i(t)− o(t)u(t)=k p(err(t)+1T i.∫err(t)d t+T D d err(t)d t)二、PID算法的数字离散化假设采样间隔为T,则在第K个T时刻:偏差err(k)=i(k) - o(k)积分环节用加和的形式表示,即err(k) + err(k+1) + …微分环节用斜率的形式表示,即[err(k)- err(k−1)]/T; PID算法离散化后的式子:u(k)=k p(err(k)+TT i.∑err(j)+T DT(err(k)−err(k−1)))则u(k)可表示成为:u(k)=k p(err(k)+k i∑err(j)+k d(err(k)−err(k−1)))其中式中:比例参数k p:控制器的输出与输入偏差值成比例关系。
系统一旦出现偏差,比例调节立即产生调节作用以减少偏差。
特点:过程简单快速、比例作用大,可以加快调节,减小误差;但是使系统稳定性下降,造成不稳定,有余差。
积分参数k i:积分环节主要是用来消除静差,所谓静差,就是系统稳定后输出值和设定值之间的差值,积分环节实际上就是偏差累计的过程,把累计的误差加到原有系统上以抵消系统造成的静差。
微分参数k d:微分信号则反应了偏差信号的变化规律,或者说是变化趋势,根据偏差信号的变化趋势来进行超前调节,从而增加了系统的快速性。
什么是数字PID控制(dcs离散PID控制)

什么是数字PID控制(dcs离散PID控制)
数字回路控制器,dcs的基本控制方式采用的大多还是常规PID控制规律,就是复杂的控制系统也还是以常规PID控制规律为中心的。
即数字PID控制算式的程序编制,仍然是以常规PID控制规律的模拟量表达式为蓝本进行的。
常规模拟PID控制的表达式如下:
公式中:P为控制器的输出信号;e为偏差信号;KP、TI、TD分别是控制器的比例增益、积分时间和微分时间。
当采集周期T0相对于输入信号变化周期很小时,可用矩形法来求积分的近似值,用一阶的差分来代替微分。
经替换最终就可得到离散PID的表达式,离散PID的表达式通常有:位置型,即PID运算控制调节阀的开度;增量型,即PID运算控制调节阀开度的增量(阀位的改变量);速度型,即PID运算控制伺服机的旋转速度。
在计算机控制中增量型算式由于易于实现手动和自动的无扰动切换,比较容易克服积分饱和,得到广泛的应用,其表达式如下:
公式中:△Pn为第n次控制器输出对前次控制器输出的增量;en为
第n次采样的偏差;KI为积分系数,TS为采样周期;KD为微分系数
由于数字PID控制比模拟控制更容易实现各种算法,所以为了改善控制质量,在实际应用中对PID算式进行了改进,如不完全微分型算式、微分先行PID控制算式、积分分离的PID算式等,都获得了很好的控制效果。
PID算法的通俗讲解及调节口诀
PID算法的通俗讲解及调节口诀PID算法是一种常用的控制算法,它可以帮助我们将实际测量值与期望值进行比较,并根据比较结果进行相应的控制。
PID算法由三个部分组成,分别是比例控制(P)、积分控制(I)和微分控制(D)。
在实际应用中,我们可以根据实际情况来调节PID算法的参数,以实现更准确的控制效果。
比例控制(P)是PID算法的核心部分之一,它根据误差的大小来调整输出量。
具体来说,比例控制会将误差与一个常数进行相乘,然后输出到系统中。
当误差较大时,输出量也会较大,从而加快系统的响应速度;当误差较小时,输出量也会较小,从而减小系统的超调量。
积分控制(I)是为了解决系统存在的稳态误差而引入的,它通过对误差的累加来调整输出量。
具体来说,积分控制会将误差乘以一个常数,并加到一个累加器中,然后输出到系统中。
通过积分控制,系统可以在长时间内逐渐减小误差,从而达到期望值。
微分控制(D)是为了解决系统存在的超调问题而引入的,它通过对误差的变化率进行调整。
具体来说,微分控制会将误差的变化率与一个常数进行相乘,并输出到系统中。
通过微分控制,系统可以在误差大幅度变化时降低输出量的变化速度,从而减小超调量。
除了PID算法的三个部分,还需要根据实际情况来调节PID算法的参数,以实现更准确的控制效果。
调节PID算法的口诀有三个重要的方面:1.比例项(P项)的调节:-当P项过大时,系统容易产生超调,并且响应速度较快,但稳定性较差;-当P项过小时,系统的响应速度较慢,并且稳态误差较大;-因此,需要通过改变P项的大小来调节系统的超调量和响应速度。
2.积分项(I项)的调节:-当I项过大时,系统容易产生超调,并且响应速度较慢;-当I项过小时,系统的稳态误差较大;-因此,需要通过改变I项的大小来调节系统的超调量和稳态误差。
3.微分项(D项)的调节:-当D项过大时,系统容易产生振荡,并且响应速度较快;-当D项过小时,系统的超调量较大;-因此,需要通过改变D项的大小来调节系统的振荡情况和超调量。
DTC的基本控制原理
DTC的基本控制原理
DTC (Direct Torque Control) 是一种控制电动机的技术,它通过直接控制电机转矩和磁通,实现了高性能和高效率的驱动。
DTC的基本控制原理如下:
1.状态估计:DTC首先需要估计电机的状态,如转速、转矩和磁通。
通常使用编码器或传感器来测量电机的转速和转矩,而磁通通常使用电流传感器来估计。
2.转矩和磁通控制:DTC的核心思想是直接控制电机的转矩和磁通,而不需要传统的PI控制器。
通过改变转矩和磁通的参考值,可以实现对电机的精确控制。
3.转矩控制:DTC使用一个转矩误差比较器来计算实际转矩和期望转矩之间的误差。
该误差通过与转矩误差阈值比较,并与转矩控制器中的两个开关相连,产生不同的电压矢量。
4.电压矢量选择:DTC使用电压矢量选择器根据实际转矩误差,选择合适的电压矢量,以使实际转矩与期望转矩尽可能接近。
电压矢量通过改变电机的磁通和转矩来达到这一目的。
5.磁通控制:DTC使用一个磁通误差比较器来计算实际磁通和期望磁通之间的误差。
该误差通过与磁通误差阈值比较,并与磁通控制器中的两个开关相连,产生不同的电压矢量。
6.状态选择:根据磁通误差和转矩误差的比较结果,DTC选择适当的电压矢量,以使电机的转矩和磁通尽可能接近期望值。
这种状态选择的方法可以提高系统的动态响应和控制精度。
7. PWM控制:最后,DTC使用PWM (Pulse Width Modulation) 控制电压矢量的功率开关,以产生适当的电压构成,进而驱动电机。
PWM控制具有精确控制输出电压幅值和相位的能力,可以帮助提高电机的效率和响应性能。
调速器PID控制算法
小调PID 控制算法一、 控制原理PID 控制器是一种线性控制器,其根据给定值c f 与实际值g f 构成控制偏差c g f f f ∆=-将偏差的比例P 、积分I 和微分D 通过线性组合构成控制量,其控制规律为p i dpid P K f I K fdtd fD K dty P I D=∆=∆∆==++⎰(1) 对(1)式经行拉氏变换,得p id pid P K F K I F SD K S F Y P I D=∆=∆=∆=++简单说来,PID 控制器各部分的作用如下:比例环节:即时成比例地反映控制系统的偏差信号,偏差一旦产生,控制器立即产生控制作用,以减少偏差。
当仅有比例控制时系统输出存在稳态误差。
积分环节:主要用来消除静态偏差。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。
微分环节:能反映偏差信号的变化趋势,在偏差信号值变得太大前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减小调节时间。
PID 算法的框图如图一:图一有几点说明:1、微分环节采用不完全微分,因为理想微分对系统系统产生较大噪声,抗干扰性能也差。
2、开度给定与实际开度的差参与积分运算,也就是说实际控制量有频差和开度差共同决定。
二、 PID 离散算法与增量式算法由于PLC 控制是一种采样控制,因此前面的积分和微分不能直接使用,需要对(1)式进行离散化处理,以一系列的采样时刻k 代替连续时间t ,以和式代替积分,以增量代替微分,以τ表示采样周期即PLC 扫描周期,可得()*()p p Y k K F k =∆()*()*ki i i Y k K I i τ==∆∑1()(1)()(1)()d d d vdY k Y k F k F k Y k T K ττ--∆-∆-+=这种算法的缺点是,由于全量输出,每次输出均与过去的状态有关,计算时要对()F k ∆进行累加,PLC 运算工作量大。
第5章数字PID及其算法
第5章数字PID及其算法数字PID是指使用数字信号处理器(DSP)或微处理器实现的PID控制算法。
它将传统的模拟PID控制器转换为数字信号,通过数值计算和运算来实现对控制系统的稳定和优化。
本章将介绍数字PID的基本原理和常用的数字PID算法。
一、数字PID的基本原理数字PID与传统的模拟PID控制器在基本原理上是一致的,都是通过调整控制器的输出来实现对系统的控制。
数字PID的基本原理包括三个部分:1. 比例(Proportional)部分:根据系统的偏差(即期望值与实际值之差)与设定的比例增益,计算出控制器的比例调节量。
比例调节量通过放大或缩小偏差,反映了控制器对于系统偏差的敏感程度。
2. 积分(Integral)部分:通过对偏差的积分,将系统之前的误差累积起来。
积分调节量考虑了系统在一段时间内的偏差总和,用于消除系统的稳态误差。
3. 微分(Derivative)部分:通过对偏差的微分,计算出系统的变化速率。
微分调节量根据偏差的变化率来预测系统的未来变化趋势,并对控制器的输出进行调整,以减少系统的震荡和振荡。
通过比例、积分和微分三个部分的调节,数字PID可以实现对系统的稳定和响应速度的平衡。
二、常用的数字PID算法1. Ziegler-Nichols算法:Ziegler-Nichols算法是最为常用的数字PID调参方法之一、该算法通过开环试验,观察系统的响应曲线,从而确定合适的比例增益和积分时间。
2. Pole-Zero Canceling算法:Pole-Zero Canceling算法是一种基于系统分析的数字PID调参方法。
它通过分析系统的传递函数,在前向通路中取消极点和零点,从而得到更稳定的闭环系统。
3. Smith Predictor算法:Smith Predictor算法是一种针对具有时延的系统的数字PID调参方法。
它通过引入状态估计器,对系统的时延进行补偿,从而提高系统的响应速度和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例名稱台達產品應用於以DTB/DTC類比輸入/輸出轉換(配合PID設定)
發行單位應用技術部發行日期Dec. 22 2008 頁數 4
適用機種溫度控制器
機器設備名稱:
DTB/DTC類比輸入/輸出轉換(配合PID設定)
機器設備本身的規格或特點:
於DTA系列溫控器由於只能以白金電阻或熱電耦做為輸入,並不支援類比輸入功能,因此通常只單純應用於標準的溫度控制。
而DTB/DTC系列溫控器由於內建類比輸入功能,此時各種類比輸出的元件(如壓力、流量等…),皆可利用DTB來做為轉換器,一方面可以取代類比輸入模組取得數位數值,一方面配合溫控器的PID運算可用來做些定壓力、定流量方面的控制需求。
控制系統的功能說明或功能方塊圖:
1)壓力控制:
以壓力表量測管路水壓,壓力由小至大依序輸出4~20mA電流,此時藉由溫控器即可測量目前壓力並形成閉迴路,配合PID運算達到定壓控制需求。
DTB並內建RS485通訊硬體,此時也可將壓力及變頻馬達出力情形提供給遠端PC監控。
品質至上QUALITY
2) 流量控制
相同於壓力控制原理,利用流量計輸出訊號至溫控器中,再藉由PID原理設定出所希望的控制反應來調整閥門的開度,以達到閉迴路控制的目地。
系統整合使用的效益說明:
類比量轉為數位值當然可以用PLC+AD模組來達成,並且再搭配人機來監控。
但於某些單機需求時,我們即可利用DTB類比輸入功能以非常經濟的方式來實現。
並且於溫控器中的PID設定相較於PLC更容易操作及了解,若是需要類比轉換後的數位值,藉由溫控器本身內建的RS485通訊埠再配合上/下限範圍的操作即可輕易的取得所需數位數
值。
並且內建的多種溫度警報方式,依需要選擇後即可藉由Relay的輸出提供最多3組的I/O警報功能。
品質至上QUALITY
品
質至上 QUALITY
設備上使用的台達機電產品:
配線圖: (以4848機種為例)
型號 參數設定
溫控器 DTB/DTC 感測器輸入方式選擇 InPt = mA4 (4~20mA 輸入) 當選擇為電流訊號輸入時,需並接250歐姆電阻 上限設定TP-H = 100.0 (當20mA 輸入時,顯示100.0) 下限設定TP-L = 0.0 (當4mA 輸入時,顯示0.0) 控制方式 CTrL = Pid (以PID 方式控制) 加熱/冷卻方式 S-HC = HEAT (選為加熱方式) 警報設定ALA1 = 5 (絕對值上/下限警報動作) P = 100.0、I=0、D=0
AL1H = 90.0 當PV 數值超過90時,警報1動作 AL1L = 10.0 當PV 數值低於10時,警報1動作
SV=100.0
品
質
至上 QUALITY 操作說明:
1) 由於設定為加熱控制,並且SV=100、P 值=100,因此輸出量和輸入訊號關係如下圖所示。
也由於輸出量是從PV=0線性遞減至PV=100,所以P 值即100- 0= 100。
因此當溫控器接收到較小的電流訊
號(即壓力較小)時,即輸出較大的輸出量來增強壓力。
反之,當接收到較大的電流訊號(壓力過大)時,即減小輸出量來減輕壓力。
2) 當然於實際運做的情形中,可能只用P 控制是不足夠的(會產生略大的振盪情形),此時先約略的輸入一個較大的I
值(如250),再依實際的穩定情形來慢慢增加或減小。
若到達穩定的速度太慢,請略減I 值後觀察其結果,反之,若仍持續難達到穩定情形,請增加I 值後觀察其情形。
3) 上述是以4~20mA 的輸入對應100%~0%的輸出,當然如果需做反相控制(如下圖),此時只需將控制方式由
HEAT(加熱)改為COOL(冷卻)並且把SV 值改設定為0即可。
4) 總合上述加熱/冷卻控制方式,當愈接近設定值時,輸出量將會趨近於零。
而加熱控制是對於低於設定值區域執行
線性P(比例)控制,因此SV 值需設定在高值。
反之,而冷卻控制是對高於設定值區域執行線性P 控制,而SV 值則需設定在最低值。
5) 藉由此加熱/冷卻的方式,有時可以做為轉換器功能,當客戶只是單純想將類比訊號透過溫控器轉送再從中藉由
RS485取得數位值,我們即可利用此方式來完成。
