电网络分析选论5章动态电路的时域方程练习题
(自动控制原理)最近几年考试时域分析法的题总汇

自动控制原理时域分析考试试题总汇3-1设二阶控制系统的单位阶跃响应曲线如图所示,若该系统为单位反馈控制系统, 试确定其单位传递函数。
解:由图知,该系统为欠阻尼二阶系统,从图中直接得出%30%=σ s t p 1.0=根据公式3.0%21==--ζπζσe1.012=-=ζωπn p t,解得358.0)(ln )(ln 222=+=σπσζ1265.331-=-=s t p n ζπω于是开环传递函数为)1.24(3.1132)2()(2+=+=s s s s s G n ζωω 3-2单位反馈控制系统的微分方程为)(200)(200)(10)(t r t c t c t c =++•••(1) — (2) 求系统的传递函数C(s)/R(s)(3) 求系统的阻尼比和自然振荡频率 (4) 求系统的开环传递函数 (5) 若r(t)=1+2t,求稳态误差(6) 若r(t)=2sin(10t+5),求稳态输出3-4设电子心率起搏器系统如图所示,其中模仿心脏的传递函数相当于一纯积分器。
要求: (1) 若5.0=ζ对于最佳响应,问起搏器的增益K 应为多大(2) 若期望心速为60次/min ,并突然接通起搏器,问1s 后实际心速为多少瞬时最大心速为多大解:(1)系统的开环传递函数为:)105.0()(+=s s Ks G:所以闭环传递函数 Ks s KK s s K s 202020)105.0()(2++=++=φ5.0,202,202===ζζωωn n K解之得:K=20 20=n ω (2) 闭环传递函数写为40020400)(2++=s s s φ 闭环极点 j s 310102,1±-= 所以系统单位脉冲响应为)310sin 310(cos )(10t j t et h t+=- 所以阶跃响应 ⎰=τ)(60)(dt t h t c =)1(6010τ-+ec(1)=次/min 峰值时间181.025.0120141.312=-⨯=-=ζωπn p t s{%5.16%75.05.012===⨯---πζπζσee最大心率为m in /9.69%)5.161(60次=+⨯3-5已知控制系统结构如图所示,(1) 当b=0时,试确定单位阶跃输入时系统的阻尼系数、自然频率、最大超调量以及单位斜坡输入所引起的稳态误差。
(完整版)电路作业题答案..

第1章电路模型和电路定律一、填空:1、—1.5A2、电路中某支路电流为1A-,表示该支路电流的真实方向与参考方向相反。
若电路电流I的参考方向由a→b,若电压与电流为非关联参考方向,则电压参考方向为 b→a 。
已知I=3A,U= -5V,则功率P= -15W ,是吸收功率(吸收或发出)。
3、电路中A、B两点的电位分别为U A=20V,U B=-20V,则两点间电压U AB= 40V 。
4、一个理想电流源串联5Ω电阻时,流过电阻电流为2A,当改变电阻阻值为10Ω时,流过电阻电流为 2A 。
5、电压源不允许短路,电流源不允许开路。
6、电路中电压U= 115 V。
7、6Ω; 8、U =16 V、R = 2Ω;9、2Ω;10、20V;11、理想电压源,串联,理想电流源,并联 .12、-6Ω二、选择1-5、D、B、B、A、A、6-11、A、C、C、A、B、A三、计算1.在指定的电压u和电流i参考方向下,写出下列元件u和i的约束方程(VCR)。
解:(a)u = -10i(b)u = —10V2、如图所示电路,已知15i A=-,21i A =,62i A=,求4i.解:i3 = i1+i2 = -5+1 = 4A ; i4 = i6-i3= 2-4 = —2A3、求电路中电流I、电压U及电阻的功率P。
解:(a)I = 2—4 = —2A U = 3I = —6V P = UI = 12W(b) I= 6-2 = 4A U = 2I= 8V P= UI= 32W4、图示电路中,分别计算两个电流源的功率,并判断是吸收还是发出功率。
图7解:3A 电流源吸收9w ;6A 电流源发出18w5、U ab=16V6、如图11所示,试计算UAC , UAD 。
解:闭合回路中电流为1A ,UAC =UBC = —1×(20+10)+ 2 = -28 V UAD =UBD =UBC + 2 = -26 V7、图示电路中,求: (1)当开关K合上及断开后,UAB =? (2)当开关K断开后,UCD =?解:(1)当开关合上时,UAB = 0 V当开关断开时,沿最大回顺时针绕行,其电流I = -20/7 A UAB =12-6I —9 UAB = -99 / 7 V(2) 当开关K断开后,UCD = 9 – I ×1 = 43 / 7 V 8、试求图示电路的入端电阻R ab ,图中电阻的单位为欧。
初三电路动态分析的练习题

初三电路动态分析的练习题电路动态分析是电路学习中的重要内容之一,它通过分析电路中元件的电流和电压随时间的变化,帮助我们更好地理解电路的工作原理和特性。
下面是一些初三电路动态分析的练习题,通过解答这些问题,可以加深对电路动态分析的理解。
问题一:RC电路充电过程考虑一个由电阻R和电容C构成的串联RC电路,初始时刻电容上没有电荷,开关S关闭,通过S的瞬间切换将电源与电路连接。
已知电阻R=10Ω,电容C=100μF,电源电压E=12V,请回答以下问题:1. 连接电源时,电路中的电流是多少?2. 充电的时间常数τ等于多少?3. 在t=τ时,电容上的电压达到了多少?问题二:RL电路的开关与电感考虑一个由电阻R和电感L构成的串联RL电路,初始时刻电感内没有电流,开关S关闭,通过S的瞬间切换将电源与电路连接。
已知电阻R=20Ω,电感L=0.1H,电源电压E=10V,请回答以下问题:1. 连接电源时,电路中的电流是多少?2. 电感充电的时间常数τ等于多少?3. 在t=τ时,电感中的电流达到了多少?问题三:RLC电路的振荡现象考虑一个由电阻R、电容C和电感L构成的串联RLC电路,初始时刻电容未充电且电感内没有电流,电源频率f为50Hz,电源电压E=20V,请回答以下问题:1. 连接电源后,电路中的电流是多少?2. 在LC谐振频率下,电路中电流的最大值是多少?3. 在LC谐振频率下,电容上的电压达到了多少?问题四:二阶RLC电路的阻尼效应考虑一个由电阻R、电感L和电容C构成的串联RLC电路,已知R=10Ω,L=2H,C=10μF,电源频率f为100Hz,电源电压E=10V,请回答以下问题:1. 连接电源后,电路中的电流是多少?2. 在阻尼比ξ小于1的情况下,电路呈现的是哪种振荡形式?3. 在阻尼比ξ大于1的情况下,电路呈现的是哪种振荡形式?通过解答以上问题,可以更好地理解电路动态分析的应用和原理,掌握相关的计算方法和技巧。
动态电路的时域分析
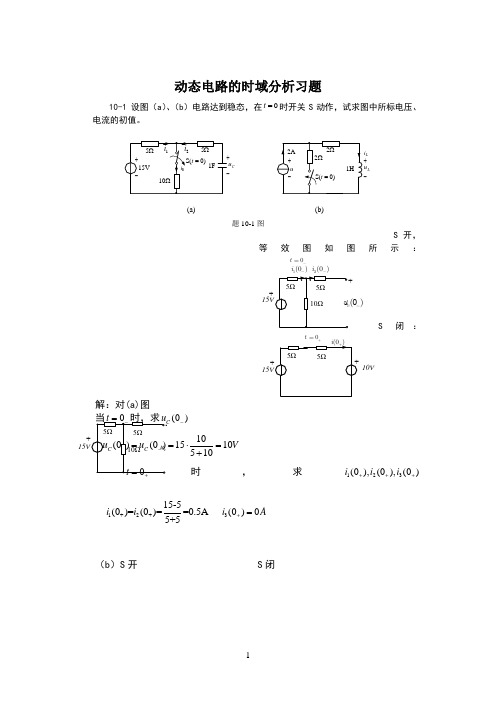
动态电路的时域分析习题10-1 设图(a )、(b )电路达到稳态,在0=t 时开关S 动作,试求图中所标电压、电流的初值。
C u L i L(a)(b)题10-1图S 开,等效图如图所示:+_t)1(0)i 2(0)i S 闭:t 10V解:对(a)图(0)-101510510V =⋅=+ 时,求123(0),(0),(0)i i i +++1+2+15-5(0)=(0)==0.5A 5+5i i 3(0)0i A +=(b )S 开 S 闭_(0)L i _(0)(0)2L i A_(0)u(0)L u (0)L对(b)图当0t -=时,求(0)L i -(0)(0)2L L i i A +-==当0t +=时,求(0),(0)L L u u -+42(0)4L u +⨯+=(0)4L u +=-(0)2240u +=⨯-=10-2 电路如图所示,已知Ω==421R R ,Ω=23R ,H L 1=,V U S 121=,V U S 62=。
电路原来处于稳定状态,0=t 时,开关S 闭合,试求)0(+L i 和)0(+L u 。
题10-2 图 题10-2 图解:S 开t(0)L i 6 VS 闭 0t(0)L u 12 V 6 V1A当0t -=时,求(0)L i -223(0)(0)1S L L U i i A R R +-===+当0t +=时,求(0)L u +R S U -+2S L111813421253246(0)10(0)3L L i i i i i i i u u ++⎧⎫=⎪⎪=+⎧⎫⎪⎪⎨⎬⎨⎬+=⎩⎭⎪⎪=⎪⎪⎩⎭+=+=10-3 设图示电路达到稳态,在0t =时开关S 动作,试求(0)c u +、(0)L i +、(0)i +、dt du C /)0(+和(0)Ldidt +。
t+__(0)L (a)_(0)c i (0)L u (b)解:当0t -=时,求(0),(0)c L u i --,等效电路如图(a )15(0)(0).(60//20)530(60//20)C C u u V +-===+_1560(0)(0).0.2530(60//20)6020L L i i A +===++当0t +=时,求(0),(0)L c u i ++,等效电路如图(b )(0)5200.250L u V +=-⨯=15101(0)0.253010c i A +-=-=(0)(0)1/6C C du i V s dt C ++== (0)(0)0A/s L L di u dt L++==10-4 设图示电路达到稳态,在0t =时开关S 动作,试求(0)c u +、(0)L i +、(0)R u +、(0)c du dt +和(0)L di dt +。
电网络分析选论第五章(动态电路的时域方程)

➢目前线性非时变问题的状 态方程,理论上都已解决, 你们已学过的“矩阵论及其 应用”第四章矩阵微分方程 就有专门的论述。
主要内容
• 状态变量分析的基本概念 • 状态方程的建立 • 线性状态方程的解析解法 • 状态方程的小信号分析 • 建立状态方程的五种方法
• 建立状态方程的五种方法 直观法 系统法(特有树) 稀疏表格法 改进节点法 端口分析法
k 1
k 1
k 1
k 1
nDE
其中 min( nDk ) 为第k个广义C-E回路中所含电 容和D型元件中最低阶元件的阶数(电容的阶 数为1);
其中 min( nEk ) 为第k个广义L-J回路中所含电感 和E型元件中最低阶元件的阶数(电感的阶数 为1)。
确定C-E回路和L-J割集的拓扑方法 用拓扑法决定独立的(广义)C-E 回路和(广义)L-J割集
是一组独立完备变量。
初始状态: 电路在初始时刻t=t0的状态
状态向量: n个状态变量
x1 (t) x2(t) 、…、xn (t) 构成的向量x(t)
状态空间:以状态向量的各
个分量x1、x2、…、xn为轴
所构成的n维欧氏空间。
状态方程
• 状态方程
(1)线性时不变网络
x Ax Bu
A为系数矩阵,B为控制矩阵
第五章 动态电路的时域方程
线性时不变系统为重点介 绍状态方程的列写和求解
电网络分析的状态变量法就 是状态方程法,是一种系统 或电路分析的有效方法。
➢这种方法列方程容易,不必化为 一个变量的函数,状态变量的变 化率可以用状态变量来表示,物 理意义清楚,很适合用数值法求 解,而且以状态方程为基础的状 态空间分析对非线性和时变系统 也很有效。
电网络分析选论5章动态电路的时域方程练习题

C 1+ -u S (t)R 3+-u 2(t)i 2(t)0 24题图1. (15%)图示网络中0U 为输出,试写出其状态方程,并求网络函数H(s)S U Ω10U +-+-1题图1u Ω1Ω1F1F 1+-2. (10%)列出图示电路的状态方程Ω2F12题图+-)(t εF 2H13. (10%)试写出图示网络的状态方程。
其中22dt u d i =。
R3题图-i S u iu +-G4. (15%)列出图示电路的状态方程,其中高阶E 元件的赋定关系为:。
22228dti d u =5. (15%)建立图示动态电路的s 域改进节点方程(MNA )方程(设电路中动态元件的初始储能为零)6. (15%)题6图中的二端口N 的特性为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321*********i u u u i i ,试写出图示网络的标准状态方程。
Nau 1i 2i 1u 2u F23u 3i7. (15%)图示的四端口网络N的特性为:112233442114123021411203i u u i i u i u ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,非线性电感的特性为322i ψψ=+,非线性电容的特性为342u q q =+,D元件的特性为23324d u i dt=, 试写出该网络的状态方程。
()s i t **1L 2L M2C 1G 2G 1C 3C ①②5题图6题图8. (15%)设图示电路中动态元件的初始储能为零,试建立该电路的s 域改进节点法方程(MNA )方程。
G 2i S①MG 1 i 3C 1L 1L 2C 2*3i 3C *②8题图N+-u 2i 2 +-u 1i 1+_u s2i 3+-u 3i 4+ -u 47题图9. (15%)图示的三端口网络N 的特性为:112233123214i u u i ⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,非线性电容的特性为323u q q =+,E 元件的特性为23322d i u dt =, 试写出该网络的状态方程。
电气工程学概论第5章习题解
L
(2) 因为
U2 R U1 j L R
所以 H ( j ) ( j )
L arctan R R 2 ( L)2 R
5.5 二端口网络如题 5.5 图所示。其中,R1=R2=500 ,L=10mH,C=1000pF。试求: (1)该网络的传递函数 | H ( j) | ∠ ( j ) ; (2)画出它的幅频特性和相频特性; (3)和题 5-8 的结果作一比较,并说明该滤波器的特性。
2
1 ) Z C
2 2
阻抗模
10 6 1 4 Z R L 10 10 3 C
阻抗角
1 1 3 L C 10 106 104 arctan arctan arctan 5 R 100 10
R
u1
L
C
题 5.6 图
u2
解: (1) 该电路的传递函数:
1 j L / / U2 j C H j U 1 R j L / / 1 j C j L R(1 LC ) j L
2
L 90 arctan 2 R 1 2 LC 2 2 2 R 1 LC ( L)
R1
j L
R2 1 jC
题 5.5 图
U1
U2
解: (1) H ( j) H ( j) ( j)
U2 1 j R2C 1 jC ( R1 R2 ) 2 LC U 1 R j L R 1 1 2 j C
R2
1 j C
H ( j )
电网络分析选论梁贵书
+
iL u
2、非线性电感 (1)流控电感
Li
三、电感元件 (续)
(2)链控电感 约夫逊结(Josephson Junction)
i I0 sin K (3)单调电感
绝大多数线圈的电感模型 属于此类,且具有饱和特性。
0
i
(4)多值电感 铁芯线圈的电感模型属于此类,具有磁滞回线
2 i2
i0 i1 i2
in
1 i1
in n
n口元件的端口电压、电流列向量
i0
0
u u1,u2 , ,un T
i i1,i2 , ,in T
5. 容许信号偶和赋定关系
• 可能存在于(多口)元件端口的电压、电流向量随时 间的变化或波形称为容许的电压—电流偶,简称容许信
号偶(Admissible Signal Pair),记作 u(t),i(t) 3Ω电阻的伏安关系为 u 3i 3cost,cost 容许信号偶
四、忆阻元件(Memristor)
定义:赋定关系为Ψ和q之间的代数关系的元件
M (q, ) : fM (q, ) 0
分类:
(1)荷控忆阻 (2)链控忆阻 (3)单调忆阻
+i
u
-
(4)多值忆阻
建议符号
四、忆阻元件(续)
在线性情况下
Mq
与线性电阻等价。
d M dq u Mi
dt
dt
线性电路无需忆阻元件
● 基本变量和高阶基本变量又可统一成 u( )和 i( ) 两种
变量 ,其中α和β为任意整数。
动态关系
• 基本表征量之间存在着与网络元件无关 的下述普 遍关系:
u(t) d(t) dt
动态电路分析习题
uC2(0+)= uC2(0)=50V
i(0 ) 10 uC2 (0 ) 60 0.12A
500
500
三、判断下图电路过渡过程的性质(过阻尼,欠阻尼,临界阻尼)。
2
+ 5/6H
1V
4
1F 4
+
0.5 1
1/5F
2V
+
12 (t)V
1F
+ u1
+
2u1 2
(a)
(b)
解 (a) 电路简化为
+ 1 5/6H 1/5F uC
–பைடு நூலகம்
uC 1 duC 6
R 5 dt 5
uC dt 0
d 2uC dt 2
5 duC dt
6uC
0
特征根为:p1= 2 ,p2= 3
非振荡衰减(过阻尼)。
(b)
un1 1F un2
0.5
1 +
1F u1
+
2u1 2
un2 2u1
un1
RC 1
du1 dt
iC
C1
duC 1 dt
C2
duC 2 dt
C1[uC1 (0 ) uC1 (0 )] C 2[uC 2 (0 ) uC 2 (0 )]
上式表明:不包括电压源支路的孤立节点上电荷总和瞬时守恒。
可
解
得
:uC
1
(0
uC 2 (0
) )
C 2U S
C1 C2 C1U S
C1 C2
S
+
US
US
3. C1 R2 C1 C 2 R1 R2
C1 R1 C 2 R2
电网络分析理论练习题
1文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持.1. (15%)图示R-C 梯形电路,试用Mason 公式求该电路的电压传输比 )()(0s U s U i2. (15%)用信号流图法求图示网络中的)(/)(3s I s U S3. 5.(15%)画出题5图所示电路的信号流图。
用Mason 公式计算电流I 。
3题图4. (15%)画出图示电路的信号流图(要求选一个树,以未知树支电压和未知连支电流为变量),用Mason 公式计算电流I 。
5. (15%)画出图示电路的信号流图(要求选一个树,以未知树支电压和未知连支电流为变量),用Mason 公式计算电流I 。
6. (10%)画出图示电路的信号流图,用Mason 公式求I 2。
7. (10%) 对图示阻容移相电路,要求用信号流图的方法求在正弦电源作用下,0•U 与1•U 4题图10.5U1Ω9VI1Ω2Ω1ΩI6题图I.Sx x ac 间的相位差为090时,R 、C 值应如何选择?此时?10=••U U8. (15%)图示R-C 梯形电路,试用Mason 公式求该电路的电压传输比)()(0s U s U i 9. (10%)用Mason 公式计算图示信号流图的传递函数S ox x 。
10. (10%)用Mason 公式计算图示信号流图的传递函数Sox x 。
11. (15%)画出图示电路的信号流图,用Mason 公式求I 2。
hSx ox a c e9题图10题图I I 2 G 2 G 3G 411题图3文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C 1
u S (t)
R 3
4题图
1. (15%)图示网络中0U 为输出,试写出其状态方程,并求网络函数H(s)
2. (10%)列出图示电路的状态方程
3. (10%)试写出图示网络的状态方程。
其中2
2dt u d i =。
4. (15%)列出图示电路的状态方程,其中高阶E 元件的赋定关系为:。
2
2
228dt
i d u =
5. (15%)建立图示动态电路的s 域改进节点方程(MNA )方程(设电路中动态元件的初始储能为零)
6. (15%)题6
图中的二端口N 的特性为:
⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321*********i u u u i i ,试写出图示网络的标准状态方程。
7. (15%)图示的四端口网络
N
的特性为:
(
s i 2
G 5题图
6题图
112233442114123021411
203i u u i i u i u ⎡⎤⎡⎤
⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥
⎢⎥=⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥
⎢⎥⎣⎦⎣⎦⎣⎦
,非线性电感的特性为
322i ψψ=+,非线性电容的特性为342u q q =+,D
元件的特性为
23
32
4d u i dt
=, 试写出该网络的状态方程。
8. (15%)设图示电路中动态元件的初始储能为零,试建立该电路的s 域改进节点法方程(MNA )方程。
G 2
i S
3
i α8题图
u s
3
7题图
9. (15%)图示的三端口网络N 的特性为:112233*********i u i u u i ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦
,非线性电容的特性为3
23u q q =+,E 元件的特性为2
332
2d i u dt =, 试写出
该网络的状态方程。
10. (15%)图示的三端口网络N 的特性为:112233*********i u u i i u ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦
,非线性电感的特性为3
22i ψψ=+,D 元件的特性为2
332
4d u i dt =, 试写
出该网络的状态方程。
2
u s 3
9题图
11. (10%)图示的四端口网络N 的特性为:
112233442114123021411
203i u u i i u i u ⎡⎤⎡⎤
⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥
⎢⎥=⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥
⎢⎥⎣⎦⎣⎦⎣⎦
,非线性电感的特性为
322i ψψ=+,非线性电容的特性为342u q q =+,D
元件的特性为
23
32
4d u i dt
=, 试写出该网络的状态方程。
i 2
u s 3
10题图
12. (10%).线性电路如图示,试求
12题图
(1) 以1c u 、2c u 为状态变量,o i 为输出量,求电路的状态方程和输出方程。
(2) 求传递函数
()()
S U S I S o .
u s
3
11题图。
