波动光学课后习题答案(第三章)
物理光学第三章课后作业解答
2nh
2
当 h=0时， ，因此右边中央条纹为暗条纹。
2
(2) 对于左边，由于1.50< 1.62 < 1.75 ，因此入射光小 角度入射时，从空隙上下表面反射的两束光的光程差 无半波损失，即
IP 3.4I1 0.85 I0 4I1
5(P119) 在杨氏实验装置中，两小孔的间距为0.5mm, 光屏离小孔的距离为50cm。当以折射率为1.60的透明 薄片贴住小孔 S2 时，发现屏上的条纹移动了1cm，试 确定该薄片的厚度。
解：
(n 1)l 0.6l l
0.6
yd 1 0.05 0.001cm
解: (1)
n1 sin1 n2 sin2
2
arcsin
sห้องสมุดไป่ตู้n 300 1.5
19.470
2n2hcos2 / 2 m
m 21.5hcos19.470 / 2 / 200
(2)
2 300
2n2hcos2 m
m 2 0.005 cos300 / 122
14(P120) 如图所示，平板玻璃由两部分组成(冕牌玻 璃n=1.50，火石玻璃n=1.75)，平凸透镜用冕牌玻璃制 成，其间隙充满二硫化碳(n=1.62)，这时牛顿环是何 形状?
y D
d
15 1.5cm
10
D 1.5mm
d
1.5d 1.5 0.45 0.58μm
D 1150
k=2 k=1 k=0 k=-1 k=-2
8(P119) 一波长为0.55m的绿光入射到间距为0.2mm 的双缝上，求离双缝2m远处的观察屏上干涉条纹的 间距。若双缝间距增加到2mm，条纹间距又是多少?
波动光学试题答案版3
波动光学一、概念选择题1. 如图所示，点光源S 置于空气中，S 到P 点的距离为r ，若在S 与P 点之间置一个折射率为n （n ＞1），长度为l 的介质，此时光由S 传到P 点的光程为（ D ）（A ）r （B ）l r - （C ）nl r - （D ）)1(-+n l r2. 在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中（ C ）（A ）传播的路程相等，走过的光程相等；（B ）传播的路程相等，走过的光程不相等；（C ）传播的路程不相等，走过的光程相等；（D ）传播的路程不相等，走过的光程不相等。
3. 来自不同光源的两束白光，例如两束手电筒光照射在同一区域内，是不能产生干涉图样的，这是由于（ C ）（A ）白光是由不同波长的光构成的 （B ）两光源发出不同强度的光（C ）两个光源是独立的，不是相干光源 （D ）不同波长,光速不同4. 真空中波长为λ的单色光，在折射率为n 的均匀透明媒质中，从A 点沿某一路径传播到B 点，路径的长度为l , 则A 、B 两点光振动位相差记为∆ϕ, 则（ C ）（A ） 当l = 3 λ / 2 ,有∆ϕ = 3 π（B ） 当 l = 3 λ / (2n ) , 有∆ϕ = 3 n π.（C ） 当 l = 3 λ /(2 n ) ,有∆ϕ = 3 π（D ） 当 l = 3 n λ / 2 , 有∆ϕ = 3 n π.5. 用单色光做双缝干涉实验，下述说法中正确的是 （ A ）（A ）相邻干涉条纹之间的距离相等（B ）中央明条纹最宽，两边明条纹宽度变窄（C ）屏与缝之间的距离减小，则屏上条纹宽度变窄（D ）在实验装置不变的情况下，红光的条纹间距小于蓝光的条纹间距6. 用单色光垂直照射杨氏双缝时，下列说法正确的是（ C ）（A ）减小缝屏距离，干涉条纹间距不变（B ）减小双缝间距，干涉条纹间距变小（C ）减小入射光强度, 则条纹间距不变（D ）减小入射波长, 则条纹间距不变7. 一束波长为 λ 的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使透射光得到干涉加强，则薄膜最小的厚度为（ D ）（A ） λ / 4 （B ） λ / (4 n ) （C ） λ / 2 （D ） λ / (2 n )8. 有两个几何形状完全相同的劈尖：一个由空气中的玻璃形成，一个由玻璃中的空气形成。
光学教程第3章_参考答案
13.1 证明反射定律符合费马原理。
证明：证明：设两个均匀介质的分界面是平面，设两个均匀介质的分界面是平面，设两个均匀介质的分界面是平面，它们的折射率为它们的折射率为n 1和n 2。
光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。
为了确定实际光线的路径，通过A,B 两点作平面垂直于界面，'OO 是它们的交线，则实际光线在界面上的反射点C 就可由费马原理来确定，如下图所示。
(1)反证法：如果有一点'C 位于线外，则对应于'C ，必可在'OO 线上找到它的垂足''C .由于''AC 'AC >,''BC 'BC >,故光线B AC'总是大于光程B ''AC 而非极小值，这就违背了费马原理，故入射面和反射面在同一平面内得证。
面内得证。
(2)在图中建立坐XOY 坐标系，则指定点A,B 的坐标分别为（x1，y1）和（x2，y2），未知点C 的坐标为（x ，0）。
C 点是在'A 、'B 之间的，光程必小于C 点在''B A 以外的相应光程，以外的相应光程，即即21vx x <<，于是光程ACB 为 yx x n y x x n CB n AC n ACB n 2211221221111)()(+-++-=+=根据费马原理，它应取极小值，即0)(1=ACB n dx d0)sin (sin )()()()()()(21112222211212111=-=¢-¢=+---+--=i i n CB B C AC C A n y x x x x n y x x x x n ACB n dx d 所以当11'i i =，取的是极值，符合费马原理。
，取的是极值，符合费马原理。
3.2 根据费马原理可以导出在近轴条件下，从物点发出并会聚倒像点的所有光线的光程都相等。
波动光学习题参考答案页PPT文档共145页文档
谢பைடு நூலகம்！
波动光学习题参考答案页PPT文档
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
波动光学大学物理答案
习题1313.1选择题（1）在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是[ ](A) 使屏靠近双缝．(B) 使两缝的间距变小．(C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源． [答案：C]（2）两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的[ ] (A) 间隔变小，并向棱边方向平移． (B) 间隔变大，并向远离棱边方向平移． (C) 间隔不变，向棱边方向平移．(D) 间隔变小，并向远离棱边方向平移． [答案：A]（3）一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为[ ] (A) λ / 4 ． (B) λ / (4n )．(C) λ / 2 ． (D) λ / (2n )． [答案：B]（4）在迈克耳孙干涉仪的一条光路中，放入一折射率为n ，厚度为d 的透明薄片，放入后，这条光路的光程改变了[ ](A) 2 ( n -1 ) d ． (B) 2nd ． (C) 2 ( n -1 ) d +λ / 2． (D) nd ．(E) ( n -1 ) d ． [答案：A]（5）在迈克耳孙干涉仪的一条光路中，放入一折射率为n 的透明介质薄膜后，测出两束光的光程差的改变量为一个波长λ，则薄膜的厚度是 ［ ］(A) λ / 2 ． (B) λ / (2n )． (C) λ / n ． (D) λ / [2(n-1)]． [答案：D]13.2 填空题 （1）如图所示，波长为λ的平行单色光斜入射到距离为d 的双缝上，入射角为θ．在图中的屏中央O 处(O S O S 21=)，两束相干光的相位差为________________． [答案：2sin /d πθλ]（2）在双缝干涉实验中，所用单色光波长为λ＝562.5 nm (1nm ＝10-9 m)，双缝与观察屏的距离D ＝1.2 m ，若测得屏上相邻明条纹间距为∆x ＝1.5 mm ，则双缝的间距d ＝__________________________．[答案：0.45mm]（3）波长λ＝600 nm 的单色光垂直照射到牛顿环装置上，第二个明环与第五个明环所对应的空气膜厚度之差为____________nm ．(1 nm=10-9 m)[答案：900nm ]（4）在杨氏双缝干涉实验中，整个装置的结构不变，全部由空气中浸入水中，则干涉条纹的间距将变 。
大学物理-波动光学习题(包括振动、波动、波的干涉、光的干涉、光的衍射、光的偏振)
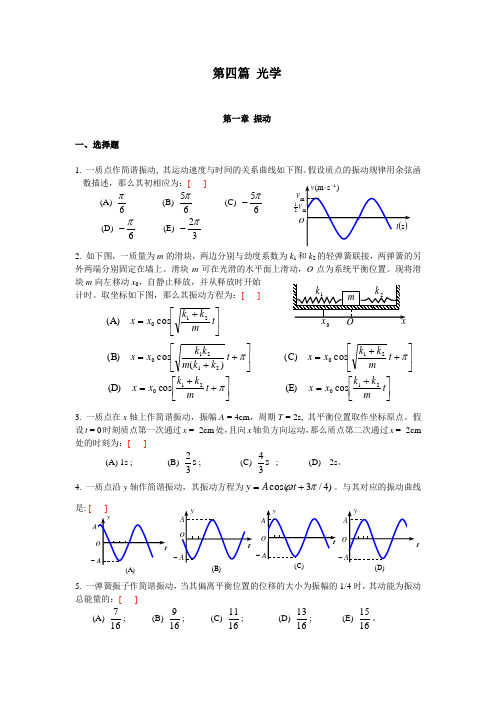
第四篇 光学第一章 振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。
假设质点的振动规律用余弦函数描述，那么其初相应为：[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图，一质量为m 的滑块，两边分别与劲度系数为k 1和k 2的轻弹簧联接，两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动，O 点为系统平衡位置。
现将滑块m 向左移动x0，自静止释放，并从释放时开始计时。
取坐标如下图，那么其振动方程为：[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动，振幅A = 4cm ，周期T = 2s, 其平衡位置取作坐标原点。
假设t = 0时刻质点第一次通过x = -2cm 处，且向x 轴负方向运动，那么质点第二次通过x = -2cm 处的时刻为：[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。
4. 一质点沿y 轴作简谐振动，其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的：[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。
(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线，假设 这两个简谐振动可叠加，那么合成的余弦振动 的初相为： [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ，0=t 时的初位移为0.04m, s -1，那么振幅A = ，初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动，经过0.5s 后，第二个振子才从正方向的端点开始运动，那么这两振动的相位差为 。
波动光学案例习题(含答案)
x (2k 1) d
d2
11/5 条纹间距
x
xk 1
xk
d
d
4
2.薄膜干涉 （分振幅法）
光程差
2d
n22
n12
s in 2
i
2
i
①
② n1 n2 d
n1 n2 n3 n1 n2 n3 n1 n2 n3
n1 n2 n3
11/5
n3
光程差不附加
2
光程差附加
2
5
光程差
2d
答： （C）
11/5
21
例： 在牛顿环实验装置中，曲率半径为R的平 凸透镜与平玻璃板在中心恰好接触，它们之间 充满折射率为n的透明介质，垂直入射到牛顿 环装置上的平行单色光在真空中的波长为λ， 则反射光形成的干涉条纹中暗环半径的表达式 为：
( A)r kR (C)r knR
(B)r kR / n (D)r k /(nR)
解： 条纹间距 x d D
dd
中央明纹两侧的第10级明纹中心间距
210x 210 D 0.11m
d
11/5
32
（2）将此装置用一厚度为 e 6.6106 m ，折射率
解： 据明环半径公式 rk
( k 1 )R
2
充液前： r120 19R / 2 充液后： r102 19R /( 2n )
n r120 1.36
11/5
r102
20
例，在相同的时间内，一束波长为λ的单色光在 空气中和在玻璃中：
（A）传播的路程相等，走过的光程相等 （B）传播的路程相等，走过的光程不相等 （C）传播的路程不相等，走过的光程相等 （D）传播的路程不相等，走过的光程不相等
波动光学谢书作业题参考解答
n0 N d
iN iN 1 iN
r f iN f
N 1 N N 1 N
1 546nm i6 ( 7 6) 0.0032 2mm 1 546nm ( 7 6) 1.024 2mm
r f i6 320mm
r1
3.20、解：2
2h cos 2m
可见，h大，m多，对于固定的m，h大，θ变 大，反之亦然。
(1)、向中心收缩，说明θ变小，则h也变小，M1和M'2相对移近。 (2)、4h 2m h
m 25 25 589 .3nm 14.7325 m 2
(3)、 2 2h 2m 2 2h cos( i ) 2(m 11) 2 2h' 2m' 2(m 10) 2 2h' cos( i ) 2(m 16) m 11 m 16 m 22 m' m 10 12 m m 10
x k2 x k1 O α2 α1 α2 β z
α1
O
z β
Π
k2
k2-k1
k1
Π 图3.3 题目所述情况示意图
图3.3 题解所述情况示意图
3.5、解：放置玻璃片后相当于光程差的改变量为：
δΔSP=(n-1)h 不难理解，这个改变量也相当于观察屏Π上考察点P的坐标的增加， 所以放置玻璃片后条纹向上移动。因为： k0δΔSP=δm· 2π 所以： δm=k0δΔSP/2π=(n-1)h/λ=(1.5-1)×0.01mm/500nm=10 即能够移动10个条纹，即移动了5个条纹间距。
3.21、解： 两次消失之间，光程差为：
波动光学习题参考答案
结束 返回
已知：
l 589.3 q = 2nl = 2×1.52×5×10-6
=3.83×10-5 (rad) = 8´ ´
结束 返回
15、 波长为680nm的平行光垂直地 照射到12cm长的两块玻璃片上，两玻璃片 一边相互接触，另一边被厚0.048mm的纸 片隔开，试问在这l2cm内呈现多少条明条 纹?
2n k550
2n
4n
=211.5k+105.8
令 k =0 e =105.8 (nm)
结束 返回
13、 彩色电视发射机常用三基色的分 光系统，如图所示，系用镀膜方法进行分色， 现要求红光的波长为600nm，绿光的波长为 520nm,设基片玻璃的折射率n3 =15.0，膜 材料的折射率 n2 =2.12。 空气的折射率为 0 n1 ，设入射角i =45 。 白光 i 试求膜的厚度。 红光 绿光 兰光
结束 返回
解：水膜正面反射干涉加强 l kl 2ne + 2 = k=2 4ne 4×1.33×380 =674 (nm) 红 l2 = = 2×2-1 2k-1 k=3
4ne 4×1.33×380 =404 (nm) 紫 l3 = = 2×3-1 2k-1 所以水膜呈现紫红色 k 的其它取值属于红外光或紫外光范围结束
x ´为k 级新的明条纹位置
x´
原来的光程差为 d = r 2 r 1 = dsinj = d x = kl D d b + d (x ´ x ) =0 两式相减得到： D´ D D Δ x ´= b (x ´ x ) <0 D´
即条纹向下移动，而条纹间距不变
D´ S 2
o
D
结束 返回
7、 用单色光源S照射双缝，在屏上形 成干涉图样，零级明条纹位于O 点，如图所 示。若将缝光源 S 移至位置S ´，零级明条 纹将发生移动。欲使零级明条纹移回 O 点， 必须在哪个缝处覆盖一薄云母片才有可能? 若用波长589nm的单 色光，欲使移动了4个 屏 S1 明纹间距的零级明纹 S´ O 移回到O点，云母片的 S 厚度应为多少?云母片 S2 的折射率为1.58。
大学物理下册波动光学习题解答杨体强
波动光学习题解答1-1 在杨氏实验装置中，两孔间的距离等于通过光孔的光波长的100倍，接收屏与双孔屏相距50cm 。
求第1 级和第3级亮纹在屏上的位置以及它们之间的距离。
解： 设两孔间距为d ，小孔至屏幕的距离为D ，光波波长为λ，则有=100d λ. (1)第1级和第3级亮条纹在屏上的位置分别为 (2)两干涉条纹的间距为 1-2 在杨氏双缝干涉实验中，用06328A =λ的氦氖激光束垂直照射两小孔，两小孔的间距为1.14mm ，小孔至屏幕的垂直距离为1.5m 。
求在下列两种情况下屏幕上干涉条纹的间距。
（1）整个装置放在空气中； （2）整个装置放在n=1.33的水中。
解： 设两孔间距为d ，小孔至屏幕的距离为D ，装置所处介质的折射率为n ，则两小孔出射的光到屏幕的光程差为所以相邻干涉条纹的间距为（1）在空气中时，n ＝1。
于是条纹间距为 （2）在水中时，n ＝1.33。
条纹间距为 1-3 如图所示，1S 、2S 是两个相干光源，它们到P 点的距离分别为1r 和2r 。
路径1S P 垂直穿过一块厚度为1t 、折射率为1n 的介质板，路径2S P 垂直穿过厚度为2t ，折射率为2n 的另一块介质板，其余部分可看做真空。
这两条路径的光程差是多少？解：光程差为 222111[r (n 1)t ][r (n 1)t ]+--+-1-4 如图所示为一种利用干涉现象测定气体折射率的原理性结构，在1S 孔后面放置一长度为l的透明容器，当待测气体注入容器而将空气排出的过程中幕上的干涉条纹就会移动。
由移过条纹的根数即可推知气体的折射率。
（1）设待测气体的折射率大于空气折射率，干涉条纹如何移动？（2）设 2.0l cm =，条纹移过20根，光波长为589.3nm ，空气折射率为 1.000276，求待测气体（氯气）的折射率。
解：（1）条纹向上移动。
（2）设氯气折射率为n,空气折射率为n 0=1.002760，则有：所以0k n =n + 1.00027600.0005893 1.0008653lλ=+=1-5 用波长为500 nm 的单色光垂直照射到由两块光学平玻璃构成的空气劈尖上。
大学物理波动光学习题答案
第七章波动光学习题答案1．从一光源发出的光线，通过两平行的狭缝而射在距双缝100 cm的屏上，如两狭缝中心的距离为0.2 mm，屏上相邻两条暗条纹之间的距离为3 mm，求光的波长(Å为单位)。
已知 D=100cm a=0.2mm δx=3mm 求λ[解]λ=aδx/D=3×10-3×0.2×10-3/100×10-2=0.6×10-6m=6000 Å2．用波长为7000 Å的红光照射在双缝上，距缝1 m处置一光屏，如果21个明条纹(谱线以中央亮条为中心而对称分布)共宽2.3 cm，求两缝间距离。
[解]明条纹间距cm a=6.084．用波长为4800 Å的蓝光照射在缝距为0.1 mm的双缝上，求在离双缝50 cm处光屏上干涉条纹间距的大小。
[解]=2.4mm5．什么是光程?在不同的均匀媒质中，单色光通过相等光程时，其几何路程是否相同? 需要时间是否相同?[解]光程=nx。
在不同的均匀媒质中，单色光通过相等光程时，其几何路程是不同。
需要时间相同6．在两相干光的一条光路上，放入一块玻璃片，其折射率为1.6，结果中央明条纹移到原是第六级明条纹处，设光线垂直射入玻璃片，入射光波长为6.6×103 Å。
求玻璃片厚度。
已知 n=1.6 λ=6.6×103Å求 d[解]光程差MP-d+nd-NP=0∵ NP-MP=6λ∴（n-1）d=6λd=6λ/(n-1)=6.6×10-6m7．在双缝干涉实验中，用钠光灯作光源(λ=5893 Å)，屏幕离双缝距离D=500mm，双缝间距a=1.2mm，并将干涉实验装置整个地浸在折射率1.33的水中，相邻干涉条纹间的距离为多大?若把实验装置放在空气中，干涉条纹变密还是变疏?(通过计算回答)已知n水=1.33 λ=5893 Å D=500 mm a=1.2mm 比较δx水和δx空气[解]δx水=Dλ/na=500×5893×10-10×10-3/(1.2×10-3×1.33)=1.85×10-4mδx空气=Dλ/a=500×5893×10-10×10-3/(1.2×10-3)=2.46×10-4m∴干涉条纹变疏8．用白光垂直照射到厚度为4×10-5 cm的薄膜上，薄膜的折射率为1.5。
波动光学大学物理答案解读
习题1313.1选择题（1）在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是[ ](A) 使屏靠近双缝．(B) 使两缝的间距变小．(C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源． [答案：C]（2）两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的[ ] (A) 间隔变小，并向棱边方向平移． (B) 间隔变大，并向远离棱边方向平移． (C) 间隔不变，向棱边方向平移．(D) 间隔变小，并向远离棱边方向平移． [答案：A]（3）一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为[ ] (A) λ / 4 ． (B) λ / (4n )．(C) λ / 2 ． (D) λ / (2n )． [答案：B]（4）在迈克耳孙干涉仪的一条光路中，放入一折射率为n ，厚度为d 的透明薄片，放入后，这条光路的光程改变了[ ](A) 2 ( n -1 ) d ． (B) 2nd ． (C) 2 ( n -1 ) d +λ / 2． (D) nd ．(E) ( n -1 ) d ． [答案：A]（5）在迈克耳孙干涉仪的一条光路中，放入一折射率为n 的透明介质薄膜后，测出两束光的光程差的改变量为一个波长λ，则薄膜的厚度是 ［ ］(A) λ / 2 ． (B) λ / (2n )． (C) λ / n ． (D) λ / [2(n-1)]． [答案：D]13.2 填空题 （1）如图所示，波长为λ的平行单色光斜入射到距离为d 的双缝上，入射角为θ．在图中的屏中央O 处(O S O S 21=)，两束相干光的相位差为________________． [答案：2sin /d πθλ]（2）在双缝干涉实验中，所用单色光波长为λ＝562.5 nm (1nm ＝10-9 m)，双缝与观察屏的距离D ＝1.2 m ，若测得屏上相邻明条纹间距为∆x ＝1.5 mm ，则双缝的间距d ＝__________________________．[答案：0.45mm]（3）波长λ＝600 nm 的单色光垂直照射到牛顿环装置上，第二个明环与第五个明环所对应的空气膜厚度之差为____________nm ．(1 nm=10-9 m)[答案：900nm ]（4）在杨氏双缝干涉实验中，整个装置的结构不变，全部由空气中浸入水中，则干涉条纹的间距将变 。
波动光学课后习题
波动光学篇习题十二·光的干涉12-1 某单色光从空气射入水中，其频率、波速、波长是否变化?怎样变化?12-2 在杨氏双缝实验中，作如下调节时，屏幕上的干涉条纹将如何变化?试说明理由． (1)使两缝之间的距离变小；(2)保持双缝间距不变，使双缝与屏幕间的距离变小； (3)整个装置的结构不变，全部浸入水中； (4)光源作平行于1S ，2S 联线方向上下微小移动；(5)用一块透明的薄云母片盖住下面的一条缝．12-3 什么是光程? 在不同的均匀媒质中，若单色光通过的光程相等时，其几何路程是否相同?其所需时间是否相同?在光程差与位相差的关系式∆λπϕ∆2=中,光波的波长要用真空中波长,为什么?12-4 如题12-4图所示，A ，B 两块平板玻璃构成空气劈尖，分析在下列情况中劈尖干涉条纹将如何变化?(1) A 沿垂直于B 的方向向上平移［见图(a)］； (2) A 绕棱边逆时针转动［见图(b)］．题12-4图12-5 用劈尖干涉来检测工件表面的平整度，当波长为λ的单色光垂直入射时,观察到的干涉条纹如题12-5图所示，每一条纹的弯曲部分的顶点恰与左邻的直线部分的连线相切．试说明工件缺陷是凸还是凹?并估算该缺陷的程度．题12-5图题12-6图12-6 如题12-6图，牛顿环的平凸透镜可以上下移动，若以单色光垂直照射，看见条纹向中心收缩，问透镜是向上还是向下移动?12-7 在杨氏双缝实验中，双缝间距d=0.20mm，缝屏间距D＝1.0m，试求：(1)若第二级明条纹离屏中心的距离为6.0mm，计算此单色光的波长；(2)相邻两明条纹间的距离．12-8 在双缝装置中，用一很薄的云母片(n=1.58)覆盖其中的一条缝，结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明纹的位置．若入射光的波长为5500oA，求此云母片的厚度．12-9 洛埃镜干涉装置如题12-9图所示，镜长30cm，狭缝光源S在离镜左边20cm的平面内，与镜面的垂直距离为2.0mm，光源波长=λ7.2×10-7m，试求位于镜右边缘的屏幕上第一条明条纹到镜边缘的距离．题12-9图12-10 一平面单色光波垂直照射在厚度均匀的薄油膜上，油膜覆盖在玻璃板上．油的折射率为1.30，玻璃的折射率为1.50，若单色光的波长可由光源连续可调，可观察到5000 o A 与7000 oA 这两个波长的单色光在反射中消失．试求油膜层的厚度．12-11 白光垂直照射到空气中一厚度为3800 oA 的肥皂膜上，设肥皂膜的折射率为1.33，试问该膜的正面呈现什么颜色?背面呈现什么颜色?12-12 在折射率1n =1.52的镜头表面涂有一层折射率2n =1.38的Mg 2F 增透膜，如果此膜适用于波长λ=5500 oA 的光，问膜的厚度应取何值?12-13 如题12-13图，波长为6800oA 的平行光垂直照射到L ＝0.12m 长的两块玻璃片上，两玻璃片一边相互接触，另一边被直径d =0.048mm 的细钢丝隔开．求： (1)两玻璃片间的夹角=θ?(2)相邻两明条纹间空气膜的厚度差是多少? (3)相邻两暗条纹的间距是多少? (4)在这0.12 m 内呈现多少条明条纹?题12-13图12-14 用=λ5000oA 的平行光垂直入射劈形薄膜的上表面，从反射光中观察，劈尖的棱边是暗纹．若劈尖上面媒质的折射率1n 大于薄膜的折射率n (n =1.5)．求： (1)膜下面媒质的折射率2n 与n 的大小关系； (2)第10条暗纹处薄膜的厚度；(3)使膜的下表面向下平移一微小距离e ∆，干涉条纹有什么变化?若e ∆=2.0 μm ，原来的第10条暗纹处将被哪级暗纹占据?12-15 (1)若用波长不同的光观察牛顿环，1λ＝6000oA ，2λ＝4500oA ，观察到用1λ时的第k 个暗环与用2λ时的第k+1个暗环重合，已知透镜的曲率半径是190cm ．求用1λ时第k 个暗环的半径．(2)又如在牛顿环中用波长为5000oA 的第5个明环与用波长为2λ的第6个明环重合，求未知波长2λ．12-16 当牛顿环装置中的透镜与玻璃之间的空间充以液体时，第十个亮环的直径由1d ＝1.40×10-2m 变为2d ＝1.27×10-2m ，求液体的折射率．12-17 利用迈克耳逊干涉仪可测量单色光的波长．当1M 移动距离为0.322mm 时，观察到干涉条纹移动数为1024条，求所用单色光的波长．12-18 把折射率为n =1.632的玻璃片放入迈克耳逊干涉仪的一条光路中，观察到有150条干涉条纹向一方移过．若所用单色光的波长为λ=5000oA ，求此玻璃片的厚度．习题十三·光的衍射13-1 衍射的本质是什么?衍射和干涉有什么联系和区别?13-2 在夫琅禾费单缝衍射实验中，如果把单缝沿透镜光轴方向平移时，衍射图样是否会 跟着移动?若把单缝沿垂直于光轴方向平移时，衍射图样是否会跟着移动?13-3 什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗 条纹，单缝处波面各可分成几个半波带?13-4 在单缝衍射中，为什么衍射角ϕ愈大（级数愈大）的那些明条纹的亮度愈小?13-5 若把单缝衍射实验装置全部浸入水中时，衍射图样将发生怎样的变化?如果此时用公式),2,1(2)12(sin =+±=k k a λϕ来测定光的波长，问测出的波长是光在空气中的还是在水中的波长?13-6 在单缝夫琅禾费衍射中，改变下列条件，衍射条纹有何变化?(1)缝宽变窄；(2)入 射光波长变长；(3)入射平行光由正入射变为斜入射．13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似，两者是否矛盾?怎样 说明?13-8 光栅衍射与单缝衍射有何区别?为何光栅衍射的明条纹特别明亮而暗区很宽?13-9 试指出当衍射光栅的光栅常数为下述三种情况时，哪些级次的衍射明条纹缺级?(1) a+b=2a;(2)a+b=3a;(3)a+b=4a.13-10 若以白光垂直入射光栅，不同波长的光将会有不同的衍射角．问(1)零级明条纹能 否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什 么因素有关?13-11 一单色平行光垂直照射一单缝，若其第三级明条纹位置正好与6000οA 的单色平行光的第二级明条纹位置重合，求前一种单色光的波长．13-12 单缝宽0.10mm ，透镜焦距为50cm ，用5000=λoA 的绿光垂直照射单缝．求：(1)位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少?(2)若把此装置浸入水中(n=1.33)，中央明条纹的半角宽度又为多少?13-13 用橙黄色的平行光垂直照射一宽为a=0.60mm 的单缝，缝后凸透镜的焦距f=40.0cm ，观察屏幕上形成的衍射条纹．若屏上离中央明条纹中心1.40mm 处的P 点为一明条纹；求：(1)入射光的波长；(2)P 点处条纹的级数；(3)从P 点看，对该光波而言，狭缝处的波面可分成几个半波带?13-14 用5900=λoA 的钠黄光垂直入射到每毫米有500条刻痕的光栅上，问最多能看到第几级明条纹?13-15 波长为5000o A 的平行单色光垂直照射到每毫米有200条刻痕的光栅上，光栅后的透镜焦距为60cm ．求：(1)屏幕上中央明条纹与第一级明条纹的间距；(2)当光线与光栅法线成 30°斜入射时，中央明条纹的位移为多少?13-16 波长6000=λo A 的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在20.0sin =ϕ与30.0sin =ϕ处，第四级缺级．求：(1)光栅常数；(2)光栅上狭缝的宽度；(3)在90°＞ϕ＞-90°范围内，实际呈现的全部级数．13-17 一双缝，两缝间距为0.1mm ，每缝宽为0.02mm ，用波长为4800oA 的平行单色光垂直入射双缝，双缝后放一焦距为50cm 的透镜．试求：(1)透镜焦平面上单缝衍射中央明条纹的宽度；(2)单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹?13-18 在夫琅禾费圆孔衍射中，设圆孔半径为0.10mm ，透镜焦距为50cm ，所用单色光波长为5000oA ，求在透镜焦平面处屏幕上呈现的爱里斑半径．13-20 已知入射的X 射线束含有从0.95～1.30oA 范围内的各种波长，晶体的晶格常数为2.75oA ，当X 射线以45°角入射到晶体时，问对哪些波长的X 射线能产生强反射?习题十四·光的偏振14-1 自然光是否一定不是单色光?线偏振光是否一定是单色光?14-2 用哪些方法可以获得线偏振光?怎样用实验来检验线偏振光、部分偏振光和自然光?14-3 一束光入射到两种透明介质的分界面上时，发现只有透射光而无反射光，试说明这束光是怎样入射的?其偏振状态如何?14-4 什么是光轴、主截面和主平面?什么是寻常光线和非常光线?它们的振动方向和各自的主平面有何关系?14-5 在单轴晶体中，e 光是否总是以e n c /的速率传播?哪个方向以0/n c 的速率传播?14-6是否只有自然光入射晶体时才能产生O 光和e 光?14-7投射到起偏器的自然光强度为0I ，开始时，起偏器和检偏器的透光轴方向平行．然后使检偏器绕入射光的传播方向转过130°，45°，60°，试分别求出在上述三种情况下，透过检偏器后光的强度是0I 的几倍?14-8 使自然光通过两个偏振化方向夹角为60°的偏振片时，透射光强为1I ，今在这两个偏振片之间再插入一偏振片，它的偏振化方向与前两个偏振片均成30°，问此时透射光I 与1I 之比为多少?14-9 自然光入射到两个重叠的偏振片上．如果透射光强为，(1)透射光最大强度的三分之一，(2)入射光强的三分之一，则这两个偏振片透光轴方向间的夹角为多少?14-10 一束自然光从空气入射到折射率为1.40的液体表面上，其反射光是完全偏振光．试求：(1)入射角等于多少?(2)折射角为多少?14-11 利用布儒斯特定律怎样测定不透明介质的折射率?若测得釉质在空气中的起偏振角为58°，求釉质的折射率．14-12 光由空气射入折射率为n 的玻璃．在题14-12图所示的各种情况中，用黑点和短线把反射光和折射光的振动方向表示出来，并标明是线偏振光还是部分偏振光．图中.arctan ,00n i i i =≠题图14-12*14-13如果一个二分之一波片或四分之一波片的光轴与起偏器的偏振化方向成30°角，试问从二分之一波片还是从四分之一波片透射出来的光将是：(1)线偏振光?(2)圆偏振光?(3)椭圆偏振光?为什么?题14-13图*14-14 将厚度为1mm且垂直于光轴切出的石英晶片，放在两平行的偏振片之间，对某一波长的光波，经过晶片后振动面旋转了20°．问石英晶片的厚度变为多少时，该波长的光将完全不能通过?。
高中物理 波动光学( 光的偏振)习题及答案
一. 选择题[A ]1. 一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片．若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的5倍，那么入射光束中自然光与线偏振光的光强比值为(A) 1 / 2． (B) 1 / 3． (C) 1 / 4． (D) 1 / 5．提示：[ D ]2. 某种透明媒质对于空气的临界角(指全反射)等于45°，光从空气射向此媒质时的布儒斯特角是(A) 35.3°．(B) 40.9°．(C) 45°． (D) 54.7°． (E) 57.3°．[ ]3. 一束自然光自空气射向一块平板玻璃(如图)，设入射角等于布儒斯特角i 0，则在界面2的反射光(A) 是自然光． (B) 是线偏振光且光矢量的振动方向垂直于入射面． (C) 是线偏振光且光矢量的振动方向平行于入射面． (D) 是部分偏振光． 提示：[ ]4. 一束自然光通过两个偏振片，若两偏振片的偏振化方向间夹角由α1转到α2，则转动前后透射光强度之比为2212cos :cos αα提示：二. 填空题1. 如图所示的杨氏双缝干涉装置，若用单色自然光照射狭缝S ，在屏幕上能看到干涉条纹．若在双缝S 1和S 2的一侧分别加一同质同厚的偏振片P 1、P 2，则当P 1与P 2的偏振化方向相互___平行________时，在屏幕上仍能看到很清晰的干涉条纹．提示：要相互平行。
致”，两个偏振片方向为了满足“振动方向一致，相位差恒定。
频率相同，振动方向一件：两束光必须满足相干条为了看到清晰的条纹，2. 要使一束线偏振光通过偏振片之后振动方向转过90°，至少需要让这束光通过_____2_____块理想偏振片．在此情况下，透射光强最大是原来光强的___1/4_____倍 。
提示：如图P 2P 1S 1S 2S3. 在以下五个图中，前四个图表示线偏振光入射于两种介质分界面上，最后一图表示入射光是自然光．n 1、n 2为两种介质的折射率，图中入射角i 0＝arctg (n 2/n 1)，i ≠i 0．试在图上画出实际存在的折射光线和反射光线，并用点或短线把振动方向表示出来．提示：作图时注意细节。
波动光学习题参考答案
=5.19×10-4 (mm) =590 (nm)
结束 返回
18、 一柱面平凹透镜A，曲率半径为R放在平玻 璃片B上，如图所示。现用波长为l 的单色平行光 自上方垂直往下照射，观察A和B间空气薄膜的反 射光的干涉条纹，如空气膜的最大厚度d =2l ， (1)分析干涉条纹的特点(形状、分布、级次高 低)，作图表示明条纹； (2)求明条纹距中心线的距离； (3)共能看到多少条明条纹； (4)若将玻璃片B向下 A 平移，条纹如何移动? d 若玻璃片移动了l /4， B 问这时还能看到几条明条纹?
结束 返回
解：由暗纹条件 解：
l = (k 1 )l 2ne = (2k+1) 2 +2
设 l 1 =500nm 为第k级干涉极小
l2 =700nm 为第(k-1)级干涉极小
1 1 1 l (k + 2 ) 1 = (k 1) 2 + 2 l2
l 1+ l 2 500+700 k= = 2(700-200) 2( l2 l1 )
x ´为k 级新的明条纹位置
x´
原来的光程差为 d = r 2 r 1 = dsinj = d x = kl D d b + d (x ´ x ) =0 两式相减得到： D´ D D Δ x ´= b (x ´ x ) <0 D´
即条纹向下移动，而条纹间距不变
D´ S 2
o
D
结束 返回
7、 用单色光源S照射双缝，在屏上形 成干涉图样，零级明条纹位于O 点，如图所 示。若将缝光源 S 移至位置S ´，零级明条 纹将发生移动。欲使零级明条纹移回 O 点， 必须在哪个缝处覆盖一薄云母片才有可能? 若用波长589nm的单 色光，欲使移动了4个 屏 S1 明纹间距的零级明纹 S´ O 移回到O点，云母片的 S 厚度应为多少?云母片 S2 的折射率为1.58。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
角色散为
d m d 2nh sin
其中干涉角满足如下关系
2nh cos m
已知 m=1， 0.6328m ， h 4cm ，则得到
1.5707rad
8
则进一步得到
d 1.25 108 rad / nm d
（2）对于光栅（参考教材 166 页到 168 页） 自由光谱范围为
d sin m
在两个极大之间有一个干涉极小值。 已知 d 7.0 102 cm ， b 8.8 103 cm ，则可以确定在单缝衍射第一 个暗点至中央峰值点之间有近似 8 个（7.95 个）干涉最大值，因此有 28=16 个干涉极小值。 同时，根据公式 d sin m 知，在中央峰值附近相邻两个亮条纹 之间的间距为
0 1.22 f
2a
同时，根据题意知： f 4 105 km, 2a 2m, 600nm ，计算得到：
0 146.4m
3.5 解：根据教材 139 页的公式(3.2-21)和(3.2-22)公式非常容易的确定 衍射光斑的角宽度和线宽度，具体计算略。 3.6 解：根据教材 142 的公式(3.2-34)可知，显微物镜的分辨最小值由 如下公式确定
a sin 。
(2) 当全部敞开后，衍射光场可以看成是两个错开距离为 2a、缝数为 N 的衍射光栅相互作用的结果。 则根据教材 144 页的公式(3.2-41)可知， 缝数为 N 的其中一个衍射光栅的衍射光场振幅为
E P Cae
i N 1
2
sin
sin
N 2
3.16 解： （1）根据教材 162 页图 3-40 的描述，当光束垂直入射到光栅上是， 经过相邻两个光栅缝并沿着角衍射时，两条光束相遇时产生的光程 差和相位差分别为
d sin , 2
2
d sin
则当 d sin 3 时，此时相邻狭缝的两束光的光程差为 3 ，经过第 1 条和第 n 条狭缝的两条光束的光程差为 3 n 1 。此时，经过任意两 个狭缝的光束沿着角衍射时的光程差都是波长的整数倍，根据干涉 的基本原理，此时光的叠加都会加强。
x 10 f a
根据题意已知 x 6.3cm, f 5m, 0.63m ，则可知
a 0.5mm
3.11 解： 根据巴比涅原理， 单丝衍射的强度分布和单缝衍射的强度分 布相同（除了中心点） 。则根据教材 143 页的公式(3.2-37)可知，单缝 衍射中央主极大的宽度为
(3) 当数值孔径为 1.60，则
0.61 0.61 0.275 0.105 m NA 1.60
3.7 解：参考教材 141 页“ （3）照相物镜的分辨本领”部分。具体略。 3.8 解：根据公式（3.2-30）可知，
N 1 D 1 1 429 6 mm 1.22 f 1.22 546 10 3.5
f
分辨本领为
m
0.6328 0.6328 m 1
A mN 1 30 1200 36000
角色散为
d m d d cos
其中衍射根据光栅方程 d sin m 确定，为
49.4o
则进一步求得
d 1.844 103 rad / nm d
2 cos 2
2
当 2m
m 称为衍射级次。 m 0, 1, 2, 时对应干涉亮纹的位置，
利用上述公式很容易确定第 1、2、3 级亮纹的相对强度分别为
sin 4 4 sin sin 3 、 2 、 4
m d
2.5 3.6 0.69
取 m=3。 当光束以倾斜角 90 度入射时，对应的最大干涉级次为
m 2d
5 7.24 0.69
取 m=7。 3.19 解：F-P 标准具和光栅都是典型的分光器件，通常利用如下三个 量来衡量器件的分光性能：自由光谱范围、分辨本领、角色散或线色 散。 （1）对于 F-P 标准具（参考教材 91 至 93 页） 自由光谱范围为
x f f
d据题意已知 0.6328m, d 7 102 cm, f 457.2cm ，计算得
x 0.4133cm
3.13 解： (1) 利用 3.12 题的分析可知，双缝衍射场相邻两个亮条纹的间距为
x f f
d cos
2 d 2 2 sin N 2 sin a sin sin 6 N I0 I0 d 6 a 2
其中，
2
另一光栅产生的衍射光场相对于这一光栅的衍射光场仅多一个常数 相移因子 ei 2 ，其中
2
a sin 。则总的衍射光场振幅为
5
E P Cae
i N 1
2
sin
sin
N 2 1 e i 2
2
则衍射光场的强度为
I P E P
I I 0 0.047182 0.0022 I 0
其中， 1.430 。同理可确定第 6 个次极大的强度值。 3.2 解：根据教材 134 页的公式(3.2-8)可知，中央衍射光斑在 x 轴和 y 轴上的第一个暗点位置分别位于：
x f f ,y a b
根据题意，已知 488nm, a 0.75mm, b 0.25mm, f 2.5m ，则可知
因此用 500/mm 的底片记录是满足要求的。 3.9 解：白光经过棱镜将实现分光，再经过狭缝后会发生衍射，衍射 条纹的亮暗间距与波长成正比，波长越大条纹间距越大，因此形成如 图所示的弯曲衍射条纹分布。 3.10 解：根据教材 134 页公式(3.2-8)可知，衍射条纹左右两个第五级 最小之间的间距为
2
sin sin 6 N 2 4I0 cos 2 6
2 2
3.15 解：根据题意可知光栅周期为 d=a+b=0.041mm，N=1000，则 （1）根据单缝衍射的公式(3.2-40)可知中央主峰的角宽度为
2 2 624 106 0.104rad a 0.012
f
d
根据题意， f 50cm, 632.8nm, x 1.5mm ，则可知
d 0.21mm
同时根据缺级的基本性质可知，
d 4 a
则， a 0.0525mm (2) 根据教材 145 页的公式(3.2-44)，并结合（1）的计算结果可知，
4
sin 8 I P 4I0 8
f 2500 0.488 103 1.62mm a 0.75 f 2500 0.488 103 4.88mm b 0.25
则中央衍射斑是一个 3.24mm 9.76mm 的矩形光斑。 整体的衍射强度分布可根据公式(3.2-6)通过计算机编程形象的显 示出来。 3.3 解：根据教材 140 页的“ （1）人眼的分辨本领”部分的介绍可知， 人瞳孔的范围在 1.5-6mm，选择人比较敏感的光波长 0.55m，则人眼
f
m
2
2nh
0.6328 10
2 1 0.04
6 2
5 1012 m 0.005nm
分辨本领为
A 0.97 2h
N 0.97
2h R 2 0.04 0.891 0.97 3.34 106 6 1 R 0.6328 10 1 0.891
x 2 f a
则根据题意已知 x 1cm, 0.63m, f 50cm ，则求得
a 63 m
3.12 解：根据教材 145 页的介绍可知，双缝衍射的强度分布是单缝衍
3
射因子和双缝干涉强度分布共同作用的结果。 单缝衍射的位置由如下 公式确定
b sin m
干涉极大由如下公式确定
(2) 根 据 d/a=0.041/0.012=3.41 ， 表 明 在 中 央 峰 内 有 7 个 极 大 （ m 0, 1, 2, 3 ） 。 (3) 根据教材 147 页的公式（3.2-48）可知相邻两个亮纹之间的角宽度 为
Nd cos
Nd
624 106 1.52 105 rad 1000 0.041
2 2 2
2
3
4
即为 0.810、0.405、0.090。 3.14 解： （1）当挡住偶数缝时，缝的总数量为 N，缝宽依然为 a，缝的间距为 d=6a，则根据教材 145 页的公式(3.2-43)可知，衍射场的强度分布为
N 2 sin sin 2 I P I0 2
0.61 NA
其中，NA 为物镜的数值孔径（关于数值孔径的概念参看应用光学的 相关知识） 。因此，可知，提高分辨率或减小最小分辨尺度的方法是 增大透镜的数值孔径或减小使用波长。 由上述公式很容易分析该题目： (1) 紫外光比可见光波长小一半，则分辨率提高一倍。 (2) 最小尺寸为
2
0.61 0.61 0.275 0.186 m NA 0.90
第三章 光的衍射 习题答案
3.1 解： 根据教材 134 的公式(3.2-6)可知， 矩形孔对应的夫琅和费衍射 场的强度分布为：
sin sin I x, y I 0