反比例函数中K的几何含义详解
反比例函数中k的几何意义及应用.

反比例函数中k的几何意义及应用.例析反比例函数中k 的几何意义及应用陆智勇(云南省广南县篆角初级中学邮编:663312 电话:135********) 反比例函数中k 的几何意义就是反比例函数图象上的任意一点的横坐标与纵坐标的乘积都等于比例系数K 的值,如图①所示.过P 作x 轴、y 轴的垂线PA 、PB ,垂足为A 、B ,连结OP,则有(1)AOBP S 矩形=PA ·PB=|y|·|x|=|xy|=|k|;(2)K PA OA S S BOP AOP 2121=?==??.能灵活运用这两个结论解有关反比例函数的问题,会给解题带来很多方便。
现略举说明。
一、求交点坐标和面积例1如图②,已知反比例函数与xy 8-=一次函数2+-=x y 的图象交于A、B两点。
(1)求A,B两点的坐标;(2)求△AOB的面积。
图②+-=-=.2,8)1(:x y x y 联立解??=-=-==.4,2;2,4y x y x 或解得).2,4(),4,2(--∴B A ).0,2(,2,0,2:)2(M x y x y ==+-=时当解法一二、比较面积的大小例2如图⑤,在χχ(1=y >0)的图像上有三点A,B,C,经过三点分别向χ轴引垂线,交χ轴于111,,C B A 三点,连接OA ,OB ,OC ,记△,1OAA △,1OBB △,1OCC 的面积分别为,,,321S S S 则有 ..642=+=+=∴OAM OMB AOB S S S .,D x BD C x AC 轴于轴于作⊥⊥,2,4==BD AC ,2222121=??=??=∴?BD OM S OMB .4422121=??=??=?AC OM S OMA ). 2,0(,2,0,2:)2(N y x x y ==+-=时当解法二图⑤.2=∴ON .,D y BD C y AC 轴于轴于作⊥⊥,4,2==BD AC ,4422 121=??=??=∴?BD ON S ONB.2222121=??=??=?AC ON S ONA .624=+=+=∴O NA O NB AO B S S SA.S 1 = S 2 = S 3B. S 1 < S 2 < S 3C. S 3 < S 1 < S 2D. S 1 > S 2 >S 3 解:由性质(1)得三、确定解析式例3如图⑥,反比例函数K xKy (=﹤0) 的图象经过点A (,3-m ),过A 作AB ⊥χ轴于点B ,.3=?AO B S (1)求K 和m 的值.(2)若过A 点的直线y=a χ+b 与χ轴交于点C ,且∠ACO=30, 求直线的解析式.解: (1)由性质(2)得,21K S AOB =∴.213K =.,,21||21,21||21,21||21321111A S S S k S k S k S OOC BOB AOA 故选即========.32=K ,图像在二、四象限又 .32-=∴K .32χ-=∴y 解析式为得代入,把(χ32)3-=-y m 图⑥(2)①连接,2AC 则在Rt △AB 2C 中,∵AB=2,∠A 2C O=30,.32,422==∴BC AC.322=-=∴BO BC OC ).0,32的坐标为(C ∴得)代入,(和(把b a y A C +=-χ23)0,32② 连接,1AC 则在Rt △AB 1C 中,∵AB=2,∠A 1C O=30,.32,411==∴BC AC.3311=+=∴BO BC OC ).0,331-∴的坐标为(C.133+-=∴χy 解析式为=+-=+.23,03)1(:b a b a 解??=-=.1,33b a 解方程组得.2=m得)代入,(和(把b a y A C +=--χ23)0,331四、求函数值例4两个反比例函数χχ6,3==y y 在第一象限内的图象如图⑦所示,2005321...,P P P P ,点在反比例函数χ6=y 的图象上,它们的横坐标分别是,...,2005321χχχχ,纵坐标分别是1,3,5,…,共2005个连续奇数, 2005321...,P P P P ,过点分别作y 轴的平行线,χ3=y 与的图象的交点依次),,(),,(),,(332222111y Q y Q y Q χχχ …, ),,(200520052005χχQ 则=2005y .解: 2005321...,P P P P ,点在反比例函数χ6=y 的图象上,它们的纵坐标分别取1,3,5…,4009时相应的横坐标分别=+-=+-.23,033b a b a ??==.3,33b a 解方程组得.333+=∴χy 解析式为图⑦图⑧为,40096,...,56,36,16),,(),,(),,(332222111y Q y Q y Q χχχ…, ),,(200520052005χχQ 函数的图象上,χ3=y 且这些点的横坐标分别与点2005321...,P P P P ,横坐标相同, 的点2005Q 横坐标是.40096所以的点2005Q 纵坐标是=2005y χ3=.24009400963= 五、确定K 的取值范围例5如图⑧所示,已知一次函数8+-=χy 和反比例函数χKy =(K ≠0)的图象在第一象限内有两个不同的公共点A 、B.(1)求实数K 的取值范围;(2)若△AOB 的面积S=24,求K 的值..082=+-k χχ依据题意得△=64-4K >0,∴K <16.设两公共点的坐标为).y ,(),y ,(2211χχB A 又1χ>0, 2χ>0,∴1χ+2χ=8>0, 1χ2χ=K >0. ∴实数K 的取值范围为0<K <16.(2)在y=-χ+8中,令χ=0,得y=8,∴OC=8.(4212112=?-?=-=χχOC OC S S S COA COB AOB 2χ-1χ) =.2446444)(421221=-=-+K χχχχ得消去联立解y Ky y ??=+-=.,8)1(:χχ∴.6464=-K ∴K=7.六、确定自变量χ的取值范围例6如图⑨是一次函数和b K y +=χ1和反比例函数χmy =2的图象,观察图象写出1y >2y 时,χ的取值范围 .解:由图⑨得y >2y ,χmy =2的图象在一、三象限,∴第三象限χ的取值范围为-2<χ<0.第一象限χ的取值范围为χ>3.∴图象1y >2y 时,χ的取值范围为-2<χ<0或χ>3. 七、求点的坐标例7如图⑩所示,正方形OABC 、正方形ADEF 的顶点A 、D 、C 在坐标轴上,点F 在AB 上,点B 、E 在函数χ1=y (χ>0)的图象上,则点E 的坐标是().的增大而增大,随χ1y .2的增大而增小随χy M >0 图⑨)215,215.(-+A )253,253.(-+B )215,215.(+-C )253,253.(+-D 解:连接OB ,则.1,12121==∴?=?=?AOB AB OA AB OA S连接OE ,则,12121?=?=?O DE OD S DE 设则,a AD DE == ,01,1)12=-+=+a a a a 即(=1a 解得.(215,2152舍去)--=-a .2512151,215+=-+=+=-=∴AD OA OD DE ∴点E 的坐标是).215,215(-+图⑩。
反比例函数中比例系数k的几何意义

反思小结
在反比例函数 y 10 的图象上,有一系列点A1,A2, x A3…..An,An+1,若A1横坐标为2,且以后每点的 横坐标与它前一个点的横坐标的差都为2. 现分别 过点A1,A2,A3…..An,An+1作X轴与Y轴的垂线 段,构成若干个矩形如图10所示,将图中阴影部 分的面积从左到右依次记为S1、S2、S3、…Sn, 5 5 15 2 5 2 (5 _____, ) 则S1=________, S +S +S =____ S1+S2 2 1 2 3 4 2 5 10 n 2 (5 ) +S3+….+Sn=________________.( 用n的代数式表 n 1 n 1 A 示)
C
S SOAD SABD SBCD SOCD 4 1 4
达标测试
已知几何图形的面积S,求比例系数k
5、如图,已知双曲线 (k>0) 经过矩形OABC边AB的中点F,交BC于点E, 且四边形OEBF的面积为2,则k的值为( B )。
y
y
k x
A 1
所以
B 2
C 4
S OAB 4
O
y
已知几何图形的面积S,求比例系数k k y 变式、如图,已知双曲线 x ( k>0 )经
B
D
C E A
x
而
SOAB SOBC SOAC
即
S ODE 1 S OAB 1 4 k 3 2
1 k 2
相似三角形的面积比 等于相似比的平方 k 4;
k 0 k 4
k 0 k 4
4 y x
达标测试
4、如图,在平面直角坐标系中, 点O为原点,菱形OABC的对角线 OB在x轴上,顶点A在反比例函数 2 的图像上,求菱形的面积。 y B
反比例函数中k的几何意义的应用

反比例函数中k的几何意义的应用
k在反比例函数中具有重要的几何意义,以下列举一些它的应用。
1. 直线反比例函数:k反映直线斜率的倒数,即斜率m=-k。
当给定直
线k值时,由定点和k值可以求出斜率m,从而可以绘制出这条直线。
2. 圆反比例函数:k反映圆半径r的倒数,即r=1/k。
当给定圆k值时,由定点和k值可以求出圆半径,从而可以绘制出这个圆。
3. 抛物线反比例函数:k反映抛物线的开口方向,当k > 0时,抛物线
向右开口;当k < 0时,抛物线向左开口。
4. 双曲线反比例函数:k反映双曲线的开口方向,当k>0时,双曲线
开口向右;当k<0时,双曲线开口向左。
5. 其他函数反比例函数:k可以反映此类函数中曲线的凹凸,当k > 0时,曲线是凹曲线;当k < 0时,曲线是凸曲线。
总之,k在反比例函数中应用广泛,几乎所有的函数都可以用反比例函
数表示。
它的几何意义非常重要,不仅仅可以根据k值绘制出各种曲线,而且可以了解曲线的开口方向以及凹凸方向。
因此,k在反比例函
数绘制中发挥着重要的作用。
反比例函数中K的几何意义课件

k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中,k值决定了图 像的形状和位置。当k>0时,图像出 现在第一象限和第三象限;当k<0时 ,图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时,图像分布在第一象限和第三象限;当k<0时,图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展,反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域,如经济学、生物学等,以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念,与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系,以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小,反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用,如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解,但仍有许多未知的性质等待我们去发 现和研究。例如,反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质:当 x 增大时,y 值会减小;当 x 减小 时,y 值会增大。这是因为 xy =
k 的关系。
在图像上,反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的,且无限接近于坐标轴
。
Part
02
反比例函数中K的几何意义

反比例函数中K的几何意义
在反比例函数中,K表示比例系数或常数,也被称为反比例常数。
它
是用来确定两个变量之间反比关系的重要参数。
反比例函数的一般形式为:y=K/x,其中K表示比例系数。
K的几何意义可以通过分析反比例函数的图像得出。
反比例函数的图
像是一个双曲线,特点是曲线趋向于两个坐标轴。
下面将详细讨论K的几
何意义。
1.K的符号对于曲线的位置以及开口方向具有重要影响。
如果K为正数,那么曲线将位于第一和第三象限,并且开口方向为右上和左下。
如果
K为负数,那么曲线将位于第二和第四象限,并且开口方向为左上和右下。
2.K的绝对值越大,曲线就越“陡峭”。
当K增大时,曲线将更加接
近于坐标轴,并且在原点附近的斜率会越来越大。
反之,当K变小时,曲
线将更加平缓,斜率将减小。
3.K决定了特定坐标点的函数值。
例如,在函数y=K/x中,当x为K 时,y的值将为1、这是因为x与y成反比关系,而K是这种关系的常数。
4.K还决定了曲线相对于坐标轴的位置。
具体而言,当K增大时,曲
线将向坐标轴移动,而当K减小时,曲线将远离坐标轴。
总之,K代表了反比例函数中的比例系数或常数,它对于函数的位置、开口方向、陡峭程度以及特定坐标点的函数值都具有重要影响。
通过对K
的分析,我们可以更好地理解和解释反比例函数的几何特征。
反比例函数中k的几何意义

【主干必备】 反比例函数中比例系数k的几何意义 设点P(m,n)是双曲线y= k (k≠0)上任意一点
x
(1)过点P作x轴或y轴的垂线,垂足为点A,则
S△OAP=
1 2
·OA·AP=
1 |m|·|n|=
2
1 |mn|=
2
1 2
|k|.
(2)过点P分别作x轴、y轴的垂线,垂足为A,B,
值为 世纪金榜导学号( D )
A.5
B.-5
C.10
D.-10
3.(2019·哈尔滨木兰期末)已知P是反比例函数y= k
x
(k≠0)图象上一点,PA⊥x轴于A,若S△AOP=4,则这个反
比例函数的解析式是 ( C )
A.y= 8
x
C.y= 8 =- 8
x
D.y= 4 或y=- 4
则S矩形OAPB=OA·AP=|m|·|n|=|mn|=|k|.
【微点警示】 因为反比例函数y= k (k是常数,k≠0)中的k有正、负之
x
分,所以在利用解析式求矩形或三角形的面积时,都应 加上绝对值符号;已知矩形或三角形的面积求反比例函 数的解析式或k的值时,要根据函数的图象所在的象限 确定k的正负.
x
x轴于点B交反比例函数y= 2 的图象于点C,连接OA,OC,
x
则△OAC的面积为 ( B )
A.2
B.3
C.6
D.8
2.(2019·达州达川区期末)如图所示,点A是反比例函
数y= k 的图象上的一点,过点A作AB⊥x轴,垂足为B,点
x
C为y轴上的一点,连接AC,BC.若△ABC的面积为5,则k的
【核心突破】
反比例函数中“k”的几何意义
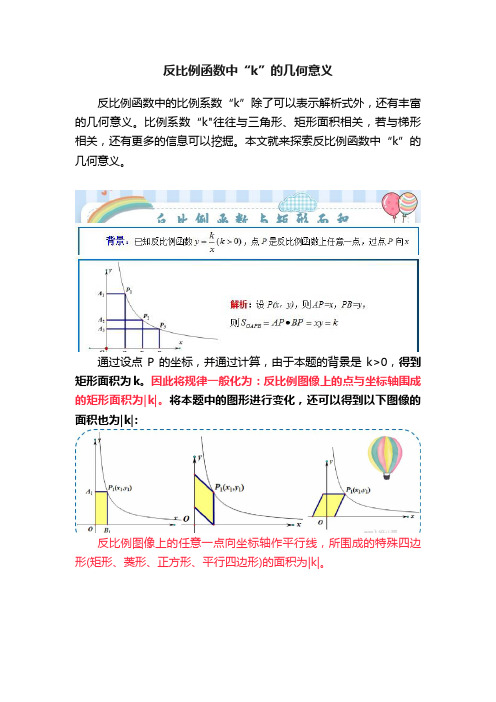
反比例函数中“k”的几何意义
反比例函数中的比例系数“k”除了可以表示解析式外,还有丰富的几何意义。
比例系数“k"往往与三角形、矩形面积相关,若与梯形相关,还有更多的信息可以挖掘。
本文就来探索反比例函数中“k”的几何意义。
通过设点P的坐标,并通过计算,由于本题的背景是k>0,得到矩形面积为k。
因此将规律一般化为:反比例图像上的点与坐标轴围成的矩形面积为|k|。
将本题中的图形进行变化,还可以得到以下图像的面积也为|k|:
反比例图像上的任意一点向坐标轴作平行线,所围成的特殊四边形(矩形、菱形、正方形、平行四边形)的面积为|k|。
反比例图像上若有两点关于原点对称,且三角形有一边平行于坐标轴,那么此时三角形的面积为|k|。
由反比例函数与矩形面积的关系,我们可以得到反比例函数与三角形面积的关系如下:反比例图像上的点与坐标轴围成的三角形面积为1/2|k|。
我们还可以做如下变式:这些三角形都有一条边与坐标轴平行,以下三角形的面积也均为1/2|k|。
掌握了上述三角形的面积特点,我们可以利用转化的方法得到面积相等的三角形。
转化的方法就是利用平行得到同底等高的三角形面积相等。
如图,S▲AOB=S▲ABC=1/2|k|。
因此要学会转化成“k” 的几何意义,更重要的是要能从图形中发现这些基本图形。
将以上两类问题综合,我们可以得到下列几个图形的面积为2|k|。
轴作垂线形成的梯形面积。
反比例图像上的任意两点分别向坐标轴作垂线,这两点的连线与垂足的连线互相平行。
反比例函数的几何意义

1、定义:一般地,如果两个变量x,y之间的关系可以表示成 (k为变量x的函数,x的取值范围是不等于0的一切实数,且y也不能等于0。
2、图像:k>0时,图像在一、三象限,y随x的增大而减小;k<0时,图像在二、四象限,y随x的增大而增大。
k值相等的反比例函数图像重合,k值不相等的反比例函数图像永不相交。
|k|越大,反比例函数的图像离坐标轴的距离越远。
3、k的几何意义
反比例函数的图像属于以原点为对称中心的中心对称的双曲线,反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(y≠0)。
反比例函数的图像既是轴对称图形,又是中心对称图形,它有两条对称轴y=±x(即第一三,二四象限角平分线),对称中心是坐标原点。
反比例函数图像不与x轴和y轴相交的渐近线为:x轴与y轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
3、若四边形OABC是边长为1的正方形,反比例函数
k 的 y 的图象过点B,则k的值为( x y
B A
)
C
o
x
4.如图,点P是反比例函数 图象上的一点, 若矩形OMNP的面积是3,则K=( )
k y x
y
M
o x
N
P
5.如图,点P是反比例函数 图象上的一点, 若矩形ONPM的面积是4,则K=( )
6 1、若点P(m,n)在反比例函数 y 图像上, x
则mn= 。 , . 2
B
3 A D
1 2
2.如图,S矩形ABCD= S△ABD=
S矩形ABCD=
C
1.理解并掌握反比例函数中∣K∣的几何意义; 2.能灵活运用∣K∣的几何意义求图形面积; 3.能根据图形面积求出K值。
k 1.如图,点P(3,2)在反比例函数 y 图像上 x 则K=( ),过P作PA⊥x轴,PB⊥y轴,则OA=( ),
PA=( ),S矩形ABCD=(
y
)
B
P(3,2) A
o
x
若E(1,6)也在该图像上,则绿色矩形面积为( )
若F(4,-1.5)
y
E
6 在y - x
图像上,则黄色矩形面积为
B
P(3,2)
o
A
F(4,-1.5)
x
(1)过P(m, n)分别作x轴, y轴的垂线, 垂足分别为A, B, 则S矩形OAPB OA AP | m | | n || k | (如图所示).
y
A.S1 = S2 = S3 B. S1 < S2 < S3 C. S3 < S1 < S2 D. S1 > S2 >S3
A S1 B S2
C
o
A1
S3 B1 C1
x
k 1.已知,点P是反比例函数 y x 图象上一点,作
PA⊥ x轴 于A,若 S△AOP是3,则这个反比例函 数的解析式为( )
y
P(m,n)
o
A
x
2 1.如图,点P是反比例函数 y 图象上 x 的一点,PD⊥x轴于D.则△POD的面积为1
S△POD
1 = OD· PD 2
1 = 2
y P (m,n) o D x
m n
1 = k 2
2.如图:SRt△OAP=
.
y
y
3 x
P
A
o x
2 3.如图:A、C是函数y 图像上任意两点, Rt△ AOB的 x 面积记作S1,Rt△OCD的面积记作S 2,则下列结论正确 的是()
y
E
S2S2
o
S1
A
S1
B D
x
C
2.如图,下列图像中阴影部分面积不是2的是( ) y
y 4 x
y
o
M P
y 2 x
x
P
A
y
o
D
y
x
B
N
3 x
2 y x
y
A
P
C
oS
2
C
A
o x
B
x
D
3.如图,反比例函数
y
k x
与正比例函数y=-
1 2
x交
于A、B点,AC⊥x轴,若S△ABC=2,求k的值。 y
则四边形AOBP的面积为 k ;且S△AOP =
S△BOP k
。
2
1.理解并掌握反比例函数中∣K∣的几何意义; 2.能灵活运用∣K∣的几何意义求图形面积; 3.能根据图形面积求出K值。
2 1.如图,过反比例函数 y 图像上两点A、C分别作 x Rt△OAB、矩形CDOE,则S1=( ) , S2=( )
则S△AOB=(
) y
A
4 y x
o
S2
C
x
B
如图,反比例函数
y-
4 x
与正比例函数y=-x交于A、B ) y
两点,AC⊥x轴B
x
4 如图,A是反比例函数 y x 上任意一点,
P是x轴上一点,过A作AB⊥y轴,垂足为B,则 S△ABP=( ).
y B A
P
O
X
k y x
y o N
M
x
P
1.如图,S矩形OAPB=
y
,S△OAP=
.
P B
O
4 y x P
A
x
2.观察图中各个三角形的面积,你有什么发现?
y P(m,n)
4 x
y
o
A
x
k (2)设P(m, n)是双曲线y (k 0)上任意一点 ,有: x 过P作x轴的垂线, 垂足为A, 则 1 1 1 SOAP OA AP | m | | n | | k | 2 2 2
A.S1>S2 B.S1<S2 C.S1 = S2 D.不能确定.
C
y
A
o
S2 S2
SS 1
1
B D
x
3 4.如图, 在y ( x 0)的图像上有三点 A, B, C , x 经过三点分别向 x轴引垂线 , 交x轴于A1 , B1 , C1三点, 边结OA, OB, OC, 记OAA 的 1 , OBB 1 , OCC1 面积分别为S1 , S 2 , S3 , 则有 __ .
y
B
P(m,n)
A
o
x
3 1.如图,点P是反比例函数 y 图象 x 上的一点,过点P分别向x轴、y轴作垂线,
则长方形ONPM的面积是多少?
y
P
N
O
M
x
3 2.如图,点P是反比例函数y 图象 x
上的一点,过点P分别向x轴、y轴作垂线, 则长方形ONPM的面积是多少?
y
y
3 x
P
N
A
o
C
S2
B
x
如图,A是反比例函数 上任意一点,P是 x轴上一动点,过A作AB⊥y轴,垂足为B,则关于 S△ABP正确的说法是( )
y A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定 P O X B A
4 y x
k 反比例函数 y 上一点P(x0,y0),过点P x
作PA⊥y轴,PB⊥X轴,垂足分别为A、B,
1.已知,点P是反比例函数 图象上一点,作 PA⊥ x轴 于A,若 S△AOP是4,求这个反比例函 数的解析式。 2.已知,点P是反比例函数 图象上一点,作 PA⊥ y轴 于A,若 S△AOP是2,求这个反比例函 数的解析式。
k y x
y
k x
如图,反比例函数与正比例函数图像交于A、B两点,
