拉普拉斯变换和Z变换表
常用拉普拉斯变换及反变换
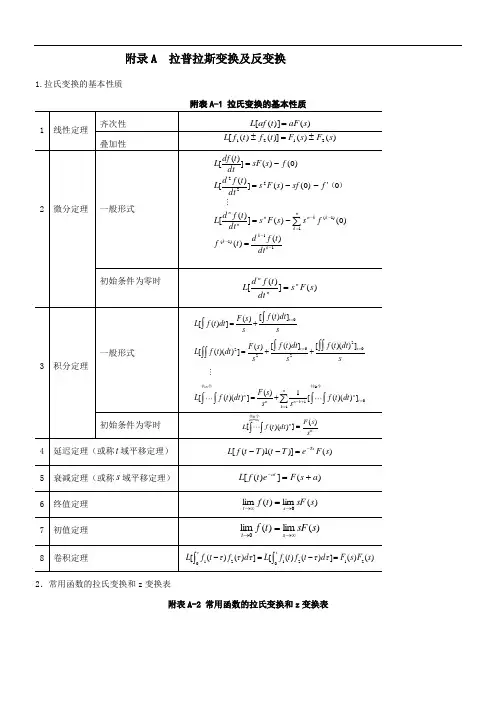
419附录A 拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质 齐次性)()]([s aF t af L =1线性定理叠加性)()()]()([2121s F s F t f t f L ±=±一般形式=−=][′−ٛ−=−=−−−−=−∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n n n dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L M ）（ 2微分定理初始条件为0时)(])([s F s dtt f d L n nn =一般形式 }}∑∫∫∫∫∫∫∫∫∫∫∫==+−===+=++=+=nk t n n k n n n n t t t dt t f ss s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共L L M3积分定理初始条件为0时}nnn s s F dt t f L )(]))(([=∫∫个共L4 延迟定理（或称t 域平移定理）)()](1)([s F e T t T t f L Ts−=−− 5 衰减定理（或称s 域平移定理）)(])([a s F e t f L at +=−6 终值定理 )(lim )(lim 0s sF t f st →∞→=7 初值定理 )(lim )(lim 0s sF t f s t ∞→→=8 卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =−=−∫∫τττττ4202．表A-2 常用函数的拉氏变换和z 变换表 序号 拉氏变换E(s)时间函数e(t) Z 变换E(z)1 1δ(t)12 Ts e −−11∑∞=−=0)()(n T nT tt δδ 1−z z3 s1 )(1t 1−z z 421s t2)1(−z Tz5 31s 22t32)1(2)1(−+z z z T6 11+n s!n t n )(!)1(lim 0aTn n n a e z z a n −→−∂∂− 7 as +1ate −aTe z z−− 8 2)(1a s + atte− 2)(aT aT e z Tze −−−9 )(a s s a +ate−−1 ))(1()1(aT aT e z z z e −−−−− 10 ))((b s a s ab ++− btate e−−−bTaT e z z e z z −−−−− 11 22ωω+st ωsin 1cos 2sin 2+−T z z Tz ωω12 22ω+s st ωcos1cos 2)cos (2+−−T z z T z z ωω 13 22)(ωω++a s t eatωsin −aTaT aT eT ze z T ze 22cos 2sin −−−+−ωω 14 22)(ω+++a s a st e at ωcos −aTaT aTe T ze z T ze z 222cos 2cos −−−+−−ωω15aT s ln )/1(1−T t a/az z −4213． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
拉氏变换和z变换表
附录A 拉普拉斯变换及反变换1.拉氏变换的基本性质1()([n n k f t dt s s-+=+∑⎰个2．常用函数的拉氏变换和z变换表附表A-2 常用函数的拉氏变换和z变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式，即1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中，系数n n a a a a ,,...,,110-和011,,,,m m b b b b -都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
（1）0)(=s A 无重根：这时，F(s)可展开为n 个简单的部分分式之和的形式，即∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根；i c 为待定常数，称为()F s 在i s 处的留数，可按下列两式计算：lim()()ii i s s c s s F s →=- （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数为[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝1in s ti i c e =∑ (F -4) （2）0)(=s A 有重根：设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…，n s 为F(s)的n r -个单根；其中，1+r c ，…，n c 仍按式(F-2)或式(F-3)计算，r c ，1-r c ，…，1c 则按下式计算：)()(lim 11s F s s c r s s r -=→11lim[()()]ir r s s dc s s F s ds-→=-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。
拉氏变换和z变换表
附录A 拉普拉斯变换及反变换1.拉氏变换的基本性质1()([n n k f t dt s s-+=+∑⎰个2．常用函数的拉氏变换和z 变换表附表A-2 常用函数的拉氏变换和z 变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式，即1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中，系数n n a a a a ,,...,,110-和011,,,,m m b b b b -都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
（1）0)(=s A 无重根：这时，F(s)可展开为n 个简单的部分分式之和的形式，即∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根；i c 为待定常数，称为()F s 在i s 处的留数，可按下列两式计算：lim()()ii i s s c s s F s →=- （F-2）或iss is A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数为[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝1in s ti i c e =∑ (F-4) （2）0)(=s A 有重根：设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…，n s 为F(s)的n r -个单根；其中，1+r c ，…，n c 仍按式(F-2)或式(F-3)计算，r c ，1-r c ，…，1c 则按下式计算：)()(lim 11s F s s c r s s r -=→11lim[()()]ir r s s dc s s F s ds-→=-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。
Z变换与拉普拉斯变换的关系
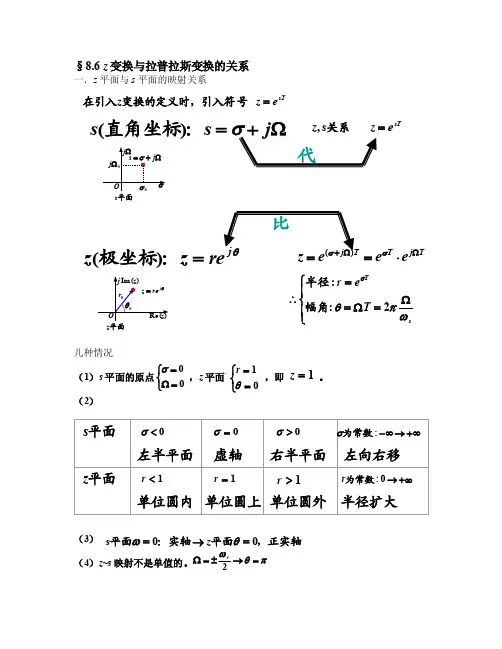
§8.6 z 变换与拉普拉斯变换的关系一．z 平面与s 平面的映射关系几种情况（1）s 平面的原点 ，z 平面 ，即 。
（2）（3） （4）z ~s 映射不是单值的。
sT e z s z = ,关系Ω+=j s s σ：直角坐标)(θj rez z =：极坐标)(T j T T j e e e z ΩΩ+⋅==σσ)(⎪⎩⎪⎨⎧Ω=Ω==∴s T T e r ωπθσ2::幅角半径代比sT ez z = 号变换的定义时，引入符在引入⎩⎨⎧=Ω=00σ⎩⎨⎧==01θr 1=z s 平面z 平面0<σ0=σ0>σ+∞→-∞:为常数σ1<r 1=r 1>r +∞→0:为常数r 左半平面 虚轴 右半平面 左向右移 单位圆内 单位圆上 单位圆外 半径扩大 ，正实轴平面：实轴平面00=→=θωz s πθω=→±=Ω2s二．z 变换与拉式变换表达式之对应注意：连续时间信号的突变点函数值与对应的序列样值有区别。
容易求得，它的拉式变换为注意跳变值()()()[]()()[]()()()?,z X s X z X n x Z s X t x L n x t x 写出能否借助，均匀抽样==−−−→−()()10;210定义为在点 阶跃序列点定义为在例如，阶跃信号==n n u t t u ()成项指数信号相加组合而由若连续时间信号N t x ˆ()()()()t x t x t x t x n ˆˆˆˆ21+++= ()()t u e A t x N i t p i N i i i ∑∑====11ˆ()[]∑=-=N i i i p s A t x L 1ˆ()成项指数序列相加组合而由若序列N nT x ()()()()nT x nT x nT x nT x N +++= 21()()nT u e A nT x N i nT p i N i i i ∑∑====11变换为它的z ()[]∑=--=N i T p i z e A nT x Z i 111例8-6-1解：解： 已知 2221j A j A =-=及()可以展成部分分式于是，s X()()()()⎪⎪⎩⎪⎪⎨⎧>=<=0020 0ˆt e A t A t t x t p i i i i ()()()()⎪⎩⎪⎨⎧>=<=000 0t e A t A t nT x nt p i i i i 即点补足系时必须在按抽样规律建立二者联,20i A ()()()()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=≠==02ˆ0 ˆn A nT t t u t x n nT t t u t x n u nT x i i i i 当当()()变换。
拉普拉斯变换表
序 号 拉氏变换 E(s)
时间函数 e(t)
1
1
2
1 1 − e−Ts
3
1
s
δ(t)
∞
δT (t) = ∑δ (t − nT ) n=0 1(t )
4
1
t
s2
Z 变换 E(z)
1
z z −1
z z −1
Tz (z − 1) 2
5
1
t2
s3
2
T 2 z(z + 1) 2(z − 1)3
6
1 s n+1
7
1
s+a
8
1 (s + a)2
9
a s(s + a)
10
b−a (s + a)(s + b)
11
ω
s2 +ω2
12
s
s2 +ω2
13
ω (s + a)2 + ω 2
14
s +a (s + a)2 + ω 2
tn n! e −at te −at 1 − e −at e −at − e −bt
sin ωt cos ωt
6 终值定理 7 初值定理
lim f (t) = lim sF (s)
t→∞
s→0
lim f (t) = lim sF (s)
t→0
s→∞
419
8 卷积定理
∫ ∫ L[
t 0
f1(t
−τ )
f2(τ )dτ ]
=
L[
t 0
f1 (t )
f2 (t
−τ )dτ ] =
F1(s)F2 (s)
(完整版)拉普拉斯变换及其逆变换表
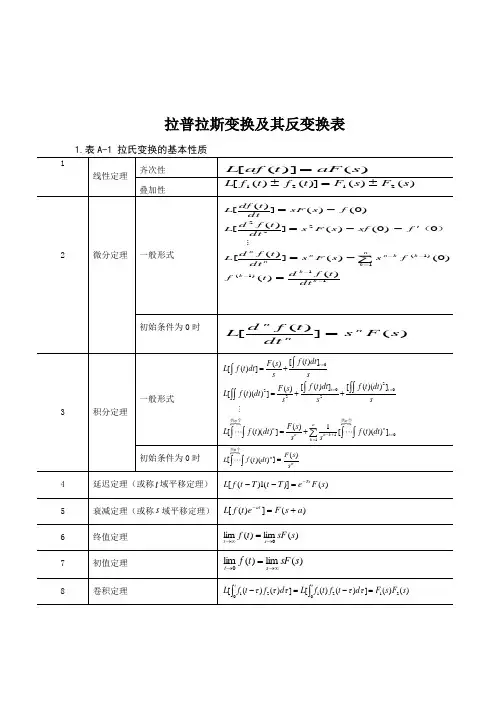
拉普拉斯变换及其反变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- （m n >）式中系数n1n 1a ,a ,...,a ,a-，m1m 1b ,b ,b ,b - 都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中，Sn 2S 1S ，，， 是特征方程A(s)＝0的根。
i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= （F-6）。
拉氏变换表
① 无重根
这时，F(s)可展开为n个简单的部分分式之和的形式。
（F-1）
式中，是特征方程A(s)＝0的根。为待定常数，称为F(s)在处的留数，可
按下式计数。根据拉氏变换的性质，从式（F-1）可求得原
函数
＝
(F-4)
2 有重根
设有r重根，F(s)可写为
=
式中，为F(s)的r重根，，…, 为F(s)的n-r个单根；
A 拉普拉斯变换及反变换
1.表A-1 拉氏变换的基本性质
1
齐次性
线性定
理
叠加性
2 微分定 一般形式
理 初始条件为0
时
一般形式
3 积分定
理
初始条件为0
时
4 延迟定理（或称域平移 定理）
5 衰减定理（或称域平移 定理）
6 终值定理
7 初值定理
8 卷积定理
2．表A-2 常用函数的拉氏变换和z变换表
序 拉氏变换
其中，，…, 仍按式(F-2)或(F-3)计算，，，…, 则按下式计算：
(F-5)
原函数为
（F-6）
号
E(s)
时间函数e(t)
1
1
δ(t)
2
3
4
t
5
6
7
8
9
10
11
12
13
14
15
Z变换E(z) 1
3． 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，
然后逐项查表进行反变换。设是的有理真分式 （）
式中系数，都是实常数；是正整数。按代数定理可将展开为部分分式。 分以下两种情况讨论。
拉氏变换定义 计算 公式及常用拉氏变换反变换
拉氏变换定义计算公式及常用拉氏变换反变换拉氏变换定义计算公式及常用拉氏变换反变换拉氏变换定义.计算.公式及常用拉氏变换反变换****拉普拉斯转换及反华转换****定义：如果定义：就是一个关于的函数，使当就是一个为丛藓科扭口藓变量；是一个运算符号，它代表对其对象进行拉普拉斯积分的拉普拉斯变换结果。
则的拉普拉斯转换由以下式子得出：2．表a-2常用函数的拉氏变换和z变换表3．用换算法展开拉氏反华转换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设f(s)是s的有理真分式b(s)bmsm bm1sm1b1s b0f(s)（n m）a(s)ansn an1sn1a1s a0式中系数a0,a1,...,an1,an，b0,b1,bm1,bm都是实常数；m,n是正整数。
按代数定理可将f(s)展开为部分分式。
分以下两种情况讨论。
①a(s)0无重根这时，f(s)可以进行为n个直观的部分分式之和的形式。
cicncc1c2f(s)i（f-1）s s1s s2s sis sni1s si式中，s1,s2,,sn就是特征方程a(s)＝0的木。
ci为未定常数，称作f(s)在si处的留数，可以按下式排序：或ci lim(s si)f(s)（f-2）a(s)s s式中，a(s)为a(s)对s的一阶导数。
根据拉氏变换的性质，从式（f-1）可求得原函数n nci stf(t)l f(s)l＝(f-4)ce ii1s si i1a(s)0有重根设a(s)0存有r重根s1，f(s)展毛为(s s1)(s sr1)(s sn)cicncrcr1c1cr1rr1(s s1)(s s1)(s s1)s sr1s sis sn式中，s1为f(s)的r重根，sr1，…,sn为f(s)的n-r个单根；其中，cr1，…,cn仍按式(f-2)或(f-3)排序，cr，cr1，…,c1则按下式排序：cr lim(s s1)rf(s)cr1lim[(s s1)rf(s)]dslim(j)(s s1)rf(s)(f-5)j!s s1ds1d(r1)c1lim(r1)(s s1)rf(s)(r1)!s s1ds原函数f(t)为f(t)lcrcicn cr1c1cr1l1rr1(s s1)s sr1s sis sn(s s1)(s s1)crtr1cr1tr2c s1(r1)!r2)!2t c1 e i ciest(r1。
拉氏变换表
附录A 拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质__________________________________________________2．表A-2 常用函数的拉氏变换和z变换表____________________________________________________________________________________________________3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。
i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )()(lim s F s s c i s s i i-=→ （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts n i i ie c -=∑1(F-4)②0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+__________________________________________________=nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。
拉氏变换及Z变换表
c b e b c e a b c a te at
bt
2
at
c b z b c z
s s b s a
s a s b b a s c s a s b
ab s s a s b
ba
e at e bt
c a e at b c e bt
1 be ae ab ab
at bt
c a z b c z
z
2
2z aTe aT z aT 2 ze z e aT
a b s b s a 2 a b s c s b s a 2
2
a b Te aT z z z 2 z e bT z e aT z e aT
拉氏变换及 Z 变换表
拉氏变换 Y ( s ) 时间函数 y (t ) Z 变换 Y ( z )
e nTs
(t nT )
(t )
1(t )
z n
1或z
0
1
1 s 1 s2 1 s3 1 s n 1
1 s (1 T ) ln a
z z 1
T 2 z z 1 3 2z 1
abc s s a s b s c
1
b a c a
ab
bc
e at
c b a b
ca
e bt
a c b c
(完整版)拉普拉斯变换表
拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质12．表A-2 常用函数的拉氏变换和z变换表233． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==----ΛΛ （m n >）式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110-Λ都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=ni iin n i i s s c s s c s s c s s c s s c s F 12211)(ΛΛ （F-1）式中，n s s s ,,,21Λ是特征方程A(s)＝0的根。
i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算：)()(lim s F s s c i s s i i-=→ （F-2） 或is s i s A s B c ='=)()(（F-3）式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts ni i i e c -=∑1(F-4)4② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r r s s s s s s s B s F ---=+Λ=n n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11111111)()()(式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r ss r -=→ )]()([lim111s F s s dsdc r s s r -=→- M)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5) M)()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L ΛΛΛ111111111)()()( t s nr i i t s r r r r i e c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1(Λ （F-6）。
信号的拉普拉斯变换和z变换
⎰∞∞--=t e t f s F st b d )()(⎰∞--=0def d e )()(t t f s F st)(d e )(j 21)(j j deft s s F t f st επσσ⎥⎦⎤⎢⎣⎡=⎰∞+∞-第三章信号的拉普拉斯变换和z 变换一、拉普拉斯变换的定义1.双边拉普拉斯变换只有选择适当的σ值才能使积分收敛，信号f(t)的双边拉普拉斯变换存在。
※象函数相同，但收敛域不同。
双边拉氏变换必须标出收敛域。
2.单边拉氏变换3.常见函数的拉普拉斯变换及其⎰∞+∞-=j j d e )(j21)(σσπs s F t f st b Fb(s)称为f(t)的双边拉氏变换（或象函数），f(t)称为Fb(s)的双边拉氏逆变换（或原函数）。
从0-开始收敛域二、拉普拉斯变换性质线性性质尺度变换证明：[]⎰∞--=de)()(tatfatf L st，则令atτ=时移特性与尺度变换相结合复频移（s域平移）特性时域的微分特性（微分定理）若f(t)←→F(s),Re[s]>σ0,则f’(t)←→sF(s)–f(0-)证明：()()()())(deedessFfttsft ftt f ststst+-=⎥⎦⎤⎢⎣⎡--='--∞-∞---∞-⎰⎰推广：()()[])0()0()()0(d)(d22----'--='--=⎥⎦⎤⎢⎣⎡fsfsFsffsF sttfL∑-=----=⎥⎦⎤⎢⎣⎡1)(1)0()(d)(d nrrrnnnfssFsttfL若f1(t)←→F1(s)Re[s]>σ1,f2(t)←→F2(s)Re[s]>σ2则a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)Re[s]>max(σ1,σ2)若f(t)←→F(s),Re[s]>σ0，且有实数a>0，则f(at)←→)(1asFa若f(t)<----->F(s),Re[s]>σ0,且有实常数t0>0,则f(t-t0)ε(t-t0)<----->e-st0F(s),Re[s]>σ0若f(t)←→F(s),Re[s]>σ0,且有复常数s a=σa+jΩa,则f(t)e s a t←→F(s-s a),Re[s]>σ0+σas-→2：?)(sin ←→t t t ε=三、拉普拉斯逆变换三种方法：（1）查表（2）利用性质（3）部分分式展开-----结合∴......,,321为不同的实数根，n p p p p nn p s K p s K p s K s F -++-+-= 2211)(ip s i i s F p s K =-=)()()(e ]1[1t p s L t p i i ε=--若象函数F(s)是s 的有理分式，可写为1110111.......)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=----若m ≥n （假分式）,可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。
常用函数Laplace变换表
3． 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行
反变换。设 F (s) 是 s 的有理真分式
F (s)
B(s) A(s)
bm s m an s n
bm1s m1 b1s b0 an1s n1 a1s a0
（n m）
cn
n
ci
s s1 s s2
s si
s sn i1 s si
（F-1）
式中， s1, s2 ,, sn 是特征方程 A(s)＝0 的根。 ci 为待定常数，称为 F(s)在 si 处的留数，可
按下式计算：
ci
lim(s
ssi
si
)
F
(
s
)
或
（F-2）
B( s) ci A(s)
s si
附录 A 拉普拉斯变换及反变换
1.表 A-1 拉氏变换的基本性质 1 齐次性 线性定理 叠加性
2 微分定理 一般形式
L[af (t)] aF (s) L[ f1 (t) f 2 (t)] F1 (s) F2 (s)
L[ df (t)] sF (s) f (0) dt
d2 L[
f
(t)]
式中系数 a0 , a1,...,an1, an ， b0 ,b1,bm1,bm 都是实常数； m, n 是正整数。按代数定理可 将 F (s) 展开为部分分式。分以下两种情况讨论。
① A(s) 0 无重根
这时，F(s)可展开为 n 个简单的部分分式之和的形式。
F (s) c1 c2 ci
（F-3）
式中， A(s) 为 A(s) 对 s 的一阶导数。根据拉氏变换的性质，从式（F-1）可求得原函数
(完整word版)拉普拉斯变换公式
附录A 拉普拉斯变换及反变换1.表A—1 拉氏变换的基本性质4192．表A-2 常用函数的拉氏变换和z变换表4204213． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数.按代数定理可将)(s F 展开为部分分式.分以下两种情况讨论。
① 0)(=s A 无重根这时，F(s ）可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s ）＝0的根。
i c 为待定常数，称为F （s ）在i s 处的留数，可按下式计算： )()(lim s F s s c i s s i i-=→ （F-2） 或iss i s A s B c ='=)()( (F —3）式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式（F —1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts n i i ie c -=∑1(F —4）②0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s ）可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ,…， n s 为F （s)的n —r 个单根；其中，1+r c ，…， n c 仍按式(F-2）或（F —3）计算,r c ，1-r c ,…， 1c 则按下式计算:422)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→- )()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5）)()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为[])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F —6）。
拉普拉斯变换与Z变换
tia
e − at
l
f (t ) = L−1 [ F ( s )] 。
例 1 求单位阶跃函数 u (t ) = 解 由拉氏变换的定义有：
C
0, t < 0 的拉氏变换。 1, t > 0
+∞
on
0 0
F(s)称为 f(t)的拉氏变换（或称为象函数） 。 若 F(s)是 f(t)的拉氏变换，则称 f(t)为 F(s)的拉氏反变换（或称为象原函数） ，记为：
定义：设函数 f(t)当 t≥0 时有定义，而且积分 某一域内收敛，则由此积分所描述的函数可写为
∫
+∞
0
f (t )e − st dt （s 是一个复参量）在 s 的
F ( s) = ∫
+∞
0
f (t )e − st dt
en
Z 变换 F(z) 1
其中 s = σ + jω 为复变量，σ为实部，ω为虚部。
2
ny
11 12
sinωt
cosωt
pa
13
e − at sin ωt
ω (s + a) 2 + ω 2 s+a (s + a) 2 + ω 2
om
14
e − at cos ωt
C
fid
2
ze −T sin ωT z 2 − 2 ze −T cos ωT + e −2 aT z 2 − ze − aT cos ωT ) z 2 − 2 ze −aT cos ωT + e − 2 aT
1 1 − e −Ts 1 s 1 s+a 1 s − (1 / T ) ln a 1 s2