拉普拉斯变换拉普拉斯变换表
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表1.表A-1 拉氏变换的基本性质2.表A-2 常用函数的拉氏变换和z变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n n n 011m 1m m m a s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==----ΛΛ (m n >)式中系数n 1n 10a ,a ,...,a ,a -,m1m 10b ,b ,b ,b -Λ都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n 1i iin n i i 2211s s c s s c s s c s s c s s c )s (F ΛΛ 式中,Sn 2S 1S ,,,Λ是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:或式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为 =nni i 1r 1r 111r 11r r 1r s s c s s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++--ΛΛΛ 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算: 原函数)(t f 为ts n 1r i i t s 122r 1r 1r r 1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=Λ (F-6)。
(完整版)拉普拉斯变换表

拉普拉斯变换及反变换1. 表 A-1 拉氏变换的基本性质1齐次性线性定理叠加性2微分定一般形式理L[af ( t)] aF (s)L[ f1 (t ) f 2 ( t )] F1 ( s) F2 ( s) L[ df (t ) ] sF (s) f (0)dtL[d 2 f (t) 2f()dt 2 ] s F (s) sf (0) 0n nd f (t ) n n k ( k 1 )L dt n s F (s) k 1 s f (0) f ( k 1) (t ) d k 1 f (t )dt k 1初始条件为 0 时一般形式3积分定理初始条件为 0 时4延迟定理(或称 t 域平移定理)5衰减定理(或称 s 域平移定理)6终值定理7初值定理8卷积定理L[d n f (t) ndt n ] s F (s)L[ f (t)dt]F (s) [ f (t)dt] t 0s sL[ f (t)(dt)2 ] F (s)[ f (t )dt]t 0[ f (t)( dt) 2 ] t 0s2 ss2共 n个n共 n个nF (s) 1 nL[ f (t )(dt) ] 1 [ f (t)( dt) ] t 0nk 1 sn ks共 n个F (s)L[ f (t )( dt) n ]s nL[ f (t T )] e Ts F ( s)L[ f ( t)e at ] F (s a)lim f (t ) lim sF (s)t s0lim f (t ) lim sF ( s)t 0 st 1 ( ) 2 ( ) ] [ t 1 ( ) 2 ( ) ] 1() 2()[ f d L f f t dL f t t F s F s0 012.表 A-2 常用函数的拉氏变换和z 变换表拉氏变换E(s)111 e Ts1s12s13s1s n 11s a1( s a) 2as( s a)b a( s a)(s b)s2 2ss2 2( s a) 2 2s a( s a)2 21s (1 / T ) ln a 时间函数 e(t)δ(t)T (t )(t nT )n01(t )tt 22ntn!e atte at1 e ate at e btsin tcos te at sin te at cos ta t / T23.用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
拉普拉斯变换表word版本

拉普拉斯变换表附录A 拉普拉斯变换及反变换收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==----ΛΛ (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110-Λ都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)(ΛΛ (F-1) 式中,n s s s ,,,21Λ是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:)()(lim s F s s c is s i i-=→ (F-2) 或is s i s As B c ='=)()( (F-3)式中,)(s A'为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(=t s n i i ie c -=∑1 (F-4) ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为())()()()(11nr rs s s s s s s B s F ---=+Λ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11111111)()()(收集于网络,如有侵权请联系管理员删除式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)()(lim 11s F s s c rs s r -=→ )]()([lim 111s F s s dsd c rs s r -=→- M)()(lim !11)()(1s F s s dsd j c rj j s s j r -=→- (F-5) M)()(lim )!1(11)1()1(11s F s s dsd r c rr r s s --=--→ 原函数)(t f 为[])()(1s F L t f -= ⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L ΛΛΛ111111111)()()( t s nr ii t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1(Λ (F-6)。
拉普拉斯变换表.
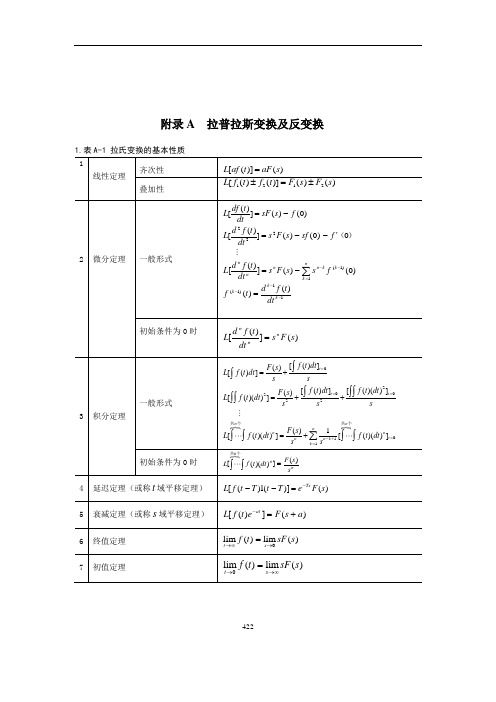
附录A 拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质4222.表A-2 常用函数的拉氏变换和z变换表4224223. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110- 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=ni iin n i i s s c s s c s s c s s c s s c s F 12211)( (F-1)式中,n s s s ,,,21 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )()(lim s F s s c i s s i i-=→ (F-2)或iss i s A s B c ='=)()( (F-3)式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(=ts n i i ie c -=∑1(F-4)② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+422=nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()(式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为[])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( (F-6)。
(完整版)拉普拉斯变换及其逆变换表
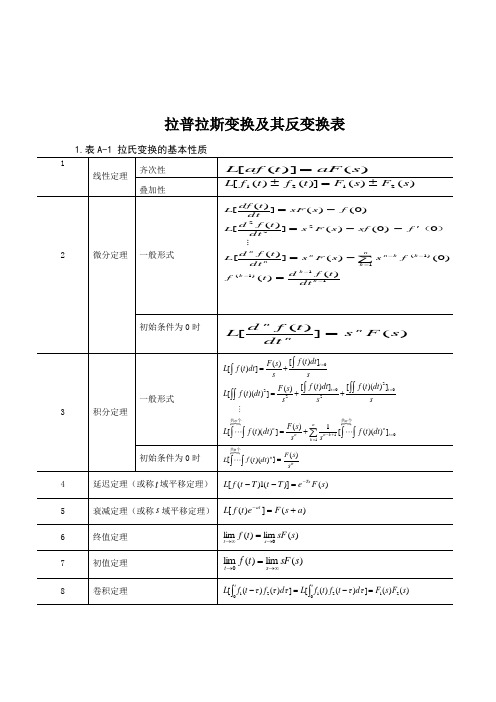
拉普拉斯变换及其反变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换表

拉普拉斯变换表第一篇:拉普拉斯变换基础拉普拉斯变换是一种重要的数学工具,在工程、物理、经济等领域都有重要的应用。
拉普拉斯变换可以将一个复杂的函数转换成另一个更易于处理的函数,从而为解决实际问题提供了便利。
1. 拉普拉斯变换定义拉普拉斯变换是一种线性运算,它将一个函数f(t)转换成另一个函数F(s),数学上可以表示成:F(s)=∫0 ^∞e^(-st)f(t)dt其中,s是一个复数,称为变换参数。
实际上,s的实部和虚部分别对应于指数函数e^(-st)中的衰减因子和频率。
2. 拉普拉斯变换性质拉普拉斯变换有很多重要的性质,这些性质可以帮助我们更好地理解和使用拉普拉斯变换。
(1) 线性性质拉普拉斯变换是一种线性运算,即对于任意常数a和b,有:L{af(t)+bg(t)}=aF(s)+bG(s)(2) 平移性质拉普拉斯变换具有平移性质,即:L{f(t-a)}=e^(-as)F(s)(3) 尺度变换性质拉普拉斯变换还具有尺度变换性质,即:L{f(at)}=1/aF(s/a)(4) 求导性质拉普拉斯变换对时间的一阶和二阶导数的变换分别为:L{f'(t)}=sF(s)-f(0)L{f''(t)}=s^2F(s)-sf(0)-f'(0)(5) 初值定理和终值定理拉普拉斯变换有两个重要的极限定理,分别是初值定理和终值定理。
初值定理描述了原函数在t=0时的值与拉普拉斯变换之间的关系,可以表示为:lim_(s→+∞)sF(s)=f(0)终值定理则描述了原函数在t趋近于无穷时的极限值与拉普拉斯变换之间的关系,可以表示为:lim_(s→0) sF(s)=lim_(t→∞) f(t)3. 常见函数的拉普拉斯变换下面是几种常见函数的拉普拉斯变换:(1) 矩形波函数rect(t)L{rect(t)}=1/s(2) 单位阶跃函数u(t)L{u(t)}=1/s(3) 指数衰减函数e^(-at)L{e^(-at)}=1/(s+a)(4) 三角函数sin(at)L{sin(at)}=a/(s^2+a^2)(5) 三角函数cos(at)L{cos(at)}=s/(s^2+a^2)第二篇:拉普拉斯变换表1下面是一份拉普拉斯变换表,其中包含了一些常见函数的拉普拉斯变换。
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表\3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s ii-=→或is s i)s (A )s (B c='=:式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+ =nnii1r 1r 111r 11r r1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r1-=→)]s (F )s s ([dsdlimc r 1s s 1r 1-=→-)s (F )s s (dsd lim !j 1c r1)j ()j (s s jr 1-=→-)s (F )s s (dsdlim )!1r (1c r1)1r ()1r (s s 11--=--→原函数)(t f 为[])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---nnii1r 1r 111r 11r r1r1s s c s s c s s c )s s (c )s s (c )s s (c L ts n1r i its 122r 1r 1r r1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表1. 表A-1 拉氏变换的基本性质1 L [ af ( t )] aF ( s )齐次性线性定理L [ f 1 ( t ) f 2 ( t )] F 1 ( s ) F 2 ( s ) 叠加性L [ df ( t )]sF ( s ) f ( 0 )L [ ddt2 f ( t )dt 2] s 2 F ( s ) sf ( 0 ) f (0 )L d n f ( t ) ndt ns n F ( s ) s n k f ( k 1 ) ( 0 )k 1f ( k 1 ) ( t ) d k 1 fdt( t )k 12 微分定理一般形式初始条件为0 时L [ d n f ( t )dt n] s n F ( s )L[ f (t )dt ]F ( s)s [ f (t )dt ]t 0s[ 2L[ f ( t)( dt ) ] 2 F ( s)s 2f (t) d t ]t 0s[2f (t )(dt ) ]t 0s共n个共n个L[ f (t)(dt )n ] F ( s)s nnk 1 s1n k 1[ f (t)(dt ) n ] t 0一般形式共n个3 积分定理初始条件为0 时L[ f ( t)( dt) n ]F ( s)s nTs4 延迟定理(或称t 域平移定理)L[ f (t T)1(t T )] e F ( s)精品资料精品资料5衰减定理(或称 s 域平移定理)L[ f (t )eat] F ( s a)6终值定理lim f ( t )lim tssF ( s)lim f (t ) lim sF(s)7初值定理t 0 s8卷积定理tL[ f 1( t) f 2 ( ) d ]tL[ f 1( t ) f 2 ( t) d ]F 1 (s) F 2 ( s )2. 表 A-2 常用函数的拉氏变换和 z 变换表序号拉氏变换 F(s)时间函数 f(t)Z 变 换 F(z)1 1δ(t)11 2 1 eTsT( t)(t nT )zn 0z 1 1 1(t )z sz 11 4 s2tTz ( z 1)21 t 5 s32T 2z(z 1) 2( z 1)1 t n6 n 1lim( 1) z n ( aT ) sn!a 0n!a z e17 s aeatzz e1 atTze 8 ( s a) 2tea at( z e(1 eaT )2aT) z9s(s a)1 e(z 1)( z 2 3n)3 naTaT e aT精品资料2m m 1n 1b aat btz z 10(s11a)(s b)e esin tz eaTz ebTz sin T s2 2z22 z cos T 1scos tz( z cos T )12 s2z 2 2 zcos T 1atzeaTsin T13 (s a)2 2e sin t z22 ze aTcos T e2 aTs a14 22e atcos tz2zeaTcos T( s 15s a)1 (1 / T ) ln aat / Tz22zeaTz z acos T e2 aT3.用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通常,在线性控制系统中,复变函数G(s)是复数s的单值
函数。即:对应于s的一个给定值,G(s)就有一个唯一确定的
值与之相对应。
当复变函数表示成 G(s) k(s zi )
(s pj)
分子为零
(a) 当s=-zi时,G(s)=0,则si=-zi称为G(s)的 零点 ;
(b) 当s=-pj时,G(s)→∞,则sj=-pj称为G(s)的 极点 。
分母为零
2.2.1 复数和复变函数
例:
当s= +j时,求复变函数G(s) =s2+1的实部u和虚部v。
解:
G(s)=s2+1=( +j)2 + 1 = 2 + j(2 ) - 2 + 1
=( 2 - 2 + 1) + j(2 )
复变函数的实部 u 2 2 1
复变函数的虚部 v 2
2.2 拉普拉斯变换
其拉普拉斯变换为:
L 1(t)
1(t
)e
st
dt
estdt 1 est
0
0
s0
lim 1 est 1 e0 1 t s s s
2.2.3 典型时间函数的拉普拉斯变换
(2) 单位脉冲函数
单位脉冲函数定义:
(t
)
, 0,
t 0 t0
且:
(t)dt 1
(t) f (t)dt f (0)
象函数
拉氏变换符号
原函数 复变量
拉普拉斯变换:在一定条件下,把实数域中的实变函数 f(t) 变 换到复数域内与之等价的复变函数 F(t) 。
2.2.2 拉普拉斯变换的定义
拉氏变换是否存在取决于定义的积分是否收敛。拉氏变 换存在的条件:
① 当t≥0时,f(t) 分段连续,只有有限个间断点; ② 当t →∞时,f(t) 的增长速度不超过某一指数函数,即
0
2j 0
1 2j
0
e e -(s-j)t -(s j)t
dt
1 2j
1
s-j
s
1jຫໍສະໝຸດ s222.2.3 典型时间函数的拉普拉斯变换
(6) 余弦信号函数
余弦信号函数定义:
两 e jt cost jsin t
式
f
(t)
0
cost,
t0 t0
相 加
e-jt cost jsin t
由欧拉公式,余弦函数表达为: cost 1 e jt e-jt
拉普拉斯变换的定义
拉氏变换是控制工程中的一个基本数学方法,其优点是能 将时间函数的导数经拉氏变换后,变成复变量s的乘积,将时 间表示的微分方程,变成以s表示的代数方程。
设有时间函数 f(t),当 t < 0 时,f(t)=0;在 t≥0时定义函
数 f(t) 的拉普拉斯变换为:
F (s) L f (t) f (t)estdt 0
其拉普拉斯变换为:
2
L cost cost estdt 1 ejt e-jt estdt
复数的三角函数表示法:
s = r (cos + j sin )
欧拉公式:
j
e j cos jsin
s1
复数的指数表示法:
s2
s re j
1 2
o
2.2.1 复数和复变函数
③ 复变函数、极点与零点的概念
以复数s= +j为自变量构成的函数G(s)称为复变函数:
G(s) = u + jv
式中:u、v 分别为复变函数的实部和虚部。
拉普拉斯变换-拉普拉斯变换表
20140107
2. 数学模型与传递函数
拉普拉斯变换
系统的数学模型以微分方程的形式表达输出与输入的关 系。经典控制理论的系统分析方法:时域法、频域法。
时域分析法
求解数学模型微分方程,获得系统 输出随时间变化的规律。
频域分析法
借助于系统频率特性分析系统的性 能,拉普拉斯变换是其数学基础。
正弦信号函数定义:
两 e jt cost jsin t
式
f
(t)
0 sin
t,
t0 t0
相 减
e-jt cost jsin t
由欧拉公式,正弦函数表达为:sin t 1 e jt e-jt
2j
其拉普拉斯变换为:
L sin t sin t estdt 1 e jt e-jt estdt
① 复数的向量表示法
复数 s= +j 可以用从原点指向点( , )的向量表示。
向量的长度称为复数的模:
s r 2 2
j
向量与 轴的夹角 称
为复数s的复角:
s1 s2
arctan( / )
1 2
o
2.2.1 复数和复变函数
② 复数的三角函数表示法与指数表示法
根据复平面的图示可得: = r cos , = r sin
频域分析法是经典控制理论的核心,被广泛采用,该方 法间接地运用系统的开环频率特性分析闭环响应。
2.2 拉普拉斯变换
复数和复变函数
复数的概念
复数 s= +j
j 1 称为虚数单位
(有一个实部 和一个虚部, 和 均为实数)
两个复数相等:当且仅当它们的实部和虚部分别相等。
一个复数为零:当且仅当它的实部和虚部同时为零。
estdt
0
1 s2
est
0
1 s2
2.2.3 典型时间函数的拉普拉斯变换
(4) 指数函数
指数函数表达式:
式中:a是常数。
f (t) eat
其拉普拉斯变换为:
L eat eatestdt e(sa)tdt 1
0
0
sa
2.2.3 典型时间函数的拉普拉斯变换
(5) 正弦信号函数
2.2.1 复数和复变函数
复数的表示法
对于复数 s= +j
复平面:以 为横坐标(实轴)、 为纵坐标(虚轴)所构成
的平面称为复平面或[s]平面。复数 s= +j 可在复平面[s]中用
点( , )表示:一个复数对应于复平面上的一个点。
j
复平面[s]
1
s1=1+j1
2
s2=2+j2
o
1 2
2.2.1 复数和复变函数
f (t) Meat
式中:M、a为实常数。
在复平面上,对于Res>a的所有复数s (Res表示s的实部)都 使积分式绝对收敛,故Res >a是拉普拉斯变换的定义域, a称 为收敛坐标。
2.2 拉普拉斯变换
典型时间函数的拉普拉斯变换
(1) 单位阶跃函数
单位阶跃函数定义:
1(t)
0, 1,
t0 t0
其拉普拉斯变换为:
L (t)
(t )e st dt
est
1
0
t 0
2.2.3 典型时间函数的拉普拉斯变换
(3) 单位速度函数(单位斜坡函数)
单位速度函数定义:
f
(t)
0 t,
t0 t0
其拉普拉斯变换为:
L t testdt 1 tdest
0
s0
1 test 1 s 0s
