各类滚动轴承轴向载荷分析及计算
滚动轴承的受力分析载荷计算失效和计算准则
滚动轴承的受力分析载荷计算失效和计算准则滚动轴承是一种常用的机械元件，它能够在高速旋转的条件下承受并转移载荷。
在设计和应用滚动轴承时，关键的工作之一是进行受力分析和载荷计算，以确保轴承能够正常工作并减少失效的风险。
本文将从受力分析、载荷计算、失效和计算准则几个方面详细介绍滚动轴承。
一、滚动轴承的受力分析滚动轴承受到的力主要有径向力和轴向力两种。
径向力是垂直于轴线的力，它可以分为径向载荷和径向惯性力两部分。
轴向力是平行于轴线的力，它可以分为轴向载荷和轴向惯性力两部分。
受力分析的目的是确定轴承所受的载荷大小和方向，以便选择适当的轴承型号和设计。
二、滚动轴承的载荷计算载荷计算是根据受力分析的结果，确定轴承承受的载荷大小和方向。
在实际应用中，轴承承受的载荷通常包括静载荷和动载荷两部分。
静载荷是指静止条件下轴承所承受的最大力，动载荷是指旋转条件下轴承所承受的最大力。
根据载荷计算的结果，可以选择适当的轴承并确定其使用寿命。
滚动轴承的失效可以分为疲劳失效和磨损失效两种。
疲劳失效是由于载荷作用下轴承材料的疲劳破裂引起的，磨损失效是由于轴承表面的磨损引起的。
根据滚动轴承的失效机理，制定了一系列的计算准则，用于评估轴承的寿命和失效风险。
常用的滚动轴承计算准则包括基本额定寿命、等效动载荷、寿命调整系数和动接触角等。
基本额定寿命是指在特定载荷下，轴承能够连续工作的寿命。
等效动载荷是指在复杂工况下，将径向载荷和轴向载荷转化成等效的径向载荷。
寿命调整系数则考虑了不同工作条件下的调整因素，用于修正基本额定寿命。
动接触角是指滚动元件与外圈之间的接触角度，它可以影响轴承的刚度和额定寿命。
综上所述，滚动轴承的受力分析、载荷计算、失效和计算准则是设计和应用滚动轴承时的重要内容，它们能够帮助我们选择适当的轴承型号、确保轴承的使用寿命并减少失效的风险。
在实际工程中，我们应该根据具体的工作条件和要求，进行合理的受力分析和载荷计算，并遵循相关计算准则，以确保滚动轴承的安全可靠运行。
轴承载荷
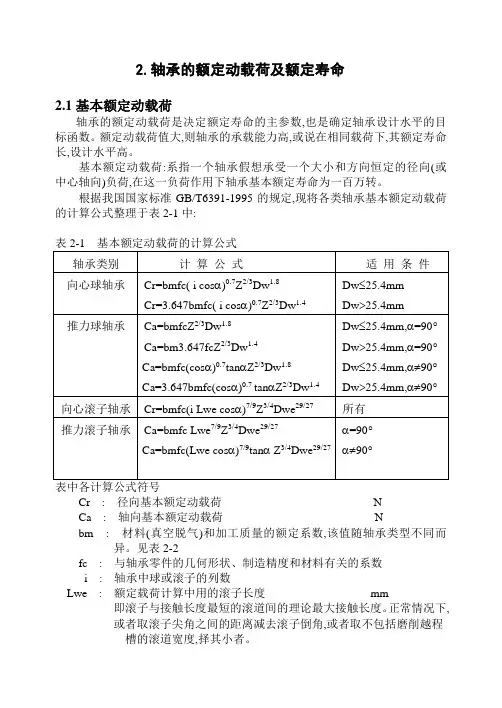
2.轴承的额定动载荷及额定寿命2.1基本额定动载荷轴承的额定动载荷是决定额定寿命的主参数,也是确定轴承设计水平的目标函数。
额定动载荷值大,则轴承的承载能力高,或说在相同载荷下,其额定寿命长,设计水平高。
基本额定动载荷:系指一个轴承假想承受一个大小和方向恒定的径向(或中心轴向)负荷,在这一负荷作用下轴承基本额定寿命为一百万转。
根据我国国家标准GB/T6391-1995的规定,现将各类轴承基本额定动载荷的计算公式整理于表2-1中:Cr : 径向基本额定动载荷NCa : 轴向基本额定动载荷Nbm : 材料(真空脱气)和加工质量的额定系数,该值随轴承类型不同而异。
见表2-2fc : 与轴承零件的几何形状、制造精度和材料有关的系数i : 轴承中球或滚子的列数Lwe : 额定载荷计算中用的滚子长度mm即滚子与接触长度最短的滚道间的理论最大接触长度。
正常情况下,或者取滚子尖角之间的距离减去滚子倒角,或者取不包括磨削越程槽的滚道宽度,择其小者。
α: 轴承的公称接触角度Z: 单列轴承中的球或滚子数。
每列球或滚子数相同的多列轴承中每列的球或滚子数Dw : 球直径mmDwe : 额定载荷计算中用的滚子直径mm对于圆锥滚子取滚子端面和小端面理论尖角处直径的平均值。
对于非对称外凸滚子近似地取零载荷下滚子与无挡边滚道间接触点处滚子的直径现将GB/T6391-1995所定的额定系数bm值列于表2-22.2 额定动载荷的修正滚动轴承基本额定动载荷的计算方法适用于优质淬硬钢(系指真空脱气钢),按良好的加工方法制造,且滚动接触表面的形状为常规设计。
超越上述规定,额定动载荷应予修正。
2.2.1 材质轴承钢因冶炼方法不同,材料中夹杂物的大小、分布、含量亦不同。
夹杂物是造成金属材料疲劳裂纹产生的主要成因,是影响滚动轴承疲劳寿命的主要因素。
如采用夹杂物含量高于真空脱气的普通电炉冶炼轴承钢,则轴承的载荷能力将会有不同程度的下降。
当采用诸如真空重熔、电渣重熔等方法冶炼的轴承钢或其它等效材质的钢材时,其夹杂物的含量显著减少,轴承的载荷能力将会得到提高。
圆锥滚子轴承轴向载荷计算
圆锥滚子轴承轴向载荷计算
圆锥滚子轴承是一种常见的轴承类型，广泛应用于机械设备中。
在设计和选择轴承时，轴向载荷是一个非常关键的参数。
本文将介绍圆锥滚子轴承轴向载荷的计算方法。
首先，需要确定轴向载荷的大小和方向。
轴向载荷是指沿轴承轴线方向的力，可以是向内或向外的。
在实际应用中，轴向载荷通常由以下几种力组成：
1.主要轴向负载：由机械设备在运行过程中所承受的重力或惯性力造成的载荷。
2.外部轴向负载：由连接到轴承的外部部件所产生的载荷，例如传动装置或负载扭矩。
3.轴向定位力：由轴向定位装置所产生的力，用于保持轴承的位置和方向。
在确定了轴向载荷的大小和方向之后，可以使用以下公式计算圆锥滚子轴承的轴向载荷：
Fa = XFr + YFa
其中，Fa表示轴向载荷，Fr表示径向载荷，X和Y是系数，需要根据轴承的类型和工作条件确定。
需要注意的是，当轴承在工作时，由于受到载荷的影响，轴承内部会产生一定的变形。
这种变形会影响到轴承的滚动性能和寿命，因此需要进行相关的计算和分析。
在计算轴向载荷时，需要考虑轴承的内部几何结构、材料力学性能等因素，以确保轴承在工作时能够承受
所要求的载荷并保持良好的性能和寿命。
总之，圆锥滚子轴承轴向载荷的计算是一个复杂的过程，需要考虑多个因素。
在设计和选择轴承时，需要根据实际工作条件和要求进行详细的计算和分析，以确保轴承能够满足所要求的性能和寿命。
滚动轴承承载能力计算分析
滚动轴承承载能力计算分析目录1分析基础 (1)1.1理论基础：Hertz弹性体接触理论 (1)1.2实验基础：许用接触应力 (2)2承载分析 (3)2.1曲率计算 (3)2.2轴向承载 (4)2.3径向承载 (6)2.4倾覆承载能力 (10)2.5当量轴向力 (12)3静容量系数f o系数确定 (13)3.1许用接触应力 (13)3.2静容量系数 (14)4算例 (16)4.1基本参数 (16)4.2曲率计算 (16)4.3计算接触应力常数Cp值 (16)4.4计算许用接触应力 (16)4.5计算静容量系数f0值 (17)4.6静容量计算 (17)5简化(统一)计算法 (18)5.1简化公式 (18)5.2不同曲率比时的静容量系数值 (18)6附录 (19)附表1:曲率函数F (p )有关的椭圆积分 (19)附表2:不同球数时的Jr值 (21)1分析基础1.1理论基础：Hertz弹性体接触理论由Hertz推导出的点接触弹性变形和接触应力计算基本公式丄——材料泊松比Q一一使两接触体压紧的法向载荷 (N) 刀P ——接触处主曲率之和K(e) ---- 第一类椭圆完全积分。
(1-1)CT — -------------■ max2 -：2K (e) (1— ~)=1.52K(e)m-QEa(mm)(1-2) (1-3) (1-4)式中a——接触椭圆长半轴b ---- 接触椭圆短半轴(T max— -一最大接触应力S(mm)2 (N/mm)(mm)u、E —与曲率函数F ( p )有关的椭圆积分，取值见附表材料弹性模量(N/mm2)a「I1・2实验基础：许用接触应力Hertz 弹性接触理论不可能包括塑性变形，但在塑性变形区仍然引用Hertz接触理论，并假定塑性变形：b 与滚动体直径D w 有关，即用:-b /D w 来表示塑性变 形。
试验证明，在接触条件保持不变的情况下，单位塑性变形 :.b /D w 随着负荷增 长的幕级数而增长，随着曲率比的降低而增加，对于点接触，可得出图1所示的 实验曲线图：图1-1点接触塑性变形、接触应力常数与许用接触应力间关系 上图中的实验曲线符合下列方程式式中[(T max]——最大许用接触应力Cp —接触应力常数S b ——塑性变形量Dw ——滚动体直径根据Cp 值计算点接触接触应力的计算公式如下:(1-6)D w,4 3 1 0pC.(1-5)110150 200 250 3C0 360 400 450 500 550 600 650 700 750 300ODQOODO-nuDQOODOODDO ooc 755025g755025g 75E5025[m 7a5025g75c 7666655554 4 4433332笛亠亘-焉吾一12.1曲率计算如图2-1所示：滚动球直径D w ，回转支承滚道中心直径 D pw ，接触角a 。
滚动轴承当量动载荷计算
ft
106 动载荷——选择轴承
三、滚动轴承的当量动载荷
当量动载荷：是由轴承实际所受载荷转换得到的与基本额定动 载荷 C 的确定条件及性质相同的假想载荷，用 P表示。
滚动轴承的寿命计算
当量动载荷
P f p ( XFr YFa )
式中：Fr 、Fa — 分别为轴承承受的径向载荷和轴向载荷；
X 、Y — 分别为轴承的径向与轴向动载荷系数 (查表13－5）
滚动轴承的寿命计算
向心推力轴承的轴向载荷Fa 计算方法：
1）求径向载荷；
2）求派生轴向力 （大小、方向、作用点）；
滚动轴承的寿命计算
3）判断 Fae Fd 2与Fd1 大小，
“放放松”轴承的 Fa 等与自身的派生轴向力；
被“压紧”轴承的 Fa 等与除自身派生轴向力以外，其余各轴向力代数和
滚动轴承的寿命计算
一、基本概念 1）滚动轴承的寿命：是指轴承中的滚动体或套圈首次出现点蚀
之前，两套圈的相对总转数或在一定转速下的运转小时数。
轴承寿命的离散性是相当大的。 20
轴承的寿命/（106r）
2）基本额定寿命：指一批相同的轴承， 在相同的条件下运转，其可靠度为90％的 寿命，用 L10 。——标准寿命
3）基本额定动载荷： 指L10恰为 106 转
时，轴承所能承受的载荷，用 C 表示。
10
5
1 100 90 80 70 60 50 40 30 20 10 0
未失效轴承数量／%
C 是单一性质的载荷。 C表征不同型号轴承的承载特性，可查手册。
二、滚动轴承寿命计算公式
滚动轴承的寿命计算
1、滚动轴承寿命计算解决问题： 1）轴承所受当量载荷P≠基本额定载荷C时的寿命； 2）已知P且要求轴承具有的预期寿命时，应选用具有多大基 本额定动载荷的轴承？
标准滚动轴承承载能力计算
标准滚动轴承承载能力计算在跟踪架通用轴系中，标准滚动轴承是重要的部件，轴承的承载能力计算是轴系设计中的关键问题。
采用通用轴系后，地平式跟踪架水平轴两端的轴承主要承受径向载荷，同时承受一定量的轴向载荷。
垂直轴上的轴承要承载垂直轴及上部转体的负荷，载荷较大；另一方面垂直轴为了满足强度和刚度的要求，轴径一般较大，轴承的尺寸与轴要相互配合，因此使用时必须考虑轴承的尺寸和轴向承载能力。
同时为了减少跟踪架的成本，尽量采用轴承厂批量生产的轴承。
角接触球轴承按公称接触角分为15 °、25°、40°三种类型，公称接触角越大，轴向承载能力越强。
目前批量生产的角接触球轴承，尺寸最大是接触角为25 °的7244AC,其外形尺寸为220 X 400X 65。
下表中给岀了7244AC轴承的相关参数轴承额定载荷选取的流程为：(1)计算滚动轴承的当量载荷在实际应用中，根据跟踪架承载状况先估算出轴承承受的径向载荷r和轴向载荷°，则可计算出此时轴承的当量动载荷P为：式中X 径向动载荷系数；丫一一轴向动载荷系数；® ――载荷系数。
(2)基本额定动载荷C选取计算岀轴承实际工作时的当量载荷后，当轴承的预期使用寿命卜工」选定，轴承最大转速n可知时，可计算出轴承应具有的基本额定动载荷C',在手册中选择轴承时，所选轴承应满足基本额定载荷C > C '。
式中A ――温度系数，可从机械设计手册中查得;£ ——寿命指数，球轴承取3,滚子轴承取10/3。
由于角接触轴承的径向承载能力大于轴向承载能力，而其在垂直轴上的应用主要承受较大轴向载荷，因此必须考虑其轴向承载能力。
（3）轴承受轴向载荷时承载能力分析在轴承转速不高时，可以忽略钢球离心力和陀螺力矩的影响，钢球与内外套圈的接触角相等。
由赫兹接触理论得到轴承滚动体与内外滚道的接触变形和负荷之间的相互关系，可以表示为式中■—滚动体与内外滚道接触变形总量；K —系数；Q —滚动体承受载荷；。
滚动轴承的选择计算
滚动轴承的选择计算16. 3 滚动轴承的选择计算16.3.0滚动轴承类型的选择1.轴承的载荷大小:滚子轴承优于球轴承方向:径向R(6、1、N)轴向A(5)R+ A(7、3、6)轴承的载荷方向2.轴承的转速极限转速n:滚动轴承允许的最高工作转速称为lim 极限转速。
对高转速的轴承:1).优先选用球轴承(润滑的阻力)2).轻系列轴承优于中、重系列(离心力) 3).实体保持架优于冲压保持架(易形成油膜减小摩擦)4).提高公差等级、改善润滑条件等推力轴承的主要承载能力表现在轴向，离心力过大时无法通过径向反力平衡，将引起较大的反力，发热大，极限转速较低3. 轴承的调心性能表16-24. 轴承的安装与拆卸5. 经济性:球比滚子便宜，精度适宜比较球轴承和滚子轴承有:16.3.1滚动轴承的工作情况分析1.运动关系:内外圈相对回转;滚动体既自转又公转。
2.轴承中载荷的分布: ,推力轴承 F=F/z 0 a,向心轴承，在载荷F 的作用下,根据变形关系，轴承r下部中间滚动体受力最大，向两边逐渐减小。
也就是说～最多只有半圈滚动体受载～且各滚动体的受载大小也不同。
应力循环特性:内、外圈～滚动体的受力可以认为是脉动循环。
16.3.2 滚动轴承的失效形式及设计准则设计失效形式准则点蚀(一般轴承) 寿命计算静载永久变形荷计算密封;磨损、烧伤润滑、散热限制胶合极限转速元件破裂，重新正确安装。
对可分离的高精度轴承不能互换安装.在正确使用下，滚动轴承的最主要的失效形式是点蚀，点蚀可能发生在滚动体和任意座圈上，由于滚动轴承的接触应力较大，通常不按永久寿命设计，设计滚动轴承的寿命是滚动轴承设计的重要内容.由于滚动轴承工作中的接触应力较大，在接触应力作用下元件表面可能发生塑性变形，过大的塑性变形会影响轴承的工作平稳性和旋转精度，除过大的工作应力会造成塑性变形以外，拆卸和装配中的不正确操作也会引起塑性变形;在润滑不良的情况下，会造成轴承磨损，在使用滚动轴承中应保证充足的润滑，在设计中应为正确的润滑提供条件，应为添加润滑剂和保持润滑剂的合理量设置必要的装置，如加油孔，油面显示装置等。
各类滚动轴承轴向载荷分析及计算
各类滚动轴承轴向载荷分析及计算王志云（山东省东营职业学院，山东东营２５７０９１）摘要：总结了滚动轴承设计中其轴向载荷分析需考虑的因素，以及生产中几种常用滚动轴承支撑的轴向载荷分析方法，使得轴承的轴向载荷分析及计算更清晰、明了，内容更全面、系统。
关键词：滚动轴承；支撑形式；安装方式；轴向载荷中图分类号：ＴＨ１３３．３３文献标识码：Ａ文章编号：１００８－８０８３（２００８）０３－００６０－０２在滚动轴承的设计计算中，轴承轴向载荷计算是设计中的关键也是难点，它由轴承类型、支撑形式和安装方式等因素决定，在生产实际中，有关轴承的支撑类型多、形式多，必须对轴系结构进行详细、合理的受力分析，才能正确的进行计算，现就几种常用形式作以分析总结，并进行其轴向载荷的计算，从而为各种形式轴承轴向载荷分析计算提供方法依据。
一、滚动轴承轴向载荷计算中考虑的因素１．轴承类型滚动轴承按不同的分类方式有许多不同的类型，如按滚动体的形状不同有球轴承和滚子轴承，按调心性能不同有调心轴承和非调心轴承等，若按承载情况不同有向心轴承、推力轴承和角接触轴承三大类，向心轴承是指主要或只受径向载荷的轴承，推力轴承是指只受轴向载荷的轴承，角接触轴承是指同时承受径向和轴向载荷的轴承。
２．轴承的支撑形式一般对于两端支撑的情况，有全固式、固游式和全游式三种支撑形式，全固式是指两端都单向固定的支撑，固游式是指一端固定一端游动的支撑，全游式是指两端都游动的支撑。
３．轴承的安装方式对于成对使用的角接触轴承，通常有正装和反装两种安装方式。
轴承外圈窄边相对称为正装，又叫＂面对面＂安装，轴承外圈窄边相背称为反装，又叫＂背靠背＂安装。
二、滚动轴承轴向载荷分析１．向心轴承轴向载荷分析（１）全固式向心轴承轴向载荷分析普通工作温度下的短轴，常用两端都单向固定的形式，如图１所示。
图１１）当外载荷ＦＡ向右时，轴有向右移动的趋势，载荷传到右端轴承内圈上，又通过滚动体传到外圈，由于右端轴承外圈右端被轴承盖固定，使得右端轴承受到向左的支反力Ｆ＇Ａ２而被压紧，而左端轴承处于放松状态。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
各类滚动轴承轴向载荷分析及计算
王志云
（山东省东营职业学院，山东东营２５７０９１）
摘要：总结了滚动轴承设计中其轴向载荷分析需考虑的因素，以及生产中几种常用滚动轴承支撑的轴向载荷分析方法，使得轴承的轴向载荷分析及计算更清晰、明了，内容更全面、系统。
关键词：滚动轴承；支撑形式；安装方式；轴向载荷中图分类号：ＴＨ１３３．３３文献标识码：Ａ文章编号：１００８－８０８３（２００８）０３－００６０－０２
在滚动轴承的设计计算中，轴承轴向载荷计算是设计中
的关键也是难点，它由轴承类型、支撑形式和安装方式等因素决定，在生产实际中，有关轴承的支撑类型多、形式多，必须对轴系结构进行详细、合理的受力分析，才能正确的进行计算，现就几种常用形式作以分析总结，并进行其轴向载荷的计算，从而为各种形式轴承轴向载荷分析计算提供方法依据。
一、滚动轴承轴向载荷计算中考虑的因素
１．轴承类型
滚动轴承按不同的分类方式有许多不同的类型，如按滚动体的形状不同有球轴承和滚子轴承，按调心性能不同有调心轴承和非调心轴承等，若按承载情况不同有向心轴承、推力轴承和角接触轴承三大类，向心轴承是指主要或只受径向载荷的轴承，推力轴承是指只受轴向载荷的轴承，角接触轴承是指同时承受径向和轴向载荷的轴承。
２．轴承的支撑形式
一般对于两端支撑的情况，有全固式、固游式和全游式三种支撑形式，全固式是指两端都单向固定的支撑，固游式是指一端固定一端游动的支撑，全游式是指两端都游动的支撑。
３．轴承的安装方式
对于成对使用的角接触轴承，通常有正装和反装两种安装方式。
轴承外圈窄边相对称为正装，又叫＂面对面＂安装，轴承外圈窄边相背称为反装，又叫＂背靠背＂安装。
二、滚动轴承轴向载荷分析
１．向心轴承轴向载荷分析
（１）全固式向心轴承轴向载荷分析
普通工作温度下的短轴，常用两端都单向固定的形式，如图１所示。
图１
１）当外载荷ＦＡ向右时，轴有向右移动的趋势，载荷传到
右端轴承内圈上，又通过滚动体传到外圈，由于右端轴承外圈右端被轴承盖固定，使得右端轴承受到向左的支反力Ｆ＇Ａ２而被压紧，而左端轴承处于放松状态。
根据力平衡条件压紧端轴承轴向力Ｆａ２＝Ｆ＇Ａ２＝ＦＡ，
放松端轴承轴向力Ｆａ１＝０。
２）当外载荷ＦＡ向左时，轴有向左移动的趋势，载荷传到左端轴承内圈上，又通过滚动体传到外圈，由于左端轴承外圈左端被轴承盖固定，使得左端轴承受到向左的支反力Ｆ＇Ａ１而被压紧，而右端轴承处于放松状态。
根据力平衡条件压紧端
轴承轴向力Ｆａ１＝Ｆ＇Ａ１＝ＦＡ，
放松端轴承轴向力Ｆａ２＝０。
（２）固游式向心轴承轴向载荷分析当轴较长或工作温度较高时，常用一端固定一端游动的形式，以保证轴伸缩时能自由游动（如图２所示）。
图２
１）当外载荷ＦＡ向右时，轴有向右移动的趋势，载荷通过螺母传到左端轴承内圈，又通过滚动体传到外圈，由于左端轴承外圈右端被箱体固定，使得左端轴承受到向左的支反力Ｆ＇Ａ１而被压紧，
而右端轴承由于外圈没固定处于放松状态。
根据力平衡条件压紧端轴承轴向力Ｆａ１＝Ｆ＇Ａ１＝ＦＡ，放松端轴承轴向力Ｆａ２＝０。
２）当ＦＡ向左时，轴有向左移动的趋势，载荷传到左端轴承内圈，又通过滚动体传到外圈，由于左端轴承外圈左端被
箱体固定，使得左端轴承受到向左的支反力Ｆ＇Ａ１而被压紧，
而右端轴承由于外圈没固定处于放松状态。
根据力平衡条件压紧端轴承轴向力Ｆａ１＝Ｆ＇Ａ１＝ＦＡ，
放松端轴承轴向力Ｆａ２＝０。
（３）全游式向心轴承轴向载荷分析
要求能左右双向游动的轴，可采用两端游动的形式，如
作者简介：王志云（１９６４－），女，山东青州人，山东省东营职业学院副教授，现从事机械类科研和教学工作。
第２２卷第３期胜利油田职工大学学报
Ｖｏｌ．２２Ｎｏ．３２００８年６月
ＪＯＵＲＮＡＬＯＦＳＨＥＮＧＬＩＯＩＬＦＩＥＬＤＳＴＡＦＦＵＮＩＶＥＲＳＩＴＹ
Ｊｕｎ．２００８
６０
图３所示人字齿轮传动中的小齿轮轴支撑，此时两轴承均不
承受轴向力，故Ｆａ１＝０，
Ｆａ２＝０。
图３
２．角接触轴承轴向载荷分析
该类轴承由于存在公称接触角，受径向载荷Ｆｒ时会产生内部轴向力Ｆｓ，其方向由外圈宽边指向窄边，因此，轴承轴向力包括内部轴向力和外载荷两部分。
（１）角接触轴承正装时轴向载荷分析（如图４）
图４
１）若Ｆｓ１＋ＦＡ＞Ｆｓ２
则：轴承２“压紧”轴承１“放松”Ｆａ２＝ＦＡ＋Ｆｓ１Ｆａ１＝Ｆｓ１２）若Ｆｓ１＋ＦＡ＜Ｆｓ２则：轴承１“压紧”轴承２“放松”Ｆａ１＝Ｆｓ２－ＦＡＦａ２＝Ｆｓ２３）若Ｆｓ１＋ＦＡ＝Ｆｓ２则：轴承１、２都“放松”Ｆａ１＝Ｆｓ１Ｆａ２＝Ｆｓ２
（２）角接触轴承反装时轴向载荷分析（如图５）
图５
１）若Ｆｓ２＋ＦＡ＞Ｆｓ１则：轴承１“压紧”轴承２“放松”Ｆａ１＝ＦＡ＋Ｆｓ２Ｆａ２＝Ｆｓ２２）若Ｆｓ２＋ＦＡ＜Ｆｓ１则：轴承２“压紧”轴承１“放松”Ｆａ２＝Ｆｓ１－ＦＡＦａ１＝Ｆｓ１
３）若Ｆｓ２＋ＦＡ＝Ｆｓ１
则：轴承１、２都“放松”Ｆａ１＝Ｆｓ１Ｆａ２＝Ｆｓ２
３．推力轴承（如图６）
图６
压紧轴承承受轴向载荷Ｆａ。
三、结论
以上对不同类型，不同支撑方式和安装方式轴承轴向载荷进行了较详细的分析，用类似方法可对生产中多种形式轴承进行分析，从而可以确切计算轴承轴向载荷，正确进行轴承设计。
如图７所示减速箱内轴承支撑形式属于向心轴承两端全固式，其轴承轴向载荷分析与计算同上述图１所述。
图７
参考文献：
［１］邱宣怀．机械设计［Ｍ］．北京：高等教育出版社，１９８９．［２］濮良贵．机械零件［Ｍ］．北京：高等教育出版社，１９８２．
［３］葛中民．机械设计基础［Ｍ］．北京：中央广播电视大学出版社，
１９９１．
［４］卢玉明．机械设计基础［Ｍ］．北京：高等教育出版社，１９９８．［５］陈立德．机械设计基础［Ｍ］．北京：高等教育出版社，２００４．
（责任编辑周永红）
６１。