滚动轴承轴向力算
机械设计基础第章滚动轴承轴向力的计算

机械设计基础第章滚动轴承轴向力的计算滚动轴承是一种重要的机械传动部件,广泛应用于各种机械设备中。
在滚动轴承的设计中,轴向力的计算是重要的一环。
轴向力是指作用在轴承上的沿轴向方向的力,它对轴承的正常工作和寿命具有重要影响。
轴承在工作过程中,常常受到来自外部或内部的轴向力的作用。
外力主要包括:1.传动装置的轴向力:在一些传动装置中,由于齿轮、联轴器、皮带轮等传动元件的轴向对各来的作用,会使得轴承受到轴向力的作用。
2.轴向定位力:当轴承所选择的结构形式为非推力轴承,即由轴承的其他结构形式来决定轴承承受的轴向力,比如圆锥滚子轴承、调整心形滚子轴承等。
3.实际工况的影响力:比如离心力、旋转不平衡力等,由于转子的形状和运动特性,往往会使得轴承受到轴向力的作用。
内力主要包括:1.轴的伸长引起的力:当轴受到拉伸力或拉压力时,会产生轴向力作用于滚动轴承上。
2.温度变化引起的力:由于温度变化引起的轴线伸长或缩短导致的轴向力。
3.轴的变形引起的力:由于轴的变形导致的轴向力,如轴端的盖板,轴承座两侧安装的螺钉张紧方式的变形。
1.当轴承承受的轴向力为外力时,根据传动装置的轴向力大小和方向来计算。
一般可以通过传动装置的设计手册或相关文献来获取。
2.当轴承承受的轴向力为内力时,可以通过相关的计算公式来计算。
比如,当轴受到拉伸力时,轴向力可以通过公式F=σ×A计算,其中F为轴向力,σ为轴的应力,A为轴截面积。
3.当轴承承受的轴向力为温度变化引起的力时,可以通过计算轴线伸长或缩短的量来计算轴向力。
在滚动轴承的设计中,合理计算轴向力是十分重要的,轴向力过大或者过小都会对轴承的使用寿命和运行效果产生负面影响。
因此,在设计滚动轴承时,需要结合实际应用情况,充分考虑轴向力的计算,以确保轴承正常工作并具有较长的使用寿命。
轴及轴承计算

-
-
-
-
-
70000B
α=25˚
α=40˚
—
—
1
0
0.35
0.57
1.14
重新查表选取判断系数e e1=0.422 e2=0.401 重新计算派生轴向力 Fd1=e1Fr1 =0.422×875.65=369.52 N Fd2=e2Fr2 =0.401×1512.62=606.56 N 重新计算轴向力 Fa1= Fae +Fd2 =400+606.56=1006.56 N Fa2= Fd2 =606.56 N Fa1/C0= 1006.56/20000 =0.05033 Fa2/C0= 606.56/20000 =0.03033 两次计算 Fa2/C0 结果相差不大,故取 e1=0.422
M aH F1H L M /aV 2 8700 0.193/ 2
840 N m
6) 求F力产生的弯矩图
927 N maV 4500
d
L/2 a
a— a 截面F力产生的弯矩为:
M 0.193/ 2 M aF F1F L /2 aV 4803
a
潘存云教授研制
L/2 a
Ft d2
L Fr Fa 2
K
F
Fr Fa F2v
Fr L 2 Fa d 2 2 6410 193 2 2860 2860 146 146 2 2 对2点取矩 F1v 2123 N L 193 193
F F2v Fr F 1v 1 v 6410 2123 4287 N
轴承类型 相对轴向载荷 名 称 代 号 f 0Fa / C0r Fa / C0 调心球轴承 10000 — — 调心滚子轴承 20000 — — 推力调心滚子轴承 29000 — — 圆锥滚子轴承 30000 — — 0.172 0.345 0.689 1.030 深沟球轴承 60000 1.380 — 2.070 3.450 5.170 6.890 0.015 0.029 0.058 0.087 70000C 0.120 α=15˚ 0.170 0.290 角接触球轴承 0.440 0.580 70000AC — — 70000B
机械设计基础第节滚动轴承轴向力的计算

机械设计基础第节滚动轴承轴向力的计算滚动轴承是一种常用的机械元件,用于支撑与传递轴向载荷和径向载荷。
在机械设计中,计算滚动轴承轴向力是非常重要的一部分,涉及到轴承的选型和设计。
本文将介绍滚动轴承轴向力的计算方法。
一、轴向载荷的种类在机械系统中,轴向载荷分为静载荷和动载荷两种。
1.静载荷:轴向载荷恒定不变的情况下的载荷称为静载荷。
静载荷通常由设备的自重、安装在轴上的其他零件的重量、负荷的重量等构成。
2.动载荷:轴向载荷大小在运行过程中有变化的载荷称为动载荷。
动载荷通常通过计算得出,可以是来自于负载的力或力矩引起的轴向力。
二、静载荷的计算静载荷的计算主要包括扭矩产生的轴向力、径向载荷以及其他附加载荷的计算等。
1.扭矩产生的轴向力:扭矩产生的轴向力是由于传递扭矩而引起的轴向力。
一般情况下,扭矩产生的轴向力可以通过计算得出,计算公式如下:Fa=(KT×Md)/L其中,Fa为扭矩产生的轴向力,KT为轴向力系数,Md为传递的扭矩,L为轴承的有效传递长度。
2.径向载荷:径向载荷是指垂直于轴向的力。
径向载荷通常由设备的自重、传动装置的重量、负载的重量等构成。
径向载荷的计算需要考虑设备的结构和工作环境等因素。
3.其他附加载荷:其他附加载荷通常包括轴向预紧力、温度变化引起的载荷、振动引起的载荷等。
这些附加载荷需要在设计过程中进行综合考虑。
三、动载荷的计算动载荷的计算需要考虑到设备在运行中的工况、运行速度、负载类型等因素。
常见的动载荷计算方法有以下几种:1.动载荷的估计:根据设备的工作环境和使用条件,根据经验公式或实验结果进行动载荷的估计。
2.动载荷的测量:通过测量设备在运行过程中的实际载荷,得到动载荷的大小。
3.动载荷的模拟计算:通过建立设备的动态模型,对工作过程进行模拟计算,得到动载荷的大小。
四、滚动轴承轴向力的选型在计算得到滚动轴承的轴向力后,还需要根据轴承的轴向载荷容量、速度等特性进行选型。
轴向载荷容量是指滚动轴承在承受轴向力时的极限载荷能力,通常通过轴向载荷容量图进行选型。
滚动轴承计算题题

滚动轴承计算题题 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】滚动轴承30题(当量动载荷、寿命计算等)1.有一轴由一对角接触球轴承支承,如图所示。
已知:齿轮的分度圆直径d =200mm ,作用在齿轮上的载荷为T F =1890N, =700N, =360N.轴承的内部轴向力S 与径向载荷的关系式为:S=T F 。
求两轴承所承受的轴向载荷。
题1图解:受力分析如图示。
题1答图1S 、2S 方向如图示所以轴承2被“压紧”,轴承1“放松”。
2.如图所示,某轴用一对30307圆锥滚子轴承,轴承上所受的径向负荷R 1=2500N ,R 2=5000N ,作用在轴上的向外负荷F a1=400N,F a2=2400N 。
轴在常温下工作,载荷平稳f P =1。
试计算轴承当量动负载大小,并判断哪个轴承寿命短些(注:30307轴承的Y=,e=,S=R/(2Y);当A/R>e 时,X=,Y=;当A/R<=e 时,X=1,Y=0)题2图解:受力分析如图示。
题2答图所以轴承2被“压紧”,轴承1“放松”。
所以11111()2500PN f P X R Y A =+=因为1P < 2P 所以轴承2寿命短些3.某齿轮轴由一对30212/P6X 轴承支承,其径向载荷分别为1r F =5200N,2r F =3800N ,方向如图所示。
取载荷系数f p =。
试计算: 两轴承的当量动负荷P 1、P 2:1)当该对轴承的预期寿命L h =18000h 时,齿轮轴所允许的最大工作转速N max =?附30212/P6X 轴承的有关参数如下: C r =59250N,e=,X=, Y=,S=Fr/(2Y)题3图解:受力分析如图示。
题3答图(1)115200152922 1.7r N YFS ===⨯ 1S 、2S 方向如图示所以轴承2被“压紧”,轴承1“放松”。
13 滚动轴承轴向力

5 F0 Fr z
滚动体--不稳定的脉动循环变应力
8
固定套圈---稳定的脉动循环变应力
三、滚动轴承的失效形式和计算准则 主要失效形式: 1)疲劳点蚀 安装润滑和维护良好
9
2)塑性变形
转速很低或作间歇摆动
10
3)磨损
润滑不良、 密封不严、 多尘条件
11
2、滚动轴承失效形式与设计准则 (一)滚动轴承的失效形式
径向载荷系数 轴向载荷系数,P280表16-11
仅能承受径向载荷的轴承N类 仅能承受轴向载荷的轴承 5类
P = fp Fr
P = fp Fa
例题
向心推力轴当量承载荷的计算
18
滚动轴承的寿命计算步骤
1、计算轴承上的Fr和Fa;
P = fp(X Fr+Y Fa) 2、计算P;
Fa 查Cor;计算 Cor
3)要求n<nlim——极限转速 6、7、N——nlim较高
5——nlim较低
4)轴的刚性较差,轴承孔不同心——调心轴承 5)便于装拆和间隙调整——内、外圈不分离的轴承 6)3、7两类轴承应成对使用,对称安装 7)旋转精度较高时——较高的公差等级和较小的游隙 8)优先考虑用普通公差等级的深沟球轴承
35
S0 ——静强度安全系数
30
例:已知一对7210C轴承,分别承受径向载荷 Fr1=5200N, Fr2=8000N,外加轴向载荷 Kα=5800N, e=0.4,求两轴承的轴向载荷。 1 2 О Kα О О О Fr1 Fr2 F eF
s r
解:查表得7210C轴承内部轴向力计算公式为 Fs1 eFr1 0.4 5200 2080 (N )
f t Cr L10 ( ) P
[说明]轴承相关计算
![[说明]轴承相关计算](https://img.taocdn.com/s3/m/ded23309640e52ea551810a6f524ccbff121cafb.png)
第十八章滚动轴承§18-1 滚动轴承的结构及类型一、滚动轴承的结构滚动轴承一般是由内圈、外圈、滚动体和保持架组成(图18-1)。
通常内圈随轴颈转动,外圈装在机座或零件的轴承孔内固定不动。
内外圈都制有滚道,当内外圈相对旋转时,滚动体将沿滚道滚动。
保持架的作用是把滚动体沿滚道均匀地隔开,如图18-2所示。
图18-1滚动轴承结构图18-2滚动轴承运动滚动体与内外圈的材料应具有高的硬度和接触疲劳强度、良好的耐磨性和冲击韧性。
一般用含铬合金钢制造,经热处理后硬度可达HRC61~65,工作表面须经磨削和抛光。
保持架一般用低碳钢板冲压制成,高速轴承多采用有色金属或塑料保持架。
与滑动轴承相比,滚动轴承具有摩擦阻力小,起动灵敏、效率高、润滑简便和易于互换等优点,所以获得广泛应用。
它的缺点是抗冲击能力较差,高速时出现噪声,工作寿命也不及液体摩擦的滑动轴承。
由于滚动轴承已经标准化,并由轴承厂大批生产,所以,使用者的任务主要是熟悉标准、正确选用。
图18-3给出了不同形状的滚动体,按滚动体形状滚动轴承可分为球轴承和滚子轴承。
滚子又分为长圆柱滚子、短圆柱滚子、螺旋滚子、圆锥滚子、球面滚子和滚针等。
图18-3 滚动体的形状二、滚动轴承的类型滚动轴承常用的类型和特性,见表18-1。
由于结构的不同,各类轴承的使用性能如下。
1.承载能力在同样外形尺寸下。
滚子轴承的承载能力约为球轴承的1.5~3倍。
所以,在载荷较大或有冲击载荷时宜采用滚子轴承。
但当轴承内径d 20mm时,滚子轴承和球轴承的承载能力已相差不多,而球轴承的价格一般低于滚子轴承,故可优先选用球轴承。
2.接触角接触角是滚动轴承的一个主要参数,轴承的受力分析和承载能力等与接触角有关。
表18-2列出各类轴承的公称接触角。
滚动体套圈接触处的法线与轴承径向平面(垂直于轴承轴心线的平面)之间的夹角称为公称接触角。
公称接触角越大,轴承承受轴向载荷的能力也越大。
滚动轴承按其承受载荷的方向或公称接触角的不同,可分为:(1) 径向轴承,主要用于承受径向载荷,其公称接触角从0 到45 ;(2) 推力轴承,主要用于承受轴向载荷,其公称接触角从大于45 到90(表18-2)。
滚动轴承计算题

所以轴承1被“压紧”,轴承2被“放松”。
,
因为
所以
18.某轴系齿轮受力如图所示,已知选用轴承型号为30206, ,e=,Y=,X=(S=R/2Y);圆锥齿轮平均分度圆直径 ,圆周力 ,径向力 ,轴向力 ,轴的转速n=600r/min,载荷系数 ,常温下工作,试求此轴承寿命为多少小时基本公式 (转)(15分)
(已知条件: =1, =, =2, =122000N, =, =, =, )
题5图
解:受力分析如图示。
题5答图
= =2353N
= =588N
、 方向如图示。
= +2000=3353N>
所以轴承2被“压紧”,轴承1“放松”。
= =2353N
= =3353N
/ = =<
/ = >力如图示。
题14答图
R1=R3= = =1667N
R2=R4= =1333N
S1=S3=R1=
S1、S3方向如图示。
S2=S4=R2=
S2、S4方向如图示。
图(a)中:S2+Fa=+500=>S1
所以轴承1被“压紧”,轴承2“放松”。
A1=S2+Fa=
A2=S2=
图(b)中:S2+Fa=+500=> S1
题6答图
= = =2100N
= = =700N
、 方向如图示。
+ =500+700=1200<
所以轴承1“放松”,轴承2“压紧”。
= =2100N
= =2100 500=1600N
= =>
= >
所以 =
= + =3057N
滚动轴承计算题(30题)
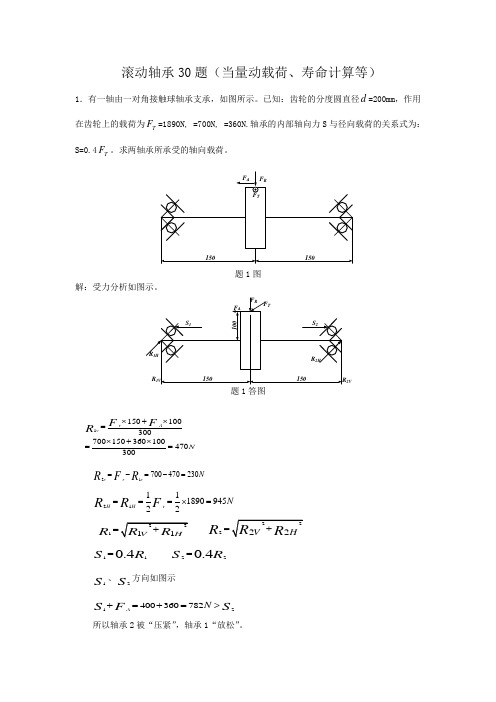
滚动轴承30题(当量动载荷、寿命计算等)1.有一轴由一对角接触球轴承支承,如图所示。
已知:齿轮的分度圆直径d =200mm ,作用在齿轮上的载荷为T F =1890N, =700N, =360N.轴承的内部轴向力S 与径向载荷的关系式为:S=0.4T F 。
求两轴承所承受的轴向载荷。
题1图解:受力分析如图示。
2V题1答图1150100300700150360100470300rA vNFF R⨯+⨯=⨯+⨯== 21700470230vrvN R FR=-=-=2111189094522HH rN R R F ===⨯=1R =2R =110.4S R = 220.4S R =1S、2S 方向如图示12400360782A N SS F +=+=>所以轴承2被“压紧”,轴承1“放松”。
1211422,782A N N SS A A F ===+=2.如图所示,某轴用一对30307圆锥滚子轴承,轴承上所受的径向负荷R 1=2500N ,R 2=5000N ,作用在轴上的向外负荷F a1=400N,F a2=2400N 。
轴在常温下工作,载荷平稳f P =1。
试计算轴承当量动负载大小,并判断哪个轴承寿命短些?(注:30307轴承的Y=1.6,e=0.37,S=R/(2Y);当A/R>e 时,X=0.4,Y=1.6;当A/R<=e 时,X=1,Y=0)题2图解:受力分析如图示。
题2答图11250078122 1.6N YRS ===⨯ 225000156322 1.6N Y R S ===⨯211278124004002781a a N S S F F+-=+-=>所以轴承2被“压紧”,轴承1“放松”。
112111781,2781a a N N SS A A F F ===+-=117810.312500e AR==< 2227810.565000e A R==< 所以11111()2500PN f PX R Y A =+=22222()6450PN f PX R Y A =+=因为1P < 2P 所以轴承2寿命短些3.某齿轮轴由一对30212/P6X 轴承支承,其径向载荷分别为1r F =5200N,2r F =3800N ,方向如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滚动轴承所承受的载荷取决于
所支承的轴系部件承担的载荷。
右图
为一对角接触球轴承反装支承一个
轴和一个斜齿圆柱齿轮的受力情况。
图中的F re、F te、F ae分别为所支承零
件(齿轮)承受的径向、切向和轴向
载荷,F d1和F d2为两个轴承在径向
载荷F r1和F r2(图中未画出)作用下
所产生的派生轴向力。
这里,轴承所
承受的径向载荷F r1和F r2可以依据
两个角接触球轴承反装的受力分析
(径向反力)
F re、F te、F ae经静力分析后确定,而轴向载荷F a1和F a2则不完全取决于外载荷F re、F te、F ae,还与轴上所受的派生轴向力F d1和F d2有关。
对于向心推力轴承,由径向载荷F r1和F r2所派生的轴向力F d1和F d2的大小可按下表所列的公式计算。
注:表中Y和e由载荷系数表中查取,Y是对应表中F a/F r>e的Y 值
下图中把派生轴向力的方向与外加轴向载荷F ae的方向一致的轴承标为2,另一端则为1。
取轴和与其相配合的轴承内圈为分离体,当达到轴向平衡时,应满足:F ae+F d2=F d1
由于F d1和F d2是按公式计算的,不一定恰好满足上述关系式,这时会出现下列两种情况:
当F ae+F d2>F d1时,则轴有向左窜动的趋势,相当于轴承1被“压紧”,轴承2被“放松”,但实际上轴必须处于平衡位置,所以被“压紧”的轴承1所受的总轴向力F a1必须与F ae+F d2平衡,即
F a1=F ae+F d2
而被“放松”的轴承2只受其本身派生的轴向力F d2,即F a2=F d2。
当F ae+F d2<F d1时,同前理,被“放松”的轴承1只受其本身派生的轴向力F a1,
即F a1=F d1
而被“压紧”的轴承2所受的总轴向力为: F a2=F d1-F ae
综上可知,计算向心推力轴承所受轴向力F a的方法可以归纳为:先通过派生轴向力及外加轴向载荷的计算与分析,判断被“放松”或被“压紧”的轴承;然后确定被“放松”轴承的轴向力仅为其本身派生的轴向力,被“压紧”轴承的轴向力则为除去本身派生的轴向力后其余各轴向力
的代数和。
返回。
