第五章作业————振动作业及答案
05 机械振动 作业及参考答案 2015

一. 选择题:【 D 】1 (基础训练2) 一劲度系数为k 的轻弹簧截成三等份,取出其中的两根,将它们并联,下面挂一质量为m 的物体,如图13-15所示。
则振动系统的频率为 : (A)m k32π1. (B)m k2π1 .(C)m k 32π1. (D)mk62π1.提示:劲度系数为k 的轻弹簧截成三等份,每份的劲度系数为变为3k ,取出其中2份并联,系统的劲度系数为6k .【 C 】 2 (基础训练4) 一质点作简谐振动,周期为T .当它由平衡位置向x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12. (B) T /8. (C) T /6. (D) T /4.提示:从从二分之一最大位移处到最大位移处这段路程在旋转矢量图上,矢量转过的角位移为13π,对应的时间为T/6.[ B ] 3、(基础训练8) 图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成的余弦振动的初相为(A) π23. (B) π.(C) π21. (D) 0. 提示:使用谐振动的矢量图示法,合振动的初始状态为初相位为π[ D ] 4、(自测提高4)质量为m 的物体,由劲度系数为k 1和k 2的两个轻质弹簧串联后连接到固定端,在光滑水平轨道上作微小振动,则振动频率为:(A) m k k v 212+=π. (B) mk k v 2121+=π. (C) 212121k mk k k v +=π. (D) )(212121k k m k k v +=π.提示:两根劲度系数分别为k1和k2的两个轻质弹簧串联后,可看成一根弹簧,其弹A/ -图13-15性系数满足:21111k k k +=,2121k k k k k +=,)(21212k k m k k +=ω,可计算得到v【 B 】 5、(自测提高5)一简谐振动曲线如图所示.则振动周期是 (A) 2.62 s . (B) 2.40 s . (C) 2.20 s . (D)2.00 s . 提示:使用谐振动的矢量图示法,初始状态旋转矢量位于第四象限,初始相位到第一次回到平衡位置时,旋转矢量转过的角度为1s 2.4s【 D 】6、(自测提高6)弹簧振子在水平光滑桌面上作简谐振动,其弹性力在半个周期内所做的功为:( )A 2kA B 221kA C 241kA D 0提示:振动方程为)cos(0φω+=t A x ,经过半个周期,质点偏离平衡位置的位移为)cos(0πφω++=t A x ,这两个位置弹簧所具有的弹性势能221kx E p =相同,所以所做的功为零。
(完整版)机械制造技术基础第五章课后习题答案

《机械制造技术基础》第二次作业(制定)答案5-1 什么是主轴展转偏差,它包含哪些方面?主轴在每一刹时展转轴线相关于轴线均匀线的改动量。
角度摇动。
它包含纯轴向窜动, 纯径向挪动、 纯5-2 在卧式镗床上来用工件送进方式加工直径为 200 的通孔时,若刀杆与送进方向倾斜1o 30' ,则在孔径横截面将产生什么样的形状偏差?其偏差大小是多少?答:圆度偏差 偏差大小为200(1 1) 0.0343mm2cos5-3 在车床上车向来径为 80mm 、长约 2000mm 的长轴外圆,工件资料为45 钢,切削用量为 2m / s , a p 0.4mm , f0.2mm / r ,刀具资料为 YT15 ,如只考虑刀具磨损惹起的加工偏差,问该轴车后可否达到IT8 的要求。
答:切削行程为 ldL2.5km1000 f刀具的尺寸磨损量可用式K l 01000查表得初始磨损为4~12, K 8 m / km则获得因刀具惹起的偏差为2(8 2.5) (40 8 ~ 24) m1000IT8 要求 80mm 的公差精度为46 m ,显然可见偏差大于公差要求,则该轴车后不可以达到IT8 精度要求。
5-4 什么是偏差复映?偏差复映系数的大小与哪些要素相关?偏差复映是指因为背吃刀量的变化惹起了切削力的变化。
变化的切削力作用在工艺系统上使它的受力变形也发生相应的变化。
也就是将毛坯加工余量的变化复映到工件上的一种现象。
偏差复映系数跟工艺系统的刚度相关,刚度越高,偏差系数越小。
若加工过程分多次走刀,则总的偏差复映系数为每次走刀复映系数的积。
5-6 在车床上用前后顶尖装夹, 车削长为800mm ,外径要求为 5000.04 mm 的工件外圆。
已知 k 10000 N / mm ,K 尾5000 N / ,4000N/,300 N ,试求主mm K 刀架mm F y( 1)仅因为机床刚度变化所产生的工件最大直径偏差,并按比率画出工件的外形。
第五、六章作业解答

4.0
x(m)
0.10 0.05
P
B
t (s)
P
4.0
O
o0
B
AB
O
AO
o0
B
t (s)
1
由比例关系求振动的周期T
(2) 画出P点对应的旋转矢量AP,可知P点相位: P
0
t BO BO 5 6 5 T 2 2 12
T
PO P O 0 ( 3) 3 OP两点的相位差:
2
(1) 由振动曲线可知振动的振幅: 解: A 0.10m
BO B O 2 ( 3) 5 6
画出t =0时刻的旋转矢量AO,可知振动的初相:
OB两点的时间间隔:t BO 4.0s
x(m)
AO
x(m)
0.10 0.05
O 5 3 或 3
Ex5-20
3 2k 1 2k 0.75
x2+x3振幅最小的条件是: 32 3 2 ( 2k 1)
两个同频率简谐运动1和2的振动曲线如图 所示,求:(1)两简谐运动的运动方程;(2) 在同一图中画出两简谐运动的旋转矢量; (3) 若两简谐运动叠加,求合振动方程。
o0
t (s)
2 rad s 1 T
2
画出两个简谐运动在初始时刻的旋转矢量A1和A2。 由矢量图可知两个简谐运动的初相分别为: 1 2 因此两简谐运动方程分别为:
2
两简谐运动的相位差: 21 2 1 合振动振幅: A
2 1 2 2
作业————振动作业及答案

第五章作业5-1 写出本章你觉得重要旳知识点。
5-2质量为kg 10103-⨯旳小球与轻弹簧构成旳系统,按)SI ()328cos(1.0ππ+=x 旳规律作谐振动,求:(1)振动旳周期、振幅和初位相及速度与加速度旳最大值; (2)最大旳答复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻旳位相差;解:(1)设谐振动旳原则方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==m m a FJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时,有p E E 2=,即)21(212122kA kx ⋅=∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t 5-3一种沿x 轴作简谐振动旳弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表达.如果0=t 时质点旳状态分别是:(1)A x -=0;(2)过平衡位置向正向运动; (3)过2Ax =处向负向运动; (4)过2A x -=处向正向运动.试求出相应旳初位相,并写出振动方程.解:由于 ⎩⎨⎧-==0000sin cos φωφA v A x将以上初值条件代入上式,使两式同步成立之值即为该条件下旳初位相.故有)2cos(1πππφ+==t T A x)232cos(232πππφ+==t T A x)32cos(33πππφ+==t T A x)452cos(454πππφ+==t T A x5-4一质点同步参与两个在同始终线上旳简谐振动,振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x 试分别用旋转矢量法和振动合成法求合振动旳振动幅和初相,并写出谐振方程。
江西理工大学大学物理(下)习题册及答案详解

班级_____________ 学号___________姓名________________ 简谐振动1. 一质点作谐振动, 振动方程为X=6COS (8πt+π/5) cm, 则t=2秒时的周相为:π5116, 质点第一次回到平衡位置所需要的时间为:s 0375.0.2. 一弹簧振子振动周期为T 0, 若将弹簧剪去一半, 则此弹簧振子振动周期T 和原有周期T 0之间的关系是:022T T =.3. 如图为以余弦函数表示的谐振动的振动曲线, 则其初周相φ=3π-,P 时刻的周相为:0.4. 一个沿X 轴作谐振动的弹簧振子, 振幅为A , 周期为T , 其振动方程用余弦函数表示, 如果在t=0时, 质点的状态分别是:(A) X 0=-A; (B) 过平衡位置向正向运动;(C) 过X=A/2 处向负向运动; (D) 过A x 22-= 处向正向运动.2 1 0 P t(s) X(m)试求出相应的初周相之值, 并写出振动方程.)2cos()(ππ+=t TA x A ; )22cos()(ππ-=t T A x B)32cos()(ππ+=t T A x C ; )452cos()(ππ+=t T A x D5.一质量为0.2kg 的质点作谐振动,其运动议程为:X=0.60 COS(5t -π/2)(SI)。
求(1)质点的初速度;(2)质点在正向最大的位移一半处所受的力。
解(1))5sin(00.32π--==t dtdxv 10.00.3,0-==s m v t(2)x x dtdv a 2520-=-==ω 22.5.7,30.0--===s m a m x AN ma F 5.1-==班级_____________ 学号___________姓名________________简谐振动的合成1. 两个不同的轻质弹簧分别挂上质量相同的物体1和2, 若它们的振幅之比A 2 /A 1=2, 周期之比T 2 / T 1=2, 则它们的总振动能量之比E 2 / E 1 是( A )(A) 1 (B) 1/4 (C) 4/1 (D) 2/11)()(;)(2222221122112=⋅==A A T T E E T A m E π2.有两个同方向的谐振动分别为X 1=4COS(3t+π/4)cm ,X 2 =3COS(3t -3π/4)cm, 则合振动的振幅为:cm A 1=, 初周相为:4πφ=. 3. 一质点同时参与两个同方向, 同频率的谐振动, 已知其中一个分振动的方程为X 1=4COS3t cm, 其合振动的方程为分振动的振幅为A 2 =cm 44. 动方程分别为X 1=A COS(ωt+π/3), X 2 =A COS (ωt+5π/3), X 3 =A COS(ω程为:)6cos(3πω+=t A x5. 频率为v 1和v 2的两个音叉同时振动时,可以听到拍音,可以听到拍音,若v 1>v 2,则拍的频率是(B )(A)v 1+v 2 (B)v 1-v 2 (C)(v 1+v 2)/2 (D)(v 1-v 2)/26.有两个同方向,同频率的谐振动,其合成振动的振幅为0.20m ,周相与第一振动周相差为π/6。
振动力学课程作业

《振动力学》2015春节学期作业一、无阻尼自由振动1、如图所示,T型结构可绕水平轴O作微小摆动,已知摆动部分的质量为w,机构绕O轴的转动惯量为J,两弹簧的弹簧系数均为k,且当①=0时(即机构处于平衡位置时),两弹簧无伸缩,试求该机构的摆动频率。
2、如图所示,长度为L的刚性杆件,在O点铰支,自由端固定一质量为m的小球。
在距离铰支端a处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:①喈喘一D)(答案:①=)3、如图所示,悬臂梁长为L,截面抗弯刚度为EI,梁的自由端有质量为m 的质量块,弹簧刚 度为k ,求系统的固有频率。
4、如图所示,半径为R 的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有 角频率。
(答案:①)君篇5、如图所示,抗弯刚度为EI = 30义106(N ・m 2)的梁AB ,借弹簧支撑于A,B 两点处,弹簧系数均为k = 300(N / m )。
忽略梁的质量,试求位于B 点左边3m 处,重量为W = 1000(N )的物块自由振动的周期。
(答案:T=0.533s )借助四根端点嵌固的竖置管柱支撑着。
每根柱子的长为L,抗弯刚度为 EI 。
试求该水箱顺水平方向自由振动的周期。
(管柱的质量忽略不计) 6、一个重W 的水箱, (答案:)(答案:T = 2)1、如图所示,库伦曾用下述方法测定液体的粘性系数c ':在弹簧上悬挂一薄板A ,先测出薄板在空气中 的振动周期J 然后测出在待测粘性系数的液体中的振动周期「设液体对薄板的阻力等于2A c ′ -其 中2A 为薄板的表面面积,v 为薄板的速度。
如薄板重W ,试有测得的数据T 和T 2,求出粘性系数c 。
空 气对薄板的阻力不计。
»2 冗 W 二~~—(答案:C ’二祈口22 一 T :)12(答案:196Ns/m )3、挂在弹簧下端的物体,质量为1.96kg ,弹簧常数k=0.49N/cm,阻尼系数c=0.196Ns/cm 。
机械振动基础作业(有答案-全版)
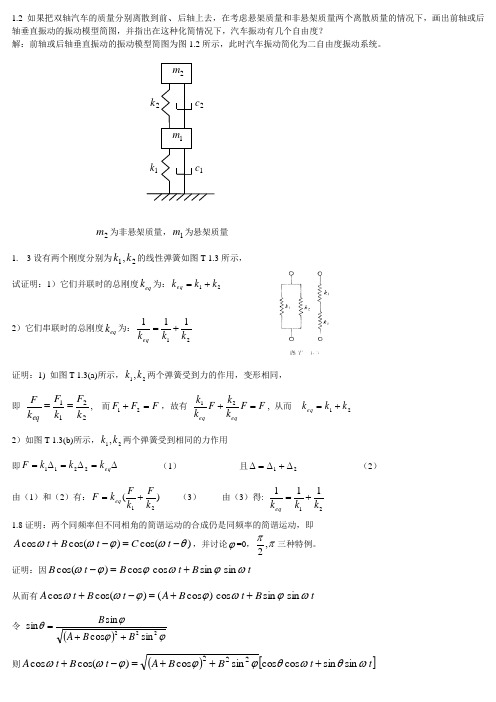
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?解:前轴或后轴垂直振动的振动模型简图为图1.2所示,此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量,1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示, 试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 为:21111k k k eq +=证明:1) 如图T-1.3(a)所示,21,k k 两个弹簧受到力的作用,变形相同, 即2211k F k F k F eq ==, 而F F F =+21,故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2)如图T-1.3(b)所示,21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 (1)且21∆+∆=∆ (2)由(1)和(2)有:)(21k Fk F k F eq += (3) 由(3)得:21111k k k eq += 1.8证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论ϕ=0,ππ,2三种特例。
证明:因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++,则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时,C=A+B ;当ϕ=2π时,22B A C +=,22BA arcsin +=B θ ;当ϕ=π时,B A -=C ,0=θ1.13汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T-1.13所示。
航空发动机强度与振动--各章作业

三、计算题
1、某等截面、无扭向、根部固装的转子叶片长 l = 16cm , E = 5.0 ×105 cm / s , J = 0.8cm4 , A = 5cm2 , ρ
( 1 ) 请 求 出 前 三 阶 弯 曲 振 动 的 固 有 频 率 ( 固 有 频 率 的 单 位 为 Hz )。 计 算 公 式 已 经 给 出 :
4、旋转着叶片的自振频率称为
;静止叶片的自振频率称为
。
5、叶片的振动阻尼有
,
,
三类。
6、列举出一些常用的提高叶片抗振阻尼的结构措施。
7、从气动和结构两个方面分析下带冠叶片的优缺点。
8、燕尾形、枞树形、销钉式三种榫头榫槽的连接方式中,哪种叶片和轮盘的连接方式抗振阻尼最好?
9、如图,试解释双榫根构造的叶片,抗振阻尼较好的原因?
8、判断弹性元件的串联或者并联。
6
第一章 转子叶片强度计算
9、在图(a)中,两弹簧是并联还是串联?在图(b)中,若将弹簧的长度变为原来的一半,则此一半长度的弹簧 的刚度系数是多少?
10、系统受外界激励作用而产生的振动称为( )振动。激励根据其来源可分为两类:一类是( ),
另一类是(
)。
7
第一章 转子叶片强度计算
5、不管是实心盘还是空心盘,热应力σθ 在轮盘外缘处呈压应力状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章作业 5-1写出本章你认为重要的知识点。
5-2质量为
kg 10103-⨯的小球与轻弹簧组成的系统,按)SI ()328cos(1.0ππ+=x 的规律作谐振动,
求: (1)振动的周期、振幅和初位相及速度与加速度的最大值;
(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等?
(3)s 52=t 与s 11=t 两个时刻的位相差;
解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知: 又πω8.0==A v m 1s m -⋅51.2=1s m -⋅ (2)N 63.0==m m a F
当p k E E =时,有p E E 2=, 即)2
1(212122kA kx ⋅= ∴m 20222±=±
=A x (3)ππωφ32)15(8)(12=-=-=∆t t
5-3一个沿x 轴作简谐振动的弹簧振子,振幅为
A ,周期为T ,其振动方程用余弦函数表示.如果0=t 时质点的状态分别是:
(1)A x -=0;
(2)过平衡位置向正向运动;
(3)过2
A x =处向负向运动; (4)过2A
x -
=处向正向运动. 试求出相应的初位相,并写出振动方程.
解:因为⎩⎨⎧-==00
00sin cos φωφA v A x 将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有
5-4一质点同时参与两个在同一直线上的简谐振动,振动方程为
试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。
解:∵πππφ
=--=∆)65(6 ∴m 1.021=-=A A A 合
∴6π
φ=
其振动方程为
5-5图为两个谐振动的t x -曲线,试分别写出其谐振动方程.
题图
解:由题图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即1s rad 2-⋅==ππω
T 故m )2
3cos(1.0ππ+=t x a 由题图(b)∵0=t 时,3
5,0,2000πφ=∴>=v A x 01=t 时,22,0,0111ππφ+
=∴<=v x 又ππωφ2
53511=+⨯= ∴πω6
5= 故m t x b )3
565cos(1.0ππ+= 5-6一轻弹簧的倔强系数为k ,其下端悬有一质量为M 的盘子.现有一质量为m 的物体从离盘底h 高度处自由下落到盘中并和盘子粘在一起,于是盘子开始振动.
(1)此时的振动周期与空盘子作振动时的周期有何不同?
(2)此时的振动振幅多大?
(3)取平衡位置为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初位相并写出物体与盘子的振动方程.
解:(1)空盘的振动周期为k
M π2,落下重物后振动周期为k m M +π2,即增大. (2)按(3)所设坐标原点及计时起点,0=t 时,则k
mg x -=0.碰撞时,以M m ,为一系统动量守恒,即 则有M
m gh m v +=
20 于是 (3)g m M kh x v )(2tan 000+=-=ωφ(第三象限),所以振动方程为。
