线性系统理论郑大钟307页PPT
合集下载
线性系统理论全课件
称一个系统为确定性系统,当且仅当不论是系统的特性和参数还是系统的输入 和扰动,都是随时间按确定的规律而变化的. 称一个动态系统为不确定性系统,或者系统的特性和参数中包含某种不确定性, 或者作用于系统的输入和扰动是随机变量
2/2,13/50
2.4 由系统输入输出描述导出状态空间描述
由输入输出描述导出状态空间描述
5/7,9/50
离散时间线性系统的状态空间描述 状态空间描述形式 离散时间线性时不变系统 X (k 1) Gx(k) Hu (k) Y (k) Cx(k) Du (k)
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
离散时间线性时变系统 X (k 1) G(k)x(k) H (k)u(k ) Y (k) C(k)x(k) D(k)u(k)
cM
J
ce La f
J
ia
1
La 0
e
0
1ia
上式可表为形如 X AX Bu Y CX Du
Ra
i f const
J,F
La
2/7,6/50
连续时间线性系统的状态空间描述 动态系统的结构
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
u1
yq
外部描述常被称作为输出—输入描述
u2
x1, x2 , , xn
y2
up
yq
例如.对SISO线性定常系统:时间域的外部描述:
y(n) an1 y(n1) a1 y(1) a0 y bn1u(n1) b1u (1) b0u
复频率域描述即传递函数描述
2/2,13/50
2.4 由系统输入输出描述导出状态空间描述
由输入输出描述导出状态空间描述
5/7,9/50
离散时间线性系统的状态空间描述 状态空间描述形式 离散时间线性时不变系统 X (k 1) Gx(k) Hu (k) Y (k) Cx(k) Du (k)
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
离散时间线性时变系统 X (k 1) G(k)x(k) H (k)u(k ) Y (k) C(k)x(k) D(k)u(k)
cM
J
ce La f
J
ia
1
La 0
e
0
1ia
上式可表为形如 X AX Bu Y CX Du
Ra
i f const
J,F
La
2/7,6/50
连续时间线性系统的状态空间描述 动态系统的结构
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
u1
yq
外部描述常被称作为输出—输入描述
u2
x1, x2 , , xn
y2
up
yq
例如.对SISO线性定常系统:时间域的外部描述:
y(n) an1 y(n1) a1 y(1) a0 y bn1u(n1) b1u (1) b0u
复频率域描述即传递函数描述
线性系统理论全PPT课件
17550机电系统状态空间描述的列写示例dtdi上式可表为形如ducxbuax27650连续时间线性系统的状态空间描述动态系统的结构动力学部件输出部件连续时间线性系统的状态空间描述线性时不变系统ducxbuax37750连续时间线性系统的方块图47850人口分布问题状态空间描述的列写示例假设某个国家城市人口为102的乡村人口迁移去城市整个国家的人口的自然增长率为1设k为离散时间变量城市人口迁移乡村而一个单位负控制措施会导致5x1010051005亦可表为57950离散时间线性系统的状态空间描述状态空间描述形式离散时间线性时不变系统671050离散系统状态空间描述的特点
若f(x,u,t),g(x,u,t)的全部组成元为x、u的 线性函数,该系统称为线性系统
A(t ) X B(t )u X 对于线性系统 Y C (t ) X D(t )u
1/ቤተ መጻሕፍቲ ባይዱ,12/50
若f(x,u,t),g(x,u,t)的全部或至少一个 组成元素为x、u的非线性函数,该系 统称为非线性系统 。 非线性系统可以用泰勒展 开方法化为线性系统。
线性系统理论
电子信息学院
1
1、线性系统理论的研究对象 • 系统是系统理论研究的对象； • 系统是由相互关联和相互作用的若干组 成部分按一定规律组合而成的具有特定 功能的整体； • 系统模型，是对系统或其简化形式的一 种描述；
2
• 动态系统---动力学系统 • 动力学系统--可用一组微分方程或差分方程 来描述； • 系统的线性性和非线性性; • 当数学方程具有线性属性时，相应的系统
5
• 建立数学模型 • 数学模型的基本要素是变量、参量、常数 和它们之间的关系 • 变量：状态变量、输入变量、输出变量、
扰动变量
若f(x,u,t),g(x,u,t)的全部组成元为x、u的 线性函数,该系统称为线性系统
A(t ) X B(t )u X 对于线性系统 Y C (t ) X D(t )u
1/ቤተ መጻሕፍቲ ባይዱ,12/50
若f(x,u,t),g(x,u,t)的全部或至少一个 组成元素为x、u的非线性函数,该系 统称为非线性系统 。 非线性系统可以用泰勒展 开方法化为线性系统。
线性系统理论
电子信息学院
1
1、线性系统理论的研究对象 • 系统是系统理论研究的对象； • 系统是由相互关联和相互作用的若干组 成部分按一定规律组合而成的具有特定 功能的整体； • 系统模型，是对系统或其简化形式的一 种描述；
2
• 动态系统---动力学系统 • 动力学系统--可用一组微分方程或差分方程 来描述； • 系统的线性性和非线性性; • 当数学方程具有线性属性时，相应的系统
5
• 建立数学模型 • 数学模型的基本要素是变量、参量、常数 和它们之间的关系 • 变量：状态变量、输入变量、输出变量、
扰动变量
线性系统理论-郑大钟(第二版)PPT课件
0
0
0
1
0
a0 a1 a2 an1 1
xn1 xn
y (b0 bna0 ), (b1 bna1), , (bn1 bnan1) x bnu
确定性系统和不确定性系统
称一个系统为确定性系统,当且仅当不论是系统的特性和参数还是系统的 输入和扰动,都是随时间按确定的规律而变化的.
称一个动态系统为不确定性系统,或者系统的特性和参数中包含某种不确 定性,或者作用于系统的输入和扰动是随机变量
2.4 由系统输入输出描述导出状态空间描述
由输入输出描述导出状态空间描述
状态空间描述形式
离散时间线性时不变系统 x(k 1) Gx(k ) Hu(k ) y(k) Cx(k) Du(k)
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
离散时间线性时变系统 x(k 1) G(k) x(k) H (k)u(k) y(k) C(k) x(k) D(k)u(k)
选择状态变量
uR2
R2 R1 R2
R1R2 R1 R2
uc
iL
R2 R1 R2
e
2.2 线性系统的状态空间描述
uc
iL
(R1
1
R2 R1
)C
L(R1 R2 )
(
R1
R1 R2 R1R2
)C
uc
iL
(R1
1
R2 R2
)C
e
L(R1 R2 )
多变量频域方法
一是频域方法
二是多项式矩阵方法
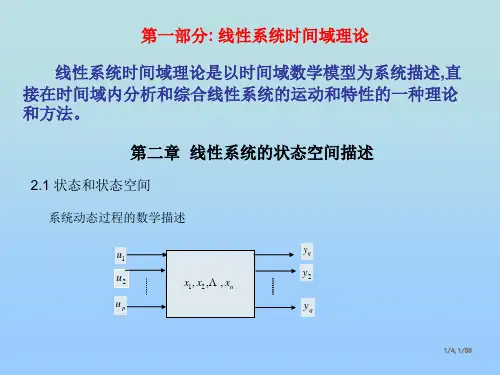
第一部分: 线性系统时间域理论
线性系统时间域理论是以时间域数学模型为系统描述,直接在时间域内分析 和综合线性系统的运动和特性的一种理论和方法
线性系统理论课件1
单变量定常系统
x(t ) Ax(t ) bu(t ), x(t 0 ) x0 , y (t ) cx(t ), t 0.
常用三元组{A,b,c}表示.
上面定常系统的拉氏变换为:
X ( s) ( sI A) 1 x(0 ) ( sI A) 1 bU ( s),
集合的积: 设A1 ,A2 ,…,
有D中唯一一个元素d与之对应, 则称ƒ是集合
A1A2…An 到 集 合 D 的 一 个 映 射 ; d 称 为 (a1,a2,…,an)在映射ƒ之下的像, (a1,a2,…,an) 称
为d在映射ƒ之下的原像.
ƒ : A1A2…AnD
or
ƒ : (a1,a2,…,an) d
线性控制系统教程
张志方 孙常胜 编著 科学出版社
预备知识
-函数 把具有下列性质的量称为-函数，记为(t)
t 0,
t 0,
(1)
t dt 1.
-函数的导数
t
d t t t lim 0 dt
设u(t)为定义在实轴R上的连续函数，则
将f(t)的定义域扩充成在t=0的任一邻域内也有定义， 并把积分 F ( s) f t e st dt 0 称为L -变换
L [ (t )] L [
(k )
0
t e st dt 1
0
(t )]
( k ) t e st dt
t
f ( , x)d
t0
t
t0
f ( , x)d x0 (t 0 )
线性系统理论PPT-郑大钟(第二版)
系统具有如下3个基本特征:
(1)整体性
1.结构上的整体性 2.系统行为和功能由整体 所决定
(2)抽象性
作为系统控制理论的研 究对象，系统常常抽去 了具体系统的物理，自 然和社会含义，而把它 抽象为一个一般意义下 的系统而加以研究。
(3)相对性
在系统的定义 中, 所谓“系统” 和“部分”这 种称谓具有相 对属性。
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
线性时不变系统
x Ax Bu
y
Cx
Du
线性时变系统
x A(t)x B(t)u
y
C (t ) x
D(t
)u
连续时间线性系统的方块图
x A(t)x B(t)u
对于单输入,单输出线性时不变系统,其微分方程描述
y (n) an1 y (n1) a1 y (1) a0 y bmu (m) bm1u (m1) b1u (1) b0u
H (k )
单位延迟
C(k)
y(k)
u(k)
G(k)
2.3.连续变量动态系统按状态空间描述的分类
线性系统和非线性系统
设系统的状态空间描述为 x f ( x,u, t) y g( x,u, t)
向量函数
f1(x,u,t)
g1(x,u,t)
f
(
x,u,
t
)
f
2
(
x,u,
e
线性系统理论全课件
内部描述则是系统的一种完全的描述,能够完全反映系统的所有动力学特性.
2/4,2/50
(3) 状态向量：以系统的 个n 独立状态变量
x t , L, x t 作为分量的向量，即
1
n
x t x t , L, x t T .
1
n
(4) 状态空间: 以状态变量 x t ,K , x t 为坐
1
n
标轴构成的 n 维空间。
际上存在无穷多种方案. (3)等价性：两个状态向量之间只差一个非奇异
变换.
(4)现实性：状态变量通常取为涵义明确的物理量. (5)抽象性：状态变量可以没有直观的物理意义. 2.1.2 状态空间表达式的一般形式： (1)线性系统
x&t At x t B t u t
yt Ct xt Dtut
g(s)
Y (s) U (s)
bm s m bm1s m1 b1s1 s n an1s n1 a1s
b0 a0
其对应的状态空间描述可按如下两类情况导出
(1)m=n,即系统为真情形
0 1 0 0 0
X 0
0
0 x u
0
0
0
1
0
a0 a1 a2 an1 1
bn1s n1 b1s b0 an1s n1 a1s a0
(2)系统的内部描述
状态空间描述是系统内部描述的基本形式,需要由两个数学方程表征,—— 状态方 程和输出方程
(3)外部描述和内部描述的比较
一般的说外部描述只是对系统的一种不完全描述,不能反映黑箱内部结构的不 能控或不能观测的部分.
x1 y x2 y xn y(n1)
6/18,19/50
4/18,17/50
写成矩阵形式： x1
2/4,2/50
(3) 状态向量：以系统的 个n 独立状态变量
x t , L, x t 作为分量的向量，即
1
n
x t x t , L, x t T .
1
n
(4) 状态空间: 以状态变量 x t ,K , x t 为坐
1
n
标轴构成的 n 维空间。
际上存在无穷多种方案. (3)等价性：两个状态向量之间只差一个非奇异
变换.
(4)现实性：状态变量通常取为涵义明确的物理量. (5)抽象性：状态变量可以没有直观的物理意义. 2.1.2 状态空间表达式的一般形式： (1)线性系统
x&t At x t B t u t
yt Ct xt Dtut
g(s)
Y (s) U (s)
bm s m bm1s m1 b1s1 s n an1s n1 a1s
b0 a0
其对应的状态空间描述可按如下两类情况导出
(1)m=n,即系统为真情形
0 1 0 0 0
X 0
0
0 x u
0
0
0
1
0
a0 a1 a2 an1 1
bn1s n1 b1s b0 an1s n1 a1s a0
(2)系统的内部描述
状态空间描述是系统内部描述的基本形式,需要由两个数学方程表征,—— 状态方 程和输出方程
(3)外部描述和内部描述的比较
一般的说外部描述只是对系统的一种不完全描述,不能反映黑箱内部结构的不 能控或不能观测的部分.
x1 y x2 y xn y(n1)
6/18,19/50
4/18,17/50
写成矩阵形式： x1
线性系统理论(郑大忠)第2章
基此，选取电容端电压uc和流经电感的电流iL作 为电路状态变量组。 显然，uc和iL必满足状态变量定义中所指出的线 性无关极大组属性。
2013/11/22
线性系统理论
23
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
R1 C + uC iL R2 iC + -
由此，得 和，
X QX
X PX PQX
X QX QPX
显然， PQ QP I
即矩阵P和Q互逆。
结论：系统的任意选取的两个状态X和 X 之间 为线性非奇异变换的关系。
2013/11/22
线性系统理论
18
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
2013/11/22
线性系统理论
2
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
一、状态和状态空间
1、系统动态过程的两类数学描述 2、状态和状态空间的定义
2013/11/22
线性系统理论
3
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、系统动态过程的两类数学描述
线性系统理论
21
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
电路系统如图所示，设各组元件的参数值为已 知，取电压源e(t)为输入变量，电阻R2端电压uR2为输 出变量。 C
R1 iC + e (t ) -
L
+ uC iL R2
2013/11/22
线性系统理论
23
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
R1 C + uC iL R2 iC + -
由此，得 和，
X QX
X PX PQX
X QX QPX
显然， PQ QP I
即矩阵P和Q互逆。
结论：系统的任意选取的两个状态X和 X 之间 为线性非奇异变换的关系。
2013/11/22
线性系统理论
18
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
2013/11/22
线性系统理论
2
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
一、状态和状态空间
1、系统动态过程的两类数学描述 2、状态和状态空间的定义
2013/11/22
线性系统理论
3
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、系统动态过程的两类数学描述
线性系统理论
21
第2章 线性系统的状态空间描述
广东工业大学 自动化学院 自动控制系 陈玮
1、电路系统状态空间描述的列写示例
电路系统如图所示，设各组元件的参数值为已 知，取电压源e(t)为输入变量，电阻R2端电压uR2为输 出变量。 C
R1 iC + e (t ) -
L
+ uC iL R2
线性系统理论课件
3
系统的线性性和非线性性 线性系统的分类 定常系统：参数不随时间变化 时变系统；参数是时间t 的函数
4
2、线性系统理论的主要任务 主要研究线性系统状态的运动规律和改变
这种运动规律的可能性和方法，建立和揭示 系统结构、参数、行为和性能间的确定的和 定量的关系。 分析问题：研究系统运动规律 综合问题：研究改变运动规律的可能性和方法
9
线性系统理论的主要学派 （1）线性系统的状态空间法 （2）线性系统的几何理论 （3）线性系统的代数理论 （4）多变量频域方法
10
7
3、线性系统理论的发展过程 20世纪50年代：古典线性系统理论已发展成熟， 传递函数，频率响应法 不足：难于处理多输入—多输出系统 20世纪60年代：现代系统与控制理论 状态空间法 解决：多输入—多输出系统
系统与控制理论 线性系统理论 最优控制理论 最优估计理论 随机控制理论 非线性系统理论 大系统理论
5
建立数学模型 数学模型的基本要素是变量、参量、常数 和它们之间的关系 变量：状态变量、输入变量、输出变量、 扰动变量 参量：系统的参数或表征系统性能的参数 常数：不随时间改变的参数
6
时间域模型：微分方程组或差分方程组 可用于常系数系统 和变系数系统
频率域模型：用传递函数、频率响应 适用于常系数系统
线性系统理论课件
1
第一章 绪论
1、线性系统理论的研究对象 线性系统，是一种理想化的模型； 可以用线性微分方程或差分方程来描述； 系统是由相互关联和相互作用的若干组成部 分按一定规律组合而成的具有特定功能的整 体； 动态系统---动力学系统
2
动力学系统--可用一组微分方程或差分方程 来描述； 当数学方程具有线性属性时，相应的系统 为线性系统； 线性系统满足叠加性； 线性系统可以用数学变换（付里叶变换， 拉普拉斯变换）和线性代数
系统的线性性和非线性性 线性系统的分类 定常系统：参数不随时间变化 时变系统；参数是时间t 的函数
4
2、线性系统理论的主要任务 主要研究线性系统状态的运动规律和改变
这种运动规律的可能性和方法，建立和揭示 系统结构、参数、行为和性能间的确定的和 定量的关系。 分析问题：研究系统运动规律 综合问题：研究改变运动规律的可能性和方法
9
线性系统理论的主要学派 （1）线性系统的状态空间法 （2）线性系统的几何理论 （3）线性系统的代数理论 （4）多变量频域方法
10
7
3、线性系统理论的发展过程 20世纪50年代：古典线性系统理论已发展成熟， 传递函数，频率响应法 不足：难于处理多输入—多输出系统 20世纪60年代：现代系统与控制理论 状态空间法 解决：多输入—多输出系统
系统与控制理论 线性系统理论 最优控制理论 最优估计理论 随机控制理论 非线性系统理论 大系统理论
5
建立数学模型 数学模型的基本要素是变量、参量、常数 和它们之间的关系 变量：状态变量、输入变量、输出变量、 扰动变量 参量：系统的参数或表征系统性能的参数 常数：不随时间改变的参数
6
时间域模型：微分方程组或差分方程组 可用于常系数系统 和变系数系统
频率域模型：用传递函数、频率响应 适用于常系数系统
线性系统理论课件
1
第一章 绪论
1、线性系统理论的研究对象 线性系统，是一种理想化的模型； 可以用线性微分方程或差分方程来描述； 系统是由相互关联和相互作用的若干组成部 分按一定规律组合而成的具有特定功能的整 体； 动态系统---动力学系统
2
动力学系统--可用一组微分方程或差分方程 来描述； 当数学方程具有线性属性时，相应的系统 为线性系统； 线性系统满足叠加性； 线性系统可以用数学变换（付里叶变换， 拉普拉斯变换）和线性代数
线性系统理论全PPT课件-309
设系统的状态空间描述为 x f (x, u, t) y g(x, u, t)
向量函数
f1(x,u,t)
g1(x,u,t)
f
(
x,
u,
t
)
f
2
(
x,
u,
t
)，g
(
x,
u,
t)
g
2
(
x,
u,
t
)
f
n
(
x,
u,
t
)
gq
(
x,
u,
t
)
若f(x,u,t),g(x,u,t)的全部或至少一个组 成元素为x、u的非线性函数,该系统 称为非线性系统 。
J,F
La
2/7,6/50
连续时间线性系统的状态空间描述 动态系统的结构
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
线性时不变系统
X Y
AX Bu CX Du
线性时变系统
X A(t)X B(t)u Y C(t)X D(t)u
3/7,7/50
y2
up
yq
1/4,1/50
(1).系统的外部描述
u1
yq
外部描述常被称作为输出—输入描述
u2
x1, x2 ,, xn
y2
up
yq
例如.对SISO线性定常系统:时间域的外部描述:
y(n) an1 y(n1) a1 y(1) a0 y bn1u(n1) b1u (1) b0u
复频率域描述即传递函数描述
线性系统理论研究对象是 (线性的)模型系统，不 是物理系统。
线性系统理论(郑大钟第二版)第3章
x (t ) = e At x (0) = diag (e λ1t , eλ2t ,L , e λnt ) x (0)
x (t ) = Px = [ν 1 ν 2 L ν n ]diag (e λ1t , e λ2t ,L , eλnt ) x (0) = [ν 1eλ1t ν 2 eλ2t L ν n eλn t ] x (0)
3. Φ (t1 ± t2 ) = Φ (t1 ) ⋅Φ (±t2 ) = Φ (±t2 ) ⋅Φ (t1 )
(Φ (t )) k = Φ (kt )
1 2 2 Ak k 1 2 2 Ak k t1 + L)( I + At2 + A t2 + L + t2 + L) Φ (t1 ) ⋅Φ (t2 ) = ( I + At1 + A t1 + L + k! k! 2 2 2 3 t2 2 1 2 1 2 t2 3 2 t1 3 t1 = I + A(t1 + t2 ) + A ( + t1t2 + ) + A ( + t1 t2 + t1t2 + ) + L 2! 2! 3! 2! 2! 3! 1 1 = I + A(t1 + t2 ) + A2 (t1 + t2 ) 2 + A3 (t1 + t2 )3 + L = Φ (t1 + t2 ) 2! 3!
= ( I + At + L +
Ak −1 k −1 t + L) A = Φ (t ) ⋅ A (k − 1)!
k
2. Φ (0) = I
将 t = 0代入 Φ (t ) = I + At + 1 A2t 2 + L + A t k + L 即可证。
x (t ) = Px = [ν 1 ν 2 L ν n ]diag (e λ1t , e λ2t ,L , eλnt ) x (0) = [ν 1eλ1t ν 2 eλ2t L ν n eλn t ] x (0)
3. Φ (t1 ± t2 ) = Φ (t1 ) ⋅Φ (±t2 ) = Φ (±t2 ) ⋅Φ (t1 )
(Φ (t )) k = Φ (kt )
1 2 2 Ak k 1 2 2 Ak k t1 + L)( I + At2 + A t2 + L + t2 + L) Φ (t1 ) ⋅Φ (t2 ) = ( I + At1 + A t1 + L + k! k! 2 2 2 3 t2 2 1 2 1 2 t2 3 2 t1 3 t1 = I + A(t1 + t2 ) + A ( + t1t2 + ) + A ( + t1 t2 + t1t2 + ) + L 2! 2! 3! 2! 2! 3! 1 1 = I + A(t1 + t2 ) + A2 (t1 + t2 ) 2 + A3 (t1 + t2 )3 + L = Φ (t1 + t2 ) 2! 3!
= ( I + At + L +
Ak −1 k −1 t + L) A = Φ (t ) ⋅ A (k − 1)!
k
2. Φ (0) = I
将 t = 0代入 Φ (t ) = I + At + 1 A2t 2 + L + A t k + L 即可证。
线性系统理论全PPT课件
详细描述
稳定性是线性系统的一个重要性质，它决定了系统在受到外部干扰后能否恢复到原始状态。如果一个系统是稳定 的，那么当外部干扰消失后，系统将逐渐恢复到原始状态。而不稳定的系统则会持续偏离原始状态。
03
线性系统的数学描述
状态空间模型
01
定义
状态空间模型是一种描述线性动态系统的方法，它通过状态变量和输入
航空航天控制系统的线性化分析
线性化分析
在航空航天控制系统中，由于非线性特性较强，通常需要进行线性化分析以简化系统模 型。通过线性化分析，可以近似描述系统的动态行为，为控制系统设计提供基础。
线性化方法
常用的线性化方法包括泰勒级数展开、状态空间平均法和庞德里亚金方法等。这些方法 可以将非线性系统转化为线性系统，以便于应用线性系统理论进行控制设计。
线性系统理论全ppt课件
• 线性系统理论概述 • 线性系统的基本性质 • 线性系统的数学描述 • 线性系统的分析方法 • 线性系统的设计方法 • 线性系统的应用实例
01
线性系统理论概述
定义与特点
定义
线性系统理论是研究线性系统的 数学分支，主要研究线性系统的 动态行为和性能。
特点
线性系统具有叠加性、时不变性 和因果性等特性，这些特性使得 线性系统理论在控制工程、信号 处理等领域具有广泛的应用。
线性系统的动态性能分析
动态性能指标
描述线性系统动态特性的性能指 标，如超调量、调节时间、振荡
频率等。
状态空间分析法
通过建立和解决线性系统的状态方 程来分析系统的动态性能，可以得 到系统的状态轨迹和响应曲线。
频率域分析法
通过分析线性系统的频率特性来描 述系统的动态性能，可以得到系统 的频率响应曲线和稳定性边界。
稳定性是线性系统的一个重要性质，它决定了系统在受到外部干扰后能否恢复到原始状态。如果一个系统是稳定 的，那么当外部干扰消失后，系统将逐渐恢复到原始状态。而不稳定的系统则会持续偏离原始状态。
03
线性系统的数学描述
状态空间模型
01
定义
状态空间模型是一种描述线性动态系统的方法，它通过状态变量和输入
航空航天控制系统的线性化分析
线性化分析
在航空航天控制系统中，由于非线性特性较强，通常需要进行线性化分析以简化系统模 型。通过线性化分析，可以近似描述系统的动态行为，为控制系统设计提供基础。
线性化方法
常用的线性化方法包括泰勒级数展开、状态空间平均法和庞德里亚金方法等。这些方法 可以将非线性系统转化为线性系统，以便于应用线性系统理论进行控制设计。
线性系统理论全ppt课件
• 线性系统理论概述 • 线性系统的基本性质 • 线性系统的数学描述 • 线性系统的分析方法 • 线性系统的设计方法 • 线性系统的应用实例
01
线性系统理论概述
定义与特点
定义
线性系统理论是研究线性系统的 数学分支，主要研究线性系统的 动态行为和性能。
特点
线性系统具有叠加性、时不变性 和因果性等特性，这些特性使得 线性系统理论在控制工程、信号 处理等领域具有广泛的应用。
线性系统的动态性能分析
动态性能指标
描述线性系统动态特性的性能指 标，如超调量、调节时间、振荡
频率等。
状态空间分析法
通过建立和解决线性系统的状态方 程来分析系统的动态性能，可以得 到系统的状态轨迹和响应曲线。
频率域分析法
通过分析线性系统的频率特性来描 述系统的动态性能，可以得到系统 的频率响应曲线和稳定性边界。
线性系统理论课件
mn ij
定义: 矩阵 A a R
ij
mn
的行秩或列秩称为矩阵A的秩
记为rank(A)。 显而易见，对于矩阵
A aij Rmn
而言，有
rank(A)≤min{m,n}
当rank(A)=m时,我们称A为行满秩矩阵; 当rank(A)=n时,我们称A为列满秩矩阵; 当rank(A)＜min{m,n}时，我们称A为降秩矩阵，
x1 x 2 x x3
xi R, i 1,2,, n
全体的集合。设 x, y R ,在Rn中规定加法和数乘为
n
x1 y1 x y 2 2 x y x y n n
ax1 ax 2 ax axn
与初等行变换矩阵相对应的初等列变换矩阵分别
记之为 Qi , j , Qi c 和 Qi, j
等价是多项式矩阵之间的一种关系，这种关系显 然具有下述三个性质：
反身性，即每一个多项式矩阵均与自身等价。
对称性，即A(s)与B(s)等价，可推出B(s)与A(s)等价。
传递性，即A(s)与B(s)等价，B(s)与C(s)等价，可推出
1
时,称T为由V1到V2的线性变换或线性算子。V1称为T 的定义域。若令 TV Tv v V V 则TV1也是一个线性 空间，它被称为T的值域空间，记为ImT=TV1。在 V1=V2时，称他为V1上的线性变换。
1 1 1 1 2
二、矩阵代数中的几个结果 定义： 矩阵 A a R 中列向量的最大无关组的个数 称为A的列秩; 其行向量的最大无关组的个数称为A的 行秩。
x y yx ( x y) z x ( y z ) 1x x k (lx) (kl) x
定义: 矩阵 A a R
ij
mn
的行秩或列秩称为矩阵A的秩
记为rank(A)。 显而易见，对于矩阵
A aij Rmn
而言，有
rank(A)≤min{m,n}
当rank(A)=m时,我们称A为行满秩矩阵; 当rank(A)=n时,我们称A为列满秩矩阵; 当rank(A)＜min{m,n}时，我们称A为降秩矩阵，
x1 x 2 x x3
xi R, i 1,2,, n
全体的集合。设 x, y R ,在Rn中规定加法和数乘为
n
x1 y1 x y 2 2 x y x y n n
ax1 ax 2 ax axn
与初等行变换矩阵相对应的初等列变换矩阵分别
记之为 Qi , j , Qi c 和 Qi, j
等价是多项式矩阵之间的一种关系，这种关系显 然具有下述三个性质：
反身性，即每一个多项式矩阵均与自身等价。
对称性，即A(s)与B(s)等价，可推出B(s)与A(s)等价。
传递性，即A(s)与B(s)等价，B(s)与C(s)等价，可推出
1
时,称T为由V1到V2的线性变换或线性算子。V1称为T 的定义域。若令 TV Tv v V V 则TV1也是一个线性 空间，它被称为T的值域空间，记为ImT=TV1。在 V1=V2时，称他为V1上的线性变换。
1 1 1 1 2
二、矩阵代数中的几个结果 定义： 矩阵 A a R 中列向量的最大无关组的个数 称为A的列秩; 其行向量的最大无关组的个数称为A的 行秩。
x y yx ( x y) z x ( y z ) 1x x k (lx) (kl) x
线性系统理论ppt课件
第五章 线性系统理论
第一节 线性关系
数学模型是由描述系统的变量和常量 构成的数学表达式，建立数学模型后，首 先要区分系统是线性还是非线性的。
以前的科学研究主要对象是线性系统， 而今正转向非线性系统，并且未来科学的 本质上是非线性科学
线性与非线性原本就是一对数学关系，用以区 分不同变量之间的两种基本的相互关系。
a11x1+a12x2+a13x3≤b1 a21x1+a22x2+a23x3≤b2
…… 它表示变量x1，x2，x3只能在给定的若干个代数 关系内变化，并且每个变量的变化都影响另 外两个变量的变化。
以上所讲的变量之间的关系都是静态相互 关系，都是用函数和代数方程进行描述。
实际上的动态过程中的诸变量的相互依存关 系要丰富的多。其数学表达式中将出现微分、 差分、积分等描述动态特性的项，反映这些 动态量对各个变量的依存关系。
xn
对于变系统系统，系统的系数为t的函数aij(t),系数矩阵为 A(t)
因此，对于最简单的一维系统就有：
x=ax
对于二维系统，有：
x=a11 x+a12 y y=a21 x+a22 y
以此类推至多维线性系统。
矩阵式描述对象整体特性的数学工具之一，方程给定后，借助代数 方法，通过分析系数矩阵，可以全面的了解系统的动态行为。
∇= a11a22 − a12a21
"鞍点"在三维空间中定义（图中的坐标原点），经过"鞍 点"平行于z轴的平面束代表无穷多个发展方向，每个平 面与曲面相交得到对应的曲线，代表该方向的发展轨迹。 不同的方向有的上升，有的下降。影射汽车市场，诸如 二手车置换的兴旺、汽车金融的产生、弱者被淘汰出局、 汽车出口呈上升态势、自主品牌的崛起、技术创新成企 业竞争王牌……不同的方面将有不同的发展。
第一节 线性关系
数学模型是由描述系统的变量和常量 构成的数学表达式，建立数学模型后，首 先要区分系统是线性还是非线性的。
以前的科学研究主要对象是线性系统， 而今正转向非线性系统，并且未来科学的 本质上是非线性科学
线性与非线性原本就是一对数学关系，用以区 分不同变量之间的两种基本的相互关系。
a11x1+a12x2+a13x3≤b1 a21x1+a22x2+a23x3≤b2
…… 它表示变量x1，x2，x3只能在给定的若干个代数 关系内变化，并且每个变量的变化都影响另 外两个变量的变化。
以上所讲的变量之间的关系都是静态相互 关系，都是用函数和代数方程进行描述。
实际上的动态过程中的诸变量的相互依存关 系要丰富的多。其数学表达式中将出现微分、 差分、积分等描述动态特性的项，反映这些 动态量对各个变量的依存关系。
xn
对于变系统系统，系统的系数为t的函数aij(t),系数矩阵为 A(t)
因此，对于最简单的一维系统就有：
x=ax
对于二维系统，有：
x=a11 x+a12 y y=a21 x+a22 y
以此类推至多维线性系统。
矩阵式描述对象整体特性的数学工具之一，方程给定后，借助代数 方法，通过分析系数矩阵，可以全面的了解系统的动态行为。
∇= a11a22 − a12a21
"鞍点"在三维空间中定义（图中的坐标原点），经过"鞍 点"平行于z轴的平面束代表无穷多个发展方向，每个平 面与曲面相交得到对应的曲线，代表该方向的发展轨迹。 不同的方向有的上升，有的下降。影射汽车市场，诸如 二手车置换的兴旺、汽车金融的产生、弱者被淘汰出局、 汽车出口呈上升态势、自主品牌的崛起、技术创新成企 业竞争王牌……不同的方面将有不同的发展。