matlab信道仿真经典源程序
基于MATLAB的移动通信信道建模与仿真精简版范文

基于MATLAB的移动通信信道建模与仿真基于MATLAB的移动通信信道建模与仿真引言移动通信是现代社会中必不可少的一部分,而移动通信信道的建模与仿真对于无线通信系统的设计与性能分析具有重要的意义。
MATLAB作为一种强大的数学建模与仿真工具,能够方便地实现移动通信信道的建模与仿真。
信道建模移动通信信道可以被看作是一个多径传播的环境,其中包含了直达信号、反射信号和散射信号等多个路径。
为了更好地描述信道的传输特性,常用的信道模型有以下几种:AWGN信道模型:假设信道中只有加性高斯噪声,是最简单的信道模型。
Rayleigh信道模型:假设信道中存在多个随机相位、高斯分布的反射路径信号,适用于城市等复杂环境。
Rician信道模型:假设信道中除了多个反射路径信号外,还存在一个主导的直达路径信号,适用于开阔区域。
信道仿真利用MATLAB进行信道仿真可以通过以下步骤实现:1. 发送信号:根据通信系统的要求,所需的发送信号。
2. 信道建模:选择合适的信道模型,并根据信道参数进行信道建模。
3. 信道传输:将发送信号通过信道进行传输,得到接收信号。
4. 接收信号处理:根据发送信号和接收信号的差异计算误码率、信号功率等性能指标。
示例代码以下是一个基于MATLAB的AWGN信道模型的移动通信信道仿真示例代码:matlab% AWGN信道模型的移动通信信道仿真示例代码SNR_dB = 10; % 信噪比(单位:dB)EbNo_dB = SNR_dB + 10 log10(1/2); % 能量比率(单位:dB)EbNo = 10^(EbNo_dB / 10); % 能量比率(单位:线性)N0 = 1 / (2 EbNo); % 噪声功率谱密度N = 1000000; % 发送信号的长度transmit_signal = randi([0, 1], 1, N); % 随机发送信号(0/1序列)receive_signal = transmit_signal + sqrt(N0/2) randn(1, N); % 添加噪声基于MATLAB的移动通信信道建模与仿真是一种快速并且有效的方法,能够帮助我们更好地理解和分析移动通信信道的性能。
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明书
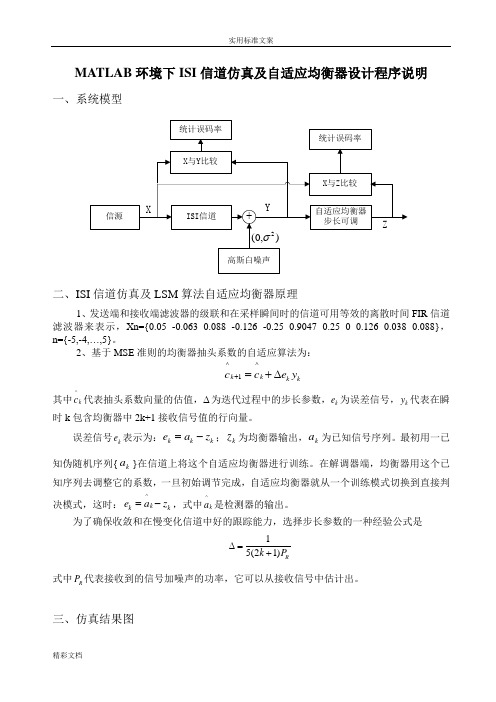
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示,Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088},n={-5,-4,…,5}。
2、基于MSE 准则的均衡器抽头系数的自适应算法为:^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值,∆为迭代过程中的步长参数,k e 为误差信号,k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为:k k k e a z =-;k z 为均衡器输出,k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端,均衡器用这个已知序列去调整它的系数,一旦初始调节完成,自适应均衡器就从一个训练模式切换到直接判决模式,这时:^k k k e a z =-,式中^k a 是检测器的输出。
为了确保收敛和在慢变化信道中好的跟踪能力,选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率,它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出,在信噪比逐渐增大的过程中,未经均衡器均衡的差错率没有明显改善,可知系统中始终存在码间干扰造成的误码;经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下,均衡器均衡之后的误码率并没有明显改善,甚至没有未均衡的差错率低,这主要是因为噪声为随机信号,功率大时对源信号影响较大,而且均衡器不易跟踪;当我们把均衡器的步长调低后,跟踪能力增强,差错率降低。
附源程序代码:main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_in_dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR_in_dB)[y,len]=channel(info,SNR_in_dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信号码元if (y(i)<0), %判决译码elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码,统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡,得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器,并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后,误码率结果图hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器,并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后,误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11',...'经自适应均衡器均衡,步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数,则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数,可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_actual_isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积%需要指出,此时码元序列长度变为N+len-1,译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss.m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参,则均方为0,标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数,则标准差为输入实参,均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lms_equalizer.m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元,一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
MATLAB仿真实例

MATLAB仿真实例通信原理是指传输信息的原理和方法。
MATLAB可以用于实现各种通信原理的仿真,包括信号的调制、发送、接收、解调等过程。
下面我将介绍一个基于MATLAB的通信原理仿真实例。
本实例以频率调制通信原理为基础,以调频调制(FM)为例进行仿真。
1.首先定义模拟信号源,生成一个基带信号。
例如,我们可以选择一个正弦波信号作为基带信号,其频率为$f_m$。
2.接下来,我们需要将基带信号进行调频调制。
在调频调制过程中,我们将基带信号的频率进行调制,生成载频为$f_c$的调制信号。
3. 在MATLAB中,我们可以使用freqmod函数来进行调频调制。
该函数接受基带信号、载频和调制指数作为输入参数,并返回调制信号。
4.在得到调制信号后,我们可以进行发送模拟。
发送模拟是指将调制信号通过信道传输,可以简单地将信号存储为一个信道矩阵。
5. 在接收端,我们需要对接收到的信号进行解调,以恢复基带信号。
在调频调制中,我们可以使用freqdemod函数进行解调。
该函数接受解调信号、载频和调制指数作为输入参数,并返回解调后的信号。
6.最后,我们可以将解调信号与原始信号进行比较,计算它们之间的误差。
可以使用均方根误差(RMSE)作为误差度量指标。
通过以上过程,我们可以完成一个简单的基于MATLAB的调频调制仿真。
为了使仿真更贴近实际通信场景,我们还可以添加信道噪声等因素。
例如,我们可以在发送模拟过程中,向信道矩阵中添加高斯白噪声。
这样可以更真实地模拟信号在传输过程中受到干扰和噪声的情况。
通过以上步骤,我们可以利用MATLAB进行通信原理的仿真实践。
这个实例不仅可以帮助我们加深理解通信原理的基本概念和过程,还可以通过实际操作和仿真结果进行验证和验证。
总之,MATLAB是一个非常强大的工具,可以用于各种通信原理的仿真。
通过利用MATLAB进行仿真实践,我们可以更深入地理解通信原理的基本原理和过程,提高我们的理论水平和实践能力。
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明
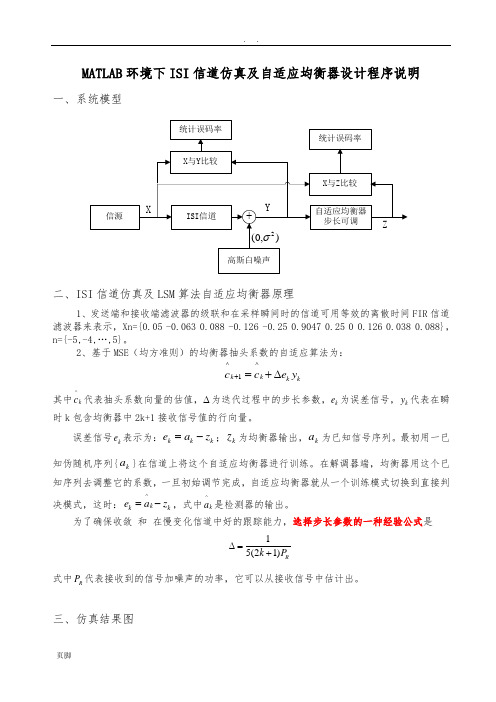
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示,Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088},n={-5,-4,…,5}。
2、基于MSE (均方准则)的均衡器抽头系数的自适应算法为:^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值,∆为迭代过程中的步长参数,k e 为误差信号,k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为:k k k e a z =-;k z 为均衡器输出,k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端,均衡器用这个已知序列去调整它的系数,一旦初始调节完成,自适应均衡器就从一个训练模式切换到直接判决模式,这时:^k k k e a z =-,式中^k a 是检测器的输出。
为了确保收敛 和 在慢变化信道中好的跟踪能力,选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率,它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出,在信噪比逐渐增大的过程中,未经均衡器均衡的差错率没有明显改善,可知系统中始终存在码间干扰造成的误码;经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下,均衡器均衡之后的误码率并没有明显改善,甚至没有未均衡的差错率低,这主要是因为噪声为随机信号,功率大时对源信号影响较大,而且均衡器不易跟踪;当我们把均衡器的步长调低后,跟踪能力增强,差错率降低。
附源程序代码:main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_ in _dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR _in_ dB)[y, len ]=channel(info, SNR _in _dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信元if (y(i)<0), %判决译码decis=-1;elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码,统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡,得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器,并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR _in _ dB, Pe ,'blacko-'); %自适应均衡器均衡之后,误码率结果图 hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器,并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后,误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11',...'经自适应均衡器均衡,步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数,则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数,可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_ actual _isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积%需要指出,此时码元序列长度变为N+len-1,译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss . m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参,则均方为0,标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数,则标准差为输入实参,均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lm _equalizer .m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元,一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
信道接收机matlab仿真

信道接收机matlab仿真1.信道化接收机MATLAB仿真代码:clc;clear;f1=2000;f2=5000;%测频范围f=input('输入待测频率 (MHz) ');if f>=f1&&f<=f2m1=4;m2=4;m3=4;%各分路器均设为5,分路器结构u=(f2-f1)/(m1*m2*m3);%频率分辨力ur=[0,0,0];%为各分路器中放带宽提供缓存ur(1)=(f2-f1)/m1; %写入各分路器中放带宽ur(2)=(f2-f1)/(m1*m2);ur(3)=(f2-f1)/(m1*m2*m3);fi=[0,0,0];%为各分路器中频频率提供缓存fi(1)=ceil(((f2-f1)/2)*1.2);%写入各分路中频频率fi(2)=ceil((ur(1)/2)*1.2);fi(3)=ceil((ur(2)/2)*1.6);fl=zeros(3,4);for j=1:1:4fl(1,j)=f1-fi(1)+(j-0.5)*ur(1);%第一本振组fl(2,j)=(fi(1)-ur(1)/2)-fi(2)+(j-0.5)*ur(2);%第二本振组fl(3,j)=(fi(2)-ur(2)/2)-fi(3)+(j-0.5)*ur(3);%第三本振组end num=zeros(1,3);%为每层的信道提供缓存for k=1:3j=1;while j<=4if f-fl(k,j)>=fi(k)-ur(k)/2&&f-fl(k,j)<=fi(k)+ur(k)/2 f=f-fl(k,j); num(k)=j-1;break;else j=j+1;endendendf=f1+num(1)*ur(1)+num(2)*ur(2)+num(3)*ur(3)+u/2;%进行频率估计fprintf('估计频率为 %f MHz\n',f);else disp('不在测频范围内 ');end仿真结果:。
基于MATLAB下的频率选择性信道仿真

基于MATLAB下的频率选择性信道仿真简介本文档旨在介绍使用MATLAB进行频率选择性信道仿真的基本方法和步骤。
背景频率选择性信道是无线通信中常见的信道类型之一,其特点是在不同的频率上具有不同的衰减和相位响应。
为了更好地理解和分析这种信道的性能,我们需要进行仿真模拟。
仿真步骤以下是在MATLAB中进行频率选择性信道仿真的基本步骤:1. 信道建模:首先,我们需要使用合适的数学模型来描述频率选择性信道。
常用的模型包括扁平衰落模型、Jakes模型、Rician衰落模型等。
根据具体的应用场景和需求,选择合适的模型进行建模。
信道建模:首先,我们需要使用合适的数学模型来描述频率选择性信道。
常用的模型包括扁平衰落模型、Jakes模型、Rician衰落模型等。
根据具体的应用场景和需求,选择合适的模型进行建模。
2. 频谱分析:通过频谱分析可以获得信号在不同频率上的衰减和相位响应。
MATLAB提供了丰富的信号处理工具箱,可以方便地对信号进行频谱分析。
频谱分析:通过频谱分析可以获得信号在不同频率上的衰减和相位响应。
MATLAB提供了丰富的信号处理工具箱,可以方便地对信号进行频谱分析。
3. 信道仿真:在信道建模和频谱分析的基础上,我们可以开始进行信道仿真。
根据所选用的信道模型和信号特性,使用MATLAB编写仿真代码,生成仿真结果。
可以考虑包括信号衰落、传输误码率等性能指标。
信道仿真:在信道建模和频谱分析的基础上,我们可以开始进行信道仿真。
根据所选用的信道模型和信号特性,使用MATLAB编写仿真代码,生成仿真结果。
可以考虑包括信号衰落、传输误码率等性能指标。
4. 结果分析:对于信道仿真的结果,我们需要进行详细的分析和评估。
根据仿真结果,可以评估系统在频率选择性信道下的性能表现,并针对性地进行优化。
结果分析:对于信道仿真的结果,我们需要进行详细的分析和评估。
根据仿真结果,可以评估系统在频率选择性信道下的性能表现,并针对性地进行优化。
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明书
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示,Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088},n={-5,-4,…,5}。
2、基于MSE 准则的均衡器抽头系数的自适应算法为:^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值,∆为迭代过程中的步长参数,k e 为误差信号,k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为:k k k e a z =-;k z 为均衡器输出,k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端,均衡器用这个已知序列去调整它的系数,一旦初始调节完成,自适应均衡器就从一个训练模式切换到直接判决模式,这时:^k k k e a z =-,式中^k a 是检测器的输出。
为了确保收敛和在慢变化信道中好的跟踪能力,选择步长参数的一种经验公式是15(21)Rk P ∆=+ 式中R P 代表接收到的信号加噪声的功率,它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出,在信噪比逐渐增大的过程中,未经均衡器均衡的差错率没有明显改善,可知系统中始终存在码间干扰造成的误码;经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下,均衡器均衡之后的误码率并没有明显改善,甚至没有未均衡的差错率低,这主要是因为噪声为随机信号,功率大时对源信号影响较大,而且均衡器不易跟踪;当我们把均衡器的步长调低后,跟踪能力增强,差错率降低。
附源程序代码:main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_in_dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR_in_dB)[y,len]=channel(info,SNR_in_dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信号码元if (y(i)<0), %判决译码decis=-1;elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码,统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡,得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器,并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后,误码率结果图hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器,并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后,误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11',...'经自适应均衡器均衡,步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数,则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数,可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_actual_isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积%需要指出,此时码元序列长度变为N+len-1,译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss.m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参,则均方为0,标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数,则标准差为输入实参,均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lms_equalizer.m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元,一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
matlab实现频域瑞利(Rayleigh)信道仿真
plot(GaussN2);
title('频域复数高斯信号2');
xlabel('实部');
ylabel('虚部');
grid;
figure(5)
subplot(2,1,1)
plot(sqrt(SEf).*GaussN1);
title('高斯噪声与多普勒功率谱相乘1');
plot(Gauss_time2);
title('时域高斯信号2');
xlabel('N');
ylabel('V');
grid;
subplot(2,2,3)
plot(GaussN1);
title('频域复数高斯信号1');
xlabel('实部');
ylabel('虚部');
grid;
GaussN2=fft(Gauss_time2);
% 产生瑞利衰落信道
x = ifft(sqrt(SEf).*GaussN1);
y = ifft(sqrt(SEf).*GaussN2);
rayleigh_amp = sqrt(abs(x).^2+abs(y).^2);
rayleigh_db = 20*log10(rayleigh_amp); %用dB表示瑞利信号
figure(2);
plot(rayleigh_db);
% axis([0 140 -100 20]);
title('瑞利信号衰落');
Matlab通信系统建模与仿真例题源代码-第五章
% ch5example2prg1.mSNR_in_dB=-10:2:30;SNR_in=10.^(SNR_in_dB./10); % 信道信噪比m_a=0.3; % 调制度P=0.5+(m_a^2)/4; % 信号功率for k=1:length(SNR_in)sigma2=P/SNR_in(k); % 计算信道噪声方差并送入仿真模型sim('ch5example2.mdl');% 执行仿真SNRdemod(k,:)=SNR_out; % 记录仿真结果endplot(SNR_in_dB, SNRdemod);xlabel('输入信噪比dB');ylabel('解调输出信噪比dB');legend('包络检波','相干解调');% ch5example7prog1.mclear;Fs=10000; % 仿真的采样率t=1/Fs:1/Fs:1; % 仿真时间点m_t(Fs*1)=0; % 基带信号变量初始化for F=150:400 % 基带信号发生:频率150Hz~400Hzm_t=m_t+0.003*sin(2*pi*F*t)*(400-F); % 幅度随线性递减endm_t90shift=imag(hilbert(m_t)); % 基带信号的希尔伯特变换carriercos=cos(2*pi*1000*t); % 1000Hz载波coscarriersin=sin(2*pi*1000*t); % 1000Hz正交载波sins_SSB1=m_t.*carriercos-m_t90shift.*carriersin; % 上边带SSBs_SSB2=m_t.*carriercos+m_t90shift.*carriersin; % 下边带SSB% 下面作出各波形以及频谱figure(1);subplot(4,2,1); plot(t(1:100),carriercos(1:100),...t(1:100),carriersin(1:100),'--r'); % 载波subplot(4,2,2); plot([0:9999],abs(fft(carriercos))); % 载波频谱axis([0 2000 -500 6000]);subplot(4,2,3); plot(t(1:100),m_t(1:100)); % 基带信号subplot(4,2,4); plot([0:9999],abs(fft(m_t))); % 信号频谱axis([0 2000 -500 6000]);subplot(4,2,5); plot(t(1:100),s_SSB1(1:100)); % SSB波形上边带subplot(4,2,6); plot([0:9999],abs(fft(s_SSB1))); % SSB频谱上边带axis([0 2000 -500 6000]);subplot(4,2,7); plot(t(1:100),s_SSB2(1:100)); % SSB波形下边带subplot(4,2,8); plot([0:9999],abs(fft(s_SSB2))); % SSB频谱下边带axis([0 2000 -500 6000]);% ch5example8prog1.mclear;Fs=10000; % 仿真的采样率t=1/Fs:1/Fs:1; % 仿真时间点m_t(Fs*1)=0; % 基带信号变量初始化for F=150:400 % 基带信号发生:频率150Hz~400Hzm_t=m_t+0.003*sin(2*pi*F*t)*(400-F); % 幅度随线性递减endm_t90shift=imag(hilbert(m_t)); % 基带信号的希尔伯特变换carriercos=cos(2*pi*1000*t); % 1000Hz载波coscarriersin=sin(2*pi*1000*t); % 1000Hz正交载波sins_SSB1=m_t.*carriercos-m_t90shift.*carriersin; % 上边带SSBout=s_SSB1.*carriercos; % 相干解调[a,b]=butter(4, 500/(Fs/2)); % 低通滤波器设计4阶,截止频率为500Hz demodsig=filter(a,b,out); % 解调输出% 下面作出各波形以及频谱figure(1);subplot(3,2,1); plot(t(1:100),s_SSB1(1:100)); % SSB波形subplot(3,2,2); plot([0:9999],abs(fft(s_SSB1))); % SSB频谱axis([0 5000 -500 6000]);subplot(3,2,3); plot(t(1:100),out(1:100)); % 相干解调波形subplot(3,2,4); plot([0:9999],abs(fft(out))); % 相干解调频谱axis([0 3000 -500 6000]);subplot(3,2,5); plot(t(1:100),demodsig(1:100)); % 低通输出信号subplot(3,2,6); plot([0:9999],abs(fft(demodsig)));% 低通输出信号的频谱axis([0 3000 -500 6000]);% ch5example8prog2.mclear;Fs=10000; % 仿真的采样率t=1/Fs:1/Fs:1; % 仿真时间点m_t(Fs*1)=0; % 基带信号变量初始化for F=150:400 % 基带信号发生:频率150Hz~400Hzm_t=m_t+0.003*sin(2*pi*F*t)*(400-F); % 幅度随线性递减endm_t90shift=imag(hilbert(m_t)); % 基带信号的希尔伯特变换carriercos=cos(2*pi*1000*t); % 1000Hz载波coscarriersin=sin(2*pi*1000*t); % 1000Hz正交载波sins_SSB1=m_t.*carriercos-m_t90shift.*carriersin; % 上边带SSBout=s_SSB1.*cos(2*pi*1018*t+1);% 存在频率误差的相位误差时的相干解调[a,b]=butter(4, 500/(Fs/2)); % 低通滤波器设计4阶,截止频率为500Hz demodsig=filter(a,b,out); % 解调输出% 下面作出各波形以及频谱figure(1);subplot(3,2,1); plot(t(1:100),s_SSB1(1:100)); % SSB波形subplot(3,2,2); plot([0:9999],abs(fft(s_SSB1))); % SSB频谱axis([0 5000 -500 6000]);subplot(3,2,3); plot(t(1:100),out(1:100)); % 相干解调波形subplot(3,2,4); plot([0:9999],abs(fft(out))); % 相干解调频谱axis([0 3000 -500 6000]);subplot(3,2,5); plot(t(1:100),demodsig(1:100)); % 低通输出信号subplot(3,2,6); plot([0:9999],abs(fft(demodsig)));% 低通输出信号的频谱axis([0 3000 -500 6000]);% ch5example9prog1.m[wav,fs]=wavread('GDGvoice8000.wav');t_end=1/fs *length(wav); % 计算声音的时间长度Fs=50000; % 仿真系统采样率t=1/Fs:1/Fs:t_end; % 仿真系统采样时间点% 设计300Hz~3400Hz的带通预滤波器H(z)[fenzi,fenmu]=butter(3,[300 3400]/(fs/2));% 对音频信号进行预滤波wav=filter(fenzi,fenmu,wav);% 利用插值函数将音频信号的采样率提升为Fs=50KHzwav=interp1([1/fs:1/fs:t_end],wav,t,'spline');wav_hilbert=imag(hilbert(wav)); % 音频信号的希尔伯特变换fc=10000; % 载波频率HzSSB_OUT=wav.*cos(2*pi*fc*t)-wav_hilbert.*sin(2*pi*fc*t); % 单边带调制figure(1); % 观察调制前后频谱subplot(2,2,1); plot(wav(53550:53750)); axis([0 200 -0.3 0.3]);subplot(2,2,2); psd(wav, 10000, Fs); axis([0 25000 -20 10]);subplot(2,2,3); plot(SSB_OUT(53550:53750)); axis([0 200 -0.3 0.3]);subplot(2,2,4); psd(SSB_OUT, 10000, Fs); axis([0 25000 -20 10]); wavwrite(0.5*SSB_OUT,Fs,'SSB_OUT.wav'); % 将SSB调制输出存盘备用% ch5example9prog2.mfunction out=ch5example9prog2(in, SNRdB)% SNR_dB设定信噪比% in 输入信号序列% out 信道输出序列Fs=50000; %系统采样率Power_of_in=var(in);Power_of_noise=Power_of_in/(10.^(SNRdB/10));bandwidth=13500-10000; % 信道带宽N0=Power_of_noise/bandwidth; % 噪声功率谱密度值W/HzGauss_noise=sqrt(N0*Fs/2).*randn(size(in));[num, den]=butter(4, [10000 13500]/(Fs/2)); % 带通信道10KHz到13.5KHz signal_of_filter_out=filter(num, den, in);noise_of_filter_out=filter(num, den, Gauss_noise);SNR_dB=10*log10(var(signal_of_filter_out)/var(noise_of_filter_out))% 测量得出的信噪比out=signal_of_filter_out+noise_of_filter_out; % 信道输出% ch5example9prog3.mclear;[recvsignal, Fs]=wavread('Channel_OUT.wav');% 读入信道输出信号数据t=(1/Fs:1/Fs: length(recvsignal)/Fs)';fc_local=10000-200; % 本地载波频率9.8KHzlocal_carrier=cos(2*pi*fc_local.*t); % 本地载波xianggan_out=recvsignal.*local_carrier; % 相干解调[fenzi,fenmu]=butter(3,[300 3400]/(Fs/2)); % 设计300Hz~3400Hz的带通滤波器demod_out=filter(fenzi,fenmu,xianggan_out); % 对相干输出信号进行滤波sound(demod_out/max(demod_out), Fs); % 播放解调音频wavwrite(demod_out,Fs,'SSBDemod_OUT.wav'); % 保存输出信号% ch5example10prog1.mclear;Y=[1:-1/7:0].*255; % 8级灰度N=8; % 8*N 列数S=ones(N,1);Y=S*Y;Y=reshape(Y,1,N*8);% 将矩阵扩大指定列数的一行M=40; % M 行数S=ones(M,1);Y=S*Y; % 重复M次矩阵行,得出图像矩阵I=uint8(Y); % 转换为uint8格式imshow(I); % 显示imwrite(I,'graybar.tif','tif'); % 并保存为图像文件% ch5example11prog1.mclear;I=imread('graybar.tif');% 读入图像(由上例生成)img=double(I')/255; % 转换为双精度数以便计算[M,N]=size(img);for K=1:2for column=K:2:N % K=1扫描奇数行for row=1:Mdot=img(row,column); % 取当前扫描点的灰度值greydot=[dot,dot,dot]; % R,G,B均设置为相同值,即显示灰度plot(row,N-column,'s','MarkerFaceColor',greydot,...'MarkerEdgeColor',greydot,'MarkerSize',6);hold on; % 保持扫描点axis([1,M, 1, N]); % 作图范围set(gcf,'DoubleBuffer','on');% 双缓冲避免作图闪烁drawnow; % 立即作图endendend% ch5example12prg1.mclear;R=zeros(100,100);G=zeros(100,100);B=zeros(100,100);R(1:50,30:100)=255;G(30:100,50:100)=255;B(1:70,1:70)=255; % 三基色产生I(:,:,1)=R;I(:,:,2)=G;I(:,:,3)=B; % 合成为100*100图像矩阵imshow(uint8(I));% 显示% ch5example13prg1.m% 生成400*480彩条图像clear;R=[1 1 0 0 1 1 0 0];G=[1 1 1 1 0 0 0 0];B=[1 0 1 0 1 0 1 0];N=60; % N*8列S=ones(N,1);R=S*R; R=reshape(R,1,N*8);G=S*G; G=reshape(G,1,N*8);B=S*B; B=reshape(B,1,N*8);M=400; % 行数S=ones(M,1);R=S*R; G=S*G; B=S*B; % 得出三基色矩阵I(:,:,1)=R; I(:,:,2)=G; I(:,:,3)=B; % 组合I=uint8(I*255); % 类型转换imshow(I); % 显示并保存imwrite(I,'colorbar.tif','tif');% ch5example14prg1.mclear;I=imread('colorbar.tif');% 或用autumn.tif,sydney.JPG等图像文件figure(1);imshow(I);I=double(I);[m,n,p]=size(I);I=-(0.75-0.125)./(255).*I+0.75; % 换算为0.125到0.75电平R=I(:,:,1);G=I(:,:,2);B=I(:,:,3);% 三基色分离R=reshape(R',1,m*n); % 转换为1维(红)G=reshape(G',1,m*n); % 转换为1维(绿)B=reshape(B',1,m*n); % 转换为1维(蓝)Y=0.30*R+0.59*G+0.11*B;% 亮度R_Y=R-Y; % 色差R0B_Y=B-Y; % 色差B0V=0.877*R_Y; % 色差电平压缩U=0.493*B_Y; % 色差电平压缩f_c=283.5*15625; % 副载波频率tvY=[interp1(Y,(1:n/980:m*n),'nearest')];% 插值:行采样980点tvV=[interp1(V,(1:n/980:m*n),'nearest')];% 插值tvU=[interp1(U,(1:n/980:m*n),'nearest')];% 插值% 全电视信号产生for h=1:(m-2)s(1280*h+(1:102))=0.75; % 消隐脉冲s(1280*h+(103:197))=1; % 行同步头s(1280*h+(198:300))=0.75;% 消隐脉冲s(1280*h+(301:1280))=tvY(h*980+(-1:978));% 图像一行像素-亮度% 色差VsV(1280*h+(1:300))=0; % 消隐部分sV(1280*h+(220:265))=0.12;% 色同步选通sV(1280*h+(301:1280))=tvV(h*980+(-1:978));% 图像信号部分% 色差UsU(1280*h+(1:300))=0;sU(1280*h+(301:1280))=tvU(h*980+(-1:978));endt=0:0.5e-7:0.5e-7*(length(s)-1);% 计算时间点序列,采样率20MHzF_v=sV.*cos(2*pi*f_c.*t); % 色差信号正交调制F_u=sU.*sin(2*pi*f_c.*t);c=F_v+F_u; % 调制输出的色差信号TVsignal=s+c; % 合成彩色电视信号figure(2); plot(t,TVsignal); xlabel('时间');% 彩色电视信号figure(3); plot(t,s); xlabel('时间'); % 亮度信号% 功率谱计算[Pxxcc,F]=psd(c,1e5,2e7);figure(4); plot(F,10*log10(Pxxcc),'g');hold on;% 调制后的色差信号频谱[Pxx,F]=psd(s,1e5,2e7); % FFT长度为1e5点,故频率分辨率100Hz figure(4); plot(F,10*log10(Pxx),'k'); % 亮度信号频谱xlabel('频率Hz');ylabel('功率谱密度dB');% ch5example15prg1.mclear;ch5example14prg1; % 用实例5.14程序产生彩色全电视信号%---带限高斯信道---TVsignal=TVsignal+0.1*randn(size(TVsignal)); % 加入噪声[b,a]=butter(2,5e6/(20e6/2)); % 传输信道带宽5MHzTVsignal=filter(b,a,TVsignal); % 通过带限信道%---接收部分---[b,a]=butter(2,0.5e6/(20e6/2)); % 行同步滤波h_pulse=filter(b,a,TVsignal);h_pulse=h_pulse>0.87; % 行同步脉冲选出。
调制解调matlab仿真源码
一、概述调制解调技术是无线通信中的重要组成部分,它能够将数字信号转换成模拟信号,通过无线信道传输,并在接收端将模拟信号转换成数字信号。
在通信系统中,调制解调技术的准确性和稳定性对整个系统的性能起着至关重要的作用。
而Matlab作为一种强大的数学计算软件,其仿真源码能够帮助工程师们更好地理解调制解调原理,优化系统设计。
二、调制解调技术概述1. 调制技术调制技术是指利用某种载波信号来传送信息信号的过程。
常见的调制技术包括幅度调制(AM)、频率调制(FM)和相位调制(PM)等。
2. 解调技术解调技术是指将调制后的信号还原成原始信号的过程。
解调技术根据调制技术的不同可以分为幅度解调、频率解调和相位解调等。
三、调制解调Matlab仿真源码1. 调制仿真源码在Matlab中,可以利用Simulink工具箱进行调制仿真源码的编写。
对于AM调制可以通过搭建AM调制系统模型,设置载波频率、调制信号频率和调制指数等参数,然后进行仿真验证调制效果。
另外,Matlab还提供了丰富的调制函数库,如ammod()函数用于进行AM调制,fmmod()函数用于进行FM调制,pmmod()函数用于进行PM调制等。
工程师们可以通过编写简单的脚本文件调用这些函数,实现调制仿真源码的编写。
2. 解调仿真源码同样地,在Matlab中可以利用Simulink工具箱进行解调仿真源码的编写。
对于AM解调可以通过搭建AM解调系统模型,设置解调信号频率和解调环节参数,然后进行仿真验证解调效果。
Matlab还提供了一系列的解调函数库,如amdemod()函数用于进行AM解调,fmdemod()函数用于进行FM解调,pmdemod()函数用于进行PM解调等。
工程师们同样可以通过编写简单的脚本文件调用这些函数,实现解调仿真源码的编写。
四、调制解调Matlab仿真实例下面我们以AM调制解调为例,展示如何使用Matlab编写调制解调仿真源码。
1. AM调制仿真源码``` matlab设置参数fc = 1000; 载波信号频率fm = 100; 调制信号频率ka = 1; 调制指数t = 0:0.001:1; 时间范围生成调制信号m_t = cos(2*pi*fm*t); 调制信号c_t = cos(2*pi*fc*t); 载波信号s_t = (1+ka*m_t).*c_t; AM调制信号绘制调制信号图像subplot(3,1,1);plot(t,m_t);title('调制信号');绘制载波信号图像subplot(3,1,2);plot(t,c_t);title('载波信号');绘制AM调制信号图像subplot(3,1,3);plot(t,s_t);title('AM调制信号');```2. AM解调仿真源码``` matlab设置解调参数fs = xxx; 采样频率t = 0:1/fs:1; 时间范围s_t = (1+ka*m_t).*c_t; AM调制信号解调信号y = amdemod(s_t,fc,fs,0,ka);t = 0:1/fs:1; 时间范围绘制解调信号图像subplot(2,1,1);plot(t,m_t);title('调制信号');绘制解调信号图像subplot(2,1,2);plot(t,y);title('解调信号');```通过上述实例,我们可以清晰地了解到如何利用Matlab编写调制解调的仿真源码,从而深入理解调制解调原理,优化系统设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%
% Rayleigh Fading Channel Signal Generator
% Using the Dent Model (a modification to the Jakes Model)
%
% Last Mouthor: Avetis Ioannisyan (avetis@)
% Number of oscillators
N0 = NumAngles/4;
% Maximum Doppler shift of carrier at some wavelength
omega_m = (2*pi) * fm(Velocity, carrierFreq);
% specify variance of the Rayleigh channel
%
% Usage Examples:
% [omega_mTau, Tk] = ai_RayCh(2^7, 2^18, 64, 2, 900, 100)
%
% where
%
% NumAngles=2^7, Length=2^18, symbolRate=64, NumWaveforms=2, carrierFreq=900, Velocity=100
% use this for *constant* variange - requires changing other params in prog
sigma2 = 10;
% make sigma2 a gaussian RV around u = sigma2 and var = sigma2/5
%
%
% Usage:
% [omega_mTau, Tk] =
% ai_RayCh(NumAngles, Length, SymbolRate, NumWaveforms, CarrierFreq, Velocity)
%
% Where the output omega_mTau is a time scaling factor for plotting
% number of equally strong rays arriving at the receiver. It used to
% compute the number of oscillators in the Dent model with N0 = numAngles/4
%
% Length - scalar preferably power of 2 for faster computation, Length > 2^17
%
% NumWaveforms - scalar used to specify how many 'k' waveforms to generate
% in the model. NumWaveforms > 2 to properly display plots
%
% CarrierFreq - scalar expressed in MHz is the carrier frequency of the
% normalized correlations. The LAGS value output by [C,LAGS] = XCORR(...)
% should be multiplied by the omega_mTau scaling factor to properly display
% axis. Tk is a two dimensional vector [M, N] = SIZE(Tk) with
% use for *non constant* variaance - requires changing other params in prog
sigma2 = sigma2 + sqrt(sigma2/5) .* randn(1,NumWaveforms);
% [omega_mTau, Tk] = RayCh(NumAngles, Length, symbolRate, NumWaveforms,
% carrierFreq, Velocity);
%
%
function [omega_mTau, Tk] = ai_RayCh(NumAngles, Length, symbolRate, NumWaveforms, carrierFreq, Velocity)
% M=numWaverorms and N=Length specified in the RayCh(...) function call
%
% And the input variables are:
%
% NumAngles - scalar power of 2, NumAngles > 2^7 is used to specify the
% tranmitter. Normally 800 or 1900 MHz for mobile comms
%
% Velocity - scalar expressed in km/hr is the speed of the receiver.
% 100 km/hr = 65 mi/hr. Normal values are 20-130 km/hr
% is used to specify the length of the generated sequence. Lengths near 1E6
% are close to realistic signals
%
% SymbolRate - scalar power of 2 and is in kilo-symbols-per-sec is used to
% specify what should be the transmission data rate. Slower rates will
% provide slowly fading channels. Normal voice and soem data rates are
% 64-256 ksps
