三次样条插值作业题(教育教学)
计算方法大作业1 克服Runge现象

x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )
S
'
(xi
0) S
xi' (
0 )i
S
'
'
x(i
0)S
xi' ' (
0)
1 ,n2, . . . , 1
(1)
这里共有了 3n-3 个条件,再加上条件(2)中的 n+1 个插值条件,共有 4n-2 个条件,
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边
dn1
1
2
Mn
dn
(6)
2 1
2
2
2
1 M1 d1
M2
d2
n 1
2
n
1
M
n
1
dn1
n
n 2 M n dn
由式(1)内点拼接条件,可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
(3) (4)
其中
i
hi 1 hi1
, hi
i
hi hi 1
三次样条插值作业题

例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%============================= % 本段代码解决作业题的例1 %============================= clear all clc% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];LeftBoun = 0.2;RightBoun = -1;% 区间长度向量,其各元素为自变量各段的长度h = zeros(1, length(IndVar) - 1);for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i);end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 1;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 1;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i)); end% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 6 * ( (DepVar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1); for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) ); S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i - 1, polyval(Part_1, 3), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ), '-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-',num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14)hold onend% 过x=1和x=2两个横轴点作垂线 %line([1, 1], [2.5, -0.5], 'LineStyle', '--');line([2, 2], [2.5, -0.5], 'LineStyle', '--');% 为x轴和y轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ...'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s曲线的图像如图所示:例2 已知函数值表:试求在区间[1,5]上满足上述函数表所给出的插值条件的三次自然样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
三次样条插值PPT学习教案

x1,x2,…,xn 称为
Sm(x1, x2, …, xn)
第2页/共31页
m=1时,样条函数是分段线性函数; m=2时,是1阶连续可微的分段二次多 项式; 显然, m次样条函数比一般的m次分段插值多 项式的 光滑性 好。 问题: 如何判断一个分段的多项式函数是样条 函数? 设
s(x)
p0 (x), x x1
从而,
a b c 3 3a 2b c 5 6a 2b 8
a 2, b 2, c 3。
第10页/共31页
5.3.2 三 次样条 插值及 其收敛 性(简 介,学 生自学)
有些实际问题中提出的插值问题,要求 插值曲 线具 有较高的光滑性和几何光顺性。 模线员用压铁压住弹性均匀的窄木条 (样条 )的两 端, 强迫样条通过一组已知离散的型值点 。 的形状后,再沿着样条画出所需的曲 线。 形下,该曲线可以由三次样条函数表 示。 插值不仅具有较好的收敛性和稳定性 ,而且 其光滑 性也 较高,因此,样条函数成为了重要的 插值工 具。
进一步可得,
光滑因子
pj (x) pj1(x) qj (x)
第4页/共31页
j 1, 2, , n
对于满足上述性质的如下形式的分段 m次多 项式s(x) ,
p0 (x), x x1
s(x)
p1(x), x1 x x2
pj (x), xj x xj1
pn (x), xn x
pj (x) Pm( j 0,1,...,n)
a 11 a 2 ,
b 1 3 b 2 , c 3。
2)由连续性,应有
ax3 bx2 cx 1 x3 x2
即,
x 1
x 1
a b c 1 13 12 2 a b c 3
科学计算实习题二 三次样条插值
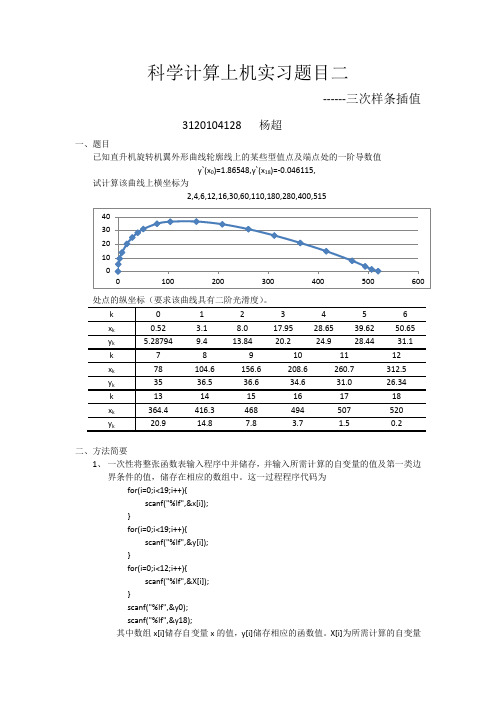
for(i=0;i<12;i++){ for(k=1;k<19;k++){
if((X[i]>x[k-1])&&(X[i]<x[k]))
S[i]=M[k-1]/(6*h[k])*pow(x[k]-X[i],3)+M[k]/(6*h[k])*pow(X[i]-x[k-1],3)+(y[k-1]-M[k-1]/ 6*pow(h[k],2))*(x[k]-X[i])/h[k]+(y[k]-M[k]/6*pow(h[k],2))*(X[i]-x[k-1])/h[k];
} 3、 利用解三对角线方程组的追赶法解出在结处的二阶导数值,这一过程程序代码如
下 bt[0]=1.0/2; for(i=1;i<=17;i++){ bt[i]=v[i]/(2-u[i]*bt[i-1]); } f[0]=g[0]*1.0/2; for(i=1;i<=18;i++){ f[i]=(g[i]-u[i]*f[i-1])/(2-u[i]*bt[i-1]); } M[18]=f[18]; for(i=17;i>=0;i--){ M[i]=f[i]-bt[i]*M[i+1];
的值。 2、 按照课本第 92 页的公式(4.44)计算确定 M 的线性方程组的系数数组 u、v、g,
并储存在相应的数组中。这一过程程序代码为 for(i=1;i<19;i++){ h[i]=x[i]-x[i-1]; } for(i=1;i<18;i++){ u[i]=h[i]/(h[i]+h[i+1]); v[i]=1-u[i]; } g[0]=6/h[1]*((y[1]-y[0])/h[1]-y0); g[18]=6/h[18]*(y18-(y[18]-y[17])); for(i=1;i<18;i++){ g[i]=6/(h[i]+h[i+1])*((y[i+1]-y[i])/h[i+1]-(y[i]-y[i-1])/h[i]);
计算方法大作业——三次样条插值

计算方法上机报告
此完成所有数据的输入。继续按 Enter 键会出现提示“选择封闭方程组的边界条件: 第 一类边界条件输入 1,第二类边界条件输入 2,第三类边界条件输入 3。 ”根据已知情况 选择相应的边界条件,若为自然三次样条插值,则选 1,并将插值区间两端点的二阶导 数值设置为 0。输入完成之后按 Enter 开始求解,程序运行结束后命令窗口会显示要求 的三次样条插值函数,同时会出现该插值函数以及插值节点的图像,便于直接观察。 2.3 算例及计算结果 (1) 《数值分析》课本第 137 页的例题 4.6.1,已知函数 y=f(x)的数值如下表,求它 的自然三次样条插值函数。 xi yi -3 7 -1 11 0 26 3 56 4 29
2 三次样条插值
2 三次样条插值
2.1 算法原理及程序框图 设在区间[a, b]上给定 n+1 个节点 xi(a ≤ x0 < x1 < … < xn ≤ b),在节点 xi 处的函数 值为 yi = f(xi) (i = 0,1,…,n)。若函数 S(x)满足以下三个条件: (1) 在每个子区间[xi-1, xi] (i = 0,1,…,n)上,S(x)是三次多项式; (2) S(xi) = yi (i = 0,1,…,n); (3) 在区间[a, b]上,S(x)的二阶导数 S”(x)连续, 则称 S(x)为函数 yi = f(x) 在区间[a, b]上的三次样条插值函数。 由定义可知 S(x)共有 4n 个待定参数,根据条件(3)可得如下 3n-3 个方程,
S x
x x i
6hi
3
M i 1
x xi 1
6hi
3
x x hi2 M i yi 1 M i 1 i 6 hi
三次样条插值作业题

例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:%=============================% 本段代码解决作业题的例1%============================= clear all clc% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];LeftBoun = 0.2; RightBoun = -1;% 区间长度向量,其各元素为自变量各段的长度 h = zeros(1, length(IndVar) - 1); for i = 1 : length(IndVar) - 1h(i) = IndVar(i + 1) - IndVar(i); end% 为向量μ赋值mu = zeros(1, length(h));for i = 1 : length(mu) - 1mu(i) = h(i) / (h(i) + h(i + 1));endmu(i + 1) = 1;% 为向量λ赋值lambda = zeros(1, length(h));lambda(1) = 1;for i = 2 : length(lambda)lambda(i) = h(i) / (h(i - 1) + h(i));end% 为向量d赋值d = zeros(1, length(h) + 1);d(1) = 6 * ( (DepV ar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1);for i = 2 : length(h)a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );d(i) = 6 * c;endd(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);% 为矩阵A赋值% 将主对角线上的元素全部置为2A = zeros( length(d), length(d) );for i = 1 : length(d)A(i, i) = 2;end% 将向量λ的各元素赋给主对角线右侧第一条对角线for i = 1 : length(d) - 1A(i, i + 1) = lambda(i);end% 将向量d的各元素赋给主对角线左侧第一条对角线for i = 1 : length(d) - 1A(i + 1, i) = mu(i);end% 求解向量MM =A \ d';% 求解每一段曲线的函数表达式for i = 1 : length(h)Coefs_1 = M(i) / (6 * h(i));Part_1 = conv( Coefs_1, ...conv( [-1, IndVar(i + 1)], ...conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) );S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_2 = M(i + 1)/(6 * h(i));Part_2 = conv( Coefs_2, ...conv( [1, -IndVar(i)], ...conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);Part_4 = conv(Coefs_4, [1, -IndVar(i)]);S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);S = S_1 + S_2 + S_3 + S_4;plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)% 在样条插值曲线的相应位置标注该段曲线的函数表达式text(i - 1, polyval(Part_1, 3), ...['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ), '-x)^{3}+', ...num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-', num2str( IndVar(i) ), ')'], ...'FontName', 'Times New Roman', 'FontSize', 14)hold onend% 过x=1和x=2两个横轴点作垂线%line([1, 1], [2.5, -0.5], 'LineStyle', '--');line([2, 2], [2.5, -0.5], 'LineStyle', '--');% 为x轴和y轴添加标注xlabel( '\itx', 'FontName', 'Times New Roman', ...'FontSize', 14, 'FontWeight', 'bold');ylabel( '\its(x)', 'FontName', 'Times New Roman', ...'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');最终,三次样条插值函数s(x)表达式为:[][][]⎪⎩⎪⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s曲线的图像如图所示:例2 已知函数值表:试求在区间[1,5]上满足上述函数表所给出的插值条件的三次自然样条插值函数)(x s本算法求解出的三次样条插值函数将写成三弯矩方程的形式:)()6()()6()(6)(6)(211123131j j jj j j jj j j j jj j jj x x h h M y x x h h M y x x h M x x h M x s --+--+-+-=+++++其中,方程中的系数jj h M 6,jj h M 61+,jj j j h h M y )6(2-,jjj j h h M y )6(211++-将由Matlab代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
三次样条插值

(2)设给定 yf(x) 函数表 (x i,f(x i)( ) i ,0 ,1 , ,n ) (8.1)
若(1)中3次样条函数 S( x) 还满足插值条件: S (x i) f(x i)(i, 0 ,1 , ,n )
称 S( x) 为 f ( x) 关于剖分 的3次样条插值函数。
cj,1 mj
已知
cj,2(3(yj h 1jyj)2m jm j1)h 1j
cj,3(mj1mj2yj1 h j yj)h 12 j
h jxj 1xj,x [xj,xj 1], j0,1, ,n1 问题:设给定 yf(x)函数表 (x i,f(x i)( ) i ,0 ,1 , ,n )(8.1)
举例: 1 汽车、船的外形设计,流体力学等要求流线型(光滑); 2 木样条的来源。
二 、 样条函数的定义 定义 9 (3次样条函数)
(1) 设有对[a,b]的剖分 :a x 0 x 1 x n b ,如果函数 S(x)
满足下述条件:
(a )S (x ) C 2a ,b ,即具有连续的一阶,二阶导数。 bS(x)在每一个小区间 xj,xj1 j 0 ,1 ,n 1 上是次数 3
8.2 三次样条插值函数的表达式 (一阶导数表示)
一、推导公式:
回忆:分段3次Hermite插值 Ih ( x), 当x[xj,xj1]时
I h ( x ) I j( x ) y j c j,1 ( x x j) c j,2 ( x x j) 2 cj,3(xxj)3
cj,1 mj
基本思路:以分段三次Hermite插值为基础,由(1)函数表(xi , yi ), (i0,1, ,n );(2 )S ( jv)(x j) S ( jv ) 1 (x j)v , 0 ,1 ,2 ;(3)三种边界条件中 的某一种推导3次样条插值函数。
MATLAB大作业 给定一个时间序列,使用三次样条插值方法进行均匀内插

MATLAB作业给定一个时间序列,使用三次样条插值方法进行均匀内插(题目的相关说明:按题目要求编写一个MATLAB程序函数,并把自己编制程序所得的结果与MATLAB库函数分析结果进行对比。
)理论基础:时间序列的概念:时间序列是一种定量预测方法,又称简单外延法,时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论与方法,时间序列分析可分为以下三种情况(1)把一个时间序列的值变动为N 个组成部分,通常可以分为四种 a、倾向变动,又称长期趋势变动 b、循环变动,又称周期变动 c、季节变动,即每年有规则的反复进行变动 d、不规则变动,即随机变动。
然后把这四个综合到一起得出预测的结果。
虽然分成这四部分,但这四部分之间的相互关系是怎么样的呢,目前一般采用相乘的关系,其实各个部分都是在其他部分作用的基础上进行作用的,所以采用相乘是有一定依据的,此种方法适合于短期预测和库存预测(2)把预测对象、预测目标和对预测的影响因素都看成为具有时序的,为时间的函数,而时间序列法就是研究预测对象自身变化过程及发展趋势,如果未来预测是线性的,其数学模型为YT+L=aT+bTL,YT+L为未来预测值,aT为截距,bT为斜率,L为由T到需要预测的单位时间数(如5年、10年等)(3)根据预测对象与影响因素之间的关系及影响程度来推算未来,与目标的相关因素很多,只能选择那些因果关系较强的为预测影响的因素,此时间序列法用于短期预测比较有效,若要用于长期预测,还需要结合其他方法才行。
三次样条插值的实际应用:在制造船体和汽车外形等工艺中传统的设计方法是,首先由设计人员按外形要求,给出外形曲线的一组离散点值,施工人员准备好有弹性的样条(一般用竹条或有弹性的钢条)和压铁,将压铁放在点的位置上,调整竹条的形状,使其自然光滑,这时竹条表示一条插值曲线,我们称为样条函数。
从数学上看,这一条近似于分段的三次多项式,在节点处具有一阶和二阶连续微商。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表:
x i 0 1 2 3 y i
0.5
2
1.5
且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s
本算法求解出的三次样条插值函数将写成三弯矩方程的形式:
)
()6()()
6()(6)(6)(211123131j j j
j j j j
j j j j j
j j j
j x x h h M y x x h h M y x x h M x x h M x s --
+
--
+
-+-=
+++++其中,方程中的系数
j
j h M 6,
j
j h M 61+,j
j j j h h M y )6(2-
,
j
j
j j h h M y )
6(211++-
将由Matlab
代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。
以下为Matlab 代码:
%=============================
% 本段代码解决作业题的例1
%============================= clear all clc
% 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];
LeftBoun = 0.2; RightBoun = -1;
% 区间长度向量,其各元素为自变量各段的长度 h = zeros(1, length(IndVar) - 1); for i = 1 : length(IndVar) - 1
h(i) = IndVar(i + 1) - IndVar(i); end
% 为向量μ赋值
mu = zeros(1, length(h));
for i = 1 : length(mu) - 1
mu(i) = h(i) / (h(i) + h(i + 1));
end
mu(i + 1) = 1;
% 为向量λ赋值
lambda = zeros(1, length(h));
lambda(1) = 1;
for i = 2 : length(lambda)
lambda(i) = h(i) / (h(i - 1) + h(i));
end
% 为向量d赋值
d = zeros(1, length(h) + 1);
d(1) = 6 * ( (DepV ar(2) - DepVar(1) ) / ( IndVar(2) - IndVar(1) ) - LeftBoun) / h(1);
for i = 2 : length(h)
a = ( DepVar(i) - DepVar(i - 1) ) / ( IndVar(i) - IndVar(i - 1) );
b = ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) );
c = (b - a) / ( IndVar(i + 1) - IndVar(i - 1) );
d(i) = 6 * c;
end
d(i + 1) = 6 *( RightBoun - ( DepVar(i + 1) - DepVar(i) ) / ( IndVar(i + 1) - IndVar(i) ) ) / h(i);
% 为矩阵A赋值
% 将主对角线上的元素全部置为2
A = zeros( length(d), length(d) );
for i = 1 : length(d)
A(i, i) = 2;
end
% 将向量λ的各元素赋给主对角线右侧第一条对角线
for i = 1 : length(d) - 1
A(i, i + 1) = lambda(i);
end
% 将向量d的各元素赋给主对角线左侧第一条对角线
for i = 1 : length(d) - 1
A(i + 1, i) = mu(i);
end
% 求解向量M
M =A \ d';
% 求解每一段曲线的函数表达式
for i = 1 : length(h)
Coefs_1 = M(i) / (6 * h(i));
Part_1 = conv( Coefs_1, ...
conv( [-1, IndVar(i + 1)], ...
conv( [-1, IndVar(i + 1)], [-1, IndVar(i + 1)] ) ) );
S_1 = polyval (Part_1, [IndVar(i) : 0.01 : IndVar(i + 1)]);
Coefs_2 = M(i + 1)/(6 * h(i));
Part_2 = conv( Coefs_2, ...
conv( [1, -IndVar(i)], ...
conv( [1, -IndVar(i)], [1, -IndVar(i)] ) ) );
S_2 = polyval (Part_2, [IndVar(i) : 0.01 : IndVar(i + 1)]);
Coefs_3 = (DepVar(i) - M(i) * h(i)^2 / 6) / h(i);
Part_3 = conv(Coefs_3, [-1, IndVar(i + 1)]);
S_3 = polyval (Part_3, [IndVar(i) : 0.01 : IndVar(i + 1)]);
Coefs_4 = (DepVar(i + 1) - M(i + 1) * h(i)^2 / 6) / h(i);
Part_4 = conv(Coefs_4, [1, -IndVar(i)]);
S_4 = polyval (Part_4, [IndVar(i) : 0.01 : IndVar(i + 1)]);
S = S_1 + S_2 + S_3 + S_4;
plot ([IndVar(i) : 0.01 : IndVar(i + 1)], S, 'LineWidth', 1.25)
% 在样条插值曲线的相应位置标注该段曲线的函数表达式
text(i - 1, polyval(Part_1, 3), ...
['\itS', num2str(i), '(x)=', num2str(Coefs_1), '(', num2str( IndVar(i + 1) ), '-x)^{3}+', ...
num2str(Coefs_2), '(x-', num2str( IndVar(i) ), ')^{3}+', num2str(Coefs_3), ...
'(', num2str( IndVar(i + 1) ), '-x)+', num2str(Coefs_4), '(x-', num2str( IndVar(i) ), ')'], ...
'FontName', 'Times New Roman', 'FontSize', 14)
hold on
end
% 过x=1和x=2两个横轴点作垂线%
line([1, 1], [2.5, -0.5], 'LineStyle', '--');
line([2, 2], [2.5, -0.5], 'LineStyle', '--');
% 为x轴和y轴添加标注
xlabel( '\itx', 'FontName', 'Times New Roman', ...
'FontSize', 14, 'FontWeight', 'bold');
ylabel( '\its(x)', 'FontName', 'Times New Roman', ...
'Rotation', 0, 'FontSize', 14, 'FontWeight', 'bold');
最终,三次样条插值函数s(x)表达式为:
[][][]⎪⎩
⎪
⎨⎧∈-+-+-+--∈-+-+---∈+-++--=.3,2,)2(44.1)3(62.2)2(06.0)3(62.0,2,1,)1(62.2)2(08.0)1(62.0)2(42.0,1,0,08.0)1(06.042.0)1(06.0)(333333x x x x x x x x x x x x x x x x s
曲线的图像如图所示:。
