您的位置：360文档中心› 高三数学下册基础达标复习题16.doc

高三数学下册基础达标复习题16.doc

合集下载

专题16 全等三角形的核心知识点精讲(讲义)-备战2024年中考数学一轮复习考点帮

专题16 全等三角形的核心知识点精讲(讲义)-备战2024年中考数学一轮复习考点帮

专题16 全等三角形的核心知识点精讲1.熟悉全等三角形常考5种模型2.掌握全等三角形性质，并运用全等三角形性质解答。

考点1：全等三角形的概念及性质考点2：全等三角形的判定模型一：平移型模型分析：此模型特征是有一组边共线或部分重合，另两组边分别平行，常要在移动的方向上加（减）公共线段，构造线段相等，或利用平行线性质找到对应角相等.模型示例概念两个能完全重合的三角形叫做全等三角形．性质1.两全等三角形的对应边相等，对应角相等．2.全等三角形的对应边上的高相等，对应边上的中线相等，对应角的平分线相等．3.全等三角形的周长、面积相等．模型二：轴对称模型模型分析:所给图形可沿某一直线折叠，直线两旁的部分能完全重合，重合的顶点就是全等三角形的对应顶点，解题时要注意隐含条件，即公共边或公共角相等.模型三：旋转型模型解读：将三角形绕着公共顶点旋转一定角度后，两个三角形能够完全重合，则称这两个三角形为旋转型三角形．旋转后的图形与原图形存在两种情况：①无重叠：两个三角形有公共顶点，无重叠部分，一般有一对隐含的等角②有重叠：两个三角形含有一部分公共角，运用角的和差可得到等角.模型四：一线三垂直型模型解读：一线：经过直角顶点的直线；三垂直：直角两边互相垂直，过直角的两边向直线作垂直，利用“同角的余角相等”转化找等角【题型1：平移型】【典例1】（2023•广州）如图，B是AD的中点，BC∥DE，BC＝DE．求证：∠C＝∠E．1．（2022•淮安）已知：如图，点A、D、C、F在一条直线上，且AD＝CF，AB＝DE，∠BAC＝∠EDF．求证：∠B＝∠E．2．（2022•柳州）如图，点A，D，C，F在同一条直线上，AB＝DE，BC＝EF．有下列三个条件：①AC＝D F，②∠ABC＝∠DEF，③∠ACB＝∠DFE．（1）请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为（填写序号）（只需选一个条件，多选不得分），你判定△ABC≌△DEF的依据是（填“SSS”或“SAS”或“ASA”或“AAS”）；（2）利用（1）的结论△ABC≌△DEF．求证：AB∥DE．【题型2：对称型】【典例2】（2023•福建）如图，OA＝OC，OB＝OD，∠AOD＝∠COB．求证：AB＝CD．1．（2023•长沙）如图，AB＝AC，CD⊥AB，BE⊥AC，垂足分别为D，E．（1）求证：△ABE≌△ACD；（2）若AE＝6，CD＝8，求BD的长．2．（2022•西藏）如图，已知AD平分∠BAC，AB＝AC．求证：△ABD≌△ACD．【题型3：旋转型】【典例3】（2023•大连）如图，AC＝AE，BC＝DE，BC的延长线与DE相交于点F，∠ACF+∠AED＝180°．求证：AB＝AD．1．（2023•乐山）如图，已知AB与CD相交于点O，AC∥BD，AO＝BO，求证：AC＝BD．2．（2023•泸州）如图，点B在线段AC上，BD∥CE，AB＝EC，DB＝BC．求证：AD＝EB．3．（2023•西藏）如图，已知AB＝DE，AC＝DC，CE＝CB．求证：∠1＝∠2．【题型4：一线三等角】【典例4】（2023•陕西）如图，在△ABC中，∠B＝90°，作CD⊥AC，且使CD＝AC，作DE⊥BC，交BC 的延长线于点E．求证：CE＝AB．1．（2021•南充）如图，∠BAC＝90°，AD是∠BAC内部一条射线，若AB＝AC，BE⊥AD于点E，CF⊥A D于点F．求证：AF＝BE．一．选择题（共8小题）1．下列各组图案中，不是全等形的是（）A．B．C．D．2．已知图中的两个三角形全等，则∠1等于（）A．50°B．58°C．60°D．72°3．如图，△ABC≌△DEC，点E在AB边上，∠B＝70°，则∠ACD的度数为（）A．30°B．40°C．45°D．50°4．如图，△ABD≌△ACE，若AB＝6，AE＝4，则CD的长度为（）A．10B．6C．4D．25．如图，点B、F、C、E在一条直线上，∠A＝∠D＝90°，AB＝DE，添加下列选项中的条件，能用HL 判定△ABC≌△DEF的是（）A．AC＝DF B．∠B＝∠E C．∠ACB＝∠DFE D．BC＝EF6．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（）A．∠B＝∠C B．BE＝CD C．BD＝CE D．AD＝AE7．如图，BE⊥AC于点E，CF⊥AB于点F，若BE＝CF，则Rt△BCF≌Rt△CBE的理由是（）A．AAS B．HL C．SAS D．ASA8．如图所示，已知在△ABC中，∠C＝90°，AD＝AC，DE⊥AB交BC于点E，若∠B＝28°，则∠AEC ＝（）A．28°B．59°C．60°D．62°二．填空题（共4小题）9．如图是两个全等三角形，图中的字母表示三角形的边长，那么∠1的度数为．10．已知：如图，△ABC和△BAD中，∠C＝∠D＝90°，再添加一个条件就可以判断△ABC ≌△BAD．11．请仔细观察用直尺和圆规作一个角∠A'O'B'等于已知角∠AOB的示意图．请你根据所学的三角形全等的有关知识，说明画出∠A'O'B'＝∠AOB的依据是．12．如图，若AC平分∠BCD，∠B+∠D＝180°，AE⊥BC于点E，BC＝13cm，CD＝7cm，则BE＝．三．解答题（共4小题）13．如图，点B、E、C、F在一条直线上，AB＝DE，AC＝DF，BE＝CF．（1）求证：△ABC≌△DEF；（2）若∠D＝45°，求∠EGC的大小．14．如图，∠ACB＝90°，∠BAC＝45°，AD⊥CE，BE⊥CE，垂足分别是D，E，BE＝0.8，DE＝1.7，求AD的长．15．如图，点A，B，C在一条直线上，△ABD、△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q．（1）求证：△ABE≌△DBC；（2）求∠DMA的度数．16．如图，AC＝DC，E为AB上一点，EC＝BC，并且∠1＝∠2．（1）求证：△ABC≌△DEC；（2）若∠B＝75°，求∠3的度数．一．选择题（共7小题）1．如图，任意画一个∠A＝60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC＝120°；②AP平分∠BAC；③AP＝PC；④BD+CE＝BC；⑤S△PBA：S△PCA＝AB：AC，其中正确的个数是（）个．A．5B．4C．3D．22．如图，在△ABC中，∠BAC＝60°，BE、CD为△ABC的角平分线．BE与CD相交于点F，FG平分∠BFC，有下列四个结论：①∠BFC＝120°；②BD＝CE；③BC＝BD+CE；④若BE⊥AC，△BDF≌△CE F．其中正确的是（）A．①③B．②③④C．①③④D．①②③④3．如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC＝∠EAD＝90°，BD，CE交于点F，连接A F，下列结论：①BD＝CE②∠AEF＝∠ADF③BD⊥CE④AF平分∠CAD⑤∠AFE＝45°其中结论正确的序号是（）A．①②③④B．①②④⑤C．①③④⑤D．①②③⑤4．如图，在Rt△AEB和Rt△AFC中，∠E＝∠F＝90°，BE＝CF，BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N，∠EAC＝∠F AB．有下列结论：①∠B＝∠C；②ED＝FD；③AC＝BE；④△ACN≌△ABM．其中正确结论的个数是（）A．1个B．2个C．3个D．4个5．在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+2S2+2S3+S4＝（）A．6B．8C．10D．126．如图，△ABC和△CDE都是等边三角形，B，C，D三点在一条直线上，AD与BE相交于点P，AC、B E相交于点M，AD、CE相交于点N，则下列四个结论：①AD＝BE；②∠BMC＝∠ANC；③∠APM＝60°；④CP平分∠MCN．其中，一定正确的结论的个数是（）A．1B．2C．3D．47．如图，△ABC中，∠BAC＝60°，∠BAC的平分线AD与边BC的垂直平分线MD相交于D，DE⊥AB 交AB的延长线于点E，DF⊥AC于点F，现有下列结论：①DE＝DF；②DE+DF＝AD；③MD平分∠E DF；④若AE＝3，则AB+AC＝6．其中正确的个数为（）A．1个B．2个C．3个D．4个二．填空题（共5小题）8．如图，以△ABC的每一条边为边，在边AB的同侧作三个正三角形△ABD、△BCE和△ACF．已知这三个正三角形构成的图形中，甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和．则∠FCE＝°．9．如图，在△ACB中，∠ACB＝90°，AC＝BC，点C的坐标为（﹣2，0），点A的坐标为（﹣8，3），点B的坐标是．10．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，则下列结论中，正确的是（填序号）．①∠AED＝90°；②∠ADE＝∠CDE；③DE＝BE；④AD＝AB+CD．11．如图，已知等腰△ABC中，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下面的结论：①∠APO+∠DCO＝30°；②△OPC是等边三角形；③A C＝AO+AP；④S△ABC＝S四边形AOCP，其中正确的是．（填序号）12．如图，在等腰直角三角形ABC中，∠ACB＝90°，AC＝BC＝4，点D是AB的中点，E、F在射线AC 与射线CB上运动，且满足AE＝CF，则在运动过程中△DEF面积的最小值为．三．解答题（共4小题）13．如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．（1）如图1，若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°，求证：AD＝BE；（2）如图2，若∠ACB＝∠DCE＝90°，CF为△DCE中DE边上的高，试猜想AE，CF，BE之间的关系，并证明你的结论．14．如图所示，等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ．（1）求证：AP＝AQ；（2）试判断△APQ是什么形状的三角形？并说明你的理由．15．（1）【模型启迪】如图1，在△ABC中，D为BC边的中点，连接AD并延长至点H，使DH＝AD，连接BH，则AC与BH的数量关系为，位置关系为．（2）【模型探索】如图2，在△ABC中，D为BC边的中点，连接AD，E为AC边上一点，连接BE交A D于点F，且BF＝AC．求证：AE＝EF．16．如图1，AC＝BC，CD＝CE，∠ACB＝∠DCE＝α，AD、BE相交于点M，连接CM．（1）求证：BE＝AD；（2）用含α的式子表示∠AMB的度数（直接写出结果）；（3）当α＝90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图2，判断△CPQ的形状，并加以证明．1．（2023•甘孜州）如图，AB与CD相交于点O，AC∥BD，只添加一个条件，能判定△AOC≌△BOD的是（）A．∠A＝∠D B．AO＝BO C．AC＝BO D．AB＝CD2．（2023•北京）如图，点A，B，C在同一条直线上，点B在点A，C之间，点D，E在直线AC同侧，AB ＜BC，∠A＝∠C＝90°，△EAB≌△BCD，连接DE．设AB＝a，BC＝b，DE＝c，给出下面三个结论：①a+b＜c；②a+b＞；③（a+b）＞c．上述结论中，所有正确结论的序号是（）A．①②B．①③C．②③D．①②③3．（2022•黑龙江）如图，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件，使△AOB≌△COD．4．（2023•成都）如图，已知△ABC≌△DEF，点B，E，C，F依次在同一条直线上．若BC＝8，CE＝5，则CF的长为．5．（2023•重庆）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC上一点，连接AD．过点B 作BE⊥AD于点E，过点C作CF⊥AD交AD的延长线于点F．若BE＝4，CF＝1，则EF的长度为3．6．（2023•南通）如图，四边形ABCD的两条对角线AC，BD互相垂直，AC＝4，BD＝6，则AD+BC的最小值是．7．（2023•淮安）已知：如图，点D为线段BC上一点，BD＝AC，∠E＝∠ABC，DE∥AC．求证：DE＝B C．8．（2023•吉林）如图，点C在线段BD上，△ABC和△DEC中，∠A＝∠D，AB＝DE，∠B＝∠E．求证：AC＝DC．9．（2022•兰州）如图1是小军制作的燕子风筝，燕子风筝的骨架图如图2所示，AB＝AE，AC＝AD，∠B AD＝∠EAC，∠C＝50°，求∠D的大小．10．（2022•安顺）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝1，D是BC边上的一点，以AD为直角边作等腰Rt△ADE，其中∠DAE＝90°，连接CE．（1）求证：△ABD≌△ACE；（2）若∠BAD＝22.5°时，求BD的长．。

2022届北京市第一次普通高中高三学业水平合格性考试数学试题(解析版)

2022届北京市第一次普通高中高三学业水平合格性考试数学试题(解析版)

2022届北京市第一次普通高中高三学业水平合格性考试数学试题一、单选题1．已知集合{2,1,0,2},{0,1,2}A B =--=，则A B =（ ） A ．{2,1}-- B ．{2,0}- C ．{0,1} D ．{0,2}【答案】D【分析】根据集合的交集运算，可求得答案. 【详解】集合{2,1,0,2},{0,1,2}A B =--=, 故{0,2}A B ⋂=， 故选：D2．在复平面内，复数z 对应的点的坐标是(1,2)-，则z =（ ） A ．2i + B ．2i - C ．12i + D ．12i -【答案】D【分析】利用复数的几何表示即得.【详解】∵复数z 对应的点的坐标是(1,2)-， ∴z =12i -. 故选：D.3．()sin 45-︒=（ ）A B ．C ．12D ．12-【答案】B【分析】利用诱导公式求得正确答案.【详解】()sin 45sin 45-︒=-︒=. 故选：B4．已知函数2(),f x x x =∈R ，则（ ） A ．()f x 是奇函数B ．()f x 是偶函数C ．()f x 既是奇函数又是偶函数D ．()f x 既不是奇函数也不是偶函数【答案】B【分析】由函数奇偶性的定义即可判断答案.【详解】由题意，()()()22R,x f x x x f x ∈-=-==，即函数为偶函数. 故选：B.5．sin cos θθ=（ ）A ．1sin 22θB ．1cos 22θC ．sin 2θD ．cos2θ【答案】A【分析】利用二倍角公式即得.【详解】由二倍角公式可得，sin cos θθ=1sin 22θ.故选：A.6．函数()y f x =的图象如图所示，则不等式()0f x >的解集为（ ）A ．(1,0)-B ．()0,1C ．(1,2)D ．(2,3)【答案】C【分析】结合图象确定正确选项.【详解】由图象可知，当()1,2x ∈时，()0f x >. 故选：C7．某天甲地降雨的概率为0.2，乙地降雨的概率为0.3．假定这一天甲、乙两地是否降雨相互之间没有影响，则两地都降雨的概率为（ ） A ．0.24 B ．0.14 C ．0.06 D ．0.01【答案】C【分析】根据相互独立事件概率计算公式，计算出正确答案. 【详解】依题意，两地都降雨的概率为0.20.30.06⨯=. 故选：C8．下列函数中，在区间(0,)+∞上单调递减的是（ ） A ．()f x x = B ．1()f x x=C ．2()log f x x =D ．()sin f x x =【答案】B【分析】根据基本初等函数的单调性即可求解.【详解】()f x x =在(0,)+∞上单调递增，故A 不符题意； 1()f x x=在(0,)+∞上单调递减，故B 符合题意；2()log f x x =在(0,)+∞上单调递增，故C 不符题意；()sin f x x =在(0,)+∞上不单调，故D 不符题意.故选：B.9．如图，在直三棱柱111ABC A B C -中，ABC 是等腰直角三角形．若14,3AB AC AA ===，则该直三棱柱的体积为（ ）A ．6B ．12C ．18D ．24【答案】D【分析】根据棱柱的体积计算公式，可直接求得答案.【详解】因为在直三棱柱111ABC A B C -中，ABC 是等腰直角三角形，14,3AB AC AA ===，则BAC ∠ 为直角， 故可得：11111114432422AB BC B A C A C V S AA AB AC AA -=⋅=⨯⨯⨯=⨯⨯⨯= , 故选：D10．已知向量(1,0),(1,1)a b ==，则a b ⋅=（ ） A ．0 B ．1 C ．2 D ．3【答案】B【分析】由平面向量数量积的坐标运算即可求得答案. 【详解】11011a b →→⋅=⨯+⨯=. 故选：B.11．“四边形ABCD 为矩形”是“四边形ABCD 为平行四边形”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 【答案】A【分析】利用充分条件与必要条件的定义判断即可. 【详解】若四边形ABCD 是矩形，则它是平行四边形，反之,若四边形ABCD 为平行四边形，四边形ABCD 不一定是矩形，所以“四边形ABCD 为矩形”是“四边形ABCD 为平行四边形”的充分不必要条件. 故选：A.12．函数2()log (3)f x x =-的定义域为（ ） A ．(3,)+∞ B ．(0,)+∞C ．(3),-∞D ．(,0)-∞【答案】A【分析】由真数大于0可得. 【详解】由30x ->，得3x >. 故选：A13．如图，已知四边形ABCD 为矩形，则AB AD +=（ ）A ．BDB ．DBC ．ACD ．CA【答案】C【分析】根据向量加法的平行四边形法则求得正确答案. 【详解】根据向量加法的平行四边形法则可知AB AD AC +=. 故选：C14．甲、乙两个学习小组各有5名同学，两组同学某次考试的语文、数学成绩如下图所示，其中“+”表示甲组同学，“”表示乙组同学．从这两个学习小组数学成绩高于80分的同学中任取一人，此人恰为甲组同学的概率是（ ） A ．0.25 B ．0.3C ．0.5D ．0.75【答案】C【分析】利用古典概型概率计算公式，计算出所求概率. 【详解】根据图象可知，两个小组高于80分的同学各有2人，所以从中任取一人，此人恰为甲组同学的概率是21222=+. 故选：C15．设m ，n 是两条不同的直线，,αβ是两个不同的平面，则下列命题中的真命题为（ ）A ．若,m n αα∥∥，则m n ∥B ．若,m n αα⊥⊥，则m n ∥C ．若,m m αβ∥∥，则αβ∥D ．若,m m αβ⊂∥，则αβ∥【答案】B【分析】在正方体中取直线和平面可排除ACD ，由线面垂直的性质可得B 正确. 【详解】在正方体ABCD EFGH -中，记底面ABCD 为α，EF 为m ，EH 为n ，显然A 不正确；记底面ABCD 为α，EF 为m ，平面CDHG 为β，故排除C ；记底面ABCD 为α，EF 为m ，平面ABFE 为β，可排除D ；由线面垂直的性质可知B 正确. 故选：B16．在ABC 中，1,2,60a c B ===︒，则b =（ ） A ．1 B ．2 C 2D 3【答案】D【分析】根据由余弦定理，可得2222cos b a c ac B =+-，代入数据即得.【详解】由余弦定理，得2222212cos 1221232b ac ac B =+-=+-⨯⨯⨯=， ∴ 3b =故选：D.17．已知a ，b 是实数，且a b >，则（ ） A ．a b -<- B ．22a b <C ．11a b> D ．||||a b >【答案】A【分析】根据不等式的性质确定正确答案.【详解】由于a b >，所以a b -<-，A 选项正确.221,1,,a b a b a b ==-==，BD 选项错误.112,1,a b a b==<，C 选项错误. 故选：A18．已知0,0x y >>，且1xy =，则x y +的最小值为（ ） A ．1 B ．2 C ．3 D ．4【答案】B【分析】由基本不等式即可求得答案.【详解】因为,0x y >，所以2x y +≥=，当且仅当1x y ==时取“=”. 故选：B.19．已知函数()2x f x =，[0,)x ∈+∞，则()f x （ ） A ．有最大值，有最小值 B ．有最大值，无最小值 C ．无最大值，有最小值 D ．无最大值，无最小值【答案】C【分析】根据指数函数的知识确定正确选项.【详解】()2xf x =在[)0,∞+上是增函数，所以最小值为()0f ，没有最大值. 故选：C20．对于正整数n ，记不超过n 的正奇数的个数为()K n ，如(1)1K =，则(2022)K =（ ） A ．2022 B ．2020 C ．1011 D ．1010【答案】C【分析】根据题意求出正奇数的个数即可. 【详解】由题意，不超过2022的正奇数有202210112=个. 故选：C. 二、填空题21．计算：lg 2lg5+=___________． 【答案】1【详解】lg2lg5lg101+==. 故答案为122．某校举行演讲比赛，五位评委对甲、乙两位选手的评分如下：甲 8.1 7.9 8.0 7.9 8.1 乙 7.9 8.0 8.1 8.5 7.5记五位评委对甲、乙两位选手评分数据的方差分别为22,S S 甲乙，则：2S 甲______2S 乙（填“>”，“=”或“<”）． 【答案】<【分析】计算出22,S S 甲乙，由此确定正确答案. 【详解】甲的得分平均值为8.17.98.07.98.18.05++++=，()2210.040.1455S =⨯=甲. 乙的得分平均值为7.98.08.18.57.58.05++++=，()22210.520.120.5255S =⨯+⨯=乙， 所以22S S <甲乙. 故答案为：<23．对于温度的计量，世界上大部分国家使用摄氏温标（℃），少数国家使用华氏温标（℉），两种温标间有如下对应关系：根据表格中数值间呈现的规律，给出下列三个推断： ①25℃对应77℉； ②20-℃对应4-℉；③存在某个温度，其摄氏温标的数值等于其华氏温标的数值． 其中所有正确推断的序号是_____________． 【答案】①②③【分析】根据条件可得 1.832y x =+，然后逐项分析即得. 【详解】设摄氏温标为x ℃，对应的华氏温标为y ℉,根据表格数据可知.,.,.,503268328632181818100200300---===---∴.32180y x -=-，即 1.832y x =+， ∴25℃x =时，77℉y =，20℃x =-时，4℉y =-，故①②正确；由.1832y x x =+=，可得40x =-，即摄氏温标40-℃对应的华氏温标为40-℉，故③正确.故答案为：①②③. 三、双空题24．已知函数()2,0,0,x x f x x <⎧⎪=≥则(1)f -=________；方程()1f x =的解为________．【答案】 －2 1【分析】根据分段函数的性质求解即可. 【详解】(1)f -=2×(－1)＝－2；x ＜0时，f (x )＜0，故f (x )＝1＞0时，x ≥01=，解得x ＝1. 故答案为：－2；1. 四、解答题25．已知函数2()1f x x mx =++（m 是常数）的图象过点(1,2)． (1)求()f x 的解析式；(2)求不等式()21f x x <+的解集． 【答案】(1)2()1f x x =+； (2)(0,2).【分析】（1）把点代入解析式可得0m =，即得； （2）利用一元二次不等式的解法即得. (1)由题意，(1)22f m =+=， 所以0m =．所以()f x 的解析式为2()1f x x =+． (2)不等式()21f x x <+等价于220x x -<． 解得02x <<．所以不等式()21f x x <+的解集为(0,2)．26．已知函数()sin 3f x x π⎛⎫=- ⎪⎝⎭．(1)写出()f x 的最小正周期； (2)求()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值．【答案】(1)2π (2)12【分析】（1）根据解析式写出最小正周期；（2）根据正弦函数的单调性判断函数在区间上的单调性，从而求出最值. (1)()f x 的最小正周期为：221T ππ==. (2) 因为02x π≤≤，所以336x πππ-≤-≤．当36x ππ-=，即2x π=时，()f x 取得最大值12．27．阅读下面题目及其解答过程． 如图，已知正方体1111ABCD A B C D -．（Ⅰ）求证：1AC BD ⊥；（Ⅱ）求证：直线1D D与平面1AB C 不平行．解：（Ⅰ）如图，连接11,BD B D ．因为1111ABCD A B C D -为正方体，所以1D D ⊥平面ABCD ．所以①___________． 因为四边形ABCD 为正方形， 所以②__________． 因为1D D BD D⋂=，所以③____________． 所以1AC BD ⊥．（Ⅱ）如图，设ACBD O =，连接1B O ．假设1//D D 平面1AB C ． 因为1D D ⊂平面11D DBB ，且平面1AB C平面11D DBB =④____________，所以⑤__________． 又11//D D B B，这样过点1B 有两条直线11,B O B B 都与1D D 平行，显然不可能．所以直线1D D与平面1AB C 不平行．以上题目的解答过程中，设置了①~⑤五个空格，如下的表格中为每个空格给出了两个选项，其中只有一个符合推理，请选出符合推理的选项，并填写在答题卡的指定位置（只需填写“A”或“B”）． 空格序号 选项 ①A ．1D D AC⊥ B ．1D D BD⊥②A ．AB BC ⊥ B ．AC BD ⊥ ③A ．1BD ⊥平面1ABC B ．AC ⊥平面11D DBB④A ．1B OB ．1B B⑤ A ．11//D D B OB ．1D D与1B O为相交直线【答案】（Ⅰ）①A ②B ③B ；（Ⅱ）④A ⑤A【分析】结合线面垂直、线面平行的知识对“解答过程”进行分析，从而确定正确答案. 【详解】要证明1AC BD ⊥，可通过证明AC ⊥平面11D DBB 来证得，要证明AC ⊥平面11D DBB ，可通过证明1,D AC A BD D C ⊥⊥来证得， 所以①填A ，②填B ，③填B.平面1AB C 与平面11D DBB 的交线为1B O ，所以④填A ， 由于1//D D 平面1AB C ，因为1D D ⊂平面11D DBB ，且平面1AB C 平面111D DBB B O =，根据线面平行的性质定理可知，11//D D B O ，所以⑤填A.28．给定集合(,0)(0,)D =-∞+∞，()f x 为定义在D 上的函数，当0x <时，24()4xf x x =+，且对任意x D ∈，都有___________．从条件①、条件②、条件③这三个条件中选择一个作为已知，补充在横线处，使()f x 存在且唯一确定．条件①：()()1f x f x -+=； 条件②：()()1f x f x -⋅=； 条件③：()()1f x f x --=． 解答下列问题：（1）写出(1)f -和(1)f 的值；（2）写出()f x 在(0,)+∞上的单调区间；（3）设()()()g x f x m m =-∈R ，写出()g x 的零点个数． 【答案】答案详见解析【分析】判断条件③不合题意.选择条件①②、则先求得当0x >时，()f x 的表达式，然后结合函数的解析式、单调性、零点，对（1）（2）（3）进行分析，从而确定正确答案. 【详解】依题意()f x 的定义域为(,0)(0,)D =-∞+∞， 当0x <时，24()4xf x x =+. 对于条件③，对任意x D ∈，都有()()1f x f x --=，以x -替换x ，则()()1f x f x --=，这与()()1f x f x --=矛盾，所以条件③不合题意. 若选条件①，当0x >时，0x -<，()()224411144x xf x f x x x -=--=-=+++. （1）()()44491,11145145f f --==-=+=++. （2）对于函数()()2404xh x x x =≠+， 任取120x x <<，()()()()()()221221121222221212444444444x x x x x x h x h x x x x x +-+-=-=⨯++++()()22121122221244444x x x x x x x x +--=⨯++()()()()12212122124444x x x x x x x x ---=⨯++ ()()()()122122124444x x x x xx --=⨯++，其中210x x ->，当122x x <<-时，1240x x ->，()()()()12120,h x h x h x h x ->>， 所以()h x 在(),2-∞-上递减.当1220x x -<<<时，1240x x -<，()()()()12120,h x h x h x h x -<<， 所以()h x 在()2,0-上递增.所以在区间(),0∞-，()()()20,10h h x h x -≤<-≤<.同理可证得：()h x 在()0,2上递增，在()2,+∞上递减，()()()02,01h x h h x <≤<≤. 当0x >时，()()24114xf x h x x =+=++， 由上述分析可知，()f x 在()0,2上递增，在()2,+∞上递减.且()12f x <≤. （3）()()()0,g x f x m m f x =-==，由（2）的分析可画出()f x 的大致图象如下图所示，所以，当1m <-或01m ≤≤或2m >时，()g x 的零点个数是0； 当1m =-或2m =时，()g x 的零点个数是1； 当10m -<<或12m <<时，()g x 的零点个数是2．若选条件②，当0x >时，0x -<，由()()1f x f x -⋅=得()()2144x f x f x x+==--，（1）()()441451,114544f f -+-==-==-+-. （2）对于函数()()2404xh x x x =<+， 根据上述分析可知：()h x 在(),2-∞-上递减，在()2,0-上递增， 且在区间(),0∞-，()()()20,10h h x h x -≤<-≤<. 对于()()2404x f x x x+=>-，任取120x x <<，()()2222122112122144441444x x x x f x f x x x x x ⎛⎫++++-=-=- ⎪--⎝⎭()2212121212414x x x x x x x x -+-=⋅()()12212112414x x x x x x x x ---=⋅()()122112414x x x x x x --=⋅.其中210x x ->.当1202x x <<<时，()()()()12121240,0,x x f x f x f x f x -<-<<，()f x 递增；当122x x <<时，()()()()12121240,0,x x f x f x f x f x ->->>，()f x 递减.所以()f x 的增区间为()0,2，减区间为()2,+∞.且()()21f x f ≤=-. （3）()()()0,g x f x m m f x =-==，结合上述分析画出()f x 的大致图象如下图所示，所以当0m ≥时，()g x 的零点个数是0；当0m <时，()g x 的零点个数是2．【点睛】利用函数的单调性的定义求函数的单调性，主要是计算出()()12f x f x -的符号.求解函数零点问题，可利用分离参数法，结合函数图象来进行求解.。

高中数学复习专题讲座(第16讲)三角函数式的化简与求值

高中数学复习专题讲座(第16讲)三角函数式的化简与求值

题目高中数学复习专题讲座三角函数式的化简与求值 高考要求三角函数式的化简和求值是高考考查的重点内容之一 通过本节的学习使考生掌握化简和求值问题的解题规律和途径，特别是要掌握化简和求值的一些常规技巧，以优化我们的解题效果，做到事半功倍 重难点归纳1 求值问题的基本类型 ①给角求值，②给值求值，③给式求值，④求函数式的最值或值域，⑤化简求值2 技巧与方法 ①要寻求角与角关系的特殊性，化非特角为特殊角，熟练准确地应用公式 ②注意切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用 ③对于条件求值问题，要认真寻找条件和结论的关系，寻找解题的突破口，很难入手的问题，可利用分析法 ④求最值问题，常用配方法、换元法来解决 快速阅读记忆：英语单词速记：/?id=330 更多资料下载：典型题例示范讲解例1不查表求sin 220°+cos 280°+3cos20°cos80°的值命题意图 本题主要考查两角和、二倍角公式及降幂求值的方法，对计算能力的要求较高知识依托 熟知三角公式并能灵活应用 错解分析 公式不熟，计算易出错技巧与方法 解法一利用三角公式进行等价变形；解法二转化为函数问题，使解法更简单更精妙，需认真体会解法一 sin 220°+cos 280°+3sin 220°cos80°=21 (1－cos40°)+21(1+cos160°)+ 3sin20°cos80° =1－21cos40°+21cos160°+3sin20°cos(60°+20°)=1－21cos40°+21(cos120°cos40°－sin120°sin40°)+3sin20°(cos60°cos20°－sin60°sin20°) =1－21cos40°－41cos40°－43sin40°+43sin40°－23sin 220°=1－43cos40°－43(1－cos40°)= 41 解法二 设x =sin 220°+cos 280°+3sin20°cos80°y =cos 220°+sin 280°－3cos20°sin80°，则 x +y =1+1－3sin60°=21， x －y =－cos40°+cos160°+3sin100° =－2sin100°sin60°+3sin100°=0 ∴x =y =41， 即x =sin 220°+cos 280°+3sin20°cos80°41 例2设关于x 的函数y =2cos 2x －2a cos x －(2a +1)的最小值为f (a )，试确定满足f (a )=21的a 值，并对此时的a 值求y 的最大值 命题意图 本题主要考查最值问题、三角函数的有界性、计算能力以及较强的逻辑思维能力知识依托 二次函数在给定区间上的最值问题错解分析 考生不易考查三角函数的有界性，对区间的分类易出错 技巧与方法 利用等价转化把问题化归为二次函数问题，还要用到配方法、数形结合、分类讲座等解 由y =2(cos x －2a )2－2242+-a a 及cos x ∈［－1，1］得f (a )＝⎪⎪⎩⎪⎪⎨⎧≥-<<-----≤)2( 41)22( 122)2(12a a a a a a∵f (a )=21, ∴1－4a =21⇒a =81∉［2,+∞)或 －22a －2a －1=21，解得a =－1(2,2)∈-，此时，y =2(cos x +21)2+21， 当cos x =1时，即x =2k π，k ∈Z ，y max =5例3已知函数f (x )=2cos x sin(x +3π)－3sin 2x +sin x cos x(1)求函数f (x )的最小正周期；(2)求f (x )的最小值及取得最小值时相应的x 的值； (3)若当x ∈［12π，127π］时，f (x )的反函数为f －1(x )，求f -－1(1)的值 命题意图 本题主要考查三角公式、周期、最值、反函数等知识，还考查计算变形能力，综合运用知识的能力知识依托 熟知三角函数公式以及三角函数的性质、反函数等知识错解分析 在求f -－1(1)的值时易走弯路 技巧与方法 等价转化，逆向思维解 (1)f (x )=2cos x sin(x +3π)－3sin 2x +sin x cos x=2cos x (sin x cos3π+cos x sin3π)－3sin 2x +sin x cos x=2sin x cos x +3cos2x =2sin(2x +3π)∴f (x )的最小正周期T =π (2)当2x +3π=2k π－2π，即x =k π－125π(k ∈Z )时，f (x )取得最小值－2 (3)令2sin(2x +3π)=1，又x ∈［27,2ππ］,∴2x +3π∈［3π,23π］,∴2x +3π=65π，则x =4π，故f -－1(1)=4π例4 已知2π＜β＜α＜43π,cos(α－β)=1312,sin(α+β)=－53,求sin2α的值_________解法一 ∵2π＜β＜α＜43π,∴0＜α－β4π π＜α+β＜43π,∴54sin(),cos().135αβαβ-=+==- ∴sin2α=sin ［(α－β)+(α+β)］=sin(α－β)cos(α+β)+cos(α－β)sin(α+β).6556)53(1312)54(135-=-⨯+-⨯=解法二 ∵sin(α－β)=135,cos(α+β)=－54,∴sin2α+sin2β=2sin(α+β)cos(α－β)=－6572sin2α－sin2β=2cos(α+β)sin(α－β)=－6540∴sin2α=56)65406572(21=--学生巩固练习1 已知方程x 2+4ax +3a +1=0(a ＞1)的两根均tan α、tan β，且α，β∈(－2,2ππ)，则tan2βα+的值是( )A21B －2 C34 D21或－2 2 已知sin α=53，α∈(2π，π)，tan(π－β)= 21，则tan(α－2β)=______3 设α∈(43,4ππ)，β∈(0，4π)，cos(α－4π)=53，sin(43π+β)=135，则sin(α+β)=_________4 不查表求值:.10cos 1)370tan 31(100sin 130sin 2︒+︒+︒+︒5 已知cos(4π+x )=53，(1217π＜x ＜47π)，求x x x tan 1sin 22sin 2-+的值6 已知α－β=38π，且α≠k π(k ∈Z ) 求)44(sin 42sin2csc )cos(12βπαααπ-----的最大值及最大值时的条件7 如右图，扇形OAB 的半径为1，中心角60°，四边形PQRS 是扇形的内接矩形，当其面积最大时，求点P 的位置，并求此最大面积8 已知cos α+sin β=3，sin α+cos β的取值范围是D ，x ∈D ，求函数y =10432log 21++x x 的最小值，并求取得最小值时x 的值参考答案1 解析 ∵a ＞1，tan α+tan β=－4a ＜0 tan α+tan β=3a +1＞0,又α、β∈(－2π,2π)∴α、β∈(－2π,θ),则2βα+∈(－2π,0), 又tan(α+β)=342tan 12tan2)tan(,34)13(14tan tan 1tan tan 2=β+α-β+α=β+α=+--=βα-β+α又a a , 整理得2tan 222tan 32-β+α+β+α=0 解得tan 2β+α=－2 答案 B2 解析 ∵sin α=53,α∈(2π,π),∴cos α=－54 则tan α=－43,又tan(π－β)=21可得tan β=－21,2212()2tan 42tan 2.11tan 31()2βββ⨯-===---- 234()tan tan 743tan(2)341tan tan 2241()()43αβαβαβ-----===+⋅+-⨯- 答案247 3 解析 α∈(43,4ππ),α－4π∈(0, 2π),又cos(α－4π36556)sin(.655613554)1312(53)43sin()4sin()43cos()4cos()]43()4cos[(]2)43()4sin[()sin(.1312)43cos(,135)43sin().,43(43).4,0(,54)4sin(=β+α=⨯+-⨯-=β+π⋅π-α+β+π⋅π-α-=β+π+π-α-=π-β+π+π-α=β+α∴-=β+π∴=β+πππ∈β+π∴π∈β=π-α∴即答案6556 4 答案 2752853)54(257)4cos()4sin(2sin sin cos cos )cos (sin sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 54)4sin(,2435,471217.257)4(2cos 2sin ,53)4cos(:.522=-⨯=++=-+=-+=-+-=+∴<+<∴<<=+-=∴=+x x x xx xx x x x x x x x x x x x x x x x x ππππππππππ又解 2)322sin(22)21()322sin(4.32243824,3822cos 2sin 42)2sin 2(sin 2)2sin 2121(42cos 2cos 22sin 2)22cos(142sin 1)cos 1(2sin )44(sin 42sin 2csc )cos(1:.62222-π-α-=--⨯π-α=∴π-α=π-α=β-α∴π=β-α-β-αβ+α=-β+α=β--αα⋅α=β-π--α-α+α=β-π-α-αα-π-=t t 令解π≠αk （k ∈Z ）,322322π-π≠π-α∴k （k ∈Z ） ∴当,22322π-π=π-αk 即34π+π=αk （k ∈Z ）时,)322sin(π-α的最小值为－17 解 以OA 为x 轴 O 为原点，建立平面直角坐标系， 并设P 的坐标为(cos θ,sin θ)，则｜PS ｜=sin θ 直线OB 的方程为y =3x ，直线PQ 的方程为y =sin θ 联立解之得Q (33sin θ；sin θ)，所以｜PQ ｜=cos θ－33sin θ 于是S PQRS =sin θ(cos θ－33sin θ)=33(3sin θcos θ－sin 2θ)=33(23sin2θ－2cos 1θ-)=33(23sin2θ+21cos2θ－21)= 33sin(2θ+6π) ∵0＜θ＜3π,∴6π＜2θ+6π＜65π ∴21＜sin(2θ+6π)≤1∴sin(2θ+6π)=1时，PQRS 面积最大，且最大面积是63，此时，θ=6π，点P 为 AB 的中点，P (21,23)8 解 设u =sin α+cos β 则u 2+(3)2=(sin α+cos β)2+(cos α+sin β)2=2+2sin(α+β)≤4∴u 2≤1,－1≤u ≤1 即D =［－1,1］,设t =32+x ,∵－1≤x ≤1,∴1≤t x 232-t2max 0.5min 0.50.50.514248242,,8log 0,5log log log 8,821.2t M t t tt t M t y M M y t x ∴===≤=++====>∴======- 当且仅当即在时是减函数时此时 课前后备注。

2023苏州中考数学第16题

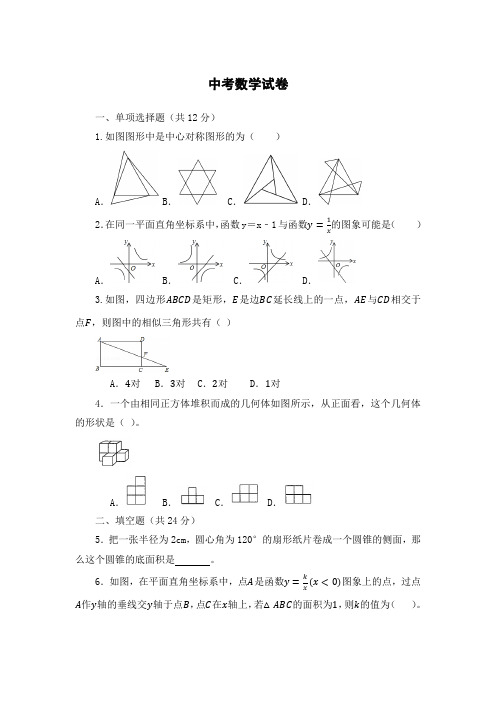
2023苏州中考数学第16题

中考数学试卷一、单项选择题（共12分）1.如图图形中是中心对称图形的为（）A．B． C． D．的图象可能是（）2．在同一平面直角坐标系中，函数y＝x﹣1与函数y=1xA．B． C．D．3.如图，四边形ABCD是矩形，E是边BC延长线上的一点，AE与CD相交于点F，则图中的相似三角形共有（）A．4对 B．3对C．2对D．1对4．一个由相同正方体堆积而成的几何体如图所示，从正面看，这个几何体的形状是（）。

A．B．C．D．二、填空题（共24分）5．把一张半径为2cm，圆心角为120°的扇形纸片卷成一个圆锥的侧面，那么这个圆锥的底面积是。

(x<0)图象上的点，过点6．如图，在平面直角坐标系中，点A是函数y=kxA作y轴的垂线交y轴于点B，点C在x轴上，若△ABC的面积为1，则k的值为（）。

三、解答题7.如图，D，E分别是△ABC的边AB，AC上的点，DE∥BC，AB＝7，AD＝5，DE＝10，求BC的长．8．如图，在矩形ABCD中，AB=4，BC=6，M是BC的中点，DE⊥AM于点E。

(1)求证：△ADE∽△MAB；(2)求DE的长。

9.如图，在四边形A BCD中，A D∥BC，A B⊥BC，点E在A B上，∠DEC=90°。

求证：△ADE∽△BEC。

10.已知△ABC和△DEF中，有ABDE =BCEF=CAFD=23，且△DEF和△ABC的周长之差为15厘米，求△ABC和△DEF的周长。

11．吉万家超市今年的营业额为280万元，计划两年后的营业额为403.2万元，求平均每年增长的百分率？12.已知关于x的方程x2+kx﹣2＝0的一个解与方程x+1x−1=3解相同。

（1）求k的值；（2）求方程x2+kx﹣2＝0的另一个解．13．如图，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限，B，C，在x轴的正半轴上（C在B的右侧），BC=2，AB=2根号3，△ADC与△ABC关于AC所在的直线对称。

高三数学填空题练习试题集

高三数学填空题练习试题集

高三数学填空题练习试题答案及解析1.函数的定义域为_____________．【答案】(0，1]【解析】有，可得0<x≤1【考点】函数的定义域2.设f(x)是定义在R上的奇函数，当x<0时，f(x)＝x＋e x(e为自然对数的底数)，则f(ln 6)的值为________．【答案】ln 6－【解析】由f(x)是奇函数得f(ln 6)＝－f(－ln 6)＝－(－ln 6)－e－ln 6＝ln 6－.3.函数的最大值为 .【答案】【解析】函数的定义域为，设，，则，所以，当时，.【考点】函数最值.4.若x，y满足约束条件，则的最大值为 .【答案】【解析】画出可行域，如图所示，将目标函数变形为，当取到最大值时，直线的纵截距最大，即将直线经过可行域，尽可能向上移动到点时，．【考点】线性规划.5.如图所示点是抛物线的焦点，点、分别在抛物线及圆的实线部分上运动，且总是平行于轴，，则的周长的取值范围是_______________.【答案】.【解析】易知圆的圆心坐标为，则圆心为抛物线的焦点，圆与抛物线在第一象限交于点，作抛物线的准线，过点作垂直于直线，垂足为点，由抛物线的定义可知，则，当点位于圆与轴的交点时，取最大值，由于点在实线上运动，因此当点与点重合时，取最小值为，此时与重合，由于、、构成三角形，因此，所以，因此的周长的取值范围是.6.设，向量且，则．【答案】【解析】因为a⊥c,b∥c，所以有2x-4=0且2y+4=0，解得x=2,y=-2，即，所以，则．7.甲、乙两地都位于长江下游，根据天气预报记录知，一年中下雨天甲市占20%，乙市占18%，假定在这段时间内两市是否降雨相互之间没有影响，则甲、乙两市同时下雨的概率为________．【答案】0.036【解析】设甲市下雨为事件A，乙市下雨为事件B，由题设知，事件A与B相互独立，且P(A)＝0.2，P(B)＝0.18，则P(AB)＝P(A)P(B)＝0.2×0.18＝0.036.8.某程序框图如右图所示，则输出的结果S为．【答案】【解析】第一次运行,，不满足；第二次运行，，不满足；第三次运行，，满足，输出S为.【考点】算法与程序框图9.设x>0,y>0,a=x+y,b=·,则a与b的大小关系是.【答案】b<a【解析】当sin θ=0时,cos2θ=1,∴b=x<x+y=a即b<a,当cos θ=0时,sin2θ=1,b=y<x+y=a,即b<a,当sin θ≠0且cos θ≠0时,∵x>0,y>0,∴x<x+y,y<x+y,∴<,<,∴b=·<·==x+y=a.综上b<a.10.已知G是△ABC的重心,O是空间与G不重合的任一点,若++=λ,则λ=.【答案】3【解析】因为+=,+=,+=,且++=0,所以++=3.11.设a>0,b>0,若lga和lgb的等差中项是0,则+的最小值是.【答案】2【解析】由已知得lga+lgb=0,即ab=1,于是+==a+b≥2=2,当且仅当a=b=1时取等号,故+的最小值是2.12.若点P是曲线y＝x2－ln x上任意一点，则点P到直线y＝x－2的最小值为________．【答案】【解析】y′＝2x－，令y′＝1，得方程2x2－x－1＝0，解得x＝－(舍去)或x＝1，故与直线y＝x－2平行且与曲线y＝x2－ln x相切的直线的切点坐标为(1，1)，该点到直线y＝x－2的距离d ＝即为所求13.若函数f(x)＝－x2＋4x－3ln x在[t，t＋1]上不单调，则t的取值范围是______．【答案】(0,1)∪(2,3)【解析】对f(x)求导，得f′(x)＝－x＋4－＝.由f′(x)＝0得函数f(x)的两个极值点为1,3，则只要这两个极值点有一个在区间(t，t＋1)内，函数f(x)在区间[t，t＋1]上就不单调，所以t<1<t＋1或t<3<t＋1，解得0<t<1或2<t<3.14.在平面直角坐标系中，若中心在坐标原点上的双曲线的一条准线方程为，且它的一个顶点与抛物线的焦点重合，则该双曲线的渐进线方程为 .【答案】【解析】因为抛物线的焦点为所以又所以而双曲线的渐近线方程为即.解答本题需注意双曲线的焦点位置.【考点】双曲线的渐近线及准线，抛物线焦点.15.已知定义在上的偶函数满足:,且当时,单调递减,给出以下四个命题:①;②为函数图像的一条对称轴;③函数在单调递增;④若关于的方程在上的两根,则.以上命题中所有正确的命题的序号为_______________.【答案】①②④【解析】∵，∴当时，，∴，又∵函数是偶函数，∴，∴①正确；∵，，∴，∴，又是函数图像的对称轴，∴是函数图像的对称轴，∴②正确；∵函数的周期是4，∴在上的单调性与上的单调性相同，∴在上为减函数，∴③错误；∵是函数图像的对称轴，∴方程的两根关于对称，∴，∴④正确.【考点】1.函数的周期性；2.函数的奇偶性；3.函数的对称性；4.函数的单调性.16.已知点，过点的直线总与线段有公共点，则直线的斜率取值范围为______（用区间表示）.【答案】【解析】如图，，根据斜率的定义可知，当直线逆时针转时，斜率增大，当直线顺时针转时，斜率减小，故直线的斜率取值范围为.【考点】直线斜率的计算、直线斜率的定义.17.函数的最小正周期为 .【答案】【解析】因为，，所以，函数的最小正周期为.【考点】三角函数的和差倍半公式，三角函数的性质.18.设与抛物线的准线围成的三角形区域（包含边界）为，为内的一个动点，则目标函数的最大值为 .【答案】3【解析】由题意，抛物线的准线，它和不等式共同围成的三角形区域为，目标函数为，作出可行域如下图，由图象可知当直线经过点时，直线的截距最小，此时最大，点的坐标为，此时，故答案为：3．【考点】简单线性规划．19.曲线与直线所围成的平面图形的面积为.【答案】【解析】画出图形可知，所求面积,而,，，故.【考点】定积分求面积.20.在正项等比数列中，，，则满足的最大正整数的值为 .【答案】12【解析】设正项等比数列首项为，公比为，由题意可得解得，，故其通项公式为.记，由，即化简得，，因此只须即，解得由于为正整数，因此最大为的整数部分，也就是12．故答案为12.【考点】等比数列的求和公式，一元二次不等式的解法.21.在中，分别是的对边，已知，若，则的面积等于 .【答案】【解析】因为，所以，，∴.由余弦定理得，∴.∴.【考点】1.余弦定理；2.三角形面积公式；3.平方关系.22.在处有极大值，则常数的值为________.【答案】6【解析】由题意知在处导数为零且时，，而，所以，解得，而当时，，不合题意，所以.【考点】利用导数求函数的极值、利用导数判断函数单调性.23.在展开式中的系数为,则实数的值为 .【答案】【解析】通项公式：，所以展开式中的系数为，解得：.【考点】1.二项式通项；2.二项式系数.24.设AB是椭圆的长轴，点C在上，且，若AB=4，，则的两个焦点之间的距离为________【答案】【解析】不妨设椭圆的标准方程为，于是可算得，得．【考点】考查椭圆的定义及运算，属容易题。

高三数学不等式试题答案及解析

高三数学不等式试题答案及解析

高三数学不等式试题答案及解析1.已知，则A．n＜m＜1B．1＜n＜m C．1＜m＜n D．m＜n＜1【答案】B【解析】函数是减函数，所以故选B2.现将一个质点随即投入区域中，则质点落在区域内的概率是【答案】【解析】略3.不等式的解集为或，则实数的取值范围．【答案】【解析】略4.如果实数满足条件，那么的最大值为（）A．B．C．D．【答案】B【解析】解：当直线过点(0，-1)时，最大，故选B5.一元二次不等式的解集为，则的最小值为．【答案】【解析】由已知得，解得，又，则。

【考点】一元二次不等式的解法及基本不等式的应用。

6.设，则函数的最小值是（）A．2B．C．D．3【答案】C【解析】因为，所以，令，则，由于，故知函数是减函数，因此；故选C．【考点】1．换元法；2．函数的最值．7.若变量x，y满足约束条件，则的最小值为．【答案】-6【解析】在坐标系中画出约束条件的可行域，得到的图形是一个平行四边形，目标函数z=x+2y，变化为，当直线沿着y轴向上移动时，z的值随着增大，当直线过A点时，z取到最小值，由与的交点得到，∴，故答案为：﹣6．【考点】简单线性规划．8.已知的大小关系是（）A．a<c<b B．b<a<e C．c<a<b D．a<b<c【答案】D【解析】因为.所以,故D正确.【考点】指数函数,对数函数.9.设，则，，的大小关系是__________________．（用“<”连接）【答案】【解析】令，则，∴函数为增函数，∴，∴，∴，∴，又，∴．【考点】利用导数研究函数的单调性、作差比较大小．10.对一切实数x，不等式恒成立，则实数a的取值范围是（）A．（-，-2）B．[-2，+）C．[-2,2]D．[0，+）【答案】B【解析】对一切实数x，不等式恒成立，等价于对任意实数，恒成立，因此有或，解得，故选B．【考点】不等式恒成立，二次函数的性质．【名师点晴】本题考查不等式恒成立问题，由于题中含有绝对值符号，因此解题的关键是换元思想，设，这样原来对一切实数恒成立，转化为对所有非负实数，不等式恒成立，也即二次函数在区间上的最小值大于或等于0，最终问题又转化为讨论二次函数在给定区间的最值问题，解题中始终贯彻了转化与化归的数学思想．11.设不等式组所表示的区域为，函数的图象与轴所围成的区域为，向内随机投一个点，则该点落在内的概率为．【答案】【解析】如图所示区域是及其内部．即，所以其面积为．区域是图中阴影部分，面积为．所以所求概率为．【考点】1几何概型概率；2定积分的几何意义．12.已知实数x、y满足，如果目标函数的最小值为－1，则实数m＝（）．A．6B．5C．4D．3【答案】B【解析】将化为，作出可行域和目标函数基准直线（如图所示），当直线向左上方平移时，直线在轴上的截距增大，即变小，所以当直线过点时，取得最小值，即，解得；故选B．【考点】简单的线性规划．13.已知正数满足，则的最小值为（）A．2B．0C．-2D．-4【答案】D【解析】作出题设约束条件表示的可行域，如图内部（含边界），作直线，直线的纵截距是，因此向上平移直线，当过点时，取得最小值，故选D．【考点】简单的线性规划问题．14.已知，满足约束条件若的最小值为，则（）A．B．C．D．【答案】B【解析】先根据约束条件画出可行域，设，将最大值转化为轴上的截距，当直线经过点时，最小，由得：，代入直线，解得故答案选【考点】线性规划．15.选修4-5：不等式选讲已知函数．（1）当时，解不等式；（2）若时，，求实数的取值范围．【答案】（1）（2）【解析】（1）把要解的不等式等价转化为与之等价绝对值不等式，再求出此不等式的解集，即得所求（2）当时，即由此得讨论即可得到实数的取值范围试题解析：(1）当时，不等式为当时，不等式化为，不等式不成立；当时，不等式化为，解得；当时，不等式化为，不等式必成立．综上，不等式的解集为．（2）当时，即由此得当时，的最小值为7，所以的取值范围是【考点】绝对值不等式16.已知函数，其中且．（1）当时，若无解，求的范围；（2）若存在实数，（），使得时，函数的值域都也为，求的范围．【答案】（1）；（2）．【解析】（1）分析题意可知，不等式无解等价于恒成立，参变分离后即再进一步等价为，即可求解；（2）分析函数的单调性，可知其为单调递增函数，换元令，从而可将问题等价转化为二次方程根的分布，列得关于的不等式即可求解．试题解析：（1）∵，∴无解，等价于恒成立，即恒成立，即，求得，∴；（2）∵是单调增函数，∴，即，问题等价于关于的方程有两个不相等的解，令，则问题等价于关于的二次方程在上有两个不相等的实根，即，即，得．【考点】1．恒成立问题；2．二次方程的根的分布；3．转化的数学思想．17.选修4-5：不等式选讲已知函数（1）解不等式（2）若不等式对任意的恒成立，求实数的取值范围．【答案】（1）；（2）．【解析】（1）解绝对值不等式，主要是分类讨论，分类标准由绝对值的定义确定；（2）不等式对任意的恒成立，即的最小值满足，由（1）的讨论，可得．试题解析：（1），当时，由，此时无解当时，由当时，由综上，所求不等式的解集为（2）由（1）的函数解析式可以看出函数在区间上单调递减，在区间上单调递增，故在处取得最小值，最小值为，不等式，对任意的恒成立即，解得故的取值范围为．【考点】解绝对值不等式，不等式恒成立问题，函数的最值．18.若不等式组表示的平面区域为，不等式表示的平面区域为．现随机向区域内撒下一粒豆子，则豆子落在区域内的概率为．【答案】．【解析】不等式组表示的平面区域为，不等式表示的平面区域为．的面积为，其中满足的图形面积为，所以随机向区域内撒下一粒豆子，则豆子落在区域内的概率为．【方法点晴】本题属于几何概型的问题，通常在几何概型中，事件的概率计算公式为：用几何概率公式计算概率时，关键是构造出随机事件所对应的几何图形，并对几何图形进行相应的几何度量．因此本题解题思路清晰，作出图形，计算相关三角形的面积，代入上述公式便得答案．19.实数满足，则的最大值是（）A．2B．4C．6D．8【答案】B【解析】试题解析：依题画出可行域如图，可见及内部区域为可行域，令，则为直线在轴上的截距，由图知在点处取最大值是4，在处最小值是-2，所以，所以的最大值是4，故选B．【考点】简单线性规划20.选修4－5：不等式选讲已知命题“，”是真命题，记的最大值为，命题“，”是假命题，其中．（Ⅰ）求的值；（Ⅱ）求的取值范围．【答案】（Ⅰ）．（Ⅱ）．【解析】试题解析：（Ⅰ）因为“，”是真命题，所以，恒成立，又，所以恒成立，所以，．又因为，“”成立当且仅当时．因此，，于是．（Ⅱ）由（Ⅰ）得，因为“，”是假命题，所以“，”是真命题．因为（），因此，，此时，即时．即，，由绝对值的意义可知，．【考点】不等式选讲21.已知实数满足不等式组则的最小值为______．【答案】【解析】由得,则当直线在y轴上的截距最大时取得最小值,所以当直线经过A（2,3）时,z最小,即当x=2,y=3,取得最小值-4．【考点】线性规划22.若关于的不等式组，表示的平面区域是直角三角形区域，则正数的值为（）A．1B．2C．3D．4【答案】B【解析】如图，易知直线经过定点，又知道关于的不等式组，表示的平面区域是直角三角形区域，且，所以，解得，故选B.【考点】线性规划.23.已知函数，且关于的不等式的解集为R．（1）求实数的取值范围；（2）求的最小值．【答案】（1）；（2）9【解析】（1）由绝对值的性质可知，由此解不等式即可求出结果；（2）由（1），根据基本不等式的性质，即可求出结果.试题解析：解：（1）依题意，（2）时，当且仅当，即时等号成立。

2023年数学高考复习真题演练(2021-2022年高考真题)16 极值与最值(含详解)

2023年数学高考复习真题演练(2021-2022年高考真题)16 极值与最值(含详解)

专题16极值与最值【考点预测】 知识点一：极值与最值 1．函数的极值函数()f x 在点0x 附近有定义，如果对0x 附近的所有点都有0()()f x f x <，则称0()f x 是函数的一个极大值，记作0()y f x =极大值．如果对0x 附近的所有点都有0()()f x f x >，则称0()f x 是函数的一个极小值，记作0()y f x =极小值．极大值与极小值统称为极值，称0x 为极值点．求可导函数()f x 极值的一般步骤 （1）先确定函数()f x 的定义域； （2）求导数()f x '； （3）求方程()0f x '=的根；（4）检验()f x '在方程()0f x '=的根的左右两侧的符号，如果在根的左侧附近为正，在右侧附近为负，那么函数()y f x =在这个根处取得极大值；如果在根的左侧附近为负，在右侧附近为正，那么函数()y f x =在这个根处取得极小值.注①可导函数()f x 在点0x 处取得极值的充要条件是：0x 是导函数的变号零点，即0()0f x '=，且在0x 左侧与右侧，()f x '的符号导号.②0()0f x '=是0x 为极值点的既不充分也不必要条件，如3()f x x =，(0)0f '=，但00x =不是极值点.另外，极值点也可以是不可导的，如函数()f x x =，在极小值点00x =是不可导的，于是有如下结论：0x 为可导函数()f x 的极值点0()0f x '⇒=；但0()0f x '=⇒0x 为()f x 的极值点.2．函数的最值函数()y f x =最大值为极大值与靠近极小值的端点之间的最大者；函数()f x 最小值为极小值与靠近极大值的端点之间的最小者．导函数为21212()()()()f x ax bx c a x x x x m x x n =++=--<<<（1）当0a >时，最大值是1()f x 与()f n 中的最大者；最小值是2()f x 与()f m 中的最小者． （2）当0a <时，最大值是2()f x 与()f m 中的最大者；最小值是1()f x 与()f n 中的最小者．一般地，设()y f x =是定义在[]m n ，上的函数，()y f x =在()m n ，内有导数，求函数()y f x =在[]m n ，上的最大值与最小值可分为两步进行：（1）求()y f x =在()m n ，内的极值（极大值或极小值）； （2）将()y f x =的各极值与()f m 和()f n 比较，其中最大的一个为最大值，最小的一个为最小值． 注①函数的极值反映函数在一点附近情况，是局部函数值的比较，故极值不一定是最值；函数的最值是对函数在整个区间上函数值比较而言的，故函数的最值可能是极值，也可能是区间端点处的函数值；②函数的极值点必是开区间的点，不能是区间的端点；③函数的最值必在极值点或区间端点处取得. 【方法技巧与总结】（1）若函数()f x 在区间D 上存在最小值()min f x 和最大值()max f x ，则 不等式()f x a >在区间D 上恒成立()min f x a ⇔>； 不等式()f x a ≥在区间D 上恒成立()min f x a ⇔≥； 不等式()f x b <在区间D 上恒成立()max f x b ⇔<； 不等式()f x b ≤在区间D 上恒成立()max f x b ⇔≤；（2）若函数()f x 在区间D 上不存在最大（小）值，且值域为(),m n ，则不等式()()()f x a f x a >≥或在区间D 上恒成立m a ⇔≥．不等式()()()f x b f x b <≤或在区间D 上恒成立m b ⇔≤．（3）若函数()f x 在区间Ｄ上存在最小值()min f x 和最大值()max f x ，即()[],f x m n ∈，则对不等式有解问题有以下结论：不等式()a f x <在区间D 上有解()max a f x ⇔<； 不等式()a f x ≤在区间D 上有解()max a f x ⇔≤； 不等式()a f x >在区间D 上有解()min a f x ⇔>； 不等式()a f x ≥在区间D 上有解()min a f x ⇔≥；（4）若函数()f x 在区间D 上不存在最大（小）值，如值域为(),m n ，则对不等式有解问题有以下结论：不等式()()()a f x f x <≤或a 在区间D 上有解a n ⇔<不等式()()()b f x f x >≥或b 在区间D 上有解b m ⇔>（5）对于任意的[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212max max f x g x f x g x ≤⇔≤； （6）对于任意的[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212min min f x g x f x g x ≥⇔≥； （7）若存在[]1,x a b ∈，对于任意的[]2m,x n ∈，使得()()()()1212min min f x g x f x g x ≤⇔≤； （8）若存在[]1,x a b ∈，对于任意的[]2m,x n ∈，使得()()()()1212max max f x g x f x g x ≥⇔≥； （9）对于任意的[]1,x a b ∈，[]2m,x n ∈使得()()()()1212max min f x g x f x g x ≤⇔≤；（10）对于任意的[]1,x a b ∈，[]2m,x n ∈使得()()()()1212min max f x g x f x g x ≥⇔≥；（11）若存在[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212min max f x g x f x g x ≤⇔≤（12）若存在[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212max min f x g x f x g x ≥⇔≥． 【题型归纳目录】题型一：求函数的极值与极值点 题型二：根据极值、极值点求参数 题型三：求函数的最值（不含参） 题型四：求函数的最值（含参） 题型五：根据最值求参数题型六：函数单调性、极值、最值得综合应用 题型七：不等式恒成立与存在性问题 【典例例题】题型一：求函数的极值与极值点例1．（2022·江西·上饶市第一中学模拟预测（文））已知函数()()()1xf x a x a =--∈e R ．当1a =时，求函数()y f x =的极值；例2．（2022·湖北·襄阳四中模拟预测）设()e sin x f x x =.(1)求()f x 在[],ππ-上的极值； (2)若对[]12,0,x x π∀∈，12x x ≠，都有()()1222120f x f x a x x -+>-成立，求实数a 的取值范围. 例3．（2022·天津市咸水沽第一中学模拟预测）已知函数ln()()eln (e 2.71828ax f x x x=-=……自然对数底数）. (1)当e a =时，求函数f （x ）的单调区间； (2)当e a >时，（i ）证明：()f x 存在唯一的极值点：（ii ）证明：()(1)e f x a <- 例4．（2022·江西师大附中三模（理））已知函数()sin ,()e xxf x xg x =-为()f x 的导函数． (1)判断函数()g x 在区间π0,2⎛⎫ ⎪⎝⎭上是否存在极值，若存在，请判断是极大值还是极小值；若不存在，说明理由；(2)求证：函数()f x 在区间(,π)-∞上只有两个零点．例5．（2022·江苏苏州·模拟预测）函数()sin cos f x x x x =--．(1)求函数()f x 在(),2ππ-上的极值；(2)证明：()()ln F x f x x =-有两个零点．【方法技巧与总结】1．因此，在求函数极值问题中，一定要检验方程()0f x '=根左右的符号，更要注意变号后极大值与极小值是否与已知有矛盾．2．原函数出现极值时，导函数正处于零点，归纳起来一句话：原极导零．这个零点必须穿越x 轴，否则不是极值点．判断口诀：从左往右找穿越（导函数与x 轴的交点）；上坡低头找极小，下坡抬头找极大．题型二：根据极值、极值点求参数例6．（2022·四川·绵阳中学实验学校模拟预测（文））若函数()322f x x ax bx a =--+在1x =处有极值10，则a b -=（ ） A ．6B ．15-C ．6-或15D ．6或15-例7．（2022·江苏南通·模拟预测）已知函数()()()e x f x x a x b =--在x a =处取极小值，且()f x 的极大值为4，则b =（ ） A ．-1B ．2C ．-3D ．4例8．（2022·四川绵阳·二模（文））若2x =是函数()()2224ln f x x a x a x =+--的极大值点，则实数a 的取值范围是（ ） A ．(),2-∞-B ．()2,-+∞C ．()2,+∞D ．()2,2-例9．（2022·河南·模拟预测（文））已知函数()2ln f x x ax =-的极值为12-，则=a （ ）A ．eB ．1e 2C ．12D ．14例10．（2022·河南·高三阶段练习（文））若函数()()22e xx a f x x =++⋅在R 上无极值，则实数a 的取值范围（ ）A ．()2,2-B ．(-C ．⎡-⎣D ．[]22-,例11．（2022·四川省南充高级中学高三阶段练习（理））已知函数322()3f x x mx nx m =-++在1x =-处取得极值0，则m n +=（ ） A ．2B ．7C ．2或7D ．3或9例12．（2022·全国·高三专题练习）函数()(ln )xe f x a x x x =--在(0,1)内有极值，则实数a 的取值范围是（ ）A ．(,)e -∞B ．(0,)eC ．(,)e +∞D ．[),e +∞例13．（2022·陕西·西北工业大学附属中学模拟预测（理））已知函数()()24143e xf x ax a x a ⎡⎤=-+++⎣⎦，若2x =是()f x 的极小值点，则实数a 的取值范围是（ ）A ．2,3⎛⎤-∞ ⎥⎝⎦B ．1,2⎛⎫+∞ ⎪⎝⎭C ．(),0-∞D ． ()1,-+∞例14．（2022·全国·高三专题练习）已知函数()321132f x x ax x =-+在区间1,32⎛⎫⎪⎝⎭上既有极大值又有极小值，则实数a 的取值范围是（ ） A ．()2,+∞B ．[)2,+∞C ．52,2⎛⎫ ⎪⎝⎭D ．102,3⎛⎫ ⎪⎝⎭例15．（2022·全国·高三专题练习）函数()()()321112132f x x m x m x =-++-在()0,4上无极值，则m ＝______．例16．（2022·吉林长春·模拟预测（文））已知函数()sin f x ax x =+，()0,πx ∈．(1)当1a =时，过()0,1做函数()f x 的切线，求切线方程；(2)若函数()f x 存在极值，求极值的取值范围．例17．（2022·北京市第十二中学三模）已知函数()ln ,af x x a x=+∈R .(1)当1a =时，求函数()f x 的单调递增区间； (2)设函数()1()f x g x x-=，若()g x 在21,e ⎡⎤⎣⎦上存在极值，求a 的取值范围. 例18．（2022·天津·耀华中学二模）已知函数()ln (0)xae f x x x a x =+->.(1)若1a =，求函数()f x 的单调区间；(2)若()f x 存在两个极小值点12,x x ，求实数a 的取值范围.例19．（2022·河北·石家庄二中模拟预测）已知函数()32f x x ax bx =-++．(1)当0,1a b ==时，证明：当()1,x ∈+∞时，()ln f x x <；(2)若2b a =，函数()f x 在区间()1,2上存在极大值，求a 的取值范围．题型三：求函数的最值（不含参）例20．（2022·江苏徐州·模拟预测）函数12()||cos f x x x =-的最小值为_____________．例21．（2022·全国·高三专题练习）函数()e ln 1x x f x x x -=+的最小值为______．例22．（2022·四川·模拟预测（文））对任意a ∈R ，存在(0,)b ∈+∞，使得1eln a b +=，则b a -的最小值为_________．例23．（2022·河南郑州·三模（文））()x f x e x =-在区间[]1,1-上的最小值是（ ）A ．11e+B ．1C ．1e +D ．1e -例24．（2022·全国·高三专题练习）函数1(1),[3,4]x y x e x +=+∈-的最大值为（ ） A ．22e -B ．55eC ．54eD ．1e --例25．（2022·全国·高三专题练习）已知函数()()1cos 0f x ax x a =-≠. （1）当1a =时，求曲线()y f x =在点()()0,0f 处的切线方程；（2）求函数()f x 在0,4π⎡⎤⎢⎥⎣⎦的最小值.例26．（2022·山东·临沭县教育和体育局高二期中）已知函数32(),1f x x bx x a x =+-+=是()f x 的一个极值点．(1)求b 的值；(2)当[2,2]x ∈-时，求函数()f x 的最大值．题型四：求函数的最值（含参）例27．（2022·北京通州·高二期中）已知函数()32392f x x x x =--+．(1)求函数()f x 的单调区间；(2)求函数()f x 在区间[]0,a 上的最小值．例28．（2022·河南·高二阶段练习（理））已知函数f (x )=x -m ln x -m . (1)讨论函数f (x )的单调性；(2)若函数f (x )有最小值g (m )，证明：g (m ) 1e≤在(0)+∞，上恒成立. 例29．（2021·江苏·高二单元测试）已知函数()2ln f x x ax =-．（1）讨论()f x 的单调性；（2）当0a >时，求()f x 在区间[]1,2上的最大值．题型五：根据最值求参数例30．（2022·河北·模拟预测）已知0a >，函数()12ag x x x+=+-在[)2,+∞上的最小值为1，则=a __________． 例31．（2022·山西运城·模拟预测（理））已知函数()32112132x x f x x =+-+，若函数()f x 在()22,23a a -+上存在最小值.则实数a 的取值范围是________.例32．（2022·浙江湖州·高三期末）若函数()()2221e x f x x x a +=+++存在最小值，则实数a 的取值范围是___________.例33．（2022·陕西·模拟预测（理））若函数3()31f x x x =--在区间(2,23)a a -+上有最大值，则实数a 的取值范围是_________．题型六：函数单调性、极值、最值得综合应用例34．（2022·全国·高三专题练习（理））已知函数f （x ）＝e x ＋ax ·sin x ． (1)求y ＝f （x ）在x ＝0处的切线方程； (2)当a ＝－2时，设函数g （x ）＝()f x x，若x 0是g （x ）在（0，π）上的一个极值点，求证：x 0是函数g （x ）在（0，π）上的唯一极小值点，且e －2<g （x 0）<e ．例35．（2022·四川泸州·三模（文））已知函数()313f x x ax =-+，R a ∈．(1)讨论函数()f x 的单调性；(2)若()()xg x f x e =⋅有且只有一个极值点，求a 的取值范围．例36．（2022·广东·深圳市光明区高级中学模拟预测）已知函数()e sin 1xf x ax x =-+-.(1)当2a =时，求函数()f x 的极值点； (2)当12a ≤<时，试讨论函数()f x 的零点个数.例37．（2022·北京市十一学校高三阶段练习）已知函数()()()211e 12ax f x x ax a x =--+-(1)当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程； (2)判断函数()f x 的极值点的个数，并说明理由.例38．（2022·重庆巴蜀中学高三阶段练习）已知函数2()e (3)ln xf x x x x=---． (1)求曲线()y f x =在点(1,(1))f 处的切线方程；(2)证明：()f x 存在唯一极大值点0x ，且()072e 22f x --<<-．例39．（2022·全国·模拟预测（文））已知函数()()2ln 1f x x x x =---． (1)证明：()f x 存在唯一的极值点； (2)m 为整数，()f x m >，求m 的最大值．题型七：不等式恒成立与存在性问题例40．（2022·辽宁·二模）若关于x 的不等式ln 1e x x x ax ++≤恒成立，则实数a 的取值范围为___________. 例41．（2022·北京·景山学校模拟预测）已知函数()ln 2f x x x ax =++．(1)当0a =时，求()f x 的极值；(2)若对任意的21,e x ⎡⎤∈⎣⎦，()0f x ≤恒成立，求实数a 的取值范围．例42．（2022·新疆克拉玛依·三模（文））已知函数()ln f x x x =，()()23g x x ax a R =-+-∈.(1)求函数()f x 的单调递增区间； (2)若对任意()0,x ∞∈+，不等式()()12f xg x ≥恒成立，求a 的取值范围. 例43．（2022·陕西·西北工业大学附属中学模拟预测（文））已知函数()()122211ln 2x f x x x x -+=+-++-.(1)求函数()f x 的单调区间；(2)若对1x ∀、[]20,2x ∈，使()()1212f x f x a-≤-恒成立，求a 的取值范围.例44.（2022·内蒙古赤峰·三模（文））已知函数()()ln 1f x x x =+. (1)求()f x 的最小值；(2)若()()212f x x m x -++-恒成立，求实数m 的取值范围.【方法技巧与总结】在不等式恒成立或不等式有解条件下求参数的取值范围，一般利用等价转化的思想其转化为函数的最值或值域问题加以求解，可采用分离参数或不分离参数法直接移项构造辅助函数．【过关测试】 一、单选题1．（2022·全国·哈师大附中模拟预测（文））已知0x 是函数()12sin cos 3f x x x x =-的一个极值点，则20tan x 的值是（ ） A ．1B ．12C ．37D ．572．（2022·宁夏·吴忠中学三模（理））下列函数中，既是奇函数又存在极值的是（ ） A ．y x =B ．()ln y x =-C ．e x y x =+D ．4y x x=+3．（2022·河南新乡·二模（文））已知0a >，函数()2313f x a x x =-的极小值为43-，则=a （ ）AB ．1C D4．（2022·内蒙古包头·一模（理））设0m ≠ ，若x m =为函数()()()2f x m x m x n =--的极小值点，则（ ） A ．m n >B ．m n <C ．1nm< D ．1n m> 5．（2022·河南·模拟预测（文））当x m =时，函数()3232ln f x x x x x =-+-取得最小值，则m =（ ）A ．23B ．1C ．32D ．26．（2022·四川凉山·三模（理））函数()2sin 2a f x x x =-，若()f x 在(0,)2π上有最小值，则实数a 的取值范围是（ ） A ．()0,∞+B ．()0,1C ．(),0∞-D ．()1,0-7．（2016·天津市红桥区教师发展中心高三学业考试）已知函数2()(4)()f x x x a =--，a 为实数，(1)0f '-=，则()f x 在[]22-,上的最大值是（ ） A ．92B ．1C ．35D ．5027-8．（2022·宁夏·高三阶段练习（文））若函数()22e xx x af x +-=在区间(,1)a a +上存在最小值，则实数a 的取值范围为（ ） A ．(),1-∞-B ．()2,1--C ．⎛-∞ ⎝⎭D ．1⎫-⎪⎪⎝⎭二、多选题9．（2022·重庆·三模）已知函数()21e xx x f x ++=（e 为自然对数的底数，e 2.72≈），则关于函数()f x ，下列结论正确的是（ ） A ．有2个零点B ．有2个极值点C ．在()0,1单调递增D ．最小值为110．（2022·湖北·宜城市第一中学高三阶段练习）已知()e xx f x =．则下列说法正确的有（ ）A ．函数()y f x =有唯一零点0x =B ．函数()y f x =的单调递减区间为()(),01,-∞⋃+∞C ．函数()y f x =有极大值1eD ．若关于x 的方程()f x a =有三个不同的根．则实数a 的取值范围是10,e ⎛⎫⎪⎝⎭11．（2022·福建省德化第一中学模拟预测）设函数()f x 的定义域为R ，()000x x ≠是()f x 的极大值点，以下结论一定正确的是（ ） A ．x R ∀∈，()()0f x f x ≥ B ．0x -是()f x -的极大值点 C ．0x -是()f x -的极小值点D ．0x -是()f x --的极小值点12．（2022·全国·模拟预测）已知函数()()e e e x xf x a x x -=-+的图象关于直线12x =对称，则下列说法正确的是（ ） A ．e a = B ．()f x 在1,2⎛⎫+∞ ⎪⎝⎭上单调递增C ．12x =为()f x 的极小值点 D ．()f x 仅有两个零点三、填空题13．（2022·全国·高三专题练习）函数()()()321112132f x x m x m x =-++-在()0,4上无极值，则m ＝______．14．（2022·天津河西·二模）若函数32()9f x x ax x =+--在1x =-处取得极值，则()2f =____________． 15．（2022·湖南·长郡中学高三阶段练习）函数()1ln f x x x=+的极值点为___________. 16．（2022·全国·高三专题练习）已知函数()3,,43,,x x a f x x x x a ≥⎧=⎨-<⎩则下列命题正确的有：___________.①若()f x 有两个极值点，则0a =或112a <<②若()f x 有极小值点，则12a >③若()f x 有极大值点，则12a >-④使()f x 连续的a 有3个取值四、解答题17．（2021·四川省叙永第一中学校高三阶段练习（文））已知函数32()f x x ax bx c =+++在1x =与23x =-时，都取得极值．(1)求a ，b 的值；(2)若3(1)2f -=，求()f x 的单调增区间和极值． 18．（2022·河南郑州·高三阶段练习（文））已知函数()21xf x x a-=+． (1)若0a =，求曲线()y f x =在点()()1,1f 处的切线方程；(2)若()f x 在1x =-处取得极值，求()f x 的单调区间及其最大值与最小值． 19．（2022·陕西·武功县普集高级中学高三期末（文））已知函数()ln a f x x x=-.(1)若3a =-，求函数()f x 的极值；(2)若函数()f x 在3,e e ⎡⎤⎣⎦上单调递增，求a 的取值范围.20．（2022·全国·高三专题练习）已知函数()32213f x x x ax =+++在()1,0-上有两个极值点，12,x x ，且12x x <． (1)求实数a 的取值范围；(2)证明：当102x -<<时，()1112f x >．21．（2022·北京·人大附中三模）设函数()()24143e xf x ax a x a ⎡⎤=-+++⎣⎦.(1)若曲线()y f x =在点()()1,1f 处的切线与x 轴平行，求a ； (2)若()f x 在2x =处取得极大值，求a 的取值范围.22．（2022·浙江嘉兴·模拟预测）已知函数2()e e,x f x ax a =+-∈R ．（注：e 2.71828=是自然对数的底数）(1)当1a =时，求曲线()y f x =在点(1,(1))f 处的切线方程； (2)若()f x 只有一个极值点，求实数a 的取值范围；(3)若存在b ∈R ，对与任意的x ∈R ，使得()f x b≥恒成立，求-a b 的最小值．专题16极值与最值【考点预测】 知识点一：极值与最值 1．函数的极值函数()f x 在点0x 附近有定义，如果对0x 附近的所有点都有0()()f x f x <，则称0()f x 是函数的一个极大值，记作0()y f x =极大值．如果对0x 附近的所有点都有0()()f x f x >，则称0()f x 是函数的一个极小值，记作0()y f x =极小值．极大值与极小值统称为极值，称0x 为极值点．求可导函数()f x 极值的一般步骤 （1）先确定函数()f x 的定义域； （2）求导数()f x '； （3）求方程()0f x '=的根；（4）检验()f x '在方程()0f x '=的根的左右两侧的符号，如果在根的左侧附近为正，在右侧附近为负，那么函数()y f x =在这个根处取得极大值；如果在根的左侧附近为负，在右侧附近为正，那么函数()y f x =在这个根处取得极小值.注①可导函数()f x 在点0x 处取得极值的充要条件是：0x 是导函数的变号零点，即0()0f x '=，且在0x 左侧与右侧，()f x '的符号导号.②0()0f x '=是0x 为极值点的既不充分也不必要条件，如3()f x x =，(0)0f '=，但00x =不是极值点.另外，极值点也可以是不可导的，如函数()f x x =，在极小值点00x =是不可导的，于是有如下结论：0x 为可导函数()f x 的极值点0()0f x '⇒=；但0()0f x '=⇒0x 为()f x 的极值点.2．函数的最值函数()y f x =最大值为极大值与靠近极小值的端点之间的最大者；函数()f x 最小值为极小值与靠近极大值的端点之间的最小者．导函数为21212()()()()f x ax bx c a x x x x m x x n =++=--<<<（1）当0a >时，最大值是1()f x 与()f n 中的最大者；最小值是2()f x 与()f m 中的最小者． （2）当0a <时，最大值是2()f x 与()f m 中的最大者；最小值是1()f x 与()f n 中的最小者．一般地，设()y f x =是定义在[]m n ，上的函数，()y f x =在()m n ，内有导数，求函数()y f x =在[]m n ，上的最大值与最小值可分为两步进行：（1）求()y f x =在()m n ，内的极值（极大值或极小值）； （2）将()y f x =的各极值与()f m 和()f n 比较，其中最大的一个为最大值，最小的一个为最小值． 注①函数的极值反映函数在一点附近情况，是局部函数值的比较，故极值不一定是最值；函数的最值是对函数在整个区间上函数值比较而言的，故函数的最值可能是极值，也可能是区间端点处的函数值；②函数的极值点必是开区间的点，不能是区间的端点；③函数的最值必在极值点或区间端点处取得. 【方法技巧与总结】（1）若函数()f x 在区间D 上存在最小值()min f x 和最大值()max f x ，则 不等式()f x a >在区间D 上恒成立()min f x a ⇔>； 不等式()f x a ≥在区间D 上恒成立()min f x a ⇔≥； 不等式()f x b <在区间D 上恒成立()max f x b ⇔<； 不等式()f x b ≤在区间D 上恒成立()max f x b ⇔≤；（2）若函数()f x 在区间D 上不存在最大（小）值，且值域为(),m n ，则不等式()()()f x a f x a >≥或在区间D 上恒成立m a ⇔≥．不等式()()()f x b f x b <≤或在区间D 上恒成立m b ⇔≤．（3）若函数()f x 在区间Ｄ上存在最小值()min f x 和最大值()max f x ，即()[],f x m n ∈，则对不等式有解问题有以下结论：不等式()a f x <在区间D 上有解()max a f x ⇔<； 不等式()a f x ≤在区间D 上有解()max a f x ⇔≤； 不等式()a f x >在区间D 上有解()min a f x ⇔>； 不等式()a f x ≥在区间D 上有解()min a f x ⇔≥；（4）若函数()f x 在区间D 上不存在最大（小）值，如值域为(),m n ，则对不等式有解问题有以下结论：不等式()()()a f x f x <≤或a 在区间D 上有解a n ⇔<不等式()()()b f x f x >≥或b 在区间D 上有解b m ⇔>（5）对于任意的[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212max max f x g x f x g x ≤⇔≤； （6）对于任意的[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212min min f x g x f x g x ≥⇔≥； （7）若存在[]1,x a b ∈，对于任意的[]2m,x n ∈，使得()()()()1212min min f x g x f x g x ≤⇔≤； （8）若存在[]1,x a b ∈，对于任意的[]2m,x n ∈，使得()()()()1212max max f x g x f x g x ≥⇔≥； （9）对于任意的[]1,x a b ∈，[]2m,x n ∈使得()()()()1212max min f x g x f x g x ≤⇔≤；（10）对于任意的[]1,x a b ∈，[]2m,x n ∈使得()()()()1212min max f x g x f x g x ≥⇔≥；（11）若存在[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212min max f x g x f x g x ≤⇔≤（12）若存在[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212max min f x g x f x g x ≥⇔≥． 【题型归纳目录】题型一：求函数的极值与极值点 题型二：根据极值、极值点求参数 题型三：求函数的最值（不含参） 题型四：求函数的最值（含参） 题型五：根据最值求参数题型六：函数单调性、极值、最值得综合应用 题型七：不等式恒成立与存在性问题 【典例例题】题型一：求函数的极值与极值点例1．（2022·江西·上饶市第一中学模拟预测（文））已知函数()()()1xf x a x a =--∈e R ．当1a =时，求函数()y f x =的极值； 【解析】由题知，当1a =时，()e (1)x f x x =--，x ∈R∴()e 1xf x '=-，令()0f x '=，0x =． ∴(),0x ∈-∞时，()0f x '<，()f x 单调递减；()0,x ∈+∞时，()0f x '>，()f x 单调递增．∴0x =是()f x 的极小值点，∴()f x 的极小值为()02f =，无极大值．例2．（2022·湖北·襄阳四中模拟预测）设()e sin xf x x =.(1)求()f x 在[],ππ-上的极值； (2)若对[]12,0,x x π∀∈，12x x ≠，都有()()1222120f x f x a x x -+>-成立，求实数a 的取值范围. 【答案】(1)极小值为42eπ34π (2)e ,2ππ⎡⎫+∞⎪⎢⎣⎭ 【解析】 【分析】（1）直接求导计算即可．（2）将问题转化为()()222211f x ax f x ax +>+，构造新函数()()2g x f x ax =+在[]0,π上单调递增即可，然后参变分离或者分类讨论都可以． (1)由()()e sin cos 0xf x x x '=+≤，[],x ππ∈-得()f x 的单调减区间是,4ππ⎡⎤--⎢⎥⎣⎦，3,4ππ⎡⎤⎢⎥⎣⎦，同理，()f x 的单调增区间是3,44ππ⎡⎤-⎢⎥⎣⎦.故()f x 的极小值为442e f ππ⎛⎫-= ⎪⎝⎭343e 42f ππ⎛⎫=⎪⎝⎭. (2)由对称性，不妨设120x x π≤<≤， 则()()1222120f x f x a x x -+>-即为()()222211f x ax f x ax +>+. 设()()2g x f x ax =+，则()g x 在[]0,π上单调递增，故()()e sin cos 20xg x x x ax '=++≥在[]0,π上恒成立. 方法一：（含参讨论）设()()()e sin cos 20xh x g x x x ax '==++≥，则()010h =>，()e 20h a πππ=-+≥，解得e 2a ππ≥. ()()2e cos xh x x a '=+，()()0210h a '=+>，()()2e h a ππ'=-.①当e a π≥时，()()2e cos sin x h x x x ''=-⎡⎤⎣⎦，故，当0,4x π⎡⎤∈⎢⎥⎣⎦时，()()2e cos sin 0x h x x x ''=-≥⎡⎤⎣⎦，()h x '递增； 当,4x ππ⎡⎤∈⎢⎥⎣⎦时，()()2e cos sin 0x h x x x ''=-≤⎡⎤⎣⎦，()h x '递减； 此时，()()(){}()()min 0,20h x h h h a e πππ''''≥==-≥，()()h x g x '=在[]0,π上单调递增，故()()()010h x g x g ''=≥=>，符合条件.②当e e 2a πππ≤<时，同①，当0,4x π⎡⎤∈⎢⎥⎣⎦时，()h x '递增；当,4x ππ⎡⎤∈⎢⎥⎣⎦时，()h x '递减；∵()()02104h h a π⎛⎫''>=+> ⎪⎝⎭，()()2e 0h a ππ'=-<，∴由连续函数零点存在性定理及单调性知，0,4x ππ⎛⎫∃∈ ⎪⎝⎭，()00h x '=.于是，当[)00,x x ∈时，()0h x '>，()()h x g x '=单调递增；当(]0,x x π∈时，()0h x '<，()()h x g x '=单调递减.∵()010h =>，()e 20h a πππ=-+≥，∴()()()(){}min 0,0g x h x h h π'=≥≥，符合条件.综上，实数a 的取值范围是e ,2ππ⎡⎫+∞⎪⎢⎣⎭.方法二：（参变分离）由对称性，不妨设120x x π≤<≤，则()()1222120f x f x a x x -+>-即为()()222211f x ax f x ax +>+. 设()()2g x f x ax =+，则()g x 在[]0,π上单调递增， 故()()e sin cos 20xg x x x ax '=++≥在[]0,π上恒成立.∵()010g '=>，∴()(),e sin cos 20xg x x x ax '=++≥在[]0,π上恒成立()e sin cos 2x x x a x+⇔-≤，(]0,x π∀∈.设()()e sin cos x x x h x x+=，(]0,x π∈，则()()2e 2cos sin cos x x x x x h x x --'=，(]0,x π∈.设()2tan 1x x x ϕ=--，0,,22x πππ⎛⎫⎛⎤∈⋃ ⎪ ⎥⎝⎭⎝⎦，则()212cos x x ϕ'=-，0,,22x πππ⎛⎫⎛⎤∈⋃ ⎪ ⎥⎝⎭⎝⎦.由()0x ϕ'>，0,,22x πππ⎛⎫⎛⎤∈⋃ ⎪ ⎥⎝⎭⎝⎦，得()x ϕ在0,4π⎛⎫ ⎪⎝⎭，3,4ππ⎛⎤⎥⎝⎦上单调递增；由()0x ϕ'<，0,,22x πππ⎛⎫⎛⎤∈⋃ ⎪ ⎥⎝⎭⎝⎦，得()x ϕ在,42ππ⎛⎫ ⎪⎝⎭，3,24ππ⎛⎤⎥⎝⎦上单调递减.故0,2x π⎛⎫∈ ⎪⎝⎭时()2042x ππϕϕ⎛⎫≤=-< ⎪⎝⎭；,2x π⎛⎤∈π ⎥⎝⎦时()33042x ππϕϕ⎛⎫≥=> ⎪⎝⎭. 从而，()cos 2cos sin cos 0x x x x x x ϕ=--<，0,,22x πππ⎛⎫⎛⎤∈⋃ ⎪ ⎥⎝⎭⎝⎦，又2x π=时，2cos sin cos 10x x x x --=-<，故()()2e 2cos sin cos 0x x x x x h x x --'=<，(]0,x π∈，()()e sin cos x x x h x x+=，(]0,x π∈单调递减，()()min e h x h πππ==-，(]0,x π∈. 于是，e e 22a a ππππ-≤-⇔≥.综上，实数a 的取值范围是e ,2ππ⎡⎫+∞⎪⎢⎣⎭. 例3．（2022·天津市咸水沽第一中学模拟预测）已知函数ln()()eln (e 2.71828ax f x x x=-=……自然对数底数）. (1)当e a =时，求函数f （x ）的单调区间；(2)当e a >时，（i ）证明：()f x 存在唯一的极值点： （ii ）证明：()(1)e f x a <-【答案】(1)函数()f x 的单调递增区间为10,e ⎛⎫ ⎪⎝⎭，单调递减区间为1,e ⎛⎫+∞ ⎪⎝⎭(2)证明见详解 【解析】 【分析】（1）求导，利用导数判断函数单调性；（2）利用导数判断单调性，利用零点存在性定理判断零点，进而确定极值点，利用零点代换结合函数最值处理极值的范围． (1)21ln()e ()ax x f x x--'=，构建()1ln()e x ax x ϕ=-- 当e a =时，则()1ln(e )e x x x ϕ=--在()0,∞+上单调递减，且1()0eϕ=当10,e ⎛⎫∈ ⎪⎝⎭x 时，()0x ϕ>，当1,e x ⎛⎫∈+∞ ⎪⎝⎭时，()0x ϕ<则函数()f x 的单调递增区间为10,e ⎛⎫ ⎪⎝⎭，单调递减区间为1,e ⎛⎫+∞ ⎪⎝⎭(2)（i ）由（1）可知：当e a >时，()ϕx 在()0,∞+上单调递减11e ()1ln 0,()10e a a a ϕϕ=-<=->∴()ϕx 在()0,∞+内存在唯一的零点011,e x a ⎛⎫∈ ⎪⎝⎭当()00,x x ∈时，()0x ϕ>，当()0,x x ∈+∞时，()0x ϕ<则函数()f x 的单调递增区间为()00,x ，单调递减区间为()0,x +∞ ∴()f x 存在唯一的极值点0x（ii ）由（i ）可知：0000ln(())el (n )x f x f x x x a -≤=∵001ln()e 0ax x --=，即001e ln()x ax -=000000ln()e 1)e (ln eln x f x x x x x a ==---，且011,e x a ⎛⎫∈ ⎪⎝⎭∵()el e 1n g x x x --=在11,e a ⎛⎫⎪⎝⎭单调递减则()1eln e g x g a a a ⎛⎫<=+- ⎪⎝⎭构建()()()e 1eln e x h x x x =-->，则()()e 1e 0x xh x -'-=>当e x >时恒成立则()h x 在()e,+∞上单调递增，则()()()e e 20e h x h ≥=->则()()e 1eln e e x x x x ->+->，即()1e eln e a a a ->+- ∴()(1)e f x a <-例4．（2022·江西师大附中三模（理））已知函数()sin ,()ex xf x xg x =-为()f x 的导函数． (1)判断函数()g x 在区间π0,2⎛⎫ ⎪⎝⎭上是否存在极值，若存在，请判断是极大值还是极小值；若不存在，说明理由；(2)求证：函数()f x 在区间(,π)-∞上只有两个零点． 【答案】(1)存在；极小值 (2)证明见解析 【解析】 【分析】（1）转化为判断导函数是否存在变号零点，对()g x '求导后，判断()g x '的单调性，结合零点存在性定理可得结果；（2）当0x <时，利用单调性得()0f x <恒成立，此时()f x 无零点；当0x =时，()0f x =；当0πx <<时，利用导数得到单调性，结合零点存在性定理可得()f x 在(0,π)上只有一个零点.由此可证结论正确. (1)由()sin e x xf x x =-，可得2e e 1()cos cos (e )e x x x x x xg x x x --=-=-， 则2e (1)e 2π()sin sin ,0,(e )e 2x x x x x x g x x x x ----⎛⎫'=+=+∈ ⎪⎝⎭， 令2()sin e x x h x x -=+，其中π0,2x ⎛⎫∈ ⎪⎝⎭，可得2e (2)e 3()cos cos 0(e )e x x x x x x h x x x ---'=+=+>， 所以()h x 在π0,2⎛⎫ ⎪⎝⎭上单调递增，即()g x '在π0,2⎛⎫ ⎪⎝⎭上单调递增，因为π2π2π2(0)20,102e g g -⎛⎫''=-<=+> ⎪⎝⎭，所以存在0π0,2x ⎛⎫∈ ⎪⎝⎭，使得()00g x '=，当()00,x x ∈时，()0,()g x g x '<单调递减；当0,2x x π⎛⎫∈ ⎪⎝⎭时，()0,()g x g x '>单调递增，所以当0x x =时，函数()g x 取得极小值． (2)由e ()sin x x f x x =-，当0x <时，11e x x ->，所以()()f x g x '==1cos ex xx --0>，所以()f x 在(,0)-∞上为增函数，所以()(0)0f x f <=，此时函数()f x 在(,0)-∞上没有零点；当0x =时，可得00(0)sin 00e f =-=，所以0x =是函数()f x 的一个零点；当0πx <<时，由()1()sin e sin e exx x x f x x x x =-=- ，令()e sin ,(0,π)xm x x x x =-∈，可得()1e (sin cos )x m x x x '=-+，令()ϕx 1e (sin cos )x x x =-+ 则()e (sin cos )e (cos sin )2e cos x x x x x x x x x ϕ'=-+--=-，当π0,2x ⎛⎫∈ ⎪⎝⎭，可得()2e cos 0x x x ϕ'=-<；当π,π2x ⎛⎫∈ ⎪⎝⎭，可得()2e cos 0x x x ϕ'=->，即()m x '在π0,2⎛⎫⎪⎝⎭上单调递减，在π,π2⎛⎫ ⎪⎝⎭上单调递增，又因为ππ2π1e 0,(π)1e 02m m ⎛⎫''=-<=+> ⎪⎝⎭，所以存在1π,π2⎛⎫∈ ⎪⎝⎭x 使得()10m x '=，当()10,x x ∈时，()0m x '<；当()1,πx x ∈时，()0m x '>，又因为()1(0)0,(π)π0m x m m <==>，所以存在()21,πx x ∈使得()20m x =，即2x 是函数()f x 的一个零点． 综上可得，函数()f x 在(,π)-∞上有且仅有两个零点． 【点睛】关键点点睛：第二问中，分段讨论并利用导数和零点存在性定理求解是解题关键. 例5．（2022·江苏苏州·模拟预测）函数()sin cos f x x x x =--．(1)求函数()f x 在(),2ππ-上的极值；(2)证明：()()ln F x f x x =-有两个零点．【答案】(1)极大值，12π-；极小值，1-；(2)详见解析. 【解析】 【分析】（1）由题可得()14f x x π⎛⎫'=- ⎪⎝⎭，进而可得；（2）当30,4x π⎛⎫∈ ⎪⎝⎭时，利用导数可得函数的最小值，进而可得函数有两个零点，当37[,)44x ππ∈，7[,)4x π∈+∞时，利用导数可得()0F x >，即得. (1)∵()sin cos f x x x x =--，∴()1cos sin 14f x x x x π⎛⎫=-+=+' ⎪⎝⎭，,2x ππ⎛⎫∈- ⎪⎝⎭，由()0f x '=，可得2x π=-，或0x =，∴,2x ππ⎛⎫∈-- ⎪⎝⎭，()()0,f x f x '>单调递增，,02x π⎛⎫∈- ⎪⎝⎭，()()0,f x f x '<单调递减，0,2x π⎛⎫∈ ⎪⎝⎭，()()0,f x f x '>单调递增，∴2x π=-时，函数()f x 有极大值()122f ππ-=-，0x =时，函数()f x 有极小值(0)1f =-；(2)∵()()ln sin cos ln ,0F x f x x x x x x x =-=--->，∴()1()1cos sin ,0h x F x x x x x'==-+->，∴()2211sin cos 4h x x x x x x π⎛⎫'=++=++ ⎪⎝⎭，当30,4x π⎛⎫∈ ⎪⎝⎭时，()()0,h x h x '>单调递增，即()F x '单调递增，又42()10,()2042F F ππππ''=-<=->，故存在0,42x ππ⎛⎫∈ ⎪⎝⎭，0()0F x '=，所以()()()00,,0,x x F x F x '∈<单调递减，()()()03,,0,4x x F x F xπ'∈<单调递增， ∴30,4x π⎛⎫∈ ⎪⎝⎭时，函数()()()0min 11sin1cos10F x F x F =<=--<，2222(e )e sin e cos e 20F ----=--+>，333()ln 0444F πππ=->， 故30,4x π⎛⎫∈ ⎪⎝⎭时，()()ln F x f x x =-有两个零点，当37[,)44x ππ∈0,()sin cos ln ln ln 44x F x x x x x x x x x x ππ⎛⎫⎛⎫+≤=---=+-≥- ⎪ ⎪⎝⎭⎝⎭，对于函数()ln x x x ϕ=-，则()1110x x x xϕ-'=-=>，又()10ϕ=， ∴37[,)44x ππ∈，()()10x ϕϕ>=，即()0F x >，此时函数()()ln F x f x x =-没有零点，当7[,)4x π∈+∞时，()sin cos ln ln ln 4F x x x x x x x x x x π⎛⎫=---=+-≥ ⎪⎝⎭，由上可知77()ln 044F x ππ≥>，故当7[,)4x π∈+∞时，函数()()ln F x f x x =-没有零点， 综上，函数()()ln F x f x x =-有两个零点． 【点睛】利用导数研究零点问题：（1）确定零点的个数问题：可利用数形结合的办法判断交点个数，如果函数较为复杂，可用导数知识确定极值点和单调区间从而确定其大致图象；（2）方程的有解问题就是判断是否存在零点的问题，可参变分离，转化为求函数的值域问题处理.可以通过构造函数的方法，把问题转化为研究构造的函数的零点问题；（3）利用导数硏究函数零点或方程根，通常有三种思路：①利用最值或极值研究；②利用数形结合思想研究；③构造辅助函数硏究.【方法技巧与总结】1．因此，在求函数极值问题中，一定要检验方程()0f x '=根左右的符号，更要注意变号后极大值与极小值是否与已知有矛盾．2．原函数出现极值时，导函数正处于零点，归纳起来一句话：原极导零．这个零点必须穿越x 轴，否则不是极值点．判断口诀：从左往右找穿越（导函数与x 轴的交点）；上坡低头找极小，下坡抬头找极大．题型二：根据极值、极值点求参数例6．（2022·四川·绵阳中学实验学校模拟预测（文））若函数()322f x x ax bx a =--+在1x =处有极值10，则a b -=（ ） A ．6 B ．15- C ．6-或15 D ．6或15- 【答案】B【解析】 【分析】先求出函数的导函数()'f x ，然后根据在1x = 时()f x 有极值10，得到232010a b a b a --=⎧⎨--+=⎩，求出满足条件的,a b ，然后验证在1x = 时()f x 是否有极值，即可求出-a b 【详解】()322f x x ax bx a =--+，2()32f x x ax b '∴=--又1x = 时()f x 有极值10∴ 232010a b a b a --=⎧⎨--+=⎩，解得411a b =-⎧⎨=⎩ 或33a b =⎧⎨=-⎩当3,3a b ==- 时，22()3633(1)0f x x x x '=-+=-≥ 此时()f x 在1x = 处无极值，不符合题意 经检验，4,11a b =-= 时满足题意 15a b ∴-=-故选：B例7．（2022·江苏南通·模拟预测）已知函数()()()e xf x x a x b =--在x a =处取极小值，且()f x 的极大值为4，则b =（ ） A ．-1 B ．2 C ．-3 D ．4 【答案】B 【解析】 【分析】对()f x 求导，由函数()()()e xf x x a x b =--在x a =处取极小值，所以0f a，所以a b =，()()2e xf x x a ∴=-，对()f x 求导，求单调区间及极大值，由()f x 的极大值为4，列方程得解.【详解】解：()()()e xf x x a x b =--()2e x x ax bx ab =--+，所以()()()22e ex x f x x a b x ax bx ab '=--+--+()2e 2x x a b x ab a b ⎡⎤=+--+--⎣⎦因为函数()()()e xf x x a x b =--在x a =处取极小值，所以()()()2e 2e 0a af a a a b a ab a b a b '⎡⎤=+--+--=-=⎣⎦，所以a b =，()()2e xf x x a ∴=-，()()()()22e 222=e 2x xf x x a x a a x a x a '⎡⎤=+-+----⎡⎤⎣⎦⎣⎦， 令()0f x '=，得=x a 或=2x a -，当()2x a ∈-∞-，时，()0f x '>，所以()f x 在()2a -∞-，单调递增，当()2x a a ∈-，时，()0f x '<，所以()f x 在()2a a -，单调递增，当()x a ∈∞，+时，()0f x '>，所以()f x 在()a ∞+，单调递增，所以()f x 在=2x a -处有极大值为()22e ==44a f a --，解得=2a ，所以=2b .故选：B 例8．（2022·四川绵阳·二模（文））若2x =是函数()()2224ln f x x a x a x =+--的极大值点，则实数a 的取值范围是（ ） A ．(),2-∞-B ．()2,-+∞C ．()2,+∞D ．()2,2-【答案】A 【解析】 【分析】求出()f x '，分0a ≥，2a <-，20a -<<，2a =-分别讨论出函数的单调区间，从而可得其极值情况，从而得出答案. 【详解】()()()()()22224224222x a x a x x a a f x x a x x x+---+'=+--==，()0x > 若0a ≥时，当2x >时，()0f x '>；当02x <<时，()0f x '<； 则()f x 在()0,2上单调递减；在()2,+∞上单调递增.所以当2x =时，()f x 取得极小值，与条件不符合,故满足题意.当2a <-时，由()0f x '>可得02x <<或x a >-；由()0f x '<可得2x a <<- 所以在()0,2上单调递增；在()2,a -上单调递减，在(),a -+∞上单调递增. 所以当2x =时，()f x 取得极大值，满足条件.当20a -<<时，由()0f x '>可得0x a <<-或2x >；由()0f x '<可得2a x -<< 所以在()0,a -上单调递增；在(),2a -上单调递减，在()2,+∞上单调递增. 所以当2x =时，()f x 取得极小值，不满足条件.当2a =-时，()0f x '≥在()0,∞+上恒成立，即()f x 在()0,∞+上单调递增. 此时()f x 无极值.综上所述：2a <-满足条件 故选：A例9．（2022·河南·模拟预测（文））已知函数()2ln f x x ax =-的极值为12-，则=a （ ）A ．eB ．1e 2C ．12 D ．14【答案】C 【解析】 【分析】求导得到导函数，考虑0a ≤和0a >两种情况，根据函数的单调性得到极值，计算得到答案. 【详解】函数()f x 的定义域为()0,∞+，()21122ax f x ax x x-'=-=，当0a ≤时，()0f x '>，所以()f x 在()0,∞+上单调递增，()f x 无极值，不符合题意；当0a >时，()2122a x a f x x⎛⎫- ⎪⎝⎭'=-，当x ⎛∈ ⎝时，()0f x '>，当x ⎫∈+∞⎪⎪⎭时，()0f x '<， 所以()f x在⎛ ⎝上单调递增，在⎫+∞⎪⎪⎭上单调递减，则()()111ln 2222f x f a ==--=-极大值，解得12a =．故选：C.例10．（2022·河南·高三阶段练习（文））若函数()()22e xx a f x x =++⋅在R 上无极值，则实数a 的取值范围（ ） A ．()2,2-B．(-C．⎡-⎣ D ．[]22-, 【答案】D 【解析】 【分析】求()()222e x x a f x x a ⎡⎤++++⋅⎣⎦'=，由分析可得()2220y x a x a =++++≥恒成立，利用0∆≤即可求得实数a 的取值范围. 【详解】由()()22e xx a f x x =++⋅可得。

三年级（下册）数学100分综合练习卷（16）--（22）

三年级（下册）数学100分综合练习卷（16）--（22）

三年级（下册）数学100分综合练习卷（16）--（22）三年级（下册）数学100分综合练习卷(16) 班别姓名座号比赛时间：40分钟满分：100分挑战计算极限，争当计算明星！加油！3×10＝80×40＝18×5＝40×60＝30÷10＝13×4＝25×20＝160×4＝300÷5＝720÷9＝16×6＝720÷0＝180÷20＝0÷90＝10×40＝12×50＝85÷5＝57÷3＝ 0＋8＝32×30＝70÷5＝25×4＝15×6＝630÷9＝450÷5＝12×40＝240÷6＝16×60＝84÷42＝600－50＝500×3＝0×930＝27×30＝84÷12＝420÷3＝910÷3＝91－59＝11×70= 1000÷5＝75÷15＝320－180＝30×40= 40＋580＝560÷4= 95÷1＝480＋90＝510÷7＝200÷4＝72÷4＝8000÷2＝102＋20＝4000÷50＝125－25×2＝50×0×8＝75＋25÷5＝32÷47×12＝45＋55÷5＝70×（40－32）＝90÷5×3＝10÷10×30＝6×（103－98）＝7＋3×0＝51－4×6＝420÷2×8＝ 750－（70+80）＝300÷2÷5＝三年级（下册）数学100分综合练习卷(17) 班别姓名座号二、笔算。

专题16 复数(习题)-2021届沪教版高考数学一轮复习(上海专用)

专题16 复数(习题)-2021届沪教版高考数学一轮复习(上海专用)

2021届高考数学一轮复习 专题16复数一、填空题1．（2020·上海松江·期末）已知复数z 满足，则2z i -（其中i 是虚数单位）的最小值为____________. 【答案】1 【解析】复数z 满足||1(z i =为虚数单位）， 设cos sin z i θθ=+，[0θ∈，2)π．则|2||cos (sin 2)|1z i i θθθ-=+-，当且仅当时取等号．故答案为：1．2．（2020·上海高三其他）若复数z 满足i 12i01z+=，其中i 是虚数单位，则z 的虚部为________ 【答案】1- 【解析】i 12i 01z +=即12(12)0,2iiz i z i i+-+===-，z 的虚部为1-故答案为1- 【点睛】本题考查了行列式的计算，复数的虚部，意在考查学生的计算能力. 3．（2020·上海普陀·高三一模）设i 是虚数单位，若11z ai i=++是实数，则实数a = 【答案】12【解析】依题意，由于z 为实数，故110,22a a -==.4．（2020·上海市建平中学高三月考）已知x C ∈，且，则_____． 【答案】4或-1【解析】由()()54321110x x x x x x -=-++++=,得1x =,或43210x x x x ++++=,进而得到答案．∵x C ∈，且()()54321110x x x x x x -=-++++=,故1x =,或43210x x x x ++++=， 当1x =时,,当43210x x x x ++++=时， ， 故，或-1故答案为：4或-1．5．（2020·上海市建平中学高三月考）设复数z 满足||1z =，使得关于x 的方程有实根，则这样的复数z 的和为________ 【答案】32- 【解析】设z a bi =+，（且），将原方程变为，则2220ax ax ++=①且220bx bx -=②；再对b 分类讨论可得；设z a bi =+，（且） 则原方程变为所以2220ax ax ++=，①且220bx bx -=，②；（1）若0b =，则21a =解得1a =±，当1a =时①无实数解，舍去；从而1a =-，此时1x =-，故1z =-满足条件；（2）若0b ≠，由②知，0x =或2x =，显然0x =不满足，故2x =，代入①得14a =-，b =所以14z =-±综上满足条件的所以复数的和为 故答案为：32-6．（2019·上海市建平中学高三月考）设复数z 满足(4)32i z i -=+（i 是虚数单位），则z 的虚部为_______． 【答案】-3 【解析】试题分析：由题意得：32436iz i i+=+=-+，其虚部为-3 7．（2019·上海市建平中学高三月考）已知复数z 满足(1i)1i z +=-，则Re()z =________ 【答案】0 【解析】因为，所以()Re 0z =. 故答案为0.8．（2020·上海普陀·三模）在复平面内，点()2,1A -对应的复数z ，则1z +=___________【解析】由题意2z i =-+，∴。

高中数学经典50题(附答案)

高中数学经典50题(附答案)

高中数学题库1. 求下列函数的值域：解法2 令t ＝sin x ，则f (t )＝－t 2＋t ＋1，∵ |sin x |≤1, ∴ |t |≤1.问题转化为求关于t 的二次函数f (t )在闭区间[－1,1]上的最值．本例题(2)解法2通过换元，将求三角函数的最值问题转化为求二次函数在闭区间上的最值问题，从而达到解决问题的目的，这就是转换的思想．善于从不同角度去观察问题，沟通数学各学科之间的内在联系，是实现转换的关键，转换的目的是将数学问题由陌生化熟悉，由复杂化简单，一句话：由难化易．可见化归是转换的目的，而转换是实现化归段手段。

2. 设有一颗慧星沿一椭圆轨道绕地球运行，地球恰好位于椭圆轨道的焦点处，当此慧星离地球相距m 万千米和m 34万千米时，经过地球和慧星的直线与椭圆的长轴夹角分别为32ππ和，求该慧星与地球的最近距离。

解：建立如下图所示直角坐标系，设地球位于焦点)0,(c F -处，椭圆的方程为12222=+by a x （图见教材P132页例1）。

当过地球和彗星的直线与椭圆的长轴夹角为3π时，由椭圆的几何意义可知，彗星A 只能满足)3(3/ππ=∠=∠xFA xFA 或。

作m FA FB Ox AB 3221B ==⊥，则于故由椭圆第二定义可知得⎪⎪⎩⎪⎪⎨⎧+-=-=)32(34)(22m c c a a c m c ca a c m两式相减得,23)4(21.2,3231c c c m c a m a c m =-==∴⋅=代入第一式得 .32.32m c c a m c ==-∴=∴答：彗星与地球的最近距离为m 32万千米。

说明：（1）在天体运行中，彗星绕恒星运行的轨道一般都是椭圆，而恒星正是它的一个焦点，该椭圆的两个焦点，一个是近地点，另一个则是远地点，这两点到恒星的距离一个是c a -，另一个是.c a +（2）以上给出的解答是建立在椭圆的概念和几何意义之上的，以数学概念为根基充分体现了数形结合的思想。

【精品】备战2020年高考理科数学之高频考点专题专题16 空间向量与立体几何(学生版)

【精品】备战2020年高考理科数学之高频考点专题专题16 空间向量与立体几何(学生版)

专题16 空间向量与立体几何考点1 利用空间向量证明平行与垂直调研1 如图，在正方体1111ABCD A B C D-中，O是AC的中点，E是线段1D O上一点，且1D E EOλ=⋅u u u u r u u u r.（1）求证：11DB CD O⊥平面；（2）若平面CDE ⊥平面1CD O ，求λ的值. 【答案】（1）证明见解析；（2）2λ=.【解析】（1）不妨设正方体的棱长为1，如图建立空间直角坐标系，则1111(0,0,0),(1,1,1),(,,0),(0,1,0),(0,0,1)22D B O C D ，于是1111(1,1,1),(,,0),(0,1,1)22DB OC CD ==-=-u u u u r u u u u r u u u r ，因为1110,0DB CD DB OC ⋅=⋅=u u u r u u u r u u u u u u ru r ，所以111,DB CD DB OC ⊥⊥， 故11DB CD O ⊥平面.（2）由（1）可知1CD O 平面的一个法向量为1(1,1,1)DB ==u u u u rm ， 由1D E EO λ=⋅u u u u r u u u r，则1(,,)2(1)2(1)(1)E λλλλλ+++，设平面CDE 的法向量为(,,)x y z =n ，由·0,0CD DE =⋅=u u u r u u u r n n ，得0,02(1)2(1)(1)y x y zλλλλλ=⎧⎪⎨++=⎪+++⎩∴可取(2,0,)λ=-n ，因为1CD O CED ⊥平面平面，所以·0,2λ=∴=m n .☆技巧点拨☆直线与平面、平面与平面的平行与垂直的向量判定方法设直线l 的方向向量为a =(a 1，b 1，c 1)，平面α，β的法向量分别为μ=(a 2，b 2，c 2)，v =(a 3，b 3，c 3)，则 （1）线面平行：l ∥α⇔a ⊥μ⇔a·μ=0⇔a 1a 2＋b 1b 2＋c 1c 2=0； （2）线面垂直：l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2，b 1=kb 2，c 1=kc 2； （3）面面平行：α∥β⇔μ∥v ⇔μ=λv ⇔a 2=λa 3，b 2=λb 3，c 2=λc 3； （4）面面垂直：α⊥β⇔μ⊥v ⇔μ·v =0⇔a 2a 3＋b 2b 3＋c 2c 3=0.注意：用向量知识证明立体几何问题，仍然离不开立体几何中的定理.如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a ∥b ，只需证明向量a =λb （λ∈R ）即可.若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外.考点2 求空间角题组一 求异面直线所成的角调研1 如图所示，在三棱锥P –ABC 中，P A ⊥平面ABC ，D 是棱PB 的中点，已知P A =BC =2，AB =4，CB ⊥AB ，则异面直线PC ，AD 所成角的余弦值为A ．−3010 B ．−305 C ．305D ．3010【答案】D【解析】因为P A ⊥平面ABC ，所以P A ⊥AB ，P A ⊥BC ．过点A 作AE ∥CB ，又CB ⊥AB ，则AP ，AB ，AE 两两垂直．如图，以A 为坐标原点，分别以AB ，AE ，AP 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系，则A (0，0，0)，P (0，0，2)，B (4，0，0)，C (4，−2，0)．因为D 为PB 的中点，所以D (2，0，1)．故CP uu r =(−4，2，2)，AD uuu r =(2，0，1)．所以cos 〈AD uuu r ，CP uu r 〉=||||AD CPAD CP ⋅⋅uuu r uu ruuur uu r =－65×26=−3010. 设异面直线PC ，AD 所成的角为θ，则cos θ=|cos 〈AD uuu r ，CP uu r〉|=3010.调研 2 在正方体1111ABCD A B C D -中，点P 在1A C 上运动（包括端点），则BP 与1AD 所成角的取值范围是ABCD 【答案】D【解析】以点D 为原点，DA 、DC 、1DD 所在直线分别为x y z 、、轴建立空间直角坐标系，设正方体棱长为1，点P 坐标为(),1,x x x -，则()()11,,,1,0,1BP x x x BC =--=-u u u r u u u u r ，设1BP BC u u u ru u u u r、的夹角为α，则所以当13x =时，cos α取最大值当1x =时，cos α因为11BC AD ∥，所以BP 与1AD 所成角的取值范围是故选D. 【名师点睛】空间向量的引入为求空间角带来了方便，解题时只需通过代数运算便可达到解题的目的，由于两向量夹角的范围为[0,π]，因此向量的夹角不一定等于所求的空间角，因此在解题时求得两向量的夹角（或其余弦值）后还要分析向量的夹角和空间角大小间的关系．解题时要根据所求的角的类型得到空间角的范围，并在此范围下确定出所求角（或其三角函数值）．☆技巧点拨☆利用向量求异面直线所成的角一是几何法：作—证—算；二是向量法：把角的求解转化为向量运算，应注意体会两种方法的特点，“转化”是求异面直线所成角的关键，一般地，异面直线AC ，BD 的夹角β的余弦值为cos β=||||AC BD AC BD ⋅⋅uuu r uu u ruuur uu u r . 注意：两条异面直线所成的角α不一定是两直线的方向向量的夹角β，即cos α=|cos β|.题组二 求线面角调研3 如图，四棱锥P –ABCD 中，底面ABCD 是直角梯形，∠DAB =90°，AD ∥BC ，AD ⊥侧面P AB ，△P AB 是等边三角形，DA =AB =2，BC =12AD ，E 是线段AB 的中点．（1）求证：PE ⊥CD ；（2）求PC 与平面PDE 所成角的正弦值． 【答案】（1）见解析；（2） 35.【解析】（1）因为AD ⊥侧面P AB ，PE ⊂平面P AB ，所以AD ⊥PE . 又△P AB 是等边三角形，E 是线段AB 的中点，所以PE ⊥AB ． 因为AD ∩AB =A ，所以PE ⊥平面ABCD ， 而CD ⊂平面ABCD ，所以PE ⊥CD ．（2）以E 为坐标原点，建立如图所示的空间直角坐标系E −xyz . 则E (0，0，0)，C (1，−1，0)，D (2，1，0)，P (0，0，3)． 所以ED →=(2，1，0)，EP →=(0，0，3)，PC →=(1，−1，−3)． 设n =(x ，y ，z )为平面PDE 的法向量．由，得⎩⎨⎧2x ＋y ＝0，3z ＝0.令x =1，可得n =(1，−2，0)．设PC 与平面PDE 所成的角为θ，则sin θ=|cos 〈PC →，n 〉|=|||||PC PC ⋅⋅uu u ruu ur n n |=35. 所以PC 与平面PDE 所成角的正弦值为35.调研4 如图，四棱锥P ABCD -中，PD ABCD ⊥平面，底面ABCD 是梯形，AB ∥CD ，BC CD ⊥，AB=PD=4，CD=2，AD =M 为CD 的中点，N 为PB 上一点，且(01)PN PB λλ=<<u u u r u u u r.（1）若14λ=时，求证：MN ∥平面P AD ； （2）若直线AN 与平面PBCAD 与直线CN 所成角的余弦值. 【答案】（1）见解析；（2. 【解析】（114PN PB =u u u r u u u r ．在P A 上取点EEN ，DE ，Q 1444PN PB PE PA AB ===u u u r u u u r u u r ，，，∴EN ∥AB ，且14EN AB ==，Q M 为CD 的中点，CD=2，∴112DM CD ==，又AB ∥CD ，∴EN ∥DM ，EN =DM ，∴四边形DMNE 是平行四边形，∴MN ∥DE ，又DE ⊂平面P AD ，MN ⊄平面P AD ，∴MN ∥平面P AD ．（2）如图所示，过点D 作DH ⊥AB 于H ，则DH ⊥CD ．以D 为坐标原点建立空间直角坐标系D −xyz ． 则D （0，0，0），M （0，1，0），C （0，2，0），B （2，2，0），A （2，−2，0），P （0，0，4），∴()()2,0,0,0,2,4CB CP ==-u u u r u u u r ，()()2,2,42,2,4AN AP PN AP PB λλ=+=+=-+-u u u r u u u r u u u r u u u r u u u r()22,22,44λλλ=-+-．该平面PBC 的法向量为(),,x y z =n ，则由20240CB x CP y z ⎧⋅==⎪⎨⋅=-+=⎪⎩u u u r u u u r n n ，得02x y z =⎧⎨=⎩，令z =1，得()0,2,1=n ．该直线AN 与平面PBC 所成的角为θ，则 ，解得1,3λ=∴()228248,,,,2,2,0333333N CN AD ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭u u ur u u u r ，，， 设直线AD 与直线CN 所成的角为α所以直线AD 与直线CN．☆技巧点拨☆利用向量求直线与平面所成的角①分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)； ②通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角．注意：直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，即注意函数名称的变化．直线与平面的夹角计算设直线l 的方向向量为a =(a 1，b 1，c 1)，平面α的法向量为μ=(a 3，b 3，c 3)，直线l 与平面α的夹角为θ⎝⎛⎭⎫0≤θ≤π2，则sin θ=|a·μ||a ||μ|=|cos 〈a ，μ〉|.题组三 求二面角调研5 二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB ，已知2AB =，3AC =，4BD =，CD = A ．45︒ B ．60︒ C ．120︒D ．150︒【答案】B【解析】由已知可得：0,0AB AC AB BD ⋅=⋅=u u u r u u u r u u u r u u u r ，CD CA AB BD =++u u u r u u u u r u u r u u u r，，∴cos CA 12，即CA ，∴二面角的大小为60°，故选B.【名师点睛】这个题目考查的是立体几何中空间角的求法；解决立体几何的小题，通常有以下几种方法：一是建系法，二是用传统的方法，利用定义直接在图中找到要求的角；还有就是利用空间向量法来解决问题.注意向量夹角必须是共起点的，还有就是异面直线夹角必须是锐角或直角.调研6 如图，在四棱锥P ABCD -中，AP ，AB ，AD 两两垂直，BC AD ∥，且4AP AB AD ===，2BC =.（1）求二面角P CD A --的余弦值；（2）已知点H 为线段PC 上异于C 的点，且DC DH =，求PHPC的值. 【答案】（1）23；（2【思路分析】（1）先根据条件建立空间直角坐标系，设立各点坐标，根据方程组解得各平面法向量，利用向量数量积求向量夹角，最后根据二面角与向量夹角关系求结果；（2）设PH PC λ=u u u v u u u v，根据向量坐标表示距离，再根据距离相等解得λ，即为PHPC的值. 【解析】以{},,A AB AP D u u u r u u u r u u u r为正交基底，建立如图所示的空间直角坐标系A xyz -.则()0,0,0A ，()4,0,0B ，()4,2,0C ，()0,4,0D ，()0,0,4P .（1）易知()0,4,4DP =-u u u r ，()4,2,0DC =-u u u r.设平面PCD 的法向量为()1,,x y z =n ，则1100DP DC ⎧⋅=⎪⎨⋅=⎪⎩u u u v u u u v n n ，即440420y z x y -+=⎧⎨-=⎩，令1x =，则2y =，2z =.所以()11,2,2=n .易知平面ACD 的法向量为()20,0,1=n ，P CD A --的余弦值为23. （2）由题意可知，()4,2,4PC =-u u u r ，()4,2,0DC =-u u u r ，设()4,2,4PH PC λλλλ==-u u u r u u u r，则DH DP PH =+=u u u u r u u u r u u u r()4,24,44λλλ--， 因为DC DH ==，化简得23410λλ-+=，所以1λ=或13λ=.点H 异于点C ，所以13λ=调研7 如图，在三棱柱111ABC A B C -中，侧棱1CC ⊥底面ABC ，且122,CC AC BC AC BC ==⊥，D 是棱AB 的中点，点M 在侧棱1CC 上运动.（1）当M 是棱1CC 的中点时，求证：CD ∥平面1MAB ； （2）当直线AM 与平面ABC 所成的角的正切值为32时，求二面角11A MB C --的余弦值.【答案】（1）见解析；（2）14-. 【思路分析】（1）取线段1AB 的中点E ，连接,DE EM ，可得四边形CDEM 是平行四边形，CD EM ∥，即可证明CD ∥平面1MAB ；（2）以C 为原点，CA ，CB ，1CC 所在直线分别为x ，y ，z 轴建立空间直角坐标系，利用向量法求二面角11A MB C --的余弦值. 【解析】（1）取线段1AB 的中点E ，连接,DE EM . ∵1,AD DB AE EB ==，∴1DE BB ∥，且112DE BB =. 又M 为1CC 的中点，∴1CM BB ∥，且112CM BB =， ∴CM DE ∥，且CM DE =，∴四边形CDEM 是平行四边形，∴CD EM ∥. 又EM ⊂平面1,AB M CD ⊄平面1AB M ，∴CD ∥平面1MAB .（2）∵1,,CA CB CC 两两垂直，∴以C 为原点，1,,CA CB CC 所在直线分别为x ，y ，z 轴，建立空间直角坐标系C xyz -，如图，∵三棱柱111ABC A B C -中，1CC ⊥平面ABC ，∴MAC ∠即为直线AM 与平面ABC 所成的角. 设1AC =，则由3tanMAC ∠=，得3CM =.设平面1AMB 的一个法向量为(),,x y z =n ，2z =，得3,1x y ==-，即()3,1,2=-n .又平面11BCC B 的一个法向量为()1,0,0CA =u u ur，∴，又二面角11A MB C --的平面角为钝角，∴二面角11A MB C --的余弦值为14-.☆技巧点拨☆利用向量求二面角求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．注意：两平面的法向量的夹角不一定是所求的二面角，有可能为两法向量夹角的补角．运用空间向量坐标运算求空间角的一般步骤（1）建立恰当的空间直角坐标系； （2）求出相关点的坐标； （3）写出向量坐标；（4）结合公式进行论证、计算；（5）转化为几何结论．平面与平面的夹角计算公式设平面α，β的法向量分别为μ=(a 3，b 3，c 3)，v =(a 4，b 4，c 4)，平面α，β的夹角为θ(0≤θ≤π)，则|cos θ|=|μ·v ||μ||v |=|cos 〈μ，v 〉|.题组四 解决探索性问题调研8 如图，在五面体ABCDPE 中，PD ⊥平面ABCD ，∠ADC =∠BAD =90°，F 为棱P A 的中点，PD =BC =2，AB =AD =1，且四边形CDPE 为平行四边形．（1）判断AC 与平面DEF 的位置关系，并给予证明；（2）在线段EF 上是否存在一点Q ，使得BQ 与平面PBC 所成角的正弦值为36？若存在，请求出QE 的长；若不存在，请说明理由．【答案】（1） AC ∥平面DEF ，证明见解析；（2） 在线段EF 上存在一点Q ⎝⎛⎭⎫14，1，324，使得BQ 与平面PBC 所成角的正弦值为36，此时QE =194. 【解析】（1）AC ∥平面DEF .理由如下： 设线段PC 交DE 于点N ，连接FN ，如图所示，因为四边形PDCE 为平行四边形，所以点N 为PC 的中点， 又点F 为P A 的中点，所以FN ∥AC ， 因为FN ⊂平面DEF ，AC ⊄平面DEF ， 所以AC ∥平面DEF .（2）假设在线段EF 上存在一点Q ，使得BQ 与平面PBC 所成角的正弦值为36，设FQ →=λFE →(0≤λ≤1)，如图，以D 为坐标原点，分别以DA ，DC ，DP 所在直线为x 轴，y 轴，z 轴，建立空间直角坐标系． 因为PD =BC =2，AB =AD =1，所以CD =2，所以P (0，0，2)，B (1，1，0)，C (0，2，0)，A (1，0，0)，所以PB →=(1，1，−2)，BC →=(−1，1，0)． 设平面PBC 的法向量为m =(x ，y ，z )，则，即⎩⎨⎧ x ＋y －2z ＝0，－x ＋y ＝0，解得⎩⎨⎧x ＝y ，z ＝2x ，令x =1，得平面PBC 的一个法向量为m =(1，1，2)． 假设存在点Q 满足条件．由F ⎝⎛⎭⎫12，0，22，E (0，2，2)，可得FE →=⎝⎛⎭⎫－12，2，22.由FQ→=λFE →(0≤λ≤1)，整理得1)(,2,)22Q λλλ-+，则BQ →=1)(,21,)22λλλ-+--， 因为直线BQ 与平面PBC 所成角的正弦值为36，所以|cos 〈BQ →，m 〉|=|||||BQ BQ ⋅⋅uu u ruu ur m m |=|5λ－1|219λ2－10λ＋7=36， 化简可得14λ2－5λ－1=0， 又0≤λ≤1，所以λ=12，故在线段EF 上存在一点Q ⎝⎛⎭⎫14，1，324，使得BQ 与平面PBC 所成角的正弦值为36， 且QE=194.调研9 棱台1111ABCD A B C D -的三视图与直观图如图所示. （1）求证：平面11ACC A ⊥平面11BDD B ；（2）在线段1DD 上是否存在一点Q ，使CQ 与平面11BDDB ？若存在，指出点Q 的位置；若不存在，说明理由.【答案】（1）见解析；（2）存在，点Q 在1DD 的中点位置，理由见解析.【思路分析】（1）首先根据三视图特征可得1AA ⊥平面ABCD ，四边形ABCD 为正方形，所以AC BD ⊥.再由1AA BD ⊥即可得线面垂直，从而得出面面垂直；（2）直接建立空间直角坐标系写出各点坐标求出法向量，再根据向量的夹角公式列等式求出12λ=. 【解析】（1）根据三视图可知1AA ⊥平面ABCD ，四边形ABCD 为正方形，所以AC BD ⊥. 因为BD ⊂平面ABCD ，所以1AA BD ⊥， 又1AA AC A =I ，所以BD ⊥平面11ACC A .因为BD ⊂平面11BDD B ，所以平面11ACC A ⊥平面11BDD B .（2）以A 为坐标原点，1,,AB AD AA 所在直线分别为,,x y z 轴建立空间直角坐标系，如图所示，根据三视图可知四边形ABCD 为边长为2的正方形，四边形1111A B C D 为边长为1的正方形，1AA ⊥平面ABCD ，且11AA =.所以()11,0,1B ，()10,1,1D ，()2,0,0B ，()0,2,0D ，()2,2,0C . 因为Q 在1DD 上，所以可设()101DQ DD λλ=≤≤u u u r u u u u r.因为()10,1,1DD =-u u u u r ，所以1AQ AD DQ AD DD λ=+=+u u u r u u u u u r u u r u u u r u u u r()()()0,2,00,1,10,2,λλλ=+-=-. 所以()0,2,Q λλ-，()2,,CQ λλ=--u u u r.设平面11BDD B 的法向量为(),,x y z =n ，根据()()()()1,,2,2,00,0,,0,1,10,0x y z BD x y z DD ⎧⎧⋅-=⋅=⎪⎪⇒⎨⎨⋅-=⋅=⎪⎪⎩⎩u u u r u u u ur n n令1x =，可得1y z ==，所以()1,1,1=n .设CQ 与平面11BDD B 所成的角为θ，9==. 所以12λ=，即点Q 在1DD 的中点位置. 调研10 如图（1），在边长为4的菱形ABCD 中，∠BAD =60°，DE ⊥AB 于点E ，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1D ⊥DC ，如图（2）．（1）求证：A 1E ⊥平面BCDE . （2）求二面角E −A 1B −C 的余弦值．（3）判断在线段EB 上是否存在一点P ，使平面A 1DP ⊥平面A 1BC ？若存在，求出EPPB 的值；若不存在，说明理由．【答案】（1）见解析；（2） −77；（3）在线段EB 上不存在点P ，使得平面A 1DP ⊥平面A 1BC ． 【解析】（1）∵DE ⊥BE ，BE ∥DC ，∴DE ⊥DC ．又∵A 1D ⊥DC ，A 1D ∩DE =D ，∴DC ⊥平面A 1DE ，∴DC ⊥A 1E . 又∵A 1E ⊥DE ，DC ∩DE =D ，∴A 1E ⊥平面BCDE . （2）∵A 1E ⊥平面BCDE ，DE ⊥BE ，∴以EB ，ED ，EA 1所在直线分别为x 轴，y 轴和z 轴，建立空间直角坐标系（如图）．易知DE =23，则A 1(0，0，2)，B (2，0，0)，C (4，23，0)，D (0，23，0)，∴1BA uuu r =(−2，0，2)，BC uu u r=(2，23，0)，易知平面A 1BE 的一个法向量为n =(0，1，0)．设平面A1BC的法向量为m =(x ，y ，z )，由1BA uuu r ·m =0，BC uu u r·m =0，得⎩⎨⎧－2x ＋2z ＝0，2x ＋23y ＝0.令y =1，得m =(−3，1，−3)，∴cos 〈m ，n 〉=m·n|m |·|n |=17×1=77.由图得二面角E −A 1B −C 为钝二面角， ∴二面角E −A 1B −C 的余弦值为−77.（3）假设在线段EB 上存在一点P ，使得平面A 1DP ⊥平面A 1BC ．设P (t ，0，0)(0≤t ≤2)，则1A P uuu r =(t ，0，−2)，1A D uuu r=(0，23，−2)，设平面A 1DP 的法向量为p =(x 1，y 1，z 1)，由得⎩⎨⎧23y 1－2z 1＝0，tx 1－2z 1＝0.令x 1=2，得p =⎝⎛⎭⎫2，t 3，t .∵平面A 1DP ⊥平面A 1BC ，∴m·p =0，即23−t3＋3t =0，解得t =−3. ∵0≤t ≤2，∴在线段EB 上不存在点P ，使得平面A 1DP ⊥平面A 1BC ．☆技巧点拨☆用向量解决探索性问题的方法1．确定点在线段上的位置时，通常利用向量共线来求．2．确定点在平面内的位置时，充分利用平面向量基本定理表示出有关向量的坐标而不是直接设出点的坐标． 3．解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等，所以为使问题的解决更简单、有效，应善于运用这一方法解题．1．（山东省泰安第二中学2019-2020学年高三上学期9月月考数学试题）已知(2,1,3)=-a ，(1,4,2)=--b ，(7,5,)x =c ，若a ，b ，c 三向量共面，则实数x =A ．627 B ．637C ．607D ．6572．（四川省成都市树德中学2019-2020学年高三11月阶段性检测数学试题）如图三棱锥S ABC -中，SA ⊥底面ABC ，AB BC ⊥，2AB BC ==，SA =SC 与AB 所成角的大小为A ．90︒B ．60︒C ．45︒D ．30°3．（甘肃省天水市第一中学2020年高三上学期12月月考数学试题）如图1四边形ABCD 与四边形ADEF分别为正方形和等腰梯形，,AD EF AF =∥4,2AD EF ==，沿AD 边将四边形ADEF 折起，使得平面ADEF ⊥平面ABCD ，如图2，动点M 在线段EF 上，,N G 分别是,AB BC 的中点，设异面直线MN 与AG 所成的角为α，则cos α的最大值为A BC D 4．（山东省泰安第二中学2019-2020学年高三上学期9月月考数学试题）在正方体1111ABCD A B C D -中，点M 是1AA 的中点，已知AB =u u u r a ，AD =u u u rb ，1AA =u u u r c ，用a ，b ，c 表示CM u u u u r ，则CM =u u u u r ______. 5．（河南省天一大联考2019-2020学年高三阶段性测试（三）数学试题）在直四棱柱1111ABCD A B C D -中，底面ABCD 是菱形，60BAD ∠=o ，1122AB AA ==，E 、F 分别是线段1AA 、11C D 的中点.（1）求证：BD CE ⊥；（2）求平面ABCD 与平面CEF 所成锐二面角的余弦值.6．（四川省南充市高中2019-2020学年高三第一次高考适应性考试数学试题）如图，在四棱锥P ABCD -中，底面ABCD 是矩形，2AB =，BC a =，PA ABCD 底面⊥.（1）当a 为何值时，BD PAC ⊥平面？证明你的结论； （2）当122PA a ==时，求面PDC 与面PAB 所成二面角的正弦值.7．（河北省承德市第一中学2019-2020学年高三上学期12月月考数学试题）如图，已知点H 在正方体1111ABCD A B C D -的对角线11B D 上，∠HDA =60︒．（1）求DH 与1CC 所成角的大小；（2）求DH 与平面1A BD 所成角的正弦值．8．（湖北省“荆、荆、襄、宜四地七校考试联盟2019-2020学年高三上学期10月联考数学试题）已知在多面体ABCDE 中，DE AB ∥，AC BC ⊥，24BC AC ==，2AB DE =，DA DC =且平面DAC ⊥平面ABC .（1）设点F 为线段BC 的中点，试证明EF ⊥平面ABC ；（2）若直线BE 与平面ABC 所成的角为60o ，求二面角B AD C --的余弦值.9．（广东省广州市番禺区广东仲元中学2019-2020年高三上学期11月月考数学试题）如图1，PAD △是以AD 为斜边的直角三角形，1PA =，BC AD ∥，CD AD ⊥，22AD DC ==，12BC =，将PAD △沿着AD 折起，如图2，使得2PC =．（1）证明：平面PAD ⊥平面ABCD ； （2）求二面角A PB C --大小的余弦值．10．（天津市部分区2019-2020学年高三上学期期末数学试题）如图，在三棱柱111ABC A B C -中，P 、O 分别为AC 、11A C 的中点，11PA PC ==1111A B B C =1PB ==114A C =.（1）求证：PO ⊥平面111A B C ； （2）求二面角111B PA C --的正弦值；（3）已知H 为棱11B C 上的点，若11113B H BC =u u u u r u u u u r，求线段PH 的长度.1．（2018新课标全国Ⅱ理科）在长方体1111ABCD A B C D -中，1AB BC ==，1AA =则异面直线1AD 与1DB 所成角的余弦值为A ．15 BC ．5D ．22．（2017新课标全国Ⅲ理科）a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论： ①当直线AB 与a 成60°角时，AB 与b 成30°角； ②当直线AB 与a 成60°角时，AB 与b 成60°角； ③直线AB 与a 所成角的最小值为45°； ④直线AB 与a 所成角的最大值为60°.其中正确的是________________．(填写所有正确结论的编号)3．（2018新课标全国Ⅰ理科）如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥. （1）证明：平面PEF ⊥平面ABFD ； （2）求DP 与平面ABFD 所成角的正弦值.4．（2018新课标全国Ⅱ理科）如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30︒，求PC 与平面PAM 所成角的正弦值．5．（2018新课标全国Ⅲ理科）如图，边长为2的正方形ABCD 所在的平面与半圆弧»CD 所在平面垂直，M 是»CD上异于C ，D 的点． （1）证明：平面AMD ⊥平面BMC ；（2）当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．6．（2017新课标全国Ⅰ理科）如图，在四棱锥P−ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o . （1）证明：平面P AB ⊥平面P AD ；C（2）若P A =PD =AB =DC ，90APD ∠=o ，求二面角A −PB −C 的余弦值.7．（2017新课标全国Ⅱ理科）如图，四棱锥P −ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点． （1）证明：直线CE ∥平面P AB ；（2）点M 在棱PC 上，且直线BM 与底面ABCD 所成角为o 45，求二面角M AB D --的余弦值．8．（2017新课标全国Ⅲ理科）如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD =∠CBD ，AB =BD ．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.9．（2019年高考全国Ⅰ卷理数）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A−MA1−N的正弦值．10．（2019年高考全国Ⅱ卷理数）如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值．11．（2019年高考全国Ⅲ卷理数）图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B−CG−A的大小.。

专题16 二次函数与最短路径问题-备战2022年中考数学母题题源解密(解析版)

专题16 二次函数与最短路径问题-备战2022年中考数学母题题源解密(解析版)

专题16 二次函数与最短路径问题考向1 利用轴对称求线段之和的最小值【母题来源】2021年中考山东省东营卷【母题题文】如图，抛物线y =−12x 2+bx+c 与x 轴交于A 、B 两点，与y 轴交于点C ，直线y =−12x+2过B 、C 两点，连接AC ．（1）求抛物线的解析式；（2）求证：△AOC ∽△ACB ；（3）点M （3，2）是抛物线上的一点，点D 为抛物线上位于直线BC 上方的一点，过点D 作DE ⊥x 轴交直线BC 于点E ，点P 为抛物线对称轴上一动点，当线段DE 的长度最大时，求PD+PM 的最小值．【答案】（1）∵直线y =−12x+2过B 、C 两点，当x ＝0时，代入y =−12x+2，得y ＝2，即C （0，2），当y ＝0时，代入y =−12x+2，得x ＝4，即B （4，0），把B （4，0），C （0，2）分别代入y =−12x 2+bx+c ，得{−8+4b +c =0c =2， 解得{b =32c =2， ∴抛物线的解析式为y =−12x 2+32x+2；（2）∵抛物线y =−12x 2+32x+2与x 轴交于点A ，∴−12x 2+32x+2＝0，解得x 1＝﹣1，x 2＝4，∴点A 的坐标为（﹣1，0），∴AO ＝1，AB ＝5，在Rt △AOC 中，AO ＝1，OC ＝2，∴AC=√5，∴AOAC=√5=√55，∵ACAB=√55，∴AOAC=ACAB，又∵∠OAC＝∠CAB，∴△AOC∽△ACB；（3）设点D的坐标为（x，−12x2+32x+2），则点E的坐标为（x，−12x+2），∴DE=−12x2+32x+2﹣（−12x+2）=−12x2+32x+2+12x﹣2 =−12x2+2x=−12（x﹣2）2+2，∵−12＜0，∴当x＝2时，线段DE的长度最大，此时，点D的坐标为（2，3），∵C（0，2），M（3，2），∴点C和点M关于对称轴对称，连接CD交对称轴于点P，此时PD+PM最小，连接CM交直线DE于点F，则∠DFC＝90°，点F的坐标为（2，2），∴CD=√CF2+DF2=√5，∵PD+PM＝PC+PD＝CD，∴PD+PM的最小值为√5．【试题解析】（1）直线y=−12x+2过B、C两点，可求B、C两点坐标，把B（4，0），C（0，2）分别代入y=−12x2+bx+c，可得解析式．（2）抛物线y=−12x2+32x+2与x轴交于点A，即y＝0，可得点A的横坐标，由相似三角形的判定得：△AOC∽△ACB．（3）设点D的坐标为（x，−12x2+32x+2），则点E的坐标为（x，−12x+2），由坐标得DE=−12x2+2x，当x＝2时，线段DE的长度最大，此时，点D的坐标为（2，3），即点C和点M关于对称轴对称，连接CD交对称轴于点P，此时PD+PM最小，连接CM交直线DE于点F，则∠DFC＝90°，由勾股定理得CD=√5，根据PD+PM ＝PC+PD＝CD，即可求解．【命题意图】函数思想；应用意识．【命题方向】主要为解答题，一般为压轴题，具有很强的甄别性.【得分要点】已知：在直线l同恻有A．B两点，在l上找一点P，使得AP＋PB最小．作法：如图．作点A关于直线l的对称点A’，连结A'B，与直线，的交点就是点P考向2 利用三点共线求线段之和的最小值【母题来源】2021年中考湖北省恩施卷【母题题文】如图，在平面直角坐标系中，四边形ABCD为正方形，点A，B在x轴上，抛物线y＝x2+bx+c 经过点B，D（﹣4，5）两点，且与直线DC交于另一点E．（1）求抛物线的解析式；（2）F为抛物线对称轴上一点，Q为平面直角坐标系中的一点，是否存在以点Q，F，E，B为顶点的四边形是以BE为边的菱形．若存在，请求出点F的坐标；若不存在，请说明理由；（3）P为y轴上一点，过点P作抛物线对称轴的垂线，垂足为M，连接ME，BP，探究EM+MP+PB是否存在最小值．若存在，请求出这个最小值及点M的坐标；若不存在，请说明理由．BAPlABl【答案】（1）由点D 的纵坐标知，正方形ABCD 的边长为5，则OB ＝AB ﹣AO ＝5﹣4＝1，故点B 的坐标为（1，0），则{1+b +c =016−4b +c =5，解得{b =2c =−3故抛物线的表达式为y ＝x 2+2x ﹣3； （2）存在，理由：∵点D 、E 关于抛物线对称轴对称，故点E 的坐标为（2，5），由抛物线的表达式知，其对称轴为直线x ＝﹣1，故设点F 的坐标为（﹣1，m ），由点B 、E 的坐标得，BE 2＝（2﹣1）2+（5﹣0）2＝26，设点Q 的坐标为（s ，t ），∵以点Q ，F ，E ，B 为顶点的四边形是以BE 为边的菱形，故点B 向右平移1个单位向上平移5个单位得到点E ，则Q （F ）向右平移1个单位向上平移5个单位得到点F （Q ），且BE ＝EF （BE ＝EQ ），则{s +1=−1t +5=m 26=(2+1)2+(m −5)2或{s −1=−1t −5=m 26=(s −2)2+(t −5)2， 解得{m =5±√17s =−2t =±√17或{s =0t =5±√22m =±√22，故点F 的坐标为（﹣1，5+√17）或（﹣1，5−√17）或（﹣1，√22）或（﹣1，−√22）；（3）存在，理由：由题意抛物线的对称轴交x 轴于点B ′（﹣1，0），将点B ′向左平移1个单位得到点B ″（﹣2，0），连接B″E，交函数的对称轴于点M，过点M作MP⊥y轴，则点P、M为所求点，此时EM+MP+PB为最小，理由：∵B′B″＝PM＝1，且B′B″∥PM，故四边形B″B′PM为平行四边形，则B″M＝B′P＝BP，则EM+MP+PB＝EM+1+MB″＝B″E+1为最小，由点B″、E的坐标得，直线B″E的表达式为y=54（x+2），当x＝﹣1时，y=54（x+2）=54，故点M的坐标为（﹣1，54），则EM+MP+PB的最小值B″E+1＝1+√(−2−2)2+(0−5)2=√41+1．【试题解析】（1）求出点B的坐标为（1，0），再用待定系数法即可求解；（2）以点Q，F，E，B为顶点的四边形是以BE为边的菱形，故点B向右平移1个单位向上平移5个单位得到点E，则Q（F）向右平移1个单位向上平移5个单位得到点F（Q），且BE＝EF（BE＝EQ），即可求解；（3）由题意抛物线的对称轴交x轴于点B′（﹣1，0），将点B′向左平移1个单位得到点B″（﹣2，0），连接B″E，交函数的对称轴于点M，过点M作MP⊥y轴，则点P、M为所求点，此时EM+MP+PB为最小，进而求解．【命题意图】考查代数几何综合题；分类讨论；矩形菱形正方形；数据分析观念．【命题方向】解答题，一般设定为试卷压轴题.【得分要点】利用转化思想得三点共线，进而利用三点共线求线段的最小值.1．（2021•湖北南漳县模拟）在平面直角坐标系xOy中，矩形OABC的顶点A，C的坐标分别为（0，3），（2，0），顶点为M的抛物线y＝﹣x2+bx+c经过点A，B，且与x轴交于点D，E（点D在点E的左侧）．（1）求点B 的坐标，抛物线的解析式及顶点M 的坐标；（2）点P 是（1）中抛物线对称轴上一动点，求△PAD 的周长最小时点P 的坐标；（3）平移抛物线y ＝﹣x 2+bx+c ，使抛物线的顶点始终在直线AM 上移动，在平移的过程中，当抛物线与线段BM 有公共点时，求抛物线顶点的横坐标a 的取值范围．解：（1）∵A ，C 点的坐标分别为（0，3），（2，0），并且四边形ABCD 是矩形，∴B 点的坐标是（2，3），把A 、B 代入抛物线解析式，则{c =3−4+2b +c =3， 解得{c =3b =2， ∴抛物线的解析式为y ＝﹣x 2+2x+3，∴y ＝﹣（x ﹣1）2+4，即顶点M 为（1，4）；（2）在对称轴上取一点P ，连接PA ，PB ，PD ，由抛物线及矩形的轴对称性可知点A ，B 关于抛物线的对称轴对称，∴PA ＝PB ，∴当点P ，B ，D 在一条直线上时△PAD 的周长最小，当﹣x 2+2x+3＝0时，解得x 1＝﹣1，x 3＝3，∴点D （﹣1，0），设直线BD 的解析式为y ＝kx+q ，代入B 点、D 点坐标得（{2k +q =3−k +q =0， 解得{k =1q =1， ∴直线BD 的解析式为y ＝x+1，当x ＝1时，y ＝2，∴P 点的坐标为（1，2）；（3）设直线AM 的解析式为：y AM ＝mx+n ，代入点A 和点M 的坐标得{n =3m +n =4， 解得{m =1n =3， ∴直线AM 的解析式为y AM ＝x+3，同理得直线BM 的解析式为y BM ＝﹣x+5，∵抛物线y ＝﹣x 2+bx+c 的顶点在直线y AM ＝x+3上，∴设平移中的抛物线的解析式为y ＝﹣（x ﹣a ）2+a+3，当a ＝1时，抛物线y ＝﹣（x ﹣a ）2+a+3即y ＝﹣x 2+2x+3，此时抛物线y ＝﹣（x ﹣a ）2+a+3与线段AB 有两个交点，当a ＞1时，①抛物线y ＝﹣（x ﹣a ）2+a+3经过点M 时，有﹣（1﹣a ）2+a+3＝4，解得：a 1＝1（舍去），a 2＝2，②当抛物线y ＝﹣（x ﹣a ）2+a+3经过点B 时，有﹣（2﹣a ）2+a+3＝3，解得：a 1＝1（舍去），a 2＝4，综上可得2≤a ≤4，当a ＜1，抛物线y ＝﹣（x ﹣a ）2+a+3与直线y BA ＝﹣x+5有公共点时，则方程﹣（x ﹣a ）2+a+3＝﹣x+5即x 2﹣（2a+1）x+a 2﹣a+2＝0有实数根，∴（2a+1）2﹣4（a 2﹣a+2）≥0，即a ≥78，∴1＞a ≥78，综上可得1＞a ≥78或2≤a ≤4时，平移后的抛物线与线段BA 有公共点．2. （2021•江苏省江阴市模拟）如图，菱形ABCD 的对角线AC ，BD 交于点O ，AB ＝4．BD ＝5．点P 是线段AO 上一动点（不与A ，O 重合）．点E 与点P 在AD 所在直线的两侧．AE ⊥AB ．AE ＝BD ．点F 在AD 边上，DF ＝AP ．连接PE ，BF ．（1）补全图形，求PE ：BF 的值；（2）连接BP ，点P 在何处时BP+BF 取得最小值？并求出这个最小值．解：（1）图形如图所示：∵四边形ABCD是菱形，∴AC⊥BD，∠DAO＝∠BAO，∴∠AOD＝90°，∵EA⊥AB，∴∠EAP+∠BAO＝90°，∵∠DAO+∠ADO＝90°，∴∠EAP＝∠BDF，∵AE＝DB，AP＝DF，∴△EAP≌△BDF（SAS），∴PE＝BF，∴PE：BF＝1．（2）∵PE＝BF，∴BP+BF＝BP+PE≥BE，∴当点P在BE与OA的交点处时，BP+BF的值最小，最小值BE=√AE2+AB2=√52+42=√41．。

历年高考数学真题汇编专题16 以基本不等式为背景的应用题(解析版)

历年高考数学真题汇编专题16 以基本不等式为背景的应用题(解析版)

历年高考数学真题汇编专题16 以基本不等式为背景的应用题1、【2017年高考江苏卷】某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元．要使一年的总运费与总存储费用之和最小，则x 的值是___________．【答案】30【解析】总费用为600900464()4240x x x x +⨯=+≥⨯=，当且仅当900x x=，即30x =时等号成立．在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误．2、【2010年高考江苏卷】某兴趣小组要测量电视塔AE 的高度H (单位：m)．示意图如图所示，垂直放置的标杆BC 的高度h ＝4 m ，仰角∠ABE ＝α，∠ADE ＝β.(1) 该小组已测得一组α，β的值，tan α＝1.24，tan β＝1.20，请据此算出H 的值；(2) 该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d (单位：m)，使α与β之差较大，可以提高测量精确度．若电视塔的实际高度为125 m ，试问d 为多少时，α－β最大？规范解答 (1) 由AB ＝H tan α，BD ＝h tan β，AD ＝H tan β及AB ＋BD ＝AD ，得H tan α＋h tan β＝Htan β， 解得H ＝h tan αtan α－tan β＝4×1.241.24－1.20＝124.因此算出的电视塔的高度H 是124 m. (2) (1) 由题知d ＝AB ，则tan α＝H d.由AB ＝AD －BD ＝H tan β－h tan β，得tan β＝H －hd，所以tan(α－β)＝tan α－tan β1＋tan αtan β＝()h hH H d d-+，当且仅当d ＝555时取等号． 又0<α－β<π2，所以当d ＝555时，tan(α－β)的值最大．因为0<β<α<π2，所以当d ＝555时，α－β的值最大．3、【2013年高考江苏卷】如图，建立平面直角坐标系xOy ，x 轴在地平面上，y 轴垂直于地平面，单位长度为1 km.某炮位于坐标原点．已知炮弹发射后的轨迹在方程y ＝kx －120(1＋k 2)x 2(k >0)表示的曲线上，其中k 与发射方向有关．炮的射程是指炮弹落地点的横坐标．(1) 求炮的最大射程；(2) 设在第一象限有一飞行物(忽略其大小)，其飞行高度为3.2 km ，试问它的横坐标a 不超过多少时，炮弹可以击中它？请说明理由．本小题主要考查函数、方程和基本不等式等基础知识，考查数学阅读能力和解决实际问题的能力．满分14分．规范解答 (1)令y ＝0，得kx －120(1＋k 2)x 2＝0，由实际意义和题设条件知x >0，k >0，故x ＝20k 1＋k 2＝20k ＋1k≤202＝10，当且仅当k ＝1时取等号． 所以炮的最大射程为10km.(2) 因为a >0，所以炮弹可击中目标等价于存在k >0，使3.2＝ka －120(1＋k 2)a 2成立，即关于k 的方程a 2k 2－20ak ＋a 2＋64＝0有正根， 所以判别式Δ＝(－20a )2－4a 2(a 2＋64)≥0， 解得a ≤6，所以0<a ≤6.所以当a 不超过6km 时，炮弹可击中目标．一、解函数应用问题的步骤(1)审题：弄清题意，分清条件和结论，理顺数量关系，初步选择数学模型；(2)建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用数学知识，建立相应的数学模型；(3)解模：求解数学模型，得出数学结论；(4)还原：将数学问题还原为实际问题的意义.以上过程用框图表示如下：二、在求实际问题中的最大值或最小值时，一般先设自变量、因变量、建立函数关系式，并确定其定义域，利用求函数最值的方法求解，注意结果应与实际情况相符合.运用基本不等式解决应用题一定要注意满足三个条件：一、正；二、定；三、相等。

2019年高考数学全国卷Ｉ第16题赏析

2019年高考数学全国卷Ｉ第16题赏析

2019年高考数学全国卷Ｉ第 16题赏析2019年高考结束了，数学在热搜中让我们深思，今年的高考题真的是把文科当理科的考，理科当华罗庚的考吗？新一轮高考改革方案到底要什么？从学生到教师，从课堂到课外，从基础到创新，我们应该怎样提高学生的解题能力和应试能力？培养人才我们应站在什么样的高度？谁都知道高考是我们教与学的风向标，是为国家培养人才的选拔性考试。

不需要死记硬背的；不需要没有梦想没有开拓精神的。

需要你有持续学习能力，需要你有发散性思维品质，需要你有灵活应变与创新意识。

高考题应该有高考题的高度，它的灵活性和创新性思维，打败的不只是靠“蒙的全对，出的全会”的学困生，它还揉碎了用一年的努力就想换回两年都不努力的投机者。

高考更是一种积累，苦读十二年的学习基础，让你成长的不只是数学核心素养，更重要的是你的数学思维对其他学科的影响。

只有你的数学素养达到一定境界，你才能取得别人一生都在羡慕的成绩。

汗水背后有时间，灵巧背后有题海。

多想少算，思路和方法就会在灵感中顿悟。

今年的高考16题更是体现了数学这一核心素养的重要性。

这个题从不同的角度去思考，我们就会发现不同的解题策略，每一种解法都体现了高考的核心考点。

考基础，考热点，考通解通法，这对我们的课堂教学有着很大的启发，希望大家从以前的换汤不换药的思维中解放出来，今天不只是要换汤，还要学会换碗！（2019全国卷Ｉ）16题：已知双曲线C：的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若，，则C的离心率为___．解法一：利用双曲线渐近线倾斜角来解。

如图解法二：利用直线和圆的相交来解，由图知：解法三：利用双曲线渐近线的斜率来解：由图知解法四：利用余弦定理来解，由图知：解法五：利用面积公式来解，由图知解法六：利用射影定理来解：解法七：利用二倍角公式来解：解题感悟：这道试题命题者是以直观想象，逻辑推理和数学运算等数学核心素养为立意。

考查了学生的数形结合，转化与化归，函数与方程的数学思想。

2022年高考数学乙卷第16题解析

2022年高考数学乙卷第16题解析

(2022年，全国乙卷，理数16)己知x=x1和x=x2分别是函数f(x)=2a x-ex2(a＞0且a≠1)的极小值点和极大值点。

若x1＜x2，则a的取值范围是。

[答案](1/e,1)
[解析]函数f(x)的定义域为R。

对函数f(x)求导，得
由于函数f(x)存在极小值点和极大值点，所以函数f′(x)存在两个变号零点。

对函数f′(x)求导，得
若a＞1，则函数f″(x)在R上单调递增。

于是，存在x0使得f″(x0)=0。

从而，函数f′(x)在(-∞,x0)上单调递减，在(x0,+∞)上单调递增。

若函数f(x)在x=x1和x=x2分别取极小值点和极大值点，则x1＞x2，不符合题意。

若0＜a＜1，则函数f″(x)在R上单调递减。

于是，存在x0使得f″(x0)=0。

从而，函数f′(x)在(-∞,x0)上单调递增，在(x0,+∞)上单调递减。

若函数f(x)在x=x1和x=x2分别取极小值点和极大值点，则x1＜x2，符合题意。

此时，由于f″(x0)=0，所以解得
因此，只需满足f′(x0)＞0，即
整理得，
两边取自然对数，有
继续整理得，
解得
综上，a的取值范围为(1/e,1)。

2014年高三数学(文科)试卷(16)

2014年高三数学(文科)试卷(16)

2014年高三数学(文科)试卷(16)本试卷共 6 页，21小题，满分 150 分．考试用时 120 分钟． 注意事项：1 ．答卷前，考生首先检查答题卡是否整洁无缺损，监考教师分发的考生信息条形码是否正确；之后务必用0.5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号，同时，将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区，请保持条形码整洁、不污损．2 ．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上．不按要求填涂的，答案无效．3 ．非选择题必须用 0.5 毫米黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上，请注意每题答题空间，预先合理安排；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4 ．作答选做题时，请先用 2B 铅笔填涂选做题的题号对应的信息点，再做答．漏涂、错涂、多涂的答案无效．5 ．考生必须保持答题卡的整洁，考试结束后，将答题卡交回． 参考结论：三棱锥的体积公式：sh v 31=，其中,h s v ,,分别是三棱锥的体积、底面积和高； 回归直线的方程是 ： a bx y +=∧， .,)())((:121x b y a x x y yx x b ni ini ii-=---=∑∑==其中一、选择题：本大题共10个小题；每小题5分，共50分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1．已知 i 为虚数单位，则=-2)1(iA ． 2iB ． -2iC ．2D ．-22．已知集合{=⋂=<∈=B A C B x R x A R )(},4.3.2.1{},27|则 A ． }4,3,2,1{ B ．}4,3,2{ C ．}4,3{， D ． }4{ 3．下列函数中，最小正周期为2π的是 A. 2tanx y =, B. x y 2sin = C. 4cos xy = D. x y 4cos = 4．设f(x) 为定义在 R 上的奇函数，当 x.>0时， =-+=)2(),1(log )(3f x x f 则 1.-A 3.-B 1.C 3.D5．下列命题为真命题的是A ．若q p ∨为真命题，则 q p ∧为真命题．B ．“ x=5”是“ 0542=--x x ”的充分不必要条件．C ．命题“若 x<1，则0322=--x x ”的否命题为：“若 x<1，则0322≤--x x ”． D ．已知命题.01,:,01,:22>-+∈∀⌝<-+∈∃x x R x p x x R x p 使得则使得6．沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的左视图为 7．某容量为180布直方图共有n(n>1)个小矩形，若第一个小矩形的面积 等于其余n-1个小矩形的面积之和的51，则第一个小矩形对应的频数是 A ． 20 B ．25 C ．30 D ．358．等差数列}{n a 中，已知,0,0745<+>a a a 则}{n a 的前n 项和n S 的最大值为 A. 7S B. 6S C. 5S D. 4S9．已知抛物线)0(22>=p px y 与双曲线)0,0(12222>>=-b a by a x 的一条渐近线交于一点M(1,m)，点 M 到抛物线焦点的距离为 3 ，则双曲线的离心率等于 A ． 3 B ．4 C ．31 D ．4110．已知x>0,y>0，且 4xy-x-2y=4，则 xy 的最小值为 A ．22B ．22C ． 2D ．2 二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分． （一）必做题：第11、12、13题为必做题．11．运行如图所示的程序框图，输出的结果是_______ ．12．已知变量 x, y ，满足约束条件⎪⎩⎪⎨⎧≤-+≥≤+-.082,102y x x y x则xy的取值范围是 __________． 13．在平面直角坐标系 xoy 中，定点 A(4,3) 且动点B(m,0)在 x 轴的正半轴上移动，则||AB m的最大值为 _______． （二）选做题：第14、15题为选做题，考生只能选做一题，两题全答的，只计算第一题的得分．14．在平面直角坐标系 xOy 中，已知直线l 的参数方程为⎩⎨⎧-=+=.24,1t y t x ),(R t ∈参数若以 O 为极点， x 轴的正半轴为极轴， 曲线 C 的极坐标方程为,sin 4θρ=则直线 l 被曲线 C 所截得的弦长为________ ．15．如图， PA 是⊙O 的切线， A 为切点，直线 PB 交⊙O于D 、B 两点，交弦AC 于E 点，且AE=4, EC=3，BE=6 , PE=6， 则 AP = ______．三、解答题：本大题6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）在平面直角坐标系xOy 中，2sin ,1M θ（ ），21,2cos N θ-（ ）（θ∈R ），且32OM ON ⋅=- . （1）求点,M N 的坐标；（2）若角,αβ的顶点都为坐标原点且始边都与x 轴的非负半轴重合，终边分别经过点,M N ，求tan αβ+()的值.一次考试中，五名学生的数学、物理成绩如下表所示：（1）要从5名学生中选2人参加一项活动，求选中的 学生中至少有一人的物理成绩高于90分的概率； （2）请在所给的直角坐标系中画出它们的散点图，并求这些数据的线性回归方程ˆybx a =+．18．（本小题满分14分）如图甲，O ⊙的直径2AB =，圆上两点C D 、在直径AB 的两侧，使4CAB π∠=，3DAB π∠=．沿直径AB 折起，使两个半圆所在的平面互相垂直（如图乙），F 为BC 的中点，E 为AO 的中点．根据图乙解答下列各题： （1）求三棱锥C BOD -的体积； （2）求证：CB DE ⊥；（3）在BD 弧上是否存在一点G ，使得//FG 平面ACD ？若存在，试确定点G 的位置；若不存在，请说明理由．19．（本题满分14分）设{}n a 是公比大于1的等比数列，n S 为数列{}n a 的前n 项和．已知37S =，且23a 是 13a +和34a +的等差中项．（1）求数列{}n a 的通项公式；（2）设111n n n n a b a a +=++()()，数列{}n b 的前n 项和为n T ，求证：12n T <．A B C O D · (第18题图甲) A B FO D ·(第18题图乙)· E G已知椭圆C 的中心为原点O ，焦点在x，且点1,（在该椭圆上． （1）求椭圆C 的方程；（2）如图，椭圆C 的长轴为AB ，设P 是椭圆上异于A 、B 的任意一点，PH x ⊥轴，H 为垂足，点Q满足PQ HP = ，直线AQ 与过点B 且垂直于x 轴的直线交于点M ，4BM BN =．求证：OQN ∠为锐角．21．（本小题满分14分）已知函数2ln , , 1x f x a x x a b a b a =+-- ∈>R （）（），e 是自然对数的底数．（1）试判断函数f x （）在区间0, +∞（）上的单调性； （2）当e a =，4b =时，求整数k 的值，使得函数f x （）在区间, 1k k +（）上存在零点； （3）若存在12, 1, 1x x ∈-[]，使得12||e 1f x f x -≥-（）（），试求a 的取值范围．（第20题图）答案及评分标准说明：一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分． 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四、只给整数分数，选择题和填空题不给中间分数．一、选择题：本大题每小题5分，满分50分． BDDAB BCCAD二、填空题：本大题每小题5分；第14、15两小题中选做一题，如果两题都做，以第14题的得分为最后得分)，满分20分． 11．63. 12．[26]，. 13．53． 1415．三、解答题：本大题6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．解：(1) 3,2OM ON ⋅=- 223sin 2cos ,2θθ∴-=- ………….2分223sin 2(1sin ),2θθ∴--=- 解得21sin 6θ=，25cos 6θ=, 所以1(,1)6M ，5(1,)3N - ….6分（2）由（1）可知1(,1)6M ，5(1,)3N -tan 6α∴=，5tan 3β=- ……….10分tan tan tan()1tan tan αβαβαβ+∴+=-⋅ 563516()3-=-⨯-1333=……….12分 【说明】 本小题主要考查了同角三角函数的关系、三角函数的定义、两角和正切公式，以及向量的有关知识.考查了运算能力．17． 解：（1）从5名学生中任取2名学生的所有情况为:45(,)A A 、41(,)A A 、42(,)A A 、43(,)A A 、51(,)A A 、52(,)A A 、53(,)A A 、12(,)A A 、13(,)A A 、23(,)A A 共种情10况.………3分其中至少有一人物理成绩高于90分的情况有：45(,)A A 、41(,)A A 、42(,)A A 、43(,)A A 、51(,)A A 、52(,)A A 、53(,)A A 共7种情况， 故上述抽取的5人中选2人，选中的学生的物理成绩至少有一人的成绩高于90分的概率7P 10=.…5分（2）散点图如右所示. ……………6分可求得：x =59795939189++++=93，y =59392898987++++=90， …8分51()()30iii x x y y =--=∑，∑=-51i 2i)x x (=22222420)2()4(+++-+-=40，3040b ==0.75， a y bx =-=20.25， ……………………11分 故y 关于x 的线性回归方程是： ˆ0.7520.25y x =+. ……………12分18． 解:（1）C 为圆周上一点，且AB 为直径，90C ∴∠=︒,4CAB π∠=,AC BC ∴= ∵O 为AB 中点，CO AB ∴⊥，2,1AB CO =∴= .∵两个半圆所在平面ACB 与平面ADB 互相垂直且其交线为AB ， ∴CO ⊥平面ABD ，CO ∴⊥平面BOD . ∴CO 就是点C 到平面BOD 的距离，在Rt ABD ∆中，11112224BOD ABD S S ∆∆==⨯⨯=，11133412C BOD BOD V S CO -∆∴=⋅=⨯=. ………………4分 （2）在AOD ∆中，60,,OAD OA OD ∠=︒=AOD ∴∆为正三角形，又E 为OA 的中点，DE AO ∴⊥，∵两个半圆所在平面ACB 与平面ADB 互相垂直且其交线为AB ， DE ∴⊥平面ABC . ∴CB DE ⊥. …………9分（3）存在，G 为 BD的中点.证明如下： 连接,,OG OF FG ，∴OG BD ⊥， ∵AB 为⊙O 的直径，∴AD BD ⊥∴//OG AD ，OG ⊄平面ACD ，AD ⊂平面ACD ， ∴OG //平面ACD .在ABC ∆中，,O F 分别为,AB BC 的中点，//OF AC ∴，OF ⊄平面ACD ，//OF ∴平面ACD ， ,OG OF O =∴平面//OFG 平面ACD ，又FG ⊂平面OFG ，//FG ∴平面ACD .…………………………14分【说明】本题主要考察空间点、线、面位置关系，考查空间想象能力、运算能力和逻辑推理能力．19． 解：（1）由已知，得1231327(3)(4)3.2a a a a a a ++=⎧⎪⎨+++=⎪⎩，………3分 解得22a =．设数列{}n a 的公比为q ，则12a q =， ∴213122a a a q q q===，．由37S =，可知2227q q ++=， ∴22520q q -+=，解得12122q q ==，．由题意，得12q q >∴=，． ……………5分∴11a =．故数列{}n a 的通项为12n n a -=． …………………7分(2)∵1(1)(1)n n n n a b a a +=++112(21)(21)n n n --=++1112121n n-=-++， …………11分 ∴n S 112231111111111121212121212121n n-⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-⎪ ⎪ ⎪ ⎪++++++++⎝⎭⎝⎭⎝⎭⎝⎭ 111121n =-++11221n =-+12<.………………………14分【说明】考查了等差数列、等比数列的概念及其性质，考查了数列求和的“裂项相消法”；考查了学生的运算能力A BFO D·(第18题图乙)·E GABCOD·(第18题图甲)20．解：（1）设椭圆C 的方程为22221,(0)x y a b a b+=>>，由题意可得c e a == ,又222c b a +=，∴224b a =. …………………2分∵椭圆C 经过(1,)2，代入椭圆方程有 2231414b b+=，解得21b =. ……………5分 ∴24a =， 故椭圆C 的方程为 2214x y +=. …………6分（2）设()00,P x y 0(22)x -<<， …………7分 ∵()2,0A -，∵PQ HP =，∴()00,2Q x y ，∴直线AQ 的方程为()00222y y x x =++． …………………9分 令2x =，得0082,2y M x ⎛⎫⎪+⎝⎭． ∵()2,0B ，4BM BN = ，∴002,2y N x ⎛⎫ ⎪+⎝⎭．∴()00,2QO x y =-- ，00002(1)2,2y x QN x x ⎛⎫-+=- ⎪+⎝⎭．∴()()2000000000002(1)4(1)2(2)222y x y x QO QN x x y x x x x -++⋅=--+-⋅=-+++ ∵220014x y +=，∴220044y x =-∴02QO QN x ⋅=- ……………………12分 ∵022x -<<，∴020QO QN x ⋅=->．又O 、Q 、N 不在同一条直线， ∴OQN ∠为锐角. ……………………14分【说明】本题主要考查椭圆的方程与性质、向量等基础知识，考查学生运算能力、推理论证以及分析问题、解决问题的能力．21． 解：（1）()ln 2ln 2(1)ln x xf x a a x a x a a '=+-=+- ……………1分 由于1a >，故当(0,)x ∈+∞时，ln 0,10xa a >->，所以()0f x '>，…………2分故函数()f x 在(0,)+∞上单调递增 . …………………3分 （2）2()4xf x e x x =+--，'()21xf x e x ∴=+-，(0)0f '∴=，……………4分当0x >时，1xe >，()0f x '∴>，故()f x 是(0,)+∞上的增函数； 同理，()f x 是(,0)-∞上的减函数. ……………5分2(0)30,(1)40,(2)20f f e f e =-<=-<=->，当2x >，()0f x >， 故当0x >时，函数()f x 的零点在(1,2)内，1k ∴=满足条件；211(0)30,(1)20,(2)20f f f e e=-<-=-<-=+>，当2x <-，()0f x >，故当0x <时，函数()f x 的零点在(2,1)--内，2k ∴=-满足条件. 综上所述 1k =或2-. ………………………7分（3）2()ln x f x a x x a b =+--，因为存在12,[1,1]x x ∈-，使得12|()()|1f x f x e -≥-，所以当[1,1]x ∈-时， max min max min |()()|()()1f x f x f x f x e -=-≥-………………8分()ln 2ln 2(1)ln xx f x a a x a x a a '=+-=+-，①当0x >时，由1a >，可知10xa ->，ln 0a >，∴()0f x '>；③当0x =时，()0f x '=.∴()f x 在[1,0]-上递减，在[0,1]上递增，……………………11分∴当[1,1]x ∈-时，{}min max ()(0)1,()max (1),(1)f x f b f x f f ==-=-， 而11(1)(1)(1ln )(1ln )2ln f f a a b a b a a a a--=+---++-=--， 设1()2ln (0)g t t t t t =-->，因为22121()1(1)0g t t t t '=+-=-≥（当1t =时取等号）， ∴1()2ln g t t t t=--在(0,)t ∈+∞上单调递增，而(1)0g =，∴当1t >时，()0g t >，∴当1a >时，12ln 0a a a-->，∴(1)(1)f f >-，∴(1)(0)1f f e -≥-，∴ln 1a a e -≥-，即ln ln a a e e -≥-，设()ln (1)h a a a a =->，则 11()10a h a a a-'=-=>.∴函数()ln (1)h a a a a =->在(1,)+∞上为增函数，∴a e ≥.即a 的取值范围是[),e +∞………14分【说明】本小题主要考查函数、导数、不等式证明等知识,通过运用导数知识解决函数、不等式问题,考查考生综合运用数学知识解决问题的能力，同时也考查函数与方程思想、化归与转化思想.。

课时训练 定积分的概念与微积分基本定理(北师大版)

课时训练 定积分的概念与微积分基本定理(北师大版)

A 级 基础达标演练 (时间：40分钟 满分：60分)一、选择题(每小题5分，共25分)1．与定积分∫3π1－cos x d x 相等的是( )． A.2∫3π0sin x 2d x B.2∫3π0⎪⎪⎪⎪⎪⎪sin x 2d x C.⎪⎪⎪⎪⎪⎪2∫3π0sin x 2d x D ．以上结论都不对解析 ∵1－cos x ＝2sin 2x2，∴∫3π1－cos x d x ＝ ∫3π02|sin x 2|d x ＝2∫3π0|sin x 2|d x . 答案 B2．(2012·芜湖一中月考)⎠⎛0e 1＋ln xx d x ＝( )．A ．ln x ＋12ln 2x B.2e －1 C.32 D.12解析⎪⎪⎪⎠⎛0e1＋ln x x d x ＝(ln x ＋ln 2x 2)e 1＝32. 答案 C3．(2012·长春质检)以初速度40 m/s 竖直向上抛一物体，t 秒时刻的速度v ＝40－10t 2，则此物体达到最高时的高度为( )． A.1603 m B.803 m C.403 mD.203 m解析 v ＝40－10t 2＝0，t ＝2，⎠⎛02(40－10t 2)d t ＝⎪⎪⎪⎝ ⎛⎭⎪⎫40t －103t 320＝40×2－103×8＝1603(m)． 答案 A4．一物体在变力F (x )＝5－x 2(力单位：N ，位移单位：m)作用下，沿与F (x )成30°方向作直线运动，则由x ＝1运动到x ＝2时F (x )作的功为( )． A. 3 J B.233 J C.433 JD ．2 3 J解析 由于F (x )与位移方向成30°角．如图：F 在位移方向上的分力F ′＝F ·cos 30°，W ＝⎠⎛12(5－x 2)·cos 30°d x＝32⎠⎛12(5－x 2)d x＝32⎝ ⎛⎪⎪⎪⎭⎪⎫5x －13x 321 ＝32×83＝433(J)． 答案 C5．(2011·全国新课标)由曲线y ＝x ，直线y ＝x －2及y 轴所围成的图形的面积为( )．A.103 B ．4 C.163D ．6解析 由y ＝x 及y ＝x －2可得，x ＝4，所以由y ＝x 及y ＝x －2及y 轴所围成的封闭图形面积为⎠⎛04(x －x ＋2)d x ＝⎝ ⎛⎭⎪⎫23x 32－12x 2＋2x | 40＝163.答案 C二、填空题(每小题4分，共12分)6．一物体以初速度v ＝9.8t ＋6.5 m/s 的速度自由落下，则下落后第二个4 s 内经过的路程是__________． 解析⎪⎪⎠⎛48(9.8t ＋6.5)d t ＝(4.9t 2＋6.5t )84＝4.9×64＋6.5×8－4.9×16－6.5×4＝313.6＋52－78.4－26 ＝261.2(m)． 答案 261.2 m7．(2012·榆林模拟)曲线y ＝1x 与直线y ＝x ，x ＝2所围成的图形的面积为____________． 答案 32－ln 28.⎠⎛3－3(9－x 2－x 3)d x ＝________. 答案 9π2三、解答题(共23分)9．(11分)如图在区域Ω＝{(x ，y )|－2≤x ≤2,0≤y ≤4}中随机撒900粒豆子，如果落在每个区域的豆子数与这个区域的面积近似成正比，试估计落在图中阴影部分的豆子数．解 区域Ω的面积为S 1＝16. 图中阴影部分的面积 S 2＝S 1－⎪⎪⎪⎠⎛2－2x 2d x ＝16－13x 32－2＝323.设落在阴影部分的豆子数为m ， 由已知条件m 900＝S 2S 1，即m ＝900S 2S 1＝600.因此落在图中阴影部分的豆子约为600粒．10．(12分)如图所示，直线y ＝k x 分抛物线y ＝x －x 2与x 轴所围图形为面积相等的两部分，求k 的值．解 抛物线y ＝x －x 2与x 轴两交点的横坐标为x 1＝0，x 2＝1， 所以，抛物线与x 轴所围图形的面积S ＝⎠⎛01(x －x 2)d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫x 22－13x 310＝16. 又⎩⎨⎧y ＝x －x 2，y ＝k x ， 由此可得，抛物线y ＝x －x 2与y ＝k x 两交点的横坐标为 x 3＝0，x 4＝1－k ，所以， S 2＝∫1－k 0(x －x 2－k x )d x ＝⎝ ⎛⎪⎪⎪⎭⎪⎫1－k 2x 2－13x 31－k 0＝16(1－k )3. 又知S ＝16， 所以(1－k )3＝12，于是k ＝1－ 312＝1－342.B 级 综合创新备选 (时间：30分钟 满分：40分)一、选择题(每小题5分，共10分)1．(2012·洛阳模拟)已知a ＝∑i ＝1n1n ⎝ ⎛⎭⎪⎫i n 2，n ∈N *，b ＝⎠⎛01x 2d x ，则a ，b 的大小关系是( )． A ．a >b B ．a ＝b C ．a <bD ．不确定答案 A 2．下列积分中①⎠⎛1e 1x d x ；②⎠⎛2－2x d x ；③⎠⎛024－x 2πd x ；④∫π20cos 2x2(cos x －sin x )d x ，积分值等于1的个数是( )．A ．1B ．2C ．3D ．4 解析 ①⎪⎪⎪⎠⎛1e 1x d x ＝ln x e 1＝1， ②⎪⎪⎪⎠⎛2－2x d x ＝12x 22－2＝0，③⎠⎛024－x 2πd x ＝1π(14π22)＝1，④∫π20cos 2x 2(cos x －sin x )d x ＝12∫π20(cos x ＋sin x )d x＝12(sin x －cos)|0π2＝1.答案 C二、填空题(每小题4分，共8分) 3．(2012·福州模拟)⎠⎛12|3－2x |d x ＝________.解析∵|3－2x |＝⎩⎪⎨⎪⎧－2x ＋3，x ≤32，2x －3，x ＞32，∴⎠⎛12|3－2x |d x ＝∫321(3－2x )d x ＋⎠⎛232(2x －3)d x＝ |(3x －x 2)321＋(x 2－3x )|232＝12. 答案 124．(2012·新余模拟)抛物线y ＝－x 2＋4x －3及其在点A (1,0)和点B (3,0)处的切线所围成图形的面积为________．解析 如图所示，因为y ′＝－2x ＋4，y ′|x ＝1＝2，y ′|x ＝3＝－2，两切线方程为y ＝2(x －1)和y ＝－2(x －3)． 由⎩⎨⎧y ＝2(x －1)，y ＝－2(x －3)得x ＝2.所以S ＝⎠⎛12[2(x －1)－(－x 2＋4x －3)]d x ＋⎠⎛23[－2(x －3)－(－x 2＋4x －3)]d x＝⎠⎛12(x 2－2x ＋1)d x ＋⎠⎛23(x 2－6x ＋9)d x ＝ ⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－x 2＋x 21＋⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－3x 2＋9x 32＝23. 答案 23三、解答题(共22分)5．(10分)曲线C ：y ＝2x 3－3x 2－2x ＋1，点P ⎝ ⎛⎭⎪⎫12，0，求过P 的切线l 与C 围成的图形的面积．解 设切点坐标为(x 0，y 0) y ′＝6x 2－6x －2， 则y ′|x ＝x 0＝6x 20－6x 0－2， 切线方程为y ＝(6x 20－6x 0－2)⎝ ⎛⎭⎪⎫x －12， 则y 0＝(6x 20－6x 0－2)⎝ ⎛⎭⎪⎫x 0－12，即2x 30－3x 20－2x 0＋1＝(6x 20－6x 0－2)⎝⎛⎭⎪⎫x 0－12.整理得x 0(4x 20－6x 0＋3)＝0，解得x 0＝0，则切线方程为y ＝－2x ＋1. 解方程组⎩⎨⎧y ＝－2x ＋1，y ＝2x 3－3x 2－2x ＋1， 得⎩⎨⎧x ＝0，y ＝1或⎩⎪⎨⎪⎧x ＝32，y ＝－2.由y ＝2x 3－3x 2－2x ＋1与y ＝－2x ＋1的图象可知 S ＝∫320[(－2x ＋1)－(2x 3－3x 2－2x ＋1)]d x ＝∫320(－2x 3＋3x 2)d x ＝2732.6．(12分)由曲线y ＝x 2和直线x ＝0，x ＝1，y ＝t 2，t ∈(0,1)所围成的图形(如图阴影部分)，求其面积的最小值．解 S 1＝t 3－⎠⎛0t x 2d x ＝t 3－13t 3＝23t 3，S 2＝⎠⎛t 1x 2d x －(1－t )t 2＝13－13t 3－(1－t )t 2，＝23t 3－t 2＋13，S 1＋S 2＝43t 3－t 2＋13，t ∈(0,1)．可由导数求得当t ＝12时，S 1＋S 2取到最小值，最小值为14.。

高考数学复习第16讲 与圆相关的定点、定值问题

高考数学复习第16讲 与圆相关的定点、定值问题

微专题17 与圆相关的定点、定值问题圆的综合问题还可能会考查与圆有关的定点、定值问题，这类问题的解决往往先从特例题：已知圆O ：x 2＋y 2＝9.点A (－5，0)，在x 轴上存在定点B (不同于点A )，满足：对于圆O 上任一点P ，都有PBP A为一常数，试求所有满足条件的点B 的坐标．变式1已知圆O 的方程为x 2＋y 2＝1，直线l 1过点A(3，0)，且与圆O 相切．(1)求直线l 1的方程；(2)设圆O 与x 轴交于P ，Q 两点，M 是圆O 上异于P ，Q 的任意一点，过点A 且与x 轴垂直的直线为l 2，直线PM 交直线l 2于点P′，直线QM 交直线l 2于点Q′.求证：以P′Q′为直径的圆C 总过定点，并求出定点坐标．变式2已知过点A(0，1)，且斜率为k 的直线l 与圆C ：(x －2)2＋(y －3)2＝1相交于M ，N 两点．求证：AM →·AN →为定值7.串讲1如图，已知以点A(－1，2)为圆心的圆与直线l 1：x ＋2y ＋7＝0相切．过点B(－2，0)的动直线l 与圆A 相交于M ，N 两点，Q 是MN 的中点，直线l 与l 1相交于点P.BQ →·BP →是否为定值？如果是，求出其定值；如果不是，请说明理由．串讲2设O 为坐标原点，F(1，0)，M 是l ：x ＝2上的点，过点F 作OM 的垂线与以OM 为直径的圆D 交于P ，Q 两点．(1)若PQ ＝6，求圆D 的方程；(2)若M 是l 上的动点，求证点P 在定圆上，并求该定圆的方程．(2018·江苏模拟卷)如图，在平面直角坐标系xOy 中，A ，B 是圆O ：x 2＋y 2＝1与x 轴的两个交点(点B 在点A 右侧)，点Q(－2，0)，x 轴上方的动点P 使直线PA ，PQ ，PB 的斜率存在且依次成等差数列．(1)求证：动点P 的横坐标为定值；(2)设直线PA ，PB 与圆O 的另一个交点分别为S ，T ，求证：点Q ，S ，T 三点共线．(2017·江苏模拟卷)在平面直角坐标系xOy 中，已知定点A(－4，0)，B(0，－2)，半径为r 的圆M 的圆心M 在线段AB 的垂直平分线上，且在y 轴右侧，圆M 被y 轴截得的弦长为3r.(1)若r ＝2，求圆M 的方程； (2)当r 变化时，是否存在定直线与圆相切？如果存在，求出定直线的方程；如果不存在，请说明理由．答案：(1)(x －1)2＋(y －5)2＝4；(2)存在两条直线y ＝3和4x ＋3y －9＝0与圆相切．解析：(1)设圆心M(m ，n)，由题意可知⎩⎪⎨⎪⎧⎝⎛⎭⎫32r 2＋m 2＝r 2，m ＞0，（m ＋4）2＋n 2＝m 2＋（n ＋2）2，解得⎩⎪⎨⎪⎧m ＝12r ，n ＝r ＋3，4分∴圆M 的方程为(x －1)2＋(y －5)2＝4.5分(2)设直线l ：y ＝kx ＋b ，则⎪⎪⎪⎪k·r 2－r －3＋b 1＋k 2＝r 对任意r ＞0恒成立，7分由⎪⎪⎪⎪⎝⎛⎭⎫k 2－1r ＋b －3＝r 1＋k 2，得⎝⎛⎭⎫k 2－12r 2＋(k －2)(b －3)r ＋(b －3)2 ＝r 2(1＋k 2)，9分∴⎩⎪⎨⎪⎧⎝⎛⎭⎫k 2－12＝1＋k 2，（k －2）（b －3）＝0，（b －3）2＝0，计算得出⎩⎪⎨⎪⎧k ＝0，b ＝3或⎩⎪⎨⎪⎧k ＝－43，b ＝3，13分 ∴存在两条直线y ＝3和4x ＋3y －9＝0与圆相切.14分微专题17 与圆相关的定点、定值问题巩固练习1.圆C ：x 2＋y 2－2tx －2t 2y ＋4t －4＝0，则圆过定点________．2．已知以曲线y ＝2x 上任意点C 为圆心的圆与x 轴交于点O ，A ，与y 轴交于点O ，B ，其中O 为原点，则△AOB 的面积为________．3．已知直线l ：mx －y ＋m ＝0，圆C ：(x －a)2＋y 2＝4.若对任意a ∈[1，＋∞)，存在l 被C 截得弦长为2，则实数m 的取值范围是________．4．设m ∈R ，过定点A 的动直线x ＋my ＝0和过定点B 的动直线mx －y －m ＋3＝0交于点P (x ，y )，则2P A ＋PB 的最大值是________．5．在平面直角坐标系xOy 中，已知圆C ：x 2＋y 2－(6－2m)x －4my ＋5m 2－6m ＝0，直线l 经过点(－1，1)．若对任意的实数m ，定直线l 被圆C 截得的弦长为定值，则直线l 的方程为________．6．在平面直角坐标系xOy 中，圆C 的方程为(x －1)2＋y 2＝4，P 为圆C 上一点．若存在一个定圆M ，过P 作圆M 的两条切线PA ，PB ，切点分别为A ，B ，当P 在圆C 上运动时，使得∠APB 恒为60°，则圆M 的方程为________．7．已知圆C 的方程为(x ＋4)2＋y 2＝16，直线l 过圆心且垂直于x 轴，其中G 点在圆上，F 点坐标为(－6，0)．(1)若直线FG 与直线l 交于点T ，且G 为线段FT 的中点，求直线FG 被圆C 所截得的弦长；(2)在平面上是否存在定点P ，使得对圆C 上任意的点G 有GF GP ＝12？若存在，求出点P 的坐标；若不存在，请说明理由．8．如图，在平面直角坐标系xOy 中，已知F 1(－4，0)，F 2(4，0)，A(0，8)，直线y ＝t(0＜t ＜8)与线段AF 1，AF 2分别交于点P ，Q ，过点Q 作直线QR ∥AF 1交F 1F 2于点R ，记△PRF 1的外接圆为圆C.(1)求证：圆心C 在定直线7x ＋4y ＋8＝0上；(2)圆C 是否恒过异于点F 1的一个定点？若过，求出该点的坐标；若不过，请说明理由．微专题17参考答案例题答案：B ⎝⎛⎭⎫－95，0. 解法1如图，假设存在这样的点B(t ，0)，当P 为圆O 与x 轴左交点(－3，0)时，PB PA ＝|t ＋3|2；当P 为圆O 与x 轴右交点(3，0)时，PB PA ＝|t －3|8，依题意，|t ＋3|2＝|t －3|8，解得，t ＝－5(舍去)，或t ＝－95.下面证明：点B ⎝⎛⎭⎫－95，0对于圆O 上任一点P ，都有PBPA为一常数． 设P(x ，y)，则y 2＝9－x 2，所以PB 2PA 2＝⎝⎛⎭⎫x ＋952＋y 2（x ＋5）2＋y 2＝x 2＋185x ＋8125＋9－x 2x 2＋10x ＋25＋9－x 2＝1825（5x ＋17）2（5x ＋17）＝925，从而PB PA ＝35为常数．解法2假设存在这样的点B(t ，0)，使得PBPA 为常数λ，则PB 2＝λ2PA 2，所以(x －t)2＋y 2＝λ2[(x ＋5)2＋y 2]，将y 2＝9－x 2代入得，x 2－2xt ＋t 2＋9－x 2＝λ2(x 2＋10x ＋25＋9－x 2)，即2(5λ2＋t)x ＋34λ2－t 2－9＝0对x ∈[－3，3]恒成立，所以⎩⎨⎧5λ2＋t ＝0，34λ2－t 2－9＝0，解得⎩⎨⎧λ＝35，t ＝－95，或⎩⎨⎧λ＝1，t ＝－5，(舍去)，所以存在点B ⎝⎛⎭⎫－95，0对于圆O 上任一点P ，都有PB PA 为常数35. 变式联想变式1 答案：(1)y ＝±24(x －3)；(2)(3±22，0)． 解析：(1)因为直线l 1过点A(3，0)，且与圆O ：x 2＋y 2＝1相切，设直线l 1的方程为y ＝k(x －3)，即kx －y －3k ＝0，则圆心O(0，0)到直线l 1的距离为d ＝|3k|k 2＋1＝1，解得k ＝±24，所以直线l 1的方程为y＝±24(x －3)． (2)对于圆方程x 2＋y 2＝1，令y ＝0，得x ＝±1，即P(－1，0)，Q(1，0)， 又直线l 2过点A 且与x 轴垂直，所以直线l 2方程为x ＝3，设M(s ，t)，则直线PM 的方程为y ＝ts ＋1(x ＋1)．解方程组⎩⎪⎨⎪⎧x ＝3，y ＝t s ＋1（x ＋1）， 得P′⎝⎛⎭⎫3，4t s ＋1同理可得，Q ′⎝⎛⎭⎫3，2t s －1.所以以P′Q′为直径的圆C 的方程为(x －3)(x －3)＋⎝⎛⎭⎫y －4t s ＋1⎝⎛⎭⎫y －2ts －1＝0，又s 2＋t 2＝1，所以整理得x 2＋y 2－6x ＋1＋6x －2t y ＝0，若圆C 经过定点，只需令y ＝0，从而有x 2－6x ＋1＝0，解得x ＝3±22，所以，圆C 总经过定点坐标为(3±22，0)．变式2证法1设M(x 1，y 1)，N(x 2，y 2)，联立⎩⎨⎧y ＝kx ＋1，（x －2）2＋（y －3）2＝1，得(k 2＋1)x 2－4(k ＋1)x ＋7＝0，所以⎩⎪⎨⎪⎧x 1＋x 2＝4（k ＋1）k 2＋1，x 1x 2＝7k 2＋1.因为AM →＝(x 1，y 1－1)，AN →＝(x 2，y 2－1)，所以AM →·AN →＝x 1x 2＋(y 1－1)(y 2－1)＝x 1x 2＋k 2x 1x 2＝(1＋k 2)x 1x 2＝(1＋k 2)x 1x 2＝(1＋k 2)71＋k 2＝7.所以AM →·AN →为定值7.证法2由于M ，N 共线，所以AM →·AN →＝AM·AN ＝(AC －1)(AC ＋1)＝AC 2－1＝7.串讲激活串讲1答案：BQ →·BP →＝－5.解析：因为AQ ⊥BP ，所以AQ →·BP →＝0，所以BQ →·BP →＝(BA →＋AQ →)·BP →＝BA →·BP →＋AQ →·BP →＝BA →·BP →.当直线l 与x 轴垂直时，得P ⎝⎛⎭⎫－2，－52.则BP →＝⎝⎛⎭⎫0，－52， 又BA →＝(1，2)，所以BQ →·BP →＝BA →·BP →＝－5.当直线l 的斜率存在时，设直线l 的方程为y ＝k(x ＋2)．由⎩⎨⎧y ＝k （x ＋2），x ＋2y ＋7＝0，解得P ⎝ ⎛⎭⎪⎫－4k －71＋2k ，－5k 1＋2k .所以BP →＝⎝ ⎛⎭⎪⎫－51＋2k ，－5k 1＋2k .所以BQ →·BP →＝－51＋2k －10k 1＋2k ＝－5.综上所述，BQ →·BP →是定值，且BQ →·BP →＝－5.串讲2答案：(1)圆D 的方程：(x －1)2＋(y －1)2＝2或(x －1)2＋(y ＋1)2＝2； (2)点P 在定圆x 2＋y 2＝2上． 解析：(1)设M(2，t)，则圆D的方程：(x －1)2＋⎝⎛⎭⎫y －t 22＝1＋t 24， 直线PQ 的方程：2x ＋ty －2＝0，由PQ ＝6， 2⎝⎛⎭⎫1＋t 24－⎝⎛⎭⎪⎪⎫⎪⎪⎪⎪2＋t 22－24＋t 22＝6，解得t ＝±2. 所以圆D 的方程为(x －1)2＋(y －1)2＝2或(x －1)2＋(y ＋1)2＝2.(2)解法1设P(x 0，y 0)，由(1)知⎩⎪⎨⎪⎧（x 0－1）2＋⎝⎛⎭⎫y 0－t 22＝1＋t 24，2x 0＋ty 0－2＝0，即⎩⎨⎧x 02＋y 02－2x 0－ty 0＝0，2x 0＋ty 0－2＝0，消去t 得x 02＋y 02＝2.所以点P 在定圆x 2＋y 2＝2上．解法2设P(x 0，y 0)，则直线FP 的斜率为k FP ＝y 0x 0－1，因为FP ⊥OM ，所以直线OM 的斜率为k OM ＝－x 0－1y 0，所以直线OM 的方程为y ＝－x 0－1y 0x.点M 坐标为⎝⎛⎭⎫2，－2（x 0－1）y 0.因为MP ⊥OP ，所以OP →·MP →＝0，所以x 0(x 0－2)＋y 0⎣⎡⎦⎤y 0＋2（x 0－1）y 0＝0，所以x 02＋y 02＝2，所以点P在定圆x 2＋y 2＝2上．解法3设直线PQ 与OM 交于点H ，A(2，0)，由射影定理知OP 2＝OH·OM ，由此知，OH ·OM ＝OF·OA ＝2，所以OP 2＝2，所以点P 在定圆x 2＋y 2＝2上．新题在线证明：(1)由题设知A(－1，0)，B(1，0)． 设P(x 0，y 0)(y 0＞0)，则k PQ ＝y 0x 0＋2，k PA ＝y 0x 0＋1，k PB ＝y 0x 0－1. 因为直线PA ，PQ ，PB 的斜率存在且依次成等差数列，所以2k PQ ＝k PA ＋k PB ，即2y 0x 0＋2＝y 0x 0＋1＋y 0x 0－1，解得x 0＝－12，即动点P 的横坐标为定值．(2)由(1)知P ⎝⎛⎭⎫－12，y 0，k PA ＝2y 0，k PB ＝－23y 0，直线PA 的方程为y ＝2y 0(x ＋1)，代入x 2＋y 2＝1得(x ＋1)[(1＋4y 02)x －(1－4y 02)]＝0，所以点S 的横坐标x S ＝1－4y 021＋4y 02，从而y S ＝4y 01＋4y 02. 同理：x T ＝－9＋4y 029＋4y 02，y T＝12y 09＋4y 02， 所以k QS ＝4y 01＋4y 021－4y 021＋4y 02＋2＝4y 03＋4y 02，k QT ＝12y 09＋4y 02－9＋4y 029＋4y 02＋2＝4y 03＋4y 02，所以k QS＝k QT，所以点Q，S，T三点共线．微专题17巩固练习参考答案1．答案：(2，0)． 解析：圆C 的方程可以改写为(x －2)(x ＋2－2t )＋y (y －2t 2)＝0，表示以(2，0)，(2t －2，2t 2)为直径的圆． 2．答案：4.解析：设C ⎝⎛⎭⎫t ，2t (t ∈R ，t ≠0)，由题意知，圆C 的方程为(x －t )2＋⎝⎛⎭⎫y －2t 2＝t 2＋4t 2，化简得x 2－2tx ＋y 2－4t y ＝0，当y ＝0时，x ＝0或2t ，则A (2t ，0)；当x ＝0时，y ＝0或4t ，则B ⎝⎛⎭⎫0，4t ，所以S △AOB ＝12OA ·OB ＝12|2t |·⎪⎪⎪⎪4t ＝4. 3．答案：[－3，0)∪(0，3]． 解法1由题意可得，圆心C 到l 的距离d ＝22－⎝⎛⎭⎫222＝3，即|am ＋m |m 2＋1＝3，所以m 2＝3（a ＋1）2－3，又因为a ≥1，所以0＜m 2≤3，－3≤m ＜0或0＜m ≤ 3.解法2由题意可得，圆心C 到l 的距离d ＝22－⎝⎛⎭⎫222＝3，又l ：mx －y ＋m ＝0恒过定点A (－1，0)，a ≥1，所以AC ≥2，另设直线l 的倾斜角为θ，所以sin θ＝3AC ∈⎝⎛⎦⎤0，32，所以l 的斜率m ＝tan θ∈[－3，0)∪(0，3]．4．答案：5 2.解析：由条件知定点A (0，0)，B (1，3)，且P A ⊥PB ，所以P A 2＋PB 2＝10(定值)，所以(2P A ＋PB )2≤(P A 2＋PB 2)(22＋12)＝50，即2P A ＋PB ≤5 2.5．答案：2x ＋y ＋1＝0.解析：由条件知圆心C (3－m ，2m )在直线2x ＋y －6＝0上，若对任意的实数m ，定直线l 被圆C 截得的弦长都是定值，则直线l 与圆心所在直线平行，再代入点(－1，1)得直线l 的方程为2x ＋y ＋1＝0.6．答案：(x －1)2＋y 2＝1.解析：设定圆圆心M (a ，b )，半径为r ，动点P (x ，y )，由题意知MP ＝2r ，即(x －a )2＋(y －b )2＝4r 2，由于点P 在圆C ：(x －1)2＋y 2＝4上，所以(2－2a )x －2by ＋a 2＋b 2－4r 2＋3＝0，对任意x ，y 都成立，所以a ＝1，b ＝0，r 2＝1，所求圆方程为(x －1)2＋y 2＝1.7．答案：(1)直线FG 被圆C 截得的弦长为7；(2)平面上存在定点P (－12，0)，使得结论成立． 解析：(1)由题意，设G (－5，y G )，代入(x ＋4)2＋y 2＝16，得y G ＝±15，所以FG 的斜率为k ＝±15，FG 的方程为y ＝±15(x ＋6)．设圆心C (－4，0)到FG 的距离为d ，由点到直线的距离公式得d ＝|±215|15＋1＝152.则直线FG 被圆C 截得的弦长为26－⎝⎛⎭⎫1522＝7.故直线FG 被圆C 截得的弦长为7. (2)设P (s ，t )，G (x 0，y 0)，则由GF GP ＝12，得（x 0＋6）2＋y 02（x 0－s ）2＋（y 0－t ）2＝12，整理得3(x 02＋y 02)＋(48＋2s )x 0＋2ty 0＋144－s 2－t 2＝0.① 又G (x 0，y 0)在圆C ：(x ＋4)2＋y 2＝16上，所以x 02＋y 02＋8x 0＝0.②将②代入①，得(2s ＋24)x 0＋2ty 0＋144－s 2－t 2＝0.又由G (x 0，y 0)为圆C 上任意一点可知，11 / 11 ⎩⎪⎨⎪⎧2s ＋24＝0，2t ＝0，144－s 2－t 2＝0.解得s ＝－12，t ＝0.所以在平面上存在定点P (－12，0)，使得结论成立． 8．答案：(1)略；(2)圆C 恒过异于点F 1的一定点，该点坐标为⎝⎛⎭⎫413，3213.解析：(1)解法1：易得直线AF 1：y ＝2x ＋8；AF 2：y ＝－2x ＋8，所以P ⎝⎛⎭⎫t －82，t ，Q ⎝⎛⎭⎫8－t 2，t ，再由QR ∥AF 1，得R (4－t ，0)，则线段F 1R 的中垂线方程为x ＝－t 2，线段PF 1的中垂线方程为y ＝－12x ＋5t －168，由⎩⎨⎧y ＝－12x ＋5t －168，x ＝－t 2，得△PRF 1的外接圆的圆心坐标为⎝⎛⎭⎫－t 2，7t 8－2， 经验证，该圆心在定直线7x ＋4y ＋8＝0上．解法2：易得直线AF 1：y ＝2x ＋8；AF 2：y ＝－2x ＋8，所以P ⎝⎛⎭⎫t －82，t ，Q ⎝⎛⎭⎫8－t 2，t ，再由QR ∥AF 1，得R (4－t ，0)，设△PRF 1的外接圆C 的方程为x 2＋y 2＋Dx ＋Ey ＋F ＝0，则⎩⎪⎨⎪⎧（4－t ）2＋（4－t ）D ＋F ＝0，（－4）2－4D ＋F ＝0，⎝⎛⎭⎫t －822＋t 2＋t －82D ＋tE ＋F ＝0， 解得⎩⎪⎨⎪⎧D ＝t ，E ＝4－74t ，F ＝4t －16，所以圆心坐标为⎝⎛⎭⎫－t 2，7t 8－2，经验证，该圆心在定直线7x ＋4y ＋8＝0上． (2)由(1)可得圆C 的方程为x 2＋y 2＋tx ＋⎝⎛⎭⎫4－74t y ＋4t －16＝0，该方程可整理为(x 2＋y 2＋2y －16)＋t ⎝⎛⎭⎫x －74y ＋4＝0，则由⎩⎪⎨⎪⎧x 2＋y 2＋4y －16＝0，x －74y ＋4＝0，解得⎩⎨⎧x ＝413，y ＝3213，或⎩⎨⎧x ＝－4，y ＝0，所以圆恒过异于点F 1的一个定点，该点坐标为⎝⎛⎭⎫413，3213.。

专题16 函数与导数的综合问题- 2022届高考数学二模试题分类汇编(新高考卷)(原卷版)

专题16 函数与导数的综合问题- 2022届高考数学二模试题分类汇编(新高考卷)(原卷版)

《专题16 函数与导数的综合问题- 2022届高考数学二模试题分类汇编（新高考卷）》1．【利用导数研究极值问题】（2022·河南焦作·二模）已知函数()(2)e x f x x =-. (1)求()f x 的极值；(2)若函数()()(ln )g x f x k x x =--在区间1,12⎛⎫⎪⎝⎭上没有极值，求实数k 的取值范围.2．【利用导数研究极值问题】（2022·四川泸州·三模）已知函数()313f x x ax =-+，R a ∈．(1)讨论函数()f x 的单调性；(2)若()()xg x f x e =⋅有且只有一个极值点，求a 的取值范围．3．【利用导数研究最值问题】（2022·甘肃兰州·模拟预测）已知函数()2e sin xf x ax x =--，e为自然对数的底数．(1)求()f x 在0x =处的切线方程；(2)当0x ≥时，()1sin f x x x ≥--，求实数a 的最大值． 4．【利用导数研究最值问题】（2022·北京·一模）已知函数()21x af x x -=-． (1)若曲线()y f x =在点()()22f ,处的切线斜率为1-，求a 的值； (2)若()f x 在()1,+∞上有最大值，求a 的取值范围.5．【利用导数证明不等式】（2022·湖北·二模）已知函数()e 1,()(ln )x f x x g x a x x =-=+． (1)若不等式()()f x g x ≥恒成立，求正实数a 的值； (2)证明：2e (2)ln 2sin x x x x x >++．6．【利用导数证明不等式】（2022·四川省泸县第四中学模拟预测）设函数()ln f x ax x =，其中R a ∈，曲线()y f x =在点()()1,1f 处的切线经过点()3,2. (1)求函数()f x 的极值； (2)证明：()2e ex x f x >-. 7．【利用导数解决恒成立问题】（2022·吉林·延边州教育学院一模）已知函数()()e R x f x ax a =+∈．(1)讨论函数()f x 的极值点个数；(2)若()1ln(1)≥-+f x x 对任意的[0,)x ∈+∞恒成立，求实数a 的取值范围．8．【利用导数解决恒成立问题】（2022·云南·二模）己知e 是自然对数的底数，()e 1x f x ax =-+，常数a 是实数.(1)设e a =，求曲线()y f x =在点(1,(1))f 处的切线方程； (2)1x ∀≥，都有(1)ln f x x -≤，求a 的取值范围.9．【利用导数解决能成立问题】（2022·辽宁·一模）已知函数()321sin 1,,462f x x x x ππαα⎡⎤=-++∈-⎢⎥⎣⎦， (1)讨论函数()f x 的单调性；(2)证明：存在,62ππα⎡⎤∈-⎢⎥⎣⎦，使得不等式()e xf x > 有解（e 是自然对数的底）.10．【利用导数解决能成立问题】（2022·广西广西·模拟预测）已知函数()()()221ln f x x a x a x a R =-++∈.(1)若()f x 在区间[]1,2上是单调函数，求实数a 的取值范围；(2)函数()()1g x a x =-，若[]01,e x ∃∈使得()()00f x g x ≥成立.求实数a 的取值范围. 11．【利用导数解决零点问题】（2022·广西南宁·二模）设函数()()212ln x f x a x x x -=-+，a ∈R ．(1)当1a =时，讨论()f x 的单调性；(2)若()f x 有两个零点，求实数a 的取值范围．12．【利用导数解决零点问题】（2022·山东枣庄·一模）已知函数()()e sin xf x x a x a =-∈R ．(1)若[]0,πx ∀∈，()0f x ≥，求a 的取值范围；(2)当59a ≥-时，试讨论()f x 在()0,2π内零点的个数，并说明理由．13．【利用导数解决方程的根问题】（2022·宁夏·固原一中一模）设函数()2ln 25f x x x x =+-.（1）求函数()f x 的极小值；（2）若关于x 的方程()()226f x x m x =+-在区间2[1,e ]上有唯一实数解，求实数m 的取值范围.14．【利用导数解决方程的根问题】（2022湖北襄阳五中高三模拟）已知函数()1e 2ln 46x f x x x -=-+-，e 是自然对数的底数．（1）求曲线()y f x =在()()1,1f 处的切线方程；（2）若()0,x ∈+∞，证明：曲线()y f x =不落在()32y x =-图像的下方．15．【利用导数解决双变量问题】（2022·黑龙江齐齐哈尔·二模）已知函数()()2ln f x a x a R x=+∈. (1)求函数()f x 的单调区间；(2)若函数()()2g x x f x =-有两个极值点12,x x ，且(]11,x e ∈（e 为自然对数底数，且2.71828e =⋯），求()()12g x g x -的取值范围.16．【利用导数解决双变量问题】（2022·河南·汝州市第一高级中学模拟预测）已知函数()()1ln f x x ax a R x=--∈.(1)当3a =时，证明：()sin 3f x x <--；(2)若()f x 的两个零点分别为()1212,x x x x <，证明：2122e x x ⋅>.。

相关主题
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A.- 6
C. D.
(数学4必修)第二章平面向量
［提高训练c组］
一、选择题
1.若三点A(2,3),B(3,d),C(4,b)共线，则有( )
A. a = 3,b = —5 B・a-b-¥\ =0 C. 2a- b = 3 D. a-2b = 0
2.设O<0 <27c ,己知两个向量OR = (cos&, sin。

)，
亦=(2 + sinO,2-cos&),则向量屈长度的最大值是( )
A. 72
B. V3
C. 3^2
D. 2^3
3.卜列命题正确的是( )
A •单位向量都相等
B・若2与乙是共线向量，与：是共线向量，贝叮与7是共线向量( )
C. \a + b\=\ a-b I,贝^\a-b = 0
D・若°o与％是单位向量,则&0厨=1
4.已知万，方均为单位向量，它们的夹角为60。

，那么a^b =( )
A. V7
B. Vio
C. V13
D. 4
5.已知向量d ,乙满足”1 = 1" =4,且Q.乙=2 ,则G与乙的夹角为
6.若平面向量乙与向量：=(2,1)平行，且1^1= 2^5，贝叮=(
A. (4,2) B・(一4,一2) C. (6,-3) D. (4,2)或(-4,-2)
二、填空题
1.已知向量a = (cos 0, sin ff),向量b =(73,-1) , WJ 2a-b的最大值是
2 若4(l,2),B(2,3),C(-2,5),试判断则厶ABC 的形状 ________________ .
3.若5 = (2,-2),则与2垂直的单位向量的坐标为______________ .
4.若向量G 1=1,1力=2,G—力=2,贝山方+力二____ .
5.平面向量a,方屮,已知a = (4,-3) , b =1, JEa b = 5 ,则向量方= __________ .
三、解答题
1.已知是三个向量，试判断下列各命题的真假.
(1)若乳5 =乳0且方工0,贝iJ5 = e
(2)向量万在方的方向上的投影是-•模等寸-同cos& (&是N与方的夹
角)，方向与Q在方相同或相反的一个向量・
2.证明:对于任意的a,b,c,d G R ,怛有不等式(ac+bd)2 < (a2 +/?2)(c2+d2)
3・平而向量5 = (V3,-1)J = 若存在不同时为0的实数£和r, 使
丘二万+(尸_3)方了二_転+厉,且丘丄歹，试求函数关系工弋£二.fa)・
4.如图，在直角AABC中，已知BC = a,若长为2d的线段PQ以点A 为中
点，问甩与荒
的夹角&取何值时丽•页的值最大？并求出这个方c
A D
数学4（必修）第二章平面向量［提高训练C组］
参考答案
一、选择题
1. C 殛=（1卫一3）,疋=（2』一3）,而〃紀"一3 = 20-6,2。

一/? = 3
2. C P}P2 =（2 + si n&-cos &,2-cos&-sin&）,
胴=j2（2-cos&）2+2sinS = J10-8cos&<718=3^2
3. C 单位向量仅仅长度相等而已，方向也许不同；当10时，7与7可以为任意向量；
G+庆i=G-亦,即对角线相等,此时为矩形，邻边垂直;还要
考虑夹角
4. C 0 + 3习二J矿+6厅方+ 9戸=Jl + 6cos600+9=V^
5. C cos0 = -^- = - = -,0 = -
砌 | 4 2 3
6 ・ D 设 b = ka = (2k,k\, 而\b\= 2^5 , 则屈
7 = 2 厉,k = ±，方二(4,2),或(一4, -2)
二、填空题
1. 4 2刁一7 = (2cos&—的,2sin& + l), 2a-h =^8 + 8sin(^-|) < V16 =4
2 直角三角形AB = (1,1), AC = (-3,3),AB AC = O,AB 丄犹
V2 V2 r V2 V2
(*亍或(-亍盲)
设所求的向量为(x,y\2x-2y = 0, x2 + y2
4.V6由平行四边形屮对角线的平方和等于四边的平方和得
a+h2 + a-h =2 犷+ 2b => 万 + b =2 茁+2b -a-b =2 + 2x4 —4 = 6
5. (f，一£)= (x,y\4x-3y = 5,x2 4-y2 = = = -|
三、解答题
1.解：(1 )若a-b =a-c且万北0,贝ljb=0,这是一个假命题
因为a^b=ac,a\b-c) = O9仅得Q 丄0-c)
(2)向量刁在丘的方向上的投影是一模等于同cos& (&是刁与方的夹角)，方向与万在5相同或相反的一个向量.这是一个假命题因为向量刁在方的方向上的投影是个数量，而非向量.
3. a =2, b = \
4. 解:•・•而丄 AC y
.\ABAC = 0. -AP = -AQ,~BP = AP-AB y CQ = AQ-AC,
.\~BPCQ =(AP-AB)(AQ-AC) = APAQ-APAC-ABAQ + ABAC
= -tz 2-AP AC + AB AP
=-a 2-AP (AB-^C)
2. 证明：设x = (a,b),y = (c,d) , WO x y = ac + bd,\x = yla 2 +/??, y = >Jc~ +cl 而丘 y
= |j||y|cos 3,\x y = x y|cos^ < x y
即 \x y < |^||.y| » 得 |ac + bd| 5 J a? +/?2 Jc? +c 厂
・・・(ac + bd)2 <(a 2 +/?2)(c 2 +d?)
i R
解：由 a = ^-l).b =(-,-)得 [a + (f 2 一3)b] (-ka +tb) = 0-ka 2+td b-k (r 2 -3)ab+t(t 2-3)b 2 = 0 _4R + F _ 3/ = 0,R =丄(r 3-3f ),/(/) = - (? 一 3r) 4 4
= -a 2 +-PQBC = -a 2 +-PQBC
— —a 1 + a 2 cos 0.
故当cos 。

= 1,即& = ()(P0与向相同)时,BP • C0最大.其最大值为0. Q H。

相关文档
最新文档