流体流动管路计算
管道流动阻力计算

流动阻力的计算流体在管道中流动,其流动阻力包括有:(1)( 1)直管阻力:流体流经直管段时,由于战胜流体的粘滞性及与管内壁间的磨擦所产生的阻力。
它存在于沿流动方向的整个长度上,故也称沿程直管流动阻力。
记为 h fz。
(2)( 2)局部阻力:流体流经异形管或管件(如阀门、弯头、三通等)时,由于流动发生突然变化引起涡流所产生的能量损失。
它仅存在流体流动的某一局部范围办。
记为 h fJ。
因此,柏努利方程中h f项应为:h f h fz h fJ说明:流动阻力可用不相同的方法表示,h f——1kg质量流体流动时所损失的机械能,单位为J/kg;h fm;—— 1N 重量流体流动时所损失的机械能,单位为gh f——1m3体积流体流动时所损失的机械能,单位为Pa 或N / m2。
1. 1. 直管段阻力(h fz)的计算流体流经直管段时,流动阻力可依下述公式计算:h fzl u2d [J/kg]2或h fz l u2g [m]d 2gl u2[pa]h fz2d式中,——磨擦阻力系数;l——直管的长度( m); d——直管内直径(m);——流体密度 (kg / m3 ) ;u——流体在直管段内的流速(m/s)2.局部阻力 (h fJ)的计算局部阻力的计算可采用阻力系数法或当量长度法进行。
1)1)阻力系数法:将液体战胜局部阻力所产生的能量损失折合为表示其动能 若干倍的方法。
其计算表达式可写出为:le u 2 ( a )h fJ[J/kg]d2或h fJ le u 2 (b)gd [m]2g[pa]le u 2 (ch fJ[pa] d 2其中, 称为局部阻力系数,平时由实验测定。
下面列举几种常用的局部阻力 系数的求法。
* 突然扩大与突然减小管路由于直径改变而突然扩大或减小,所产生的能量损失按(b )或 (c)式计算。
式中的流速 u 均以小管的流速为准, 局部阻力系数可依照小管与大管的截面积之比从管件与阀门当量长度共线图 曲线上查得。
第二节 流体流动的基本方程式

第二节 流体流动的基本方程式化工厂中流体大多是沿密闭的管道流动,液体从低位流到高位或从低压流到高压,需要输送设备对液体提供能量;从高位槽向设备输送一定量的料液时,高位槽所需的安装高度等问题,都是在流体输送过程中经常遇到的。
要解决这些问题,必须找出流体在管内的流动规律。
反映流体流动规律的有连续性方程式与柏努利方程式。
1-2-1 流量与流速一、流量单位时间内流过管道任一截面的流体量称为流量。
若流体量用体积来计量,称为体积流量,以V s 表示,其单位为m 3/s ;若流体量用质量来计量,则称为质量流量,以w s 表示,其单位为kg/s 。
体积流量与质量流量的关系为:w s =V s ·ρ (1-16) 式中 ρ——流体的密度,kg/m 3。
二、流速单位时间内流体在流动方向上所流经的距离称为流速。
以u 表示,其单位为m/s 。
实验表明,流体流经管道任一截面上各点的流速沿管径而变化,即在管截面中心处为最大,越靠近管壁流速将越小,在管壁处的流速为零。
流体在管截面上的速度分布规律较为复杂,在工程计算中为简便起见,流体的流速通常指整个管截面上的平均流速,其表达式为: A V u s = (1-17)式中 A ——与流动方向相垂直的管道截面积,m 2。
流量与流速的关系为:w s =V s ρ=uA ρ (1-18) 由于气体的体积流量随温度和压强而变化,因而气体的流速亦随之而变。
因此采用质量流速就较为方便。
质量流速,单位时间内流体流过管路截面积的质量,以G 表示,其表达式为:ρρu A V A w G s s === (1-19)式中 G ——质量流速,亦称质量通量;kg/(m 2·s )。
必须指出,任何一个平均值都不能全面代表一个物理量的分布。
式1-17所表示的平均流速在流量方面与实际的速度分布是等效的,但在其它方面则并不等效。
一般管道的截面均为圆形,若以d 表示管道内径,则 24d V u s π= 于是 uV d sπ4=(1-20) 流体输送管路的直径可根据流量及流速进行计算。
化工原理第一章 流体流动

例1-10 20℃的水在内径为 50mm的管内流动,流速为 2m/s,是判断管内流体流动的 型态。
三.流体在圆管内的速度分布
(a)层流
(b)湍流
u umax / 2 u 0.82umax
hf
le
d
u2 2
三.管内流体流动的总摩擦阻力损失计算 总摩擦阻力损失 =直管摩擦阻力损失+局部摩擦阻力损失
hf hf 直 hf局
l u2 ( le u2 z u2 )
d2 d 2
2
[
(
l
d
l
e
)
z
]
u2 2
管内流体流动的总摩擦阻力损失计算 直管管长 管件阀件当量长度法
hf
l
制氮气的流量使观察瓶内产生少许气泡。 已知油品的密度为850 kg/m3。并铡得水 银压强计的读数R为150mm,同贮槽内的 液位 h等于多少?
(三)确定液封高度 h p ρg
H 2O
气体 压力 p(表压)
为了安全, 实际安装
水 的管子插入 液面的深度
h 比上式略低
第二节 流体流动中的基本方程式
截面突然变化的局部摩擦损失
突然扩大
突然缩小
A1 / A2 0
z (1 A1 )2
A2
z 0.5(1 A2 )2
A1
当流体从管路流入截面较 大的容器或气体从管路排 到大气中时z1.0
当流体从容器进入管的入 口,是自很大截面突然缩 小到很小的截面z=0.5
局部阻力系数法
hf
z
u2 2
流体流速与管径的关系

流体流速与管径的关系
【原创版】
目录
1.流体流速与管径的基本关系
2.流量、流速和管径的计算公式
3.影响流速的其他因素
4.管径对流速的实际应用
正文
流体流速与管径的关系是流体力学中一个基本的概念。
在一般的情况下,流速与管径成反比。
也就是说,当流量保持不变时,管径越大,流速越慢;管径越小,流速越快。
在实际应用中,我们可以通过一些公式来计算流速和流量。
例如,在水管路中,常用的公式为:流量 = 管截面积×流速。
而管截面积又可以通过管径来计算,即:管截面积 = π× (管径/2)。
通过这两个公式,我们可以看出,在流量一定的情况下,流速与管径的平方成反比。
除了管径,还有其他因素会影响流速,比如流体的粘度、温度、压力等。
这些因素都会通过改变流体的流动性,从而影响流速。
在实际应用中,管径对流速的影响也非常明显。
例如,在家庭用水中,我们通常使用的水龙头的出水口直径都比较小,这样可以保证水流的速度较快,使用起来更加方便。
而在大型的水利工程中,由于需要输送大量的水流,所以往往需要使用较大的管道,以保证流速适中,不会造成水流过于缓慢。
总的来说,流体流速与管径的关系是一个基本的物理规律,它在我们的日常生活中有着广泛的应用。
第1页共1页。
化工原理ppt-第一章流体流动

其单位为J/kg。
2022/8/11
34
二、流体系统的质量守恒与能量守恒
2. 柏努利方程
(1) 总能量衡算
4)外加能量 流体输送机械(如泵或风机)向流体作功。单位质量流体所获得
的机械能。用We表示,单位J/kg。 5)能量损失
液体流动克服自身粘度而产生摩擦阻力,同时由于管路局部装置 引起的流动干扰、突然变化而产生的阻力。流体流动时必然要消耗 部分机械能来克服这些阻力。单位质量流体克服各种阻力消耗的机 械能称为能量损失。用Σhf ,单位J/kg。
2022/8/11
27
知识运用
【1-3】某自来水厂要求安装一根输水量为30m3/h的管道,试选择一合 适的管子。
解:水的密度:1000kg/m3, 体积流量:Vs=30000/(3600×1000)=0.0083(m3/s)
查表水流速范围,取u=1.8m3/s
根据d 4Vs
u
d 4Vs 4 30 / 3600 0.077 m 77mm
22
一、流体流量和流速
2.流速
单位时间内流体质点在流动方向上所流经的距离。
(1)平均流速:u=Vs/A (m/s)
关系:G =u
(2)质量流速:G=Ws/A (kg/(m2·s))
2022/8/11
23
一、流体流量和流速
3.圆形管道直径的选定
2022/8/11
24
一、流体流量和流速
3.圆形管道直径的选定
2022/8/11
8
二、流体压力
2.表压与真空度
表压和真空度
p 当地大气压,
表压强=绝对压强-大气压强
p 当地大气压,
真空度=大气压强-绝对压强
《流体力学》第五章孔口管嘴管路流动
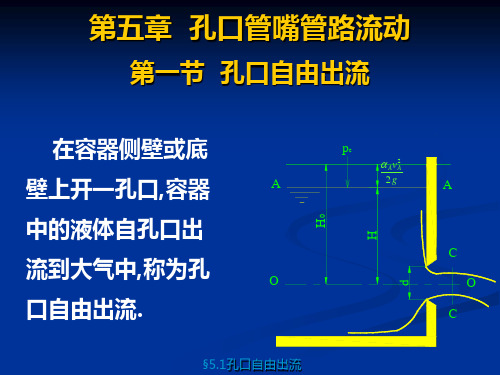
2g
A
C O
C
(C
1)
vc2 2g
(ZA
ZC )
pA
pC
Av
2 A
2g
令
H0
(Z A
ZC )
pA
pC
AvA2
2g
§5.1孔口自由出流
1
则有
vc
c 1
2gH0
H0
(Z A
ZC )
pA
pC
AvA2
2g
H0称为作用水头,是促使
力系数是不变的。
§5.4 简单管路
SH、Sp对已给定的管路是一个定数,它综合 反映了管路上的沿程和局部阻力情况,称为 管路阻抗。
H SHQ2
p SpQ2
简单管路中,总阻力损失与体积流量平方成 正比。
§5.4 简单管路
例5-5:某矿渣混凝土板风道,断面积为1m*1.2m, 长为50m,局部阻力系数Σζ=2.5,流量为14m3/s, 空气温度为20℃,求压强损失。
2v22
2g
1
vc2 2g
2
vc2 2g
令 H0 (H1 ζH12:局)液部体p阻1 经力p孔2系口数处1v的122g1 2v22
1
H1 H
H2
2
2
H0 (1 2 ) 2vcg2突ζ然2:液扩体大在的收局缩部断阻面力之系后数 C
C
§5.2 孔口淹没出流
1
c 1
2gH0
Q A 2gH0 A 2gH0
出流
H0
环境工程原理第03章流体流动

pa
101.3
J/kg
E3 E2 所以药剂将自水槽流向管道
第一节 管道系统的衡算方程
本节思考题
(1)用圆管道输送水,流量增加1倍,若流速不变或 管径不变,则管径或流速如何变化?
(2)当布水孔板的开孔率为30%时,流过布水孔的 流速增加多少?
(3)拓展的伯努利方程表明管路中各种机械能变化 和外界能量之间的关系,试简述这种关系,并 说明该方程的适用条件。
p2d p p
p1
1
2
um2
+ gz +
p2 dp
p1
We
hf
1
2
um2
+
gz
+
p
We
hf
(3.1.16)
在流体输送过程中,流体的流态几乎都为湍流,令α=1
1
2
um2
+
gz
+
p
We
hf
1
2
um2 1
+
um
1 A
udA
A
1 2
u
2
m
1 A
A
1 u2dA 2
1 2
u2
m
1 2
um2
由于工程上常采用平均速度,为了应用方便,引入动能
校正系数α,使
1 2
u2
m
1 2
um
2
α的值与速度分布有关,可利用速度分布曲线计算得到。经证
管子流量计算公式

管子流量计算公式首先,我们需要根据流体性质和管道参数来确定所使用的流量计算公式。
常见的流量计算公式有以下几种:容积流量法、质量流量法、1/2经验公式、修正压降法和重力流量法。
1.容积流量法:容积流量公式适用于压力较低、流体密度较小的情况,其公式为:Qv=A*V其中,Qv表示容积流量(单位为m³/s),A表示管道截面积(单位为m²),V表示流动速度(单位为m/s)。
2.质量流量法:质量流量公式适用于流体密度变化较大的情况,如气体等。
质量流量公式为:Qm=A*ρ*V其中,Qm表示质量流量(单位为kg/s),A表示管道截面积(单位为m²),ρ表示流体密度(单位为kg/m³),V表示流动速度(单位为m/s)。
3.1/2经验公式:1/2经验公式适用于一般流体情况。
该公式为:Q=Kv*A*√(2*Δp/ρ)其中,Q表示流量(单位为m³/s),Kv表示计算系数,A表示管道截面积(单位为m²),Δp表示压力差(单位为Pa),ρ表示流体密度(单位为kg/m³)。
4.修正压降法:修正压降法适用于粘性流体的流量计算,该方法要根据实验数据来确定修正因子。
修正压降法的公式为:Q=Kv*A*(Δp/μ)^(1/n)其中,Q表示流量(单位为m³/s),Kv表示计算系数,A表示管道截面积(单位为m²),Δp表示压力差(单位为Pa),μ表示流体动力粘度(单位为Pa·s),n表示修正因子。
5.重力流量法:重力流量法适用于较大坡度或管道倾斜角较小的情况。
重力流量法的公式为:Q=K*A*√(2*g*h)其中,Q表示流量(单位为m³/s),K表示流量系数,A表示管道截面积(单位为m²),g表示重力加速度(单位为m/s²),h表示液位差(单位为m)。
通过以上公式,可以根据实际情况选择适合的流量计算方法。
在实际应用中,还需考虑管道摩阻、压力损失等因素,以及根据具体工况来选择合适的公式进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 0.027 C 0.027
uB
78.31C1uC 2 19.6
并联管路
(1)主管路中流体的质量等于各并联支路中流体质量 流量之和,即
WW 1W 2W 3 对不可压缩性气体,还有
VV1V2V3
(2)由于各并联支路的起、止端均为分点支 A 和汇合 点B,因此各支路的起、止端截面的总比能差相等,则各 并联支路单位质量流体的阻力损失相等,即
hf1 hf2 hf3
另外,由于阻力损失的单位为J/kg,即以单位质量 流体为计算基准,所以在计算并联管路段的阻力损失时, 只需要考虑其中任一支路的阻力损失即可,绝不能把各 并联支路的阻力损失全部加在一起作为并联管路段的阻 力损失。也就是说,主管路与并联管路段的总阻力损失 应为
V
4
d
2 p
u
2
0 .0 5 4 2 1 .3 9 4
0 .0 0 3 1 8 m 3 s
1 1 .4 m 3 h
(2)管路布局一定,要求核算操作条件改变时, 流动参数的变化情况
如图所示,高位槽A内的液体通过一等径管流向槽B。在 管线上装有阀门,阀门前后M、N处分别安装压力表。假设 槽A、B液面维持不变,阀门前后管长分为 l1、l2 。现将阀门 关小,试分析管内流量及M、N处压力表的读数如何变化?
及 Re 数计算
1
1
dp0.004h 5f750.00 44 05750.1631 5
1
d p 0.163 5来自Redpudp4V ds2pdp3610.002 0754d12p0 3998.29d48p5
1
设 =0.03,由式 d p 0.163 5 算出
1
dp0.1630.0350.081
l leOu C C 2 d2
比较上两式,可得
g B u z 2 B 2 p B
l d l e O u 2 B 2 B g C u z 2 C 2 p C
l l e O u C 2 C d2
代入数据,得
9 .8 2 .5 1 u 2 B 2 0 B 0 6 .0 u 0 2 B 7 2 9 .8 1 .5 1 u 2 C 2 0 C 0 . 5 0 0 u 6 2 C 2
(1)管路布局一定,要求核算在某给定条件下管 路的输送能力
例 如图所示的输送管路,已知进料管口处的压力 p2=
1.96104Pa(G),管子的规格为 60×3mm、直管长度35m,
管路上有3个标准弯头、1个1/4〞闸阀,管子绝对粗糙度为 0.2mm,高位槽内液面距进料管口中心的高度 z=4.2m,液 体的密度和粘度分别为1100kg/m3和1.7×10-3Pa·s。试问该管 路能达到多大的供液流量。
70×3mm;其长度(包括当量长度)分别控制在80m、60m和 50m;z2和z3分别为2.5m和1.5m;管壁的绝对粗糙度均取 0.2mm。常温水的密度和粘度分别为1000kg/m3和l×10-3 Pa·S;若要求供水的总流量为52m3/h,试确定高位槽内液 面的高度z1。
1 A
z1
G
1’ 高
高
分为设计计算和校核计算
简单管路的设计计算
❖设计计算是给定输送任务,要求设计经济上合理的 管路。
❖典型的设计计算内容: 规定输送任务V,确定最经济 (适宜)的管径及泵的有效压头He (或确定高位槽的高 度)。
例:钢管的总长为100m,用以输送20℃的水,已知水的流率为
27m3/h。要求输送过程中摩擦阻力不大于40Nm/kg,试确定输 送管路的最小直径。已知20℃时水的粘度 =1.00510 -3 pas, 密度ρ=998.2kg/m3。
高 2
B
2’
O
3
C 3’ z3
z2 G’
解:主管路A中的流量为
V4dA 2uA40.12uA356200
uA1.84 ms
对OB段和OC段进行能量衡算
g 0 z u 2 0 2 p 0 g B zu 2 B 2 p B
l leOu B B 2 d2
g 0 z u 2 0 2 p 0 g C z u 2 C 2 p C
化工原理
Reporter
第一章 流 1 基础知识 体流动 2 流体静力主学 要 内 容
3 流体动力学
4 流体流动的类型
5 流体流动阻力的计算 6 管路计算 7 流量测量
管路计算
管路计算是连续性方程式、柏努利方程式和阻 力公式的综合应用。根据管路有无分支,可分 为简单管路和复杂管路。
简单管路
无分支或汇合的管路,称为简单管路。简单管 路可以是由直径相同的管路,也可以是由直径 不同的管路串联而成。
整理得
uB
78.31C1uC 2 19.6
85.17B1
又因为 V4dB 2uB4dC 2uC
代入数据,得
V 40.027 u B 40.06 2u 4 C356200
整理得
uC4.4 91.2uB
0.2 0.0029
dB 70
0.2 0.003
dC 64
用试差法:假设B、C均处于完全湍流区,查莫狄图,得
l1
l2
MN
解: 取阀门的高度Z=0,阀门关闭时流体静止,由静力
学方程有
P AP aP M G 1 .0 1 15 3 00 .9 9 .8 140
1 .9 0 150 N m 2
P BP a P N G 1 .0 1 15 3 0 0 .4 5 9 .8 140
1 .4 5 150 N m 2 A
pa
B
pb
阀门开度为四分之一时,列 A 至 B 界面的伯努利方程
PAu2A 2 PBu2B 2
hl1 f
P
P
MN
l2
uA= uB =0
hf
lu2
d2
现假设管内为层流,则有 64 64 Re ud
P P 32 lu
A B
d2
u3 PA 2 P B ld23 21 3.9 01 1 5 0 3 0 1 .5 4 0 52 15 0 030 0.024
由图查出 =0.025,与假设值相符。因此,管内径应为 78mm, 查附录无缝钢管规格表,选用3寸( 88.54)的有缝
钢管。
校验: 管内实际流速
V
27
u4d2 p360040.080521.46ms
Re 94851.17105 0.0805
0.2
0.0025 dp 80.5
由图查出 =0.025
A
p1
B
p2
P
P
l1
l2
M
N
例:已知, =30cp, =900kg/m3,d =40mm,l1=50m,
l2=20m,阀全关,PM(G)=0.9at,PN(G)=0.45at。若阀打 开至四分之一时,le=30m。
求: (1)V(流量)的大小;(2)阀打开时,PM、 PN如何变化?
A
pa
B
pb
P
P
8i2ldiVi5i2
将上式代入式 h f主 h f1 h f主 h f2 h f主 h f3,得
81l1V12 2d15
822ld2V 2522
812ld1V 3532
81l1V12 2d15
822ld2V 2522
812ld1V 3532
故
V1:V2:V3
d15
1l1
:
d25
2l2
:
d35
l
dp
u 2 2 2
代入数据,得
9 . 8 4 . 1 2 0 0 0 u 2 2 1 . 9 1 6 4 03 5 2 . 2 0 . 5 9 0 . 5 u 2 2 2 11 0 0 . 0 0 54 2
9 . 8 4 . 1 2 0 0 0 u 2 2 1 . 9 1 6 4 03 5 2 . 2 0 . 5 9 0 . 5 u 2 2 2 11 0 0 . 0 0 54 2
h f h f 主 h f 1 h f 主 h f 2 h f 主 h f 3
(3)各并联支路的流量分配
尽管各并联支路的阻力相等,但由于各支路的管径、 管长、粗糙度情况一般不相同,所以各支路的流量也不相 等。各支路的流量分配关系可由计算得到。
ui
4V i
d
2 i
hf
i
li di
ui2 2
设 =0.03,算出 u21.39 ms
R e d p u 0 .0 5 4 1 . 7 1 .3 1 9 0 3 1 1 0 0 4 .8 6 1 0 4
钢管绝对粗糙度 0.2mm,则
0.2 0.0037
dp 54
查图,得 =0.03,与假设相符,所以 u21.39 ms
由 u21.39 ms 可算出
此外,在设计计算中,如要确定分支管路所需的外加 能量We时,为了确保完成整个管路的输送任务,必须按 所需能量较大的支路来计算。操作中,可通过关小其他支 路上的阀门开度,将其流量调节到所要求的数值。
例: 如图所示,为一由高位槽稳定供水系统,主管路A、
支管路B和C的规格分别为 l08×4mm、 76×3mm和
lu 2
1 0 0 1 .4 6 2
h fd p2 0 .0 2 5 0 .0 8 0 5 2 3 3 N m k g
满足要求。
应该注意的是,算出的管径 dp 必须根据管子标准进行圆整。
校核计算
校核计算常见有以下两种情况
❖(1)管路布局一定,要求核算在某给定条件下管路的 输送能力;
❖ (2)管路布局一定,要求核算操作条件改变时,流动 参数的变化情况;
3l3
ui
4V i
d
2 i
WW 1W 2W 3 VV1V2V3
