四波混频波形
第四章三次谐波与四波混频

三次谐波
II. 气体、原子蒸汽(惰性气体He, Xe, Kr 等;碱金属、碱土金 气体、原子蒸汽(惰性气体He, 碱金属、 属蒸汽Na, Hg等 属蒸汽Na, Rb, Cs, Ti, Ca, Hg等) (1)尖锐的吸收线----共振增强效应显著。 尖锐的吸收线----共振增强效应显著 共振增强效应显著。 (2)激光损伤强度阈值比晶体中高几个数量级, 激光损伤强度阈值比晶体中高几个数量级, 可以采用高强度的入射激光场。 可以采用高强度的入射激光场。 (3)气体大多有很宽的透明范围(20nm~可见、红外区) 气体大多有很宽的透明范围(20nm~可见 红外区) 可见、 所以,在高强度激光作用下, 所以,在高强度激光作用下,气体中的三阶极化强度可以和 晶体中的二阶极化强度相比拟, 晶体中的二阶极化强度相比拟,特别适合用来产生 XUV(20nm~100nm)和VUV(100nm~200nm)波段的相干辐射 XUV(20nm~100nm)和VUV(100nm~200nm)波段的相干辐射。 波段的相干辐射。
三次谐波
实验结果: 实验结果: 基频光; (1)30ps、300MW、1064nm基频光;长度 ) 、 、 基频光 长度50cm、 、 Rb(3Torr):Xe(2000Torr)样品;输出 样品; 三次谐波, 样品 输出354.7nm三次谐波,转 三次谐波 换效率10% 换效率 基频光, 混合气体, (2) 532nm基频光,样品为 ) 基频光 样品为Cd:Ar混合气体,产生 混合气体 产生177.3nm三 三 次谐波输出。 次谐波输出。 (3) 354nm基频光,样品为 基频光, 混合气体, 基频光 样品为Xe:Ar混合气体,产生 混合气体 产生118.2nm三 三 次谐波输出,转换效率最大为0.3% 次谐波输出,转换效率最大为
波分复用系统中的四波混频估算

是落入该信道内各个四波混频项
/6 7 8 /6 7 89
0 12 !
: 6 )+
; " 直 接 利用 式进 行计算十 分 繁 琐 但 对 于 典 型 波 分 复 用 光 纤 通 信 系 统 而 言 ’, < " < /+ ) 时对应于 = ? 设 ( / > <3 4 A@ ) > -@ ) 且 = = / > / < ? <@ ) B A@ ) A+ ) ’ / > C+ ) 则 中的最小值 ,/ > <@ ) 上式可化简为
其中 假设各信道功率同为 为光纤的非线性系数 为光纤的损耗因子 为简并因 子 即当 时 为 否则 为 波矢失配因子 为
" " " " " ! ! # % & 式中 是参考角频率 取为色散绝对值 ! $ $ ’ $ ’ ’ ( $ $ )* + 最小的信道角频率 ( , . . $ )* + " $ / /为零色散点处的色散 % & % & ’ $ 光速和 ’ 斜率 而 ’ $ & ( )* + 分别是参考波长 $下的光纤色散参数 由于波分复用情况下每个信道内都可能落入多个四波混频项 而各个激光器的相位是独 立分布的随机变量 故信道 ! 内四波混频功率的期望值 0 12 $ 以 为5 功率的和 其归一化数值 ! 3 4计
光子学四波混频技术的研究与应用

光子学四波混频技术的研究与应用光子学四波混频技术简介光子学四波混频技术(Phenomenon of Four Wave Mixing,FWM)是一种非线性光学过程,通过使用光纤、激光器、光源和光探测器等设备,可以实现三个或更多光信号的混频,最终产生新的频率与调制信号。
FWM技术产生的新信号,不仅具有与原信号不同的频率,还具有根据原信号的幅度和相位关系,而形成的非线性扰动产生的新频率与既有频率之间存在着特定的相互关系。
FWM技术的应用FWM技术在通讯、光电子学、量子信息、光谱学等领域都有广泛的应用。
其中,FWM技术在通信领域的应用,可以实现紧凑型、低成本且高速率的光通信系统。
此外,FWM还可在生物医学成像、量子量测和光声成像等领域应用。
例如,这项技术可以通过准确测量光子的数量,产生高分辨率的生物化学成像。
在光学传感领域,由于FWM技术可监测和测量温度、压力、流速、水平和其他物理量的变化,而被广泛应用。
此外,该技术还可以实现基于光子信号的微型传感器,用于监测环境的变化。
光子学四波混频技术的研究过去的几十年中,FWM技术得到了广泛的研究,并结合了不同的技术和原理来进一步规范化,在实现实时通讯、光传感、光量子计算等技术方面已经取得了很大的进展。
例如,研究人员已经成功开发出紧凑型的FWM光滤波器,可以提高光子信号的效率和可靠性。
这些成果和技术的开发,将在今后的光通讯和光电子学领域发挥重要作用。
在物理学和电子学领域,又有一些有趣的研究进展:例如,研究人员用于有效的减少光子信号的色散,或用于在量子技术等领域实现频谱管理。
未来展望随着科学技术的进步和创新,FWM技术将继续发展和应用。
未来,我们可以期望这项技术实现更高效、可靠和高分辨率的光子元件与光子传输,进一步推进通讯和传感技术的发展。
在量子技术和纳米技术中,FWM技术将逐渐得到广泛的应用。
这个技术的广泛应用将带来更快速、可靠、高安全性的通讯和其他应用,同时推动人类的科技、工业和文化的前进。
四波混频实验报告

四波混频实验报告1. 引言四波混频是一种实验技术,通过将不同频率的波形进行混合,可以产生新的频率。
这种技术被广泛应用于无线通信、雷达等领域。
本实验旨在通过混合四个不同频率的信号,观察其混频效果并分析各频率之间的相互影响。
2. 实验材料和装置- 信号发生器:用于产生不同频率的信号- 混频器:用于将多个信号进行混频- 示波器:用于观察混频后的波形3. 实验步骤1. 将信号发生器的四个输出分别连接到混频器的四个输入端口。
2. 设置信号发生器的输出频率为100Hz、200Hz、300Hz和400Hz。
3. 设置混频器的工作模式为线性混频。
4. 连接混频器的输出端口到示波器的通道一,选择适当的量程和触发方式。
5. 打开示波器,并观察混频后的波形。
4. 实验结果与分析实验中,我们将100Hz、200Hz、300Hz和400Hz的信号进行混频,并观察示波器上的显示结果。
结果显示,混频后的波形呈现出新的频率。
通过观察混频后的波形,我们可以发现以下几个特点:- 混频后的波形频率为四个输入信号频率的线性组合。
在实验中,我们得到的混频频率为100Hz + 200Hz + 300Hz + 400Hz = 1000Hz。
- 混频后的波形幅值受到各输入信号的幅值影响。
如果某一个输入信号的幅值较大,那么混频后的波形幅值也会较大;反之,如果某一个输入信号的幅值较小,那么混频后的波形幅值也会较小。
此外,我们还发现混频过程中,不同频率信号之间会相互影响。
当混频器接收到多个输入信号时,这些信号会相互影响,使得混频后的波形发生畸变。
因此,在实际应用中,需要根据实际情况选择合适的混频器和输入信号,以避免不必要的干扰和失真。
5. 实验总结通过本实验,我们深入了解了四波混频技术在无线通信等领域的应用。
通过观察混频后的波形,我们掌握了混频频率和幅值的关系,以及混频过程中的相互干扰情况。
在实际应用中,我们需要根据具体的要求和系统特点,选择合适的混频器和输入信号,以达到预期的效果。
raman—nath条件下吸收介质中的四波混频理论

raman—nath条件下吸收介质中的四波混频理论四波混频理论是四波混合在一起并在一个复杂的介质中产生交叉频率的物理学现象。
传统的理论是基于RamanNath条件下,即当复杂介质中有一个特定频率(内模)和另一个竞争频率(外模)时,四波混频理论会起作用。
四波混频理论又分为四类:模式交叉,曲率交叉,分离式混频和波恢复。
模式交叉可以产生四个独立的模式,其中每个模式都具有稳定的横向振幅和纵向振幅,在一个特定的介质中,它们会产生交叉频率,具有特定形态和角度,以此类推。
曲率交叉也叫做Kerr效应,它是一种光学和光学数字图像处理技术。
它可以在一个介质中产生弯曲变形模式,这些模式会在有竞争频率存在时产生交叉频率。
它也可以将介质中的特定频率以及竞争频率转换为另一个介质中的不同频率,以此来改变其特性。
分离式混频可以实现介质中特定频率和竞争频率的分离,并且在介质中产生一个新的特定频率,以此来实现更多的灵活性。
波恢复是当特定频率和竞争频率存在于介质中时,它可以让两个波长重新恢复到原来的振幅。
它可以有效调节介质中的竞争频率,从而改善整体的模式。
四波混频理论已经被广泛应用于多个领域,如光学传感、物理模拟、图像处理、声学处理和无线电频率等。
它主要用于实现介质的吸收,降低介质中的竞争频率,并调节四波混频的模式。
四波混频理论吸收介质中的特定频率和竞争频率,并将其转换为不同频率,这种转换过程可以保证一个特定形状的波模式,确保介质中的其他频率不会影响混频结果。
此外,四波混频理论的技术也可以用于解决复杂介质中的多倍长度传输问题,从而有效提高信号传输速率。
四波混频理论由RamanNath首先提出,它是一种物理学现象,具有广泛的应用前景。
它不仅可以吸收介质中的特定频率和竞争频率,还可以有效改善介质特性,确保良好的传输效果。
因此,在应用中,四波混频理论是一项重要的技术,用于提高介质传输效率和精度。
综上所述,四波混频理论是一种基于RamanNath条件的物理学现象,它可以吸收介质中的特定频率和竞争频率,并将它们转换为不同的频率,以此来改善介质中的特性。
四波混频波形.

第1章引言碰撞问题是物理学中常见的问题,早在1639年就有物理学家开始提出有关碰撞的问题,之后的几百年中无数科研工作着持续对碰撞问题进行探索,提出不同的假设,运用实验演示验证自己的理论,研究碰撞问题的规律和特点等。
当时的碰撞问题还只局限于宏观物体的碰撞,到近代物理研究中碰撞问题的研究已经深入到微观领域。
物质是由分子构成,碰撞效应能够对对物质的结构的检测和分析,用于研究激光制冷。
对于碰撞截面的探究有助于我们了解碰撞系统下能量的再分布,各个能级之间的跃迁几率等等。
它不仅仅在物理方向具有重要作用,而且在其它领域都具有广泛的应用,包括,天文学、等离子体学、原子物理学化学、材料和气体电子学等领域。
关于碰撞的研究与之有联系的种类相当宽泛:原子间碰撞、Au+Au碰撞等。
由于碰撞效应能够为许多实际生产应用部门都会需要相关数据,促进各个领域的飞速发展,因此碰撞效应[1-2]的研究具有重要的研究价值四波混频是一种先进的光谱学技术,随着激光技术的不断发展使得四波混频技术的应用有的巨大的提高,比以往的技术相比拥有许多技术优势,因而四波混频技术是一种常用技术手段。
本文中我们就应用四波混频来研究多普勒系统中的碰撞效应。
1.1 碰撞效应近代物理学中无数科研工作着对微观领域的碰撞问题进行探索,发现碰撞的的特点之一就是粒子之间发生碰撞之后,辐射频率发生改变。
一个原子或者分子和其它物质产生碰撞时,能导致其固有辐射频率的改变,这个现象就叫做碰撞效应。
宇宙中的物质都是由原子分子构成的,碰撞效应的理论可以用来分析原子或分子内部的结构,为众多学科的研究和发展奠定了理论基础,提供了实验方法,具有非常重要的研究价值。
关于碰撞问题的研究包括对碰撞截面的研究,对谱线线性的研究,对谱线展宽的研究等等。
碰撞效应在物理化学甚至其它领域都具有广泛的应用,包括,天文学[3]、等离子体学[4-6]、原子物理学化学[7-9]、材料和气体电子学[10-14]等领域。
第四章三次谐波与四波混频

分类: 分类:
2、非参量过程---非参量过程---介质在与光场相互作用后的终态与初态不同了, 介质在与光场相互作用后的终态与初态不同了,发生 质间的能量转移。 了光场与介 质间的能量转移。
受激拉曼散射(SRS)、受激布里渊散射(SBS)。 受激拉曼散射(SRS)、受激布里渊散射(SBS)。 双光子吸收(TPA)。 双光子吸收(TPA)。 饱和吸收(SA)。 饱和吸收(SA)。
实现三次谐波的困难
(1)晶体中的激光损伤强度阈值较低,无法使用高强度的入射激光。 晶体中的激光损伤强度阈值较低,无法使用高强度的入射激光。 (2)晶体中的双折射特性难以实现三次谐波所要求的位相匹配。 晶体中的双折射特性难以实现三次谐波所要求的位相匹配。 所以,一般难以在晶体中直接实现三次谐波(THG), 所以,一般难以在晶体中直接实现三次谐波(THG),方解石直接实现 THG相位匹配的晶体 THG相位匹配的晶体。 相位匹配的晶体。 −6 目前实验结果: 4mm长方解石晶体中以 目前实验结果:在4mm长方解石晶体中以 3 × 10 的转换效率得到了 三次谐波输出。 三次谐波输出。 (3) 对紫外光吸收较强
三次谐波
实现三次谐波的介质 I. 晶体: 晶体:
χ (3) ~ 10− 20 − 10− 23 ( SI制) χ (3) ( SI ) = χ ( 2) ~ 10 −11 − 10−13 ( SI制)
4π ×10 −8 χ ( 3) (esu ) 9 4π χ ( 2) ( SI ) = ×10 − 4 χ ( 2 ) (esu ) 3
三阶非线性光学效应概述
主要特点: 及耦合波方程描述。 主要特点:1、基于 χ (3) 及耦合波方程描述。 2、无论介质有何种对称性,总存在一些非零的 无论介质有何种对称性, χ ( 3) 张量元,原则上三阶非线性光学效应可 张量元, 所有介质中观察到 中观察到。 在所有介质中观察到。 3、比二阶效应弱几个数量级( χ (3) << χ ( 2) ),更难 比二阶效应弱几个数量级( ), 于观察。 于观察。 4、三阶效应中参与相互作用的有四个光电场, 三阶效应中参与相互作用的有四个光电场, 现象更加丰富。 现象更加丰富。
四波混频
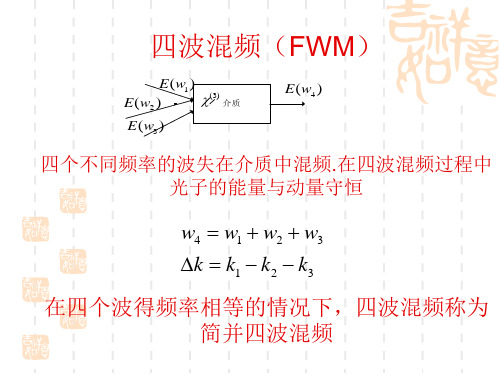
E ( w1 ) χ(3) E ( w2 )
E ( w3 )
E ( w4 )
四个不同频率的波失在介质中混频.在四波混频过程中 光子的能量与动量守恒
w4 = w1 + w2 + w3 ∆k = k1 − k2 − k3
在四个波得频率相等的情况下,四波混频称为 简并四波混频
虽然简并四波混件下,必须保证 。
改变信道间距
用适当不等间距的波长信道配置设计来实现 ,通常选择通 道频率,使产生的新频率分量大部分落在通道滤波器通带 之外,这种技术用于10个信道,每个信道速率为10G/s 以下 的系统可大大减小四波混频的影响 加大信道间距也可抑 制四波混频的效率,却是以牺牲系统带宽为代价的 实际上 , 采用部分等间距信道更为有意义,其核心在于使通道间隔 相对远的信道之间的四波混频所产生的频率分量落在信道 滤波器通带内,由于四波混频的效率随着波长间隔加大而 降低,引入的恶化并不严重,这样可使系统容纳更多的波长。
∆k = k4 − (k1 − k2 − k3 ) = 0
考虑一种特殊情况,如下图,存在两对波矢方向相反的光,输 出为-k‘,它们满足如下相位匹配条件 k ' + (−k ' ) = k + (−k ) 。
简并四波混频的相位匹配
四波混频效应
这种简并四波混频非线性过程与典型的全息照过程很 相似。可以将k‘当做物光,k当做参考光,两者在介质 中互相干涉,形成全息图,如果全息图被记录下来了, 在参考光k的照射下,沿物光k’相反的方向-k‘可见物得 虚像。若挡住物光k’,在另一参考光-k的照射下,会 产生-k‘方向的赝像,该赝像就是原物光的相位共轭光。 虽然全照息过程和四波混频过程都产生相位共轭光, 但两者根本不同之处:全息照相的记录和重现过程在 时间上式分段进行的,而四波混频的相位共轭光与原 入射光几乎是同时产生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章引言碰撞问题是物理学中常见的问题,早在1639年就有物理学家开始提出有关碰撞的问题,之后的几百年中无数科研工作着持续对碰撞问题进行探索,提出不同的假设,运用实验演示验证自己的理论,研究碰撞问题的规律和特点等。
当时的碰撞问题还只局限于宏观物体的碰撞,到近代物理研究中碰撞问题的研究已经深入到微观领域。
物质是由分子构成,碰撞效应能够对对物质的结构的检测和分析,用于研究激光制冷。
对于碰撞截面的探究有助于我们了解碰撞系统下能量的再分布,各个能级之间的跃迁几率等等。
它不仅仅在物理方向具有重要作用,而且在其它领域都具有广泛的应用,包括,天文学、等离子体学、原子物理学化学、材料和气体电子学等领域。
关于碰撞的研究与之有联系的种类相当宽泛:原子间碰撞、Au+Au碰撞等。
由于碰撞效应能够为许多实际生产应用部门都会需要相关数据,促进各个领域的飞速发展,因此碰撞效应[1-2]的研究具有重要的研究价值四波混频是一种先进的光谱学技术,随着激光技术的不断发展使得四波混频技术的应用有的巨大的提高,比以往的技术相比拥有许多技术优势,因而四波混频技术是一种常用技术手段。
本文中我们就应用四波混频来研究多普勒系统中的碰撞效应。
1.1 碰撞效应近代物理学中无数科研工作着对微观领域的碰撞问题进行探索,发现碰撞的的特点之一就是粒子之间发生碰撞之后,辐射频率发生改变。
一个原子或者分子和其它物质产生碰撞时,能导致其固有辐射频率的改变,这个现象就叫做碰撞效应。
宇宙中的物质都是由原子分子构成的,碰撞效应的理论可以用来分析原子或分子内部的结构,为众多学科的研究和发展奠定了理论基础,提供了实验方法,具有非常重要的研究价值。
关于碰撞问题的研究包括对碰撞截面的研究,对谱线线性的研究,对谱线展宽的研究等等。
碰撞效应在物理化学甚至其它领域都具有广泛的应用,包括,天文学[3]、等离子体学[4-6]、原子物理学化学[7-9]、材料和气体电子学[10-14]等领域。
例如通过对谱线展宽、II碰撞截面的研究能够获得气体的密度和温度,从而可以得到恒星表面的引力大小[15]。
经由对碰撞引发的放射跃迁的探究能够对等离子体确认判断。
B. Sun 和 F. Robicheaux 等人在2008年经由对气态物质谱线展宽的探究,得出分离现象中的成对波动现象[16]的存在是引起谱线展宽主导因素的结论,并得到一个计算模型。
1.1.1 碰撞问题的分类诺贝尔物理奖获得者赫兹和弗兰克在1925年在对电子和惰性气体碰撞后的性质的探究时发现弹性碰撞[17-18]。
物理学家里查德·泰勒和凯德尔在对碰撞进行实验研究时发现了非弹性碰撞[19]。
根据实验过程中是否有原子激发我们可以将碰撞效应进行分类。
(1)弹性碰撞在碰撞过程中,假如碰撞没有导致粒子系统的能量的改变,原子并没有引发能级跃迁,这种碰撞就叫作弹性碰撞。
弹性碰撞能够产生无辐射跃迁来引发能量改变,从而使粒子位置产生变化,因此,弹性碰撞能够导致谱线展宽和频移。
一些学者研究了气体分子间的弹性碰撞对声波衰减的影响,提出了一组基于分子弹性碰撞的干空气-水汽双流体方程,利用该方程探究了水汽对大气声波衰减的影响,得出了声波频率与分子间的弹性碰撞频率的之比是衡量分子间弹性碰撞对声波衰减影响[20]的重要参数的结论。
对于某一特定波长的声波,其衰减系数依据弹性碰撞频率改变而变化,波长越小衰减越小,大气内氧分子-氮分子的弹性碰撞频率能够达到109hz,因此二者的弹性碰撞对一定频率的声波的衰减的影响完全可以忽略。
(2)非弹性碰撞两个粒子发生碰撞之后,一个粒子获得了另外一个粒子的动能,使得内能发生改变,足以使这个粒子由低能级跃迁到高能级,而它包含着原子的辐射,那么这个就叫做非弹性碰撞。
例如,让高能电子激发质子,电子与质子之间发生了弹性碰撞,但是也会出现产生了π介子的情况,说明电子有能量的转移,π介子接收了电子的能量,因此电子的能量减少。
这就是非弹性碰撞导致的,非弹性碰撞能够引起原子发生改变。
它为激光器件的赶紧提供了基础。
非弹性碰撞可以导致能量传递,发生原子跃迁,原子跃迁必须遵守某种规律,就原子而言,它符合选择定则:△J=0,±1和△ν=±1。
精选资料,欢迎下载非弹性碰撞可以包含两类,第一类是指碰撞导致动能改变成内能的类型,通过碰撞系统将动能传递给粒子,变成粒子的内能(包括电离能,激发能等)。
实验中最常使用的氦-氖气体激光器来说,通过外加电场对质量较小的电子进行加速,这样能够使动能以最高的传输效率转化给粒子,使粒子在基态具有很大的内能,最终导致氖原子粒子数反转布居,即He原子和Ne原子分别由基态跃迁到两个亚稳态[21]。
第二类碰撞在微粒参与碰撞的过程中有内能的减少,粒子发生碰撞后能量传递给其他的微粒[22-24],使得其他微粒因此获得能量,或者是动能或者是内能,获得能量的粒子会由原先的基态发生跃迁,由于获得的能量差异,原子激发到哪个态是不确定的。
从概率上来说,距离原子受激态较近的高激发态发生碰撞跃迁的可能越大[25,26]。
1.1.2 碰撞引起能量再分布近年来,非弹性碰撞中的能量转移引起了人们的广泛关注。
原子中存在某些光学禁戒跃迁,但用非弹性碰撞方法可实现这些跃迁[3],所以,用碰撞也可研究原子结构。
按有无原子激发可分为弹性碰撞和非弹性碰撞。
两个粒子相碰,如果只有动能的交换而不改变粒子的内部能量,并不能使原子处于较高能级,即没有发生原子激发,这类碰撞称为弹性碰撞。
这类碰撞是碰撞对之间通过无幅射跃迁进行能量交换,可以引起粒子在发光过程中的相位突变,所以弹性碰撞不但引起谱线展宽,还引起谱线的频移;如果原子与粒子碰撞后,不仅动能交换,原子的内部能量也发生了变化,使原子跃迁至较高能级,发生了原子激发,这类碰撞称为非弹性碰撞。
只有发生非弹性碰撞时才可能使原子激发。
同时,非弹性碰撞效应会使光谱出现一定的谱线移动和翅线现象,即碰撞产生能级再分布现象[4]。
使得某些光学禁戒跃迁也可以实现。
对于非弹性碰撞引起的激发态碱金属原子与原子或分子的能量转移过程在研究原子滤波器、化学反应动力学等方面有非常重要的应用。
由于受光源限制,人们最初主要集中于低激发态原子能量转移过程的研究。
直到80年代后,由于染料激光器的出现,人们才有可能研究碱金属原子中间态或高激发态的能量转移过程。
80年代,Krause系统地研究了碱金属原子精细结构能量转移过程与惰性气体的关系。
最近Krause等人又开始系统地研究碱金属原子塞曼能级间能量转移截面与惰性气体的关系。
在强激光场作用下电子同原子分子相互作用的规律,可调谐激光器向更宽频谱的范围发展,以及飞秒I V精选资料,欢迎下载脉冲技术的广泛使用,为至今尚末实现的在碰撞时对基元碰撞事件的探测提供了新的机会。
这样的实验能改变对非弹性碰撞过程和化学反应实质的新的和更深刻的理解。
光学碰撞第一次被Weisskopf 描述为下面类型的过程[5]B f A B i A +→++)()(ωη (1.1.1)这里碰撞前原子A 的初始态)(i A ,原子B 处于基态;经过碰撞激发,原子A 吸收或辐射能量为ωη的光子后跃迁到)(f A 态,而原子B 仍旧处于基态,其作用是为原子A 提供能级微扰。
在该过程中,由于微扰气体原子B 的出现,使得A 气体原子发射或吸收的光谱出现压力展宽或频移。
这种现象之所以发生是因为,微扰气体原子B 使原子A 的能级发生移动,产生了一种新的发射或吸收频率,且此频率不能被自由原子吸收或辐射。
通过对碰撞展宽光谱的研究,可以给我们提供一些原子内部的力学信息,尤其是包含激发态的相互作用。
在早期的碰撞光谱学研究中出现过两种近似理论,其一为Weisskopf 模型,这个理论把原子辐射过程认为是经典的随时间相位变化的谐振子模型,该假设的基础是所谓的碰撞展宽引起的相位移动理论,该理论可以通过傅里叶分析可以得到谱线形状函数。
第二种近似理论是由JabloIiski 提出的准分子模型理论,在该理论中系统有谐振子组成,而微扰原子被当做准分子,谱线展宽的计算采用量子力学方法和分子电子带光谱的强度分布理论。
考虑到本文所讨论的是用密度矩阵理论研究四波混频光谱学,所以我们主要介绍第二种近似理论。
在这个模型里,由原子A 和B 组成的复合系统与辐射场的相互作用哈密顿量为 )(ε))(,()(0t d t R r H r H H T c += (1.1.2)这里0H 原子A 和B 在相距)(t R 时的原子哈密顿量求和得到的,r 表征A 和B 原子的电子坐标,))(,(t R r H c 是原子A 和B 相互作用的哈密顿量,B A T d d d +=是原子A 和B 多普勒算符之和,)(εt 是碰撞区域激光辐射的电场,并假设其形式为t t L ωcos ε)(ε0= (1.1.3)其中场强0ε在碰撞时认为是常量。
V I在LICET 和LACT 过程中,由激光辐射场发出的频率为L ω的单光子在碰撞过程中被吸收。
设A 和B 原子的初始复合状态为>>='||ii I ,末态为>>='||ff F 。
在弱场情形,相应的散射截面可由辐射场的最低阶项)(2ε计算得出。
根据Berman 的理论,哈密顿量(2-2-1)的薛定谔方程的解可用波函数>)(|t ψ表示,并可作如下展开:>∑>=)(|)()(ψ|R E t a t x x x (1.1.4)其中>>≡))((|)(|t R E R E x x 满足方程 >=+)(|)()]()([0R E E R E R H r H x x x c (1.1.5)这里不显含对r 的依赖性。
这里强度)(t a x 满足下列耦合微分方程∑)()(ε)(||)()()()(||)()()()('''x x x x x x x x T x x x x t a t R E dt d R E i t a t R E d R E t a R E t a i ≠⋅><∑⋅><=η&ηε(1.1.6)当∞→R 时,0)(→R H c ,)]()([0R H r H c +的左矢>)(|R E x 减小为复合态的左矢>>='||0ee E 。
在adiabatic 近似中,我们假设碰撞并未引起任何A-B 准分子跃迁,因而方程(1.1.6)可以省略简写为如下关于)(t a x 的等式∑)()(ε)(||)()()()('x x x T x x x x t a t R E d R E t a R E t a i •><=&η (1.1.7)这正是辐射场可能会在某些准分子态>)(|R E x 和>)(|R E x ’感生跃迁的证据,其跃迁几率依赖于)()(0R V E R E x x x += (1.1.8)这里)(R V x 是准分子在能级0x E 下的势能。
