流体力学第四章习题答案
李玉柱流体力学课后题标准答案第四章

第四章 流体动力学基础4-1 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭,0y ≥总流的动能修正系数为何值?解:172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A A B y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4-2 如图示一股水流自狭长的缝中水平射出,其厚度00.03m δ=,平均流速V 0=8m/s ,假设此射流受重力作用而向下弯曲,但其水平分速保持不变。
试求(1)在倾斜角45θ=o 处的平均流速V ;(2)该处的水股厚度δ。
解:(1)由题意可知:在45度水流处,其水平分速度仍为8m/s,由勾股定理可得:V=︒45sin 8=11.31m/s (2)水股厚度由流量守恒可得:VD D V δδ=000,由于缝狭长,所以两处厚度近似相等,所以000.0380.02111.31V V δδ⨯===m 。
4-3 如图所示管路,出口接一收缩管嘴,水流射人大气的速度V 2=20m/s ,管径d 1=0.1m ,管嘴出口直径d 2=0.05m ,压力表断面至出口断面高差H =5m ,两断面间的水头损失为210.5(/2)V g 。
试求此时压力表的读数。
解:取压力表处截面为截面1-1,收缩管嘴处截面为截面2-2,选择两截面包围的空间为控制体,由实际流体的恒定总流能量方程得:2211221222wV p V p z z h g g g g ρρ'++=+++, 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ,由上述两个方程可得压力表的读数(相对压强):222112212wV V p p z z h g g ρ⎛⎫-'-=+-+ ⎪⎝⎭, 上式计算结果为:2.48at 。
流体力学第四章习题答案

第四章习题答案选择题(单选题)4.1等直径水管,A-A 为过流断面,B-B 为水平面,1、2、3、4为面上各点,各点的流动参数有以下关系:(c )(a )1p =2p ;(b )3p =4p ;(c )1z +1p g ρ=2z +2p g ρ;(d )3z +3p g ρ=4z +4pgρ。
4.2伯努利方程中z +p g ρ+22v gα表示:(a )(a )单位重量流体具有的机械能;(b )单位质量流体具有的机械能;(c )单位体积流体具有的机械能;(d )通过过流断面流体的总机械能。
4.3水平放置的渐扩管,如忽略水头损失,断面形心点的压强,有以下关系:(c )p p 2(a )1p >2p ;(b )1p =2p ;(c )1p <2p ;(d )不定。
4.4黏性流体总水头线沿程的变化是:(a ) (a )沿程下降;(b )沿程上升;(c )保持水平;(d )前三种情况都有可能。
4.5黏性流体测压管水头线的沿程变化是:(d ) (a )沿程下降;(b )沿程上升;(c )保持水平;(d )前三种情况都有可能。
4.6平面流动具有流函数的条件是:(d )无黏性流体;(b )无旋流动;(c )具有速度势;(d )满足连续性。
4.7一变直径的管段AB ,直径A d =0.2m ,B d =0.4m ,高差h ∆=1.5m ,今测得A p =302/m kN ,B p =402/m kN , B 处断面平均流速B v =1.5s m /.。
试判断水在管中的流动方向。
解: 以过A 的水平面为基准面,则A 、B 点单位重量断面平均总机械能为:42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭(m )2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯(m )∴水流从B 点向A 点流动。
流体力学第四章答案

第四章习题简答4-2 管径cm d 5=,管长m L 6=的水平管中有比重为0.9油液流动,水银差压计读数为cm h 2.14=,三分钟内流出的油液重量为N 5000。
管中作层流流动,求油液的运动粘度ν。
解: 管内平均流速为s m d Q v /604.1)4/05.0/(180/)9.09800/(5000)4//(22=⨯⨯==ππ 园管沿程损失h f 为γ(h 水银γ/油)1-=0.142(13.6/0.9-1)=2.004m园管沿程损失h f 可以用达西公式表示: g v d l h f 22λ=,对层流, Re /64=λ, 有fgdh lv 264Re 2=, 但νvd =Re , 从而lv h gd f 6422=ν, 代入已知量, 可得到s m /10597.124-⨯=ν题 4-2 图4-4 为了确定圆管内径,在管内通过s cm /013.02=ν的水,实测流量为s cm /353,长m 15管段上的水头损失为cm 2水柱。
试求此圆管的内径。
解:422222212842642642642Re 64gd lQ d d g lQ gd lv g v d l vd g v d l h f πνπννν=⎪⎭⎫ ⎝⎛==== m gd lQ d 0194.002.08.9210013.0351********4=⨯⨯⨯⨯⨯⨯==∴-ππν 4-6 比重85.0, s m /10125.024-⨯=ν的油在粗糙度mm 04.0=∆的无缝钢管中流动,管径cm d 30=,流量s m Q /1.03=, 求沿程阻力系数λ。
解: 当78)(98.26∆d >Re>4000时,使用光滑管紊流区公式:237.0Re221.00032.0+=λ。
园管平均速度s m d q v /4147.1)4//(2==π, 流动的33953Re ==νvd , : 723908)(98.2678=∆d , 从而02185.0Re /221.00032.0237.=+=o λ4-8 输油管的直径mm d 150=,流量h m Q /3.163=,油的运动黏度s cm /2.02=ν,试求每公里长的沿程水头损失。
工程流体水力学第四章习题答案
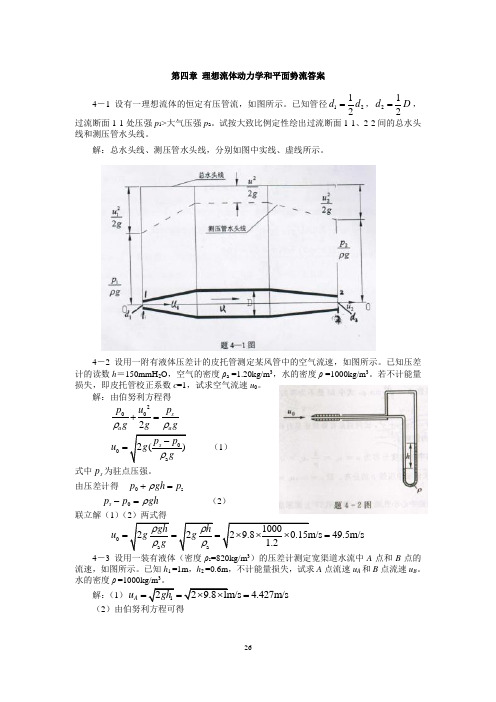
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
李玉柱流体力学课后题答案-第四章

第四章 流体动力学基础4-1 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭,0y ≥总流的动能修正系数为何值?解:172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A A B y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4-2 如图示一股水流自狭长的缝中水平射出,其厚度00.03m δ=,平均流速V 0=8m/s ,假设此射流受重力作用而向下弯曲,但其水平分速保持不变。
试求(1)在倾斜角45θ=o 处的平均流速V ;(2)该处的水股厚度δ。
解:(1)由题意可知:在45度水流处,其水平分速度仍为8m/s,由勾股定理可得:V=︒45sin 8=11.31m/s (2)水股厚度由流量守恒可得:VD D V δδ=000,由于缝狭长,所以两处厚度近似相等,所以000.0380.02111.31V V δδ⨯===m 。
4-3 如图所示管路,出口接一收缩管嘴,水流射人大气的速度V 2=20m/s ,管径d 1=0.1m ,管嘴出口直径d 2=0.05m ,压力表断面至出口断面高差H =5m ,两断面间的水头损失为210.5(/2)V g 。
试求此时压力表的读数。
解:取压力表处截面为截面1-1,收缩管嘴处截面为截面2-2,选择两截面包围的空间为控制体,由实际流体的恒定总流能量方程得:2211221222wV p V p z z h g g g g ρρ'++=+++, 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ,由上述两个方程可得压力表的读数(相对压强):222112212w V V p p z z h g g ρ⎛⎫-'-=+-+ ⎪⎝⎭,上式计算结果为:2.48at 。
流体力学第四章答案(DOC)

第四章习题简答4-2 管径cm d 5=,管长m L 6=的水平管中有比重为0.9油液流动,水银差压计读数为cm h 2.14=,三分钟内流出的油液重量为N 5000。
管中作层流流动,求油液的运动粘度ν。
解: 管内平均流速为s m d Q v /604.1)4/05.0/(180/)9.09800/(5000)4//(22=⨯⨯==ππ 园管沿程损失h f 为γ(h 水银γ/油)1-=0.142(13.6/0.9-1)=2.004m园管沿程损失h f 可以用达西公式表示: g v d l h f 22λ=,对层流, Re /64=λ, 有fgdh lv 264Re 2=, 但νvd =Re , 从而lv h gd f 6422=ν, 代入已知量, 可得到s m /10597.124-⨯=ν题 4-2 图4-4 为了确定圆管内径,在管内通过s cm /013.02=ν的水,实测流量为s cm /353,长m 15管段上的水头损失为cm 2水柱。
试求此圆管的内径。
解:422222212842642642642Re 64gd lQ d d g lQ gd lv g v d l vd g v d l h f πνπννν=⎪⎭⎫ ⎝⎛==== m gd lQ d 0194.002.08.9210013.0351********4=⨯⨯⨯⨯⨯⨯==∴-ππν 4-6 比重85.0s m /10125.024-⨯=ν的油在粗糙度mm 04.0=∆的无缝钢管中流动,管径cm d 30=,流量s m Q /1.03=, 求沿程阻力系数λ。
解: 当78)(98.26∆d >Re>4000时,使用光滑管紊流区公式:237.0Re221.00032.0+=λ。
园管平均速度s m d q v /4147.1)4//(2==π, 流动的33953Re ==νvd , : 723908)(98.2678=∆d , 从而02185.0Re /221.00032.0237.=+=o λ4-8 输油管的直径mm d 150=,流量h m Q /3.163=,油的运动黏度s cm /2.02=ν,试求每公里长的沿程水头损失。
吴望一《流体力学》第四章习题参考答案
15.初始流体静止,因而流体初始无旋。该流动满足理想、正压、体力有势条件,根据涡旋 不生不灭定理,初始无旋则永远无旋。 16. 流动满足理想、不可压缩、体力有势条件,根据亥姆霍兹方程有:
K K K dΩ − ( Ω ⋅∇ ) V = 0 。 dt K K K K K K ∂V ∂V 设流动在 x − y 平面上,则涡度 Ω = Ωk ,且 = 0 ,于是 ( Ω ⋅∇ ) V = Ω =0 ∂z ∂z K dΩ 所以 = 0 ,即沿轨迹涡度不变。 dt
通过全平面的涡通量 lim Γ = lim Γ 0 (1 − e
R →∞ R →∞
−
R2 4 vt
) = Γ0 。
K K K K
11.解: 取平面内流线切向 τ 、法向 n 和平面的法向 k 作为三个正交单位向量,τ ,n 和 k 组成笛卡尔坐标系。
K
K
K rotV =
其中
1 ⎡ ∂ ( vn H n ) ∂ ( vτ Hτ ) ⎤ K − ⎢ ⎥k , ∂n ⎦ H n Hτ ⎣ ∂τ
涡线为
2
K j ∂ ∂y xy 2 z
K k K K K ∂ = ( xz 2 − xy 2 ) i + ( xy 2 − yz 2 ) j + ( zy 2 − zx 2 ) k ∂z xyz 2
dx dy dz 。 = = 2 2 2 2 x ( z − y ) y ( x − z ) z ( y − x2 )
z0 是常量。它的原本对于该流动某横截面上的涡通量的贡献为 Ω ( r ) S ,其中 S 代表该横截
面在球形流体内截出的圆面积。设球形流体固化后的角速度为 ω ′ ,则小球所在位置处的涡 度 = 2ω ′ 。由该横截面上涡通量守恒可知,固化前后球形流体内的截面 S 上的涡通量相等, 即 2ω ′S = Ω S ,可得 ω ′ =
《流体力学》第四章作业答案
解:设受水平推力为 R,管道流速和支管流速分别为 v1,v2 ,压强为 p1,p2
(1) p1 A1 + ρQ1v1 = 2(p2 A2 + ρQ2v2)cos300 + R
①
A1
πd 2 =
4
= 0.385m2 , A2
= 0.196m2
v1
=
Q A1
= 1.56m / s
, v2
= 1.53m / s
(1.2 − 0.7)gH = 159.8 pa
总能量=159.8 − 98.07 = 61.7 pa
v2 ρ
2
= 29 pa
pm
=
三角形中位线(负值)
=
−
1(159.8 2
−
61.7
+
29)=
−63.5 pa
4.25
4.28
30. 径 为 d1=700mm 的 管 道 在 支 承 水 平 面 上 分 支 为 d2=500 的 两 支 管 , A-A 断 面 压 强 为 70kN / m2 ,管道流量 Q = 0.6m3 / s ,两支管流量相等:(1)不计水头损失,求支墩受水平 推力。(2)水头损失为支管流速水头的 5 倍,求支墩受水平推力。不考虑螺栓连接的作用。
解:
以圆盘为基准面,列 1-1、2-2 两断面的能量方程:
3 + 0 + V12 = δ + 0 + V22
2g 2 2g
①
列 1-1、3 点的能量方程:
3 + 0 + V12 = 0 + p3 + 0
2g
γ
②
据连续性方程:
Q
工程流体力学课后习题答案4-7章
第四章 流体动力学【4-1】直径d =100mm 的虹吸管,位置如图所示。
求流量和2、3点的压力(不计水头损失)。
【解】列1、4点所在断面的伯努利方程,以过4点的水平面为基准面。
24500 0029.8v ++=++⨯得 4 =9.9 m/s v 2234 3.140.19.90.078 m /s 44π==⨯⨯=Q d v列1、2点所在断面的伯努利方程,以过1点的水平面为基准面222000 02p v g gρ++=++ (v 2=v 4)得 2242210009.9 4.910Pa 22ρ⨯=-=-=-⨯v p列1、3点所在断面的伯努利方程,以过1点的水平面为基准面233000 22p v g gρ++=++ (v 3=v 4)得 2439.9298001000 6.8610Pa 2=-⨯-⨯=-⨯p【4-2】一个倒置的U 形测压管,上部为相对密度0.8的油,用来测定水管中点的速度。
若读数△h =200mm ,求管中流速u =?【解】选取如图所示1-1、2-2断面列伯努利方程,以水管轴线为基准线212 0 002w w p p u g g gρρ++=++其中:p 1和p 2分别为1-1、2-2断面轴线上的压力。
设U 形测压管中油的最低液面到轴线的距离为x ,选取U 形测压管中油的最高液面为等压面,则12()w o w p gx g h p g x h ρρρ--∆=-+∆题 4-1图21()w o p p g h ρρ-=-∆则0.885m/s u ==【4-3】图示为一文丘里管和压力计,试推导体积流量和压力计读数之间的关系式。
当z 1=z 2时,ρ=1000kg/m 3,ρH =13.6×103kg/m 3,d 1=500mm ,d 2=50mm ,H =0.4m ,流量系数α=0.9时,求Q =? 【解】列1-1、2-2断面的伯努利方程、以过1-1断面中心点的水平线为基准线。
流体力学第四章参考答案
流体力学第四章参考答案流体力学是研究流体运动和力学性质的学科,它在工程学、物理学和地球科学等领域中具有重要的应用价值。
第四章是流体力学中的一个重要章节,主要讨论了流体的运动方程和流体的动力学性质。
在本文中,将对流体力学第四章的参考答案进行详细的论述和解释。
首先,我们来讨论流体的运动方程。
流体的运动方程是描述流体运动的基本方程,它包括连续性方程、动量方程和能量方程。
连续性方程描述了流体的质量守恒,即单位时间内通过某一截面的质量流量等于该截面内质量的减少量。
动量方程描述了流体的动量守恒,即单位时间内通过某一截面的动量流量等于该截面内动量的减少量。
能量方程描述了流体的能量守恒,即单位时间内通过某一截面的能量流量等于该截面内能量的减少量。
其次,我们来讨论流体的动力学性质。
流体的动力学性质包括粘性、密度、压力和速度等。
粘性是流体的一种性质,它描述了流体内部分子之间的摩擦力。
密度是流体的另一种性质,它描述了单位体积内的质量。
压力是流体的一种性质,它描述了单位面积上受到的力的大小。
速度是流体的运动状态,它描述了单位时间内流体通过某一截面的体积。
在解答流体力学问题时,我们需要根据具体情况选择合适的运动方程和动力学性质。
首先,我们可以根据问题中给出的条件和要求选择适当的运动方程。
例如,如果问题中要求求解流体的速度分布,则我们可以选择动量方程。
其次,我们可以根据问题中给出的条件和要求选择适当的动力学性质。
例如,如果问题中给出了流体的密度和压力分布,则我们可以选择密度和压力作为动力学性质。
在解答流体力学问题时,我们还需要运用一些基本的解题方法和技巧。
首先,我们可以利用物理规律和数学方法建立数学模型。
例如,我们可以利用连续性方程、动量方程和能量方程建立流体的运动方程。
其次,我们可以利用数学工具和计算方法求解数学模型。
例如,我们可以利用微积分和偏微分方程求解流体的运动方程。
最后,我们可以利用实验和观测数据验证数学模型和解题结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章习题答案选择题(单选题)4、1等直径水管,A-A 为过流断面,B-B 为水平面,1、2、3、4为面上各点,各点的流动参数有以下关系:(c)(a)1p =2p ;(b)3p =4p ;(c)1z +1p g ρ=2z +2p g ρ;(d)3z +3p g ρ=4z +4pgρ。
4、2伯努利方程中z +p g ρ+22v gα表示:(a)(a)单位重量流体具有的机械能;(b)单位质量流体具有的机械能;(c)单位体积流体具有的机械能;(d)通过过流断面流体的总机械能。
4、3水平放置的渐扩管,如忽略水头损失,断面形心点的压强,有以下关系:(c)p p 2(a)1p >2p ;(b)1p =2p ;(c)1p <2p ;(d)不定。
4、4黏性流体总水头线沿程的变化就是:(a)(a)沿程下降;(b)沿程上升;(c)保持水平;(d)前三种情况都有可能。
4、5黏性流体测压管水头线的沿程变化就是:(d)(a)沿程下降;(b)沿程上升;(c)保持水平;(d)前三种情况都有可能。
4、6平面流动具有流函数的条件就是:(d)无黏性流体;(b)无旋流动;(c)具有速度势;(d)满足连续性。
4、7一变直径的管段AB ,直径A d =0、2m,B d =0、4m,高差h ∆=1、5m,今测得A p =302/m kN ,B p =402/m kN , B 处断面平均流速B v =1、5s m /、。
试判断水在管中的流动方向。
解: 以过A 的水平面为基准面,则A 、B 点单位重量断面平均总机械能为:42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭(m)2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯(m)∴水流从B 点向A 点流动。
答:水流从B 点向A 点流动。
4、8利用皮托管原理,测量水管中的点速度v 。
如读值h ∆=60mm,求该点流速。
解: 3.85u ====(m/s)答:该点流速 3.85u =m/s 。
4、9水管直径50mm,末端阀门关闭时,压力表读值为212/m kN 。
阀门打开后读值降至5、52/m kN ,如不计水头损失,求通过的流量。
解:(1)水箱水位 321100 2.1410009.807p H z g ρ⨯=+=+=⨯(m)(2)阀门开启后,从水箱液面到仪表处列伯努利方程,可得:22p v H g g ρ=+∴ 5.57v ===(m/s) 20.055.570.0114Q vA π⨯==⨯=(m 3/s)答:通过的流量0.011Q =m 3/s 。
4、10水在变直径竖管中流动,已知粗管直径1d =300mm,流速1v =6s m /。
为使两断面的压力表读值相同,试求细管直径(水头损失不计)。
解: 以过下压力表处的水平面为基准面,列伯努利方程如下:22111222121222w p v p v z z h g g g gααρρ-++=+++∵120w h -=,13z =m,20z = 取12αα=,当12p p =时,有:222211229.8073694.842v gz v =+=⨯⨯+=29.74v =(m/s)由连续性方程 2211v A vA = ∴2300235.5d d ===(mm) 答:细管直径为235.5mm 。
4、11为了测量石油管道的流量,安装文丘里流量计,管道直径1d =200mm,流量计喉管直径2d =100mm,石油密度ρ=8503/m kg ,流量计流量系数μ=0、95。
现测得水银压差计读书p h =150mm,问此时管中流量Q 就是多少。
解: Q μ= 其中:0.95μ=;2210.20.0359d K ππ⨯===0.15p h =(m)Q μμ==0.950.0359=⨯0.0511575=(m 3/s)51.2=(l /s)答:此时管中流量Q 51.2=l /s 。
4、12水箱中的水从一扩散短管流到大气中,直径1d =100mm,该处绝对压强1p =0、5大气压,直径2d =150mm,试求水头H ,水头损失忽略不计。
解:(1)以出水管轴线为基准面,列管径1d 与2d 处的伯努利方程,可得:2211122222p v p v g g g gααρρ+=+ 取12 1.0αα==,20p =,10.5101.32550.663p =-⨯=-kPa ∵ 221122p v v ρ-=-∴ 432221250.663101101.325d v d ρ⎡⎤⎛⎫⨯⨯⎢⎥-== ⎪⎢⎥⎝⎭⎣⎦1224101.325 4.9940.1510.1v ⎡⎤⎢⎥⎢⎥==⎢⎥⎛⎫-⎢⎥ ⎪⎝⎭⎣⎦(m/s)(2)从液面到短管出口列能量(伯努利)方程。
222 4.994 1.27229.807v H g ===⨯(m)答:水头H 1.27=m 。
4、13离心式通风机用集流器A 从大气中吸入空气,直径d =200mm 处接一根细玻璃管,已知管中的水上升H =150mm,求进气流量(空气的密度ρ=1、293/m kg )。
解: 以集流器轴线的水平面为基准面,从距进口一定距离的水平处列到测管处的伯努利方程,可得:22a H p p v g g gαρρ=+不计损失,取 1.0α= ∴v =其中 0a p =,则 H p H g ρ=-⋅水∴47.76v ===(m/s) 247.760.2 1.54Q vA π==⨯⨯=(m 3/s)答:进气流量 1.5Q =m 3/s 。
4、14一吹风装置,进排风口都直通大气,风扇前、后断面直径1d =2d =1m,排风口直径3d =0、5m,已知排风口风速3v =40s m /,空气的密度ρ=1、293/m kg ,不计压强损失,试求风扇前、后断面的压强1p 与2p 。
解: 以过轴线的水平面为基准面,以2d 及3d 截面列伯努利方程:2233322222p v p v g g g gααρρ+=+其中30p =,340v =(m/s),23 1.0αα==,232322d v v d =⋅∴()442222332322 1.290.51401967.5222 1.0v d p v v d ρρ⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥=-=-=⨯⨯-=⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦(Pa)从大气到1d 断面,列伯努利方程:2111002a p p v g g gαρρ+=++其中 1 1.0α=,0a p =(相对压强),2312322d v v v d ==⋅∴42211 1.290.54064.522 1.0p v ρ⎛⎫=-=-⨯⨯=- ⎪⎝⎭(Pa)答:风扇前、后断面的压强164.5p =-Pa,2p 967.5=Pa 。
4、15两端开口的等直径U 形管,管内液柱长度为L ,使液面离开平衡位置而造成液柱振荡,水头损失忽略不计,求液柱的振荡方程z =()t f 。
解: 取0-0断面为基准面,由非恒定流的伯努利方程:221122120122Lp u p u u z z dl g g g g g tρρ∂++=+++∂⎰∵1z z =-,2z z =,120p p ==,12u u =∴012Lu L uz dl g t g t∂∂-==∂∂⎰ ∴2u gzt L∂-=∂ ∵()(),u z t u t =()dzu t dt=∴222d z gz dt L=-令 cos z c tω=,则ω=00sin 2z z z π⎫==+⎪⎪⎭答:液柱的振荡方程00sin 2z z z π⎫==+⎪⎪⎭。
4、16水力采煤用水枪在高压下喷射强力水柱冲击煤层,喷嘴出口直径d =30mm,出口水流速度v =54s m /,求水流对煤层的冲击力。
解: 取控制体如图,受力如图。
P a1F()2Q v v Fρ-=-∴22220.03100054 2.06144dF Qv vππρρ⨯==⋅=⨯⨯=(kN)水流对煤层的作用力与F构成作用力与反作用力,大小为2.061kN,方向向右。
答:水流对煤层的冲击力 2.061F=kN,方向向右。
4、17水由喷嘴射出,已知流量Q=0、4sm/3,主管直径D=0、4sm/,喷口直径d=0、1m,水头损失不计,求水流作用在喷嘴上的力。
d解:(1)取过轴线的水平面为基准面,列螺栓断面与出口断面的伯努利方程:2211122022p v v g g gααρ+=+∴()4222211212122vd p v v d ρρ⎡⎤⎛⎫⎢⎥=-=- ⎪⎢⎥⎝⎭⎣⎦()22100050.93 3.181291.8542=⨯-=(kPa)1210.44 3.180.4Q v A π⨯===⨯(m/s) 2220.4450.930.1Q v A π⨯===⨯(m/s) (2)取控制体如图所示,列动量方程。
p 1p 2v 2()2111Q v v p A F ρ-=-∴()1121F p A Q v v ρ=--()20.41291.85410.450.93 3.18143.2394π⨯=⨯-⨯⨯-=(kN)答:水流作用在喷嘴上的力为143.239kN 。
4、18闸下出流,平板闸门宽b =2m,闸前水深1h =4m,闸后水深2h =0、5m,出流量Q =8s m /3,不计摩擦阻力,试求水流对闸门的作用力,并与按静水压强分布规律计算的结果相比较。
解:(1)由连续方程 1122Q h b v h b v =⋅⋅=⋅⋅∴118124Q v h b ===⨯(m/s) 228820.5Q v h b ===⨯(m/s) (2)由动量方程,取控制体如图。
()211122Q v v p A p A F ρ-=--∴()12122122h hF g h b g h b Q v v ρρρ=⋅-⋅-- ()22122122h h gb Q v v ρρ⎛⎫=--- ⎪⎝⎭()2240.510009.8072100088122⎛⎫=⨯⨯⨯--⨯⨯- ⎪⎝⎭98.46=(kN)()221140.510009.807 3.52120.1422F g b ρ=-⋅⋅=⨯⨯⨯⨯=静(kN)答:水流对闸门的作用力98.46F =kN,按静水压强分布规律计算的结果120.14F =静kN 。
4、19矩形断面的平底渠道,其宽度B 为2、7m,渠底在某断面处抬高0、5m,该断面上游的水深为2m,下游水面降低0、15m,如忽略边壁与渠底阻力,试求:(1)渠道的流量;(2)水流对底坎的冲力。
0.m解:(1)以上游渠底为基准面,列上、下游过水断面的能力方程:221112221222p v p v z z g g g gααρρ++=++其中:120a p p p ===,1 2.0z =m,2 2.00.15 1.85z =-=m111Q Q v A Bh ==,222Q Q v A Bh == 1 2.0h =m,2 2.00.150.5 1.35h =--=m∴ ()2222112222221112v v Q z z g B h B h ⎛⎫-=-=-⋅⎪⎝⎭()()11221212222222212122111g z z g z z Q Bh h h B h B h ⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥==⋅⎢⎥⎢⎥⎛⎫-- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦()12229.8070.152.7 1.35 1.3512⎡⎤⨯⨯⎢⎥=⨯⨯⎢⎥-⎢⎥⎣⎦8.47=(m 3/s)1118.47 1.572.72Q Q v A Bh ====⨯(m/s) 2228.47 2.322.7 1.35Q Q v A Bh ====⨯(m/s) (2)取控制体如图,列动量方程、()211122Q v v p A p A F ρ-=--∴ ()112221F p A p A Q v v ρ=---()22122122h h gB gB Q v v ρρρ=--- ()2212212h h gB Q v v ρρ⎛⎫-=-- ⎪⎝⎭()222 1.3510009.807 2.710008.47 2.32 1.572⎛⎫-=⨯⨯⨯-⨯⨯- ⎪⎝⎭22.48=(kN)答:(1)渠道的流量8.47Q =m 3/s;(2)水流对底坎的冲力22.48F =kN 。
