大学物理-功能原理 机械能守恒定律
(大学物理课件)§3.6功能原理及机械能守恒教程教案

机械能守恒定律的表述及含义
1
机械能守恒定律的表述
机械能守恒定律表述了一个系统内机械能的总量不会改变的事实。
2
机械能守恒定律的含义
机械能守恒定律的含义是,当一个物体的机械能发生变化时,它的动能和势能相互转换,但 总能量不变。
3
机械能守恒定律的应用
机械能守恒定律可以用于求解多种物理问题,如摆锤、小球自由落体等。
杠杆原理简介
什么是杠杆?
杠杆是指在一个支点绕着物体的悬挂点旋转的长条 形物体。
什么是杠杆原理?
杠杆原理是指在平衡状态下,杠杆两侧的力矩相等。
杠杆原理分类
1 一类杠杆
一类杠杆是指支点处的力作用在杠杆的一侧,称为杠杆的顶端。
2 二类杠杆
二类杠杆是指支点处的力作用于杠杆的中间,使其在顶端和底端之间移动。
焦耳定律简介
1 什么是热?
热是物体的分子或原子内部运动所产生的一种形式,是一种能量。
2 什么是焦耳定律?
焦耳定律是指热量的大小跟物体的质量、温度差以及物体的热容量等相关。
焦耳定律的表述及含义
1
焦耳定律的表述
热量的大小跟物体的质量、温度差以及物体的热容量等相关。
2Leabharlann 焦耳定律的含义焦耳定律的含义是物体温度的提高或降低是由吸收或释放的热量所决定的。
2 动能定理的应用有哪些?
动能定理可以用于求解运动物体的速度、加速度等问题。
动量守恒定律简介
1 什么是动量?
动量指物体的质量和速度 乘积。
2 什么是动量守恒定律? 3 动量守恒定律的应用
动量守恒定律指出,在一
有哪些?
个系统中,当没有外力作
动量守恒定律可以用于求
用时,系统的总动量保持
大学物理-机械能守恒定律

解:重力的功:W=mgl( cosf-cos45°) ,根据动能定理有:
1 mv 2 mgl(cosf cos45)
2
O
所以 v 2gl (cosf cos45)
当f=10°时, v=2.33 m/s (亦可用功能原理求解)
45 °
f
l T
B'
B
C'
A
C mg
19
三、计算题
1.一质量为m的质点在沿x轴方向的合外力 F F0ekx作用下(其中,F0 ,k 为正的恒量),从x=0处自静止出发,求它沿x轴运动时所能达到的最大速 率。
Fy
dy
Fz
dz)
xB
Ax xA Fxdx
yB
Ay yA Fydy
zB
Az zA Fzdz
A Ax Ay Az
6
功的单位(焦耳)
1J 1Nm
平均功率 P A
t
瞬时功率
P
lim
ΔA
dW
Fv
t0 Δt
dt
P Fvcos
功率的单位(瓦特)
1 W 1 J s1 1 kW 103 W
(a)
即,各力作功之和等于合力作的功。 但对质点系:写不出像质点那样的简单式子, 即,各力作功之和不一定等于合力的功。
10
例 1 一质量为 m 的小球 竖直落入水中, 刚接触水面时
其速率为 v0 .设此球在水中所
受的浮力与重力相等,水的阻
力为 Fr bv , b 为一常量.
求阻力对球作的功与时间的函
v
ds
P
17
m 1.0 kg l 1.0 m
0 30o
θ 10o
A mgl (cos cos0 )
大学物理:2-1 机械能守恒定律

26
例2 求使物体不仅摆脱地球引力作用, 而且脱离太 阳引力作用的最小速度。(第三宇宙速度)
解 根据机械能守恒定律有
1 2
mv22
G
m ms r0
0
v2
2Gms 42.1103 m s-1 r0
地球公转速度 v1 物体相对于地球速度
Gms 29.7 103 m s-1 r0
v v2 v1 (42.1103 29.7 103 )m s- 1 12.4 103 m s-1
y
A
小mg球和在F滚N 两动个过力程的中作受用到。 h
合力为
F mg FN
O
FN
mg
B
x
根据动能定理有
B A
F
d
r
1 2
mvB2
1 2
mv
2 A
即
B mg d r
A
B A FN
d
r
1 2
mvB2
1 2
mv2A
12
因
FN
始终垂直于
dr
,
所以
B A FN dr 0
(2)功和动能都是与参照系有关的量。但动能定理 在不同惯性系中都成立,这是力学相对性原理的必 然结果。在一般情况下,如无特别声明,就是指以 地面为参照系。
11
例3 小球以初速率vA 沿光滑曲面向下滚动,
如图所示。问当小球滚到距出发点A的垂直距离
为h 的B 处时, 速率为多大 ?
解 建立右图的坐标系,
F3 F3n Fn3 Fn
所以 A外 + A非保内 = (EkQ +EpQ ) (EkP + EpP ) 22
系统的动能与势能之和称为系统的机械能,用E表示 于是有 A外 + A非保内 = E(Q) E(P)
大学物理复习第四章知识点总结

大学物理复习第四章知识点总结大学物理复习第四章知识点总结一.静电场:1.真空中的静电场库仑定律→电场强度→电场线→电通量→真空中的高斯定理qq⑴库仑定律公式:Fk122err适用范围:真空中静止的两个点电荷F⑵电场强度定义式:Eqo⑶电场线:是引入描述电场强度分布的曲线。
曲线上任一点的切线方向表示该点的场强方向,曲线疏密表示场强的大小。
静电场电场线性质:电场线起于正电荷或无穷远,止于负电荷或无穷远,不闭合,在没有电荷的地方不中断,任意两条电场线不相交。
⑷电通量:通过任一闭合曲面S的电通量为eSdS方向为外法线方向1EdS⑸真空中的高斯定理:eSoEdSqi1int只能适用于高度对称性的问题:球对称、轴对称、面对称应用举例:球对称:0均匀带电的球面EQ4r20(rR)(rR)均匀带电的球体Qr40R3EQ240r(rR)(rR)轴对称:无限长均匀带电线E2or0(rR)无限长均匀带电圆柱面E(rR)20r面对称:无限大均匀带电平面EE⑹安培环路定理:dl0l2o★重点:电场强度、电势的计算电场强度的计算方法:①点电荷场强公式+场强叠加原理②高斯定理电势的计算方法:①电势的定义式②点电荷电势公式+电势叠加原理电势的定义式:UAAPEdl(UP0)B电势差的定义式:UABUAUBA电势能:WpqoPP0EdlEdl(WP00)2.有导体存在时的静电场导体静电平衡条件→导体静电平衡时电荷分布→空腔导体静电平衡时电荷分布⑴导体静电平衡条件:Ⅰ.导体内部处处场强为零,即为等势体。
Ⅱ.导体表面紧邻处的电场强度垂直于导体表面,即导体表面是等势面⑵导体静电平衡时电荷分布:在导体的表面⑶空腔导体静电平衡时电荷分布:Ⅰ.空腔无电荷时的分布:只分布在导体外表面上。
Ⅱ.空腔有电荷时的分布(空腔本身不带电,内部放一个带电量为q的点电荷):静电平衡时,空腔内表面带-q电荷,空腔外表面带+q。
3.有电介质存在时的静电场⑴电场中放入相对介电常量为r电介质,电介质中的场强为:E⑵有电介质存在时的高斯定理:SDdSq0,intE0r各项同性的均匀介质D0rE⑶电容器内充满相对介电常量为r的电介质后,电容为CrC0★重点:静电场的能量计算①电容:②孤立导体的电容C4R电容器的电容公式C0QQUUU举例:平行板电容器C圆柱形电容器C4oR1R2os球形电容器CR2R1d2oLR2ln()R1Q211QUC(U)2③电容器储能公式We2C22④静电场的能量公式WewedVE2dVVV12二.静磁场:1.真空中的静磁场磁感应强度→磁感应线→磁通量→磁场的高斯定理⑴磁感应强度:大小BF方向:小磁针的N极指向的方向qvsin⑵磁感应线:是引入描述磁感应强度分布的曲线。
功能原理 机械能守恒定律
``````
2GmE RE
2
2 gRE
E 0
第二宇宙速度
11.2km/s
4 – 5
功能原理
机械能守恒定律
3) 飞出太阳系 第三宇宙速度 第三宇宙速度 v3 ,是抛体脱离太阳引力所需的 最小发射速度 .
h
v
设
地球质量 mE , 抛体质量 m , 地球半径 RE , 太阳质量 mS , 抛体与太阳相距 RS .
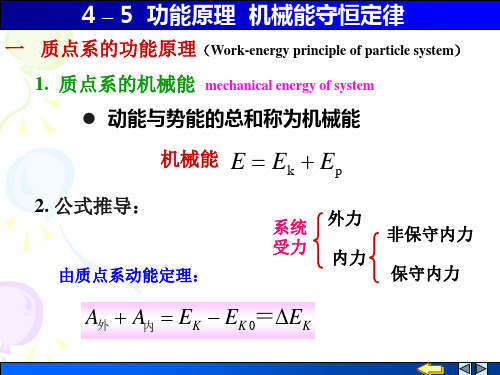
2. 公式推导:
由质点系动能定理:
A外 A内 EK EK 0=EK
4 – 5
功能原理
机械能守恒定律
由质点系动能定理:
A外 A内 EK EK A内保+A内非
则 又
A外+A内保+A内非=EK-EK 0=EK
A内保 E p
即保守内力作的功等于质点系势能增量的负值.
3、功能原理与动能定理并无本质的区别。它们的区别
仅在于功能原理中引入了势能而无需考虑保守内力的功,这正 是功能原理的优点;因为计算势能增量常比直接计算功方便。
4 – 5
二
功能原理
机械能守恒定律
机械能守恒定律 (law of conservation of mechanical energy) 由质点系的功能原理
4 – 5
功能原理
机械能守恒定律
作 业:
4.5.1 , 4.5.3.
4 – 5
四 宇宙速度
功能原理
机械能守恒定律
牛顿的《自然哲学的数学原理》插图,抛体 的运动轨迹取决于抛体的初速度
4 – 5
功能原理
机械能守恒定律
1) 人造地球卫星 第一宇宙速度 第一宇宙速度 v1,是在地面上发射人造地球卫星 所需的最小速度 . 设 地球质量
功能原理(大学物理)

va a
4R E
RE
2R E
∵G
m Em R2
E
=m
g
设:卫星在a 点的速率为va
所受的向心力是由万有引力
提供,由牛顿第二定律可得:
b vb
F向心力= m a =m
v2 R
G (m2RE mE)2 =m
v2 a
2R E
∴
Gm R2
E
E
=g
代入上式得:
∴ va=
gR E 2
va a
≥
5 2
R
C
(2)小球在 A 点受重力mg 及
A
轨道对小球的正压力N 作用。
H
B
·R
N0
(3)如果小球由H =2R 的高处滑下
mg 小球将不能到达A点就掉下来了。
本题结束
例题: 如图所示,子弹水平地射入一端固定在弹簧上
的木块内,已知:子弹质量是0.02kg ,木块质量是 8.98kg。弹簧的劲度系数是100N/m,子弹射人木块 后,弹簧被压缩10cm。设木块与平面间的滑动摩擦系 数为0.2,求:子弹的速度。
和轨道对小 球的正压力
N
+mg
=
m
v2 A
R
(1 )
不脱轨的条件为: N = mRvA2-m g ≥ 0
m
v2 A
R
≥
mg
(2)
N
+mg
=
m
v2 A
R
(1)
m
v2 A
R
≥
mg
(2)
0+mg( H
-
2R
)=
1 2
m
v
大学物理(3.4.2)--功能原理机械能守恒定律能量守恒定律
第四讲功能原理 机械能守恒定律 能量守恒定律k k k i i i i ii e E E E v m v m W W ∆=-=-=+∑122122)2121(系统的外力和内力作功的总和等于系统动能的增量。
回顾前面学过的知识点:1. 质点系动能定理P1p 2p )(E E E W ∆-=--=2. 保守力作功等于势能的减少3. 成对力的功只与作用力和相对位移有关:r d F dW '⋅= 22/16※ 质点系功能原理1、系统的机械能: 动能与势能的总和称为机械能3、由势能的定义,保守内力的功总等于系统势能的减少pin c E W ∆-= 2、内力的功可分为: 保守内力的功和非保守内力功pk E E E +=(保守内力的功由势能代替)第四讲 功能原理 机械能守恒定律 能量守恒定律 in ncin c in in W W W W i i+==∑非保守内力的功将导致机械能与其他形式的能量转换。
inncex p k W W E E E +=∆+∆=∆k in ncp ex in nc in c ex in ex E W E W W W W W W ∆=+∆-=++=+ 4、系统的功能原理 (由质点系动能定理)在选定的质点系内,在任一过程中,质点系总机械能的增量等于所有外力的功与非保守内力的功的代数和。
4/16※ 机械能守恒定律问题1:有非保守内力作功,系统的机械能不守恒 ?例如:摩擦力作功,机械能转变成热能。
0=+in nc ex W W 0=∆+∆=∆p k E E E 常量=+p k E E 由功能原理:则:或:如果: 如果系统内只有保守内力作功,其他内力和一切外力都不作功,或元功之和恒为零,则系统内各物体的动能和势能可以相互转换,但总机械能保持不变。
问题2:有摩擦力作功:机械能守恒?in nc ex p k W W E E E +=∆+∆=∆力 f 作正功,f ' 作负功,总和为零,机械能守恒。
3-6功能原理机械能守恒定律
又是怎样认识黑洞的呢 ?
2 E
第三宇宙速度
mE 1 2 -1 v3 ( v' 2G ) 16.4 km s RE
5 简谐运动的振幅 周期 频率和相位 3 ––16简谐运动 功能原理 机械能守恒定律
探路者无人飞船俯视火星
探路者飞船在火星着陆点地貌
5 简谐运动的振幅 周期 频率和相位 3 ––16简谐运动 功能原理 机械能守恒定律
5 简谐运动的振幅 周期 频率和相位 3 ––16简谐运动 功能原理 机械能守恒定律
* 四 宇宙速度
牛顿的《自然哲学的数学原理》插图,抛体的运轨 迹取决于抛体的初速度
5 简谐运动的振幅 周期 频率和相位 3 ––16简谐运动 功能原理 机械能守恒定律
(1) 人造地球卫星
第一宇宙速度
第一宇宙速度v1,是在地面上发射人造地球卫星所 需的最小速度 . 设:地球质量 mE , 抛体质量 m ,地球半径 RE
5 简谐运动的振幅 周期 频率和相位 3 ––16简谐运动 功能原理 机械能守恒定律
一
质点系的动能定理 对第 i 个质点,有
ex in
Wi Wi Eki Eki 0
外力功 内力功 对质点系,有
m1
ex Fi
in m i m2 Fi
W
i
ex
i
Wi Eki Eki 0 Ek Ek 0
2
va
va ( gRE / 2) 1/ 2 同理 vb ( gR E / 4)
1/ 2
a
4RE
o
RE
b
vb
1 mE m 1 2 Ea mva G m gR 1 E 2 2 RE 4 E mgR E 8 1 2 mE m 1 Eb mvb G m gR 10 E 2.3510 J 2 4 RE 8
大学物理3-3机械能守恒定律 能量守恒定律
1. 机械能守恒定律
机械能守恒定律:如果一个系统内只有保守内力 做功(常见),或者非保守内力与外力的总功为零, 则系统内各物体的动能和势能可以互相转换,但机械 能的总值保持不变。这一结论称为机械能守恒定律。
条件 Ae 0,Aid 0;或 Ae Aid 0
E
弹 p1
1 2
kx02
如果物体因惯性继续下降的微小距离为h,并且
以这最低位置作为重力势能的零位置,那么,系统
初时的重力势能为
E
重 p1
mgh
守恒定律
系统在这初始位置的总机械能为
E1=Ek
1+E
弹 p1+E
重 p1
1 2
mv
2 0
1 2
kx02
mgh
在物体下降到最低位置时,物体的动能 Ek,2 系0统
定律 EKa EPa EKb EPb
或 E EK EP 常量
能量守恒定律
2. 能量守恒定律
一个孤立系统经历任何变化时,该系统的 所有能量的总和是不变的,能量只能从一种 形式变化为另外一种形式,或从系统内一个 物体传给另一个物体。这就是普遍的能量守 恒定律。
守恒定律
例题3-5 起重机用钢丝绳吊运一质量为m 的物体,以 速度v0作匀速下降,如图所示。当起重机突然刹车时, 物体因惯性进行下降,问钢丝绳再有多少微小的伸长? (设钢丝绳的劲度系数为k,钢丝绳的重力忽略不计)。 这样突然刹车后,钢丝绳所受的最大拉力将有多大?
T
x0
G
h
v0
守恒定律
解 我们考察由物体、地球和钢丝绳所组成的系统。 除重力和钢丝绳中的弹性力外,其它的外力和内力都 不作功,所以系统的机械能守恒。
大学物理-第三章三大守恒定律
i
i
1 若质点系动量守恒,则动量在三个坐标轴上的分量都守恒。
2、在系统内质点间的碰撞,打击,爆炸过程中,内力很大,可 忽略重力、摩擦力等外力,可近似认为动量守恒。
上一页 下一页
3、虽然有时系统总动量不守恒,但只要系统在某个方向受 的合外力为0,则系统在该方向动量守恒。
即 F x 当 F ix 0 时 p x , m iv ix 常量
mv1
得 F (0 .3 )22 0 32 0 2 2 0 3c0o 3 s()0 14 (N )51
0 .01
根据正弦定理
sm i 2 nvsiF n t() 18 ,即力的 v 夹 方 角 1向 6 。 为 2
上一页 下一页
例2-6质量为m=30kg的铁锤(彩电)从1m高处由静止下落,碰撞
Ixt1 t2F xd tpx2px1mx2 vmx1v Iyt1 t2F yd tpy2py1my2v my1v Izt1 t2F zd tpz2pz1mz2 vmz1v
4 . 对于碰撞、打等 击过 、程 爆, 炸物体互 之作 间用 的
称为冲力, 值其 大特 , 点 变 t短是 化 ,峰 大 在, 某
b v2
d v
d(m v )
d p
t 2
Fm am
Fdtdp
dt dt
微分形式
dt
a
v1
I 定义 :t1 t动2F 量 d ptp p 1 m 2d vp p 2 t 1 p 1 P 2m mv( 2v I2 t1t2v F1 d)t
( M d)v M (d v ) d( v M d v u ) Mv
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ex in nc
i
W W ( Ek Ep ) ( Ek 0 Ep 0 )
2
3-6 功能原理
机械能守恒定律
W
ex
W ( Ek Ep ) ( Ek 0 Ep 0 )
in nc
机械能 E Ek Ep
W W E E0
ex in nc
——质点系的功能原理
W Ek E k 0
in
1
i
注意
内力可以改变质点系的动能
3-6 功能原理
机械能守恒定律
二
质点系的功能原理
W
ex
W Ek E k 0
in
W
in c
in
Wi
i
in
in Wc
in Wnc
非保守 力的功
W ( Epi Epi 0 ) ( Ep Ep0 )
13
3-6 功能原理
机械能守恒定律
解(1)将物体、槽、地球视为系统,仅有保守内 力重力做功,系统机械能守恒。以 v 和V分别表 示物体刚离开槽时物体和槽的速度,则有
1 1 2 2 mgR mv MV 2 2
对物体和槽,水平方向动量守恒
mv MV 0
联解可得
v
2 MgR M m
2 gR V m M (M m)
3-6 功能原理
机械能守恒定律
一
质点系的动能定理
对第 i 个质点,有
m1
ex Fi
Wi Wi Eki Eki 0
ex in
in m i m2 Fi
外力功 内力功
对质点系,有
W
i
ex
i
Wi Eki Eki 0 Ek Ek 0
in i i
ex
质点系动能定理 W
2 MgR M m
2 gR M m
(1)
15
3-6 功能原理
根据牛顿定律 将式(1)代入,得
机械能守恒定律
v'2 N ' mg m R
'2
v 2m N ' mg m (3 )mg R M
16
3-6 功能原理
机械能守恒定律
例:一陨石从距地面 h 高处由静止开始落向地面, 忽略空气阻力,求: (1)陨石下落过程中,地球引力做的功; (2)陨石落地时速度多大? 解(1)取地心为原点,从 o 指向陨石为 r 的正方向, 如图。陨石从 a 落到 b ,地球引力的功为
8
3-6 功能原理
机械能守恒定律
例2: 长为l 的均质链条,部分置于水平面上, 另一部分自然下垂, 已知链条与水平面间静摩 擦系数为0 , 滑动摩擦系数为 O 求:
(1) 满足什么条件时,链条将开始滑动 (2) 若下垂部分长度为b 时,链条自静 止开始滑动,当链条末端刚刚滑离 桌面时,其速度等于多少? y
l
11
3-6 功能原理
机械能守恒定律
根据动能定理有
1 1 1 2 2 2 g( l b ) g( l b) lv 2 0 2 2 2
v g 2 g 2 (l b ) ( l b )2 l l
12
3-6 功能原理
机械能守恒定律
例2.3.9 一质量为m的物体,从质量为M的园弧形 槽顶由静止滑下,设园弧形槽的半径为R、张角 为 ,如忽略所有摩擦,求:(1) 物体刚离开槽底 端时,物体和槽的速度各为多少?(2) 在物体从A滑 到B的过程中,物体对滑槽做的功; (3) 物体到达B 时对槽的压力。
Ek Ep
5
3-6 功能原理
机械能守恒定律
四、守恒定律的意义 1.守恒定律 · 力学中:动量守恒定律 机械能守恒定律 角动量守恒定律
· 自然界中还有: 质量守恒定律、 电荷守恒定律; (粒子物理中的)重子数、轻子数、 奇异数、 宇称守恒定律
6
3-6 功能原理
机械能守恒定律
2.守恒定律的特点 (1)方法上:针对一过程,但不究过程细节, 给出始末态的情况。 (2)适用范围广:宏观、微观、高速、低速 均适用。
在应用功能原理时,应只计及非保守内力和含外力
做功对质点系机械能改变的贡献。
4
3-6 功能原理
机械能守恒定律
三
机械能守恒定律
当W
ex
W
in nc
0 时,有 E E0
——只有保守内力作功的情况下,质点 系的机械能保持不变.
E Ek Ep
Ek Ek 0 ( Ep Ep 0 )
讨论:关于功能原理的理解 (1) 功能原理的适用条件:仅对惯性参照系适用;
3
3-6 功能原理
机械能守恒定律
(2) 功能原理描述质点系的运动规律。在应用功能
原理求解问题时,必须正确确定质点系的范围,
保证引入势能时,涉及势能的所有质点都包含在 所研究的质点系中; (3) 功能原理与动能定理的不同之处在于它把质点 系内的保守内力做功用质点势能改变来替代,因此,
14
3-6 功能原理
机械能守恒定律
(2) 对槽,只有物体对它的压力N对它做功,依 据动能定理,物体对槽做的功应等于槽动能的 增量,即
1 m 2 gR WN MV 2 2 Mm
(3) 物体到达B的瞬间,槽在水平方向不受外力, 加速度为0,视为惯性参照系。此时,物体的水 平速度为
v' v V
9
例
3-6 功能原理
机械能守恒定律
解: (1) 以链条的水平部分 为研究对象,设链条每单位 长度的质量为,沿铅垂向 下取Oy 轴。
O
y
设链条下落长度 y =b0 时,处于临界状态 0 b0 l b0 g 0 ( l b0 ) g 0 1 0
当 y >b0 ,拉力大于最大静摩擦力时,链 条将开始滑动。
7
讨论
3-6 功能原理
机械能守恒定律
(1) 内力和为零,内力功的和是否为零?
f1f 2 W 1 f 1L
不一定为零
f 0
f1
B A
f2
B A
W 2 f 2S
1
W f ( L S )
(2) 内力的功也能改变系统的动能
S L
例:炸弹爆炸,过程内力和为零,但内 力所做的功转化为弹片的动能。
10
3-6 功能原理
机械能守恒定律
(2) 以整个链条为研究对象,链条在运动过程中 各部分之间相互作用的内力的功之和为零, 重力的功
1 W b ygdy g ( l 2 b 2 ) 2
l
摩擦力的功
1 W ' b ( l y ) gdy g ( l b )2 2
