指数函数图像及性质学生

合集下载

指数函数的图像和性质-学案

指数函数的图像和性质
知识与技能：理解指数函数的概念与意义，理解指数函数的图像和性质，并会运用图像和性质解决有关问题。

过程与方法：利用数形结合的方法，理解并熟记典型指数函数和一般指数函数的图像和性质。

情感态度与价值观：体验指数函数与现实世界的密切联系及其在刻画现实问题中的作用，培养学生运用现代技术学习、探索
和解决问题的能力。

教学重点：指数函数的图像和性质。

教学难点：底数a>1与0<a<1时指数函数的不同性质的理解及应用。

教学过程：
一、指数函数的概念：
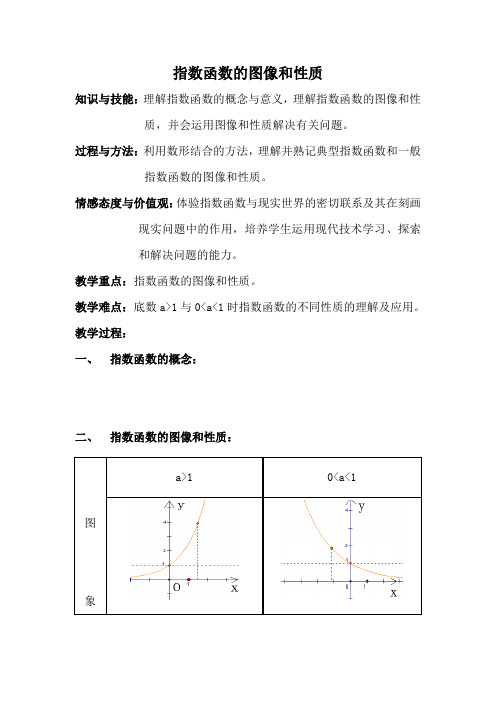
二、指数函数的图像和性质：
7.09.0
三、指数函数的图像和性质的应用：例1、比较下列各题中两数值的大小
① 1.72.5,1.73.
② 0.8-0.1 ,0.8-0.2
解：①
②
例2、比较下列各题中两数值的大小
①（ )0.4 ,1
②0.8－0.3 ,4.9－0.1
解：①
②
归纳：
例3、已知下列不等式，比较m、n的大小。

① 2m < 2n
②0.2m > 0.2n
③ a m > a n (a≠1且a>1)
解：①
②
③
四、课堂作业：
教材P77 2 （4）、（5）、（6）
4 （1）、（2）。

《指数函数》图像与性质学情分析

A1 技术支持的学情分析
A1 技术支持的学情分析（一）学情分析方案
教学主题学情分析目的
二、学情分析方案《指数函数》图像与性质
可以进一步深化学生对函数概念的理解与认识；指数函数的学习可以为研究对数函数打下基础，为了更好的学习函数知识，以免影响整个高中数学学习。
教学内容
指数函数的图象、性质及其简单应用
教学目标
1、知识目标：理解指数函数的定义，掌握指数函数的图象、性质及其简单应用.
2、能力目标：体会数形结合和分类讨论思想，体验从特殊到一般的学习方法.
3、情感态度与价值观：培养学生勇于提出问题，善于探索的思维品质.
教学对象及学情分析
（4）（6）班级学生数学基础较好，学生已掌握函数的一般性质和简单的指数运算；从学生原有的知识和能力出发，在教师的带领下创设疑问，通过合作交流，共同探索，逐步解决问题.
教学重点
指数数函数图象和性质的发现，以及指数函数图象与底数的关系.
学情分析方法和工具
1、课堂检测+课后检查 2、数学考试，检测掌握能力
学情分析：通过考试结果及调查问卷了解学习情况，对结果进行统计图表工具进行分析。
其他
2

高一数学人必修件指数函数的图象和性质

生物繁殖
在生物学领域，指数函数用于描述生物种群的繁殖速度。某些生物种群的增长符合指数函数的规律，如细菌繁殖、昆虫数量增长等。
其他领域应用案例
放射性衰变
在物理学中，指数函数用于描述放射性物质的衰变过程。放射性元素的原子数量随时间呈指数减少。
化学反应速率
化学领域中，指数函数可用于描述某些化学反应的速率。反应速率与反应物浓度的关系可以用指数函数表示。
同底数幂相乘
幂的乘方
底数不变，指数相加。即$a^m times a^n = a^{m+n}$。
底数不变，指数相乘。即$(a^m)^n = a^{m times n}$。
同底数幂相除
底数不变，指数相减。即$a^m div a^n = a^{m-n}$。
幂的乘方法则
1 2
正整数指数幂的乘法
$(a^m)^n = a^{m times n}$，其中$m, n$为正整数。
指数函数图像与坐标轴交点
指数函数的图像与x轴没有交点，与y轴的交点是(0,1)。
指数函数性质总结
指数函数的单调性
当a>1时，指数函数在定义域内单调递增；当0<a<1时，指数函数在定义域内单调递减。
指数函数的奇偶性
指数函数既不是奇函数也不是偶函数。
指数函数的值域
指数函数的值域是(0, +∞)。
形如y=a^x（a>0且a≠1）的函数叫做指数函数。
指数函数表达式
y=a^x，其中a是自变量，x是指数，y是因变量。
指数函数图像特征
指数函数图像形状
指数函数的图像是一条从坐标原点出发，向右上方或右下方无限延伸的曲线。
指数函数图像位置
当a>1时，图像位于第一象限和第二象限；当0<a<1时，图像位于第一象限和第四象限。

指数函数的图像及性质教学设计

2、指数函数的图象及其性质一、教学内容分析本节课是《普通高中课程标准实验教科书·数学（1）》（人教A版）第二章第一节第二课（2.1.2）《指数函数及其性质》。

根据我所任教的学生的实际情况，我将《指数函数及其性质》划分为三节课（探究图象及其性质，指数函数及其性质的应用），这是第一节课“探究图象及其性质”。

指数函数是重要的基本初等函数之一，作为常见函数，它不仅是今后学习对数函数和幂函数的基础，同时在生活及生产实际中有着广泛的应用，所以指数函数应重点研究。

二、学生学习况情分析指数函数是在学生系统学习了函数概念，基本掌握了函数的性质的基础上进行研究的，是学生对函数概念及性质的第一次应用。

教材在之前的学习中给出了两个实际例子（GDP的增长问题和炭14的衰减问题），已经让学生感受到指数函数的实际背景，但这两个例子背景对于学生来说有些陌生。

本节课先设计一个看似简单的问题，通过超出想象的结果来激发学生学习新知的兴趣和欲望。

三、设计思想1.函数及其图象在高中数学中占有很重要的位置。

如何突破这个即重要又抽象的内容，其实质就是将抽象的符号语言与直观的图象语言有机的结合起来，通过具有一定思考价值的问题，激发学生的求知欲望――持久的好奇心。

我们知道，函数的表示法有三种：列表法、图象法、解析法，以往的函数的学习大多只关注到图象的作用，这其实只是借助了图象的直观性，只是从一个角度看函数，是片面的。

本节课，力图让学生从不同的角度去研究函数，对函数进行一个全方位的研究，并通过对比总结得到研究的方法，让学生去体会这种的研究方法,以便能将其迁移到其他函数的研究中去。

2.结合参加我校实际，在本课的教学中我努力实践以下两点：（1）.在课堂活动中通过同伴合作、自主探究培养学生积极主动、勇于探索的学习方式。

（2）.在教学过程中努力做到生生对话、师生对话，并且在对话之后重视体会、总结、反思，力图在培养和发展学生数学素养的同时让学生掌握一些学习、研究数学的方法。

高一数学必修1第二章指数函数图像和性质-学生

(3)(ab )r ＝a r b r (a ＞0，b ＞0，r ∈Q )． 5．无理数指数幂无理数指数幂a α(a ＞0，α是无理数)是一个确定的实数．有理数指数幂的运算性质对于无理数指数幂同样适用．例1 (1)计算：0.06431-－⎝⎛⎭⎫－780＋[(－2)3]34-＋16－0.75＋|－0.01|21；(2)化简： 3329-a a÷33137--⋅a a (a ＞0)．例2 (1)⎝⎛⎭⎫－33832-＋(0.002)21-－10(5－2)－1＋(2－3)0； (2)3323-a a ·()1321-215-⎪⎪⎭⎫ ⎝⎛⋅-a a.【新知识梳理与重难点点睛】1．指数函数的定义一般地，函数y ＝a x (a ＞0，且a ≠1)叫做指数函数，其中x 是自变量，函数的定义域是R .2．指数函数的图象与性质a ＞10＜a ＜1图象性质定义域R ，值域(0，＋∞) 图象过定点(0,1)，即x ＝0时，y ＝1当x ＞0时，y ＞1；当x ＜0时，0＜y ＜1 当x ＞0时，0＜y ＜1；当x ＜0时，y ＞1 在R 上是增函数在R 上是减函数要点一指数函数的概念例1给出下列函数：①y＝2·3x；②y＝3x＋1；③y＝3x；④y＝x3；⑤y＝(－2)x.其中，指数函数的个数是() A．0 B．1 C．2 D．4跟踪演练1若函数y＝(4－3a)x是指数函数，则实数a的取值范围为________．答案{a|a＜43，且a≠1}要点二指数函数的图象例2如图是指数函数①y＝a x，②y＝b x，③y＝c x，④y＝d x的图象，则a，b，c，d与1的大小关系是()A．a＜b＜1＜c＜d B．b＜a＜1＜d＜cC．1＜a＜b＜c＜d D．a＜b＜1＜d＜c跟踪演练2(1)函数y＝|2x－2|的图象是()(2)直线y＝2a与函数y＝|a x－1|(a＞0且a≠1)的图象有两个公共点，则a的取值范围是________．要点三指数型函数的定义域、值域例3求下列函数的定义域和值域：(1)y ＝4-12x ；(2)y ＝1－2x ；(3)y ＝⎝⎛⎭⎫12322--x x .跟踪演练3 (1)函数f (x )＝1－2x ＋1x ＋3的定义域为( ) A ．(－3,0] B ．(－3,1]C ．(－∞，－3)∪(－3,0]D ．(－∞，－3)∪(－3,1] (2)函数f (x )＝⎝⎛⎭⎫13x－1，x ∈[－1,2]的值域为________．1．下列各函数中，是指数函数的是( ) A ．y ＝(－3)x B ．y ＝－3x C ．y ＝3x －1 D ．y ＝⎝⎛⎭⎫13x 2．y ＝⎝⎛⎭⎫34x 的图象可能是( )3．y ＝2x ，x ∈[1，＋∞)的值域是( ) A ．[1，＋∞) B ．[2，＋∞) C ．[0，＋∞) D ．(0，＋∞)4．函数f (x )＝a x 的图象经过点(2,4)，则f (－3)的值是________．5．函数y ＝⎝⎛⎭⎫12x 2－1的值域是________．【新方法、新技巧练习与巩固】一、基础达标 1．y ＝2x－1的定义域是( )A ．(－∞，＋∞)B ．(1，＋∞)C ．[1，＋∞)D ．(0,1)∪(1，＋∞)2．已知集合M ＝{－1,1}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪12＜2x ＋1＜4，x ∈Z ，则M ∩N 等于( ) A ．{－1,1} B ．{－1} C ．{0} D ．{－1,0} 3．函数y ＝2x＋1的图象是( )4．当x ∈[－2,2)时，y ＝3－x －1的值域是( ) A ．(－89，8] B ．[－89，8]C ．(19，9)D ．[19，9]5．指数函数y ＝(2－a )x 在定义域内是减函数，则a 的取值范围是________．6．函数y ＝a x －5＋1(a ≠0)的图象必经过点________．7．已知函数f (x )＝a x －1(x ≥0)的图象经过点(2，12)，其中a ＞0且a ≠1.(1)求a 的值；(2)求函数y ＝f (x )(x ≥0)的值域．二、能力提升 8．函数y ＝5－|x |的图象是( )。

指数函数图像和性质

图像
特
征
3、深入探究，加深理解
y
引导学生观察图像，发现图像与底的关系
在第一象限沿箭头方向底增大
1 y 2
x
1 y 3
x
y 3x y 2x
底互为倒数的两个函数图像关于y轴对称
1 0
1 y 3
x
1 y 2
x
指数函数图像和性质（二）
(一）复习回顾：
1、指数函数的定义：
2、指数函数
的图像及特征
a>1
图
0<a<1
像
图像分布在一、二象限，与y轴相交，落在x轴的上方。都过点（0，1）第一象限的点的纵坐标都第一象限的点的纵坐标都大于1；第二象限的点的大于0且小于1；第二象限纵坐标都大于0且小于1。的点的纵坐标都大于1。从左向右图像逐渐上升。从左向右图像逐渐下降。
x
有负根,则实数a 的取值范围是
____________
▲4、函数
1 y 2
x2
的单调减区间是__
（五）回顾与反思：
x
(二）学生活动： ①若指数函数 y a (a 0, a 1) 在 1,1 上最大值与最小值的差是1，则实数 a 的是
x
____________
②函数 y
1 6
x2 x 2
的定义域是
____________
③函数
1 y 3
x2 2 x
的值域是
____________
（三）数学运用：
例1 已知函数
ax 1 f ( x) x (a 0, a 1), f (1) 3. a 1

指数与指数函数图像及性质(学生版)

指数与指数函数图像及性质【知识要点】 1．根式（1）如果a x n =，那么x 叫做a 的n 次方根.其中1>n ，且*∈N n 。

（2）如果a x n=，当n 为奇数时，n a x =；当n 为偶数时，n a x ±=()0>a .其中n a 叫做根式,n 叫做根指数,a 叫做被开方数. 其中1>n ，且*∈N n 。

(3)()()*∈>==N n n a a nnn ,1,00。

,||,a n a n ⎧=⎨⎩为奇数为偶数其中1>n ，且*∈N n 。

2.分数指数幂(1)正分数指数幂的定义: n m n m a a =()1,,,0>∈>*n N n m a (2)负分数指数幂的定义: nm nm aa1=-()1,,,0>∈>*n Nn m a(3) 要注意四点：①分数指数幂是根式的另一种表示形式； ②根式与分数指数幂可以进行互化； ③0的正分数指数幂等于0； ④0的负分数指数幂无意义。

(4)有理数指数幂的运算性质:①sr sra a a +=⋅()Q s r a ∈>,,0；② ()rs sra a =()Q s r a ∈>,,0；③()r r rb a ab =()Q r b a ∈>>,,0,0.3.无理数指数幂(1)无理数指数幂的值可以用有理数指数幂的值去逼近; (2)有理数指数幂的运算性质同样适用于无理数指数幂。

4．指数函数的概念：一般地，函数()0,1xy a a a =>≠且叫做指数函数，其中x 是自变量，函数的定义域是R 。

5．指数函数的图像与性质第一课时【典例精讲】题型一根式、指数幂的化简与求值1.n a 叫做a 的n 次幂，a 叫做幂的底数，n 叫做幂的指数，规定：1a a =；2. (1,)n a n n N +=>∈,||,a n a n ⎧=⎨⎩为奇数为偶数；3. 1(0,,,)n mnmn a a m n N ma-+=>∈且为既约分数，=a a αβαβ（）. 【例1】计算下列各式的值．（1（2（3；（4)a b >.【变式1】求下列各式的值：（1*1,n n N >∈且）；（2【例2】计算)21313410.027256317--⎛⎫--+-+⎪⎝⎭【变式2】化简34的结果为（）A ．5B ．C ．﹣D ．﹣5【变式3】1332-⎛⎫ ⎪⎝⎭×76⎛⎫- ⎪⎝⎭0＋148＝________.题型二根式、指数幂的条件求值 1. 0a >时，0;b a > 2. 0a ≠时， 01a =； 3. 若,r s a a =则r s =；4. 1111222222()(0,0)a a b b a b a b ±+=±>>； 5. 11112222()()(0,0)a b a b a b a b +-=->>. 【例3】已知11223a a-+=，求下列各式的值.（1）11a a -+；（2）22a a -+；（3）22111a a a a --++++【变式1】已知,a b 是方程2640x x -+=的两根，且0,a b >>的值.【变式2】已知12,9,x y xy +==且x y <，求11221122x y x y-+的值.【变式3】已知11223a a -+=，求33221122a aa a----的值.【变式4】（1）已知122+=xa，求xx xx a a a a --++33；（2）已知a x=+-13，求6322--+-x ax a .【例4】计算下列各式的值：（1）246347625---+-；（2）()2x 3442<--+-x x x ；（3）12121751531311++-+++++++n n ；（4）()54 2222233=++--xxxx x 其中.【变式5】化简或计算出下列各式：（1）121316324(1243)27162(8)--+-+-；（2）化简65312121132ab b a b a ---⎪⎪⎭⎫ ⎝⎛；（3【课堂练习】1. 若()0442-+-a a 有意义,则a 的取值范围是()A.2≥aB.42<≤a 或4>aC. 2≠aD. 4≠a 2. 下列表述中正确的是() A.()()()273336263=-=-=- B.32213421313a a a a a a =⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⋅=⋅ C.无理数指数幂na (n 是无理数)不是一个确定的实数 D.()()()⎩⎨⎧≤-≥=00a a a a a nn3. 已知0>a ,则的值2313123131⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+--a a a a 为 ()A.3232-+aa B.4 C. 3232--aa D. 4-4. 计算：()=-+-0430625.0833416π ______.【思维拓展】1.化简⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+-----2141811613212121212121的结果是 ( )A.13212121--⎪⎪⎭⎫ ⎝⎛-B.132121--⎪⎪⎭⎫ ⎝⎛- C.32121-- D.⎪⎪⎭⎫ ⎝⎛--3212121第二课时题型三指数函数的概念【例1】已知函数()2()33x f x a a a =-+是指数函数，求实数a 的值。

指数函数的图象和性质

1
1
练习：比较大小 a3和a 2，（a 0, a 1)
方法总结
（1）构造函数法：要点是利用函数的单调性，数的特征是同底不同指（包括可以化为同底的），若底数是参变量要注意分类讨论。比较两个同底数幂的大小时,可以构造一个指数函数,再利用指数函数的单调性即可比较大小. （2）搭桥比较法：用别的数如0或1做桥。数的特征是不同底不同指。比较两个不同底数幂的大小时,通常引入第三个数作参照.
分析：(1)因为该城市人口呈指数增长，而同一指数函数的倍增期是相同的，所以可以从图象中选取适当的点计算倍增期.(2)要计算20年后的人口数，关键是要找到20年与倍增期的数量关系. 解：(1)观察图,发现该城市人口经过20年约为10万人，经过40年约为20万人，即由10万人口增加到20万人口所用的时间约为20年，所以该城市人口每翻一番所需的时间约为20年.(2)因为倍增期为 20年，所以每经过20年，人口将翻一番.因此，从80万人开始，经过20年，该城市人口大约会增长到160万人.
x
用描点法作函数y (1)x 和y (1)x的图象.
函
2
3
x … -3 -2 -1 0 1 2 3 …
数 y=2-x … 8 4 2 1 1/2 1/4 1/8 …
图 y=3-x … 27 9 3 1 1/3 1/9 1/27 …
象 y (1)x 2
特征
y (1)x 3
y
O
思考：若不用描点法，这两个函数的图象又该如何作出呢？
底数a由大变小时函数图像在第一象限内按＿＿顺＿＿
时针方向旋转.
问题三：图象中有哪些特殊的点？
答：四个图象都经过点＿(＿0＿,1＿) ．
a>1

高中数学_指数函数图象与性质教学设计学情分析教材分析课后反思

“指数函数的图象与性质”教学设计一、教材内容分析：教学内容：本节教学内容见《普通高中教科书人民教育出版社A版必修1第一册第四章第二节第二课（4.2.2）《指数函数图象与性质》》的第二节即指数函数及其性质的第二课时，所需要进行教学的内容为：指数函数的图象、性质及简单应用。

内容分析：指数函数的底数取值情况为1a且，a为底数，底数对于0≠>a指数函数来说至关重要，其影响指数函数的图象和性质。

本节课程需要学生并能够绘制指数函数图象，了解底数a对于图象如何影响，通过对图象观察、对比、分析得到指数函数的性质，从而提高学生的观察能力，通过性质的产生过程，学生逐步掌握“分类讨论”与“数型结合”的数学核心素养。

二、学生学情分析学生学习基础：在初中时期，学生已经接触到一些函数即一次函数、二次函数以及反比例函数，不仅熟悉这些函数的图象和性质，而且对于函数的研究有了一些了解与认识，其中包括描点法绘制函数图象，这一系列的函数基础，能够初步使用数形结合的思想来考虑抽象问题。

学生学习阻碍：学生的思维方式依旧以直观思维方式为主，因此尽管具备了基础的函数学习的技能，但在本节课程中要想清晰的理解底数a在对指数函数的图象和性质的影响中起到何种作用依旧存在困难。

三、教学目标分析（一）课程目标：在学生的画图过程中，发现底数a的变化是如何影响指数函数的图形及其性质，并且得到指数函数的图象，通过对图象的观察、分析，掌握指数函数的性质。

（二）课时目标及目标解析：【课时目标】1、通过分组画指数函数y=2x与y=(1/2)x，y=3x与y=(1/3)x的图象，感悟底数a的变化对指数函数的图象的影响。

2、观察指数函数图象，对图象进行细致的分析与研究，进而获得指数函数的性质，在这一学习过程中，学生的观察学习水平以及数形结合的思想均能够得到提升，培养学生的数学思维能力。

3、结合具体例题，对涉及指数函数图象和形制的问题进行解决，以此让学生掌握相关基础知识的应用，使学生对用图形来分析函数性质这一学习方式得以重视。

指数函数的图像和性质教案设计

指数函数的图像和性质教案设计一、教学目标1. 让学生理解指数函数的概念，掌握指数函数的图像和性质。

2. 培养学生运用指数函数解决实际问题的能力。

3. 提高学生对数学知识的兴趣，培养学生的逻辑思维能力。

二、教学内容1. 指数函数的定义与性质2. 指数函数的图像特点3. 指数函数的实际应用4. 指数函数的图像和性质的综合运用三、教学重点与难点1. 教学重点：指数函数的定义、图像特点和性质。

2. 教学难点：指数函数图像和性质的运用。

四、教学方法1. 采用问题驱动法，引导学生探索指数函数的图像和性质。

2. 利用多媒体课件，直观展示指数函数的图像，帮助学生理解。

3. 结合实际例子，让学生体验指数函数在实际生活中的应用。

4. 开展小组讨论，培养学生的合作能力和解决问题的能力。

五、教学过程1. 引入：通过回顾幂函数的知识，引导学生思考指数函数的定义和特点。

2. 讲解：讲解指数函数的定义，引导学生掌握指数函数的基本性质。

3. 展示：利用多媒体课件，展示指数函数的图像，引导学生观察和分析图像特点。

4. 实践：让学生绘制指数函数的图像，观察和分析图像的性质。

5. 应用：结合实际例子，让学生运用指数函数解决实际问题。

6. 总结：对本节课的内容进行总结，强调指数函数的图像和性质。

7. 作业：布置相关练习题，巩固所学知识。

六、教学评估1. 课堂问答：通过提问，了解学生对指数函数概念和性质的理解程度。

2. 练习题：布置针对性的练习题，检验学生对指数函数图像和性质的掌握情况。

3. 小组讨论：评估学生在小组讨论中的参与程度和合作能力。

七、拓展与延伸1. 引导学生思考：指数函数在实际生活中的应用场景有哪些？2. 探讨：如何利用指数函数解决实际问题？3. 布置研究性学习任务：让学生研究指数函数在其他领域的应用。

八、教学反思1. 教师总结本节课的教学效果，反思教学过程中的优点和不足。

2. 学生反馈学习感受，提出改进建议。

3. 针对教学不足，制定改进措施，为下一节课的教学做好准备。

指数函数的图象和性质教案

4.2.2 指数函数的图象和性质4号一、【教学目标】1.采用“疑、探、导、练”教学法，根据观察指数函数底数对指数函数图象的影响，并通过图象归纳指数函数的性质；2.通过画指数函数图象、归纳指数函数性质与运用过程，培养学生的观察能力及数形结合、特殊--一般、分类讨论的数学思想。

3.让学生感受数学问题探索的乐趣，体验成功的喜悦，发展学生逻辑推理、直观想象的核心素养。

二、【教学重、难点】教学重点：理解指数函数的图象及性质。

教学难点：指数函数性质的归纳与运用。

三、【教学方法】我校学生数学基础比较薄弱，学生对数学普遍不感兴趣。

本节课探究性比较强，而且突出数学图形的运用，这恰是学生学习的弱项，但是思想比较活跃的他们对新事物具有强烈的好奇心，动手能力、观察能力比较强。

因此本节课通过结合计算机软件工具，让学生更直观形象地理解指数函数的图象和性质，让学习成为一种愉悦的主动认知过程，切实做到将数学课堂还给学生。

四. 【教学过程设计】二、合作探究，探索新知6、将这四个函数图象放在同一个坐标系中图象关于和xxayay)1(== y轴对称7、归纳指数函数的性质：通过前面对图象特征的充分认识，引导学生一起将这些图象特征转化成数学语言，即得到指数函数的性质。

xy a=a＞1 0＜a＜1图象定义域R值域（0，+∞）性质过定点（0，1）当x＞0时，y＞1；x＜0时，0＜y＜1当x＞0时，0＜y＜1；x＜0时，y＞1非奇非偶函数非奇非偶函数在R上是增函数在R上是减函数教师：现在我把刚刚画的四个函数放在同一个坐标系，你有什么发现？教师：引导学生去观察底数互为倒数的两个指数函数图象关于Y轴对称。

教师：观察上面函数图象，你能归纳出指数函数y=a x(a＞0,且a≠1)的图象特征和性质吗？教师引导学生观察图象，填写表格，讨论交流，概括总结出指数函数的基本性质。

通过让学生动眼观察、动脑思考，并引导他们对所发现的知识进行归纳、分类，目的在于让学生成为数学课堂的主人，在这一过程中不仅让学生的主体意识得以充分的体现，也让学生经历知识的产生和发展过程，感受数学问题探索的乐趣，体验成功的喜悦，体会数形结合及分类讨论的数学思想，从而有效的达到对知识的理解，进一步发展学生的数学抽象、直观想象的数学核心素养。

《指数函数的图像和性质》教案、导学案与同步练习

《第四章指数函数与对数函数》《4.2.2指数函数的图像和性质》教案【教材分析】本节课在已学指数函数的概念，接着研究指数函数的图像和性质，从而深化学生对指数函数的理解，并且了解较为全面的研究函数的方法，为以后在研究对数函数幂函数等其它函数打下基础。

另外，我们日常生活中的很多方面都涉及到了指数函数的知识，例如细胞分裂，放射性物质衰变，贷款利率等，所以学习这一节具有很大的现实价值。

【教学目标与核心素养】课程目标1、掌握指数函数的图象和性质，培养学生实际应用函数的能力；2、通过观察图象，分析、归纳、总结指数函数的性质；3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.数学学科素养1.数学抽象：指数函数的图像与性质；2.逻辑推理：图像平移问题；3.数学运算：求函数的定义域与值域；4.数据分析：利用指数函数的性质比较两个函数值的大小：5.数学建模：通过由抽象到具体，由具体到一般的数形结合思想总结指数函数性质.【教学重难点】重点：指数函数的图象和性质；难点：对底数的分类，如何由图象、解析式归纳指数函数的性质．【教学方法】：以学生为主体，采用诱思探究式教学，精讲多练。

【教学过程】一、情景导入请学生用三点画图法画图像，观察两个函数图像猜测指数函12,()2x x y y ==数有哪些性质？要求：让学生自由发言，教师不做判断。

而是引导学生进一步观察.研探.二、预习课本，引入新课阅读课本116-117页，思考并完成以下问题1.结合指数函数的图象，可归纳出指数函数具有哪些性质？2.指数函数的图象过哪个定点？如何求指数型函数的定义域和值域问题？要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。

三、新知探究1、指数函数的图象和性质四、典例分析、举一反三题型一指数函数的图象问题题点一：指数型函数过定点问题例1函数y＝a x－3＋3(a＞0，且a≠1)的图象过定点________．【答案】(3,4)【解析】因为指数函数y＝a x(a＞0，且a≠1)的图象过定点(0,1)，所以在函数y＝a x－3＋3中，令x－3＝0，得x＝3，此时y＝1＋3＝4，即函数y＝a x－3＋3的图象过定点(3,4)．题点二：指数型函数图象中数据判断例2函数f(x)＝a x －b 的图象如图所示，其中a ，b 为常数，则下列结论正确的是( )A ．a ＞1，b ＜0B ．a ＞1，b ＞0C ．0＜a ＜1，b ＞0D.0＜a ＜1，b ＜0【答案】D【解析】从曲线的变化趋势，可以得到函数f(x)为减函数，从而有0＜a ＜1；从曲线位置看，是由函数y ＝a x (0＜a ＜1)的图象向左平移|－b|个单位长度得到，所以－b ＞0，即b ＜0.题点三：作指数型函数的图象例3画出下列函数的图象，并说明它们是由函数f(x)＝2x 的图象经过怎样的变换得到的．(1)y ＝2x ＋1；(2)y ＝－2x .【答案】见解析【解析】如图．(1)y ＝2x ＋1的图象是由y ＝2x 的图象向上平移1个单位长度得到的；(2)y ＝－2x 的图象与y ＝2x 的图象关于x 轴对称．解题技巧：（指数函数的图像问题）1.指数函数在同一平面直角坐标系中的图象的相对位置与底数大小的关系:在y 轴右侧,图象从上到下相应的底数由大变小;在y 轴左侧,图象从上到下相应的底数由小变大.无论指数函数的底数a 如何变化,指数函数y=ax(a>0,且a≠1)的图象与直线x=1相交于点(1,a),因此,直线x=1与各图象交点的纵坐标即为底数,由此可得底数的大小.2.因为函数y=ax 的图象恒过点(0,1),所以对于函数f(x)=kag(x)+b(k,a,b 均为常数,且k≠0,a>0,且a≠1).若g(m)=0,则f(x)的图象过定点(m,k+b).3.指数函数y=ax 与y=(1a )x(a>0,且a≠1)的图象关于y 轴对称.4.处理函数图象问题的常用方法:一是抓住图象上的特殊点;二是利用图象的变换;三是利用函数的奇偶性与单调性.跟踪训练一1、如图是指数函数:①y=a x,②y=b x,③y=c x,④y=d x的图象,则a,b,c,d 与1的大小关系是( )A.a<b<1<c<dB.b<a<1<d<cC.1<a<b<c<dD.a<b<1<d<c2、已知函数f(x)=a x+1+3的图象一定过点P,则点P 的坐标是 .3、函数y=的图象有什么特征?你能根据图象指出其值域和单调区间吗?【答案】1.B2.(-1,4)3.原函数的图象关于y 轴对称.由图象可知值域是(0,1],单调递增区间是(-∞,0],单调递减区间是(0,+∞).【解析】1、解析:(方法一)①②中函数的底数小于1且大于0,在y 轴右边,底数越小,图象向下越靠近x 轴,故有b<a,③④中函数的底数大于1,在y 轴右边,底数越大, 图象向上越靠近y 轴,故有d<c.故选B.(方法二)作直线x=1,与函数①,②,③,④的图象分别交于A,B,C,D 四点, 将x=1代入各个函数可得函数值等于底数值, 所以交点的纵坐标越大,则对应函数的底数越大. 由图可知b<a<1<d<c.故选B. 答案:B2、解析:∵当x+1=0,即x=-1时,f(x)=a 0+3=4恒成立,故函数f(x)=a x+1+3恒过(-1,4)点.3、解:∵y=(12)|x|={(12)x,x≥0,(12)-x ,x<0,∴其图象由y=(12)x(x≥0)和y=2x (x<0)的图象合并而成.||1()2x而y=(12)x(x>0)和y=2x(x<0)的图象关于y 轴对称,所以原函数的图象关于y轴对称.由图象可知值域是(0,1],单调递增区间是(-∞,0],单调递减区间是(0,+∞).题型二指数函数的性质及其应用题点一：比较两个函数值的大小例4比较下列各题中两个值的大小: （1）1.72.5与1.73 （2）0.8−√2与0.8−√3 （3）1.70.3与0.93.1【答案】(1)1.72.5<1.73(2)0.8−√2<0.8−√3（3）1.70.3>0.93.1【解析】(1)(单调性法)由于1.72.5与1.73的底数是1.7,故构造函数y=1.7x,而函数y=1.7x在R 上是增函数.又2.5<3,∴1.72.5<1.73(2)(单调性法)由于0.8−√2与0.8−√3的底数是0.8,故构造函数y=0.8x,而函数y=0.8x在R 上是减函数.又0.8−√2<0.8−√3（3）(中间量法)由指数函数的性质,知0.93.1<0.90=1,1.70.3>1.70=1,则1.70.3>0.93.1题点二：指数函数的定义域与值域问题例5求下列函数的定义域与值域 (1)y=21x−4; (2)y=(23)-|x|.【答案】(1)定义域为{x|x ∈R,且x≠4},值域为(0,1)∪(1,+∞). (2)定义域为R,值域为[1,+∞). 【解析】(1)∵由x-4≠0,得x≠4,∴函数的定义域为{x|x ∈R,且x≠4}.∵1x−4≠0,∴21x−4≠1.∴y=21x−4的值域为(0,1)∪(1,+∞).（2）函数的定义域为R.∵|x|≥0,∴y=(23)-|x|=(32)|x|≥(32)0=1.故y=(23)-|x|的值域为[1,+∞).解题技巧：（指数函数的性质及其应用） 1.函数y=af(x)(a>0,且a≠1)的定义域、值域:(1)定义域的求法.函数y=a f(x)的定义域与y=f(x)的定义域相同.(2)函数y=af(x)的值域的求法如下.①换元,令t=f(x); ②求t=f(x)的定义域x ∈D; ③求t=f(x)的值域t ∈M;④利用y=a t的单调性求y=a t(t ∈M)的值域. 2.比较幂的大小的常用方法:跟踪训练二1、比较下面两个数的大小: (a-1)1.3与(a-1)2.4(a>1,且a≠2). 2、比较下列各题中两个值的大小: ①2.53,2.55.7; ②1.5-7,(827)4;③2.3-0.28,0.67-3.1.【答案】1.当a>2时,(a-1)1.3<(a-1)2.4;当1<a<2时,(a-1)1.3>(a-1)2.4. 2.①2.53<2.55.7..②1.5-7>(827)4.③2.3-0.28<0.67-3.1.【解析】1、因为a>1,且a≠2,所以a-1>0,且a-1≠1, 若a-1>1,即a>2,则y=(a-1)x是增函数,∴(a-1)1.3<(a-1)2.4.若0<a-1<1,即1<a<2,则y=(a-1)x 是减函数,∴(a-1)1.3>(a-1)2.4. 故当a>2时,(a-1)1.3<(a-1)2.4; 当1<a<2时,(a-1)1.3>(a-1)2.4.2.①(单调性法)由于2.53与2.55.7的底数是2.5,故构造函数y=2.5x,而函数y=2.5x在R 上是增函数.又3<5.7,∴2.53<2.55.7. ②(化同底)1.5-7=(32)-7=(23)7,(827)4=[(23)3]4=(23)12,构造函数y=(23)x.∵0<23<1,∴y=(23)x 在R 上是减函数.又7<12,∴(23)7>(23)12,即1.5-7>(827)4. ③(中间量法)由指数函数的性质,知2.3-0.28<2.30=1,0.67-3.1>0.670=1,则2.3-0.28<0.67-3.1.五、课堂小结让学生总结本节课所学主要知识及解题技巧六、板书设计七、作业课本118页习题4.2 【教学反思】本节通过运用指数函数的图像及应用解决相关问题，侧重用实操，培养学生的逻辑思维能力，提高学生的数学素养.《4.2.2 指数函数的图像和性质》导学案【学习目标】知识目标1、掌握指数函数的图象和性质，培养学生实际应用函数的能力；2、通过观察图象，分析、归纳、总结指数函数的性质；3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.核心素养1.数学抽象：指数函数的图像与性质；2.逻辑推理：图像平移问题；3.数学运算：求函数的定义域与值域；4.数据分析：利用指数函数的性质比较两个函数值的大小：5.数学建模：通过由抽象到具体，由具体到一般的数形结合思想总结指数函数性质.【重点与难点】重点：指数函数的图象和性质；难点：对底数的分类，如何由图象、解析式归纳指数函数的性质．【学习过程】一、预习导入阅读课本111-113页，填写。

指数函数的图像与性质教案

指数函数的图像与性质教案一、教学目标1. 理解指数函数的定义和基本性质。

2. 能够绘制和分析指数函数的图像。

3. 掌握指数函数在实际问题中的应用。

二、教学内容1. 指数函数的定义与表达式指数函数是一种特殊类型的函数，形式为f(x) = a^x，其中a 是底数，x 是指数。

指数函数的定义域是所有实数，值域是正实数。

2. 指数函数的图像特点(1) 当a > 1 时，指数函数的图像上升。

(2) 当0 < a < 1 时，指数函数的图像下降。

(3) 指数函数的图像经过点(0, 1)。

3. 指数函数的性质(1) 单调性：当a > 1 时，指数函数单调递增；当0 < a < 1 时，指数函数单调递减。

(2) 指数函数的值域为正实数。

(3) 指数函数的图像具有无限多条切线，且切线斜率恒为a。

三、教学方法1. 采用问题驱动的教学方法，引导学生通过观察、分析和解决实际问题，深入理解指数函数的图像与性质。

2. 利用数学软件或图形计算器绘制指数函数的图像，帮助学生直观地感受指数函数的特点。

3. 设计具有挑战性的练习题，激发学生的思考和探索能力，巩固所学知识。

四、教学评估1. 通过课堂讲解、练习题和小组讨论，评估学生对指数函数定义、图像和性质的理解程度。

2. 布置课后作业，要求学生绘制指数函数的图像，并运用指数函数解决实际问题，以评估学生的应用能力。

3. 在课程结束后，进行一次小测验，检验学生对指数函数的整体掌握情况。

五、教学资源1. 教学PPT或教案文档，包含指数函数的定义、图像和性质的相关知识点。

2. 数学软件或图形计算器，用于绘制指数函数的图像。

3. 练习题和案例分析题，供学生巩固所学知识和应用实践。

六、教学步骤1. 引入指数函数的概念，引导学生思考指数函数在实际生活中的应用场景。

2. 讲解指数函数的定义与表达式，引导学生理解指数函数的基本形式。

3. 利用数学软件或图形计算器，绘制不同底数的指数函数图像，引导学生观察和分析指数函数的图像特点。

指数函数的图像和性质教案设计

指数函数的图像和性质教案设计第一章：指数函数的定义与性质1.1 指数函数的定义引导学生回顾函数的概念，引入指数函数的定义。

通过实际例子，让学生理解指数函数的形式和特点。

1.2 指数函数的性质分析指数函数的单调性，奇偶性，周期性等基本性质。

通过图表和实际例子，让学生直观地理解指数函数的性质。

第二章：指数函数的图像2.1 指数函数图像的特点引导学生绘制简单的指数函数图像，观察其特点。

分析指数函数图像的渐近线和拐点等特殊点。

2.2 指数函数图像的应用通过实际例子，让学生了解指数函数图像在实际问题中的应用，如人口增长、放射性衰变等。

第三章：指数函数的导数3.1 指数函数的导数公式引导学生回顾导数的基本概念，引入指数函数的导数公式。

通过例题和练习，让学生掌握指数函数的导数计算方法。

3.2 指数函数的单调性分析指数函数的单调性，引导学生理解导数与单调性的关系。

通过实际例子，让学生了解如何利用导数判断指数函数的单调性。

第四章：指数函数的极限4.1 指数函数的极限定义引导学生回顾极限的概念，引入指数函数的极限定义。

通过实际例子，让学生理解指数函数在趋近于无穷大或无穷小时的极限值。

4.2 指数函数的极限性质分析指数函数的极限性质，如单调性和连续性。

通过练习题，让学生掌握指数函数极限的计算方法。

第五章：指数函数的应用5.1 指数函数在实际问题中的应用通过实际例子，让学生了解指数函数在实际问题中的应用，如人口增长、放射性衰变等。

引导学生运用指数函数解决实际问题，培养学生的应用能力。

5.2 指数函数在其他学科中的应用引导学生了解指数函数在其他学科中的应用，如物理学中的放射性衰变、生物学中的种群增长等。

培养学生的跨学科思维和综合运用能力。

第六章：指数函数与对数函数的关系6.1 对数函数的定义引导学生回顾对数函数的概念，引入对数函数的定义。

通过实际例子，让学生理解对数函数的形式和特点。

6.2 指数函数与对数函数的关系分析指数函数与对数函数的互为反函数关系。

指数函数图像与性质

指数函数图像与性质吴昊学情分析学生已经学习过函数的基本概念和基本性质，函数的零点。

还学习过基本初等函数——幂函数。

熟悉幂函数的图像与性质。

教学目标1. 理解指数函数的意义2. 知道指数函数产生是由于实践的需要，并能对一些有关的实际问题列出指数函数关系式3. 会用描点法描出指数函数的图像，掌握指数函数图像的形状和位置4. 掌握指数函数的性质教学重难点重点：（1）指数函数的概念，指数函数的定义域（2）指数函数的图像与单调性难点：利用指数函数的性质，比较幂与1的大小教学过程（一）指数函数概念的引入通过细胞分裂的例子引入函数()2,x y x N *=∈老师：大家来看这样一个例子，一个细胞，一次分裂可以分裂为两个，如果经过x 次分裂，细胞一共有y 个，那么y 与x 的函数关系是什么？学生回答：()2,x y x N *=∈老师：大家观察，这个函数和我们之前学习过的一次函数，二次函数，反比例函数有什么异同？学生：这个函数只能定义在正整数上，并且自变量x 在指数上老师：我们能不能想办法把这个函数的定义域拓展一下？使它的定义扩大一些？学生：这个函数可以定义在有理数上,0,0m y x m n n ⎛⎫==>> ⎪⎝⎭，老师：那么我们可不可以让这种形式的函数定义在实数上呢？大家一起看屏幕。

屏幕上放出一组指数函数图像上的点老师：大家可以看到在作图时，随着描出的点的增多，这些点都近似地在一条光滑的曲线上！我们可以看到，这个曲线对应的函数与原来的函数()2,x y x Q =∈在自变量取值为有理数时有相同的函数值！也就是说，我们可以定义函数()2,x y x R =∈老师：那我们接着考虑，能不能把上面的函数推广？学生：可以把底数2换掉。

老师：我们现在给出指数函数的定义。

一般地，函数()(),,0,1x y a x R a a =∈>≠叫做指数函数，自变量x 作为指数，常数a 作为底数（二）指数函数概念的深化1. 我们可以看到对于底数的要求是：0,1a a >≠，为什么有这样的要求呢？学生讨论老师总结：首先指数式中底数是负数时，指数不能为某些数，比如12；而底数为0时，指数不能为0。

高中数学_指数函数的图象和性质教学设计学情分析教材分析课后反思

《指数函数的图象和性质》教学设计一、学习目标1.能画出具体指数函数的图象；2.观察指数函数图象，归纳出指数函数的性质，培养解决问题的能力3.通过观察图象、归纳总结指数函数性质的活动，让学生在数学活动中感受数学思想方法之美、体会数学思想方法之重要。

二、数学学科素养1.数学抽象：指数函数的图像与性质；2.逻辑推理：图像平移问题；3.数学运算：求函数的定义域与值域；4.数据分析：利用指数函数的性质比较两个函数值的大小：5.数学建模：通过由抽象到具体，由具体到一般的数形结合思想总结指数函数性质.三、教学重难点教学重点：指数函数的概念和性质.教学难点：用数形结合的方法从具体到一般地探索、概括指数函数的性质.四、教法与学法教学策略：小组合作讨论策略;讲练有效结合策略;自主探究式学习策略教学手段：多媒体化课件；几何画板3、借助几何画板画出xx x x x x y y y y y y ）（）（41,31,)21(,4,3,2====== 的图象，通过图象不同的变化趋势，可以将底数分为哪两类？底数分为a>1和0<a<14、观察图中的函数图象的位置，公共点，变化趋势，总结共同特征，小组分工分别讨论a>1和0<a<1的图象，汇报小组讨论结果，师生一起画出指数函数图象：)10(<<=a a y x )1(>=a a y x4、请同学们对照x a y =的图象，得出性质归纳：指数函数图象和性质图象，独立思考后回答。

观察图象，做出分类类比、探究，独立思考后由小组讨论，由小组派代表起来发言，说出发现的结果或规律。

由图象总结性质数两种不同的变化趋势，对指数函数分类研究做铺垫。

充分利用信息技术作图，学生对图象认识更加准确直观。

自然的将指数函数分为a>1和0<a<1两类。

让学生经历观察图象、发现规律的过程，目的是让学生通过对函数图象的观察与比较，归纳出指数函数中a 对图象的影响，同时培养学生数形结合地观察、思考5、课件出示：指数函数图象的性质6、完善学案上指数函数的图象与性质 10<<a1 a图象定义域值域性质学生一起回答问题的意识与能力。

指数函数的图像和性质教学设计 (2)

指数函数的图像和性质教课方案一、教材分析( 一 ) 教材的地位和作用本课时主要学习指数函数的图像和性质看法，经过指数函数图像的研究归纳其性质。

“指数函数”是函数中的一个重要基本初等函数，是后续知识——对数函数 ( 指数函数的反函数 ) 的准备知识。

本节课的要点是指数函数的图像及性质，难点在于弄清楚底数 a 关于函数变化的影响。

经过这部分知识的学习进一步深入学生对函数看法的理解与认识，使学生获取较系统的函数知识并领会研究函数较为完好的思想方法，其余还可类比学习后边的其余函数。

( 二) 教课目标知识维度：初中已经学习了正比率函数、反比率函数和一次函数，并对一次函数、二次函数作了更深入研究，学生已经初步掌握了研究函数的一般方法，可以从初中运动变化的角度认识函数初步转变到从会集与对应的看法来认识函数。

能力维度：学生利用描点法画出函数的图像，并描述出函数的图像特色，可以为研究指数函数的性质做好准备。

素质维度：由观察到抽象的数学活动过程已有必定的领会，已初步认识了数形联合的思想。

1、知识与技术目标：(1)掌握指数函数的看法 ( 能理解对 a 的限制以及自变量的取值可推行至实数范围 );(2)会做指数函数的图像 ;(3)能初步掌握指数函数的图像，性质及其简单应用。

2、过程与方法目标：经过由指数函数的图像归纳其性质的学习过程，由图像研究指数函数的性质。

利用性质解决实质问题，培育学生研究、归纳分析问题的能力。

3、感情态度与价值观目标：(1)在学习的过程中领会研究详尽函数及其性质的过程和方法，如体验从特殊到一般的学习规律，认识事物之间的广泛联系与互相转变，培育学生用联系的看法看问题(2)经过教课互动促进师生感情，激发学生的学习兴趣，提升学生抽象、概括、分析、综合的能力经过研究领会“数形联合”的思想 ; 感觉知识之间的关系性 ; 领会研究函数由特别到一般再到特别的研究学习过程 ; 体验研究函数的一般思想方法。

( 三 ) 教课要点和难点教课要点：指数函数的图象和性质。

指数函数的图像和性质

指数函数的图像和性质
指数函数是一种特殊函数，其定义域为实数集合R，值域也是实数集合R。

指
数函数的图像是一条弧线，朝右上方抛物线式延伸，底点在坐标原点处。

其图像如下所示：
指数函数具有以下性质：
一、指数函数是定义在实数集合上的单值函数，其图象是一条朝右上方延伸的
弧线，且在坐标原点处有底点，函数值随x增大而增大，函数图像上每一点到底点的距离都不变；
二、指数函数对任何正实数都有定义，指数函数f(x)=a^x（a为正实数）的图
谱具有单调性，当a的值不同时，指数函数的函数图象具有相似的特点；
三、指数函数具有不变性，不论x的取值范围如何，函数的函数图象仍不改变；
四、指数函数的切线斜率随着x的增大而增大；
五、指数函数的斜率在同一条线上增加或减少；
六、不论指数函数是升幂函数还是降幂函数，其图象都是从坐标原点开始，一
条朝右上方延伸的弧线。

以上就是指数函数的图像与性质，根据以上描述，指数函数的函数图像与以及
其性质可以得出：指数函数是从坐标原点开始，一条朝右上方延伸的弧线，有着单调性，不变性，切线斜率随着x的增大而增大等性质。