高斯投影坐标正算公式
第6章 高斯投影简介
（4）高斯平面投影的特点：
高斯平面直角坐标系与大地坐标系
1、高斯投影坐标正算公式
（1）高斯投影正算：已知椭球面上某点的大地坐标 L , B ，求该点 在高斯投影平面上的直角坐标 x , y ，即 L , B ( x , y ) 的坐标变换。 （2）投影变换必须满足的条件： 中央子午线投影后为直线； 中央子午线投影后长度不变； 投影具有正形性质，即正形投影条件。 （3）投影过程 在椭球面上有对称于中央子午线的两点 P1 和 P 2 ,它们的大地坐标 分别为（L , B）及（l , B ），式中 为椭球面上 P 点的经度与中央子 l 午线 ( L )的经度差： L L 0 , l 点在中央子午线之东, l 为正，在西 P 则为负，则投影后的平面坐标一定 P1( x , y ) 为 P2 ( x , y ) 和。
归算的内容
水平观测方向
地面长度归算
水平观测方向归算到椭球面
三差改正：水平方向归算到椭球面上，
需进行垂线偏差改正、标高差改正和截 面差改正，通常把这三项改正简称为三 差改正
① 垂线偏差改正（δu）
定义：地面上以铅垂线为准观测的水平方向值，归 算为以椭球面法线为准的水平方向值时，顾及测站 点垂线偏差的影响所加的改正
第六章 高斯投影简介
高斯投影概述
1、投影与变形
地图投影：就是将椭球面各元素（包括坐标、方向和长度）按一 定的数学法则投影到平面上。研究这个问题的专门学科叫地图投影 学。可用下面两个方程式（坐标投影公式）表示：
x F1 ( L , B ) y F2 ( L , B )
式中L,B是椭球面上某点的大地坐标，而是x,y该点投影后的平面直角 坐标。
f f
t
高斯投影高斯投影正算公式
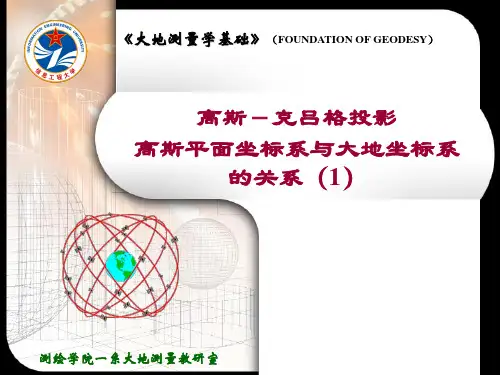
高斯－克吕格投影也称等角横切椭圆柱投 影，它可看作是等角圆柱投影（墨卡托投 影，1569）的一种，它由德国科学家高斯 处理三角测量成果时首先提出，后经克吕 格完善（1919） ，我国于1952年起正式采 用高斯－克吕格投影。
四个世纪以来，世界各国都用墨卡托投影作 为海图的数学基础。当代常用于较大比例尺 分幅海图或赤道附近的航空图。
《大地测量学基础》（FOUNDATION OF GEODESY）
高斯－克吕格投影 高斯平面坐标系与大地坐标系
的关系（1）
测绘学院一系大地测量教研室
上节课内容回顾
☺ 长度比？ m d s
dS
☺ 椭球面到平面的长度比在什么方 向取极值？
子午方向和卯酉方向 MNcosB
☺ 最大角度变形？ sin a b
② 分带的方法
1) 6°带划分 (n为带号 )
6°带中央子午线的经度计算公式 L0 6 n3
已知6°带中央子午线的经度反算带号
n
1 6
(L0
3
)
计算任意经度所在投影带的带号公式
nL的 整 数 商 （ 1有 余 数 时 ） 6
2、高斯投影的分带
Zone-dividing of Gauss Projection
② 分带的方法
2) 3°带划分 (n'为带号 )
3°带中央子午线的经度计算公式 L0 3 n
已知3°带中央子午线的经度反算带号 n L 0 3
计算任意经度所在投影带的带号公式 n L 1.5 1 3
③ UTM分带的方法
UTM的分带是从经度180°起向东每6°为一 带，即与国际百万分之一地形图的划分一致；
（135°02′30″）
南海南沙群岛的曾母 暗沙（3°52′）
高斯平面直角坐标与大地坐标的相互转换——高斯投影的正算与反算.
昆明冶金高等专科学校测绘学院 （4）计算公式
3 2 2 2 4 ( 5 3 t 9 t ) y f f f f 2M f N f 2 4M f N 3 f tf 2 4 6 (6 1 9 0t f 4 5t f ) y 7 2 0M f N 5 f 1 1 2 2 3 l y (1 2t f f ) y 3 N f co s B f 6 N f co s B f 1 2 5 (5 2 8t 2 t4 2 2 f 24 f 6 f 8 f t f )y 5 1 2 0N f co s B f B Bf tf y2 tf
式中：
2 e 2 cos2 B
t 2 tan2 B l （L L0） X为B对应子午线弧长 N为卯酉圈曲率半径 20626 5
昆明冶金高等专科学校测绘学院
2
高斯投影坐标反算公式
（1）高斯投影反算：
已知某点 x, y ，求该点 L, B ，即 x, y ( L, B) 的坐标变换。 （2）投影变换必须满足的条件
昆明冶金高等专科学校测绘学院
二、高斯投影坐标正反算得实用公式及算例
1 高斯投影坐标正算公式 （1）高斯投影正算： 已知某点的 L, B ，求该点的 x, y ，即 （2）投影变换必须满足的条件： 中央子午线投影后为直线； 中央子午线投影后长度不变； 投影具有正形性质，即正形投影条件。 （3）投影过程 在椭球面上有对称于中央子午线的两点 P1 和 P2 ,它们的大地坐标 分别为 ( L1 , B1 )或（l1 , B1）及 （L2 , B2）或(l2 , B2 ) 式中 l 为椭球面上点的经 度与中央子午线 ( L0 ) 的经度差：l L L0 ,点在中央子午线之东, l 为正，在西则为负，则投影后的平面坐标一定为P1 ( x1 , y1 ) 和 P2 ( x 2 , y 2 ) 。
高斯投影坐标计算
B
d B dq
2
dX dq dq
c
(
cos B dV V dB
2
dB dq
sin B dB V dq
2
)
2
d B dq
2
cos B c ( tan B V
2 2
3
V
sin B cos B
)
N sin B cos B
同理得
d X dq
3
N cos B ( 1
3
3
2
0
l
L
L
0
高斯投影坐标正算的函数式：
x y
l 是以弧度为单位的经度差。
F B , l F B , l
1 2
一 高斯投影坐标正算公式计算
如图，椭球面上一点投影 到平面后为d点，椭球面上 该点的平行圈（B或q为一 常数）与中央子午线的交 点为e点，若将上式中的展 开点z0设为e处，则很据高 斯投影条件，中央子午线 的长度比m=1，且纵坐标x 等于从赤道起到该平行圈 间的子午线弧长X。此时 可以写出下列方程：
4 2
二、高斯投影坐标反算公式
最后得到坐标反算的公式为：
B B
f
2M
f
t
f
y N
f
2
t 24 M
2 f
f
f
f
N
4 f
3 f
5 3 t
6
2 f
2 f
9 f t
2
2 f
y
4
t
高斯平面直角坐标系
大地测量学基础
4.9 高斯平面直角坐标系 三、高斯投影坐标正反算公式
（4）反算公式
当l＜3.5°时，上式换算精度达0.0001″。 欲使换算精确至0.01″，可对上式简化成：
大测量学基础
4.9 高斯平面直角坐标系 三、高斯投影坐标正反算公式
平 时 作 业 用编程进行高斯投影正反算。 已知
B 51 3843.9023 L 111 0213.1360
大地测量学基础
4.9 高斯平面直角坐标系 三、高斯投影坐标正反算公式
即有：
在数学上，F1为 l 的偶函数，F2为 l 的奇函数。 因为在每带中，l/ρ˝不大，是一个微小量，可展成幂级 数。
m０，ｍ１，ｍ２，…，是待定系数，它们都是纬度B的函 数。
大地测量学基础
4.9 高斯平面直角坐标系 三、高斯投影坐标正反算公式
大地测量学基础
4.9 高斯平面 直角坐标系
大地测量学基础
4.9 高斯平面直角坐标系 三、高斯投影坐标正反算公式
三、高斯投影坐标正反算公式 1、高斯投影坐标正反算的定义 （1）高斯投影正算： 已知椭球面上某点的大地坐标B、L，求其 该点在高斯平面直角坐标系中的坐标x、y的工作 叫高斯投影正算。 （2）高斯投影反算： 已知椭球面上某点在高斯平面直角坐标系中 的坐标x、y，求其该点的大地坐标B、L的工作 叫高斯投影反算。
大地测量学基础
4.9 高斯平面直角坐标系 三、高斯投影坐标正反算公式
（3）反算公式推导思路： 和正算公式基本一样，也是根据高斯投影的3个条件来 推导的。 ①由对称条件，同样可得： 把B、l 展成y的幂级数，而φ1为y的偶函数， φ2为y的奇 函数。
式中 n ０ ，ｎ １ ，ｎ ２ … 是待定系数，它们都是纵坐标 x 的函数 ,与y无关。
第四章 7高斯投影坐标正反算
——正形投影的一般条件 ——高斯投影坐标正算 ——高斯投影坐标反算 ——高斯投影几何解释
提前在黑板上写出四个m2
上一讲应掌握的内容
1、地图(数学)投影：将椭球面上元素(包括坐标，方位和 距离)按一定的数学法则投影到可展平面上。 x F1 ( L, B) 坐标投影公式： y F2 ( L, B) 2、地图投影变形几个概念： 长度比，主方向，变形椭圆 3、四种投影变形： 长度变形，方向变形，角度变形，面积变形
x m0 m 2 l 2 m 4 l 4 y m1l m3 l 3 m5 l 5
分别对l 和q 求偏导数
2) 由第三个条件正形投影条件
y x x y 和 l q l q
dm0 dm2 2 dm4 4 2 4 m1 3m3 l 5m5 l dq dq l dq l 2m l 4m l 3 dm1 l dm3 l 3 ）
将各系数代入，略去高次项，得高斯投影坐标正算公式 精度为0.001m
xX N N sin B cos Bl 2 + sin B cos 3 B(5 - t 9 2 4 4 )l 4 + 2 24
N sin B cos 5 B(61 - 58t 2 t 4 )l 6 720
dl tan Adq
2 2 2 2 E ( dq ) 2 F tan A ( dq ) G tan A ( dq ) m2 2 2 2 r2 ( dq ) tan A ( dq )
E 2 F tan A G tan 2 A = r 2 sec 2 A E cos 2 A 2 F sin A cos A G sin 2 A = r2
大地坐标BLH转平面坐标xyh（高斯投影坐标正算）Java版
⼤地坐标BLH转平⾯坐标xyh（⾼斯投影坐标正算）Java版技术背景 做过位置数据处理的⼩伙伴基本上都会遇到坐标转换，⽽基于⾼斯投影原理的⼤地坐标转平⾯坐标就是其中⼀种坐标转换，坐标转换的⽬的就是⽅便后⾯数据的处理⼯作，⼤地坐标转⾼斯平⾯坐标常⽤的有两种，即3°带和6°带，具体采⽤哪种根据实际情况⽽定。
计算原理 6°带带号n与相应的中央⼦午线L0经度的关系为： 3°带带号n’与相应的中央⼦午线L0’经度的关系为： 设参考椭球的长半轴为 a，第⼀偏⼼率为 e，并令： 设中央⼦午线的经度为 L0，再记： 则⾼斯投影正算公式为： 其中： 没学过测绘的同学对以上原理不是很理解，也很正常，⼤家可以查阅相关《⼤地测量学》书籍，具体武⼤版还是矿⼤版的，没什么区别。
具体实现 具体实现平台依然是IBM的Eclipse软件，编程语⾔为Java，下⾯是以3°带为例，进⾏⾼斯投影坐标正算，具体内容请看代码1package package1;23public class BLH_xyh {45public static double a = 6378137;6public static double e = Math.sqrt(0.0066943799013);7public static double scale_wide = 3;8public static doubleπ = 3.14159265358979323846;910public static void main(String[] args) {11// TODO ⾃动⽣成的⽅法存根12 Point3d xyh = the_coordinates_are_counting(36.0307523111,120.184664478,9.7065);13 System.out.println(xyh.getX()+","+xyh.getY()+","+xyh.getZ());14 }15public static Point3d the_coordinates_are_counting(double B,double L,double H){16double A_ = 117 +3*e*e/418 +45*e*e*e*e/6419 +175*e*e*e*e*e*e/25620 +11025*e*e*e*e*e*e*e*e/1638421 +43659*e*e*e*e*e*e*e*e*e*e/65536;22double B_ = 3*e*e/4+15*e*e*e*e/1623 +525*e*e*e*e*e*e/51224 +2205*e*e*e*e*e*e*e*e/204825 +72765*e*e*e*e*e*e*e*e*e*e/65536;26double C_ = 15*e*e*e*e/6427 +105*e*e*e*e*e*e/25628 +2205*e*e*e*e*e*e*e*e/409629 +10395*e*e*e*e*e*e*e*e*e*e/16384;30double D_ = 35*e*e*e*e*e*e/51231 +315*e*e*e*e*e*e*e*e/204832 +31185*e*e*e*e*e*e*e*e*e*e/13072;33/*34 double E_ = 315*e*e*e*e*e*e*e*e/1638435 +3465*e*e*e*e*e*e*e*e*e*e/65536;36 double F_ = 693*e*e*e*e*e*e*e*e*e*e/13072;37 */3839doubleα = A_*a*(1-e*e);40doubleβ = -B_*a*(1-e*e)/2;41doubleγ = C_*a*(1-e*e)/4;42doubleδ = -D_*a*(1-e*e)/6;43/*44 double ε = E_*a*(1-e*e)/8;45 double ζ = -F_*a*(1-e*e)/10;46 */4748double C0 = α;49double C1 = 2*β+4*γ+6*δ;50double C2 = -8*γ-32*δ;51double C3 = 32*δ;5253double x,y,sign;54double scale_number = Math.floor(L/scale_wide);55if(L > (scale_number * scale_wide + scale_wide/2)){56 scale_number =scale_number + 1;57 sign = -1;58 }else{59 sign = 1;60 }6162double L0 = scale_wide*scale_number;63double l = Math.abs(L-L0);64 B = B*π/180;65 l = l*π/180;66double t = Math.tan(B);67double m0 = Math.cos(B)*l;68doubleη = Math.sqrt(e*e*Math.pow(Math.cos(B),2)/(1-e*e));69double N = a/Math.sqrt(1-e*e*Math.pow(Math.sin(B), 2));7071double X0 = C0*B+Math.cos(B)*(C1*Math.sin(B)+C2*Math.pow(Math.sin(B),3)+C3*Math.pow(Math.sin(B), 5));7273 x = X074 +N*t*m0*m0/275 +N*t*m0*m0*m0*m0*(5-t*t+9*η*η+4*η*η*η*η)/2476 +N*t*m0*m0*m0*m0*m0*m0*(61-58*t*t+t*t*t*t)/720;77 y = N*m0+78 N*m0*m0*m0*(1-t*t+η*η)/6+79 N*m0*m0*m0*m0*m0*m0*(5-18*t*t+t*t*t*t+14*η*η-58*η*η*t*t)/120;8081 y = y*sign+500000;8283double h = H;8485 Point3d xyh = new Point3d(x,y,h);86return xyh;87 }88 }其中Point3d的定义如下：1package package1;23public class Point3d {4private double x;5private double y;6private double z;7public Point3d(double x,double y,double z){8this.x=x;9this.y=y;10this.z=z;11 }12public double getX() {13return x;14 }15public void setX(double x) {16this.x = x;17 }18public double getY() {19return y;20 }21public void setY(double y) {22this.y = y;23 }24public double getZ() {25return z;26 }27public void setZ(double z) {28this.z = z;29 }30 }测试数据为36.0307523111,120.184664478,9.7065，运⾏结果如下：⾄此结束致谢 感谢⼭东科技⼤学北⽃星光创客兴趣学习⼩组的王⽼师对于原理⽂档的整理以及郑** C++代码的技术分享！参考⽂档1、⼭东科技⼤学”北⽃星光创客”兴趣学习⼩组GNSS技术⽂档。
1 高斯投影坐标正算公式
1 高斯投影坐标正算公式（1）高斯投影正算：已知椭球面上某点的大地坐标，求该点在高斯投影平面上的直角坐标，即的坐标变换。
（2）投影变换必须满足的条件中央子午线投影后为直线；中央子午线投影后长度不变；投影具有正形性质，即正形投影条件。
（3）投影过程在椭球面上有对称于中央子午线的两点和,它们的大地坐标分别为（）及（），式中为椭球面上点的经度与中央子午线的经度差：, 点在中央子午线之东, 为正，在西则为负，则投影后的平面坐标一定为和。
（4）计算公式当要求转换精度精确至0.OOlm时，用下式计算：2 高斯投影坐标反算公式（1）高斯投影反算：已知某点的高斯投影平面上直角坐标，求该点在椭球面上的大地坐标，即的坐标变换。
（2）投影变换必须满足的条件坐标轴投影成中央子午线，是投影的对称轴；轴上的长度投影保持不变；投影具有正形性质，即正形投影条件。
（3）投影过程根据计算纵坐标在椭球面上的投影的底点纬度，接着按计算（）及经差，最后得到、。
（4）计算公式当要求转换精度至时，可简化为下式：3高斯投影相邻带的坐标换算（1）产生换带的原因高斯投影为了限制高斯投影的长度变形，以中央子午线进行分带，把投影范围限制在中央子午线东、西两侧一定的范围内。
因而，使得统一的坐标系分割成各带的独立坐标系。
在工程应用中，往往要用到相邻带中的点坐标，有时工程测量中要求采用带、带或任意带，而国家控制点通常只有带坐标，这时就产生了带同带（或带、任意带）之间的相互坐标换算问题，如图所示：（2）应用高斯投影正、反算公式间接进行换带计算计算过程把椭球面上的大地坐标作为过渡坐标。
首先把某投影带（比如Ⅰ带）内有关点的平面坐标，利用高斯投影反算公式换算成椭球面上的大地坐标，进而得到；然后再由大地坐标，利用投影正算公式换算成相邻带的（第Ⅱ带）的平面坐标。
在这一步计算时，要根据第Ⅱ带的中央子午线来计算经差，亦即此时。
算例在中央子午线的Ⅰ带中，有某一点的平面直角坐标，，现要求计算该点在中央子午线的第Ⅱ带的平面直角坐标。
高斯投影坐标计算
本节要点提要
1、高斯投影坐标正算公式 2、高斯投影坐标反算公式 3、高斯投影坐标正算的数值公式 4、高斯投影坐标反算的迭代计算公式
地图投影的分类
• 按投影变形性质分类: 等角投影 等距投影 等积投影
a=b
• 按投影面分类 : 圆锥面 正轴投影 切投影
a=1 or b=1
圆柱(椭圆柱) 面 横轴投影 割投影
(1)中央子午线投影后为直线； (2)中央子午线投影后长度不变； (3)投影具有正形性质，即正形投影 条件。
高斯投影坐标正算
l =3／ρ=0.052
1) 由第一个条件（中央子午线投影后为直线） 可知，由于地球椭球体是一个旋转椭球体，即 中央子午线东西两侧的投影必然对称于中央子 午线。 x 为 l 的偶函数，而y 则为 l 的奇函数。
由恒等式两边对应系数相等，建立求解待定系数的递推公式
d m d m d m 1 1 0 1 m m m = 2 1 2 3 d q 2 d q 3 d q
m0=?
３) 由第二条件（中央子午线投影后长度不变）可 知，位于中央子午线上的点，投影后的纵坐标 x 应 该等于投影前从赤道量至该点的子午弧长。
Байду номын сангаас
a· b=1
平面投影 斜轴投影
• 按投影的中心轴线: • 按椭球面与投影面的切割情况分:
高斯投影特性（三个）： – 中央子午线投影后为一直线，且长度不变； 其它经线为凹向中央子午线的曲线，且长 度改变。 – 投影后，赤道为一直线，但长度改变，其 它纬线呈凸向赤道的曲线。 – 投影后，中央子午线与赤道线正交，经线 与纬度也互相垂直，即高斯投影为等角投 影。
将各系数代入，略去高次项，得高斯投影 坐标正算公式精度为0.001m
高斯投影正反算
高斯投影正反算学院：资源与环境工程工程学院专业：测绘工程 学号：X51414012 姓名：孙超一、高斯投影概述想象有一个椭圆柱面横套在地球椭球体外面，并与某一条子午线相切，椭圆柱的中心轴通过椭球体的中心，然后用一定投影方法，将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上，再将此柱面展开即成为投影面。
高斯投影由于是正形投影，故保证了投影的角度不变性，图形的相似性以及在某点各方向上长度比的同一性。
由于采用了同样法则的分带投影，这即限制了长度变形，又保证了在不同投影带中采用相同的简便公式和数表进行变形引起的各项改正的计算，并且带与带间的互相换算也能用相同的公式和方法进行。
高斯投影的这些优点必将使它得到广泛的推广和具有国际意义。
二、高斯投影坐标正算公式1.高斯投影必须满足以下三个条件 1）中央子午线投影后为直线 2）中央子午线投影后长度不变 3）投影具有正形性质，即正形投影条件2.高斯正算公式推导1）由第一个条件可知，由于地球椭球体是一个旋转椭球体，所以高斯投影必然有这样一个性质，即中央子午线东西两侧的投影必然对称于中央子午线。
2）由于高斯投影是换带投影，在每带内经差ｌ是不大的，ｌρ是一个微小量，所以可以将X=X （ｌ，q ），Y=Y （l ，q ）展开为经差为l 的幂级数，它可写成如下的形式X=m 0+m 2l 2+m 4l 4+…Y=m 1l+m 3l 2+m 5l 5+…式中m 0,m1,m2,…是待定系数，他们都是纬度B 的函数。
3）由第三个条件：∂y ∂l =∂x ∂q 和∂x ∂l =-∂y∂q ，将上式分别对l 和q 求偏导2340123423401234...........x m m l m l m l m l y n n l n l n l n l =+++++=+++++可得到下式0312123403121234111,,,, 234111,,,,234dm dm dm dm n n n n dq dq dq dq dn dn dn dn m m m m dq dq dq dq ⎧====⎪⎪⎨⎪=-=-=-=-⎪⎩经过计算可以得出232244524632235242225sin cos sin cos (594)224 sin cos (6158)720cos cos (1)6cos (5181458)120N N x X B B l B B t l NB B t t l Ny N B l B t l NB t t t l ηηηηη=+⋅+-+++-+=⋅+-++-++-三、高斯投影坐标反算公式推导1.思路：级数展开，应用高斯投影三个条件，待定系数法求解。
(完整版)高斯投影正反算
高斯投影正反算学院：资源与环境工程工程学院专业：测绘工程学号：X51414012姓名：孙超一、高斯投影概述想象有一个椭圆柱面横套在地球椭球体外面，并与某一条子午线相切，椭圆柱的中心轴通过椭球体的中心，然后用一定投影方法，将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上，再将此柱面展开即成为投影面。
高斯投影由于是正形投影，故保证了投影的角度不变性，图形的相似性以及在某点各方向上长度比的同一性。
由于采用了同样法则的分带投影，这即限制了长度变形，又保证了在不同投影带中采用相同的简便公式和数表进行变形引起的各项改正的计算，并且带与带间的互相换算也能用相同的公式和方法进行。
高斯投影的这些优点必将使它得到广泛的推广和具有国际意义。
二、高斯投影坐标正算公式1.高斯投影必须满足以下三个条件1）中央子午线投影后为直线2）中央子午线投影后长度不变3）投影具有正形性质，即正形投影条件2.高斯正算公式推导1）由第一个条件可知，由于地球椭球体是一个旋转椭球体，所以高斯投影必然有这样一个性质，即中央子午线东西两侧的投影必然对称于中央子午线。
2）由于高斯投影是换带投影，在每带内经差ｌ是不大的，ｌρ是一个微小量，所以可以将 X=X （ｌ，q ），Y=Y （l ，q ）展开为经差为l 的幂级数，它可写成如下的形式X=m 0+m 2l 2+m 4l 4+…Y=m 1l+m 3l 2+m 5l 5+…式中m 0,m1,m2,…是待定系数，他们都是纬度B 的函数。
3）由第三个条件：∂y ∂l =∂x ∂q 和∂x ∂l =-∂y ∂q ，将上式分别对l 和q 求偏导2340123423401234...........x m m l m l m l m l y n n l n l n l n l =+++++=+++++可得到下式0312123403121234111,,,, 234111,,,,234dm dm dm dm n n n n dq dq dq dq dn dn dn dn m m m m dq dq dq dq ⎧====⎪⎪⎨⎪=-=-=-=-⎪⎩L L 经过计算可以得出232244524632235242225sin cos sin cos (594)224sin cos (6158)720cos cos (1) 6cos (5181458)120N N x X B B l B B t l N B B t t l N y N B l B t l N B t t t l ηηηηη=+⋅+-+++-+=⋅+-++-++-三、高斯投影坐标反算公式推导1.思路：级数展开，应用高斯投影三个条件，待定系数法求解。
「高斯投影坐标正反算公式及适合电算的高斯投影公式」
「高斯投影坐标正反算公式及适合电算的高斯投影公式」高斯投影坐标正反算公式是用于计算高斯投影坐标的数学公式。
高斯投影坐标是一种地理坐标系统，常用于测量和测绘工作中。
高斯投影坐标正算是指已知一个点的经纬度坐标，通过公式计算出该点的高斯投影坐标。
而高斯投影坐标反算是指已知一个点的高斯投影坐标，通过公式计算出该点的经纬度坐标。
一、高斯投影坐标正算公式：已知一个点的经纬度坐标(φ,λ)，其中φ为纬度，λ为经度，以及椭球体参数a、f和中央经线经度L0，可以通过以下步骤计算出该点的高斯投影坐标(X,Y)：1.计算扁率f'：f'=(a-b)/a其中，b=a*(1-f)是椭球体的短半轴。
2.计算黄赤交角ε：ε = atan(b / a)3.计算辅助量t：t = tan(π/4 - φ/2) / [(1 - f' * sin²φ)⁰.⁵ * (1 + e' *sinφ)⁰.⁵]其中，e'=f'*(2-f')是椭球体的第一偏心率。
4.计算辅助量η：η = e'^2 * cos²φ5.计算系数A、B、C和D：A = (L - L0) * cosφC = (L - L0) * cos⁵φ * (5 - tan²φ + 9e'^² + 4e'^⁴ - 24e'^² * tan²φ - 45e'^⁴ * tan²φ)D = (L - L0) * cos⁷φ * (61 - 58tan²φ + tan⁴φ + 270e'^² - 330e'^² * tan²φ)6.计算高斯坐标X和Y：X=k0*a*(A+B/2+C/4+D/6)Y=k0*a*(C/2+D/8)其中，k0是比例系数，一般情况下取1二、高斯投影坐标反算公式：已知一个点的高斯投影坐标(X,Y)，以及椭球体参数a、f、中央经线经度L0、比例系数k0和起始经度L1，可以通过以下步骤计算出该点的经纬度坐标(φ,λ)：1.计算扁率f'：f'=(a-b)/a其中，b=a*(1-f)是椭球体的短半轴。
第20次课-高斯投影坐标正算公式
高斯投影的概念，即高斯投影必须满足的三个条件： （1）中央子午线投影后为直线（纵坐标轴） （2）中央子午线投影后长度不变 （3）正形投影 由第一个条件得： P1 (l , B) P2 (l , B)
P 1 ' ( x, y )
P2 ' ( x, y)
x x(q, l )，y y(q, l )
6带中央子午线： L 0 6n6 3 3带中央子午线： L 0 3n3 经度差（到中央子午线 的距离）l L L0
L 6带： n6 int 1 6 L 3带： n3 int 0.5 3
2、根据椭球选择计算子午弧长公式 克拉索夫斯基椭球上（54北京坐标系）
04sin833162sin52816038005111133??1975年国际椭球上80西安坐标系克拉索夫斯基椭球上54北京坐标系3计算正算公式中的各符号的值2vcnwanbttanbe22cosbew22sin1?4代入正算公式计算高斯平面坐标5对y的值进行加工正算公式计算出的自然值500公里前面冠以带号54255322334223422185bcos1201cos6cos95bcossin24cossin2lttnltbnlbnyltbnlbbnxx????高斯投影坐标正算高精度公式bl?xyb??????????864286222426442242254331111385cos403203302705861cos720495cos24cos2tttbnttttbnttbntbntly??????????764275222425322317947961cos504015814185cos12011cos61costttbntttbntbnbnx小结?正算公式的推导思路
高斯投影正反算公式83
§8.3高斯投影坐标正反算公式任何一种投影①坐标对应关系是最主要的；②如果是正形投影，除了满足正形投影的条件外（C-R 偏微分方程），还有它本身的特殊条件。
8.3.1高斯投影坐标正算公式： B, x,yl ⇒高斯投影必须满足以下三个条件：①中央子午线投影后为直线；②中央子午线投影后长度不变；③投影具有正形性质，即正形投影条件。
由第一条件知中央子午线东西两侧的投影必然对称于中央子午线，即(8-10)式中，x 为的偶函数，y 为的奇函数；，即，l l 0330'≤l 20/1/≈''''ρl 如展开为的级数，收敛。
l （8-33）+++=++++=553316644220l m l m l m y l m l m l m m x 式中是待定系数，它们都是纬度B 的函数。
,,10m m 由第三个条件知：qyl x l y q x ∂∂-=∂∂∂∂=∂∂,(8-33)式分别对和q 求偏导数并代入上式l (8-34)----=++++++=+++5533156342442204523164253l dqdm l dq dm l dq dm l m l m l m l dqdm l dq dm dq dm l m l m m 上两式两边相等，其必要充分条件是同次幂前的系数应相等，即l(8-35)dq dm m dqdm m dqdm m 2312013121⋅=⋅-==(8-35)是一种递推公式，只要确定了就可依次确定其余各系数。
0m 由第二条件知:位于中央子午线上的点，投影后的纵坐标x 应等于投影前从赤道量至该点的子午线弧长X ，即(8-33)式第一式中，当时有：0=l(8-36)0m X x==顾及(对于中央子午线)B V Mr M B N dq dB M dBdXcos cos 2====得：(8-37,38) B Vc B N r dq dB dB dX dq dX dq dm m cos cos 01===⋅===(8-39)B B Ndq dB dB dm dq dm m cos sin 22121112=⋅-=⋅-=依次求得并代入(8-33)式，得到高斯投影正算公式6543,,,m m m m6425644223422)5861(cos sin 720)495(cos 24cos sin 2lt t B B N lt B simB N l B B N X x ''+-''+''++-''+''⋅''+=ρηηρρ (8-42)5222425532233)5814185(cos 120)1(cos 6cos l t t t B N lt B N l B N y ''-++-''+''+-''+''⋅''=ηηρηρρ8.3.2高斯投影坐标反算公式x,y B,⇒l投影方程：(8-43)),(),(21y x l y x B ϕϕ==满足以下三个条件：①x 坐标轴投影后为中央子午线是投影的对称轴；② x 坐标轴投影后长度不变；③投影具有正形性质，即正形投影条件。
高斯投影及换带计算
x
y
o
500km
=500000+ = 636780.360m = 500000+ = 227559.720m
国家统一坐标：
（带号）
（带号）
例：有一国家控制点的坐标:x=3102467.280m ,y=19367622．380m，（1）该点位于6˚ 带的第几带？（2）该带中央子午线经度是多少？（3）该点在中央子午线的哪一侧？ （4）该点距中央子午线和赤道的距离为多少？
3)、高斯投影的特点:
（1）中央子午线投影后为直线，且长度不变。（2） 除中央子午线外，其余子午线的投影均为凹向中央子午线的曲线，并以中央子午线为对称轴。投影后有长度变形。（3） 赤道线投影后为直线，但有长度变形。
赤道
中央子午线
平行圈
子午线
O
x
y
（4） 除赤道外的其余纬线，投影后为凸向赤道的曲线，并以赤道为对称轴。（5）经线与纬线投影后仍然保持正交。 （6） 所有长度变形的线段，其长度变形比均大于l。（7）离中央子午线愈远，长度变形愈大。
工程测量采用3 º带，特殊工程可采用1.5 º带或任意带
按照6º带划分的规定，第1带中央子午线的经度为3º，其余各带中央子午线经度与带号的关系是： L。=6ºN－3º （N为6º带的带号） 例：20带中央子午线的经度为： L。＝6º× 20－3º＝117 º 按照3º带划分的规定，第1带中央子午线的经度为3º，其余各带中央子午线经度与带号的关系是： L。=3ºn （n为3º带的带号） 例：120带中央子午线的经度为 L。＝3º× 120＝360 º
2、高斯投影坐标反算公式：x,y B,l
满足以下三个条件：①x坐标轴投影后为中央子午线是投影的对称轴；② x坐标轴投影后长度不变；③投影具有正形性质，即正形投影条件。
高斯平面直角坐标系与大地坐标系相互转化
高斯平面直角坐标系与大地坐标系相互转化高斯平面直角坐标系与大地坐标系转换 1. 高斯投影坐标正算公式(1) 高斯投影正算:已知椭球面上某点的大地坐标(L，B)，求该点在高斯投影平面上的直角坐标(x，y)，即(L，B)->(x，y)的坐标变换。
(2) 投影变换必须满足的条件中央子午线投影后为直线; 中央子午线投影后长度不变; 投影具有正形性质，即正形投影条件。
(3) 投影过程在椭球面上有对称于中央子午线的两点P 1 和P 2 ，它们的大地坐标分别为(L，B)及(l，B)，式中l 为椭球面上P 点的经度与中央子午线(L 0 )的经度差:l=L-L 0 ，P 点在中央子午线之东，l 为正，在西则为负，则投影后的平面坐标一定为P 1 ’(x,y)和P 2 ’(x,-y)。
(4) 计算公式 4 ' ' 2 2 3 4 ' ' 2 ' ' 2 ' ' ) 9 5 ( cos sin 2 sin 2 l t B B N Bl N X x 5 ' ' 4 2 5 5 ' ' 3 ' ' 2 2 3 ' ' ' ' ' ' ) 18 5 ( cos 120 ) 1 ( 6 cos l t t B N l t B N Bl N y 当要求转换精度精确至0.001m时，用下式计算: 6 ' ' 4 2 5 6 ' ' 4 ' ' 4 2 2 3 4 ' ' 2 ' ' 2 ' ' ) 58 61 ( cos sin 720 ) 4 9 5 ( cos sin 24 sin 2 l t t B B N l t B B N Bl N X x5 ' ' 2 2 2 4 2 5 5 ' ' 3 ' ' 2 2 3 3 ' ' ' ' ' ' ) 58 14 18 5 ( cos 720 ) 1( cos 6 cos l t t t B N l t B N Bl N y2. 高斯投影坐标反算公式(1) 高斯投影反算:已知某点的高斯投影平面上直角坐标(x,y)，求该点在椭球面上的大地坐标(L,B)，即(x,y)->(L,B)的坐标变换。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高斯投影坐标正算公式
高斯投影坐标正反算公式
2.2.2. 1高斯投影坐标正算公式： B, x,y
高斯投影必须满足以下三个条件：
⑴中央子午线投影后为直线；⑵中央子午线投影后长度不变；⑶投影具有正形性质，即正形投影条件。
由第一条件知中央子午线东西两侧的投影必然对称于中央子午线，即
式中，x为的偶函数，y为的奇函数；，即，
如展开为的级数，收敛。
（2-10）
式中是待定系数，它们都是纬度B的函数。
由第三个条件知：
分别对和q求偏导数并代入上式
(2-11)
上两式两边相等，其必要充分条件是同次幂前的系数应相等，即
(2-12)
(2-12)是一种递推公式，只要确定了就可依次确定其余各系数。
由第二条件知:位于中央子午线上的点，投影后的纵坐标x应等于投影前从赤道量至该点的子午线弧长X，即(2-10)式第一式中，当时有：
(2-13)
顾及(对于中央子午线)
得：
(2-14,15)
(2-16)
依次求得并代入(2-10)式，得到高斯投影正算公式
(2-17)
2.2.2. 2高斯投影坐标反算公式
x,y B,
投影方程：
(2-18)
高斯投影坐标反算公式推导要复杂些。
⑴由x求底点纬度(垂足纬度),对应的有底点处的等量纬度，求x,y与
的关系式，仿照式有，
由于y和椭球半径相比较小(1/16.37)，可将展开为y的幂级数；又由于是对称投影，q必是y的偶函数，必是y的奇函数。
(2-19)
是待定系数，它们都是x的函数.
由第三条件知：
，
， (2-20)
(2-19)式分别对x和y求偏导数并代入上式
上式相等必要充分条件，是同次幂y前的系数相等，
第二条件，当y=0时，点在中央子午线上，即x=X，对应的点称为底点，其纬度为底点纬度，也就是x=X时的子午线弧长所对应的纬度，设所对应的等量纬度为。
也就是在底点展开为y的幂级数。
由(2-19)1式
依次求得其它各系数
(2-21)
(2-21)1
…………
将代入(2-19)1式得
(2-22)1
(2-22)
将代入(2-19)2式得(2-23)2式。
(最后表达式) ⑵求与的关系。
由式知：
(2-23)
(2-24)
按台劳级数在展开
(2-25)
(2-25) 由式可求出各阶导数：
(2-26)
(2-27)1
(2-27)2
…………………
将式(2-22)1(2-22)(2-26)(2-27)入(2-25)并按y幂集合得高斯投影坐标反算公式(2-28)
(2-28)
归纳由求的基本思想：由点得到底点，将底点f作为过渡，也就是说将坐标原点o移到f点，先求关系式，再将
关系式代入关系式得关系式，最后将坐标原点移回到o点,从而求得点。
2.2.2. 3高斯投影坐标正反算公式的几何解释：
（图4：高斯投影坐标正反算公式的几何解释示意图）
⑴当B=0时x=X=0，y则随的变化而变化，这就是说，赤道投影
为一直线且为y轴。
当=0时,则y=0,x=X,这就是说，中央子午线投影亦为直线，且为x轴，其长度与中央子午线长度相等。
两轴的交点为坐标原点。
⑵当=
常数时(经线),随着B值增加，x值增大，y值减小，这就告诉我们，经线是凹向中央子午线的曲线，且收敛于两极。
又因，即当用-B代替B时，y 值不变，而x值数值相等符号相反，这就说明赤道是投影的对称轴。
⑶当B=常数时(纬线)，随着的增加，x值和y值都增大，这就是说，纬线是凸向赤道的曲线。
又当用-代替时，x值不变，而y值数值相等符号相反，这就说明，
中央子午线是投影对称轴。
由于满足正形投影条件，所以经线和纬线的投影是互相垂直的。
⑷距中央子午线愈远的子午线，投影后弯曲愈厉害，表明长度变形愈大。