平面曲线的弧长
定积分的应用平面曲线弧长课件

参数方程的转换
参数方程转换为普通方程
将参数方程中的参数t消除,将参数方程转换为普通方程。
参数方程的微分形式
将参数方程转换为微分形式,以便于计算曲线的切线斜率和 弧长。
03 定积分在平面曲线弧长中 的应用
理论完善
随着定积分在平面曲线弧长中的应用越来越广泛,其理论体系也可能会得到进一步完善。例如,可能会发现新的定理 和公式,以更好地描述和解决定积分问题。
应用领域的拓展
随着科技的不断发展,定积分的应用领域也可能会进一步拓展。例如,在人工智能、机器学习等领域中, 定积分可能会被用来解决一些新的问题。
定积分在平面曲线弧长中的实际价值
弧长公式的应用
计算特定曲线的弧长
利用弧长公式,可以计算出给定参数 方程的曲线上任意一段弧的长度。这 迹的长度 等。
比较不同曲线的长度
通过比较不同曲线的弧长,可以得出 它们之间的形状差异。例如,可以利 用弧长公式比较不同函数的图像长度。
弧长公式的拓展
弧长公式的推导
弧长公式的基本概念
弧长公式是定积分的一个重要应用,它用于计算平面曲线上某段弧的长度。在推 导弧长公式之前,需要了解曲线的基本参数方程和弧长的定义。
弧长公式的推导过程
通过将曲线分割成许多小段,并利用定积分计算每小段线段的长度,然后将这些 长度相加,最终得到整个弧的长度。这个过程涉及到极限和定积分的概念。
建立方程
首先需要确定曲线的起点和终点,以 及曲线在起点和终点处的切线方向。
根据起点、终点和参数,建立曲线的 参数方程。
选择参数
选择一个合适的参数,例如时间或角 度,来表示曲线上每一点的位置。
6.4平面曲线的弧长

折线的长 Mi1Mi 的极限存在,则称此极限为曲线
i 1
弧AB的弧长.
二、平面曲线弧长的计算
1.直角坐标情形
设曲线弧为y f ( x) y
(a x b),其中f ( x)在[a,b]
上有一阶连续导数.
dy
取积分变量为x , 在[a , b]上
任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长,
小切线段的长 (dx)2 (dy)2 1 y2dx,
弧长元素ds 1 y2dx, 弧长s b 1 y2dx. a
例 1 计算曲线 y 2 x3 2 上相应于x从点 a 到 b 的 3
一段弧的长度.
解
因为
y
1
x2,
所以ds
1
(
x
1 2
)2
dx
1 xdx,
2.参数方程情形
设曲线弧为
x y
(t) (t)
( t ).
其中 (t), (t)在[ , ]上具有连续导数.
ds (dx)2 (dy)2 [ 2 (t ) 2 (t )](dt )2
2 (t ) 2 (t )dt,
所以弧长 s 2 (t) 2 (t)dt.
例4 求星形线 x2 3 y2 3 a2 3 (a 0) 的全长.
解 星形线的参数方程为
x a cos3 t
y
a
sin3
t
(0 t 2π),
设s1为第一象限部分的弧长,则根据对称性,
π
s
4s1
4
2 0
x2 y2dt
π
4 2 3a sin t cos tdt 6a. 0
平面曲线的弧长与曲率

O
ax
π
因此 s 4 2 x2(t ) y2(t )dt 0
π
4 2
3a cos2 t sin t
2
3a sin2 t cos t
2
dt
0
12a
π 2
sin
t
cos
tdt
12a
sin2
t
π 2
6a.
0
20
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
n
故 lim T 0 i1
x2(i ) y2(i )Δti
数学分析 第十章 定积分的应用
高等教育出版社
x2(t) y2(t) dt.
§3 平面曲线的弧长曲率
平面曲线的弧长
由第一章§1习题 6 可知
*平面曲线的曲率
x2(i ) y2(i ) x2(i ) y2(i ) y(i ) y(i ) . 又y(t)在[ , ]上连续,从而在[ , ]上一致连续,
b2
ab sin2 t
b2
32.
当 a b 0 时, 在 t 0, π 处曲率最大, 在 t π ,
3π 2
处曲率最小,
Kmax
a b2
, Kmin
b a2
.
2
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
*平面曲线的曲率
由例1可得,若
a
b
R,
则各点处曲率相等,
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
*平面曲线的曲率
数学分析-平面曲线的弧长与曲率

解: 利用对称性
绕 x 轴旋转
星形线
星形线是内摆线的一种.
点击图片任意处 播放开始或暂停
大圆半径 R=a
小圆半径
参数的几何意义
(当小圆在圆内沿圆周滚动
时, 小圆上的定点的轨迹为是内摆线)
内容小结
3. 平面曲线的弧长
曲线方程
参数方程方程
上
半圆为
下
它也反映了环面微元的另一种取法.
第三节、平面曲线的弧长与曲率
定义: 若在弧 AB 上任意作内接折线 ,
当折线段的最大
边长 →0 时,
折线的长度趋向于一个确定的极限 ,
此极限为曲线弧 AB 的弧长 ,
即
并称此曲线弧为可求长的.
定理: 任意光滑曲线弧都是可求长的.
则称
(1) 曲线弧由直角坐标方程给出:
弧长元素(弧微分) :
因此所求弧长
的弧长 .
解:
例12. 求阿基米德螺线
相应于 0≤≤2
一段的弧长 .
解:
第四节、旋转体的侧面积
设平面光滑曲线
求
积分后得旋转体的侧面积
它绕 x 轴旋转一周所得到的旋转曲面的侧面积 .
取侧面积元素:
例19. 计算圆
x 轴旋转一周所得的球台的侧面积 S .
解: 对曲线弧
应用公式得
当球台高 h=2R 时, 得球的表面积公式
极坐标方程
弧微分:
直角坐标方程
注意: 求弧长时积分上下限必须上大下小
4. 旋转体的侧面积
侧面积元素为
(注意在不同坐标系下 ds 的表达式)
思考与练习
1.用定积分表示图中阴影部分的边界长 s .
7-2平面曲线的弧长及旋转体的侧面积

2 2
2
π
1
1
周所得的旋转面的面积为
2 0
1 5 S 2= ∫ 2π ⋅ x ⋅ dx = 5π . 2 2
因此, 因此,所求旋转体的表面积为
练习题答案
a 2 1 3 5 3 2、 3、 一、1、1 + ln ; 2、 π ; 3、 + ln . 2 2 12 2 2 3 8 5 二、 [( ) 2 − 1]. 9 2 三、6a . 四、8a .
2 3 3 )a, a ) . 六、(( π − 3 2 2
2 2
= n∫
0
sin t + cos t + 2 sin t cos t dt 2 2 2 2
sin t + cos t dt = n∫ = 4n. 0 2 2
π
三、参数方程情形
曲线弧为
x = ϕ (t ) , y = ψ (t )
= r (θ ) + r ′ (θ )dθ ,
2 2
故弧长 s = ∫α r (θ ) + r ′ (θ )dθ .
β
2 2
例 4 求阿基米德螺线 r = aθ (a > 0)上相应
的弧长. 于 θ 从 0 到 2π 的弧长. 解Q
r′ = a,
β α
2π
∴ s=∫
′ 2 (θ )dθ r (θ ) + r
第二节 平面曲线的弧长与 旋转体的侧面积
一、 平面曲线弧长的概念 二、 直角坐标系情况 三、 参数方程情况 四、 极坐标情况 五、旋转体的侧面积 六、 小结
《微积分》第八节 平面曲线的弧长
小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
思考题
闭区间[a, b]上的连续曲线 y f ( x)
是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
作业
P236习题3_8 1(单),2(2),3,4(2), 5,7(1、4),8,10(单)
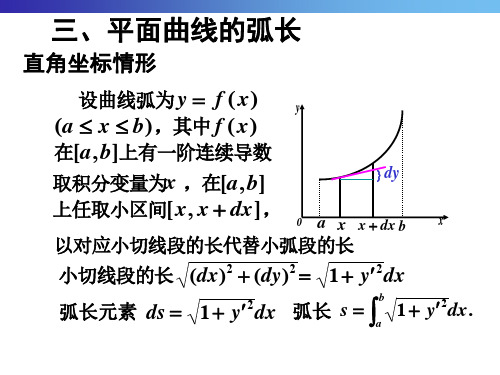
三、平面曲线的弧长
直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a, b]
dy
上任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长
小切线段的长 (dx)2 (dy)2 1 y2dx
曲线弧为 ( ) ( )
其中 ( ) 在[ , ]上具有连续导数.
x y
( (
)cos )sin
( )
dx [()cos ()sin]d,
dy [()sin ()cos]d,
ds (dx)2 (dy)2 2( ) 2( )d,
弧长
s
2( ) 2( )d .
例5
求极坐标系下曲线r
a
sin
3
3
的长.
(a 0) (0 3)
解
r
3a
sin
3
2
cos
3
1 3
a sin
2
cos
,
3 3
s
r 2( ) r2( )d
3 0
a2
sin
3
数学分析10.3平面曲线的弧长与曲率
第十章 定积分的应用 3 平面曲线的弧长与曲率一、平面曲线的弧长设平面曲线C=⌒AB. 如图所示,在C 上从A 到B 依次取分点: A=P 0,P 1,P 2,…,P n-1,P n =B ,它们成为曲线C 的一个分割,记为T. 用线段联结T 中每相邻两点,得到C 的n 条弦P i-1P i (i=1,2,…,n),这n 条弦又成为C 的一条内接折线,记:T =ni 1max ≤≤|P i-1P i |,s T =∑=n1i i 1-i |P P |,分别表示最长弦的长度和折线的总长度。
定义1:对于曲线C 的无论怎样的分割T , 如果存在有限极限:0T lim →s T =s ,则称曲线C 是可求长的, 并把极限s 定义为曲线C 的弧长.定义2:设平面曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 如果x(t)与y(t)在[α,β]上连续可微,且x ’(t)与y ’(t)不同时为零 (即x ’2(t)+y ’2(t)≠0, t ∈[α,β]),则称C 为一条光滑曲线.定理:设曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 若C 为一光滑曲线,则C 是可求长的,且弧长为:s=⎰'+'βα22(t)y (t)x dt.证:对C 作任意分割T={P 0,P 1,…,P n },并设P 0与P n 分别对应t=α与t=β, 且P i (x i ,y i )=(x(t i ),y(t i )), i=1,2,…,n-1.于是,与T 对应得到区间[α,β]的一个分割T ’: α=t 0< t 1<t 2<…t n-1<t n =β.在T ’所属的每个小区间△i =[t i-1,t i ]上,由微分中值定理得△x i =x(t i )-x(t i-1)=x ’(ξi )△t i , ξi ∈△i ;△y i =y(t i )-y(t i-1)=y ’(ηi )△t i , ηi ∈△i . 从而C 的内接折线总长为s T =∑=∆+∆n1i 2i 2i y x =∑='+'n1i i 2i 2)(ηy )(ξx △t i .记σi =)(ηy )(ξx i 2i 2'+'-)(ξy )(ξx i 2i 2'+',则s T =[]∑=+'+'n1i i i 2i 2σ)(ηy )(ξx △t i .又由三角形不等式可得:|σi |≤||y ’(ηi )|-|y ’(ξi )||≤|y ’(ηi )-y ’(ξi )|. 由y ’(t)在[α,β]上连续,从而一致连续,∴对任给的ε>0, 存在δ>0, 当T '<δ时,只要ηi , ξi ∈△i ,就有|σi |≤|y ’(ηi )-y ’(ξi )|<α-βε, i=1,2,…,n. ∴|s T -∑='+'n1i i 2i 2)(ξy )(ξx △t i |=|∑=n1i i σ△t i |≤∑=n1i i |σ|△t i <ε,∴0T lim →s T =∑=→''+'n1i i 2i 20T )(ξy )(ξx lim △t i ,即s=⎰'+'βα22(t)y (t)x dt.注:1、若曲线C 由直线坐标方程y=f(x), x ∈[a,b]表示,则看作参数方程:x=x, y=f(x), x ∈[a,b]. 因此,当f(x)在[a,b]上连续可微时,此曲线即为一光滑曲线,其弧长公式为:s=⎰'+ba 2(x )f 1dx. 2、若曲线C 由极坐标方程r=r(θ), θ∈[α,β]表示,则 化为参数方程:x=r(θ)cos θ, y=r(θ)sin θ, θ∈[α,β]. 由x ’(θ)=r ’(θ)cos θ-r(θ)sin θ, y ’(θ)=r ’(θ)sin θ+r(θ)cos θ, 得:x ’2(θ)+y ’2(θ)=r 2(θ)+r ’2(θ),∴当r ’(θ)在[α,β]连续,且r(θ)与r ’(θ)不同时为零时,此极坐标曲线为一光滑曲线, 其弧长公式为:s=⎰'+βα22 )(θr )(θr d θ.例1:求摆线x=a(t-sint), y=a(1-cost)(a>0)一拱的孤长.解:∵x’(t)=a-acost; y’(t)=asint. ∴x’2(t)+y’2(t)=2a2(1-cost)=4a2sin22t.其弧长为s=⎰2π222tsin4a dt=4a⎰2π02tsin d⎪⎭⎫⎝⎛2t=8a.例2:求悬链线y=2ee-xx+从x=0到x=a>0那一段的弧长.解:∵y’=2ee-xx-. ∴1+y’2=2x-x2ee⎪⎪⎭⎫⎝⎛+.其弧长为s=⎰+a-xx2ee dx=2ee-aa-.例3:求心形线r=a(1+cosθ) (a>0)的周长.解:∵r’(θ)=-asinθ. ∴r2(θ)+r’2(θ)=4a2cos22θ.其周长为s=⎰2π02θacos2dθ=4a⎰2π02θcos d⎪⎭⎫⎝⎛2θ=8a.注:∵s(t)=⎰'+'tα22(t)y(t)x dt连续,∴dtds=22dtdydtdx⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛,即有ds=22dydx+. 特别称s(t)的微分dx为弧微分. (如左下图)PR为曲线在点P处的切线,在Rt△PQR中,PQ为dx,QR为dy,PR则为dx,这个三角形称为微分三角形。
定积分——求曲线的弧长
2
0
x 2 2 2 2 sin 2 0 4
机动
目录
上页
下页
返回
结束
例11. 计算摆线
的弧长 . 解: d s
x 2 (d ) dt dy 2 (d t )
一拱
y
dt
o
2 a x
a 2 (1 cos t ) 2 a 2 sin 2 t d t
a 2(1 cos t ) d t t 2a sin dt 2 2 t t 2 s 2a sin d t 2a 2 cos 8a 0 2 2 0
2 2 2 1 a 1 ln 1 2 0 2
0
1 2 d (P257 积分公式)
小结
目录
上页
下页
返回
结束
MM y 2 1 ( ) MM x s s( x) lim 1 ( y) 2 x0 x
MM lim 1 x0 M M
机动
目录
上页
下页
返回
结束
弧微分公式
ds 1 ( y) dx 或
2
ds (dx) 2 (d y ) 2
x x(t ) 若曲线由参数方程表示: y y (t )
则弧长微分公式为
ds [ x ( t )]2 [ y( t )]2 d t
机动
目录
上页
下页
返回
结束
(1) 曲线弧由直角坐标方程给出:
弧长元素(弧微分) :
ds (dx) (d y ) 1 y2 d x
因此所求弧长
s
2 (t ) 2 (t ) d t
10数学分析教案-(华东师大版)第十章定积分的应用平面曲线的弧长与曲率)
§3 平面曲线的弧长与曲率一 平面曲线的弧长先建立平面曲线弧长的概念,设C=AB 是一条没有自交点的非闭的平面曲线,在C 上从A 到B 依次取分点A=P 0,P 1,P 2,…,P n =B,它们成为对曲线C 的一个分割,记为T ,然后用线段连接T 中每相邻两点,得到C 的n 条弦1(1,2,...,)i i P P i n -=,这n 条弦又成为C 的一条内接折线,记||T||=max|P i-1P i |,11||nT i ii s PP -==∑分别表示最长弦的长度和折线的总长度。
定义1 如果存在有限极限||||0lim s T T s →=,即任给ε>0,恒存在δ>0,使得对于C 的任何分割T ,只要||T||<δ,就有|s T -s|<ε,曲线C 是可求长的,并把s 定义为曲线C 的弧长。
定理10.1 设曲线C 是一条没有自交点的非闭的平面曲线,由参数方程x=x(t),y=y(t),t ∈[α,β]给出,若x(t)、y(t)在[α,β]上连续可微,则C 是可求长的,且弧长为s βα=⎰。
证明 对C 作任一分割T={ P 0,P 1,P 2,…,P n },并设P0与Pn 分别对应t=α和t=β,且P i (x i ,y i )=(x(t i ),y(t i )),i=1,2,…,n -1,于是与T 对应得到区间[α,β]的一个分割T':α=t 0,t 1,t 2,…,t n =β。
现在用反证法先证明||||0lim ||||0T T →'=.假设||||0lim ||||0T T →'≠,则存在ε0>0,对于任何δ>0,都可以找到一个分割T 使得||T||<δ而同时||T'||>ε0,从而可以找到C 上两点Q'和Q'',使得|Q''Q'|<δ,而它们对应的参量t'和t''满足|t't''|≥ε0,依次取δ=1/n,n=1,2,…,则得到两个点列{Q'n }和{Q''n }和它们对应的参量数列{t'n }和{t''n },它们满足|Q n ''Q n '|<1/n, |t'n t''n |≥ε0,由致密性定理,存在子列{}{}k kn n t t '''及,和t*和t**∈[α,β],使得lim *,lim **k knn k k t t t t →∞→∞'''==,显然|t*-t**|≥ε0,即t*≠t**。
平面曲线弧长的概念
2 2 t2
2
2 2 t2
1 2
例 5 证明正弦线 y a sin x (0 x 2)的弧长
等于椭圆
x y
cos t 1
a
2
sin
t
(0 t 2)的周长.
证 设正弦线的弧长等于s1
s1
2 0
1 y2dx
2 0
1 a2 cos2 xdx
2
1 a2 cos2 xdx,
0
无限增加且每个小弧段都缩向一点时,
n
此折线的长 | M i1M i |的极限存在,则称此极限为
i 1
曲线弧AB 的弧长.
二、直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a,b]
dy
上任取小区间[ x, x dx],
0
0
6a.
例4.求曲线 y=sin x 在[0, ]上对应弧长。
2
解: Q y cos x
ds 1 cos2 xdx
S
2
1 cos2 xdxS令 1 cos2 x t 1
2t2 dt
0
2 2 t2
1 4 2t2 4dt 2 1 2 t2 dt 4 1 1 dt
作业: P252 1;3.
x y
r( r(
)cos )sin
( )
ds (dx)2 (dy)2 r 2( ) r2( )d ,
弧长 s r 2( ) r2( )d .
例6
求极坐标系下曲线r
a
sin
3
3
的长.
(a 0) (0 3)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1 平面图形的面积
§2 由平行截面面积求体积 §3 平面曲线的弧长 §4 旋转曲面的面积 §5 定积分在物理中的应用
§6 定积分的近似计算
§1平面图形的面积
一、直角坐标系情形 二、参数方程 三、极坐标系情形
一、直角坐标系情形
y
y f ( x)
y
y f2 ( x) y f1 ( x )
y
y f ( x)
x [a , b ] 在[a , b]上任取小区 间[ x , x dx ] ,
o
x x dx
x
x 取以dx 为底的窄边梯形绕 轴旋转而成的薄 片的体积为体积元素, dV [ f ( x )]2 dx
旋转体的体积为 V [ f ( x )]2 dx
a b
解
两曲线的交点
x y2
(0,0) (1,1)
选 x 为积分变量 x [0,1] 面积元素 dA ( x x 2 )dx
y x2
2 3 x 1 A 0 ( x x )dx x 2 . 3 0 3 3
1
3
1
2
例 2
计算由曲线 y x 3 6 x 和 y x 2 所围成
因为曲线 y f ( x ) 过点( 2,3)
9 y x , 因为 f ( x ) 为单调函数 2 所以所求曲线为 y 3 2 x .
2
9 c 2
补充:定积分的微元法
回顾 曲边梯形求面积的问题
曲边梯形由连续曲线
y
y f ( x ) ( f ( x ) 0) 、 x 轴与两条直线 x a 、
y f ( x)
x b 所围成。
b
o a
b x
A a f ( x )dx
面积表示为定积分的步骤如下
(1)把区间[a , b]分成 n个长度为x i 的小区间,相 应的曲边梯形被分为n个小窄曲边梯形,第i 个小窄 曲边梯形的面积为Ai ,则 A Ai .
(2)计算Ai 的近似值 Ai f ( i )xi i xi
y
y
1
1 2 x 2
O -1
1 y 1 x2 1 3 x
例3 计算抛物线y22x 与直线yx4所围成的图形的 面积。 解:求两曲线的交点得:(2,2),(8,4)。将图形 向y轴投影得区间[2,4]。
4
1 2 1 2 1 3 4 A ( y 4 y )dy [ y y 4 y y ] 2 18 。 (8, 4) 2 4 2 2 6 1 2 1 2 1 3 4 y )dy [ y 4 y y ] 2 18 。 2 2 2 6 18。
a a
b2 2 x3 a 4 2 2 (a x ) 0 ab 2 。 3 3 a
例 2
连接坐标原点 O 及点 P ( h, r )的直线、直线
x h及 x 轴围成一个直角三角形.将它绕 x 轴旋
转构成一个底半径为 r 、高为 h 的圆锥体,计算圆 锥体的体积.
y
P
解 直线 OP方程为
x2 y2 例 1 求椭圆 2 2 1 a b 分别绕x轴与y轴旋产生的 旋转体的体积。
y
b
b y a2 x2 a
解:椭圆绕 x 轴旋转产生 的旋转体的体积:
O
a x
Vxx 2 V 20
a a
0
b2 2 2 2 b 2 (a 2 x 2 )dx y 2dx 2 2 (a x )dx y dx 2 0 2 0 a a
2
( 2,2), (8,4).
y2 2 x
选 y 为积分变量
y [2, 4]
2 4 2
y dA y 4 dy 2
2
y A ( y 4 )dy 18. 2
三、小结
求在直角坐标系下、参数方程形式 下、极坐标系下平面图形的面积.
(注意恰当的选择积分变量有助于简化 积分运算)
解: S2 2S1 S2 0 f ( x )dx
0 f ( x )dx 2[ xy 0 f ( x )dx]
两边同时对 x 求导
x x
x
y
S1
( x, y ) y f ( x )
S2
3 f ( x ) 2 y 2 xy 2 xy y
积分得
o
x
y 2 cx,
i 1 n
(3) 求和,得A的近似值 A f ( i )xi .
i 1
n
(4) 求极限,得A的精确值
A lim f ( i )xi a f ( x )dx
b
n
0 i 1
提示
若用A 表示任一小区间
面 积 元 素
[ x , x x ]上的窄曲边梯形的面积, 则 A A,并取A f ( x )dx ,
设曲线 y f ( x ) 过原点及点( 2,3) ,且 f ( x ) 为单调函数,并具有连续导数,今在曲线上任 取一点作两坐标轴的平行线,其中一条平行线 与 x 轴和曲线 y f ( x ) 围成的面积是另一条平 行线 与 y 轴和 曲线 y f ( x ) 围 成的 面积 的两 倍,求曲线方程.
于是 A f ( x )dx
y
y f (x )
dA
A lim f ( x )dx
f ( x )dx.
b a
o a
x x dxb x
当所求量 U 符合下列条件: (1)U 是与一个变量 x 的变化区间a, b有关的量;
(2)U 对于区间 a, b具有可加性,就是说,如 果把区间a, b分成许多部分区间,则 U 相应地分 成许多部分量,而U 等于所有部分量之和;
y x3 6x
的图形的面积.
解
两曲线的交点
y x3 6x y x2
(0,0), ( 2,4), ( 3,9).
y x2
选 x 为积分变量 x [2, 3]
(1) x [2, 0], dA1 ( x 3 6 x x 2 )dx ( 2) x [0,3], dA2 ( x 2 x 3 6 x )dx
作业: P242 1-6
§2 由平行截面面积求体积
一、旋转体的体积 二、平行截面面积为已知的立体的体积 三、小结
一、旋转体的体积
旋转体就是由一个平面图形饶这平面内 一条直线旋转一周而成的立体.这直线叫做 旋转轴.
圆柱
圆锥
圆台
旋转体: 由连续曲线 yf (x)、直 线 xa 、ab 及 x 轴所围成 的曲边梯形绕 x轴旋转一周 而成的立体。 讨论: 答案:
d
解
利用对称性知 1 2 2 A 2 a (1 cos ) d 2 0 2 a (1 2 cos cos 2 )d 0 3 2 3 1 a 2 2 sin sin 2 a . 2 0 2 4
例7
O 2 4 4 -2 (2, 2)
8 x
二、参数方程
设曲线C是由参数方程 x x(t ), y y(t ),t [ , ]给出,
在[ , ]上y(t )连续,x (t )连续可微且 ' (t ) 0, x
记a x( ),b x( ), (a b或b a), 则由曲线C及直线x a, x b和x轴所围图形面积公式为
x
2
例 5
求双纽线 2 a 2 cos 2 所围平面图形
的面积.
解 由对称性知总面积=4倍第一象限部分面积
y x
A 4A1
A 40
4
A1
1 2 a2 . a cos 2d 2
2 a 2 cos 2
例 6 求心形线r a (1 cos ) 所围平面图形的 面积(a 0) .
r
o
r y x h
h
x
取积分变量为x , x [0, h]
在[0, h]上任取小区间[ x , x dx ] ,
以dx 为底的窄边梯形绕x 轴旋转而成的薄片的 体积为
4b a 4b a 2 2 0 a x dx a 4 ab。 a
2
b
y
a
a2 x2
4b a 2 x 2 dx ab。 a 4
S1
O
a x
1 2 1 例 2 求曲线 y x 、y 与直线 x 3 、 2 2 1 x x 3 所围成的图形的面积。 解: 由对称性,图形面积是第一 象限部分的两倍。 2 1 3 x 1 x2 1 S 2[ ( )dx ( )dx ] 2 2 0 1 x 1 2 2 1 x
2
a
0
4ab sin2 tdt ab.
0
2
三、极坐标系情形
d
设由曲线r j ( ) 及射线
、 围成一曲边扇
形,求其面积.这里,j ( ) 在[ , ]上连续,且j ( ) 0 .
r j ( )
d
o 1 面积元素 dA [j ( )]2 d 2 1 曲边扇形的面积 A [j ( )]2 d .
(3)部分量U i 的近似值可表示为 f ( i )x i ;
就可以考虑用定积分来表达这个量 U
微元法的一般步骤:
x 1) 根据问题的具体情况,选取一个变量例如 [ 为积分变量,并确定它的变化区间 a , b] ;
2) 设想把区间[a , b]分成 n个小区间,取其中任 一小区间并记为[ x , x dx ],求出相应于这 小区间的部分量U 的近似值.如果U 能近 似地表示为[a , b]上的一个连续函数在 x 处的 值 f ( x ) 与dx 的乘积,就把 f ( x )dx 称为量 U 的元素且记作dU ,即 dU f ( x )dx ;
