2019精选教育华东师大版八年级上册第11章 数的开方 学案(无答案).doc
华东师大版八年级数学上册 第11章 数的开方 第2课时 算术平方根导学案(无答案)

【学习课题】 第2课时 算术平方根【学习目标】1、了解数的算术平方根的概念,会用根号表示一个数的算术平方根.2、了解求一个正数的算术平方根与平方是互逆的运算,会利用这个互逆运算关系求某些非负数的算术平方根.3、了解算术平方根的性质.【学习重点】了解算术平方根的概念、性质,会用根号表示一个正数的算术平方根.【学习难点】了解算术平方根的非负性【候课朗读】平方根的定义,平方根的表示,平方根的性质【学习过程】一、学习准备:1、三种表达形式①定义 ②文字叙述 ③符号语言2、一个正数有___ _个平方根,它们 ____;0有 个平方根,是 ______ ;负数 。
3、求值 (1) =±169 (2)=±-410 (3) =±14 (4) =±0 (5) =±2516 4、实例1:若正方形的面积等于5,求正方形的边长是多少?二、解读教材5、算术平方根的概念:我们规定若一个正数x 的平方等于a ,即x 2=a ,则这个正数x 就叫做a 的算术平方根。
记为“a ”,读作“根号a ”。
特别地,我们规定0的算术平方根是0,即0=0。
6、算术平方根的性质:一个正数有个算术平方根,是;0有个算术平方根,是;负数。
7、算术平方根的三种表达形式(1)定义:x2=a (a≥0,x≥0)(2)文字叙述:算术平方根(3)符号语言:a(a≥0)例2:求下列各数的算术平方根:49;(1)900;(2)1;(3)64(4)14。
解:(1) ∵302=900,∴900的算术平方根是30,即900=30;(2)(3)(4)例3:求值三、挖掘教材8、算术平方根与平方根的区别与联系(1)、平方根与算术平方根的区别:①定义不同:如果x2=a,那么x叫做a的平方根,表示为±a(a≥0)。
一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身;负数没有平方根。
如果x2=a,并且x≥0,那么非负数x叫做a的算术平方根。
新华东师大版八年级数学上册:第11章 数的开方 第6课时 导学案(无答案)

新华师大版八年级数学上册:第11章数的开方2导学案学习目标 1.了解实数与数轴上的点的一一对应关系,进一步领会数形结合思想。
2.能比较实数的大小,会进行实数的近似计算。
学习重点 比较实数的大小,实数的近似计算。
学习方法 勾画圈点法、旁批法、识记法等。
预习 一、自学1.自学教材P10-11的例1和例2。
2.自学检测:A.实数与数轴上的点的对应关系:(1)如图1,正方形边长为1,则对角线OB 的长为2(后面的14章我们会学习如何算出OB ),以O 为圆心,OB 长为半径画弧,交数轴于点A 。
数轴上A 点对应的数是什么? ,它介于哪两个整数之间? 。
(2)如果将所有的有理数都标到数轴上,那么数轴被填满了吗?(3)如图2,通过本书14章的学习,我们能得到线段AB=2,AC=3,AD=4=2,AE=5, ……图1 图2由此可见:每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数。
即:实数与数轴上的点是 的关系。
在数轴上,右边的点表示的数比左边的点表示的数 。
B.完成教材P11的练习2-3题。
二、互学1.计算:2352+(结果保留一位小数)2.比较下列各组数中的实数的大小。
2352和 (2)325π--和展示一、质疑1.试估计-(3+2)与-2π的大小关系。
2.求绝对值小于5的所有整数的积。
二、点拨(由小组提出有价值的问题,其他小组发表意见,帮助解决问题;展示过程中,教师适时引导、点拨、调控和激励。
)反馈一、小结1.实数与数轴上的点是一一对应关系。
2.实数的大小比较方法:同类比较法,近似值比较法,比差法等。
3.记住常用无理数2,3,5,π的近似值。
4.实数的近似计算方法:中间结果比最后结果多取一位。
二、当堂检测1.将下列实数按从小到大的顺序排列,并用“<”连接π,5-,52-,0,12-π2.教材P11的习题2题3.教材P11的习题3题4.写出两个-6~~-5之间的无理数。
5.已知a,b为两个连续整数,7a b<<且,则a= ,b= 。
20192108-学年华东师大版八年级上册第11章数的开方11.1.1 平方根 学案(无答案)精品教育.doc

八年级数学上册导学案01命题人:刘英明 审题人:曹金满 课型:新授课课题:11.1.1 平方根学习目标:1.理解平方根和算术平方根的概念,了解平方与开平方的关系.2.会用平方根的概念求某些数的平方根、算术平方根,并会用根号表示.3.理解平方运算与开平方运算是互逆运算的关系.学习重点:平方根、算术平方根的概念和求法.学习难点:有关平方根、算术平方根的运算的区别于联系.一、知识回顾:1.复习平方数:探究交流:一对互为相反数的的数的平方有什么关系? 2.填底数:因为=23 =-2)3( 所以( )2=9因为=25 =-2)5( 所以( )2=25探究交流:平方得25的数有几个?分别是什么?这两个数有什么关系?它们的和等于多少呢?二、引入新知:如图所示, 面积为25cm 2的正方形, 其边长为多少呢?根据正方形的面积公式,应该是(边长)2=25 由此我们得出, 其边长应该为 如果:面积为16,则边长应该为______;面积为9,则边长为________;面积为a ,则边长又如何呢?可设边长为x ,则得到:__________。
新知概念1:如果一个数x 的平方等于a ,那么这个数x 叫做a 的平方根。
就是说, 当a x =2(a ≥0)时, 称x 是a 的平方根。
而a 称为x 的平方数。
重点:怎么求一个数的平方根?在上面的问题中,我们知道因为 25=25,所以5是25的一个平方根.探究交流1:25的平方根只有一个吗?还有没有别的数的平方也等于25?因为( )2=25,所以 也是25的一个平方根 这就是说 和 都是25的平方根 探究交流2:如何求一个数的平方根?求一个数的平方根的关键是什么呢?25cm 2 231-⎪⎭⎫ ⎝⎛231)(例如:求25的平方根的关键是: 等于25,这个数就是25的平方根.三、举例应用:例1:求下列各数的平方根(试着考虑,每个数,有几个平方根?) (1)100 (2)0.49 (3)1.69 (4)2516 (5)412 例2:(1)16的平方根是什么? (2)0的平方根是什么? (3)91的平方根是什么? (4)-4有没有平方根?为什么?概括:(1)一个正数的平方根有 ,它们是互为 .(2)0的平方根是 , 就是它 .(3) 没有平方根.新知概念2:正数a 的正的平方根叫做a 的算术平方根.正数a 的算术平方根记作:a 读作根号a ;它的另一个平方根记作:-a 读作负根号a一个正数a 的平方根表示为:a 读作正负根号a四、巩固练习:1.下列叙述正确的打“ √” ,错误的打“×”:(1)16的平方根是±4( ) (2)±7是49的平方根( )(3)112的平方根是11 ( ) (4)-9是81的平方根 ( )2.(1)25的算术平方根用符号表示为 = (2)25的负平方根用符号表示为_____=_____(3)25的平方根用符号表示为__ __=_____五、小结:谈谈今天你的收获?六、作业:教材第4页练习1、2、3、4随堂检测一、选择题:1.下列说法,①16的算术平方根是4;②-36没有算术平方根;③一个数的算术平方根一定是正数;④2a 的算术平方根是a .其中正确的有( ) 注意: 0的算术平方根还是0A.1个B.2个C.3个D.4个2.当≥m 0时,m 表示( )A.m 的平方根B.一个有理数C.m 的算术平方根D.一个正数3.一个自然数的算术平方根是a ,则下一个自然数的平方根是( )A.()1+aB.()1+±aC.12+aD.12+±a4.一个自然数的算术平方根是x ,则它后面一个数的算术平方根是( )A.1+xB.12+xC.1+xD.12+x5.若42-m 与13-m 是同一个数的平方根,则m 的值是( )A.-3B.1C.-3或1D.-16.已知x ,y 是实数,且0)3(432=-++y x ,则xy 的值是( )A.4B.-4C.D. 7.已知n 是一个正整数,n 135是整数,则n 的最小值是( )A.3B.5C.15D.258.下列式子中,正确的是( )A.10< <11B.11< <12C.12< <13D.13< <149.下列计算,你认为正确的是( )A.451691=B.212214=C.05.025.0=D.525=-- 二、填空题:10.16的算术平方根是 ,2)9(-的平方根是 .11.若411+-+-=a a b ,则ab 的平方根是 .12.如果x 的平方等于a ,那么x 就是a 的 ,所以a 的平方根是 .13.非负数a 的平方根表示为 .14.因为没有什么数的平方会等于 ,所以负数没有平方根,因此被开方数一定是 .15.已知0)1(132=-+-+-z y x ,求xyz =________.16.化简:2)3(π-= .4949-12712712712717.已知:a 、b 为两个连续的整数,且a <15<b ,则b a += .18.若整数m 满足条件1)1(2+=+m m 且52<m ,则m 的值是 .19.研究下列算式,你会发现什么规律?24131==+⨯,39142==+⨯,416153==+⨯……请用含n 的式子表示出来 .三、解答题:20.求下列各式中的x 的值(1) (2)21.如果一个正数的平方根分别为2+a 和112-a ,求这个正数.22.已知12-a 的平方根是±1,13-+b a 的算术平方根是2,求b a +的值.23.若221025+=-+-b a a ,求a 、b 的值.04552=-x 025)1(362=--x。
2019八年级数学上册 第11章 数的开方教案1 (新版)华东师大版

一.你对本章数的开方知识掌握的如何?请自己 估算一下自己的分数。
二.本节课 我们一起来研究我们的单元考试题。
面向全体学生提出相关的问题。明确要研究,探索的问题是什么,明确本节课的具体任务。.
三.学生查阅试卷
四.从中发现问题.
五.学生提出问题.
六 .师生研究分析问题.共 同解决问题.
七.预习下一课的内容.
数的开方
教学目标一步理解和掌握知识,更好的利用知识解决问题,提高能力。
过程与方法
查阅试卷,发现问题,提出问题,研究讨 论,解决问题,提高能力。
情感态度与价值观
培养学生良好的学 习品质。
教学重点
试卷中存在的问题。
教学难点
认识错误,正确改正,逐步提高。
教学内容与过程
鼓励学生去研究、分析、探索解决问题的方法。
教学反思
必须手写,是检查备课的重要依据。
新华东师大版八年级数学上册第11章数开方复习学案(无)
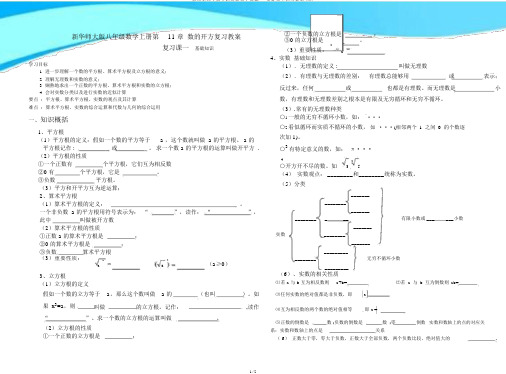
新华师大版八年级数学上册第11 章数的开方复习教案复习课一基础知识学习目标1.进一步理解一个数的平方根、算术平方根及立方根的意义;2.理解无理数和实数的意义;3.娴熟地求出一个正数的平方根、算术平方根和实数的立方根;4.会对实数分类以及进行实数的近似计算.要点:平方根、算术平方根、实数的观点及其计算.难点:算术平方根、实数的综合运算和代数与几何的综合运用一、知识概括1、平方根(1)平方根的定义:假如一个数的平方等于 a ,这个数就叫做 a 的平方根。
a 的平方根记作 :或。
求一个数 a 的平方根的运算叫做开平方 .(2)平方根的性质①一个正数有个平方根,它们互为相反数②0 有个平方根,它是。
③负数平方根。
(3)平方和开平方互为逆运算;2、算术平方根(1)算术平方根的定义:。
一个非负数 a 的平方根用符号表示为:“”,读作:“”,此中叫做被开方数(2)算术平方根的性质①正数 a 的算术平方根是;②0 的算术平方根是;③负数算术平方根(3)重要性质:22(a≥0)a a3、立方根(1)立方根的定义假如一个数的立方等于a,那么这个数叫做 a 的(也叫)。
如果 x3=a,则叫做的立方根。
记作:,读作“”。
求一个数的立方根的运算叫做。
(2)立方根的性质①一个正数的立方根是;②一个负数的立方根是;③0 的立方根是。
3a(3)重要性质:4、实数基础知识(1).无理数的定义 :叫做无理数(2).有理数与无理数的差别:有理数总能够用或表示;反过来,任何或也都是有理数。
而无理数是小数,有理数和无理数差别之根本是有限及无穷循环和无穷不循环。
(3).常有的无理数种类○1一般的无穷不循环小数,如:¨···○2看似循环而实质不循环的小数,如···(相邻两个1之间0的个数逐次加 1)。
○3有特定意义的数,如:π···4.3 ,3○开方开不尽的数。
八年级数学上册 第11章 数的开方 11.1 平方根与立方根 2 立方根学案 (新版)华东师大版

2 立方根学习目标1、了解一个数的立方根概念,并会用根号表示一个数的立方根.2、能用类比平方根的方法学习立方根,及开立方运算,并能区分立方根与平方根的异同.3、能用有理数估计一个开方开不尽数的大致范围,使学生形成估算的意识,培养学生的估算能力.4、经历运用计算器探究数学规律的过程,发展合情推理能力.课前预习1.类似平方根定义可知,若3x a,则为的立方根,记为,读作.其中,a是,3是,根指数3不能省略.例如:2的立方等于8,-2的立方等于-8,所以8的立方根为,-8的立方根为,记为 .2.求一个数的立方根的运算,叫做,与加、减、乘、除、乘方一样,都是一种运算.立方根是开立方运算的结果,与运算互为逆运算.3.用科学计算器求一个的立方根的按键顺序为: .合作探究(学透教材)探究问题:1.求下列各数的立方根.(1)8;(2)-125;(3)-0.008.272. 试用科学计算器求-3.375的立方根.讨论交流:1.在学习平方根运算时,首先是找一些数的平方值,然后再根据其逆运算过程确定某数的平方根.同样,我们来先算一算一些数的立方:32= ;()32-= ;313⎛⎫ ⎪⎝⎭= ;313⎛⎫- ⎪⎝⎭= ;30.5= ;()30.5-= ;30= . 2.经计算发现正数、0、负数的立方值与其平方值有何不同之处?3.求平方运算时,平方运算的底数为相反数,但其平方值却相等,故一个正数的平方根有两个值.求立方运算时,当底数互为相反数,其立方值有何关系?一个数的立方根有几个?负数有无立方根?4.怎样来验算开立方的结果是否正确呢?5.你知道数的立方根和数的平方根有什么区别与联系?试完成下表.问题拓展:1. 被开方数是互为相反数的两个数,其立方根仍互为相反数吗?(1=-22,由此得出 ;又=-3-3,由此得出 .= .(2)对比分析:当a ≥0,?2.a ≥0a 的取值范围有限制吗? 课堂反馈1、64的立方根是( )(A )4 (B )-4 (C )8 (D )-82、比较2)(A )2<(B )2< (C2<(D 23、已知A=m 是2m n +的立方根,B=2m -3m n ++的算术平方根,则11m n +的立方根是 .42,则a = ;若264a == .答案:1.A ;2.C ;3.3;4.64,2±;5.10或12或14 我的收获 课后巩固1、下列四种说法:①负数有一个负的立方根;②1的平方根与立方根都是1;③4•的平方根;④互为相反数的两个数的立方根仍为相反数.正确的有( ). (A )1 种 (B )2 种 (C )3种 (D )4种 答案:C20=,则,a b 的关系是( ) A 、a b = B 、1a b= C 、,a b 互为相反数 D 、无法确定 答案:C3、填空:答案:4= . 答案:4065、如果要生产容积为50L 的圆柱形热水器,使它的高等于底面直径的2倍,这种容器的底面直径应取多少?(π取3.14,结果保留三个有效数字) 解:设这种圆柱形热水器的底面直径为xdm ,则其半径为dm x2,高为2xdm ,由题意,得:502214.32=⨯⎪⎭⎫⎝⎛⨯x x ,5057.13=x ,解得:17.3≈x .答:这种容器的底面直径约为3.17dm .6、解方程:(1)274x 3-2=0; (2) 12(x+3)3=4. 答案:(1)23;(2)-17、分别求出下列各题的值:=__________,=__________,=__________,……=__________,=__________,=__________,……你能从中找出规律吗?请写出这个规律.若把3换成其他数,这个规律还成立吗?答案:3,32,33,……;3,32,33,……规律:开平方时,被开方数的指数,每增加2次,相应结果的指数增加1次;开立方时,被开方数的指数,每增加3次,相应结果的次数增加1次;成立.填一填:1、x,a,三次根号a,被开方数,根指数,2,-22,-2开立方,开立方,立方2。
华东师大版八年级数学上册 第11章 数的开方 第1课时 平方根导学案(无答案)-精选学习文档
【学习课题】 第1课时 平方根【学习目标】1、了解平方根的概念,会用根号表示一个数的平方根;2、了解开平方与平方是互逆的运算,会利用这个互逆运算关系求某些非负数的平方根。
【学习重点】平方根的概念、性质及求法。
【学习难点】对平方根的求值。
【候课朗读】30以内的平方数 【学习过程】 一、学习准备:1、填一填:22= ,()22-= ;23.0= ,()23.0-= ;232⎪⎭⎫⎝⎛= ,232⎪⎭⎫ ⎝⎛-= 。
2、想一想:一个数的平方等于4,则这个数是 ;平方等于0.09的数有 ;平方等于94的数有 ;平方等于0的数是二、解读教材: 3、填空:()12= ,()22= ,()32= ,()42= ,()52= ,()82= ,()182= ,你能填出哪些空?4、平方根的定义:一般地,如果一个数x 的平方等于a ,即x 2=a ,那么这个数x 就叫做a 的平方根(也叫做二次方根)。
例:∵(±1)2=1,∴±1叫做1的平方根,∵(±2)2=4,∴ 叫做 的平方根, ∵02=0,∴ 叫做 的平方根,∵(±0.7)2=0.49,∴ 叫做 的平方根。
问:平方等于2的数应如何表示呢?5、平方根的表示:一个正数a 的正的平方根用符号2a 表示,其中a 叫做被开方数,2叫做根指数,正数a 的负的平方根用-2a 表示。
这两个平方根合起来可以记作±2a 。
这里符号2读作“二次根号”,2a读作“二次根号a ”。
根指数是2时,通常将这个2省略不写,如2a 记作a 读作“根号a ”;±2a 记作±a ,读作“正、负根号a ”。
例:()222=±的平方根叫22±∴()332=± ∴ 叫做 的平方根。
()552=± ∴ 叫做 的平方根。
()002=± ∴ 叫做 的平方根。
6、平方根的性质:(1)一个正数有几个平方根?(2)0有几个平方根?(3)负数呢?通过前面具体数字的平方根的探讨,总结出正数、0、负数的平方根的情况:一个正数有 个平方根,它们互为 ;0有 个平方根,是 ;负数 。
华东师大版八年级上册第11章数的开方学案(无答案)
八年级数学上册导教案05命题人:刘英明审题人:曹金满课型:复习课课题:第十一章数的开方(能力提高)学习目标 :1.进一步理解一个数的平方根、算术平方根及立方根的意义.2.理解无理数和实数的意义.3.娴熟地求出一个正数的平方根、算术平方根和实数的立方根.学习要点:平方根、算术平方根、实数的观点及其计算.学习难点:算术平方根、实数的综合运算和代数与几何的综合运用.一、选择题 :1.以下说法中正确的选项是()A.4 是 8 的算术平方根B.16 的平方根是 4C. 6 是6的平方根D. a 没有平方根2.以下各式中错误的选项是()A.0.360.6B. 0.36 0.6C. 1.44 1.2D. 1.44 1.23.若x2(0.7 ) 2,则 x =()A.-0.7B.±0.74. 36的平方根是()A.6B.±6C. 6D. 65.以下语句正确的选项是()A.假如一个数的立方根是这个数自己,那么这个数必定是零;B.一个数的立方根不是正数就是负数;第1页/共4页C.负数没有立方根;D.一个数的立方根与这个数同号,零的立方根是零。
6.以下说法中,正确的选项是()A.无穷小数都是无理数B.带根号的数都是无理数C.循环小数是无理数D.无穷不循环小数是无理数7. a是无理数,则a是一个()A.非负实数B.正实数C.非完整平方数D.正有理数8.以下说法中,错误的选项是()A. 2 是无穷不循环小数B. 2 是无理数C. 2是实数D. 2 等于1.4149.与数轴上的点拥有一一对应关系的是()A.无理数B.实数C.整数D.有理数10.以下说法中,不正确的选项是()A.绝对值最小的实数是 0B. 平方最小的实数是 0C.算术平方根最小的实数是 0D.立方根最小的实数是 0二、填空题 :1.和统称为实数 .2.1 2 绝对值是,相反数是,倒数是.3.以下说法: (1)带根号的数是无理数; (2)无穷小数都是无理数; (3)无理数都是无限小数;(4)在实数范围内,一个数不是有理数,则必定是无理数,不是正数,则必定是负数 .第2页/共4页此中错误的有 ______个.三、非负数性质的应用 :1.若 x 、 y 都是实数,且 y x33 x 2 ,求 x 3y 的平方根 .已知 a 3 (5 b)2 c 1 0 ,求 a的值 .2.b c2x y x 2 9,求 3x 6 y 的立方根 .3. 已知3x四、定义的应用 :4.已知 x 2的平方根是±2, 2x y 7 的立方根是3,求 x 2y 2 的平方根 .5.假如 Ma ba b 3 是 a b3 的算术平方根, Na 2b 3a2b 是 a2b 的立方根,求 M N 的立方根 .6.已知 3 x4 ,且 ( y 2 z 1) 2z 3 0 ,求 3 x y 3 z 3 的值7.若 33 x 1与31 2 y 互为相反数,求 x的值y五、数形联合的应用 :8.点 A 在数轴上表示的数为 3 5 ,点 B 在数轴上表示的数为5 ,则 A ,B 两点的距离为 ______.9. a 、 b 在数轴上的地点如下图,化简 : ( a 1) 2(b 1) 2 ( a b) 2 .10.已知实数在数轴上的对应点如下图,化简 : a 2 a b c a(b c) 2六、实数绝对值的应用 :11.化简以下各式:(1) 2 1.4 (2)3.14(3) 23(4) x x 3 ( x3)(5) x 2 1七、实数应用题 :第3页/共4页12.有一个边长为11cm 的正方形和一个长为13cm,宽为 8cm 的矩形,要作一个面积为这两个图形的面积之和的正方形,问边长应为多少cm。
华东师大版八年级数学上册 第11章 数的开方 第3课时 立方根导学案(无答案)
【学习课题】 第3课时 立方根 【学习目标】1、理解立方根的概念。
2、会表示一个数的立方根,并学会求一个数的立方根。
3、理解立方根的意义,并会正确区分立方根与平方根。
【学习重点】了解立方根的概念,会求一个数的立方根 【学习难点】正确区分平方根与立方根。
【候课朗读】1.算术平方根的概念及其性质。
2.10以内数的立方: 113= 823= 2733= 6443=12553=21663= 34373= 51283= 72993=1000103=【学习过程】 一、学习准备1.计算:2x+3x= ;5x-2x= ; 8y ×x=_______; 8xy ÷x= ;22= ;4= ;23= ;若x 3=8,则x= 。
观察这些算式之后我们发现:我们可以采用探究的形式,利用类比平方根的方法来展开本节知识的学习。
二、解读教材 2、立方根的概念:一般地,若一个数x 的立方等于a ,即x 3=a ,则这个数x 就叫a 的 (也叫三次方根),如2是8的立方根,-32是 的立方根,0是 的立方根。
即时练习:3.立方根的符号表达:每个数a 都只有一个....立方根,表示为 3a 。
如:x 3= 7 ,x 是7的立方根,即:x=37,而(-2)3=-8 ,所以-2是-8的立方根,即38-=-24、立方根的性质:23=8,43= ; (-3)3=-27,(-5)3= ; 0 3=0。
有没有其他的数的立方也等于8,等于64,等于-27,等于-125正数有一个正的立方根;负数有一个负的立方根;0的立方根是0本身。
5、立方根的三种表达形式: (1)定义:x 3=a (2)文字叙述:立方根 (3)符号语言:3a例1:求下列各式中的x① x 3=27 ②x 3-64=0 ③ x 3= -0.008 ④x 3=216125解:x 3=27x=327∴x=3 例2:求22710的立方根。
解:22710=2764 ∵(34)3=2764=27102 ∴27102的立方根为34即327102=34 求下列各数的立方根 ①-0.008 ② -343 ③0.512 例3:38= 364-= 3125343= -3827-=三.挖掘教材 6、开立方的定义:求一个数a 的立方根的运算,叫做开立方,其中a 叫做被开方数,表示为:3a (a 为任何数),开立方与立方互为逆运算。
2019八年级数学上册 第11章 数的开方 11.1 平方根与立方根 1 平方根 第1课时 平方根学案华东师大版
11.1 平方根与立方根第1课时平方根学习目标1.从实际问题的需要出发,引进平方根概念,体现从实际到理论、具体到抽象这样一个一般的认识过程,培养学生辩证唯物主义观点;2.从求二次幂的平方运算引出求平方根的运算,突出平方运算和开平方运算的互逆性;3.使学生理解数的平方根的概念,能运用根号表示一个数的平方根;4.掌握用平方运算求某些数的平方根的方法.学习过程一、创设情境问题1 要剪出一块面积为25 cm2的正方形纸片,纸片的边长应是多少?问题2 已知圆的面积是16πcm2,求圆的半径长.(学生探索,回答问题)二、探究归纳问题1解设正方形纸片的边长为x cm,依题意有:x2=25,求出满足x2=25的x值,就可得正方形纸片的边长.因52=25,(-5)2=25,故满足x2=25的x的值可以是5,也可以是-5,但正方形边长只能取正值.所以x=5.答正方形纸片的边长为5cm.这个问题实质上就是要找一个数,这个数的平方等于25.问题2解设圆的半径为R cm,依题意有:πR2=16π,即R2=16,求出满足R2=16的R的值即可求出圆的半径.因42=16,(-4)2=16,故满足R2=16的R的值为4或-4,但圆的半径只能取正值.所以数R=4.答圆的半径为4cm.这个问题实质上就是要找一个数,这个数的平方等于16.刚才具体的二个例子,从数学意义上都是要解决这样一个共同的问题:已知某数的平方,要求这个数.用式子来表示就是如果x2=a,求x的值.概括如果一个数的平方等于a,那么这个数叫做a的平方根(square root)(也叫a的二次方根).在上述例1问题中,因为52=25,所以5是25的一个平方根.又因为(-5)2=52=25,所以-5也是25的一个平方根.这就是说,25的平方根有两个:5与-5.在上述例2问题中,因为42=16,所以4是16的一个平方根.又因为(-4)2=42=16,所以-4也是16的一个平方根.这就是说,16的平方根有两个: 4与-4.所以,根据平方根的意义,我们可以利用平方来检验或寻找一个数的平方根.三、实践应用例1求100的平方根.解因为102=100,(-10)2=100,除了10和-10以外,任何数的平方都不等于100,所以100的平方根是10和-10,也可以说,100的平方根是±10.学生试一试:(1) 144的平方根是什么?(2) 0的平方根是什么?(3)254的平方根是什么?(4)-4有没有平方根?为什么?请学生也编三道求平方根的题目,并给出解答.与同学交流,你发现了什么?1.平方根的性质:问 正数的平方根是什么?答 如果数是正数,它们都有两个平方根,这些数的两个平方根都分别是互为相反数.问 0的平方根是什么?答 0的平方根是0,这是因为02=0.由于任何不为零的数的平方都不等于零,所以零的平方根只有一个,它就是零本身.问 负数有平方根吗?为什么?答 负数没有平方根.由于正数、零和负数的平方都不是负数,所以负数没有平方根.请同学概括数的平方根的性质.答 一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身;负数没有平方根.2.一个非负数a 的平方根的表示法.当a >0时,a 的正的平方根用符号“2a ”表示,其中a 叫做被开方数,2叫做根指数,a 的负的平方根用符号“-2a ”表示,这两个平方根合起来可以记作“2a ±”.这里,符号“2”,读作“二次根号”,“2a ”读作“二次根号a ”.当根指数是2时,通常将这个2省略不写,如2a 记作a ,读作“根号a ”;2a ±记作a ±,读作“正负根号a ”.一般地,如果x 2=a (a ≥0),那么a 的平方根可以表示为x =a ±.例如,9的平方根记作9±,读作正负根号9.3.开平方.求一个数a (a ≥0)的平方根的运算,叫做开平方.开平方运算是已知指数和幂求底数.平方与开平方互为逆运算.一个数可以是正数、负数或者是0,它的平方数只有一个,正数或负数的平方都是正数,0的平方是0.但一个正数的平方根却有两个,这两个数互为相反数,0的平方根是0.负数没有平方根.因为平方与开平方互为逆运算,因此我们可以通过平方运算来求一个数的平方根,也可以通过平方运算来检验一个数是不是另一个数的平方根.例2 将下列各数开平方:(1)49, (2)1.69.分析 开方运算就是求平方根,我们可以通过平方运算来解决.解 (1)因为49)7(2=±,所以49的平方根是,7±,即749±=±.(2) 因为69.1)3.1(2=±,所以1.69的平方根是3.1±,即3.169.1±=±.例3 下列各数有平方根吗?如果有,求出它的平方根;如果没有,请说明理由.(1)-64;(2)0;(3)(-4)2.分析 因为只有正数和零才有平方根,所以首先应观察所给出的数是否为正数或0.解 (1)因为-64是负数,所以-64没有平方根;(2)0有一个平方根,它是0;(3)因为016)4(2>=-,所以2)4(-有两个平方根,且416)4(2±=±=-±.四、交流反思1.一般地,如果x2=a ,那么叫x 做a 的平方根.(也叫a 的二次方根).用a ±表示.当a >0时a 有两个平方根,即a ±,a 表示a 的正的平方根,-a 表示a 的负的平方根,它们互为相反数;当a =0时,a 有一个平方根,就是它本身;负数没有平方根.2.求一个数a 的平方根的运算,叫做开平方,平方和开平方运算有区别又有联系.区别在于,平方运算中,已知的是底数和指数,求的是幂;而在开平方运算中,已知的是指数和幂,求的是底数.在平方运算中的底数可以是任意数,平方的结果是唯一的;在开平方运算中,被开方数必须是非负数,开平方的结果不一定是唯一的.3.平方和开平方运算又有联系,二者互为逆运算.4.求一个数的平方根,可以通过平方运算来解决.五、检测反馈1.说出下列各数的平方根(1)64; (2)0.25; (3) 6449.2.求下列各数的平方根(1)8116; (2) 0.36; (3) 324.3. 平方根等于本身的数是 .4. 已知16)2(2=x ,y 是2)5(-的正的平方根,求代数式y x xy x x-++的值.答案:1. (1)±8; (2) ±0.5; (3) ±872. (1) ±94;(2) ±0.6;(3) ±183. 04.x = ±2,y =5,y x x y x x -++的值是﹣218.六、学习小结回忆一下:本节课你有什么收获?1. 平方根、开平方的定义;2. 平方根的表示;3. 平方根的性质;4. 求一个数的平方根.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学上册导学案05
命题人:刘英明 审题人:曹金满 课型:复习课
课题:第十一章 数的开方(能力提升)
学习目标:
1.进一步理解一个数的平方根、算术平方根及立方根的意义.
2.理解无理数和实数的意义.
3.熟练地求出一个正数的平方根、算术平方根和实数的立方根.
学习重点:平方根、算术平方根、实数的概念及其计算.
学习难点:算术平方根、实数的综合运算和代数与几何的综合运用.
一、选择题:
1.下列说法中正确的是( )
A.4是8的算术平方根
B.16的平方根是4
C.6是6的平方根
D.a -没有平方根
2.下列各式中错误的是( ) A.6.036.0±=± B.6.036.0= C.2.144.1-=- D.2.144.1±=
3.若22)7.0(=x ,则x =( )
A.-0.7
B.±0.7
C.0.7
D.0.49 4.36的平方根是( )
A.6
B.±6
C.6
D.6±
5.下列语句正确的是( )
A.如果一个数的立方根是这个数本身,那么这个数一定是零;
B.一个数的立方根不是正数就是负数;
C.负数没有立方根;
D.一个数的立方根与这个数同号,零的立方根是零。
6.下列说法中,正确的是( )
A.无限小数都是无理数
B.带根号的数都是无理数
C.循环小数是无理数
D.无限不循环小数是无理数 7.a 是无理数,则a 是一个( )
A.非负实数
B.正实数
C.非完全平方数
D.正有理数
8.下列说法中,错误的是( ) A.2是无限不循环小数 B.2是无理数 C.2是实数 D.2等于1.414
9.与数轴上的点具有一一对应关系的是( )
A.无理数
B.实数
C.整数
D.有理数
10.下列说法中,不正确的是( )
A.绝对值最小的实数是0
B.平方最小的实数是0
C.算术平方根最小的实数是0
D.立方根最小的实数是0
二、填空题: 1. 和 统称为实数. 2.21-绝对值是 ,相反数是 ,倒数是 .
3.下列说法:(1)带根号的数是无理数;(2)无限小数都是无理数;(3)无理数都是无限小数;
(4)在实数范围内,一个数不是有理数,则一定是无理数,不是正数,则一定是负数. 其中错误的有 ______个.
三、非负数性质的应用:
1.若x 、y 都是实数,且233+-+-=x x y ,求y x 3+的平方根.
2.已知01)5(32=++++-c b a ,求c b a +的值.
3. 已知039
22=--++x x y x ,求y x 63+的立方根.
四、定义的应用:
4.已知2-x 的平方根是±2,72++y x 的立方根是3,求22y x +的平方根.
5.如果b a b a M -++=3是3++b a 的算术平方根,322+-+=b a b a N 是b a 2+的立方根, 求N M -的立方根.
6.已知43=x ,且03)12(2=-++-z z y ,求333z y x ++的值
7.若313-x 与321y -互为相反数,求
y
x 的值 五、数形结合的应用:
8.点A 在数轴上表示的数为53,点B 在数轴上表示的数为5-,则A ,B 两点的距离为______. 9.a 、b 在数轴上的位置如图所示,化简:222)()1()1(b a b a ---++.
10.已知实数在数轴上的对应点如图所示,化简:22)(c b a c b a a -+-+--
六、实数绝对值的应用:
11.化简下列各式: (1)4.12- (2)14.3-π (3)32- (4))3(3≤--x x x (5)12+x
七、实数应用题:
12.有一个边长为11cm 的正方形和一个长为13cm ,宽为8cm 的矩形,要作一个面积为这两个图形的面积之和的正方形,问边长应为多少cm 。
八、引申提高:
13.已知29的整数部分为a ,小数部分为b ,求))((b a b a -+的值.
14.计算)12111
431
321
211
)(132(+++++++++ .。
