运筹学excel运输问题实验报告
excel运筹学实验报告

excel运筹学实验报告《Excel运筹学实验报告》摘要:本实验报告通过使用Excel软件进行运筹学实验,探讨了在实际问题中如何利用Excel进行数据分析和决策优化。
通过实验分析,我们发现Excel在运筹学领域具有广泛的应用价值,能够帮助我们更好地理解和解决实际问题。
1. 实验背景运筹学是一门研究如何通过数学模型和计算方法来进行决策优化的学科,它在工程、管理、经济等领域都有着重要的应用。
而Excel作为一种常用的数据分析工具,具有强大的计算和图表功能,可以帮助我们进行运筹学实验的模拟和分析。
2. 实验目的本实验旨在通过使用Excel软件进行运筹学实验,探讨其在实际问题中的应用和优势,以及如何利用Excel进行数据分析和决策优化。
3. 实验过程我们选取了一个实际的运筹学问题作为实验对象,利用Excel软件建立了相应的数学模型,并进行了数据输入和计算分析。
通过Excel的求解功能,我们得到了最优化的决策方案,并进行了结果的可视化展示。
4. 实验结果通过实验分析,我们发现Excel在运筹学实验中具有以下优势:- 数据处理方便快捷:Excel具有强大的数据处理和计算功能,可以帮助我们对大量数据进行快速分析和处理。
- 决策优化准确可靠:通过Excel的求解功能,我们可以得到最优化的决策方案,帮助我们在实际问题中做出更准确的决策。
- 结果可视化直观:Excel的图表功能可以帮助我们将结果进行直观的可视化展示,使得决策过程更加清晰和可理解。
5. 实验结论通过本次实验,我们深刻认识到了Excel在运筹学领域的重要应用价值,它不仅可以帮助我们更好地理解和解决实际问题,还可以提高我们的决策效率和准确性。
因此,我们应该充分利用Excel软件进行运筹学实验,不断提升自身的数据分析和决策优化能力。
综上所述,本实验报告通过对Excel运筹学实验的探讨和分析,旨在帮助读者更好地理解和应用Excel在运筹学领域的价值和优势,从而提高决策效率和准确性。
试验报告模板——Excel在物流管理中的应用

试验报告模板——Excel在物流管理中的应用一、实验目的和要求(一)知识目标1.掌握excel常用键的使用以及快捷方式2.掌握常用基本函数以及物流管理函数的使用3.掌握如何制作表格以及表格的美化4.掌握excel在运输管理、配送与仓储、采购管理等方面的使用.(二)能力目标1.能运用excel制作常见的物流管理相关表格2.能运用excel进行物流预测、分析和决策3.能通过excel解决物流中常用的普通数学、数学分析、概率和运筹学等计算难题及物流管理中的繁琐的统计计算、财务管理计算等。
(三)素质目标1、能自主学习会计信息化新知识、新技术2、具有较强的语言表达、会计职业沟通和协调能力3、具有踏实肯干的工作作风和主动、热情、耐心的服务意识4、具有良好的心理素质、诚信品格和社会责任感教学重点:(1)Excel在运输管理中的应用;(2)Excel在配送与仓储中的应用;(3)Excel在采购管理中的应用。
二、实验内容1、Excel在运输管理中的应用本章内容利用Excel作为工具解决最小成本问题、运输模式的选择问题、运输线路决策问题和网络最大流问题。
2、Excel在配送与仓储中的应用本章内容利用Excel作为工具解决配送中心选址问题。
3、Excel在采购管理中的应用本章内容利用Excel作为工具解决采购的利润杠杆效应模拟、采供控制模型和供应商的选择与评估问题。
三、实验报告填写要求1)学生自己找一个实例,根据实例数据建立合理的模型。
2)实验设计过程进行描述(包括实验目的、实验意义、实验步骤、技术关键点与难点等解决途径),不少于六百字;3)实验设计结果;(1)输入已知条件讲问题的已知条件转换为一个矩阵,在Excel中输入。
C列表示酒店A的事;D列表示酒店B的事;E列表示酒店C的事;第4行表示仓库1的事;第5行表示仓库2的事;于是,可以在【C4:E5]这个范围输入单位运输成本。
F列表示库存量的事;于是【F4]表示仓库1的库存、【F5]表示仓库2的库存·第6行表示需求量的事;于是【C6]表示酒店A的需求量、[D6]表示酒店B的需求量、[E6]表示酒店C的需求量。
运筹学excel运输问题实验报告(一)

运筹学excel运输问题实验报告(一)运筹学Excel运输问题实验报告实验目的通过运用Excel软件解决运输问题,加深对运输问题的理解和应用。
实验内容本实验以四个工厂向四个销售点的运输为例,运用Excel软件求解运输问题,主要步骤如下:1.构建运输问题表格,包括工厂、销售点、单位运输成本、每个工厂的供应量、每个销售点的需求量等内容。
2.使用Excel软件的线性规划求解工具求解该运输问题,确定每条路径上的运输量和总运输成本。
3.对结果进行分析和解释,得出优化方案。
实验步骤1.构建运输问题表格工厂/销售点 A B C D 供应量1 4元/吨8元/吨10元/吨11元/吨35吨2 3元/吨7元/吨9元/吨10元/吨50吨3 5元/吨6元/吨11元/吨8元/吨25吨4 8元/吨7元/吨6元/吨9元/吨30吨需求量45吨35吨25吨40吨2.使用Excel软件的线性规划求解工具求解该运输问题在Excel软件中选择solver,按照下列步骤完成求解:1.添加目标函数:Total Cost=4AB+8AC+10AD+11AE+3BA+7BC+9BD+10BE+5CA+6CB+11CD+8CE+8DA+7DB+6DC+9DE2.添加约束条件:•A供应量: A1+A2+A3+A4=35•B供应量: B1+B2+B3+B4=50•C供应量: C1+C2+C3+C4=25•D供应量: D1+D2+D3+D4=30•A销售量: A1+B1+C1+D1=45•B销售量: A2+B2+C2+D2=35•C销售量: A3+B3+C3+D3=25•D销售量: A4+B4+C4+D4=403.求解结果工厂/销售点 A B C D 供应量1 10吨25吨0吨0吨35吨2 0吨10吨35吨5吨50吨3 0吨0吨15吨10吨25吨4 35吨0吨0吨0吨30吨需求量45吨35吨25吨40吨单位运输成本4元/吨8元/吨10元/吨11元/吨总运输成本2785元1480元875元550元4.结果分析和解释通过求解结果可知,工厂1最终向A销售10吨、向B销售25吨;工厂2最终向B销售10吨、向C销售35吨、向D销售5吨;工厂3最终向C销售15吨、向D销售10吨;工厂4最终向A销售35吨。
使用Excel求解运输问题
使用Excel求解运输问题
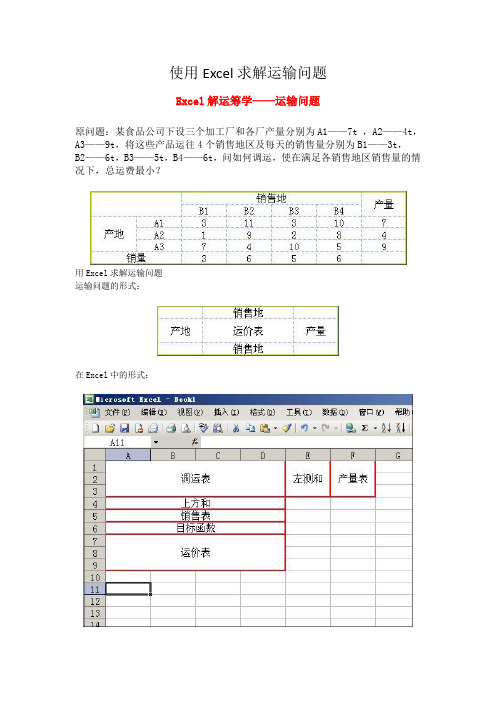
Excel解运筹学——运输问题
原问题:某食品公司下设三个加工厂和各厂产量分别为A1——7t ,A2——4t,A3——9t,将这些产品运往4个销售地区及每天的销售量分别为B1——3t,
B2——6t,B3——5t,B4——6t,问如何调运,使在满足各销售地区销售量的情况下,总运费最小?
用Excel求解运输问题
运输问题的形式:
在Excel中的形式:
步骤:
1、 F1:F3填产量表,A5:D5填售量表,A7:D9填运价表。
2、E1填=SUM(A1:D1),并复制到E3;A4填=SUM(A1:A3),并复制到D4;A6填=SUMPRODUCT(A1:D3,A7:D9)。
3、启动规划求解:
设置目标单元格:$A$6
等于:最小值
可变单元格:$A$1:$D$3
约束:A4=A5, B4=B5, C4=C5, D4=D5, E1<=F1, E2<=F2, E3<=F3在选项中选中:采用线性模型,假定非负
4、求解
得到答案:
A1给B3调运5t,B4调运2
A2给B1调运3t,B4调运1t
A3给B2调运6t,B4调运3t
A4给B1调运3t,B2调运6t,B3调运5t,B4调运6t
总运费最少为 85。
(三)运输问题的Excel建模求解
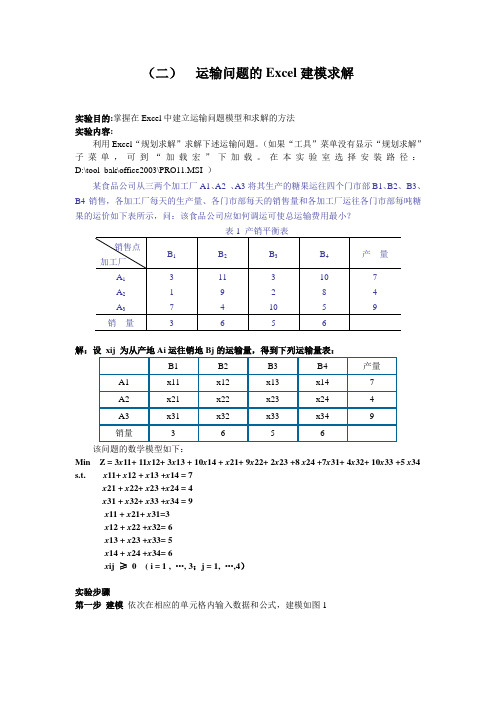
(二)运输问题的Excel建模求解实验目的:掌握在Excel中建立运输问题模型和求解的方法实验内容:利用Excel“规划求解”求解下述运输问题。
(如果“工具”菜单没有显示“规划求解”子菜单,可到“加载宏”下加载。
在本实验室选择安装路径:D:\tool_bak\office2003\PRO11.MSI )某食品公司从三两个加工厂A1、A2 、A3将其生产的糖果运往四个门市部B1、B2、B3、B4销售,各加工厂每天的生产量、各门市部每天的销售量和各加工厂运往各门市部每吨糖果的运价如下表所示,问:该食品公司应如何调运可使总运输费用最小?解:设xij 为从产地Ai运往销地Bj的运输量,得到下列运输量表:该问题的数学模型如下:Min Z = 3x11+ 11x12+ 3x13 + 10x14 + x21+ 9x22+ 2x23 +8 x24 +7x31+ 4x32+ 10x33 +5 x34 s.t. x11+ x12 + x13 +x14 = 7x21 + x22+ x23 +x24 = 4x31 + x32+ x33 +x34 = 9x11 + x21+ x31=3x12 + x22 +x32= 6x13 + x23 +x33= 5x14 + x24 +x34= 6x ij ≥0 ( i = 1 , ..., 3;j = 1, (4)实验步骤第一步建模依次在相应的单元格内输入数据和公式,建模如图1注:Sumproduct()函数:在给定的几组数组中,将数组间对应的元素相乘,并返回乘积之和。
图1运输的Excel模型第二步设置规划求解参数如图2和图3,其中,“选项”中选取“假定非负”和“采用线性模型”,其它采用默认选项,如图图2 规划求解参数设置图3 选项设置第三步求解设置完毕后,单击图2中“求解”按钮,出现如图4规划求解结果对话框图4 规划求解结果对话框如图4所示,共提供3类报告,选择你想要的报告,单击确定按钮,完成运算,最后计算结果如图5图5 计算结果思考:为什么用WINQSB最小元素法求解出来的最优解同Excel计算出来的不同,而最优值相同?(因为终表中非基变量检验数有等于0 的,说明有无穷多最优解)。
管理运筹学运输问题实验报告

管理运筹学运输问题实验报告一、实验目的通过研究和实践,掌握线性规划求解运输问题的基本模型和求解方法,了解运输问题在生产、物流和经济管理中的应用。
二、实验背景运输问题是管理运筹学中的一个重要问题,其主要目的是确定在不同生产或仓库的产量和销售点的需求之间如何进行运输,使得运输成本最小。
运输问题可以通过线性规划模型来解决。
三、实验内容1. 根据实验数据,建立运输问题的线性规划模型。
2. 使用Excel中的“规划求解器”功能求解模型。
3. 对不同情况进行敏感性分析。
四、实验原理运输问题是一种典型的线性规划问题,其目的是求解一组描述生产和需要之间的运输方案,使得总运输费用最小。
运输问题的一般模型如下:min ∑∑CijXijs.t. ∑Xij = ai i = 1,2,...,m∑Xij = bj j = 1,2,...,nXij ≥ 0其中,Cij表示从i生产地到j销售点的运输成本;ai和bj分别表示第i个生产地和第j个销售点的产量和需求量;Xij表示从第i个生产地向第j个销售点运输的物品数量。
五、实验步骤1. 根据实验数据,建立运输问题的线性规划模型。
根据题目所给数据,我们可以列出线性规划模型:min Z =200X11+300X12+450X13+350X21+325X22+475X23+225X31+275X32+400X 33s.t. X11+X12+X13 = 600X21+X22+X23 = 750X31+X32+X33 = 550X11+X21+X31 = 550X12+X22+X32 = 600X13+X23+X33 = 450Xij ≥ 02. 使用Excel中的“规划求解器”功能求解模型。
在Excel中,选择“数据”选项卡中的“规划求解器”,输入线性规划的目标函数和约束条件,并设置求解参数,包括求解方法、求解精度、最大迭代次数等。
3. 对不同情况进行敏感性分析。
敏感度分析是指在有些条件发生变化时,线性规划模型的最优解会如何变化。
物流运筹学实验报告一

实验报告一一、 实验名称:线性规划问题及运输问题 二、 实验目的:通过本实验,能掌握Spreadsheet方法,会熟练应用Spreadsheet 建模与求解方法。
在Excel (或其它)背景下就所需解决的问题进行描述与展平,然后建立线性规划模型,并使用Excel 的命令与功能进行运算与分析。
三、实验设备: 计算机、EXCEL 四、实验内容:1.线性规划问题题目:某厂生产A.B.C 三种产品,其所需劳动力、材料等有关数据见下表。
要求:(1)确定获利最大的产品生产计划;(2)如果设计一种新产品D ,单位劳动力消耗为8单位,材料消耗为2单位,每件可获利3元,问该种产品是否值得生产?解:(1)设C B A ,,各生产321,,x x x 件。
有32143min x x x z ++=⎪⎩⎪⎨⎧=≥≤++≤++)3,2,1(,03054345536321321j x x x x x x x j获利最大的生产计划是C B A ,,各生产5件、0件、3件,最大利润为273453=⨯+⨯=z 元。
( 2 ) 设新产品D 的产量为6x 。
最优计划为D C B A ,,,的产量各为0,0,5,,25最大利润为=⨯+⨯=25354z 2721元。
运用excel 可以求出两题答案,步骤如下: 第(1)题,线性规划问题的步骤:1. 进行问题描述,输入相应数据,如下图2. 建模,输入相关数据,包括:产量(变量),劳动力,材料,约束条件(资源限量),总利润3. 对表格:C11:C13编辑函数:C11 =SUMPRODUCT(C4:E4,$C$9:$E$9); C12 =SUMPRODUCT(C5:E5,$C$9:$E$9);C13 =SUMPRODUCT(C6:E6,C9:E9)4. 按“工具”----“规划求解”,进行求解:目标单元格:“$c$13” 等于“最大值”可变单元格“$C$9:$E$9” 约束“$C$11:$C$12<=$E$11:$E$12”5. 按“选项”按钮,勾选“采用线性模型”和“假定非负”,按“确定”,“求解”“确定”后可求出所需要的解注:中间的步骤很容易落下,要熟记所需的步骤,求解前检查是否有步骤遗漏。
运筹学实训报告

一、课程名称:运筹学实训二、实验名称:运输问题与Excel中的线性规划三、实验目的:1、熟练掌握运筹学软件的相关操作2、学会使用软件求解运筹学中常见的数学模型,如线性规划问题、运输问题、目标规划问题、最短路问题、最大流问题等等3、了解线性规划问题在Excel中如何建立,主要是数据单元格、输出单元格、可变单元格和目标单元格的定义以及规划求解宏定义应用设置。
4、熟练掌握Excel规划求解宏定义模块使用。
四、实验内容与要求:使用QSB+、WinQSB教学软件中的运输/转运问题软件完成运输问题的求解;进一步熟悉Excel中对一般线性规划进行灵敏度的步骤和方法、整数线性规划和运输问题这两种特殊线性规划建模与求解的步骤和方法。
在熟悉QSB+ 、WinQSB中运输问题软件基本功能基础上,能熟练操作,正确完成求解过程及分析过程。
熟悉Excel中一般线性规划的灵敏度分析、特殊线性规划的整数线性规划和运输问题的建模与求解分析过程。
五、实验任务:Ⅰ、线性规划Ⅱ、目标规划Ⅲ、运输问题Ⅳ、最短路问题Ⅴ、最大流问题六、实验过程及结果分析:1.利用规划求解:max Z=X1-2X2+X3st X1+X2+X3≤122X1+X2-X3≤6-X1+3X2≤9;X1,X2,X3≥0 解:根据步骤①建立问题模型如图所示:②加载宏,用规划求解来计算(规划求解选项、规划求解结果在以下问题讨论中操作均同)我们从电脑中得到如下数据:极限值报告:工作表:2.利用规划求解:minz=-2X1-X2+3X3-5X4 s.t X1+2X2+4X3-X4<=62X1+3X2-X3+X4<=12X1+X3+X4<=4X1,X2,X3,X4>=0解:根据步骤,我们从电脑中得到如下数据:极限值报告:工作表:3.利用规划求解解目标规划问题Min(p1(d1-+d1+),p2d2-,p3d3-,p4(5d3++3d2+)) s.t X1+X2-d1++d1-=8005X1+d2- -d2+=25003X2+d3- -d3+=1400X1,X2,d1-,d1+>=(i=1,2,3)解:根据步骤,我们从电脑中得到如下数据:极限值报告:工作表:4、利用规划求解运输问题B1 B2 B3 B4 产量A1 4 12 4 11 16 A2 2 10 3 9 10 A3 8 5 11 8 22 销量8 14 12 14解:根据步骤,我们从电脑中得到如下数据:极限值报告:工作表:5、利用规划求解解最短路径问题4V2 5V49 V65V8V7V5 V3 V167 65744解:根据步骤,我们从电脑中得到如下数据: 工作表:6、利用规划求解最大流问题解:根据步骤,我们从电脑中得到如下数据: 最大流的求解:V1V2V4V3V5V6V7 (1,1)(4,3)(3,2)(10,6)(4,2)(3,2)(5,3)(4,3)(2,2)(7,6)(8,3)极限值报告:七、实验心得:通过本次参数实训,我初步掌握了WinQSB的网络模型中的运输问题以及运用EXCEL求解线性规划问题的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学excel运输问题实验报告
运筹学Excel运输问题实验报告
实验目的
本次实验的目的是掌握运筹学中运输问题的求解方法,并能使用Excel 进行计算和求解。
实验内容
本次实验需求解以下运输问题:
供应商A产地B产地C产地供应量
X 3元/件2元/件4元/件200件
Y 4元/件1元/件3元/件300件
Z 2元/件5元/件1元/件400件
需求量300件400件200件
其中,表格左侧为供应商和需求地点,表格上方为各产地和对应的单位运费。
需求地点分别为A、B、C三个地点。
求解过程
1.将表格中的供应量和需求量累加,得到总供应量和总需求量。
本
例中,总供应量为900件,总需求量为900件。
两者相等表明运输量满足需要。
2.构造运输平衡表,计算各产地到各需求地的单位运输成本。
供应商A产地B产地C产地供应量
X 3元/件2元/件4元/件200件
Y 4元/件1元/件3元/件300件
Z 2元/件5元/件1元/件400件
需求量300件400件200件
供应商A产地B产地C产地供应量
700件800件400件
单位运输成本为:
供应商/产地 A B C
X 3 2 4
Y 4 1 3
Z 2 5 1
3.使用Excel求解运输问题:
在Excel中,按如下步骤进行操作:
1.将供应地点、需求地点和各产地到需求地点的单位运输成本输入
Excel表格。
2.创建范围使用标准化语句创建单元格范围:
$B$2:$D$4
3.在单元格范围后创建A7运算函数,使用以下语句求解运输问题:
=线性规划($B$2:$D$4,B6:B8,C5:E5)
将计算结果填入Excel表格中。
结果分析
使用Excel求解后,得到最小总运输成本为:2800元。
具体的运输方案如下表所示:
A产地B产地C产地供应量
X 0 0 200 200
Y 0 400 0 400
Z 300 0 0 300
300 400 200
可以看到,总供应量和总需求量相等,符合运输平衡的要求。
实验结论
本次实验采用Excel对运输平衡问题进行求解。
通过求解,得到最小
总运输成本和具体的运输方案。
经过结果分析,可以看到该方案符合
运输平衡的要求,同时总运输成本最小。
最终,本次实验达到了预期
目标。
结论评价
本次实验采用Excel进行运输问题的求解,相较于手工计算更为高效
且准确。
Excel中提供的线性规划函数可以方便地求解线性规划问题,使得计算过程更为简单。
同时,通过本次实验,也更深入地了解了运
输问题的求解方法和使用Excel进行计算的技巧。
但是,需要注意的是,Excel的计算结果仅为运输问题的一种解决方案,实际方案可能会受到外部因素的影响,需要在实际操作中进行实时调
整和变化。
此外,还需要考虑一些实际问题,比如物流成本的变化,
货物损失率等,这些因素都需要进一步地考虑和计算。
个人感受
本次实验让我进一步了解了运输问题的求解方法和Excel的使用技巧。
通过数学建模和Excel求解,我更加深入地了解了线性规划问题的求
解方法和计算过程,也加深了我对运筹学的理解。
同时,由于本次实
验需要进行反复计算和验证,也让我更加注重数据处理的精度和细节,从而提高了我的实验能力。
参考文献
[1] 韩乐生. 运筹学[M]. 高等教育出版社, 2007.
[2] 陈嵘, 王策. 运筹学——模型、方法与应用[M]. 清华大学出版社, 2016.
[3] 徐晓春. 运筹学基础—线性规划与整数规划[M]. 中国人民大学出
版社, 2016.
[4] Excel在运筹学中的应用. 计算机技术与发展, 2015, (12):118-119.。
