中国科学技术大学ch波尔氢原子理论
大学物理13-3 氢原子的玻尔理论

§4.氢原子的玻尔理论 / 四、氢原子的玻尔理论
例2:用 12.6eV 的电子轰击基态原子,这 些原子所能达到最高态。
解:如果氢原子吸收电子全部能量它所具 有能量
E E1 12 .6 -13.6 12.6 -1.0eV
En
E1 n2
- 13 .6 n2
-1.0eV
n 13.6 3.69 取 n 3
由
En
1 n2
-
ቤተ መጻሕፍቲ ባይዱ
me4
8
2 0
h2
,
~
m ee4
802h 3c
1 f2
-
1 i2
与
~
R
1 k2
-
1 n2
比较
R
m ee4
802h 3c
1.097373107 m-1
这一数值与实验测得结果符合很好。
§4.氢原子的玻尔理论 / 四、氢原子的玻尔理论
为此,玻尔于1922年12月10日诺贝尔诞 生100周年之际,获诺贝尔物理学奖。
n 为主量子数,上式叫量子化条件。
§4.氢原子的玻尔理论 / 四、氢原子的玻尔理论
假设3 跃迁假设
当原子从定态 Ei 跃迁到定态 Ef 要发
射或吸收频率为 的光子,
h | Ei - E f |,
|
Ei
-Ef|
h
当 Ei>Ef 原子发射光子。 当 Ei<Ef 原子吸收光子。
§4.氢原子的玻尔理论 / 四、氢原子的玻尔理论
E -1.51- (-3.39) 1.88eV
hc
。
6560 A
E
外来光提供能量使电子从n=2激发到n=5
E, -0.54 - (-3.39) 2.85eV
中国科学技术大学ch波尔氢原子理论

中国科学技术⼤学ch波尔氢原⼦理论§1—3 波尔氢原⼦理论⼀. 原⼦⾏星模型的困难卢瑟福模型把原⼦看成由带正电的原⼦核和围绕核运动的⼀些电⼦组成,这个模型成功地解释了α粒⼦散射实验中粒⼦的⼤⾓度散射现象。
α粒⼦的⼤⾓度散射,肯定了原⼦核的存在,但核外电⼦的分布及运动情况仍然是个迷,⽽光谱是原⼦结构的反映,因此研究原⼦光谱是揭⽰这个迷的必由之路。
经典理论假设:电⼦和原⼦核之间由库仑⾥作⽤,维持着电⼦在⼀定的轨道上不停的绕原⼦核旋转——原⼦的⾏星模型进⼀步的考察原⼦内部电⼦的运动规律时,却发现已经建⽴的物理规律⽆法解释原⼦的稳定性,同⼀性,再⽣性和分⽴的线光谱。
原⼦⾏星模型核外电⼦在核的库仑场中运动,受有⼼⼒作⽤Ze2 = me v24πε 0 r 2re rr+ Ze原⼦内部系统的总能量是电⼦的动能和体系的势能之和E=EK+ EV=me v 2 2Ze24πε 0 r= ? 1 ? Ze22 4πε0r电⼦在轨道中运动频率f= v = e2πr 2πZ4πε 0 me r 3卢瑟福模型提出了原⼦的核式结构,在⼈们探索原⼦结构的历程中踏出了第⼀步。
可是当我们利⽤原⼦的⾏星模型进⼊原⼦内部考察电⼦的运动规律时,却发现与已建⽴的物理规律不⼀致的现象。
经典的原⼦⾏星模型遇到了难以克服的困难。
⑴原⼦的分⽴线光谱和稳定性按经典电磁学理论,带电粒⼦做加速运动,将向外辐射电磁波,其电磁辐射频率等于带电粒⼦运动频率。
由于向外辐射能量,原⼦的能量将不断减少,则原⼦的光谱应当为连续谱;电⼦的轨道半径将不断缩⼩,最终将会落到核上,即所有原⼦将 “坍缩”。
这与事实是⽭盾的。
? ⽆法⽤经典的理论解释原⼦中核外电⼦的运动。
⑵原⼦的同⼀性任何元素的原⼦都是确定的,某⼀元素的所有原⼦之间是⽆差别的,这种原⼦的同⼀性是经典的⾏星模型⽆法理解的。
⑶原⼦的再⽣性⼀个原⼦在同外来粒⼦相互作⽤以后,这个原⼦可以恢复到原来的状态,就象未曾发⽣过任何事情⼀样。
大学物理:13-4 氢原子光谱及玻尔的氢原子理论

,
n 3,4,5,
B = 3654.7Å(经验常数)
1889年, 里德伯(J.R.Rydberg)提出普遍方程:
波数
~
1 R( k 2
Байду номын сангаас
1 n2
)
—— 里德伯方程
k 1,2,3, n k 1, k 2, k 3,
R 4 / B —— 里德伯常数
R=1.0973731568549107m-1(现代值)
~ 1 R( 1 1 )
k2 n2
n R =3
En
E1 n2
13.6 n2
可知终态 n =2,E2 = -3.4 eV
始态
n =3,E3 = -1.51 eV
“我一看到巴耳末公式,整个问题对我
来说就全部清楚了。”
—— 引自玻尔的“二月转变”
由里德伯方程
~
1
R(
1 k2
1 n2
),
双方乘hc得
h
hc
hcR(
1 k2
1 n2
),
此式右端应为能量差。
2、玻尔氢原子理论(1913):
1.定态条件: 电子绕核作圆周运动,有确定的 能量(不辐射能量)。 — 经典轨道+定态
2. 频率条件:
En ●
Ek
En Ek
h
3. 量子化条件:
vn mp ●mrn●-e
+e En
Ln mv nrn n
n=1, 2, 3…
三、氢原子轨道半径和能量的计算
e2
4 0rn2
m
v
2 n
rn
vn rn -e m
rn n2r1 ,
解得轨道半径:
玻尔氢原子理论

v e m rn 40 rn2
2 n
2
h mvn rn n 2
0h rn n me 2
2 2
nh vn 2 mrn
r =16r1
波尔半径
0 h2 10 r1 0 . 529 10 m 2 me
rn n r1
2
n 1, 2, 3,
原子能级
三、氢原子的玻尔理论
玻尔(Niels henrik David Bohr,1885-1962)
在1913年发表了《论原子结构与分子结构》 等三篇论文,提出了在卢瑟福原子有核模型基础 上的关于原子稳定性和量子跃迁的三条假设,从 而圆满地解释了氢原子的光谱规律。 玻尔的成功,使量子理论取得重大发展,推 动了量子物理的形成,具有划时代的意义。 玻尔于1922年12月10日诺贝尔诞生100周年之 际,在瑞典首都接受了当年的诺贝尔物理学奖金。 1937年,他来中国作学术访问
h Ei E f
me4 1 1 2 2 2 2 8 0 h n n i f
me 1 1 2 3 2 2 8 0 h c n n f i
4
比较前面 氢原子经 验公式
ni n f
ni n f
1 1 R n n
R T (n f ) 2 nf
R T ( ni ) 2 ni
二
卢瑟福的原子有核模型
卢瑟福(E. Rutherford,1871-1937)
1859年成为卡文迪许实验室主任J. J. Thomson的研究生。 1899年1月发现铀盐放射出α射线和β射线, 并提出天然放射性的衰变理论和衰变定律。 天然放射性的发现与电子和X射线的发现,是 20世纪三项最伟大的发现。 他于1908年获得诺贝尔化学奖金。 卢瑟福还判定α粒子是带正电的氦原子核, 他根据α粒子散射实验提出原子的有核模型。 卢瑟福被誉为原子物理之父,又是开创原子 核物理学的奠基人。
氢原子光谱实验规律 波尔理论

二、卢瑟福的原子有核模型
1. 卢瑟福的原子有核模型
1911 年卢瑟福根据 α 粒子散射实验结果建立 了原子的有核模型。
① 所有正电荷和几乎所有的原子 质量都集中在原子中心的一个 非 常 小 ( R≤10-15m ) 的 体 积 内, 这就是“原子核”;
② 原子中的电子围绕原子核转动;
③ 带正电的核和带负电的电子间 的静电引力把整个原子结合在 一起。
解: 赖曼系
1
R(112
1 n2
)
1/[R(1n12)] 其 中 R 1 .0 9 7 1 0 2 n m 1
n = 2 时对应最长波长 max 121.5nm
n = ∞时对应最短波长 min 91.2nm
帕邢系
1/[1.097
104
(
1 32
1 n2
)](nm)
53 1282nm
例题2 :
% R(612n 12) n7,8,9,L
3) 氢原子光谱规律
氢原子光谱有着内在的联系,表现在其波数可用 一普遍公式来表示:
v% 1
R
1 k2
1 n2
(广义巴尔末公式)
式中: k1,2,3L, n k 1 ,k 2 ,k 3 ,L
对应一个 k 就构成一个谱线系。
里兹组合原理:任一条谱线的波数都可以写成两 项之差的形式,即
• 每一谱线的波数都可以表示为二个光谱项之差
% T (k)T (n )
%
1
R
1 k2
1 n2
---广义巴尔末公式
表面上如此繁杂的光谱线竟然由一个式 子简单地表示,这不能不说是一项出色的成 果,但公式是凭经验凑出来的,它为什么与 实验符合得如此好,在公式问世将近三十年 内,一直是个谜。
16.4玻尔氢原子理论
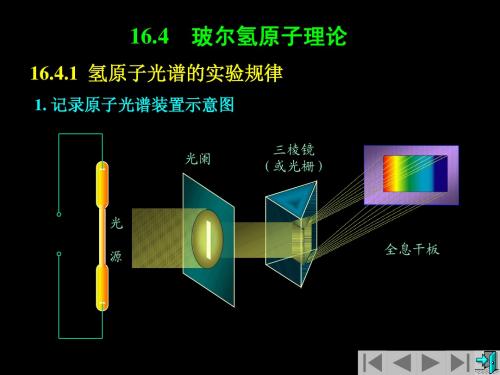
h L=m r =n v = nh 2π n 叫做量子数。 h = h 2π 叫做约化普朗克常数。 叫做量子数 量子数。 叫做约化普朗克常数 约化普朗克常数。
2. 氢原子轨道和能量
{
v 1 e m = r 4 πε0 r2 L = nh
2
2
r
r v
得到第 n 个定态的轨道半径和 氢原子能量分别为: 氢原子能量分别为:
16.4 玻尔氢原子理论
16.4.1 氢原子光谱的实验规律 氢原子光谱的实验规律
1. 记录原子光谱装置示意图
三棱镜 (或光栅)
光阑
光 全息干板 源
2. 氢原子光谱 关于氢原子光谱的研究,可追溯到十九世纪中叶。 关于氢原子光谱的研究,可追溯到十九世纪中叶。瑞典物 原子光谱的研究 理学家埃格斯特朗( 理学家埃格斯特朗(1814~1874)首先在气体放电的光谱中 ~ ) 发现了氢 后来他又发现了氢 发现了氢原子光谱的 Hα 线,后来他又发现了氢原子光谱在可 见光波段的其它三条谱线,并且精确地测量了它们的波长。 见光波段的其它三条谱线,并且精确地测量了它们的波长。
计算氢原子巴耳末系的最短波长和最长波长。 例 计算氢原子巴耳末系的最短波长和最长波长。 解 最长波长是 E3 E2 能级的跃迁产生的: 能级的跃迁产生的:
1
λmax
1 1 5 7 = R( 2 − 2 ) = 1.097 ×10 × 2 3 36
λmax = 6563A
最短波长即线系限波长: 最短波长即线系限波长: 即线系限波长
rn = n2 (
) = n2r 1 2 πme
ε0h2
(n = 1,2,3,L )
E1 1 me4 En = − 2 ( 2 2 ) = 2 n 8ε0 h n
《大学物理》氢原子的玻尔理论

原子发光是重要的原子现象之一, 光谱学 的数据对物质结构的研究具有重要意义。
氢原子谱线的波长可以用下列经验公式表示:
~
R(
1 k2
1 n2
)
k 1,2,3, n k 1, k 2, k 3,
~ 1
波数
R 1.096776 107 m-1 里德伯常量
~nk
me4
8 0 2 h3c
(
1 k2
1 n2
)
与氢原子光谱经验公式是一致的。
R
me4
8
2 0
h3c
1.0973731107
m
-1
R 理论值与实验值符合得很好。
玻尔的创造性工作对量子力学的建立有着深远的影响。
四. 玻尔理论的缺陷
● 玻尔理论仍然以经典理论为基础,定态假设 又和经典理论相抵触。
● 量子化条件的引进没有适当的理论解释。 ● 对谱线的强度、宽度、偏振等无法处理。
定态跃迁到另一能量为 射或吸收一个频率为
Ek
kn
的定态时,就要发 的光子。
kn
En
Ek h
玻尔辐射频率公式
(3)量子化条件 在电子绕核作圆周运动中,
其稳定状态必须满足电子的角动量 的整数倍的条件。
L
mvr
等于
h
2
L n h , n 1,2,3, 角动量量子化条件
2
n 为量子数
三. 氢原子轨道半径和能量的计算
根据电子绕核作圆周运动的模型及角动量 量子化条件可以计算出氢原子处于各定态时的 电子轨道半径。
rn n2 (m0he22 ),n 1,2,3,
r1 0.5291010m 玻尔 半径
氢原子的玻尔理论
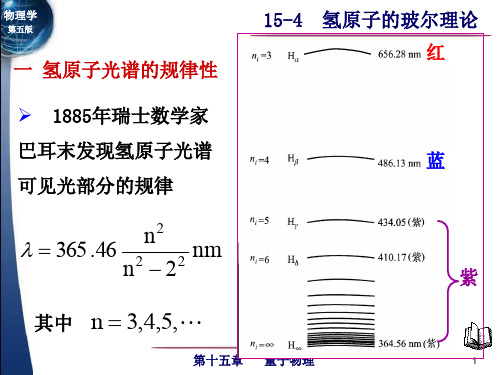
电子在原子中可以在一些特定的圆轨道上运动 而不辐射电磁波,这时,原子处于稳定状态,简称 定态.
与定态相应的能量 分别为 E1,E2… , E1 < E2< E3
是对经典概念的修改!
E1+ E3
第十五章 量子物理
24
物理学
第五版 (2)量子化条件
15-4 氢原子的玻尔理论
引入角动量量子化的概念 L mvr n h 2π
第十五章 量子物理
2
物理学
第五版
紫外 可见光
红外
15-4 氢原子的玻尔理论
莱曼系
1
R(112
1 n2
)
,
巴尔末系
1
R(
1 22
1 n2
)
,
n 2,3, n 3,4,
帕邢系
1
R(312
1 n2
),
n 4,5,
布拉开系
1
R(
1 42
1 n2
)
,
玻尔理论对氢原子光谱的解释
En
me4
8
2 0
h
2
1 n2
h Ei E f
1c Nhomakorabea
me4
8
2 0
h3c
(
1 n2f
1 ni2
)
,
ni n f
里德伯常量
R
me4
8 02 h3c
1.0973731107
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1—3 波尔氢原子理论一. 原子行星模型的困难卢瑟福模型把原子看成由带正电的原子核和围绕核运动的一些电子组 成,这个模型成功地解释了α粒子散射实验中粒子的大角度散射现象。
α粒子的大角度散射,肯定了原子核的存在,但核外电子的分布及运动 情况仍然是个迷,而光谱是原子结构的反映,因此研究原子光谱是揭 示这个迷的必由之路。
经典理论假设:电子和原子核之间由库仑里作用,维持着电子在一定 的轨道上不停的绕原子核旋转——原子的行星模型进一步的考察原子内部电子的运动规律时,却发现已经建立的物理规 律无法解释原子的稳定性,同一性,再生性和分立的线光谱。
原子行星模型核外电子在核的库仑场中运动,受有心力作用Ze2 = me v24πε 0 r 2r−e rr+ Ze原子内部系统的总能量是电子的动能和体系的势能之和E=EK+ EV=me v 2 2−Ze24πε 0 r= − 1 ⋅ Ze22 4πε0r电子在轨道中运动频率f= v = e2πr 2πZ4πε 0 me r 3卢瑟福模型提出了原子的核式结构,在人们探索原子结构的历程中踏 出了第一步。
可是当我们利用原子的行星模型进入原子内部考察电子 的运动规律时,却发现与已建立的物理规律不一致的现象。
经典的原 子行星模型遇到了难以克服的困难。
⑴ 原子的分立线光谱和稳定性¾ 按经典电磁学理论,带电粒子做加速运动,将向外辐射电磁波,其电磁 辐射频率等于带电粒子运动频率。
¾ 由于向外辐射能量,原子的能量将不断减少,则原子的光谱应当为连续 谱;电子的轨道半径将不断缩小,最终将会落到核上,即所有原子将 “坍缩”。
¾ 这与事实是矛盾的。
¾ 无法用经典的理论解释原子中核外电子的运动。
⑵ 原子的同一性 任何元素的原子都是确定的,某一元素的所有原子之间是无差别的, 这种原子的同一性是经典的行星模型无法理解的。
⑶ 原子的再生性一个原子在同外来粒子相互作用以后,这个原子可以恢复到原来的 状态,就象未曾发生过任何事情一样。
原子的这种再生性,是行星 模型所无法说明的。
二. 波尔氢原子模型玻尔(N.Bohr)基于卢瑟福原子模型,原子光谱的实验规律、普 朗克的关于黑体辐射的量子论以及爱因斯坦的光子概念,于1913 年提出了新的原子模型并成功地建立了氢原子理论。
波尔的氢原子模型成功解释了氢光谱的产生,能准确地推出巴尔末 公式,并能算出里德伯常数的理论值。
此外,玻尔理论对类氢离子 的光谱也能给出很好的解释。
因此,玻尔理论一举成功,很快为人 们接受。
不过当玻尔理论应用于复杂一些的原子时,就与实验事实产生了 较大的出入。
这说明玻尔理论还很粗略,直到1925年量子力学建 立以后,人们才建立了较为完善的原子结构理论。
⑴ 玻尔假设为了解释氢原子光谱的实验事实,玻尔于1913年提出了他的三条基本假设:①定态假设:原子的能量状态时分立的,处 于一定能量状态的原子是稳定,电子只在某− errn些特定的轨道上运动,每一个轨道对应一个+ Ze定态En。
即使电子在这些轨道上做加速运动,也不向外辐射能量。
②角动量量子化假设:电子处于上述定态时, 角动量是量子化的。
L = merv = nhr Pφ vrrrnh = h 2π③频率条件:电子并不永远处于一个轨道上,当它吸收或放出能量 时,会在不同轨道间发生跃迁,跃迁前后的能量差满足频率法则:v = En − Em h En−ern rm+ ZeEm根据上述三条基本假设,玻尔建立了他的原子模型,并成功地解 释了氢光谱的实验事实。
⑵ 玻尔模型①(类)氢原子的大小玻尔假设电子在特定的轨道上绕核作圆周运动,设核的电量为Ze(当 Z=1时,就是氢原子)。
如果原子核是固定不动的,电子绕核作匀速圆周运动,那么由牛顿第二定律,电子所受库仑力恰好提供了它作圆周 运动的向心力:即14πε 0⋅Ze2 r2=mev2 r⇒r = 1 ⋅ Ze24πε0 mev2代入量子化条件 L = mevr = nh得rn=4πε 0h 2mee2⋅n2 Z,n = 1,2,3,L我们引入a0=4πε 0h 2mee2= 0.53×10−10 m则量子化的轨道半径为rn=a0⋅n2 Z相应的轨道速率为vn=nh mern=e2 ⋅ Z4πε0h n=Zαcn当Z=1(氢原子),n=1 时电子的轨道半径与速率分别为r1 = a0氢原子的第一轨道半径——玻尔半径;rn = n2a0v1=e24πε 0hvn=αcn精细结构常数氢原子的第一玻尔速度α = e2 ≈ 1 4πε 0hc 137类氢离子:原子核外只有一个电子,而核电荷数大于1的体系。
比如一次电离的氢离子He+,二次电离的锂离子Li2+,三次电离的铍 离子Be3+,都是具有类似氢原子结构的离子。
氢原子及类氢离子的轨道半径②(类)氢原子的定态能量——量子化的波尔能级电子在原子核的库仑场中运动,所以电子的能量由动能EK和势能EV 两部分构成。
由于轨道半径 r 是量子化,所以相应的能量也必然是量子化的。
En=−14πε 0⋅Ze2 2rn=−2π 2mee4 (4πε0 )2 h2⋅Z2 n2=−Z2 2n2mec2α 2=−hcRZ2 n2R=meα 2c2h=2π 2mee4 (4πε0 )2 h3c里德伯常量上式为量子化能级的表达式,当Z=1,n=1时,就是氢原子的基态E1=−1 2mec2α 2=−hcR≈−13.6eVn≥2 的状态,称为原子的激发态En=−1 2n2mec2α 2=−hcR n2≈− 13.6 n2eVn → ∞, rn → ∞, EV → 04 3 2 n=1∞E∞=0n=6n=5-0.85 eV Pfundn=4Brackett-0.85 eVn=3Paschen-1.51 eVn=2Balmer激发态 -3.40 eV轨道模型n=1 Lyman原子能级图基态 -13.6 eV电子在轨道间跃迁时,原子在不同的能级间跃迁③(类)氢原子的光谱根据波尔理论,氢原子的光谱可以作如下的解释:氢原子在正常状态时,它的能级最小,电子位于最小的轨道,当原 子吸收或放出一定的能量时,电子就会在不同的能级间跃迁,多余 的能量便以光子的形式向外辐射,从而形成氢原子光谱。
由波尔假设的频率条件我们可以可到光谱公式hv=En−Em=hcRZ 2 ⎛⎜ ⎝1 m2−1 n2⎞⎟ ⎠ν~=RZ 2 ⎜⎛ ⎝1 m2−1 n2⎟⎞ ⎠R 为里德伯常数当 Z=1 时即为里德伯方程ν~=R⎜⎛ ⎝1 m2−1 n2⎟⎞ ⎠里德伯常数的理论值R = meα 2c = 2π 2mee4 = 1.09737315×107 m−1 2h (4πε0 )2 h3c由氢光谱的实验数据,里德伯常数的实验值RH = 1.0967758×107 m−1¾比较 R 与 RH ,我们发现两者符合的很好,说明了波尔原子模型的正确性; ¾但是它们之间依然有万分之五的差别,而当时光谱学的实验精度已达 万分之一。
④ 原子核质量的影响玻尔理论假定电子绕固定不动的核旋转,只有当核的质量无限大时 才可以作这样的近似。
而氢核只比电子重约一千八百多倍,这样的 处理显然不够精确。
实际情况是核与电子绕它们共同的质心运动。
⎩⎨⎧rM=r1= mer2 r1 + r2⎧⎪⎪r1=μMr⎨ ⎪⎪⎩r2=μmer约化质量 μ = MmeM + me波尔对原子模型进行修正,当原子核并非静止时,采用质心坐标系,在有心力场的两体问题中,只需要用约化质量 μ 代替电子的质量 me, 则上述结论就对应于质心系:En=−2π 2μe4 (4πε0 )2 h2⋅Z2 n2rn=4πε 0h 2 μe2⋅n2 ZRM=4πμe4 ⋅ (4πε0 )2 h3c=R∞μme=R∞1+1 meMRω 是原子核质量为无穷大时的里德伯常量,我们注意到,前面 我们算出的里德伯常数 R 其实是Rω。
对于氢原子,m/M=1/1836.15RA=R∞1+1 me/M= 10973731×1= 10967758 m−11 + 1 / 1836.15与实验值RH完全吻合!!里德伯常数随原子核质量变化的情况曾被用来证实氢的同位素— 氘的存在。
起初有人从原子质量的测定估计有质量是2个单位的重氢——氘。
1932年,尤雷在实验中发现,所摄液氢莱曼系的头四条谱线都是双 线,双线之间波长差的测量值与通过里德伯常数 RD 计算出的双线 波长差非常相近,从而确定了氘的存在。
美国物理学家尤雷观察到的含有氢/氘两种物质的混合 体的光谱系双线,以及测量出的双线间的波长差。
按照波尔理论:ν~H=RH⎜⎛ ⎝1 m2−1 n2⎟⎞ ⎠ν~D=RD⎜⎛ ⎝1 m2−1 n2⎟⎞ ⎠RD = 2(M H + me ) = 1+ meRH 2M H + me2M H + me因为 RD > RH ,所以对于同一谱线 v~D > v~H 即 λD < λH对于同一级谱线λD = RH λH RD⇒λH − λD = Δλ = 1 − RHλHλHRDRH = 0.999727 ⇒RDΔλ = 0.000272 λH⑤ 连续谱我们已经知道,所有的光谱线分为一系列线系,每个线系的谱线 都从最大波长到最小波长(系线);可是试验中观察到在系限之 外还有连续变化的谱线。
这是怎么回事呢?当速度为v0的自由电子被 H+ 捕获并进入第 m 轨道时ΔE=1 2mev02−Em=hνν~ = mev02 − RH2hc m2因为 Em 是一定的,而 v0 是任意的,所以可以产生连续的 λ 值,对应连续的光谱,这就是各系限外出现连续谱的原因。
处于基态的电子吸收大于 |E1| 的电磁辐射而跃迁到连续能级区, 成为自由电子——光电效应。
。
