氢原子的玻尔理论知识
氢原子光谱玻尔氢原子理论

根据电子绕核作圆周运动的模型及角动量 量子化条件可以计算出氢原子处于各定态时的 电子轨道半径。
玻尔的氢原子理论
rn n2 (m0he22 ),n 1,2,3,
r1 0.5291010m 玻尔 半径
电子处在半径为 rn的轨道上运动时,可以计
算出氢原子系统的能量 En为
En
1 n2
பைடு நூலகம்
(8m0e2h4 2 ), n
● 量子化条件的引进没有适当的理论解释。 ● 对谱线的强度、宽度、偏振等无法处理。
氢原子光谱
例题18-6 在气体放电管中,用能量为12.5eV的电子通 过碰撞使氢原子激发,问受激发的原子向低能级 跃迁时,能发射那些波长的光谱线?
解: 设氢原子全部吸收电子的能量后最高能激发到第n
个能级,此能级的能量为
态跃迁到另一能量为 Ek的定态时,就要发射
或吸收一个频率为 kn 的光子。
kn
En
Ek h
玻尔频率公式
玻尔的氢原子理论
(3)量子化条件 在电子绕核作圆周运动中,
其稳定状态必须满足电子的角动量 L等于 h
的整数倍的条件。
2
L n h , n 1,2,3,
2
n为量子数
角动量量子化条件
3. 氢原子轨道半径和能量的计算
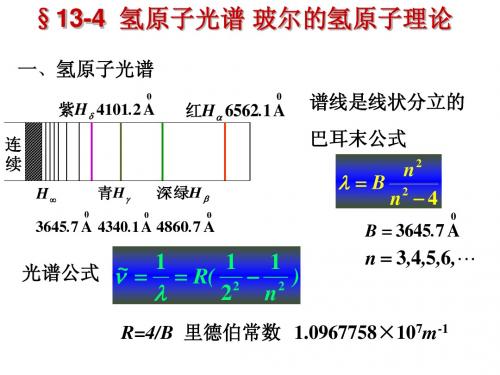
§18-4 氢原子光谱 玻尔的氢原子理论
1. 氢原子光谱的规律性
原子发光是重要的原子现象之一, 光谱学 的数据对物质结构的研究具有重要意义。
氢原子谱线的波长可以用下列经验公式表示:
~
R(
1 k2
1 n2
)
~ 1
k 1,2,3, n k 1, k 2, k 3,
波数
R 1.096776 107 m-1 里德伯常量
玻尔理论与氢原子跃迁(含答案)

玻尔理论与氢原子跃迁一、基础知识 (一)玻尔理论1、定态:原子只能处于一系列不连续的能量状态中,在这些能量状态中原子是稳定的,电子虽然绕核运动,但并不向外辐射能量.2、跃迁:原子从一种定态跃迁到另一种定态时,它辐射或吸收一定频率的光子,光子的能量由这两个定态的能量差决定,即hν=Em -En.(h 是普朗克常量,h =6.63×10-34 J·s)3、轨道:原子的不同能量状态跟电子在不同的圆周轨道绕核运动相对应.原子的定态是不连续的,因此电子的可能轨道也是不连续的.4、氢原子的能级、能级公式 (1)氢原子的能级图(如图所示) (2)氢原子的能级和轨道半径 ①氢原子的能级公式:En =1n2E1(n =1,2,3,…),其中E1为基态能量,其数值为E1= -13.6 eV .②氢原子的半径公式:rn =n 2r1(n =1,2,3,…),其中r1为基态半径,又称玻尔半径,其数值为r1=0.53×10-10m.(二)氢原子能级及能级跃迁对原子跃迁条件的理解(1)原子从低能级向高能级跃迁,吸收一定能量的光子.只有当一个光子的能量满足hν=E 末-E 初时,才能被某一个原子吸收,使原子从低能级E 初向高能级E 末跃迁,而当光子能量hν大于或小于E 末-E 初时都不能被原子吸收.(2)原子从高能级向低能级跃迁,以光子的形式向外辐射能量,所辐射的光子能量恰等于发生跃迁时的两能级间的能量差.特别提醒 原子的总能量En =Ekn +Epn ,由ke2r2n =m v2rn 得Ekn =12ke2rn ,因此,Ekn 随r 的增大而减小,又En随n 的增大而增大,故Epn 随n 的增大而增大,电势能的变化也可以从电场力做功的角度进行判断,当r 减小时,电场力做正功,电势能减小,反之,电势能增大. 二、练习1、根据玻尔理论,下列说法正确的是( )A .电子绕核运动有加速度,就要向外辐射电磁波B .处于定态的原子,其电子绕核运动,但它并不向外辐射能量C .原子内电子的可能轨道是不连续的D .原子能级跃迁时,辐射或吸收光子的能量取决于两个轨道的能量差 答案 BCD解析 根据玻尔理论,电子绕核运动有加速度,但并不向外辐射能量,也不会向外辐射电磁波,故A 错误,B 正确.玻尔理论中的第二条假设,就是电子绕核运动可能的轨道半径是量子化的,不连续的,C 正确.原子在发生能级跃迁时,要放出或吸收一定频率的光子,光子能量取决于两个能级之差,故D 正确.2、下列说法中正确的是( )A .氢原子由较高能级跃迁到较低能级时,电子动能增加,原子势能减少B .原子核的衰变是原子核在其他粒子的轰击下而发生的C .β衰变所释放的电子是原子核内的中子转化成质子而产生的D .放射性元素的半衰期随温度和压强的变化而变化 答案 AC解析 原子核的衰变是自发进行的,选项B 错误;半衰期是放射性元素的固有特性,不 会随外部因素而改变,选项D 错误.3、(2000•安徽)根据玻尔理论,某原子的电子从能量为E 的轨道跃迁到能量为E'的轨道,辐射出波长为λ的光.以h 表示普朗克常量,C 表示真空中的光速,则E ′等于( C )A .E−h λ/cB .E+h λ/cC .E−h c /λD E+hc /λ4、欲使处于基态的氢原子激发,下列措施可行的是 A.用10.2 eV 的光子照射 B.用11 eV 的光子照射 C.用14 eV 的光子照射D.用11 eV 的光子碰撞[命题意图]:考查考生对玻尔原子模型的跃迁假设的理解能力及推理能力.[解答]:由"玻尔理论"的跃迁假设可知,氢原子在各能级间,只能吸收能量值刚好等于两能级之差的光子.由氢原子能级关系不难算出,10.2 eV 刚好为氢原子n=1和n=2的两能级之差,而11 eV 则不是氢原子基态和任一激发态的能量之差,因而氢原子只能吸收前者被激发,而不能吸收后者.对14 eV 的光子,其能量大于氢原子电离能,足可使“氢原子”电离,而不受氢原子能级间跃迁条件限制.由能的转化和守恒定律不难知道,氢原子吸收14 eV 的光子电离后产生的自由电子仍具有0.4 eV 的动能.另外,用电子去碰撞氢原子时,入射电子的动能可全部或部分地为氢原子吸收,所以只要入射电子的动能大于或等于基态和某个激发态能量之差,也可使氢原子激发,故正确选项为ACD.例1、一个具有E K0=20.40eV 动能、处于基态的氢原子与一个静止的、同样处于基态的氢原子发生对心碰撞(正碰),则下列关于处于基态的氢原子向激发态跃迁的说法中正确的是( ) A.不可能发生跃迁 B.可能跃迁到n=2的第一激发态 C.可能跃迁到n=3的第二激发态 D.可能跃迁到n=4的第三激发态【解析】两个氢原子做完全非弹性碰撞时损失的动能最大,损失动能的极值0110.22E E ev ∆==,所以处于基态的氢原子只可能跃迁到n=2的第一激发态。
高中物理:玻尔理论与氢原子的能级跃迁

高中物理:玻尔理论与氢原子的能级跃迁【知识点的认识】氢原子的能级和轨道半径(1)氢原子的能级公式:E n=E1(n=1,2,3,…),其中E1为基态能量E1=﹣13.6eV.(2)氢原子的半径公式:r n=n2r1(n=1,2,3,…),其中r1为基态半径,又称玻尔半径,r1=0.53×10﹣10m.(3)氢原子能级图(如图)①能级图中的横线表示氢原子可能的能量状态﹣﹣定态.②横线左端的数字“1、2、3…”表示量子数,右端的数字“﹣13.6,﹣3.4,…”表示氢原子的能级.③相邻横线间的距离,表示相邻的能级差,量子数越大,相邻的能级差越小.④带箭头的竖线表示原子由较高能级向较低能级跃迁,放出光子的能量:hν=E m﹣E n.特别提醒:能级越高,量子数越大,轨道半径越大,电子的动能越小,电势能越大,原子的能量随能级的升高而增大.【命题方向】题型一:氢原子能级跃迁问题氦原子被电离一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为E1=﹣54.4eV,氦离子能级的示意图如图所示.在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是()A.40.8eV B.43.2eV C.51.0eV D.54.4eV分析:当光子的能量和某两个能级之间的能量差相等时才能被吸收,即体现能量的量子化.解答:根据量子理论可以知道,处于基态的离子在吸收光子能量时是成份吸收的,不能积累的.因此当其它能级和基态能量差和光子能量相等时,该光子才能被吸收.A、由能级示意图可知:第2能级和基态能级差为:△E1=E2﹣E1=﹣13.6﹣(﹣54.4)=40.8eV,故A选项中光子能量能被吸收,故A错误;B、没有能级之间的能量差和B中光子能量相等,故B正确;C、第4能级和基态能级差为:△E2=E4﹣E1=﹣3.4﹣(﹣54.4)=51.0eV;故C选项中光子能量能被吸收,故C错误;D、当光子能量大于等于基态能量时,将被处于基态离子吸收并能使其电离,故选项D中的光子能量能被吸收,故D错误故选B.点评:轨道量子化和能量量子化是量子力学的基础,是近代物理学的巨大飞跃,学生要能通过简单的计算理解其意义.【解题方法点拨】1.对原子跃迁条件的理解(1)原子从低能级向高能级跃迁,吸收一定能量的光子,当一个光子的能量满足hν=E末﹣E初时,才能被某一个原子吸收,使原子从低能级E初向高能级E末跃迁,而当光子能量hν大于或小于E末﹣E初时都不能被原子吸收.(2)原子从高能级向低能级跃迁,以光子的形式向外辐射能量,所辐射的光子能量恰等于发生跃迁时的两能级间的能量差.(3)原子跃迁条件hν=E m﹣E n只适用于光子和原子作用而使原子在各定态之间跃迁的情况.对于光子和处于基态的氢原子作用而使氢原子电离时,只要入射光子的能量E≥13.6eV,氢原子就能吸收.对于实物粒子与原子作用使原子激发时,粒子能量大于能级差即可.2.量子数为n的氢原子跃迁时辐射光子种数的判定方法:如果是一个氢原子,向低能级跃迁时辐射光子的可能频率种数为(n﹣1).如果是一群氢原子,向低能级跃迁时最多发出的光子种数为C.。
氢原子的玻尔理论1
4340.5Å 紫 。 ‥
巴耳末(J.J.Balmer)分析这些谱线后,得到
~ 1 4 ( 1 - 1 ) , n 3,4,5, 经验公式:波数 B 22 n2
B = 3645.6Å(经验常数) 里德伯(J.R.Rydberg)提出普遍方程: 1889年,
波数
~ R( 1 - 1 ) n 2 n 2
—— 里德伯方程
n 1,2,3, n n 1, n 2, n 3, R 4 / B —— 里德伯常数
R=1.0973731568549107m-1(现代值)
后来发现在紫外和红外区还有其他谱线系。 氢光谱各谱线系与 n 的关系:
~ R( 1 - 1 ) n 2 n 2
1. 玻尔的量子化假设
玻尔认为电子绕核作圆周运动不发射 电磁波,并保持原子结构的稳定。在原子 有核基础上应用量子化概念,提出三个基 本假设,该理论是经典理论和普朗克量子 化概念的混合。为半经典理论或早期氢原 子的量子理论。
假设1(定态假设) 电子在原子中,可以在一些特定的圆 轨道上运动而不辐射电磁波,这时原子处 于稳定状态(简称定态),并具有一定的 能量。 假设2(角动量量子化假设) 电子以速度 v 在半径为 r 的圆周上绕 核运动时,只有电子的角动量 L 等于h/2 的整数倍的那些轨道才是稳定的,即 n 1,2,3,4 L mvr nh / 2
氢原子的 玻尔理论
十九世纪末二十世纪初,一些实验现象相继发 现,如电子、X 射线和放射性元素的发现表明原 子是可以分割的,它具有比较复杂的结构,原子 是怎样组成的?原子的运动规律如何?对这些问 题的研究形成了原子的量子理论。
一、原子结构的探索
1897年,J.J.汤姆逊发现电子以后,人们就 知道原子中除有电子以外,一定还存在着带正 电的部分。而且原子内正、负电荷相等。电子 和正电荷是如何分布的呢?
玻尔的氢原子理论

玻尔的氢原子理论
为此,J.汤姆孙在1904年提出了原子结构的枣糕式模型.该模型认 为,原子可以看作一个球体,原子的正电荷和质量均匀分布在球内, 电子则一颗一颗地镶嵌其中.1909年,J.汤姆孙的学生卢瑟福为了验证 原子结构的枣糕式模型,完成了著名的α粒子散射实验.实验发现α粒 子在轰击金箔时,绝大多数α粒子都穿透金箔,方向也几乎不变,但 是大约有1/8 000的α粒子会发生大角度偏转,即被反弹回来.这样的 实验结果是枣糕式模型根本无法解释的,因为如果说金箔中的金原子 都是枣糕式的结构,那么整个金箔上各点的性质应该近乎均匀,α粒 子轰击上去,要么全部透射过去,要么全部反弹回来,而不可能是一 些穿透过去,一些反弹回来.
玻尔的氢原子理论
二、 原子结构模型
1897年,J.汤姆孙发现了电子.在此之前,原 子被认为是物质结构的最小单元,是不可分的,可 是电子的发现却表明原子中包含带负电的电子.那 么,原子中必然还有带正电的部分,这就说明原子 是可分的,是有内部结构的.执着的科学家就会继 续追问:原子的内部结构是什么样的?简洁的里德 伯光谱公式是不是氢原子内部结构的外在表现?
玻尔的氢原子理论
三、 玻尔的三点基本假设
为了解决原子结构有核模型的稳定性和氢原子光谱的分 立性问题,玻尔提出以下三个假设:
(1)定态假设.原子中的电子绕着原子核做圆周运动, 但是只能沿着一系列特定的轨道运动,而不能够任意转动, 当电子在这些轨道运动时,不向外辐射电磁波,原子系统处 于稳定状态,具有一定的能量.不同的轨道,具有不同的能 量,按照从小到大的顺序记为E1、E2、E3等.
玻尔的氢原子理论
可是这个模型却遭到很多物理学家的质疑.因为按照当时的物 理理论(包括经典力学、经典电磁理论及热力学统计物理),这 样一个模型是根本不可能的,原因有以下两个:
氢原子的玻尔理论

③氢原子的能级 ( energy level ) E1 基态 ( ground state ) E2 , E3 ,… ,激发态 ( excited ) ④由玻尔假设可导出广义巴尔末公式
hν = En- Ek /8ε 1/λ = ν /c = me4/8ε0h3c(1/k2 - 1/n2 ) 1/λ = R (1/k2 - 1/n2 ) , n > k
小结
1.玻尔假设 1.玻尔假设 ①定态假设 跃迁假设 ②跃迁假设 hν = En- Ek 2.德布罗意 德布罗意假设 2.德布罗意假设 λ = h / mv ; E = hν
h 1 1 λ= =h • mv 2qm U
电子的德布罗意波长: 电子的德布罗意波长: 德布罗意波长
λ e = 1.23 •
1 U
(nm)
3.电子衍射
二、电子显微镜
■光学显微镜能分辨的两点间最小距离: 光学显微镜能分辨的两点间最小距离:
λ越小,Z越小,则分辨本领越高。 越小, 越小,则分辨本领越高。 ■但可见光波长较大,即光学显微镜分辨 但可见光波长较大, 本领有限。 本领有限。 ■电子显微镜可提高分辨本领 利用电子射线代替照射光
λ = h / p = h / mv ν =E / h
(德布罗意公式) 德布罗意公式 公式)
2.德布罗意波长 德布罗意波长
设带电粒子的电量:q ,质量:m ,速度: 质量: 速度: 设带电粒子的电量: v ,加速它的电压:U 。则粒子获得的动 加速它的电压: 能为: 能为: 1 2qU 2 mv = qU 则 v = m 2 带电粒子的德布罗意波长: 德布罗意波长 带电粒子的德布罗意波长:
hν = En- Ek
辐射或吸收光子的频率: 辐射或吸收光子的频率: ν =(En- Ek)/ h
波尔的氢原子理论

2 卢瑟福的核式模型
卢瑟福1871年8月13日出生在 新西兰,1894年大学毕业,1895年 到 英 国 剑 桥 大 学 学 习 , 成 为 J.J. 汤 姆孙的研究生。1908年卢瑟福荣获 诺贝尔化学奖,同年在曼切斯特大 学任教,继续指导他的学生进行 粒子散射的实验研究。
卢瑟福的α粒子散射验证了核式模型。
19-1 波尔的氢原子理论
量子物理起源于对原子物理的研究,人们从高能粒子的 散射实验和原子光谱中获得原子内部信息。
3
4
一 玻尔理论的实验基础
1 汤姆逊葡萄干面包模型
1903年,汤姆孙提出原子结构模 型:原子里面带正电的部分均匀地 分布在整个原子球体中,而带负电 的电子镶嵌在带正电的球体之中。 带正电的球体与带负电的电子二者 电量相等,故原子不显电性。
5 6 普芳德(Pfund)系
区域 紫外 可见 可见 红外 红外
此后又发现碱金属也有类似的规律。
日期 1906年 1880年 1908年 1922年 1924年
3 里兹并合原理
~ T(m α) T(n β)
R
光谱项 : T(m) (m )2
R
T (n) (n )2 10
三 经典电磁理论遇到的困难
6
粒子散射
4 2
H
e
,
q 2e, 原子量为4,m 7500me
粒子束射向金箔:
-
(1) 多数 0
+
(2)少数 较大
1 / 8000被反射,
(3)极少数 ,反弹
大部分透过。
7
1911年,卢瑟福提出原子的 “有核结构模型”
原子的核式模型
原子由原子核和核外电子 构成,原子核带正电荷,占据 整个原子的极小一部分空间, 而电子带负电,绕着原子核转 动,如同行星绕太阳转动一样。
玻尔的氢原子理论
~ T( k ) T( n ) T( k )
R R ,T ( n ) 2 称为光谱项 2 k n
从氢原子光谱规律可以看出:
1、光谱是线状的,谱线对应一定的位置,不因观 察方式不同而改变顺序;
2、谱线间有一定的关系,各系可用一个公式表示, 不同线系有共同的光谱项; 3、每一谱线的可以用两光谱项之差表示;
2、频率假设
原子从一较大能量En的定态向另一较低能量Ek的定 态跃迁时,辐射一个光子
h En Ek
跃迁频率条件
原子从较低能量Ek的定态向较大能量En的定态 跃迁时,吸收一个光子 3、轨道角动量量子化假设
h Ln 2
轨道量子化条件
n为正整数,称为量子数
基本假设应用于氢原子:
(1)轨道半径量子化
由图可知,可见光的谱线为 n=4和n=3跃迁到n=2的两条
1 1 ~ 42 R( 2 2 ) 2 4 1 1 1.097 107 ( ) 4 16 0.21 107 m 1
n4 n3 n2 n1
42
o 1 ~ 4861 A 42
1 1 ~ 32 R( 2 2 ) 2 3
2 h rn n 2 ( 0 2 ) me
1 me4 En 2 ( 2 2 ) n 8 0 h
基态能级
(n 1, 2,3, )
E1 13.58 eV
激发态能级 En E1 13.58 eV n2 n2 氢原子的电离能
E电离 E E1 13.58 eV
二、玻尔氢原子理论 原子的核式结构的缺陷:
无法解释原子的稳定性 无法解释原子光谱的不连续性 玻尔原子理论的三个基本假设: 1、定态假设
原子系统存在一系列不连续的能量状态,处于这些状态
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ni n f
me4
8 02 h3c
1.097107 m1
R
(里德伯常数)
第十五章 量子物理
19
物理学第五版1源自-4 氢原子的玻尔理论三 氢原子玻尔理论的意义和困难
1 意义
(1)正确地指出原子能级的存在(原子 能量量子化).
(2)正确地指出定态和角动量量子化的 概念.
(3)正确地解释了氢原子及类氢离子光 谱规律.
射
Ef
L mvr n h 2π
n 1,2,3, 主量子数
第十五章 量子物理
14
物理学
第五版
15-4 氢原子的玻尔理论
3 氢原子轨道半径和能量的计算
(1)轨道半径
e2
经典力学: 4π 0rn2
m vn2 rn
+ rn
量子化条件:mvn rn
n
h 2π
rn
0h2
π me 2
n2
r1n2
(n
1,2,3,)
邢 系
开 系
-0.85 eV
-1.51 eV
系
n=2
莱 曼 系
-3.40 eV
n=1
-13.6 eV
第十五章 量子物理
18
物理学
第五版
15-4 氢原子的玻尔理论
4 玻尔理论对氢原子光谱的解释
En
me4
8
2 0
h2
1 n2
h Ei E f
1 me4 ( 1 1 ), c 8 02h3c n2f ni2
1 经典有核模型的困难
根据经典电磁理论,电子绕核作匀速 圆周运动,作加速运动的电子将不断向外 辐射电磁波.
第十五章 量子物理
9
物理学
第五版
15-4 氢原子的玻尔理论
原子不断向外辐射能量, 能量逐渐减小,电子旋转 的频率也逐渐改变,发射 光谱应是连续谱;
e
v
F
r
e
由于原子总能量减小, 电子将逐渐的接近原子核 而后相遇,原子不稳定.
第十五章 量子物理
15
物理学
第五版
15-4 氢原子的玻尔理论
rn
0h2
π me 2
n2
r1n2
(n
1,2,3,)
n 1 , 玻尔半径
r1
0h2
π me 2
5.29 10 11
m
(2) 能量
第 n 轨道电子总能量:
En
1 2
mvn2
e2
4π 0rn
第十五章 量子物理
16
物理学
第五版
15-4 氢原子的玻尔理论
3
物理学
第五版
紫外
莱曼系
15-4 氢原子的玻尔理论
1
1 R(12
1 n2
),
n 2,3,
可见光
巴耳末系
1
1 R( 22
1 n2
)
,
n 3,4,
第十五章 量子物理
4
物理学
第五版
15-4 氢原子的玻尔理论
红外
帕
邢
系
1
1 R( 32
1 n2
)
,
n 4,5,
布拉开系
1
1 R( 42
1 n2
)
,
n 5,6,
电子在原子中可以在一些特定的圆轨道 上运动而不辐射电磁波,这时,原子处于稳 定状态,简称定态.
与定态相应的能 量分别为 E1,E2… , E1 < E2< E3
E1 + E3
第十五章 量子物理
13
物理学
第五版
(2) 频率条件
h Ei E f
(3)量子化条件
15-4 氢原子的玻尔理论
吸 Ei
发
收
第十五章 量子物理
11
物理学
第五版
15-4 氢原子的玻尔理论
2 玻尔的氢原子理论 1913年玻尔在卢瑟福的原子结构模型的 基础上,将量子化概念应用于原子系统,提 出三条假设:
(1)定态假设 (2)频率条件 (3)量子化条件
第十五章 量子物理
12
物理学
第五版
15-4 氢原子的玻尔理论
(1)定态假设
布在半径为 1010 m 的球体范围内,电子浸
于其中 .
第十五章 量子物理
6
物理学
第五版
15-4 氢原子的玻尔理论
卢瑟福 (E.Rufherford, 1871—1937)
英国物理学家. 1899年发现铀 盐放射出α、β 射线,提出天然放 射性元素的衰变理论和定律.
根据 α 粒子散射实验,提出 了原子的有核模型,把原子结构 的研究引上了正确的轨道,因而
第十五章 量子物理
20
物理学
第五版
15-4 氢原子的玻尔理论
2 缺陷
(1)无法解释比氢原子更复杂的原子.
(2)微观粒子的运动视为有确定的轨道. (3)对谱线的强度、宽度、偏振等一系列 问题无法处理.
(4)半经典半量子理论,既把微观粒子看 成是遵守经典力学的质点,同时,又赋予它 们量子化的特征.
被誉为原子物理之父.
第十五章 量子物理
7
物理学
第五版
15-4 氢原子的玻尔理论
卢瑟福的原子有核模型(行星模型)
原子的中心有一带正电的原子核 , 它几乎集中了原子的全部质量,电子围绕 这个核旋转,核的尺寸与整个原子相比是 很小的.
第十五章 量子物理
8
物理学
第五版
15-4 氢原子的玻尔理论
二 氢原子的玻尔理论
e
e
第十五章 量子物理
10
物理学
第五版
15-4 氢原子的玻尔理论
玻 尔 (Bohr . Niels 1885—1962)
丹麦理论物理学家,现代 物理学的创始人之一. 在卢瑟福原子有核模型基础上 提出了关于原子稳定性和量子 跃迁理论的三条假设,从而完 满地解释了氢原子光谱的规律.
1922年玻尔获诺贝尔物理学奖.
En
me4
8 02 h 2
1 n2
E1 n2
基态能量 (n 1)
E1
me4
8
2 0
h
2
13.6 eV(电离能)
激发态能量 (n 1) En E1 n2
第十五章 量子物理
17
物理学
第五版
15-4 氢原子的玻尔理论
氢原子能级跃迁与光谱图
n= n=5 n=4
n=3
帕
布 拉
0 -0.54 eV
巴 耳 末
物理学
第五版
15-4 氢原子的玻尔理论
一 近代氢原子观的回顾
1 氢原子光谱的实验规律
1885 年瑞士数学家巴耳末发现氢原子 光谱可见光部分的规律:
365 .46
n2 n2 22
nm,
n 3,4,5,
第十五章 量子物理
1
物理学
第五版
15-4 氢原子的玻尔理论
氢原子光谱的巴耳末系
364.6 nm
410.2 nm 434.1 nm 486.1 nm
普丰德系
1
R(
1 52
1 n2
)
,
n 6,7,
汉弗莱系
1
1 R( 62
1 n2
)
,
n 7,8,
第十五章 量子物理
5
物理学
第五版
15-4 氢原子的玻尔理论
2 卢瑟福的原子有核模型
1897年, J.J.汤姆孙发现电子.
1903年,汤姆孙提出原子的“葡萄干蛋 糕模型”.
原子中的正电荷和原子的质量均匀地分
656.3 nm
第十五章 量子物理
2
物理学
第五版
15-4 氢原子的玻尔理论
1890 年瑞典物理学家里德伯给出氢原子 光谱公式
波数 1 R( 1 1 )
n n 2
2
f
i
n f 1,2,3,4,,ni nf 1,nf 2,nf 3,
里德伯常数 R 1.097 107 m1
第十五章 量子物理
