《结构力学》动力学1
一级注册结构工程师基础考试_结构力学一动力

确保结构安全性和稳定性。
风振效应研究
研究风对高层建筑、大跨度结构的 作用,通过动力学分析优化结构设 计,提高抗风能力。
振动控制
利用结构动力学原理,采取减震、 隔震等措施,降低建筑结构的振动 幅度,提高居住和工作环境的舒适 度。
机械结构的动力学分析
04 结构力学一动力考试关知识的掌握程度和应用能力。
考试内容
主要包括结构动力学的基本原理、振动与波动的基本概念、弹性 力学的基本方程等。
考试形式
闭卷考试,时间为3小时,满分100分。
考试题型解析
1 2
单项选择题
主要考查考生对基本概念和原理的理解和应用, 一般有10-15道题目,每题4分。
描述动能的变化与功的关系,即 W=ΔEk,其中W为功,ΔEk为动能的 变化。
动量定理
描述力对时间的累积作用,即Ft=mv, 其中F为力,t为时间,m为质量,v为 速度。
振动的基本原理
01
02
03
简谐振动
物体在平衡位置附近做周 期性往复运动的运动形式。
阻尼振动
由于受到阻力的作用,振 幅逐渐减小的振动。
塑性变形是材料在外力作用下发生的不可逆变形。屈服准则是描述材料开始进 入塑性变形的条件。
流动法则与增量理论
流动法则是描述塑性应变与外力之间的关系,增量理论则是描述材料在塑性变 形过程中的行为。
02 结构动力学基本原理
动力学的基本原理
牛顿第二定律
动能定理
描述物体运动与力的关系,即F=ma, 其中F为力,m为质量,a为加速度。
动力学基本概念
动力学主要研究物体运动状态随时间 变化的规律。基本概念包括牛顿第二 定律、动量、动能等。
结构力学-第十四章 结构动力学1

动的合成,为了便于研究合成运动,
令 (e)式改写成
y Asin,
v Acos
y(t) Asin( t )......... .......... ...( f )
它表示合成运动仍是一个简谐运动。其中A和可由下式确定
振幅
A
y2
v
2
.............................(g
由初始条件确定C1和C2;
设
y(0)
y(0)
y v
得 C1 y
C2
v
y r
y(t)
e t
( y
cos r t
v
r
y
sin rt)
21
y(t)
e t
(
y
cos r t
v
r
y
sin
rt
)
y(t) et Asin( rt )
2
其中
A
y2
v
y r
tg1 r y
v y
y
讨论(:a)衰减周期运动
m获得初位移y
m获得初速度 y
研究单自由度体系的自由振动重要性在于: 1、它代表了许多实际工程问题,如水塔、单层厂房等。 2、它是分析多自由度体系的基础,包含了许多基本概念。 自由振动反映了体系的固有动力特性。
要解决的问题包括:
建立运动方程、计算自振频率、周期和阻尼………. 9
一、运动微分方程的建立
(1)低阻尼情形 ( <1 )
1,2 i 1 2 , 令 r 1 2
y(t)
B e( ir )t 1
B e( ir )t 2
eix cos x i sin x
et (B1eirt B2eirt ) eix cos x i sin x
结构动力学

§1.3 体系振动的自由度
象静力计算一样,在动力计算时,首先需要选取一个 合理的计算简图。但由于需要考虑惯性力,因此在动力计 算的简图中,多了一项关于质量分布的处理问题。当体系 振动时,它的惯性力与质量的运动情况有关,所以确定质 量在运动中的位置具有重要的意义。 振动的自由度:我们把确定体系上全部质量位置所需 的独立几何参变数的数目,称为该体系的振动自由度。 例1.1 如图(a)所示跨中置一质量为m电动机的简支梁,当 梁自身的质量远小于电动机的质量时,梁的质量可忽略不 计。其计算简图如图(b)所示。
Fp
如:具有偏心质量的回旋机器它所传递 给结构上的横向力就是时间 t 的函数。
t
这类荷载称为动力荷载
图(a)
显然,结构在动力荷载作用下的计 算与静力荷载作用下的计算将有很大的 的区别,而且要复杂的多。
Fpsin t
图(b)
这是因为,在进行动力计算时,除了需要考虑惯 性力外,还需取时间作为自变量。在动力问题中,内 力与荷载不能构成静力平衡,但根据达朗伯原理,可 以将动力问题转化为静力问题,方法是任一时刻在结 构上加入假想的惯性力作为外力。即结构在形式上处 于“平衡状态”,这样,就可以应用静力学的有关原 理和方法计算在给定时刻的内力和位移等。 在实际工程中,大多数荷载都是随时间的改变而 变化的,但有一些荷载使结构产生很小的振动,以至 于其上的惯性力可以忽略不计,此时为了简化计算, 可将其视为静力荷载。仅将那些随时间变化,且使结 构产生较大的振动的荷载才作为动力荷载来考虑。
dmy Fp t dt
1 2
t m y 1 3
当质量m不随时间变化时,有 Fp
0 即:Fp t m y
因此,如果把惯性力(-mÿ)加到原来受力的质量上,则动 力学问题就可以按静力平衡来处理,这种列运动方程的 方法常称为动静法。这种方法较为方便,因此得到广泛 应用。 (2)拉格朗日(Lagrange)方程 应用虚位移原理,作用在任意质量mi上的所有力 (包括惯性力),对任意的虚位移所作的虚功总和应 等于零,得
结构动力学 结构力学分支

结构动力学结构力学分支
结构力学是应用力学原理研究多体建筑物结构动态变形、稳定性、破
坏机制等重要问题的学科。
从理论上讲,结构力学可被分为以下几个
分支:
(1)绝热动力学:研究在影响力产生热量的变形过程中,能量平衡方程,热导率温度关系等问题。
(2)动力力学:研究分析结构振动反应与模态特性,以及结构在突发
类和碰撞运动时的变形过程。
(3)刚体力学:研究力学分析旋转体的动力响应及弹性结构的变形、
局部应力分布与项势。
(4)材料力学:研究结构力学对各种材料的影响。
包括材料弹性模量、材料弹塑性行为、材料持续性及结构体之间动力相互作用。
(5)疲劳力学:研究建筑物结构产生疲劳损坏的机理,主要包括循环
加载、应力控制、结构模式和材料疲劳行为等。
(6)结构动力学:研究结构在力学和刚体作用下的运动方程和动力行为。
(7)安全可靠性工程:涉及建筑结构的可靠性,包括结构变形过程中的可靠性设计、抗震设计和生命安全设计等理论。
(8)结构优化:采用计算机技术,利用数学模型求解结构变形特性和参数最优化,实现结构设计的优化,从而得到更为有效的结构。
结构力学课件15动力学(1)
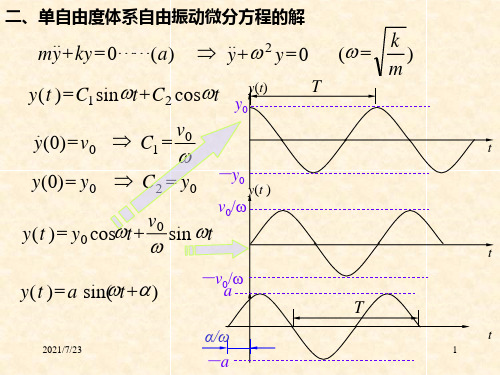
能相差很大。反之,两个外形看来并不相同的结构,如果其
2自021振/7/2周3 期相近,则在动荷载作用下的动力性能基本一致。2
例4、图示三根单跨梁,EI为常数,在梁中点有集中质量m, 不考虑梁的质量,试比较三者的自振频率。
EI
l
w=
k11 =
3EI l3
+k
m
m
•对于静定结构一般计算柔度系数方便。
•如果让振动体系沿振动方向发生单位位移时,所有刚节点
都不能发生转动(如横梁刚度为∞刚架)计算刚度系数方便。
两端刚结的杆的侧移刚度为:
12 l
EI
3
一端铰结的杆的侧移刚度为:
2021/7/23
3 EI l3
5
五、阻尼对自由振动的影响
忽略阻尼影响时所得结果 大能体不上能 反映实际结构的振动规律。
忽略阻尼的振动规律
考虑阻尼的振动规律
结构的自振频率是结构的固有特性,与外因无关。
简谐荷载作用下有可能出现共振。
自由振动的振幅永不衰减。
自由振动的振幅逐渐衰减。
共振时的振幅趋于无穷大。 共振时的振幅较大但为有限值。
产生阻尼的原因:结构与支承之间的外摩擦;材料之间的内摩
擦;周围介质的阻力。
阻尼力的确定:总与质点速度反向;大小与质点速度有如下关系:
①与质点速度成反比(比较常用,称为粘滞阻尼)。
②与质点速度平方成反比(如质点在流体中运动受到的阻力)。
③与质点速度无关(如摩擦力)。
粘滞阻尼力的分析比较简单,(因为R(t)=-Cy ).
结构动力学-1

大连理工大学建设工程学部工程抗震研究所
结构动力学 Dynamics of Structures
Tacoma Narrows Bridge
风致振动破坏 大连理工大学建设工程学部工程抗震研究所 结构动力学 Dynamics of Structures
2004年9月-2005年9月:墨西
哥湾多次飓风便造成约190座海洋平 台严重破坏和损伤。
结构动力学 Dynamics of Structures
典型动力荷载的特性和来源
简谐荷载
复杂荷载
冲击荷载
长持续时间的荷载
大连理工大学建设工程学部工程抗震研究所
结构动力学 Dynamics of Structures
动力问题的基本特性:
F F
惯性力 (a)静荷载 (b)动力荷载
荷载、反应不随时间变化 反应具有单一的解
荷载、反应随时间变化 全部时间历程上的一系列解
弯矩、剪力及挠曲形状直接
依赖于外荷载,与外力相平衡
位移与加速度有联系,加速度产
生惯性力 弯矩、剪力需平衡外力和惯性力
* 缓慢变化的荷载,其惯性力与外荷比很小,分析时仍视作静荷载。
大连理工大学建设工程学部工程抗震研究所
结构动力学 Dynamics of Structures
惯性力P(t)与加速度成正比,但方向相反。
m
P(t )
m
(t ) v
(t ) 0 P(t ) mv
抵抗质量加速 度的惯性力
P(t )
(t ) mv
形式上的平衡方程,实质上的运动方程
大连理工大学建设工程学部工程抗震研究所
结构动力学 Dynamics of Structures
§1-6 结构动力分析的一般过程
结构动力学

结构动力学第一章概述1.动力荷载类型:根据何在是否随时间变化,或随时间变化速率的不同,荷载分为静荷载和动荷载根据荷载是否已预先确定,动荷载可以分为两类:确定性(非随机)荷载和非确定性(随机)荷载。
确定性荷载是荷载随时间的变化规律已预先确定,是完全已知的时间过程;非确定性荷载是荷载随时间变化的规律预先不可以确定,是一种随机过程。
根据荷载随时间的变化规律,动荷载可以分为两类:周期荷载和非周期荷载。
根据结构对不同荷载的反应特点或采用的动力分析方法不同,周期荷载分为简谐荷载(机器转动引起的不平衡力)和非简谐周期荷载(螺旋桨产生的推力);非周期荷载分为冲击荷载(爆炸引起的冲击波)和一般任意荷载(地震引起的地震动)。
2.结构动力学与静力学的主要区别:惯性力的出现或者说考虑惯性力的影响3.结构动力学计算的特点:①动力反应要计算全部时间点上的一系列解,比静力问题复杂且要消耗更多的计算时间②于静力问题相比,由于动力反应中结构的位置随时间迅速变化,从而产生惯性力,惯性力对结构的反应又产生重要的影响4.结构离散化方法:将无限自由度问题转化为有限自由度问题集中质量法:是结构分析中最常用的处理方法,把连续分布的质量集中到质点,采用真实的物理量,具有直接直观的优点。
广义坐标法:广义坐标是形函数的幅值,有时没有明确的物理意义,但是比较方便快捷。
有限元法:综合了集中质量法与广义坐标法的特点,是广义坐标的一种特殊应用,形函数是针对整个结构定义的;有限元采用具有明确物理意义的参数作为广义坐标,形函数是定义在分片区域的。
①与广义坐标法相似,有限元法采用了形函数的概念,但不同于广义坐标法在全部体系(结构)上插值(即定义形函数),而是采用了分片的插值(即定义分片形函数),因此形函数的公式(形状)可以相对简单。
②与集中质量法相比,有限元法中的广义坐标也采用了真实的物理量,具有直接直观的优点。
5.结构的动力特性:自振频率、振型、阻尼第二章分析动力学基础及运动方程的建立1.广义坐标:能决定质点系几何位置的彼此独立的量;必须是相互独立的参数2.约束:对非自由系各质点的位置和速度所加的几何或运动学的限制;(从几何或运动学方面限制质点运动的设施)3.结构动力自由度,与静力自由度的区别:结构中质量位置、运动的描述动力自由度:结构体系在任意瞬间的一切可能的变形中,决定全部质量位置所需要的独立参数的数目静力自由度:是指确定体系在空间中的位置所需要的独立参数的数目为了数学处理上的简单,人为在建立体系的简化模型时忽略了一些对惯性影响不大的因素确定结构动力自由度的方法:外加约束固定各质点,使体系所有质点均被固定所必需的最少外加约束的数目就等于其自由度4.有势力的概念与性质:有势力(保守力):每一个力的大小和方向只决定于体系所有各质点的位置,体系从某一位置到另一位置所做的功只决定于质点的始末位置,而与各质点的运动路径无关。
结构力学Ⅱ课件:结构动力学(一)
一、动力计算的特点 • 动力计算与静力计算的本质区别:不能忽略惯性力
(1) 计算中考虑惯性力 FI ma my (2)利用达朗伯原理原理,把惯性力视为外力参与
瞬时的平衡,将动力问题转化为静力问题来处理。 (3)动力方程是二阶微分方程,方程求解复杂困难。
F (t )
动荷载:F (t) 干扰力、受迫力、激励
阻尼力: FD cy 和速度方向相反
16
刚度法建立动力方程
y (t )
FD
FI
F(t) y,y, y
FS
质点平衡方程: FI FD FS F (t )
惯性力: FI my
阻尼力: FD cy
约束力(恢复力): FS ky
刚度法的运动方程: my cy ky F(t) (2-1)
三、动力计算中体系的自由度 • 集中质量法——
假定忽略杆的轴向变形和质点的转动。 平面内每个质点最多有两个线位移。
• 质点体系的振动自由度确定方法—附加链杆法
使每个质点不发生线位移所施加的附加链杆数,即为体 系动力计算的自由度。
11
三、动力计算中体系的自由度
2个自由度
1个自由度
2个自由度 单自由度
研究对象
• 求解杆系结构在动荷载 作用下的变形和内力。
本章重点
• 单自由度体系的自振频 率及在简谐荷载作用下
的动力响应。
§10.1 概述
一、动力计算的特点
• 动力计算研究结构在动力荷载作用下的变形和内力,即 研究结构的动力反应。
• 动力荷载:大小、方向、作用点随时间变化的荷载。 • 结构的动力反应不但与动力荷载的性质有关,还与结构
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ω
vo
sin ω t................( e)
0 -yο y
yo cosω t
vo ω − vo ω
y T A
α ω• •
T t
0
ω
vo
sin ω t
0
t
α Asin ω t + ω
13
-A
三、结构的自振周期和频率
由式
y (t ) = A sin(ω t + α )
二、动力荷载分类
P(t )
按起变化规律及其作用特点可分为: 按起变化规律及其作用特点可分为:
周期荷载:随时间作周期性变化。(转动电机的偏心力) 。(转动电机的偏心力 1)周期荷载:随时间作周期性变化。(转动电机的偏心力) P
t 简谐荷载(按正余弦规律变化) 简谐荷载(按正余弦规律变化) 一般周期荷载
sin kπx —— 是根据边界约束条件选取 l
ϕ1(x),ϕ2(x),........ n (x) .ϕ
的函数,称为形状函数。 的函数,称为形状函数。
a1, a2,…….. an
y ( x , t ) = ∑ a kϕ k ( x )
k =1
ak(t) ——称广义座标,为一组待定 称广义座标,
参数,其个数即为自由度数, 参数,其个数即为自由度数,用此法可将 无限自由度体系简化为有限自由度体系。 无限自由度体系简化为有限自由度体系。
g ∆ st
T = 2π
∆ st m = 2π k g
频率 1.只与结构的质量与刚度有关,与外界干扰无关; 1.只与结构的质量与刚度有关 与外界干扰无关; 只与结构的质量与刚度有关, 和周 的平方根成正比, 成反比, 2.T与m的平方根成正比,与k成反比,据此可改变周期; 的平方根成正比 成反比 据此可改变周期; 期的 14 3.是结构动力特性的重要数量标志 是结构动力特性的重要数量标志。 讨论 3.是结构动力特性的重要数量标志。
9
一、运动微分方程的建立
方法: 方法:达朗伯尔原理 建立平衡方程。 力,建立平衡方程。 应用条件:微幅振动(线性微分方程) 应用条件:微幅振动(线性微分方程) 力学模型 刚度法: 1、 刚度法:研究作用于被隔离的质量上的 静平衡位置
k
S(t) m m W I(t)
重力
m 质量m在任一时刻的位移 y(t)=yj+yd W
y T A
α ω• •
及图可见位移方程是一个周期函数。 及图可见位移方程是一个周期函数。
0
t
-A
周期- 周期 T =
2π
ω
,
工程频率- 工程频率 f =
1 ω = ( Hz ), T 2π
园频率- 园频率 ω = 2 π f =
2π T
计算频率和周期的几种形式
ω=
k = m
1 g = = mδ Wδ
x
n
y
7
四、动力计算的方法
动力平衡法(达朗伯尔原理) 动力平衡法(达朗伯尔原理)
m
P (t ) = m&&(t ) y
P(t)
− m&&(t ) =I(t) y
m
P (t ) = m&&(t ) y
改写成 设其中 …………..运动方程 运动方程 …………..平衡方程 平衡方程
P (t ) − m&&(t ) = 0 y
改写为
k && + ω y = 0 其中 ω = y m
2
2
它是二阶线性齐次微分方程,其一般解为: 它是二阶线性齐次微分方程,其一般解为:
y (t ) = C1 sin ωt + C2 cos ωt
积分常数C 积分常数 1,C2由初始条件确定
...............(d )
11
静平衡位置
m
. y (t ) = C sin ω t + C .
振幅 相位角
vo 2 A = yo + ω −1 yoω α = tg vo
.......... .......... .........( g )
12
y (t ) = yo cos ω t +
y y
ο
y (t ) = A sin(ω t + α )........................( f )
3.计算图示刚架的频率和周期 计算图示刚架的频率和周期。 例3.计算图示刚架的频率和周期。 m EI1=∞ I I h
10 由平衡位置计量。以位移为未知量的平衡方程式,引用了刚度系数,称刚度法。 由平衡位置计量。以位移为未知量的平衡方程式,引用了刚度系数,称刚度法。
柔度法:研究结构上质点的位移,建立位移协调方程。 2、 柔度法:研究结构上质点的位移,建立位移协调方程。 静平衡位置 m
. y (t ) = I (t )δ = −m&y&(t )δ .
三、动力计算中体系的自由度
确定体系上全部质量位置所需独立参数的个数称为体系的振动自由度。 确定体系上全部质量位置所需独立参数的个数称为体系的振动自由度。 体系的振动自由度 实际结构的质量都是连续分布的,严格地说来都是无限自由度体系。 实际结构的质量都是连续分布的,严格地说来都是无限自由度体系。计算 困难,常作简化如下: 困难,常作简化如下: 1、集中质量法 把连续分布的质量集中为几个质点, 把连续分布的质量集中为几个质点,将一个无限自由度的问题简化成有限 自由度问题。 自由度问题。
1
§10-1 动力计算的特点和动力自由度 10动力计算的特点、 一、动力计算的特点、目的和内容
特点:静力荷载与动力荷载的特点及其效应。 1、特点:静力荷载与动力荷载的特点及其效应。 静力荷载”是指其大小、方向和作用位置不随时间而变化的荷载。 “静力荷载”是指其大小、方向和作用位置不随时间而变化的荷载。这 类荷载对结构产生的惯性力可以忽略不计,由它所引起的内力和变形都是确定 类荷载对结构产生的惯性力可以忽略不计, 对结构产生的惯性力可以忽略不计 的。 动力荷载”是指其大小、方向和作用位置随时间而变化的荷载。 “动力荷载”是指其大小、方向和作用位置随时间而变化的荷载。这类 荷载对结构产生的惯性力不能忽略,因动力荷载将使结构产生相当大的加速度, 荷载对结构产生的惯性力不能忽略,因动力荷载将使结构产生相当大的加速度, 对结构产生的惯性力不能忽略 由它所引起的内力和变形都是时间的函数。 由它所引起的内力和变形都是时间的函数。 与静力计算的对比:两者都是建立平衡方程,但动力计算,利用动静法, 与静力计算的对比:两者都是建立平衡方程,但动力计算,利用动静法, 建立的是形式上的平衡方程。力系中包含了惯性力,考虑的是瞬间平衡, 建立的是形式上的平衡方程。力系中包含了惯性力,考虑的是瞬间平衡,荷 内力都是时间的函数。建立的平衡方程是微分方程 平衡方程是微分方程。 载、内力都是时间的函数。建立的平衡方程是微分方程。 2、目的和内容 计算结构的动力反应:内力、位移、速度与加速度, 计算结构的动力反应:内力、位移、速度与加速度,使结构在动内力与静 内力共同作用下满足强度和变形的要求。 内力共同作用下满足强度和变形的要求。
t
3
冲击荷载:短时内剧增或剧减。(如爆炸荷载) 。(如爆炸荷载 2)冲击荷载:短时内剧增或剧减。(如爆炸荷载) P P tr t P(t ) P tr t
随机荷载: 非确定性荷载) 荷载在将来任一时刻的数值无法事先确定。 3)随机荷载:(非确定性荷载) 荷载在将来任一时刻的数值无法事先确定。 如地震荷载、风荷载) (如地震荷载、风荷载)
静平衡位置
m获得初位移yο 获得初位移
m获得初速度 yo 获得初速度 &
研究单自由度体系的自由振动重要性在于: 研究单自由度体系的自由振动重要性在于: 1、它代表了许多实际工程问题,如水塔、单层厂房等。 它代表了许多实际工程问题,如水塔、单层厂房等。 2、它是分析多自由度体系的基础,包含了许多基本概念。 它是分析多自由度体系的基础,包含了许多基本概念。 自由振动反映了体系的固有动力特性。 自由振动反映了体系的固有动力特性。 要解决的问题包括: 要解决的问题包括: 建立运动方程、计算自振频率、周期和阻尼 建立运动方程、计算自振频率、周期和阻尼………. .
1
2
cos ω t .....( d )
C2 = yo v C1 = o ω
I(t) (d)式可以写成 式可以写成
设 t=0 时
y ( 0) = y o & y (0) = vo
y (t ) = yo cos ω t +
由式可知, 由式可知,位移是由初位移yο引起的余弦运动和由初速度vο引起的正弦 运动的合成,为了便于研究合成运动, 运动的合成,为了便于研究合成运动, 令 (e)式改写成 式改写成
多自由度体系
6
m ( x)
无限自由度体系 x
y(x,t)
广义座标法: 2、广义座标法: 如简支梁的变形曲线可用三角级数来表示
y ( x, t ) = ∑ ak (t ) sin
k =1
n
k πx l
x y(x,t)
用几条函数曲线来描述体系的振动曲 线就称它是几个自由度体系, 线就称它是几个自由度体系,其中
m&&(t )δ + y = 0 y
可得与 (b) 相同的方程
.......... .( c )
I(t)
1 Qδ = k
刚度法常用于刚架类结构,柔度法常用于梁式结构。 刚度法常用于刚架类结构,柔度法常用于梁式结构。 二、自由振动微分方程的解
m&& + ky = 0 y k && + y = 0 y m ....................................(b)
