06实验六 空间图形的画法
9.1平面的基本性质第三课时 空间图形直观图的画法
首页
上一页
下一页
末页
瞻前顾后
要点突破
典例精析
演练广场
解 :点 C′的位置不对. ′ 的位置不对. 画法: 法一: (1)作 画法: 法一 : 作 CD∥x 轴交 y 轴于点 D, ∥ , 画对应轴 O′x′、 ′ y′, ∠ x′O′y′ ′ ′ O′ ′ 使 ′ ′ ′ = 45°. 1 (2)在 x′ 轴上取 O′B′= OB,在 y′ 轴的负半轴上取 O′D′ = OD,过 D′ 作 在 ′ ′ ′ , ′ ′ ′ , ′ 2 D′C′∥ ′轴且 D′C′= DC. ′ ′∥x′ ′ ′ ′∥ (3)连结 O′C′、 ′ C′, 并擦去辅助线, 连结 ′ ′ B′ ′ 并擦去辅助线, △ O′B′C′即为所画三角形的直观图. 则 ′ ′ ′即为所画三角形的直观图. 如 图.
首页
上一页
下一页
末页
瞻前顾后
要点突破
典例精析
演练广场
知识要点: 知识要点: 斜二测画法的理解及应用 (1)画图时要紧紧把握住一斜 画图时要紧紧把握住一斜 轴的线段, 画图时要紧紧把握住 一斜——在已知图形的 xOy 平面内垂直于 x 轴的线段,在直观 在已知图形的 两种度量形式, 图中均与 x′轴成 45°或 135°;二测 ′ 或 ;二测——两种度量形式,即在直观图中,平行于 x′轴或平行 两种度量形式 即在直观图中, ′ 于 z′轴的线段长度不变, 平行于 y′轴的线段长度变为原来的一半. ′ 轴的线段长度不变, ′ 轴的线段长度变为原来的一半. (2)画水平放置的平面图形的步骤为:画轴,取点,成图.图形中平行于 x 轴的线段 ,在 画水平放置的平面图形的步骤为: 轴的线段, 画水平放置的平面图形的步骤为 画轴,取点,成图. 直观图中保持不变, 轴的线段,长度变为原来的一半. 直观图中保持不变, 平行于 y 轴的线段,长度变为原来的一半 . 画立体图形的直观图,在画轴时, 画立体图形的直观图 ,在画轴时,要多画一条与平面 x′O′y′垂直的轴 O′z′,且 ′ ′ ′ ′ ′ 平行于 O′z′的线段, 长度不变,其他同平面图形的画法. ′ ′ 的线段,长度不变,其他同平面图形的画法. (3)空间几何体的直观图在数学中有重要作用 ,画得立体感强 ,在做题时立体关系就便于 空间几何体的直观图在数学中有重要作用 空间几何体的直观图在数学中有重要作用,画得立体感强, 观察,图形画得好,在科学实验和日常生活中也会大有作用. 观察,图形画得好, 在科学实验和日常生活中也会大有作用.
空间图形的认识与绘制

立体图形
特点:具有明显的三维特性,可以通过组合、旋转等方式形成各种复杂的空间结构
定义:三维空间中占有一定空间的图形,具有长、宽、高三个维度
分类:长方体、正方体、圆柱体、圆锥体、球体等
应用:在建筑、机械、航天等领域中广泛应用
组合体
添加标题
添加标题
添加标题
添加标题
分类:根据组合方式的不同,可以分为叠加型、挖切型和综合型等。
大小:空间图形的大小可以通过其尺寸来衡量,如半径、直径、边长等
方向:空间图形中的方向可以通过旋转或翻转来改变
位置:空间图形中的位置可以通过坐标系来确定,如三维空间中的x、y、z轴
空间图形的位置关系
平行:空间图形中的线段或平面在无限延伸后不相交
垂直:空间图形中的线段或平面在无限延伸后相交于一点
相交:空间图形中的线段或平面在有限长度内相交
性质:具有位置,没有方向和长度
直线
定义:直线是两点之间所有点的集合
性质:无限延伸,不可度量
表示方法:用直尺或直线命令绘制
在空间图形中的应用:构成平面、形成角度和交点
平面
定义:平面是空间中无限延展、没有厚度的几何元素
表示方法:通常用平行四边形表示平面,并加上方向箭头
空间图形的基本元素:点、直线和平面
05
空间图形的应用
建筑设计中的应用
添加标题
添加标题
添加标题
添加标题
通过运用空间图形,建筑师可以更好地实现建筑设计的功能需求,提高建筑的使用舒适度和空间效率。
空间图形在建筑设计中的应用,可以创造出独特的视觉效果,增强建筑的艺术性和表现力。
空间图形可以帮助建筑师解决建筑设计中的复杂问题,如结构、采光、通风等,提高建筑的技术性和可行性。
如何画好立体图形
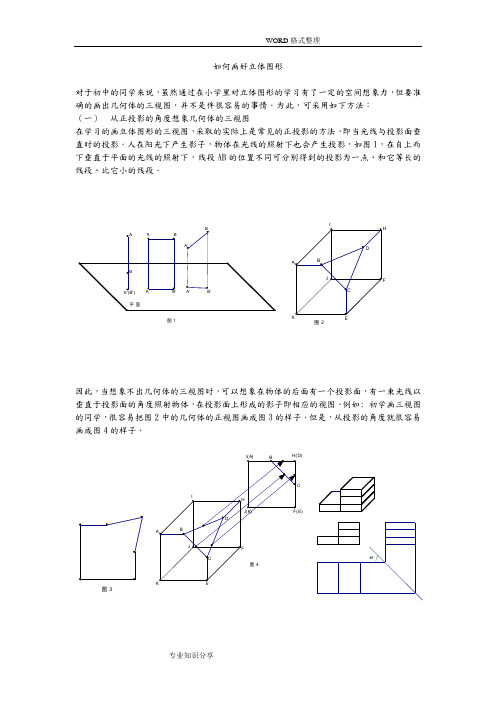
如何画好立体图形对于初中的同学来说,虽然通过在小学里对立体图形的学习有了一定的空间想象力,但要准确的画出几何体的三视图,并不是件很容易的事情.为此,可采用如下方法:(一) 从正投影的角度想象几何体的三视图在学习的画立体图形的三视图,采取的实际上是常见的正投影的方法,即当光线与投影面垂直时的投影.人在阳光下产生影子,物体在光线的照射下也会产生投影,如图1,在自上而下垂直于平面的光线的照射下,线段AB 的位置不同可分别得到的投影为一点、和它等长的线段、比它小的线段.因此,当想象不出几何体的三视图时,可以想象在物体的后面有一个投影面,有一束光线以垂直于投影面的角度照射物体,在投影面上形成的影子即相应的视图.例如: 初学画三视图的同学,很容易把图2中的几何体的正视图画成图3的样子.但是,从投影的角度就很容易画成图4的样子.图345图 1图 2(二)用45º线的方法形成对应因为三视图中的正视图和俯视图都反映几何体的长,所以在画三视图时,正视图和俯视图在长上应保持一致,同理,正视图和左视图应在高上保持一致,左视图和俯视图应在宽上保持一致.在这几种保持一致的对应上,左视图和俯视图的一致比较难掌握,而画45º线的方法则可以使它们之间保持很好的一致.具体画法为:1.确定主视图的位置,画出主视图;2.在主视图正下方画出俯视图,注意与主视图“长对正”;3.在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;4.为表示出旋转几何体(圆柱、圆锥、球等)的对称轴,可在视图中加画点划线。
《几何画板》在数学教学中的应用对于数学科学来说主要是抽象思维和理论思维,这是事实;一个没有得到形象思维培养的人会有很高的抽象思维、理论思维的能力。
同样,一个学生如果根本不具备数学想象力,要把数学学好那也是不可能的。
因此,随着计算机多媒体的出现和飞速发展,在网络技术广泛应用于各个领域的同时,也给学校教育带来了一场深刻的变革──用计算机辅助教学,改善人们的认知环境──越来越受到重视。
06实验六 空间图形的画法

图6-4
绘制二元函数图形也可用简捷绘制的ezsurf指令,它的使 用格式为: ezsurf(f(x,y),[a,b,u,v]) 即可绘制函数在区域[a,b]×[u,v]上的图形。当省略区域 时,默认区间是[-2 ,2 ]×[- 2 , 2 ]。例如输入: ezsurf('x*exp(-x^2-y^2)') 则输出如图6-5所示。
图6-12
【例7】可以证明:函数z=xy的图形是双曲抛物面。在区 域-2≤x≤2,-2≤y≤2上作出它的图形。
输入: x=-2:0.1:2; y=-2:0.1:2; [xx,yy]=meshgrid(x,y); zz=xx.*yy; surf(xx,yy,zz) 输出如图6-13所示。
图6-13
例如,画出曲面 z x y 的图形。输入: x=-2:0.1:2; y=-2:0.1:2; [x,y]=meshgrid(x,y); z=x.^2+y.^2; surf(x,y,z) z x 2 y 2,见图6-2。 得到曲面
2 2
图6-2
执行下面的程序: x=-2:0.015:2; y=-2:0.015:2; [x,y]=meshgrid(x,y); z=x.^2+y.^2; i=find(x.^2+y.^2>4); z(i)=NaN; surf(x,y,z) 同样得到曲面(见图6-3)。 由于自变量的取值范围不同,图形也不同。不过,后者比 较好地反映了旋转曲面的特点,因此是常用的方法。
图6-3
又如,参数方程: x 2sin cos , y 2sin sin , z 2cos 是以原 点为中心、2为半径的球面,其中 0 , 0 2 因此只要输入: t=0:0.1:pi; r=0:0.1:2*pi; [r,t]=meshgrid(r,t); x=2*sin(t).*cos(r); y=2*sin(t).*sin(r); z=2*cos(t); surf(x,y,z) 2 2 2 2 便作出了方程为 x y z 2 的球面(见图6-4)。
实验2 空间图形的画法(基础实验)

项目二 一元函数积分学与空间图形的画法实验2 空间图形的画法(基础实验)实验目的 掌握用Mathematica 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面 的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.基本命令1.空间直角坐标系中作三维图形的命令Plot3D命令Plot3D 主要用于绘制二元函数),(y x f z =的图形. 该命令的基本格式为Plot3D[f[x,y],{x,x1,x2},{y,y1,y2},选项]其中f[x,y]是y x ,的二元函数, x1,x2表示x 的作图范围, y1,y2表示y 的作图范围.例如,输入Plot3D[x^2+y^2,{x,-2,2},{y,-2,2}]则输出函数22y x z +=在区域22,22≤≤-≤≤-y x 上的图形(图2.1)与Plot 命令类似, Plot3D 有许多选项. 其中常用的如PlotPoints 和ViewPoint. PlotPoints 的用 法与以前相同. 由于其默认值为PlotPoints->15, 常常需要增加一些点以使曲面更加精致, 可能要 用更多的时间才能完成作图. 选项ViewPoint 用于选择图形的视点(视角), 其默认值为 ViewPoint->{1.3,-2.4,2.0},需要时可以改变视点.2.利用参数方程作空间曲面或曲线的命令ParametricPlot3D 用于作曲面时, 该命令的基本格式为ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},{u,u1,u2},{v,v1,v2},选项]其中x[u,v],y[u,v],z[u,v]是曲面的参数方程表示式. u1,u2是作图时参数u 的范围, v1,v2是参数v 的 范围.例如,对前面的旋转抛物面, 输入ParametricPlot3D[{u*Cos[v],u*Sin[v],u^2},{u,0,3},{v,0,2 Pi}]同样得到曲面22y x z +=的图形(图2.2).由于自变量的取值范围不同, 图形也不同. 不过, 后者比较好的反映了旋转曲面的特点, 因 而是常用的方法.又如, 以原点为中心, 2为半径的球面. 它是多值函数, 不能用命令Plot3D 作图. 但是, 它的 参数方程为,20,0,cos 2,sin sin 2,cos sin 2πθπϕϕθϕθϕ≤≤≤≤===z y x因此,只要输入ParametricPlot3D[{2 Sin[u]*Cos[v],2 Sin[u]*Sin[v],2 Cos[u]},{u,0,Pi},{v,0,2 Pi}]便作出了方程为22222=++y x z 的球面(图2.3)..用于作空间曲线时,ParametricPlot3D 的基本格式为ParametricPlot3D[{x[t],y[t],z[t]},{t,t1,t2},选项]其中x[t],y[t],z[t]是曲线的参数方程表示式. t1,t2是作图时参数t 的范围.例如, 空间螺旋线的参数方程为).80(10/,sin ,cos π≤≤===t t z t y t x输入ParametricPlot3D[{Cos[t],Sin[t],t/10,RGBColor[1,0,0]},{t,0,8 Pi}]则输出了一条红色的螺旋线(图2.4).在这个例子中,请读者注意选项RGBColor[1,0,0]的位置.用于作空间曲线时, ParametricPlot3D 的选项PlotPoints 的默认值是30, 选项ViewPoint 的默 认值没有改变.3.作三维动画的命令MoviPlot3D:无论在平面或空间, 先作出一系列的图形, 再连续不断地放映, 便得到动画. 例如, 输入调用作图软件包命令<<Graphics\Animation.m.执行后再输入MoviePlot3D[Cos[t*x]*Sin[t*y],{x,-Pi,Pi},{y,-Pi,Pi},{t,1,2},Frames->12]则作出了12幅曲面图, 选中任一幅图形, 双击它便可形成动画.实验举例一般二元函数作图例2.1 (教材 例2.1) 作出平面y x z 326--=的图形,其中20,30≤≤≤≤y x . 输入Plot3D[6-2x-3y,{x,0,3},{y,0,2}]则输出所作平面的图形(图2.5).如果只要位于第一卦限的部分, 则输入Plot3D[6-2x-3y,{x,0,3},{y,0,2},PlotRange->{0,6}]观察图形.2.6).图2.6例2.2 (教材 例2.2) 作出函数2214y x z ++=的图形.输入k[x_,y_]:=4/(1+x^2+y^2)Plot3D[k[x,y],{x,-2,2},{y,-2,2},PlotPoints->30,PlotRange->{0,4},BoxRatios->{1,1,1}]则输出函数的图形2.7. 观察图形, 理解选项PlotRange->{0,4}和BoxRatios->{1,1,1}的含义. 选项 BoxRatios 的默认值是{1,1,0.4}.例2.3 (教材 例2.3) 作出函数22y x xye z ---=的图形. 输入命令Plot3D[-x*y*Exp[-x^2-y^2],{x,-3,3},{y,-3,3},PlotPoints->30,AspectRatio->Automatic];则输出所求图形(图 图2.8例2.4 (教材 例2.4) 作出函数)94cos(22y x z +=的图形. 输入Plot3D[Cos[4x^2+9y^2],{x,-1,1},{y,-1,1},Boxed->False,Axes->Automatic,PlotPoints->30,Shading->False]则输出网格形式的曲面图2.9, 这是选项Shading->False 起的作用, 同时注意选项Boxed->False 的作用.二次曲面例2.5 (教材 例2.5) 作出椭球面1194222=++z y x 的图形. 这是多值函数, 用参数方程作图的命令ParametricPlot3D. 该曲面的参数方程为,cos ,sin sin 3,cos sin 2u z v u y v u x === (ππ20,0≤≤≤≤v u ).输入ParametricPlot3D[{2*Sin[u]*Cos[v],3*Sin[u]*Sin[v], Cos[u]},{u,0,Pi},{v,0,2 Pi},PlotPoints->30]则输出椭球面的图形, 可使图形更加光滑.图2.10例2.6 (教材 例2.6) 作出单叶双曲面1941222=-+z y x 的图形. 曲面的参数方程为,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u )输入ParametricPlot3D[{Sec[u]*Sin[v],2*Sec[u]*Cos[v], 3*Tan[u]},{u,-Pi/4,Pi/4},{v,0,2 Pi},PlotPoints->30]图2.11例2.7 作双叶双曲面13.14.15.1222222-=-+z y x 的图形.曲面的参数方程是,csc 3.1,sin cot 4.1,cos cot 5.1u z v u y v u x ===其中参数πππ<<-≤<v u ,20时对应双叶双曲面的一叶, 参数πππ<<-<≤-v u ,02时对应双叶双曲面的另一叶. 输入sh1=ParametricPlot3D[{1.5*Cot[u]*Cos[v],1.4*Cot[u]*Sin[v],1.3/Sin[u]},{u,Pi/1000,Pi/2},{v,-Pi,Pi}, DisplayFunction->Identity];(*DisplayFunction->Identity 是使图形暂时不输出的选项*) sh2=ParametricPlot3D[{1.5*Cot[u]*Cos[v],1.4* Cot[u]*Sin[v],1.3/Sin[u]},{u,-Pi/2,-Pi/1000}, {v,-Pi,Pi},DisplayFunction->Identity];Show[sh1,sh2,DisplayFunction->$DisplayFunction](*命令Show[sh1,sh2]是把图形sh1,sh2放置在一起, DisplayFunction->$DisplayFunction 是恢复显示图形的选项*) 输出为图2.12.例2.8 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.输入Plot3D[x*y,{x,-2,2},{y,-2,2},BoxRatios->{1,1,2}, PlotPoints->30]输出图形略. 也可以用ParametricPlot3命令作出这个图形, 输入ParametricPlot3[{r*Cos[t],r*Sin[t],r^2*Cos[t] *Sin[t]},{r,0,2},{t,0,2 Pi},PlotPoints->30]输出为图2.13例2.9 (教材 例2.7) 作出圆环v z u v y u v x sin 7,sin )cos 38(,cos )cos 38(=+=+=,(πππ22/,2/30≤≤≤≤v u )的图形.输入ParametricPlot3D[{(8+3*Cos[v])*Cos[u],(8+3*Cos[v])*Sin[u],7*Sin[v]},{u,0,3*Pi/2},{v,Pi/2,2*Pi}];图2.14例2.10 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π的图形.输入命令ParametricPlot3D[{Cos[u]*Sin[v],Sin[u]Sin[v],Cos[v]+Log[Tan[v/2]+u/5]}, {u,0,4*Pi},{v,0.001,2}];则输出所求图形(图2.15).曲面相交例2.11 (教材 例2.8) 作出球面22222=++z y x 和柱面1)1(22=+-y x 相交的图形. 输入g1=ParametricPlot3D[{2 Sin[u]*Cos[v],2 Sin[u]*Sin[v],2 Cos[u]},{u,0,Pi},{v,0,2 Pi},DisplayFunction->Identity];g2=ParametricPlot3D[{2Cos[u]^2,Sin[2u],v},{u,-Pi/2,Pi/2},{v,-3,3},DisplayFunction->Identity];Show[g1,g2,DisplayFunction->$DisplayFunction]则输出所求图形(图2.16)例2.12 作出锥面222z y x =+和柱面1)1(22=+-y x 相交的图形. 输入g3=ParametricPlot3D[{r*Cos[t],r*Sin[t],r}, {r,-3,3},{t,0,2 Pi},DisplayFunction->Identity];Show[g2,g3,DisplayFunction->$DisplayFunction]输出为图2.17.图2.17例2.13 画出以平面曲线x y cos =为准线, 母线平等Z 轴的柱面的图形. 写出这一曲面的参数方程为⎪⎩⎪⎨⎧=∈-∈==s z R s t t y t x ],,[,cos ππ 取参数s 的范围为[0, 8]. 输入命令ParametricPlot3D[{t,Cos[t],s},{t,-Pi,Pi},{s,0,8}]则输出所求图形(图2.18).例2.14 (教材 例2.9) 作出曲面x y x y x z =+--=2222,1及xOy 面所围成的立体图形. 输入g1=ParametricPlot3D[{r*Cos[t], r*Sin[t],r^2},{t,0,2*Pi},{r,0,1},PlotPoints->30]; g2=ParametricPlot3D[{Cos[t]*Sin[r],Sin[t]Sin[r],Cos[r]+1},{t,0,2*Pi},{r,0,Pi/2},PlotPoints->30];Show[g1,g2]则输出所求图形(图图2.19例2.15 (教材 例2.10) 作出螺旋线t z t y t x 2,sin 10,cos 10===(R t ∈)在xOz 面上的正投影曲线的图形.所给螺旋线在xOz面上的投影曲线的参数方程为10==.,cosx2ztt输入ParametricPlot[{2t,10Cos[t]},{t,-2Pi,2Pi}];则输出所求图形(图图2.20注:将表示曲线的方程组, 消去其中一个变量, 即得到曲线在相应于这一变量方向上的正投影曲线的方程, 不考虑曲线所在平面, 它就是投影柱面方程; 对于参数方程, 只要注意将方程中并不存在的那个变元看成第二参数而添加第三个方程即可.例2.16 (教材例2.11) 作出默比乌斯带(单侧曲面)的图形.输入Clear[r,x,y,z];r[t_,v_]:=2+0.5*v*Cos[t/2];x[t_,v_]:=r[t,v]*Cos[t]y[t_,v_]:=r[t,v]*Sin[t]z[t_,v_]:=0.5*v*Sin[t/2];ParametricPlot3D[{x[t,v],y[t,v],z[t,v]},{t,0,2 Pi},{v,-1,1},PlotPoints->{40,4},Ticks->False]则输出所求图形(图空间曲线例2.17 (教材 例2.12) 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 输入ParametricPlot3D[{t*Cos[t],t*Sin[t],2*t,RGBColor[1.0,0,0.5]},{t,0,6 Pi}]则输出所求图形(图图2.22例2.18 绘制参数曲线 ⎪⎩⎪⎨⎧===2/cos 2sin t z t y t x 的图形.输入命令ParametricPlot3D[{Sin[t],2Cos[t],t.2},{t,0,12}];则输出所求图形(图2.23).例2.19 绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.输入命令ParametricPlot3D[{Cos[t]^2,1/(1+2*t),ArcTan[t]},{t,0,8}]; 则输出所求图形(图2.24).动画制作例2.20 平面正弦曲线的运动. 输入Table[Plot[Sin[x+t*Pi],{x,0,6 Pi}],{t,0,2,1/8}]则作出了16幅具有不同相位的正弦曲线(输出图形略). 双击屏幕上某一幅画, 则可形成动画. 下面是动画的最后一幅图(图2.25).例2.21 (教材 例2.13) 作模拟水波纹运动的动画. 输入调用软件包命令<<Graphics\Animation.m执行后再输入MoviePlot3D[Sin[Sqrt[x^2+y^2]+t*2*Pi],{x,-8 Pi,8 Pi},{y,-8 Pi,8 Pi},{t,1,0},PlotPoints->50,AspectRatio->0.5,ViewPoint->{0.911,-1.682,2.791},Frames->12]则输出12幅具有不同相位的水面图形, 双击屏幕上任意一幅图, 均可观察动画效果. 下图是第一幅图(图2.26).图2.26例2.22 (教材 例2.14) 用动画演示由曲线],0[,sin π∈=z z y 绕z 轴旋转产生旋转曲面的过程.该曲线绕z 轴旋转所得旋转曲面的方程为,sin 222z y x =+ 其参数方程为])2,0[],,0[(,,sin sin ,cos sin ππ∈∈===u z z z u z y u z x输入For[i=1,i<=30,i++,ParametricPlot3D[{Sin[z]*Cos[u],Sin[z]*Sin[u],z},{z,0,Pi},{u,0,2*Pi*i/30},AspectRatio->1,AxesLabel->{"X","Y","Z"}]];则输出连续变化的30幅图形. 双击屏幕上任意一幅图, 均可观察动画效果. 下面是生成旋转曲面的过程中的第23幅图(图2.27).图2.27例2.23 将一张薄膜贴在1,0,1,0====y y x x 的方框上, 薄膜振动的函数取为)cos()sin()sin()cos 1)(cos 1(16),,(224141222t n m y m x n m n n m t y x u m n ππππππ+⋅-+=∑∑==其中t 为参数, 作出图形随t 的变动而引起薄膜振动的动画.初始位置是).0,,(y x u 通过t 的不同值得到多幅画面, 然后将这些图形连续地一张张显示出来, 即可达到运动的动画效果. 输入命令<<Graphics 'Animation '; Clear[x,y,t,m,n];u[x_,y_,t_]:=Sum[16*(1+Cos[n*Pi])*(1-Cos[m*Pi])*Sin[n*Pi*x]*Sin[m*Pi*y]*Cos[Sqrt[m^2+n^2]*Pi*t] /(m^2*n^2*Pi*2),{m,1,4},{n,1,4}]Animate[Plot3D[u[x,y,t],{x,0,1},{y,0,1}, PlotRange->{-8,8}],{t,0,1.75,0.25}];图2.28实验习题1.用Plot3D 命令作出函数)33,33(3sin 2cos ≤≤-≤≤--=y x y x z 的图形, 采用选项 PlotPoints->40.2.作出函数)sin(22y x z +=π的图形.3.用Plot3D 命令作出函数)sin (cos 228/)(22y x e z y x +=+-在ππππ≤≤-≤≤-y x ,上的图形, 采用选项PlotPoints->60.4.二元函数22y x xyz +=在点(0,0) 处不连续, 用Plot3D 命令作出在区域22,22≤≤-≤≤-y x 上的图形(采用选项PlotPoints->40).观察曲面在(0,0)附近的变化情况.5.一个环面的参数方程为),20,20(sin ,sin )cos 3(,cos )cos 3(ππ≤≤≤≤=+=+=v u u z v u y v u x 试用命令ParametricPlot3D 作出它的图形.6.一个称作正螺面的曲面的参数方程为).80,11(3/,sin ,cos ≤≤≤≤-===v u v z v u y v u x 试用命令ParametricPlot3D 作出它的图形.7.用命令Plot3D 作双曲抛物面4122y x z -=,其中1414,66≤≤-≤≤-y x (用选项 BoxRatios->{1,1,1}, PlotPoints->30).8.用命令ParametricPlot3D 作出圆柱面122=+y x 和圆柱面122=+z x 相交的图形.9.用命令ParametricPlot3D 作出抛物柱面2y x =和平面1=+z x 相交的图形.10.用命令ParametricPlot3D 作出圆柱面122=+y x 和圆柱面122=+z x 相交所成的空间曲线 在第一封内的图形.11.用命令ParametricPlot3D 作出球面22222=++z y x 和柱面1)1(22=+-y x 相交所成的空 间曲线的图形.。
实验9空间立体图形的绘制.ppt

0.5 0.25 0 -0.25 -0.5 1
1
0.75 0.5 0.25 0 0 0.25 0.5 0.75 1
空间立体图形的绘制
• 我们也把上面的两个曲面及其交线在同一坐标系 中显示,即键入:
Show t1, t2
运行后得(图6(d))
1 0.75 0.5 0.25 0 -1 -0.5
1 0.5 0 0 -0.5 0.5 1 -1
Plot3D Sqrt 1 x ^2 y^2 , x, 1, 1 , y, 1, 1
空间立体图形的绘制
• 运行后即得到该曲面 的得到该曲面的图形, 但注意到运行后出现 红色报错信息,而且 • 图形不完整(如图 一),其原因是在作 图范围内[-1,1]*[ 1,1]内某些点处无定 义。
1 0.75 0.5 0.25 0 -1 -0.5 0 0.5 1 -1 -0.5 0 0.5 1
空间立体图形的绘制
• 空间图形的叠加 • 与平面图形相类似空间的立体图形同样可 用“Show”命令,把不同的图形(曲面或 曲线)叠加并在一个坐标系中显示出来。 • 例如,现在要在同一坐标系中显示曲面, 及xoy所围成的立体图形。
空间立体图形的绘制
• 首先,我们分别作出 z 1x y x2 y2 x ,的图 形,并把它们的变量储存在变量t1和t2中,最后 用“”命令叠加并在同一坐标系中显示,即键入:
1 0.5 0 -0.5 -1 1
0.5
0 -0.5 -1 -1 -0.5 0 0.5 1
空间立体图形的绘制
• 空间曲线的绘制 • 例如,现在我们作出上半球面z=与圆柱面的交线 并储存在变量p中,首先我们把此交线方程化为参 数方程 cost 1
, x 2 sin t y , 0 t 2Pi, 从而只要键入 2 t z sin , 2
空间几何体的三视图及斜二测画法

斜二测画法是一种将三维物体投影到 二维平面的方法,通过在垂直方向上 截取物体的一部分并改变其角度来获 得。
性质
斜二测画法能够保留物体的主要特征 ,如形状、大小和相对位置,但无法 完全保留物体的所有细节。
斜二测画法的步骤
01
02
03
04
确定投影方向
选择一个垂直于平面的方向作 为投影方向。
截取物体
空间几何体的三视图
目 录
• 空间几何体的三视图概念 • 三视图的画法 • 三视图的观察与理解 • 斜二测画法 • 三视图与斜二测画法的比较
01
空间几何体的三视图概念
定义与性质
定义
空间几何体的三视图是指从三个 不同的方向观察物体,并将所看 到的图形投影到平面上的结果。
性质
三视图是相互独立的,但它们之 间存在一定的关系,即主视图、 俯视图和左视图分别表示物体的 长度、宽度和高度。
特点
俯视图主要用来表达物体 的水平宽度和垂直深度, 是三视图中表达物体上下 关系的视图。
03
三视图的观察与理解
观察角度
正视图
从几何体的正面观察,呈现几何 体的主要轮廓和特征。
左视图
从几何体的左侧观察,呈现几何体 的侧面轮廓和结构。
俯视图
从几何体的顶部观察,呈现几何体 的底部轮廓和结构。
理解空间几何体的结构
在侧视图中,物体的垂直 线段与投影面垂直,水平 线段与投影面平行,并保 持其实际长度。
特点
侧视图主要用来表达物体 的垂直高度和水平深度, 是三视图中表达物体前后 关系的视图。
俯视图
定义
俯视图是从物体的顶部方 向观察物体所得到的视图。
画法
在俯视图中,物体的水平 线段与投影面平行,垂直 线段与投影面垂直,并保 持其实际长度。
9.1.平面---空间图形直观图的画法

A D
B
)
C
o
x
练习2:如图,直观图所示的平面图形是(C ) A.任意三角形 C.直角三角形 B.锐角三角形 D.钝角三角形
y
A
B
C
o
x
练习3:如图,直观图所示的平面图形是( A.正三角形 C.钝角三角形 B.锐角三角形 D.直角三角形
A
C
)
y
B
C
o
x
作业:P11 习题 8、9.
四个步骤:取轴、画轴、平行性、长度.
练习1:下列说法是否正确? (1)水平放置的正方形的直观图可能 是梯形. (×) (2) 两条相交直线的直观图可能平行.
(×)
(3) 互相垂直的两条直线的直观图仍然 互相垂直. (×) (4)等腰三角形的水平放置的直观图 仍是等腰三角形. (×)
例3、如图,直观图所示的平面图形是(B A.任意四边形 C.任意梯形 B.直角梯形 D.等腰梯形
斜二测画法
1.如何将一个直立放置的平面图形 画在纸上?
2.将一个水平放置的平面图形 (立体图形) 画在纸上,怎样画才有立体感呢?
问题: (1)、太阳光线(假定太阳光线是平 行的)把一个长方形形状的窗框投 射到地板上,变成了什么图形?
(2)、上述窗框的投影图形与原窗 框图比较,哪些几何关系或几何量 发生了变化?哪些没有发生变化?
巩固练习 画水平放置的正五边形的直观图
二、怎样画立体图形的直观图?
例2、画棱长为2cm的正方体的直观图.
z' D' A' D A B y' B' C C'
x'
上述画直观图的方法叫做斜二测画法,规则如下: (1)在已知图形中取水平平面,取互相垂直的轴ox、oy, 再取oz轴,使 ∠ xoz=90° 且∠ yoz=90 °; (2)画直观图时,把它们画成对应的o’x’、o’y’、 o’ z’ , 使∠x’o’y’= 45 °(或135°) , ∠x’o’z’= 90 °. x’o’y’ 所确定的平面表示水平平面; (3)已知图形中平行于x轴、y轴或z轴的线段,在直观图 中分别画成平行于x’轴,y’轴,z’轴的线段; (4)已知图形中平行于x轴和z轴的线段,在直观图中保持 长度不变;平行于y轴的线段,长度为原来的一半.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图6-4
绘制二元函数图形也可用简捷绘制的ezsurf指令,它的使 用格式为: ezsurf(f(x,y),[a,b,u,v]) 即可绘制函数在区域[a,b]×[u,v]上的图形。当省略区域 时,默认区间是[-2 ,2 ]×[- 2 , 2 ]。例如输入: ezsurf('x*exp(-x^2-y^2)') 则输出如图6-5所示。
图6-5
6.2 实验内容
6.2.1 一般二元函数作图
【例1】作平面z=6-2x-3y的图形,其中0≤x≤3, 0≤y≤2。 输入: x=0:0.1:3; y=0:0.1:2; [x,y]=meshgrid(x,y); z=6-2*x-3*y; surf(x,y,z) 输出如图6-6所示。
2
输入: t=pi/1000:0.1:pi/2 ; r=-pi:0.1:pi; [r,t]=meshgrid(r,t); x1=1.5*cos(r).*cot(t); y1=1.4*sin(r).*cot(t); z1=1.3*csc(t); mesh(x1,y1,z1) hold on mesh(-x1,-y1,-z1) 输出如图6-12所示。
图6-10
x2 y 2 z 2 1 的图形。 【例5】作单叶双曲面 1 4 9
曲面的参数方程是
x sec u sin v, y 2sec u cos v, z 3tan u
其中
2
u
2
, 0 v 2 。输入:
t=-pi/4:0.1:pi/4; r=0:0.1:2*pi; [r,t]=meshgrid(r,t); x=sin(r).*sec(t); y=cos(r).*sec(t); z=3*tan(t); surf (x,y,z)
图6-3
又如,参数方程: x 2sin cos , y 2sin sin , z 2cos 是以原 点为中心、2为半径的球面,其中 0 ,0 2 因此只要输入: t=0:0.1:pi; r=0:0.1:2*pi; [r,t]=meshgrid(r,t); x=2*sin(t).*cos(r); y=2*sin(t).*sin(r); z=2*cos(t); surf(x,y,z) 2 2 2 2 便作出了方程为 x y z 2 的球面(见图6-4)。
图6-12
【例7】可以证明:函数z=xy的图形是双曲抛物面。在区 域-2≤x≤2,-2≤y≤2上作出它的图形。
输入: x=-2:0.1:2; y=-2:0.1:2; [xx,yy]=meshgrid(x,y); zz=xx.*yy; surf(xx,yy,zz) 输出如图6-13所示。
图6-13
图6-15
6.2.4 莫比乌斯带子
【例10】前面作出的曲面都是双侧曲面,它们可以分出内、 外侧或左、右侧等,而现在作出的莫比乌斯带子是单侧曲 面,它没有内外侧或左右侧之分。 输入: t=0:0.1:2.01*pi; v=-1:0.1:1; [v,t]=meshgrid(v,t); r=2+0.5*v.*cos(t/2); x=r.*cos(t); y=r.*sin(t); z=0.5*v.*sin(t/2); mesh(x,y,z) 输出如图6-16所示。观察所见到的曲面,理解它是单侧 曲面。
输入: t=0:0.1:2*pi; r=-3:0.1:3; [r,t]=meshgrid(r,t); x=r.*cos(t); y=r.*sin(t); z=r; u=-pi/2:0.1:pi/2; v=-3:0.1:3;
[u,v]=meshgrid(u,v); x1=2*cos(u).^2; y1=sin(2*u); z1=v; mesh(x,y,z) hold on mesh(x1,y1,z1)
4 1 x y
2 2
, 作出它的图形。
输入: ezsurf('4/(1+x^2+y^2)') 得到函数的图形(见图6-8)。
图6-8
【例3】画出函数
z cos(4 x 2 9 y 2 ) 的图形。
输入: x=-1:0.1:1; y=-1:0.1:1; [x,y]=meshgrid(x,y); z=cos(4*x.^2+9*y.^2); mesh(x,y,z) 则得到网格形式的曲面(见图6-9),这是选项 Shading:False起的作用,同时注意选项Boxed:False的 作用。
图6-16
6.2.5 空间曲线
【例11】作出空间曲线 x t cos t , y t sin t , z 的图形。 输入: ezplot3('t*cos(t)','t*sin(t)','2*t',[0,6*pi]) 输出如图6-17所示。
2t (0 t 6 )
图6-17
MATLAB
高等数学实验
实验六
空间图形的画法
实验目的 掌握用MATLAB绘制空间曲面和曲线的方 法。通过作图和观察,深入理解多元函数 的概念,提高空间想像能力。深入理解二 次曲面方程及其图形。
6.1 学习MATLAB命令
6.1.1 三维曲线的绘制
命令plot3主要用于绘制三维曲线,它的使用格式和plot完全相似。 该命令的基本形式是: plot3(x,y,z,'s') 例如,一条空间螺旋线的参数方程是: x=cost, y=sint, z=t/10(0≤t≤8 ) 输入: t=0:0.1:8*pi; x=cos(t); y=sin(t); z=t/10; plot3(x,y,z) xlabel('x'); ylabel('y'); zlabel('z') 则输出了一条螺旋线(见图6-1)。
图6-6
如果只要位于xoy平面上方的部分,则输入: x=0:0.1:3; y=0:0.1:2; [x,y]=meshgrid(x,y); z=6-2*x-3*y; i=find(6-2*x-3*y<0); z(i)=NaN; surf(x,y,z) 输出如图6-7所示。
【例2】设函数
z
图6-11
x2 y2 z2 2 2 1 的图形。 【例6】作双叶双曲面 2 1.5 1.4 1.3
曲面的参数方程是
x 1.5cot u cos v, y 1.4cot u sin v, z 1.3csc u
其中: 参数 0 u , v 对应双叶双曲面的一叶 2 参数 u 0, v 对应双叶双曲面的另一叶。
图6-1
同绘制二维曲线相似,也有简捷的绘制空间曲线命令 ezplot3,具体使用方法同ezplot相似,形式是: ezplot3('x(t)','y(t)','z(t)',[t1,t2]) 其中x(t), y(t), z(t)是曲线的参数方程的表示式。t1,t2 是作图时参数t的范围。 例如上述螺线也可输入下面命令得到: ezplot3('cos(t)','sin(t)','t/10',[0,8*pi]) 输出图形略。
6.1.2 三维曲面网线图与曲面图的绘制
MATLAB软件绘制曲面图要比绘制曲线图相对复杂,这里 只作简单的介绍。在绘制网线图与曲面图时,最常用的基 本形式是: (1)[X,Y]=meshgrid(x,y) (2)Z=f(x,y) (3)mesh(X,Y,Z) %绘制网线图 (4)surf(X,Y,Z) %绘制曲面图
[u,v]=meshgrid(u,v); x1=2*cos(u).^2; y1=sin(2*u); z1=v; mesh(x,y,z) hold on mesh(x1,y1,z1)
图6-14
【例9】作出锥面 相交的图形。
x y z 和柱面 ( x 1)2 y 2 1
2 2 2
图6-9
6.2.2 二次曲面
x2 y 2 z 2 1 的图形。 【例4】作椭球面 4 9 1
该曲面的参数方程是
x 2sin u cos v, y 3sin u sin v, z cos u
其中 0 u ,0 v 2 输入: t=0:0.1:pi; r=0:0.1:2*pi; [r,t]=meshgrid(r,t); x=2*sin(t).*cos(r); y=3*sin(t).*sin(r); z=cos(t); surf(x,y,z)
例如,画出曲面 z x y 的图形。输入: x=-2:0.1:2; y=-2:0.1:2; [x,y]=meshgrid(x,y); z=x.^2+y.^2; surf(x,y,z) z x 2 y 2,见图6-2。 得到曲面
2 2
图6-2
执行下面的程序: x=-2:0.015:2; y=-2:0.015:2; [x,y]=meshgrid(x,y); z=x.^2+y.^2; i=find(x.^2+y.^2>4); z(i)=NaN; surf(x,y,z) 同样得到曲面(见图6-3)。 由于自变量的取值范围不同,图形也不同。不过,后者比 较好地反映了旋转曲面的特点,因此是常用的方法。
6.2.3 曲面相交
