三视图练习
三视图练习题

三视图练习题三视图练习题1.下图是由哪个平面图形旋转得到的()A B C D2.有一个几何体的三视图如下图所示,这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对3.下列几何体各自的三视图中,有且仅有两个视图相同的是()A .①②B .①③C .①④D .②④ 4.有一个几何体的三视图及其尺寸如下(单位:cm ),则该几何体的表面积和体积为( )A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cmππ D.以上都不正确5.如左图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t变化的可能图象是()侧视正视图俯视图6.正方体的截平面不可能是(1) 钝角三角形 (2) 直角三角形 (3) 菱形 (4) 正五边形 (5) 正六边形下述选项正确的是:()(A) (1)(2)(5) (B) (1)(2)(4) (C) (2)(3)(4) (D) (3)(4)(5) 7.如图,在正方体ABCD —A1B1C1D1中,P 为BD1的中点,则△PAC 在该正方体各个面上的射影可能是()A .①④B .②③C .②④D .①②8.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为()俯视图侧视图正视图A.9.一空间几何体的三视图如图所示,则该几何体的体积为( ). A.2π+B. 4π+2π4π+10.如图,是几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是()侧(左)视图正(主)视图俯视图A B C D1A 1B 1C 1D P① ③ ④ ②俯视图左视图主视图A .5B .6C .7D .811.如果一个几何体的三视图如图所示,其中正视图中ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为 ( )A .23B .32C .12D .612.用若干个棱长为1的正方体搭成一个几何体,其正视图、侧视图都是如右图形,对这个几何体,下列说法正确的是A .这个几何体的体积一定是7 B .这个几何体的体积一定是10C .这个几何体的体积的最小值是6,最大值是10D .这个几何体的体积的最小值是7,最大值是11 二、填空题13.如图,,E F 分别为正方体的面11A ADD 、面11B BCC的中心,则四边形E B F D1在该正方体的面上的射影可能是____________。
三视图练习题及答案

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一,它能够以三个不同的视角展示一个物体的外观和内部结构,帮助人们更好地理解和分析物体的形状和构造。
为了提高对三视图的理解和应用能力,下面将给出一些三视图练习题及答案,希望对读者有所帮助。
1. 请根据给出的三视图,画出物体的立体图。
答案:根据三视图,我们可以确定物体的形状和尺寸,然后利用透视法将其转化为立体图。
在绘制过程中,需要注意比例和透视关系,以保证立体图的准确性。
2. 给出一个物体的立体图,请根据立体图绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察立体图中的各个面,然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意比例和尺寸的准确性,以确保三视图能够准确地表达立体图的形状和结构。
3. 请根据给出的三视图,判断物体的形状是什么?答案:通过观察三视图中的线条和面,我们可以判断物体的形状。
例如,如果正视图中的线条是直的,侧视图中的线条是弯曲的,那么物体可能是一个圆柱体。
通过观察三视图中的特征,我们可以逐步推断出物体的形状。
4. 给出一个物体的形状,请根据形状绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察物体的形状和结构,然后根据其特征来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意线条的粗细和长度,以确保三视图能够准确地表达物体的形状和结构。
通过以上的练习题和答案,我们可以提高对三视图的理解和应用能力。
练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构,还可以提高我们的制图能力和空间想象力。
在实际工程设计和制图中,三视图是非常重要的表达方式,掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。
总之,通过不断地练习和应用,我们可以提高对三视图的掌握程度,为工程设计和制图提供更准确、更有效的表达方式。
希望以上的练习题和答案能够对读者有所帮助,进一步提高对三视图的理解和应用能力。
物体三视图的认识 小学数学 练习题
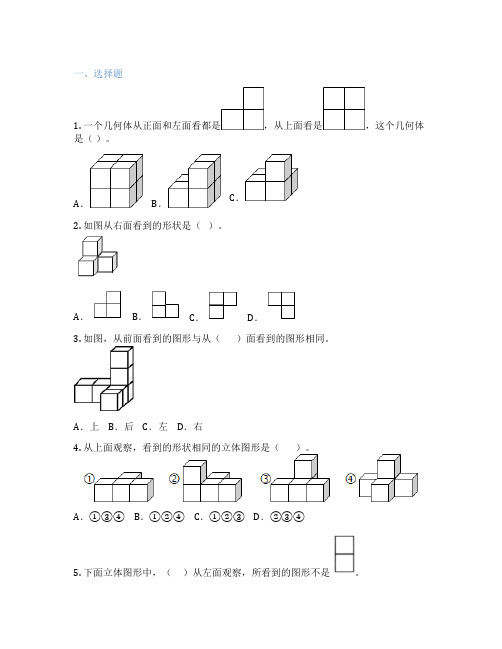
一、选择题1. 一个几何体从正面和左面看都是,从上面看是,这个几何体是()。
C.A.B.2. 如图从右面看到的形状是()。
A.B.C.D.3. 如图,从前面看到的图形与从()面看到的图形相同。
A.上B.后C.左D.右4. 从上面观察,看到的形状相同的立体图形是()。
A.①③④B.①②④C.①②③D.②③④5. 下面立体图形中,()从左面观察,所看到的图形不是。
A.B.C.二、填空题6. 分别从前面、右面和上面观察下边的物体,从( )面和( )面看到的图形完全相同。
7. 我能选择对.(1)从正面看图________,看到的是图a.(2)从正面看图________,看到的是图b.(3)从侧面看图________,看到的是图c.8. 是从物体(如图)的( )面看到的。
9. 一个几何体从上面看是,图中的数字表示在这个位置上的小正方体的个数,则这个几何体从正面看是___________,从左面看是___________,从右面看是___________。
(填序号)10. 从( )面看是,从( )面看是,从( )面看是。
三、解答题11. 把8个棱长是1厘米的小正方体拼在一起(如图),从上面,正面和左面看到的图形面积和是多少?最多取走几个小正方体使得从正面看到的图形不变?12. 下面3个几何体都是由棱长1cm的小正方体摆成的。
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个几何体的上面看到的?将序号写在括号中。
()()()(2)①的体积是②的体积的()(3)③的体积是()cm3,如果要把它继续拼搭成一个大正方体,至少还需要()个小正方体。
(4)你还能提出一个数学问题并解答吗?13. 把4个同样大小的正方体横着摆成一个长方体,说说下面的图形是从哪一面看到的.14. 看一看,写一写,画一画。
(1)上面的物体都是由()个小正方体组成的。
(2)从左面看到的图形相同的是(),从前面看到的图形相同的是()。
(填序号)(3)分别画出物体③和④从上面看到的图形。
CAD三视图练习题

CAD三视图练习题投影与三视图练习题1.填空题(1)俯视图为圆的几何体是_______,______。
(2)画视图时,看得见的轮廓线通常画成_______,看不见的部分通常画成_______。
(3)举两个左视图是三角形的物体例子:________,_______。
(4)如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称_______。
请将六棱柱的三视图名称填在相应的横线上.(6)、如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称_______。
(7)、一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有________个碟子。
(8)、某几何体的三种视图分别如下图所示,那么这个几何体可能是_____。
(9)人在观察目标时,从眼睛到目标的叫做视线。
所在的位置叫做视点,有公共的两条所成的角叫做视角。
视线不能到达的区域叫做。
(10)物体在光线的照射下,在某个内形成的影子叫做,这时光线叫做,投影所在的叫做投影面。
由的投射线所形成的投影叫做平行投影。
由的投射线所形成的投影叫做中心投影。
(11)在平行投影中,如果投射线垂直于投影面,那么这种投影就称为正投影。
(12)物体的三视图是物体在三个不同方向的。
上的正投影就是主视图,水平面上的正投影就是,上的正投影就是左视图。
2.选择题(1)圆柱对应的主视图是( )。
(A) (B) (C) (D)(2)某几何体的三种视图分别如下图所示,那么这个几何体可能是( )。
(A)长方体 (B)圆柱 (C)圆锥 (D)球(3)下面是空心圆柱在指定方向上的视图,正确的是…( )(4)一个四棱柱的俯视图如右图所示,则这个四棱柱的主视图和左视图可能是( )(5)主视图、左视图、俯视图都是圆的几何体是( )。
(A)圆锥(B)圆柱 (C)球 (D)空心圆柱(6)在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )A、小明的影子比小强的影子长B、小明的影子比小强的影子短C、小明和小强的影子一样长D、无法判断谁的影子长 3、解答题(1)根据要求画出下列立体图形的视图。
三视图识图练习

三视图1.将长方体截去一个四棱锥后,得到的几何体的直观图如图所示,则该几何体的俯视图为()2.如图,甲、乙、丙是三个立体图形的三视图,与甲、乙、丙相对应的标号是()①长方体;②圆锥;③三棱锥;④圆柱.A.③①②B.①②③C.③②④D.④②③3.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④4.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是()15.一个几何体的三视图如右图,则组成该组合体的简单几何体为()A.圆柱与圆台B.四棱柱与四棱台C.圆柱与四棱台D.四棱柱与圆台5.一个长方体截去两个三棱锥,得到的几何体如图所示,则该几何体的三视图为()6.将正方体(如图(1)所示)截去两个三棱锥,得到如图(2)所示的几何体,则该几何体的侧视图为()7.如图所示为一个简单几何体的三视图,则其对应的几何体是()8.某几何体的直观图如图所示,下列给出的四个俯视图中正确的是()9.一个几何体的三视图如图所示,则该几何体的直观图可以是()10.如果用□表示1个立方体,用表示2个立方体叠加,用■表示3个立方体叠加,那么图中由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是()11.一个几何体的三视图如图所示,则该几何体的直观图可以是()A.B.C.D.12.下列三视图所对应的直观图是()A.B.C.D.13.下面的三视图对应的物体是()A.B.C.D.14.如图是哪一个物体的三视图()A.B.C.D.16.如图是一个物体的三视图,则此三视图所描述物体的直观图是()A.B.C.D.17.某几何体的三视图如图所示,则这个几何体的直观图是图中的()A.B.C.D.18.空间几何体的三视图如图所示,则此空间几何体的直观图为()A.B.C.D.19.某建筑物的三视图如图所示,则此建筑物结构的形状是()A.圆锥B.四棱柱C.从上往下分别是圆锥和四棱柱D.从上往下分别是圆锥和圆柱20.如图所示为一个简单几何体的三视图,则其对应的几何体是()A.B.C.D.21.已知一个几何体的三视图如图所示,则此几何体的组成为()A.上面为棱台,下面为棱柱B.上面为圆台,下面为棱柱C.上面为圆台,下面为圆柱D.上面为棱台,下面为圆柱22.如图所示为长方体木块堆成的几何体的三视图,此几何体共由________块木块堆成.23.已知某组合体的正视图与侧视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是图中的________.(把你认为所有正确图象的序号都填上)24.若一个正三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.答案解析1.【答案】C【解析】俯视图从图形的上边向下边看,看到一个正方形的底面,在底面上有一条对角线,对角线是由左上角到右下角的线,故选C.2.【答案】D【解析】3.【答案】D【解析】在各自的三视图中①正方体的三个视图都相同;②圆锥有两个视图相同;③三棱台的三个视图都不同;④正四棱锥有两个视图相同.4.【答案】D【解析】根据几何体的三视图知识求解.由于该几何体的正视图和侧视图相同,且上部分是一个矩形,矩形中间无实线和虚线,因此俯视图不可能是D.5.【答案】C【解析】从该几何体可以看出,正视图是一个矩形内有一斜向上的对角线;俯视图是一个矩形内有一斜向下的对角线,没有斜向上的对角线,故排除B、D项;侧视图是一个矩形内有一斜向下的对角线,且都是实线,因为没有看不到的轮廓线,所以排除A项.6.【答案】B【解析】还原正方体后,将D1,D,A三点分别向正方体右侧面作垂线.D1A的射影为C1B,且为实线,B1C被遮挡应为虚线.7.【答案】A【解析】对于A,该几何体的三视图恰好与已知图形相符,故A符合题意;对于B,该几何体的正视图的矩形中,对角线应该是虚线,故不符合题意;对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的侧视图的矩形中,对角线应该是虚线,故不符合题意.故选A.8.【答案】B【解析】几何体的俯视图,轮廓是矩形,几何体的上部的棱都是可以看见的线段,所以C,D不正确;几何体的上部中间的棱与正视图方向垂直,所以A不正确.故选B.9.【答案】D【解析】由俯视图是圆环可排除A,B,C,进一步将三视图还原为几何体,可得选项D.10.【答案】B【解析】结合已知条件易知B正确.11.【答案】D【解析】由俯视图可知,原几何体的上底面应该是圆面,由此排除选项A和选项C.而俯视图内部只有一个虚圆,所以排除B.故选D.12.【答案】C【解析】从俯视图可以看出直观图的下面部分为长方体,上面部分为圆柱,且与下面的长方体的顶面的两边相切,由侧视图可以看出上下部分高度相同.只有C满足这两点,故选C.13.【答案】D【解析】从俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有D 满足这两点,故选D.14.【答案】C【解析】经分析可知,该物体应该是一个圆柱竖直放在一个长方体上,A中的不是一个圆柱,故排除.B中的圆柱直径小于长方体的宽.D项中上面不是一个圆柱体.故选C.15.【答案】B【解析】由已知中的三视图可得该几何体是一个组合体,由几何体上部的三视图均为矩形可知上部是四棱柱,由下部的三视图中有两个梯形可得下部为四棱台,故组成该组合体的简单几何体为四棱柱与四棱台,故选B.16.【答案】D【解析】正视图和侧视图相同,说明组合体上面是锥体,下面是正四棱柱或圆柱,由俯视图可知下面是圆柱.故选D.17.【答案】B【解析】由正视图可排除A,C选项;由侧视图可排除D选项,综合三视图可得,B选项正确.故选B.18.【答案】A【解析】由已知中三视图的上部分是锥体,是三棱锥,满足条件的正视图的选项是A与D,由侧视图可知,选项D不正确,由三视图可知该几何体下部分是一个四棱柱,选项都正确,故选A. 19.【答案】C【解析】由图可得该几何体是一个组合体,其上部的三视图有两个三角形,一个圆,故上部是一个圆锥,其下部的三视图均为矩形,故下部是一个四棱柱.故选C.20.【答案】A【解析】对于A,该几何体的三视图恰好与已知图形相符,故A符合题意;对于B,该几何体的正视图的矩形中,对角线应该是虚线,故不符合题意;对于C,该几何体的正视图的矩形中,对角线应该是从左上到右下的方向,故不符合题意;对于D,该几何体的侧视图的矩形中,对角线应该是虚线,故不符合题意.故选A.21.【答案】C【解析】结合图形分析知上为圆台,下为圆柱.故选C.22.【答案】4【解析】由三视图知,由4块木块组成.如图.23.【答案】①②③④【解析】由正视图和侧视图可知几何体为锥体和柱体的组合体.(1)若几何体为圆柱与圆锥的组合体,则俯视图为③;(2)若几何体为棱柱与圆锥的组合体,则俯视图为④;(3)若几何体为棱柱与棱锥的组合体,则俯视图为①;(4)若几何体为圆柱与棱锥的组合体,则俯视图为②.24.【答案】28√33【解析】25.【答案】三视图对应的几何体如下图所示.【解析】。
第二十九章 三视图 同步练习 2022—2023学年人教版数学九年级下册

人教版九下 29.2 三视图一、选择题(共16小题)1. 如图是某几何体的三视图,该几何体是( )A. 正方体B. 圆锥C. 四棱柱D. 圆柱2. 如图所示的几何体,其俯视图是( )A. B.C. D.3. 如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )A. B.C. D.4. 由若干个棱长为1cm的正方体堆积成一个几何体,它的三视图如图所示,则这个几何体的表面积是( )A. 15cm2B. 18cm2C. 21cm2D. 24cm25. 如图,是某几何体的三视图,该几何体是( )A. 圆柱B. 正方体C. 三棱柱D. 长方体6. 如图是由一个圆柱和一个长方体组成的几何体,则该几何体的俯视图是( )A. B.C. D.7. 若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这个几何体是( )A. 球体B. 圆锥C. 圆柱D. 正方体8. 如图①,长方体的体积为120,图②是图①的三视图,用S表示面积,若S主=24,S 左=20,则S俯=( )A. 26B. 28C. 30D. 329. 下列选项中,如图所示的圆柱的三视图画法正确的是( )A. B.C. D.10. 如图所示,从左面看该几何体,看到的图形是( )A. B.C. D.11. 图②是图①中长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯=( )A. a2+aB. 2a2C. a2+2a+1D. 2a2+a12. 一个几何体由若干个大小相同的小正方体组成,从上面看和从左面看得到的平面图形如图,那么组成该几何体所需小正方体的个数最少为( )A. 4B. 5C. 6D. 713. 如图所示的六角螺母,从上面看,得到的图形是( )A. B.C. D.14. 一个圆柱的三视图如图所示,则这个圆柱的体积为( )A. 24B. 24πC. 96D. 96π15. 如图,是一个几何体从正面、左面、上面看得到的图形,则这个几何体是( )A. B.C. D.16. 如图,下列关于物体的主视图画法正确的是( )A. B.C. D.二、填空题(共10小题)17. 如图图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为.18. 下图是由一些相同长方体的积木块拾成的几何体的三视图,则此几何体共由块长方体的积木搭成.19. 在①长方体,②球,③圆锥,④圆柱,⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是.(填上序号即可)20. 长方体的主视图、俯视图如图所示,则这个长方体的体积为;21. 一个几何体的三视图如下图所示,这个几何体是(填名称).22. 有四块如图(1)这样的小正方体摆在一起(各部分之间必须相连),其主视图如图(2),则左视图有种画法.23. 长方体直观图有多种画法,通常我们采用画法.24. 下图是由十个小正方体组成的几何体,若每个小正方体的棱长都是2,则该几何体的主视图和左视图的面积之和是.25. 图是某几何体的三视图及相关数据,则该几何体的侧面积是26. 图是由小正方体组合而成的几何体的主视图、左视图和俯视图,则至少再加个小正方体后,该几何体可成为一个正方体.三、解答题(共7小题)27. 如图是一个几何体的三视图,根据图示的数据计算出该几何体的表面积.28. 画出下列组合体的三视图.29. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:碟子的个数1234⋯碟子的高度(单位:cm)22+1.52+32+4.5⋯(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.30. 一个等腰Rt△ABC如图所示,将它绕直线AC旋转一周,形成一个几何体.(1)写出这个几何体的名称,并画出这个几何体的三视图;(2)依据图中的数据,计算这个几何体的表面积.(结果保留π)31. 如图是由一些大小相同的小立方块搭成的几何体.(1)图中有块小立方块;(2)请分别画出它的主视图,左视图和俯视图.32. 由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如下图所示,数字表示该位置上的小正方体个数.(1)请在下图中画出它的主视图和左视图;(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为.(3)在不改变主视图和俯视图的情况下,最多可添加个小正方体.33. 一个零件是由长为34mm、高和宽都为17mm的长方体与直径为34mm、高度为17mm的半圆柱组成几何体后,又切去直径为17mm的圆柱后剩下的几何体,其实物直观图如图所示,请画出这个零件的三视图.答案1. D【解析】该几何体的视图为一个圆形和两个矩形.则该几何体可能为圆柱.2. D【解析】从上面看,是一个带圆心的圆.3. A【解析】该组合体的主视图如下:4. B【解析】由三视图可知该几何体的直观图如图所示.∵各个小正方体的棱长为1cm,∴这个几何体的表面积是3×6×1×1=18(cm2).5. D6. A【解析】从上边看,是一个矩形,矩形的内部有一个与矩形两边相切的圆.7. A【解析】解答这种类型的题目时,可以像画图题一样,面出每个选项中的几何体的三视图,然后和已知三视图比较得出答案;也可以通过已知的三个视图想象出几何体,从选项中寻找和它一致的几何体,进而得出答案.8. C【解析】由题意,长方体的宽为120÷24=5,长为120÷20=6,∴俯视图的面积为6×5=30.9. A【解析】放置的圆柱的主视图是长方形,左视图是圆,俯视图是长方形.10. B【解析】从左面看是一个长方形,中间有两条水平的虚线,故选B.11. A【解析】∵S主=a2=a⋅a,S左=a2+a=a(a+1),∴俯视图的长为a+1,宽为a,=a⋅(a+1)=a2+a.∴S俯12. B【解析】由从上面看与从左面看得到的平面图形知,组成该几何体所需小正方体个数最少的分布情况如图所示(不唯一);所以组成该几何体所需小正方体的个数最少为5,故选B.13. B【解析】从上面看,是一个正六边形,六边形的中间是一个圆.14. B【解析】由三视图可知圆柱的底面直径为4,高为6,∴底面半径为2,=πr2ℎ=π⋅22×6=24π,∴V圆柱故选B.15. B【解析】观察从正面、左面、上面看得到的图形发现,这个几何体是长方体和圆锥的组合图形.故选B.16. C【解析】主视图是从正面看几何体得到的图形,在画图时规定:看得见的轮廓线画成实线,看不见的轮廓线画成虚线,显然空心圆柱的主视图画法正确的是C,故选C.17. 3π【解析】由三视图知几何体为圆柱,且底面圆的半径是1,高是3,∴这个几何体的体积为:π×12×3=3π.18. 419. ②20. 1221. 四棱锥22. 4【解析】左视图可能为以下4种.23. 斜二侧24. 48【解析】该几何体的主视图和左视图如下,∴面积之和为2×2×(6+6)=48.25. 16√7π【解析】根据三视图可知该几何体为圆锥,高为6,母线长为8,则底面半径为√82−62=2√7,所以S=π×2√7×8=16√7π.圆锥侧26. 22【解析】观察三视图,可知这个几何体各个位置上的小正方体的个数,在俯视图上标出如图所示,则由题意可知最小可以组成3×3×3的正方体,即组成的正方体共有27个小正方体,27−2−1−1−1=22,所以至少再加22个小正方体后,才能组成一个正方体.27. 由三视图可知该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,所以圆锥的母线长=√52+122=13,⋅2π⋅5⋅13=90π.所以圆锥的表面积=π⋅52+1228. 如图所示.29. (1)由图可知,每增加一个碟子高度增加1.5cm,桌子上放有x个碟子时,高度为2+1.5(x−1)=1.5x+0.5.(2)由图可知,共有3摞,左前一摞有5个,左后一摞有4个,右边一摞有3个,共有3+4+5=12(个),叠成一摞后的高度=2+1.5×11=18.5(cm).30. (1)这个几何体是圆锥,这个几何体的三视图如图所示.×2π×2×√22+22+π×22=(4√2+4)π.(2)这个几何体的表面积为1231. (1)6(2)如图所示.32. (1)该几何体的主视图和左视图如图所示.(2)32【解析】给这个几何体喷上颜色(底面不喷色),需要喷色的面有32个,所以喷色的面积为32.(3)1【解析】在俯视图中标数字“2”的正方形的位置上再添加1个小正方体,不会改变主视图和俯视图.33. 三视图如图所示:。
三视图小练习

三视图专题练习
请据题图所示形体,画出主视图,补全左视图的缺漏线条。
根据轴测图补画三视图中所缺的线条。
根据题图所示形体,画出主视图。
补全俯视图的缺漏线条。
根据两视图 , 补画第三视图
根据轴测图补全三视图中所缺的线,或补画第三个视图
如图所示的形体:根据已有的正等轴测图、主视图,补充完成视图。
并在三视图中标注出长、宽、高(说明:长5cm、宽4cm、高4cm;凹槽部分:下底面宽1cm)(8分)
根据立体图,补全俯视图和左视图中所缺漏的图线。
(高考题1)
根据轴测图,补全三视图中缺少的图线
主视
根据轴测图,补全三视图中缺少的图线
根据轴测图,补全三视图中缺少的视图及图线
根据所给的主视方向,画出三视图
如图,三视图反映的是一个模型,这个模型有数个象A 那样的正立方体叠加而成的。
你认为这个模型是由几个A 那样的正立方体组成的 ( )
A .4个
B .5个
C .6个
D .7个
为了表示工件的最高点的圆弧尺寸(弧的半径30mm ),妥当的是 ( )
A B C D
30 R30 半径30 R60
仔细观察右侧的俯视图,它和下面a 、b 、c 、d 四个模型的关系正确的是( )
A .肯定是c 的
B .可能是b 、c 、d 的
C .可能是a 、b 的
D .不可能是a 、b 的
30、根据立体图,补画俯视图和左视图中缺少的图线。
a b c
d。
三视图习题50道(含答案)

word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题(单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2(主)视图与侧(左)视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示,则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图,该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示,则其侧.面积等于(A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h=7、 一个几何体的三视图如图所示 ,则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图(也称主视图)是()8、如图,网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形,)S 2a.俯视图正(主)视图侧(左)视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示,则该几何体的体积为().A.2 2.3B. 4 2 . 3侧(左)视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c m2)为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、请补全三视图中所缺的两条图线。
每条线都为2、、根据轴测图,补全三视图中缺少的图线。
答案
3根据立体图补全三视图中所缺的图线。
答案.主视图长虚线两条(1分);短虚线两条(1分);
左视图虚线两条(1分);
俯视图实线一条(1分)。
4、
根
据
立体图,补全主视图、俯视图和左视图中所缺漏的图线。
(原创)
(1)主视图画出三条虚线 3)
(2俯视图画出一条实线 1)
(3)左视图画出两条虚线2)
5、(原创)根据轴测图,补全三视图中缺少的图线。
6、. 请补全三视图中所缺的图线。
7、.请据轴测图,请补全三视图中所缺的两条图线。
