勒让德多项式及性质 PPT课件
合集下载
14第十四章 勒让德多项式
( tan
m2 sin2
)
0，(0),
(
)
有限
记
本征值 l(l 1), l m, m 1, m 2,...
住
本征函数 Plm (cos ) (缔合勒让德函数)
结 论
m=0 时，本征函数为勒让德多项式 Pl (cos )
• 2u 0 球壳区域的通解：
u(r)
(cl rl dl rl1) Plm (cos )[am cos(m ) bm sin( m )]
[l(l
1)
m (m
1)] Pl(m)
0
证：对微分方程 [(1 x2 ) Pl] l(l 1) Pl 0
应用高阶导数公式求导 m 次
n
[ f ( x)g( x)](n) Cnk f (k) ( x) g(nk) ( x) k0 取 f 1 x2 , g Pl, n m 1
P0 ( x) 1
P1( x) x cos
P2( x) (3x2 1) / 2 P3( x) (5x3 3x) / 2
| Pl ( x) | 1, 1 x 1 Pl (1) 1, Pl (1) (1)l
Pl
(x)
1 2l l!
dl dx l
(x2
1)l
17
§14.2 勒让德多项式的性质
右边从 1 到 x 逐项积分 l 次，得到
l
m0
1 (l m)! ( x 1)ml 2m m! (l m)! (m l)!
( x 1)l 2l l!
l
Clm ( x 1)m 2l m
m0
(x
1)l ( x 2l l!
1
2)l
1 2l l!
(
数学物理方程课件第六章勒让德多项式
0
2 (2n)!
2n n!
2n n! 2n n!2n 1 2n 153
2 (2n)!
2n 1!
2 2n 1
数学物理方程与特殊函数
第6章勒让德多项式
性质2 递推公式
(n 1)Pn1 (x) (2n 1)xPn (x) nPn1 (x) 0
Pn1 (x) Pn1 (x) 2n 1Pn (x)
n0
Cn
2n 1 2
1 1
x Pn (x)dx
C0
1 2
1
1 x P0 (x)dx
1 2
1
x dx
1
1 2
C2n1 0
C2n
4n 1 2
1 1
x
P2n
(x)dx
4n
1
1 0
xP2n
( x)dx
4n 1
22n 2n!
1 d2n 0 x dx2n
(x2 1)2n dx
4n 1 22n 2n !
数学物理方程与特殊函数
第6章勒让德多项式
三 勒让德多项式
y APn (x) BQn (x)
Pn
(x)
M
(1)m
m0
2n 2m!
2n m!(n m)!(n
2m)!
xn2m
Pn
1 2n n!
dn dx n
(x2
1)n
当n为偶数时M
n 2
当n为奇数时 M
n 1 2
P0 (x) 1
P1(x) x
2)(n 1)(n 4!
3)
x4
]
c 1 c0
y2
a1[ x
(n
1)(n 3!
2)
2 (2n)!
2n n!
2n n! 2n n!2n 1 2n 153
2 (2n)!
2n 1!
2 2n 1
数学物理方程与特殊函数
第6章勒让德多项式
性质2 递推公式
(n 1)Pn1 (x) (2n 1)xPn (x) nPn1 (x) 0
Pn1 (x) Pn1 (x) 2n 1Pn (x)
n0
Cn
2n 1 2
1 1
x Pn (x)dx
C0
1 2
1
1 x P0 (x)dx
1 2
1
x dx
1
1 2
C2n1 0
C2n
4n 1 2
1 1
x
P2n
(x)dx
4n
1
1 0
xP2n
( x)dx
4n 1
22n 2n!
1 d2n 0 x dx2n
(x2 1)2n dx
4n 1 22n 2n !
数学物理方程与特殊函数
第6章勒让德多项式
三 勒让德多项式
y APn (x) BQn (x)
Pn
(x)
M
(1)m
m0
2n 2m!
2n m!(n m)!(n
2m)!
xn2m
Pn
1 2n n!
dn dx n
(x2
1)n
当n为偶数时M
n 2
当n为奇数时 M
n 1 2
P0 (x) 1
P1(x) x
2)(n 1)(n 4!
3)
x4
]
c 1 c0
y2
a1[ x
(n
1)(n 3!
2)
勒让德多项式
例1:将 x 2 在[-1,1]内展成勒让德多项式的级数形式
x 2 Cn Pn (x) n0
Cn
2n 1 2
1 1
x
2
Pn
(
x)dx
1 1
xk
Pn
( x)dx
0
n2
4 1
C2 2
1 x2 1 (3x2 -1)dx 5
1 2
4
1 3x4 x2
1
dx
5 6 2 2 45 3 3
第6章勒让德多项式
例2:将Pl(x) 在[-1,1]内展成勒让德多项式的级数形式
解：方法一
l 1
(l 1) / 2
Pl(x) CnPn (x) CnPn (x)
Cl2n1Pl2n1 ( x)
n0
n0
n0
2l 4n 1
Cl2n1
2
1
1 Pl(x)Pl2n1(x)dx
2l 4n 1 2
1 0
xd
d 2n1 dx 2 n 1
(x2
1)2n
4n 22n
1 2n
!
x
d 2 n 1 dx 2 n 1
(x2
1)2n|10源自1 0d 2 n1 dx 2 n 1
(x2
1)2n
dx
4n 22n
1 2n
!
d 1 2n1 0 dx2n1
(x2
1)2n dx
4n 22n
1 2n
!
d2n2 dx 2 n 2
0
0
0
/ 2 sin 2n1 d 2n / 2 sin 2n1 d
0
2n 1 0
1 P2n (x)dx 1
勒让德多项式
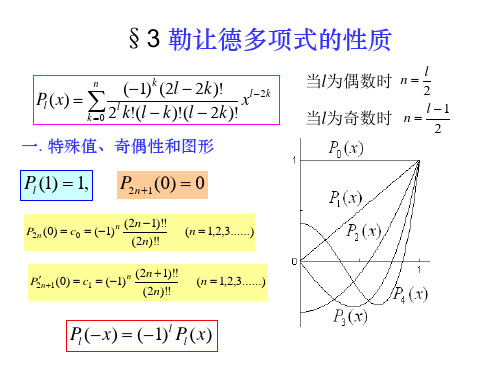
§3 勒让德多项式的性质
(1) k (2l 2k )! l 2 k Pl ( x) l x k 0 2 k!(l k )!(l 2k )!
n
一. 特殊值、奇偶性和图形
l 2 l 1 n 当l为奇数时 2
当l为偶数时 n
Pl (1) 1,
P2 n (0) c0 (1) n
六. 勒让德多项式的正交性、完备性与模
0, lk 2 1 Pl ( x)Pk ( x)dx Nl2 , l k 2l 1
1
勒让德多项式完备性 若f(x)是定义在[-1,1]区间上任意一个平方可积的函数,
那么
f ( x) cl Pl ( x)
l 0
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
2. P l ( x) P l 1 ( x) 2 xP l ( x) P l 1 ( x)
3. 4.
P l 1 ( x) xP l ( x) (l 1) P( x) Pl 1 ( x) P l 1 ( x) 2l 1P l ( x)
1 1 2rx r xr
2
r Pl ( x)
l l 0 2
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
1 2rx r 2
(1 2rx r ) lr l 1Pl ( x)
l 0
( x r ) r l Pl ( x) (1 2rx r 2 ) lr l 1Pl ( x)
证
2 l
1 dl 2 l Pl ( x) l ( x 1 ) 2 l! dx l
(1) k (2l 2k )! l 2 k Pl ( x) l x k 0 2 k!(l k )!(l 2k )!
n
一. 特殊值、奇偶性和图形
l 2 l 1 n 当l为奇数时 2
当l为偶数时 n
Pl (1) 1,
P2 n (0) c0 (1) n
六. 勒让德多项式的正交性、完备性与模
0, lk 2 1 Pl ( x)Pk ( x)dx Nl2 , l k 2l 1
1
勒让德多项式完备性 若f(x)是定义在[-1,1]区间上任意一个平方可积的函数,
那么
f ( x) cl Pl ( x)
l 0
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
2. P l ( x) P l 1 ( x) 2 xP l ( x) P l 1 ( x)
3. 4.
P l 1 ( x) xP l ( x) (l 1) P( x) Pl 1 ( x) P l 1 ( x) 2l 1P l ( x)
1 1 2rx r xr
2
r Pl ( x)
l l 0 2
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
1 2rx r 2
(1 2rx r ) lr l 1Pl ( x)
l 0
( x r ) r l Pl ( x) (1 2rx r 2 ) lr l 1Pl ( x)
证
2 l
1 dl 2 l Pl ( x) l ( x 1 ) 2 l! dx l
第六章勒让德多项式
1 d d 1 d 2 n(n 1) sin 2 2 sin d d sin d 1 d d 1 d 2 2 sin sin n ( n 1)sin 2 d d d 1 d 2u 2 m 2 1 d d 2 2 d sin sin n ( n 1)sin m d d ( ) B1 cos m B2 sin m 2 2 d d m cot [ n ( n 1) ] 0 2 2 d d sin 连带的勒让德方程
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
数学物理方程与特殊函数
第6章勒让德多项式
例2:将Pl( x) 在[-1,1]内展成勒让德多项式的级数形式 解：方法一
Pl( x) Cn Pn ( x) Cn Pn ( x)
n 0
l 1
( l 1) / 2
n 0
n 0
Cl 2 n 1Pl 2 n 1 ( x)
方法二
2l 4n 1 1 1 2 l 4 n 1 Cl 2 n 1 Pl ( x) Pl 2 n 1 ( x)dx Pl 2 n 1 ( x)dPl ( x) 1 1 2 2 1 2l 4n 1 1 Pl 2 n 1 ( x) Pl ( x) |1 Pl ( x) Pl ( x)dx 2 n 1 1 2 2l 4n 1 2 Pl 2 n1 (1) Pl (1) 0 2l 4n 1 2
第六章---数理方程勒让德多项式
y2
x
(n
1)(n 3!
2)
x3
(n
1)(n
3)(n 5!
2)(n
4)
x5
(2k 1 n)(2k 3 n) (1 n)(n 2) (n 2k) x2k1 (2k 1)!
6. 3 勒让德多项式
6. 3 勒让德多项式
将6.2中的递推公式写成
ak
(k 2) (k 1) (n k)(k n 1)
2)!
6. 3 勒让德多项式
an4
(2n 4)! 2!2n (n 2)!(n
4)!
一般地当 n 2k 0 时，有
6.1 勒让德方程的引出
第二个方程为
d 2
d 2
cot
d
d
n
n
1
m2
sin2
0
令 x cos ，并记 P( x) (cos )
1 x2
d2P dx 2
2x
dP dx
n
n
1
m2 1 x2
P
0
k0
(k c 2)(k c 1)ak2 [(k c)(k c 1) n(n 1)ak 0
a k0 k2
(k
(k＋c)(ck)(k
cc1)a1k)xk
c2
n(n
(k＋c 1)(k c 2)
0 1)
ak
数学物理方法第六章-勒让德函数课件
正整数)，则级数y0(x) 将到x2n项为止．将 k=l=2n代入式(6.1.9)，易见x2n+2项的系数为
重复应用式(6. 1. 9)，可证C2n+4, C2n+6, … 均为零。 y0(x)的最高次幂为x2n= xl．
根据物理量是有限的，舍去不合物理意义的 解，取常数C1 =0，则勒让德方程的解为
45
递推公式的证明方法: (1)母函数关系式为
对t求导得
两边乘以(1-2xt+t2), 再将母函数关系式代入 左边, 即有
两边比较 t l 的系数(l≥1), 即得式(6.2.13)
46
x Pl ( x)t l Pl ( x)t l1
l0
l0
lPl ( x)t l1 2 x Pl ( x)t l11 lPl ( x)t l12
§6.3.1 勒让德多项式的正交性与正交归一关系式 1. “正交性”与“正交归一关系式”浅析
(1)、三维欧几里得(Euclid)空间 三维欧几里得空间的基矢i，j，k如果用 ek 或
10
§6.1.2 勒让德方程的本征值问题
二阶线性齐次常微分方程
(1-x2)y"(x)-2xyʹ(x)-l(l+1)y(x)＝0
-1<x<1
(6.1.6)
称为勒让德方程.
方程中的 l(l+1)=l 是待定参数
y(x)是待求函数.
11
在x=0的邻域求勒让德方程的有界解. 在有界性条件下求解勒让德方程的问题又称
比较等式两边t l的系数, 即得式(6.2.14)
lPl (x)tl xPl(x)tl
Pl(x)tl1
l0
l0
l0
lPl (x)tl xPl(x)tl
重复应用式(6. 1. 9)，可证C2n+4, C2n+6, … 均为零。 y0(x)的最高次幂为x2n= xl．
根据物理量是有限的，舍去不合物理意义的 解，取常数C1 =0，则勒让德方程的解为
45
递推公式的证明方法: (1)母函数关系式为
对t求导得
两边乘以(1-2xt+t2), 再将母函数关系式代入 左边, 即有
两边比较 t l 的系数(l≥1), 即得式(6.2.13)
46
x Pl ( x)t l Pl ( x)t l1
l0
l0
lPl ( x)t l1 2 x Pl ( x)t l11 lPl ( x)t l12
§6.3.1 勒让德多项式的正交性与正交归一关系式 1. “正交性”与“正交归一关系式”浅析
(1)、三维欧几里得(Euclid)空间 三维欧几里得空间的基矢i，j，k如果用 ek 或
10
§6.1.2 勒让德方程的本征值问题
二阶线性齐次常微分方程
(1-x2)y"(x)-2xyʹ(x)-l(l+1)y(x)＝0
-1<x<1
(6.1.6)
称为勒让德方程.
方程中的 l(l+1)=l 是待定参数
y(x)是待求函数.
11
在x=0的邻域求勒让德方程的有界解. 在有界性条件下求解勒让德方程的问题又称
比较等式两边t l的系数, 即得式(6.2.14)
lPl (x)tl xPl(x)tl
Pl(x)tl1
l0
l0
l0
lPl (x)tl xPl(x)tl
大学物理-勒让德多项式
(三) 勒让德多项式的正交性与正交归一关系式 (I) 勒让德多项式的正交性 勒让德方程与有限性条件构成施—刘型本征值问题：
勒让德方程可化为施—刘型方程，其中 (x) = 1，a =
–1，b = 1，而本征函数 yl (x) = Pl (x) 是实函数，故有如下正 交关系
另一种形式：
(II) 勒让德多项式的完备性 根据施—刘型本征值问题的完备性定理，对于在区间
示——微分表示
证明：由二项式展开定理得到
所以
注意到：凡是指数 (2l – 2s) < l 的项经 l 次求导后为 0，故 只剩下 (2l – 2s) ≥ l 的项，即 s ≤ l / 2，于是得到
罗德里格斯公式的应用之一 因为
所以
对于 Pl (1)，利用上式，n > 0 各项的值均为 0，只有当 n = 0 的项，其值不为 0，因此
之间存在着一定的关系。具体如下：
(1) (2) (3) (4)
证明：(I) 由生成函数关系式 两边对 r 求导，有
改写为 两边乘以 (1–2 x r + r2)，再将生成函数关系式代入，得到
比较两边 rl 的系数，有 整理上式，得到 当 l = 0 时，P0(x) = 1，P1(x) = x， 所以 x P0(x) = P1(x) (II) 将生成函数关系式两边对 x 求导，得到
例3 将函数 f (x) = xn 在区间 [–1,1] 上按完备正交函数系
Pl (x) 展开为广义傅里叶级数。
解：所给函数满足斯–刘型本征函数完备性定理的条件，故
xn Cl Pl (x) l 0
广义傅里叶系数为
Cl
2l 1 2
1 1
x
n
Pl
勒让德多项式及性质1
Pl ( x) (1)l Pl ( x)
即当
l 为偶数时，勒让德多项式 Pl ( x) 为偶函数， l 为奇数时 Pl ( x) 为奇函数
一、勒让德多项式的正交关系
0
1
1
Pk ( x) P ( x)dx 0 l
(k l )
(k l )
Pk (cos ) Pl (cos ) sind 0
2 2 2
d d m 方程解出:(1 x ) 2 2 x [l (l 1) ] 0，x cos 2 dx dx 1 x d 2 d 2 m 0时，成为l阶勒让德方程： x ) 2 2 x (1 l (l 1) 0 dx dx 用常点邻域 a0 y0 ( x), l为偶数时 k , 令 y ak x a0 y0 ( x) a1 y1 ( x) 的级数解法 k 0 a1 y1 ( x)，l为奇数时
f
(l )
l! f ( ) ( z) C ( z )l 1 d 2πi
容易证明微分表示也可表示为环路积分形式
1 1 Pl ( x) 2πi 2l
C为
( 2 1)l C ( x)l 1 dx
z 平面上围绕 z x 点的任一闭合回路，
并取正方向．这叫作勒让德多项式的施列夫利积分表示式． 还可以进一步表为下述拉普拉斯积分．
同样若记
arc cos x
y( x) ( x)
l
阶勒让德方程
则上述方程也可写为下列形式的
d 2 dy [(1 x ) ] l (l 1) y 0 dx dx
轴对称球函数 现在注意：m 0时， ( ) A cos m B sin m A(常数) （r , , ） R(r )( )( ) AR(r )( ) （r , ） u u 即在以r， 构成的锥体上各点的u值相同。
第六章_勒让德多项式
6.1 勒让德方程的引出
引入参数 n n 1 分解整理得
d 2R dR 2 r 2r n n 1 R 0 2 dr dr
欧拉型方程
1 d d 1 d 2 sin d sin 2 2 n n 1 0 sin d
引入参数 分解可得两个常微分方程
" 0
d d sin sin n n 1 sin 2 0 d d
§1 勒让德方程的引出
第一个方程与自然周期条件 2 结合，构成本征值问题
d 2 dR R d d R d 2 r dr r 2 sin d sin d r 2 sin 2 d 2 0 2 r dr
用
r 遍乘各项并移项整理，即得 R
2
1 d 2 dR 1 d d 1 d 2 r dr sin d sin d sin 2 d 2 R dr
k n 1 2
这两个多项式可以统一写成
(2n 2k )! Pn ( x) (1) n x n2 k , n 0,1, 2, 2 k !(n k )!(n 2k )! k 0
k n 2
n 阶勒让德多项式
6. 3 勒让德多项式
0～4阶Legendre多项式为
(2k 2 l )(2k 4 l ) (l )(l 1)(l 2k 1) a2 k a0 (2k )!
6. 2
勒让德方程的求解
(1 l )(l 2) a3 a1 3! (3 l )(l 4) (3 l )(1 l )(l 2)(l 4) a5 a3 a1 54 5!
第四章-特殊函数(上)-勒让德多项式和球谐函数PPT课件
[l]
Pl(x)k20(1)k2lk!((l2lk)2!(kl)!2k)!xl2k （4.1.7）
上式中[l/2]表示不 大于l/2的最大整数
[2l]l22l1,,
l 2n l 2n1
(n0,1,2,)
上式具有多项式的形式，故称 P l ( x ) 为 l 阶勒让德多项式．
勒让德多项式也称为 第一类勒让德函数．
(nl) (nl)
当 n
l
时满足
1
1Pn(x)Pl(x)d，x0
(4.2.3)
称为正交性． 相等时可求出其模
N l 1 1P l2(x)dx2l2 1 (l0,1 ,2, )
(4.2.4)
下面给出公式（4.2.2），及其模(4.2.4)的证明
【证明】 （1）正交性 勒让德多项式必然满足勒让德方程(4.1.6)，故有
Pn (cos) ，这时有
f(cos) CnPn(cos) n0
(4.2.7)
其中系数为 (注意积分上、下限)
C n2 n 2 1 0 πf(c o s)P n(c o s)sin d （4.2.8）
4.2.2.勒让德多项式的应用（广义傅氏级数展开）
例4.2.1 将函数 f (x) x3 按勒让德多项式形式展开.
再进行 l 次分部积分，即得
Nl22(2 l(1 l)!l)2
1(x21)l d2l(x21)l dx
1
dx2l
(x2 1)l 是 2l 次多项式，其 2l 阶导数也就是最高幂项
x 2 l 的 2l 阶导数为 (2l )! ．故
N l2(1)l 22 (l2 (ll)!!)2
1(x1)l(x1)ldx
注意到 (x2 1 )l(x 1 )l(x 1 )l以 x1 为 l 级零点，
勒让德多项式及性质
第三篇：特殊函数
第二章 勒让德多项式
主要内容：
勒让德多项式（轴对称问题）及性质 连带勒让德函数（转动对称问题） 球函数（一般问题）
在分离变量法一章中，我们已经知道拉普拉斯方程
1 2 u 1 u 1 2u (r ) 2 (sin ) 2 2 0 2 2 r r r r sin r sin
u与 无关，只与r， 有关。意味着当r， 一定时， 可任意改变，u不变。
问题关于极轴（z轴）对称。 球函数Y ( , ) A( ) ~ 称为轴对称球函数。
r
0 0 ( ) y ( x) l为2k 1(奇数):a1 y1 ( x) ~ x 2 k 1 将它们分别乘上适当的常数，叫做l阶勒让德
Pl ( x) (1)l Pl ( x)
即当
l 为偶数时，勒让德多项式 Pl ( x) 为偶函数， l 为奇数时 Pl ( x) 为奇函数
一、勒让德多项式的正交关系
0
1
1
Pk ( x) P ( x)dx 0 l
(k l )
(k l )
Pk (cos ) Pl (cos ) sind 0
）是正交的、完备的。
可以作为广义傅立叶级数的基。 若函数 f (x) 定义在区间[1,1] 上，或
f ( ) 定义在区间
[0, ]
或
上，则
f ( x) f l Pl ( x)
l 0
f ( ) f l Pl (cos )
l 0
其中系数：
fl
或
1 2 Nl
1
f ( x) x
3 l 0
第二章 勒让德多项式
主要内容：
勒让德多项式（轴对称问题）及性质 连带勒让德函数（转动对称问题） 球函数（一般问题）
在分离变量法一章中，我们已经知道拉普拉斯方程
1 2 u 1 u 1 2u (r ) 2 (sin ) 2 2 0 2 2 r r r r sin r sin
u与 无关，只与r， 有关。意味着当r， 一定时， 可任意改变，u不变。
问题关于极轴（z轴）对称。 球函数Y ( , ) A( ) ~ 称为轴对称球函数。
r
0 0 ( ) y ( x) l为2k 1(奇数):a1 y1 ( x) ~ x 2 k 1 将它们分别乘上适当的常数，叫做l阶勒让德
Pl ( x) (1)l Pl ( x)
即当
l 为偶数时，勒让德多项式 Pl ( x) 为偶函数， l 为奇数时 Pl ( x) 为奇函数
一、勒让德多项式的正交关系
0
1
1
Pk ( x) P ( x)dx 0 l
(k l )
(k l )
Pk (cos ) Pl (cos ) sind 0
）是正交的、完备的。
可以作为广义傅立叶级数的基。 若函数 f (x) 定义在区间[1,1] 上，或
f ( ) 定义在区间
[0, ]
或
上，则
f ( x) f l Pl ( x)
l 0
f ( ) f l Pl (cos )
l 0
其中系数：
fl
或
1 2 Nl
1
f ( x) x
3 l 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
l 0
Al r0l
pl (cos )
cos2
x2
1 3
p0 (x)
2 3
p2 (x)
A0
1 3
A2
2 3
1 r0 2
Al 0 (l 0.2)
u(r, )
1 3
2 3
1 r02
r2
p2 (cos )
r 例题4：半径为 0 的半球，其球面上温度为
u0 cos ，底面绝热，试求这个半球里的稳定温度分布。
3、勒让德多项式的积分表示
根据柯西积分公式的高阶导数，并取正方向积分有
i f (l) (z) l!
2πi
C
(
f ( )
z)l 1
d
容易证明微分表示也可表示为环路积分形式
1 1 ( 2 1)l
i Pl (x) 2πi 2l C ( x)l1 dx
C 为 z 平面上围绕 z x 点的任一闭合回路，
选取球心为极点，Z轴为极轴，
Z
Z轴为对称轴，u与无关。
u 0
u rr0 u0 cos u0 x
O
Y
X
u
0 2
或 u x
x0 0
0
2 x不是直角坐标
对定解问题解析延拓到整个球形区域
x=0上满足第二类边界条件，是关于Z轴对称的。所以边界条件应进行偶延拓。
u0
cos
u rr0
(1)n
(2n 1)!! (2n)!!
式中记号 (2n)!! (2n)(2n 2)(2n 4)L 6 4 2
而 (2n 1)!! (2n 1)(2n 3)(2n 5)L 531
因此， (2n)! (2n)!!(2n 1)!!
奇偶性：
根据勒让德多项式的定义式，作代换 x (x), 容易得到
将指标n k
Pl
(x)
[l/2]
(1)k
k0
k !2l
(2l (l
2k)! k)!(l
2k)!
xl2k
,
按降幂排列的l次多项式。
一、勒让德方程的解：
我们知道：在自然边界条件下，勒让德方程的解
为
Pl (x)
[l] 2
(1)k
k 0
(2l 2k)! 2l k!(l k)!(l
xl2k 2k)!
场强为 E0，球的半径为 r0 ，介电常数为
，试求解介质球内外的场强。
解：选取球心为极点，
极点，平行于E0 的直线为Z轴。
即：Z轴为对称轴， u与 无关。
由于介质球的极化，球面上产生了束缚电荷。
场强
E u
在球面上不连续。u
u
E
在球面上无意义。 所以，球内外电势要通过衔接条件连接。
1、设球内电势为：u内 ，满足：
(231x6
315x4
105x2
5)
1 512
(231cos 6
126 cos
4
105cos
2
50)
勒让德多项式的图形可通过计算机仿真(如MATLAB仿真) 得到
图 11.1
2、勒让德多项式的微分表示
Pl (x)
1 2l l !
dl dxl
(x2
1)l
上式通常又称为勒让德多项式的罗德里格斯（Rodrigues） 表示式．
m
() Acos m B sin m, m 0,1, 2,3,...
球函数Y (,) (Acos m Bsin m)( ),其中( )需从连带勒让德
方程解出:(1 x2 ) d 2 2x d [l(l 1) m2 ] 0，x cos
dx2 dx
1 x2
m 0时，成为l阶勒让德方程：(1 x2 ) d 2 2x d l(l 1) 0 dx2 dx
Pl (x) (1)l Pl (x)
即当 l 为偶数时，勒让德多项式 Pl (x) 为偶函数，
l 为奇数时
Pl ( x) 为奇函数
一、勒让德多项式的正交关系
1
1 Pk (x)Pl (x)dx 0 (k l)
0 Pk (cos )Pl (cos )sind 0 (k l)
两式称为正交性．
二、勒让德多项式的模：
u x 展开
为广义傅立叶级数。
0
f (x) u0 x fl Pl (x)
l 0
fl
2l 1 2
1 1
f
(x)Pl (x)dx
2l 2
1
u0
1
1 Pl ( )d
可以导出： f 2n1 0
f
2n
(1)n1
(4n (2n
1)( 2n 1)(2n
1)!! 2)!!
u0
f
0
1 2
u0
比较系数得：
2)! (l
2)!
al 4
(l 2)(l 3) 4(2l 3)
al 2
(1)2
(l 2)(l 2 2!(2l
3) 3)
2l
(l
(2l 2)(2l 3)(2l 4)! 1)(l 2)(l 3)(l 4)!(l
2)!
(1)2
2!2l
(2l (l
4)! 2)!(l
4)!
前面已学：勒让德方程在x 1有自然边界条件：y 有限，从而构成 x 1
本征值问题，本征值是l(l 1), l 0,1, 2, 3..., 在l为整数条件下，勒让德方程
的两个线性独立特解y(x) a0 y0 (x) a1 y1(x)之一退化为l次多项式。z Nhomakorabea(
)
y(x)
l为l为22kk(1偶(奇数数):):aa01yy10((xx))
1 2
2
2 5
(最高幂）
f (x)
x3
l 0
fl Pl (x)
3 5
P1
(
x)
2 5
P3 (x)
另一解法：
x3
(5 2
x3
3 2
x
3 2
x)
2 5
3 5
P1(x)
2 5
P3 ( x)
推广： f (x) xn
fl
2l 1 2
1 1
x
n
Pl
(
x)dx
(2l
0 1)n!(n
l
1)!!
(n l)!(n l 1)!!
n l 奇数 n l 偶数，且n l
例题2、以勒让德多项式为基本函数族，将函数
f (x) 2x3 3x 4 在区间（-1，+1）上进行广义傅立叶展开。
n 3,1,0 l 0,1,3
f0 4
f1
21 5
f3
4 5
2x3
3x
4
4P0
(x)
21 5
P1 (x)
4 5
P3
(x)
四、解方程：要选取对称轴为球坐标的极轴，
r2
d2R dr 2
2r
dR dr
l(l
1) R
0
和球谐函数方程
1
sin
sin
Y
1
sin2
2Y
2
l(l 1)Y
0
继续分离变数，令Y (,) ( )(),得到关于的方程：
'' 0 ( 2 ) ()
(1) 0时，( (2) m2 ,()
) C1
Acos
C2 C2
m Bsin
P2 (x)
1 2
(3x2
1)
1 4
(3cos 2
1)
P3
(x)
1 2
(5x3
3x)
1 8
(5cos
3
3cos
)
P4
(x)
1 8
(35x4
30x2
3)
1 64
(35cos
4
20 cos
2
9)
P5
(x)
1 8
(63x5
70x3
15x)
1 128
(63cos
5
35
cos
3
30
cos
)
P6 (x)
1 16
用常点邻域
的级数解法
,
令
y
ak xk
k0
a0 y0 (x)
a1 y1(x)
aa10yy10(
( x), l为偶数时 x)，l为奇数时
同样若记 arc cos x y(x) (x)
则上述方程也可写为下列形式的 l 阶勒让德方程
d [(1 x2 ) dy ] l(l 1) y 0
dx
dx
u内 0 u内 r0 有限值
(r r0)
u内 Al r l Pl (cos )
l 0
N
2 l
1
[
1
Pl
(
x)]2
dx
代入 Pl (x) 的微分式得：
Nl2
2 2l 1
模为： Nl
2 2l 1
三、广义傅立叶级数
由前面的分析可以看出，勒让德多项式 Pl ( x)
为本征函数族，（ l 0, 1,2 ）是正交的、完备的。
可以作为广义傅立叶级数的基。
若函数 f (x)定义在区间[1,1] 上，或 f ( ) 定义在区间
轴对称球函数
现在注意：m 0时，() Acos m B sin m A(常数) （u r, ,） R(r)( )() AR(r)( ) （u r,） u与无关，只与r， 有关。意味着当r，一定时，可任意改变，u不变。 即在以r， 构成的锥体上各点的u值相同。 问题关于极轴（z轴）对称。球函数Y ( ,) A( ) ~ 称为轴对称球函数。