高数A下册复习总结
高数A复习题

微分方程 向量代数 多元函数微分学 重积分 曲线积分 无穷级数
第七章 微分方程
1.定义:
一般地 , n 阶常微分方程的形式是
F(x, y, y',, y(n) ) 0
或 y(n) f (x, y, y',, y(n1) ) ( n 阶显式微分方程)
例1: 3y4 y5 6y'xy 0的阶数为:4
一. 数量积 向量积 混合积
a
b
|
a
||
b
|
cos
a
b
|
a
||
b
|
cos
cos
a
b
,
| a || b |
2.
c
向 a b量 sain与 b(其的中向量为积a为与bc的 夹a 角b)
c
的方向既垂直于a
,又垂直于b
,指向符合
右手系. 向量积也称为“叉积”、“外积”.
关于向量积的说明:
(1)
a
a
0.
(2)
a
//b
( 0 sin 0)
a
b
0.
(a
0,
b 0)
向量积还可用三阶行列式表示
i j k a b ax ay az
bx by bz
3.称定向为义量这设三的已个知混向三量合个的积向混量合a 积、b, 、记c 为,[a数bc量].(a
b)
c
设
a
n M0 M = 0 而M0 M ={x x0, y y0, z z0},
z
n
M
0
M
O
x
y
得: A(x x0) +B( y y0) +C( z z0) = 0 (1)
高数下册总复习知识点归纳
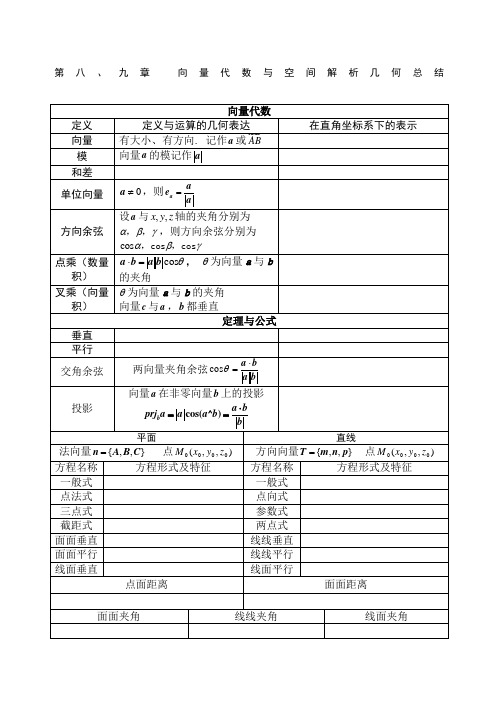
第八、九章向量代数与空间解析几何总结○1定义:四步法——分割、代替、求和、取极限;○2性质:对积分的范围具有可加性,具有线性性;○3对坐标的积分,积分区域对称与被积函数的奇偶性。
第十二章总结无穷级数常数项级数傅立叶级数幂级数一般项级数正项级数用收敛定义,nns∞→lim存常数项级数的基本性质常数项级数的基本性质○若级数收敛,各项同乘同一常数仍收敛?○两个收敛级数的和差仍收敛?注:一敛、一散之和必发散;两散和、差必发散.○去掉、加上或改变级数有限项?不改变其收敛性?○若级数收敛?则对这级数的项任意加括号后所成的级数仍收敛,且其和不变。
推论?如果加括号后所成的级数发散?则原来级数也发散?注:收敛级数去括号后未必收敛.莱布尼茨判别法若1+≥nnuu且0lim=∞→nnu,则∑∞=--11)1(nnn u收敛nu∑和nv∑都是正项级数,且nnvu≤.若nv∑收敛,则nu∑也收敛;若nu∑发散,则nv∑也发散.比较判别法比较判别法的极限形式nu∑和nv∑都是正项级数,且lvunnn=∞→lim,则○1若+∞<<l0,nu∑与nv∑同敛或同散;○2若0=l,nv∑收敛,nu∑也收敛;○3如果+∞=l,nv∑发散,nu∑也发比值判别法根值判别法nu∑是正项级数,ρ=+∞→nnn uu1lim,ρ=∞→nnnulim,则1<ρ时收敛;1>ρ(ρ=+∞)时发散;1=ρ时可能收敛也可收敛性和函数展成幂级数nnnxa∑∞=0,ρ=+∞→nnn aa1lim,1,0;,0;0,.R R Rρρρρ=≠=+∞===+∞缺项级数用比值审敛法求收敛半径)(xs的性质○在收敛域I上连续;○在收敛域),(RR-内可导,且可逐项求导;○和函数)(xs在收敛域I上可积分,且可逐项积分.(R不变,收敛域可能变化).直接展开:泰勒级数间接展开:六个常用展开式⎰-=πππnxdxxfancos)(1⎰-=πππnxdxxfbnsin)(1收敛定理x是连续点,收敛于)(xf;x是间断点,收敛于)]()([21+-+xfxf周期延拓)(xf为奇函数,正弦级数,奇延拓;)(xf为偶函数,余弦级数、偶延拓.交错。
高数下册复习知识点总结

高数下册复习知识点总结高数下册复习学问点总结高数下册复习学问点总结:8空间解析几乎与向量代数1.给定向量的坐标表达式,如何表示单位向量、方向数与方向余弦、投影。
2.向量的数量积、向量积的定义式与坐标式,把握两个向量垂直和平行的条件。
3.了解常用二次曲面的方程及其图形,以坐标轴为旋转轴的旋转曲面方程。
空间曲线在坐标平面上的投影方程。
4.平面方程和直线方程及其求法。
5.平面与平面、平面与直线、直线与直线之间的夹角,利用平面、直线的相互关系(平行、垂直、相交等)解决有关问题。
6.点到直线以及点到平面的距离。
9多元函数微分法及其应用1.有关偏导数和全微分的求解方法,偏导要求求到二阶。
2.复合函数的链式法则,隐函数求导公式和方法。
3.空间曲线的切线和法平面方程,空间曲面的切平面与法线方程;函数沿着一条直线的方向导数与梯度。
4.利用充分条件推断函数的极值问题;利用拉格朗日乘子法(即条件极值)分析实际问题或给定函数的最值问题。
10重积分1.二重积分直角坐标交换积分次序;选择合适的坐标系计算二重积分。
2.选择合适的坐标系计算三重积分。
3.利用二重积分计算曲面的面积;利用三重积分计算立体体积;4.利用质心和转动惯量公式求解问题。
11曲面积分与曲线积分1.两类曲线积分的计算与联系;2.两类曲面积分的计算与联系;3.格林公式和高斯公式的应用。
12曲面积分与曲线积分1.常数项积分的敛散性判别:(1)正项级数;(2)交叉级数;(3)一般级数2.幂级数的收敛域(1)标准型(2)非标准型幂级数的和函数,幂级数绽开3.傅里叶级数的和函数以及绽开式扩展阅读:高数下册总复习学问点归纳(1)高等数学(一)教案期末总复习第八、九章向量代数与空间解析几何总结向量代数定义与运算的几何表达定义向量模有大小、有方向.记作a 或AB向量a的模记作a在直角坐标系下的表示aaxiayjazk(ax,ay,az)axprjxa,ayprjya,azprjzaaax2ay2az2和差cabca -b单位向量cabaxbx,ayby,azbzaa0,则eaa设a与x,y,z轴的夹角分别为,,,则方向余弦分别为cos,cos,cosea(ax,ay,az)axayaz222方向余弦aaacosx,cosy,coszaaaea(cos,cos,cos)cos2+cos2cos21点乘(数量积)ababcos,为向量a与b的夹角abaxbxaybyazbziabaxbxjaybykazbzcabsin叉乘(向量积)为向量a与b 的夹角cab向量c与a,b都垂直定理与公式垂直平行abab0abaxbxaybyazbz0a//bcosa//bab0axayazbxbybz2222交角余弦ab两向量夹角余弦cosab向量a在非零向量b上的投影axbxaybyazbzaxayazbxbybz22投影prjbaacos(ab)abbprjbaaxbxaybyazbzbxbybz222平面法向量n{A,B,C}点M0(x0,y0,z0)方程名称一般式点法式方程形式及特征直线方向向量T{m,n,p}点M0(x0,y0,z0)方程名称一般式点向式方程形式及特征A1xB1yC1zD10A2xB2yC2zD20AxByCzD0A(xx0)B(yy0)C(zz0)0 xx0yy0zz0mnp高等数学(一)教案期末总复习xx1三点式yy1y2y1y3y1zz1z2z10z3z1两点式线线垂直线线平行线面平行参数式x2x1x3x1截距式面面垂直面面平行线面垂直xyz1abcA1A2B1B2C1C20A1B1C1A2B2C2ABCmnpxx0mtyy0ntzzpt0xx0yy0zz0x 1x0y1y0z1z0m1m2n1n2p1p20m1n1p1m2n2p2AmBnCp0点面距离M0(x0,y0,z0)AxByCzD0面面距离AxByCzD10AxByCzD20dAx0By0Cz0DABC222dD1D2ABC222面面夹角n1{A1,B1,C1}n2{A2,B2,C2}cos|A1A2B1B2C1C2|A1B1C1A2B2C2222222线线夹角s1{m1,n1,p1}s2{m2,n2,p2}线面夹角s{m,n,p}n{A,B,C}AmBnCpA2B2C2m2n2p2cosm1m2n1n2p1p2222m12n12p12m2 n2p2sinx(t),y(t),z(t),切“线”方程:切向量xx0yy0zz0(t0)(t0)(t0)空间(t)曲线:T((t0),(t0),(t0))法平“面”方程:(t0)(xx0)(t0)(yy0)(t0)(zz0)0切“线”方程:y(x)切向量z(x)T(1,(x),(x))xx0yy0zz01(x0)(x0)法平“面”方程:(xx0)(x0)(yy0)(x0)(zz0)0法向量切平“面”方程:Fx(x0,y0,z0)(xx0)Fx(x0,y0,z0)(yy0)F(x,y,z)0空间曲面:n(Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0))n(fx(x0,y0),fy(x0,y0) ,1)Fx(x0,y0,z0)(zz0)0法“线“方程:xx0yy0zz0Fx(x0,y0,z0)Fy(x0,y0,z0)Fz(x0,y0,z0)切平“面”方程:fx(x0,y0)(xx0)fy(x0,y0)(yy0)(zz0)0法“线“方程:zf(x,y)或n(fx(x0,y0),fy(x0,y0),1)xx0yy0zz0fx(x0,y0)fy(x0,y0)1高等数学(一)教案期末总复习第十章总结重积分计算方法(1)利用直角坐标系X型Y型积分类型二重积分典型例题f(x,y)dxdydxDab2(x)1(x)f(x,y)dyf(x,y)dxP141例1、例3f(x,y)dxdyDdcdy2(y)1(y)Ifx,ydD(2)利用极坐标系使用原则(1)积分区域的边界曲线易于用极坐标方程表示(含圆弧,直线段);(2)被积函数用极坐标变量表示较简洁(含(x2y2),平面薄片的质量质量=面密度面积为实数)P147例5f(cos,sin)ddDd2()1()f(cos,sin)d0202(3)利用积分区域的对称性与被积函数的奇偶性当D关于y轴对称时,(关于x轴对称时,有类似结论)0I2f(x,y)dxdyD1计算步骤及留意事项f(x,y)对于x是奇函数,即f(x,y)f(x,y)f(x,y)对于x是偶函数,即f(x,y)f(x,y)D1是D的右半部分P141例2应用该性质更便利1.画出积分区域2.选择坐标系标准:域边界应尽量多为坐标轴,被积函数关于坐标变量易分别3.确定积分次序原则:积分区域分块少,累次积分好算为妙4.确定积分限方法:图示法先积一条线,后扫积分域5.计算要简便留意:充分利用对称性,奇偶性高等数学(一)教案期末总复习三重积分(1)利用直角坐标投影投影法截面法bay2(x)f(x,y,z)dVdxy1(x)dyz2(x,y)z1(x,y)f(x,y,z)dzP159例1P160例2xrcos(2)利用柱面坐标yrsinzz相当于在投影法的基础上直角坐标转换成极坐标适用范围:1积分区域表面用柱面坐标表示时方程简洁;如旋转体○If(x,y,z)dvP161例3空间立体物的质量质量=密度面积22222被积函数用柱面坐标表示时变量易分别.如f(xy)f(xz)○f(x,y,z)dVdzdabr2()r1()f(cos,sin,z)dxcosrsincos(3)利用球面坐标ysinrsinsinzrcosdvr2sindrdd适用范围:1积分域表面用球面坐标表示时方程简洁;如,球体,锥体.○P16510-(1)2222被积函数用球面坐标表示时变量易分别.如,f(xyz)○Idd11222(,)1(,)f(sincos,sinsin,cos)2sind(4)利用积分区域的对称性与被积函数的奇偶性高等数学(一)教案期末总复习第十一章总结曲线积分与曲面积分积分类型参数法(转化为定积分)第一类曲线积分(1)L:y(x)IIf(x,y)ds计算方法典型例题(t)Iaf(x,y(x))1y"(x)dx曲形构件的质量(2)L:y(t)质量=线密度xr()cos弧长(3)rr()()L:f((t),(t))b"2(t)"2(t)dt2Lx(t)P189-例1P190-3yr()sinIf(r()cos,r()sin)r2()r"2()d平面其次类曲线积分(1)参数法(转化为定积分)x(t)L:(t单调地从到)y(t)P196-例1、例2、例3、例4LPdxQdy{P[(t),(t)](t)Q[(t),(t)](t)}dt(2)利用格林公式(转化为二重积分)条件:①L封闭,分段光滑,有向(左手法则围成平面区域D)②P,Q具有一阶连续偏导数结论:LPdxQdy(DQP)dxdyxy满意条件直接应用IPdxQdy应用:有瑕点,挖洞L不是封闭曲线,添加帮助线变力沿曲线所做的功P205-例4P214-5(1)(4)(3)利用路径无关定理(特别路径法)等价条件:①QP②xy③PdxQdy0LLPdxQdy与路径无关,与起点、终点有关P211-例5、例6、例7④PdxQdy具有原函数u(x,y)(特别路径法,偏积分法,凑微分法)(4)两类曲线积分的联系IPdxQdy(PcosQcos)dsLL空间其次类曲线积分(1)参数法(转化为定积分)PdxQdyRdz{P[(t),(t),(t)](t)Q[(t),(t),(t)](t)R[(t),(t),(t)](t)}d tIPdxQdyRdz(2)利用斯托克斯公式(转化其次类曲面积分)L条件:①L封闭,分段光滑,有向②P,Q,R具有一阶连续偏导数PdxQdyRdzL变力沿曲线所做结论:的功QpRQPR()dydz()dzdx()dxdyyzzxxyP240-例1 高等数学(一)教案期末总复习应用:满意条件直接应用不是封闭曲线,添加帮助线第一类曲面积分投影法:zz(x,y)投影到xoy面If(x,y,z)dv曲面薄片的质量Dxy质量=面密度类似的还有投影到yoz面和zox面的公式面积(1)投影法Pdydzp(x(y,z),y,z)dydz1○Dyz:zz(x,y),为的法向量与x轴的夹角前侧取“+”,cos0;后侧取“”,cos0Qdzdxp(x,y(x,z),z)dzdx2其次类曲面积分○Dyz:yy(x,z),为的法向量与y轴的夹角右侧取“+”,cos0;左侧取“”,cos02If(x,y,z)dvf(x,y,z(x,y))1zx2zydxdyP217-例1、例2P226-例2IPdydzQdzdxR3QdxdyQ(x,y,z(x,y))dxdy○Dyz流体流向曲面一侧的流量:xx(y,z),为的法向量与x轴的夹角上侧取“+”,cos0;下侧取“”,cos0(2)高斯公式右手法则取定的侧条件:①封闭,分片光滑,是所围空间闭区域的外侧②P,Q,R具有一阶连续偏导数结论:PdydzQdzdzRdxdy(PQR)xyzP231-例1、例2应用:满意条件直接应用不是封闭曲面,添加帮助面(3)两类曲面积分之间的联系PdydzQdzdxRdxdy(PcosQcosRcos)dSP228-例3转换投影法:dydz(全部类型的积分:z)dxdyxdzdx(z)dxdyy1定义:四步法分割、代替、求和、取极限;○2性质:对积分的范围具有可加性,具有线性性;○3对坐标的积分,积分区域对称与被积函数的奇偶性。
高数下册常用常见知识点

高数下册常用常见知识点高等数学下册常用知识点第八章:空间解析几何与向量代数一、向量及其线性运算1.向量的概念及基本性质:包括向量相等、单位向量、零向量、向量平行、共线、共面等基本概念。
2.向量的线性运算:包括加减法和数乘。
3.空间直角坐标系:包括坐标轴、坐标面、卦限和向量的坐标分解式等。
4.利用坐标进行向量的运算:设向量a=(ax。
ay。
az),向量b=(bx。
by。
bz),则a±b=(ax±bx。
ay±by。
az±bz),λa=(λax。
λay。
λaz)。
5.向量的模、方向角、投影:包括向量的模、两点间的距离公式、方向角、方向余弦和投影等。
二、数量积和向量积1.数量积:包括数量积的概念、性质和计算公式等。
2.向量积:包括向量积的概念、性质和计算公式等。
三、曲面及其方程1.曲面方程的概念:包括曲面方程的定义和基本性质等。
2.旋转曲面:包括旋转曲面的定义、方程和旋转后方程的计算等。
3.柱面:包括柱面的特点、方程和母线的概念等。
4.二次曲面:包括椭圆锥面的方程和图形等。
2.椭球面:$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$3.旋转椭球面:$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$4.单叶双曲面:$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$5.双叶双曲面:$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1$6.椭圆抛物面:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=z$7.双曲抛物面(马鞍面):$\frac{x^2}{a^2}-\frac{y^2}{b^2}=z$8.椭圆柱面:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$9.双曲柱面:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$10.抛物柱面:$2x=ay^2$空间曲线及其方程:1.参数方程:$\begin{cases}x=x(t)\\y=y(t)\\z=z(t)\end{cases}$,如螺旋线:$\begin{cases}x=a\cos t\\y=a\sin t\\z=bt\end{cases}$2.一般方程:$F(x,y,z)=0$,消去$z$,得到曲线在面$xoy$上的投影。
高等数学下册知识点归纳

高等数学下册知识点归纳
高等数学下册的知识点主要包括以下内容:
1. 向量的模、方向角、投影:向量的模是表示向量大小的度量,方向角和方向余弦是描述向量方向的量,投影则是描述向量在另一个向量上的投影。
2. 两向量的数量积、向量积:数量积是两个向量的点乘,结果是一个标量;向量积是两个向量的叉乘,结果是一个向量。
3. 平面及其方程:平面的一般方程、点法式方程等都是描述平面的重要方式。
4. 空间直线及其方程:空间直线的方程包括对称式方程、参数方程等。
5. 空间曲线的切线与法平面:空间曲线的切线方程和法平面方程是描述空间曲线的重要方式。
6. 曲面的切平面与法线:曲面的切平面和法线是描述曲面在某一点的切线和方向的重要方式。
7. 全微分:全微分是函数在某一点的变化率的度量,包括一阶偏导数和高阶偏导数。
8. 偏导计算:偏导数是函数在某个变量上的变化率,对于多元函数来说,偏导数是重要的概念。
9. 二元函数的极限:二元函数的极限是描述函数在某个点附近的性质的重要方式,包括极限的求解和证明。
10. 二重积分:二重积分是计算二维区域上的积分的重要方式,包括定积分和反常积分。
以上是高等数学下册的一些主要知识点,掌握这些知识点有助于理解和应用高等数学的基本概念和方法。
高数下册的复习总结学习资料完整.doc

高等数学 ( 向量代数— >无穷级数 ) 知识点向量与空间几何向量:向量表示((a^b)); 向量运算 (向量积 );向量的方向和投影空间方程:曲面方程(旋转曲面和垂直柱面);直线方程 (参数方程和投影方程)平面方程:点法式(法向量 )、一般式、截距式;平面夹角和距离直线方程:一般式、对称式(方向向量 )、参数式;直线夹角;平面交线(法向量积 )切平面和切线:切线与法平面;切平面与法线多元函数微分学多元函数极限:趋近方式,等阶代换偏微分和全微分:高阶微分(连续则可等 );复合函数求导(Jacobi 行列式 );多元函数极值:偏导数判定;拉格朗日乘数法(条件极值 )重积分二重积分:直角坐标和极坐标;对称性;换元法三重积分:直角坐标、柱坐标和球坐标;对称性重积分的应用:曲面面积;质心;转动惯量;引力曲线与曲面积分曲线积分:弧长积分;坐标曲线积分 (参数方程 );格林公式面积积分:对面积积分;坐标面积积分;高斯公式无穷级数级数收敛:通项极限正项级数:调和级数;比较法和比较极限法;根值法;极限法;绝对收敛和条件收敛幂级数:收敛半径和收敛域;和函数;麦克劳林级数(二次展开 )Fourier 级数:傅里叶系数 (高次三角函数积分 );奇偶延拓;正弦和余弦级数;一般周期的傅里叶级数矢量分析与场论(空间场基础 )方向导数与梯度方向导数:向量参数式;偏导数;方向余弦梯度 (grad):方向导数的最值;梯度方向;物理意义(热导方向与电场方向)格林公式:曲线积分—>二重积分;曲线方向与曲面方向全微分原函数:场的还原;折线积分通量与散度高斯公式:闭合曲面—>三重积分;曲面外侧定向;曲面补齐;向量表达(通量 )散度 (div) :通量的体积元微分;物理意义(有源场(电场 ))环流量与旋度斯托克斯公式:闭合曲线—>曲面积分;向量积定向;行列式表达;向量表达;物理意义 (环通量 )旋度 (rot) :行列式斯托克斯公式;物理意义(有旋场 (磁场 ))第八章向量与解析几何向量代数定义定义与运算的几何表达uuur 向量有大小、有方向. 记作a或AB模向量 a 的模记作 a和差在直角坐标系下的表示a a x i a y j a z k (a x, a y ,a z)r r r a x prj x a, a y prj y a,a z prj z a a a x 2 a y 2 a z 2c a b a x b x, a y b y , a z b zc a b c a- b单位向量 a 0 ,则 e a aae a( a x , a y , a z )a x2a y2a z2方向余弦点乘(数量积)叉乘(向量积)c a b 设 a 与x, y, z轴的夹角分别为,,,则方向余弦分别为 cos , cos , cosa b a b cos,为向量a与b的夹角c a b sin为向量 a 与 b 的夹角向量 c 与 a ,b都垂直定理与公式cosa x,cosa y,cosa zr r ra a ae a ( cos , cos , cos )cos2 +cos 2 cos 2 1a b a x b x a y b y a z b zi j ka b a x a y a zb x b y b z垂直平行a b a b 0 a b a x b x a y b y a z b z 0 a // b a b 0 a // ba x a y a zb x b y b za bcosa xb x a y b y a z b z交角余弦两向量夹角余弦cosa x2 a y2 a z2b x2 b y2 b z2a b向量 a 在非零向量b上的投影ax b x a y b y a z b z 投影 a b prj b a bx b y b zprj b a a cos(a b) 2 2 2b平面直线法向量 n { A, B,C }点M0( x0, y0, z0) 方向向量 T { m , n, p} 点 M 0 ( x0 , y0 , z0 )方程名称方程形式及特征方程名称方程形式及特征一般式Ax By Cz D 0 一般式A1 x B1 y C 1 z D 1 0 A 2 x B 2 y C 2 z D 2 0点法式A( x x0 ) B( y y0 ) C(z z0 ) 0 点向式x x0 y y0 z z0 m n px x1 y y1 z z1 x x0 mt 三点式x 2 x1 y2 y1 z2 z1 0 参数式y y0 nt x3 x1 y3 y1 z3 z1 z z0 pt截距式x y z1 两点式x x0 y y0 z z0 a b c x1 x0 y1 y0 z1 z0面面垂直A1 A2 B1B2 C1C2 0 线线垂直m1 m2 n1 n2 p1 p2 0面面平行A1 B1 C1线线平行m1 n1 p1 A2 B2 C 2 m2 n2 p2线面垂直A B C线面平行Am Bn Cp 0 m n p点面距离面面距离M 0 (x0 , y0 , z0 ) Ax By Cz D 0 Ax By Cz D1 0 Ax By Cz D 2 0n1 cosdAx0 By0 Cz0 DdD1 D2A2 B 2 C 2 A2 B2 C2 面面夹角线线夹角线面夹角{ A1, B1 ,C1} n2 { A2 , B2 ,C2 } s1 { m1 ,n1 , p1} s2 { m2 , n2 , p2 } s { m,n, p} n { A, B, C} | A1A2 B1 B2 C1C2 | m1 m2 n1 n2 p1 p2 sinAm Bn Cpcos A2 B2 C 2 m2 n2 p 22 2 2A222 2m12 n12 p12 m22 n22 p22A1 B1 C1 B2 C2空间曲线x(t),y(t),z(t ),(t)x x0 y y0 z z0切“线”方程:(t 0 ) (t 0 ) (t0 ) 切向量T ( (t0 ) , (t0 ) , (t0 )) 法平“面”方程:(t0 ) ( x x0 ) (t0 ) ( y y0 ) (t 0 )( z z0 ) 0:空间曲面:y(x)z (x)F ( x, y, z) 0切向量T (1 , ( x) , (x))法向量rn( F x ( x0 , y0 , z0 ) ,F y ( x0 , y0 , z0 ) ,F z ( x0 , y0 , z0 ) )切“线”方程:x x0 y y 0 z z01 ( x0 ) ( x 0 )法平“面”方程:( x x0 ) ( x0 ) ( y y0 ) ( x0 )( z z0 ) 0切平“面”方程:F x ( x0 , y 0 , z0 )( x x0 ) F x ( x0 , y0 , z0 )( y y 0 )F x ( x0 , y0 , z0 )( z z0 ) 0法“线“方程:x x0 y y 0 z z0F x ( x 0 , y 0 , z0 ) F y ( x 0 , y 0 , z0 ) F z ( x0 , y 0 , z0 )r) ,n ( f x ( x0 , y 0 切平“面”方程:f y ( x0 , y 0 ) , 1 ) f x ( x0 , y0 )( x x0 ) f y ( x0 , y0 )( y y0 ) ( z z0 ) 0z f ( x, y) 或法“线“方程:rn ( f x ( x0 , y0 ) , x x0 y y0 z z0f y (x0 , y0 ) , 1) f x ( x0 , y0 ) f y (x0 , y0 ) 1第十章重积分积分类型二重积分I f x, y dD平面薄片的质量质量 = 面密度面积重积分计算方法(1)利用直角坐标系X—型 f ( x, y)dxdy b 2 ( x)dx f (x, y)dyD a 1( x)Y—型 f (x, y) dxdy d 2 ( y)dy f (x, y) dxD c 1 ( y)(2)利用极坐标系使用原则(1)积分区域的边界曲线易于用极坐标方程表示( 含圆弧 ,直线段 );(2) 被积函数用极坐标变量表示较简单( 含( x2y2 ) ,为实数)f ( cos , sin ) d dD2(), sin ) dd f ( cos1()020 2(3)利用积分区域的对称性与被积函数的奇偶性当D 关于 y 轴对称时,(关于 x 轴对称时,有类似结论)0 f ( x, y)对于x是奇函数,即 f ( x, y ) f ( x, y )I2 f ( x, y) dxdy f ( x, y )对于x是偶函数,D1即 f ( x, y) f ( x , y )D1是 D的右半部分计算步骤及注意事项典型例题P141—例 1、例 3P147—例 5P141—例 2应用该性质更方便1 .画出积分区域2 .选择坐标系标准:域边界应尽量多为坐标轴,被积函数关于坐标变量易分离3 .确定积分次序原则:积分区域分块少,累次积分好算为妙4 . 确定积分限 方法:图示法 先积一条线,后扫积分域5 . 计算要简便注意:充分利用对称性,奇偶性投影法 (1) 利用直角坐标截面法f ( x, y, z)dVb y 2 ( x ) z 2 ( x,y ) 投影dx dy f ( x, y, z)dzay 1 ( x )z 1 ( x ,y)x r cos (2) 利用柱面坐标y r sinz zP159—例 1P160—例 2三重积分 相当于在投影法的基础上直角坐标转换成极坐标I适用范围 :f ( x, y, z)dvP161—例 3○积分区域 表面用柱面坐标表示时方程简单; 如 旋转体12变量易分离 .如 f ( x 22) f (x 22)○被积函数 用柱面坐标表示时yzf (x, y, z)dVb dr 2 ( ) cos , sin, z) ddzr 1 ( f (空间立体物的a)质量x cos r sin cos (3)利用球面坐标ysinr sin sin质 量 = 密 度z r cos面积dv r 2sindrd dP165— 10-(1)适用范围 :○1积分域 表面用球面坐标表示时 方程简单 ;如,球体,锥体 .2变量易分离 . 如, f ( x2 y2 2)○被积函数 用球面坐标表示时z2 22(, ) sin cos ,sin sin , cos ) 2sin dIdd1(f ( 1 1, )(4)利用积分区域的对称性与被积函数的奇偶性积分类型第一类曲线积分If (x, y)dsL曲形构件的质量质 量 = 线 密 度弧长第十一章曲线积分与曲面积分曲线积分与曲面积分计算方法典型例题参数法(转化为定积分)( 1) L : y (x) I f ( (t), (t)) '2 (t )'2 (t )dt( 2) L : x(t )(t) Ib1 y'2 ( x) dxf (x, y( x))y(t )aP189-例 1x r ( )cosP190- 3( 3) rr ( ) () L :y r ( )sinIf ( r ( ) cos ,r ( ) sin ) r 2 ( ) r '2 ( ) d( 1) 参数法 (转化为定积分)x ( t)(t 单调地从 到 )L :(t) yPdx Qdy{ P[ (t),( t)](t ) Q[ (t), ( t)] (t )} dtL( 2)利用格林公式 (转化为二重积分)条件: ①L 封闭,分段光滑,有向(左手法则围成平面区域D )② P , Q 具有一阶连续偏导数结论:Pdx QdyQ P()dxdyLx y平面第二类曲线 D满足条件直接应用积分应用:有瑕点,挖洞不是封闭曲线,添加辅 助线P196-例 1、例 2、例 3、例 4P205-例 4P214-5(1)(4)I Pdx QdyL变力沿曲线所做的功(3)利用路径无关定理 (特殊路径法)等价条件:①QP ②Pdx Qdyx yL③ PdxQdy 与路径无关,与起点、终点有关L④ Pdx Qdy 具有原函数 u( x, y)(特殊路径法,偏积分法,凑微分法)(4)两类曲线积分的联系P211-例 5、例 6、例 7IPdx Qdy(Pcos Qcos )dsLL( 1)参数法 (转化为定积分)空间第二类曲线Pdx Qdy Rdz{ P[ (t), (t), (t)] (t ) Q[ (t), (t), (t)] (t )积分R[ (t), (t), (t)] (t )}dt( 2)利用斯托克斯公式 (转化第二类曲面积分)IPdx Qdy Rdz 条件: ①L 封闭,分段光滑,有向L② P , Q ,R 具有一阶连续偏导数P240-例 1变力沿曲线所做的功第一类曲面积分If (x, y, z)dv曲面薄片的质量质 量 = 面 密 度面积Pdx QdyRdzL结论:R Q P R Q p()dydz (z)dzdx (x)dxdyyzxy满足条件直接应用应用:不是封闭曲线,添加辅 助线投影法: zz( x, y) 投影到 xoy 面I f (x, y, z)dvf (x, y, z(x, y)) 1 z x 2 z 2y dxdyDxy类似的还有投影到yoz 面和 zox 面的公式P217-例 1、例 2(1)投影法○1Pdydzp( x( y, z), y, z)dydzDy z: z z( x, y) , 为 的法向量与 x 轴的夹角前侧取“ +”, cos 0 ;后侧取“”, cos 0○2Qdzdxp(x, y( x, z), z)dzdxDyz第二类曲面积分: yy( x, z) , 为的法向量与 y 轴的夹角右侧取“ +”, cos 0 ;左侧取“ ”, cos 0○3QdxdyQ( x, y, z(x, y))dxdyDy z: xx( y, z) ,为 的法向量与 x 轴的夹角IPdydz Qdzdx Rdxdy”, cos上侧取“ +”, cos ;下侧取“(2 )高斯公式 右手法则取定 的侧流体流向曲面一 条件: ① 封闭,分片光滑,是所围空间闭区域的外侧侧的流量② P , Q ,R 具有一阶连续偏导数结论:Pdydz Qdzdz Rdxdy(PQR )xyz满足条件直接应用应用:不是封闭曲面,添加辅 助面(3)两类曲面积分之间的联系Pdydz Qdzdx Rdxdy (PcosQcos Rcos )dS转换投影法: dydz (z)dxdy dzdx (z)dxdyx y所有类型的积分:○1 定义:四步法——分割、代替、求和、取极限; ○2 性质:对积分的范围具有可加性,具有线性性;○3 对坐标的积分,积分区域对称与被积函数的奇偶性。
高等数学A下知识点
高等数学A下知识点
第八章
1.向量的数量积与向量积;
2.直线与平面的夹角;
第九章
1.多元函数的一阶、二阶复合偏导数;
2.二元隐函数求偏导;
3.二元函数的极值;
4.空间曲线的切线方程,空间曲面的法线方程;
第十章
1.二重积分的几何意义,二重积分的直角坐标与极坐标计算;
3.三重积分的计算;
注意积分的对称性。
第十一章
1.两类曲线积分的转化,两类曲面积分的转化;
2.用格林公式计算第二类曲线积分;
3.平面上曲线积分与路径无关的等价条件;
4.第一类曲面积分的计算;
5.第二类曲面积分的计算,高斯公式;
注意积分的对称性。
第十二章
1.数项级数的敛散性判定;
2.阿贝尔收敛性定理;
3.幂级数的收敛半径与收敛域;
4.周期为 2函数的傅里叶展开式。
高等数学下知识点总结
高等数学下知识点总结一、极限与连续1. 极限的概念极限是描述函数趋于某个特定值的概念。
对于实数函数f(x),当自变量x无限接近某个实数a时,如果函数值f(x)无限接近某个实数L,则称L为函数f(x)在x趋于a时的极限,记作$\\lim\\limits_{x\\to a}f(x)=L$。
2. 极限的性质•唯一性:一个函数在某一点的极限唯一。
•有界性:函数在某一点的极限存在,则函数在该点的附近有界。
•局部有界性:函数在无穷远处的极限存在,则函数在某一点的局部有界。
•夹逼定理:若函数在某一点的两边夹逼住一个数,则该数为函数在该点的极限。
3. 连续的概念若函数f(x)在某一点a的极限存在且等于f(a),则称函数f(x)在点a处连续。
4. 连续函数的性质•若两个函数均在某一点连续,则它们的和、差、积、商(除分母为0外)也在该点连续。
•若两个函数均在某一点连续,则它们的复合函数也在该点连续。
•若函数在闭区间[a,b]上连续,则它在该闭区间上有界。
二、导数与微分1. 导数的概念函数f(x)在点x=a处的导数,表示函数曲线在该点处的切线的斜率,记作f′(a)或$\\frac{{dy}}{{dx}}|_{x=a}$。
2. 导数的性质•可导性:若函数在某一点导数存在,则该点可导。
•右导数和左导数:对于单侧不连续点,可以讨论右导数和左导数。
•导函数:若函数在某一区间上处处可导,则该区间上存在一函数,称为原函数的导函数,记作f′(x)。
3. 常见函数的导数公式•常数函数导数为0:$f(x) = c, \\quad f'(x) = 0$。
•幂函数导数:1.$f(x) = x^n, \\quad f'(x) = nx^{n-1}, (n \ eq 0)$。
2.$f(x) = \\frac{1}{x^n}, \\quad f'(x) = -\\frac{n}{x^{n+1}}, (n \eq 0)$。
高数下知识点总结大全(通用8篇)
高数下知识点总结大全(通用8篇)高数下知识点总结大全篇11.邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
2.对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
3.垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线。
4.平行线:在同一平面内,不相交的两条直线叫做平行线。
5.同位角、内错角、同旁内角:同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
内错角:∠2与∠6像这样的一对角叫做内错角。
同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
6.命题:判断一件事情的语句叫命题。
7.平移:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移平移变换,简称平移。
8.对应点:平移后得到的新图形中每一点,都是由原图形中的某一点移动后得到的,这样的两个点叫做对应点。
9.定理与性质对顶角的性质:对顶角相等。
10垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
11.平行公理:经过直线外一点有且只有一条直线与已知直线平行。
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
12.平行线的性质:性质1:两直线平行,同位角相等。
性质2:两直线平行,内错角相等。
性质3:两直线平行,同旁内角互补。
13.平行线的判定:判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角相等,两直线平行。
本章使学生了解在平面内不重合的两条直线相交与平行的两种位置关系,研究了两条直线相交时的形成的角的特征,两条直线互相垂直所具有的`特性,两条直线平行的长期共存条件和它所有的特征以及有关图形平移变换的性质,利用平移设计一些优美的图案. 重点:垂线和它的性质,平行线的判定方法和它的性质,平移和它的性质,以及这些的组织运用. 难点:探索平行线的条件和特征,平行线条件与特征的区别,运用平移性质探索图形之间的平移关系,以及进行图案设计。
高数下册总复习知识点
d z z d u z dv dt u dt v dt
z
u v
t
公式的记忆方法:连线相乘,分线相加.
5、全微分形式不变性 无论 z是自变量 u、v的函数或中间变量 u、v 的函数,它的全微分形式是一样的.
z z dz du dv u v
6、隐函数的求导法则
偏导数,记为
z f , ,z x x0 x x0 x x x y y y y
0 0
x x0 或 y y0
f x ( x 0 , y0 ) .
y 同理可定义函数z f ( x , y ) 在点( x0 , y0 ) 处对 的偏导数, 为
f ( x 0 , y0 y ) f ( x 0 , y0 ) lim y 0 y z f 记为 , , z y x x0 或 f y ( x 0 , y 0 ) . y y0 y x x 0 y x x 0
y y0 y y0
2、全微分公式
z z dz dx dy . x y
用定义证明可微与不可微的方法 可微 不可微
z [ f x ( x0 , y0 ) x f y ( x0 , y0 ) y] z [ f x ( x0 , y0 ) x f y ( x0 , y0 ) y] 0 ( 0)
这条定曲线叫柱面 的准线,动直线叫 柱面的母线.
从柱面方程(的特征:二元方程)看柱面的特征:
只含 x , y 而缺 z 的方程 F ( x , y ) 0 ,在 空间直角坐标系中表示母线平行于 z 轴的柱 面,其准线为 x o y 面上曲线C . (其他类推)
实 例
y z 2 1 椭圆柱面 2 b c x2 y2 2 1 双曲柱面 2 a b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 向量与解析几何
向量代数
定义 定义与运算的几何表达
在直角坐标系下的表示
向量 有大小、有方向. 记作a 或AB a (,,)x y z x y z a i a j a k a a a =++=
,,x x y y z z a Prj a a Prj a a Prj a ===
模
向量a 的模记作a
a 222x y z a a a =++
和差
c a b =+ c a b =-
=+c a b {},,=±±±x x y y z z a b a b a b
单位向量
0a ≠,则a a
e a
=
a e 2
2
2
(,,)=
++x y z x y z a a a a a a
方向余弦
设a 与,,x y z 轴的夹角分别为αβγ,,,则方向余弦分别为cos αβγ,cos ,cos
cos y x z a a a a
a
a
αβγ==
=
,cos ,cos
cos a e αβγ=(,cos ,cos ) 222cos 1αβγ+=+cos cos 点乘(数量积)
θcos b a b a =⋅, θ为向量a 与b 的夹
角
z z y y x x b a b a b a ++=⋅b a
叉乘(向量积)
b a
c ⨯=
θsin b a c = θ为向量a 与b 的夹角 向量c 与a ,b 都垂直
z
y
x
z y x
b b b a a a k j i
b a =⨯ 定理与公式
垂直 0a b a b ⊥⇔⋅= 0x x y y z z a b a b a b a b ⊥⇔++=
平行
//0a b a b ⇔⨯=
//y z
x x y z
a a a a
b b b b ⇔==
交角余弦
两向量夹角余弦b
a b
a ⋅=θcos
222222
cos x x y y z z
x y z x y z a b a b a b a a a b b b θ++=
++⋅++
投影
向量a 在非零向量b 上的投影
b a b
Prj a a a b b
∧⋅==cos() x x y y z z
b x y z
a b a b a b Prj a b b b ++=
++2
2
2
第九章 多元函数微分法及其应用
x x y y z x
==∂∂00
=相当于一元函数求导数,对某一自变量求偏导,把其余变量均视为常数即可同一元函数求高阶导数
可微一定可导(偏导存在)可导不一定可微+dv z ∂
法向量
000((((x y z n F x F x F x =(((x y n f f x =--或
00(((,x y n f x f x =
,
第十章 重积分
积分类型
计算方法
二重积分
()σ
d ,⎰⎰=D
y x f I
平面薄片的质量
质量=面密度
⨯面积
(1) 利用直角坐标系
X —型 ⎰⎰
⎰⎰
=D
b
a
x x dy y x f dx dxdy y x f )
()
(21),(),(φφ
Y —型
⎰⎰
⎰⎰
=d
c
y y D
dx y x f dy dxdy y x f )
()
(21),(),(ϕϕ
(2)利用极坐标系 使用原则
(1) 积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 );
(2) 被积函数用极坐标变量表示较简单( 含22()x y α
+, α为实数 )
21()()
(cos ,sin )(cos ,sin )D
f d d d f d β
ϕθα
ϕθρθρθρρθ
θρθρθρρ
=⎰⎰⎰⎰
02θπ≤≤ 0θπ≤≤ 2πθπ≤≤
(3)利用积分区域的对称性与被积函数的奇偶性
当D 关于y 轴对称时,(关于x 轴对称时,有类似结论)
110(,)(,)(,)2(,)(,)(,)(,)D f x y x f x y f x y I f x y dxdy
f x y x f x y f x y D D ⎧
⎪⎪-=-⎪⎪
=⎨⎪⎪-=⎪⎪⎩
⎰⎰对于是奇函数,即对于是偶函数,即是的右半部分
计算步骤及注意事项
1. 画出积分区域
2. 选择坐标系 标准:域边界应尽量多为坐标轴,被积函数
关于坐标变量易分离
3. 确定积分次序 原则:积分区域分块少,累次积分好算为妙 4. 确定积分限 方法:图示法 先积一条线,后扫积分域 5. 计算要简便 注意:充分利用对称性,奇偶性
(1) 利用直角坐标⎩⎨⎧截面法
投影法
投影
⎰⎰⎰⎰⎰
⎰
=Ω
b a
y x z y x z x y x y z z y x f y x V z y x f )
,()
,()
()
(2121d ),,(d d d ),,(
第十一章曲线积分与曲面积分
所有类型的积分:
○1定义:四步法——分割、代替、求和、取极限;
○2性质:对积分的范围具有可加性,具有线性性;
○3对坐标的积分,积分区域对称与被积函数的奇偶性。
第十二章 级数
无
穷级
数
常数项级数
傅
立叶级数
幂级数
一
般项级
数
正
项级数
用收敛定义,n n s ∞
→lim 存在
常数项级数的基本性质
常数项级数的基本性质 ○
1 若级数收敛,各项同乘同一常数仍收敛. ○
2两个收敛级数的和差仍收敛. 注:一敛、一散之和必发散;两散和、差必发散.
○
3去掉、加上或改变级数有限项, 不改变其收敛性. ○
4若级数收敛, 则对这级数的项任意加括号后所成的级数仍收敛,且其和不变。
推论: 如果加括号后所成的级数发散, 则原来级数也发散. 注:收敛级数去括号后未必收敛.
○5(必要条件) 如果级数收敛, 则0lim 0
=→n
n u 莱布尼茨判别法
若1+≥n n
u u 且0lim =∞
→n n u ,则∑∞
=--1
1)1(n n
n u 收敛
n u ∑和n v ∑都是正项级数,且n n v u ≤.若n v ∑收敛,则n u ∑也收敛;若n u ∑发散,则n v ∑也发散.
比较判别法
比较判别法的极限形式
n u ∑和n v ∑都是正项级数,且l v u n
n n =∞
→lim ,则○
1若+∞<<l 0,n u ∑与n v ∑同敛或同散;○2若0=l ,n v ∑收敛,n u ∑也收敛;○
3如果+∞=l ,n v ∑发散,n u ∑也发散。
比值判别法 根值判别法
n u ∑是正项级数,ρ=+∞→n
n n u u 1lim ,ρ=∞→n n
n u lim ,则1<ρ时收敛;1>ρ(ρ
=+∞)时发散;1=ρ时可能收敛也可能发散.
收
敛性
和函数
展成幂级数
n n n
x a
∑∞
=0
,ρ=+∞
→n
n n a a 1lim ,1
,0;,0;0,.R R R ρρρρ
=
≠=+∞===+∞ 缺项级数用比值审敛法求收敛半径
)(x s 的性质○
1在收敛域I 上连续;○2在收敛域),(R R -内可导,且可逐项求导;○3和函数)(x s 在收敛域I 上可积分,且可逐项积分.(R 不变,收敛域可能变化).
直接展开:泰勒级数 间接展开:六个常用展开式
11(11)1n n x x x ∞==-<<-∑ 11 ()!
x
n n e x x n ∞==-∞<<+∞∑ 22T T l
π==
∑∞=++=1
)sin cos (2)(n n n nx b nx a a x f ⎰-
=
π
π
πdx x f a )(10
⎰-
=
π
π
πnxdx x f a n cos )(1
⎰-
=
π
π
πnxdx x f b n sin )(1
收敛定理
x 是连续点,收敛于)(x f ;x 是间断点,收敛于)]()([2
1+-+x f x f
周期 延拓
)(x f 为奇函数,正弦级数,奇延拓;)(x f 为偶函数,余弦级数、偶延拓.
交错
级数。
