神经网络PID控制
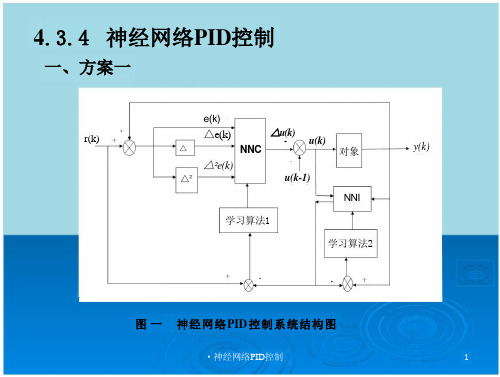
神经网络PID控制
NNI
十
十
x₁(k)=e(k)x₂(k)=△e(k)=e(k)-e(k-1)x₃(k)=△²e(k)=e(k)-2e (k-1)+e(k-2)e(k)=r(k)-y(k)NNC 的输出为:△u(k)=k₁x₁(k)+k₂x₂(k)+k₃x₃(k)式中,}i=1,2,3 为权系数,△u(k) 为输入信号的加权和。由此可见,NNC 具有增量D 控制的结构
i=1,2,…,Q-1
BP网络的输入层节点的输为
网络的隐含层输入、输为
·神经网络PID控制 20
o(k)=1
(13)
(14)
式中o 为输出层权系数 阈值,
网络的输出层的输入输出为
·神经网络PID控制 21
图二 神经网络PID控制系统结构图
·神经网络PID控制 17
二、方案二
被控对象
u
个
经典PID控制算式为u(k)=u(k-1)+Kp[e(k)-e(k-1)]+K,e(k)+K,[e(k)-2e(k-1) + e(k-2)1
7.由(20)式,计算修正输出层敝系数。(k);8.由(21)式,计算修正隐含层敝系数。)(k);9.置k=k+1, 返回到“3”,直到性能指标J 满足要求。
·神经网络PID控制 26
系数a(k)是慢时变的,a(k)=1.2(1-0.8e -01k),神经网络结构为4—5—3,输入层的个神经元分别为模型翰入r(k)、 输 出(k)、误 差(k)和常量。学习速率=0.25,动量系数=0.05,加权系数初始值取随[=0.50.5]上的随机数。当输入信号为幅值是的正弦信号(t)sin(2πt)时,取采样时间为.001s,仿真结果如图所示。·神经网络PID控制 27
基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计一、引言PID(Proportional-Integral-Derivative)控制器是一种常用的自动控制器,其通过测量系统的输出偏差,根据比例、积分和微分三个因素来控制系统的输出。
然而,传统的PID控制器难以适应复杂、非线性和时变的系统,对于这类系统的控制,神经网络已经被证明是一种有效的方法。
本文将介绍基于BP神经网络的PID控制系统设计。
二、BP神经网络简介BP神经网络(Backpropagation Neural Network)是一种常用的前向反馈型人工神经网络,其通过反向传播算法来训练网络参数,从而实现对输入数据的学习和预测。
BP神经网络拥有多层神经元,每个神经元都与下一层神经元相连,并通过权重和阈值来传递和处理输入信息。
三、PID控制器简介PID控制器由比例(Proportional)、积分(Integral)和微分(Derivative)三个部分组成,其控制输出的公式为:u(t) = Kp * e(t) + Ki * ∑e(t)dt + Kd * de(t)/dt其中,u(t)为控制器的输出,Kp、Ki、Kd为控制器的三个参数,e(t)为系统的输出偏差,∑e(t)dt为偏差的积分项,de(t)/dt为偏差的微分项。
1.数据采集和预处理:首先需要采集系统的输入和输出数据,并对其进行预处理,包括数据归一化和滤波处理等。
2.神经网络设计和训练:根据系统的输入和输出数据,设计BP神经网络的结构,并使用反向传播算法来训练网络参数。
在训练过程中,根据系统的输出偏差来调整比例、积分和微分三个参数。
3.PID控制器实现:根据训练得到的神经网络参数,实现PID控制器的功能。
在每个控制周期内,根据系统的输出偏差来计算PID控制器的输出,将其作为控制信号发送给被控制系统。
4.参数调优和性能评估:根据控制系统的实际情况,对PID控制器的参数进行调优,以提高系统的控制性能。
基于BP神经网络的PID控制器设计

基于BP神经网络的PID控制器设计PID控制器是一种常用的控制器,可以通过根据系统的误差、历史误差和误差的变化率来计算控制信号,从而实现对系统的控制。
传统的PID控制器可以通过调节PID参数来实现对系统动态特性的控制,但是参数调节过程往往需要经验和反复试验,而且很难实现对非线性系统的精确控制。
近年来,基于BP神经网络的PID控制器设计方法得到了广泛的关注。
BP神经网络是一种常用的人工神经网络模型,可以通过训练得到输入与输出之间的映射关系。
在PID控制器设计中,可以将误差、历史误差和误差的变化率作为BP神经网络的输入,将控制信号作为输出,通过训练神经网络来实现对控制信号的合理生成。
1.数据预处理:首先需要采集系统的输入输出数据,包括系统的误差、历史误差和误差的变化率以及相应的控制信号。
对这些数据进行归一化处理,以便神经网络能够更好地学习和训练。
2.网络结构设计:根据系统的特性和要求,设计BP神经网络的输入层、隐藏层和输出层的神经元数量。
通常情况下,隐藏层的神经元数量可以根据经验设置为输入层和输出层神经元数量的平均值。
3.训练网络:采用反向传播算法对神经网络进行训练,以获得输入和输出之间的映射关系。
在训练过程中,需要设置学习率和动量系数,并且根据训练误差的变化情况来确定训练的终止条件。
4.参数调整:将训练得到的神经网络与PID控制器相结合,根据神经网络的输出和系统的误差、历史误差和误差的变化率来计算控制信号,并通过对PID参数的调整来实现对系统的控制。
1.适应能力强:BP神经网络能够通过训练来学习系统的动态特性,从而实现对非线性系统的精确控制。
2.自适应性高:BP神经网络能够根据实时的系统状态来实时调整控制信号,从而实现对系统动态特性的自适应控制。
3.参数调节方便:通过BP神经网络的训练过程,可以直接得到系统的输入和输出之间的映射关系,从而减少了传统PID控制器中参数调节的工作量。
4.系统稳定性好:基于BP神经网络的PID控制器能够根据系统状态及时调整控制信号,从而提高了系统的稳定性和鲁棒性。
神经网络及其PID控制

神经⽹络及其PID控制⼀、⼈⼯神经元模型1、突触权值(连接权)每⼀个突触都由其权值作为特征表征,各个神经元之间的连接强度由突触权值来表⽰。
与神经元相连的突触上,连接的输⼊信号通过权值的加权进⼊神经元的求和单元。
2、求和单元求和单元⽤于求取各输⼊信号的突触加权和,这个操作构成⼀个线性组合器。
3、激活函数激活函数起⾮线性映射的作⽤,并⽤来限制神经元输出振幅。
激活函数也称限制函数,或传输函数。
通常⼀个神经元输出的正常范围在[0, 1]区间或[−1, 1]区间。
4、外部偏置此外,神经元模型还包括⼀个外部偏置,或外部偏置称为阀值,偏置的作⽤是根据其为正或负,相应的增加或者降低激活函数的⽹络输⼊。
5、⼀对⽅程描述神经元6、激活函数(1)阶跃函数(2)分段线性函数(3)Sigmoid函数(4)双曲正切函数:⼆、神经⽹络的结构1、前馈型⽹络这类⽹络将每⼀层的神经元串联起来,⼀层的输出是下⼀层的输⼊,⽹络中没有反馈连接(1)节点分类节点有输⼊单元、计算单元和输出单元三类(2)层级分类输⼊层:源节点构成输⼊层,输⼊层没有计算,直接将输⼊信号传递到下⼀层的计算单元可见层:输⼊、输出节点直接与外界相连,可直接受外界环境影响隐含层:中间层与外界⽆直接联系,所以称为隐含层(3)前馈型⽹络常常可以有多个隐含层,从⽽构成多层前馈⽹络,图中是⼀个n-p-q的三层前馈⽹络前馈型⽹络是⼀类静态⾮线性映射,通过简单⾮线性处理的复合映射可获得复杂的⾮线性处理能⼒。
但是,从计算的观点看,前馈型⽹络并⾮是⼀种强有⼒的计算系统,不具备丰富的动⼒学⾏为2、反馈型⽹络在反馈型⽹络中,输⼊信号决定反馈系统的初始状态,然后系统经过⼀系列状态转移后,逐渐收敛于平衡状态,这样的平衡状态就是反馈型⽹络经计算后输出的结果,需要注意的是通常有多个平衡态。
因此,稳定性是反馈⽹络最重要的问题之⼀。
如果能找到⽹络的李雅普诺夫(Lyapunov)函数,就能保证⽹络从任意初始状态都能收敛到局部最⼩点,即求得局域最优解。
基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计一、引言PID控制系统是目前工业控制中广泛应用的一种基本控制方法,它通过测量控制系统的偏差来调节系统的输出,以实现对控制对象的稳定控制。
然而,传统的PID控制器需要事先对系统建模,并进行参数调整,工作效果受到控制对象模型的准确性和外部干扰的影响。
而BP神经网络具有非线性映射、自适应性强、鲁棒性好等优点,可以有效地克服传统PID控制器的缺点。
因此,基于BP神经网络的PID控制系统设计成为当前研究的热点之一二、基于BP神经网络的PID控制系统设计理论1.PID控制器设计原理PID控制器是由比例环节(Proportional)、积分环节(Integral)和微分环节(Derivative)组成的控制器,其输出信号可以表示为:u(t) = Kp*e(t) + Ki*∫e(t)dt + Kd*(de(t)/dt),其中e(t)为控制系统的输入偏差,t为时间,Kp、Ki和Kd分别为比例系数、积分系数和微分系数。
2.BP神经网络理论BP神经网络是一种前馈型神经网络,通过反向传播算法对输入信号进行学习和训练,从而得到最优的网络结构和参数。
BP神经网络由输入层、隐层和输出层组成,其中每个神经元与上、下相邻层之间的神经元互相连接,并具有非线性的激活函数。
3.基于BP神经网络的PID控制系统设计理论基于BP神经网络的PID控制系统设计的核心思想是将BP神经网络作为PID控制器的自适应调节器,根据控制对象的输入信号和输出信号之间的误差进行训练和学习,通过调整BP神经网络的权重和阈值来实现PID 控制器的参数调节,从而提高控制系统的稳定性和鲁棒性。
三、基于BP神经网络的PID控制系统设计步骤1.系统建模首先,需要对待控制对象进行建模,获取其数学模型。
对于一些复杂的非线性系统,可以采用黑箱建模的方法,利用系统的输入和输出数据进行数据拟合,获取系统的数学模型。
2.BP神经网络训练将系统的数学模型作为BP神经网络的训练集,通过反向传播算法对BP神经网络进行训练,得到最优的网络结构和参数。
神经网络PID控制系统的研究

神经网络PID控制系统的研究一、本文概述随着科技的发展,控制理论在各个领域的应用越来越广泛,其中,PID(比例-积分-微分)控制算法以其简单、稳定、有效的特性,被广泛应用于工业控制系统中。
然而,传统的PID控制算法在面对非线性、时变、不确定性等复杂系统时,其性能往往会受到限制。
近年来,神经网络作为一种强大的非线性映射工具,其强大的自学习和自适应能力为解决这些问题提供了新的思路。
本文将研究神经网络与PID控制算法的结合,构建一种神经网络PID控制系统。
我们将概述神经网络和PID控制算法的基本原理和特点,然后分析神经网络PID控制系统的基本结构和运行机制。
接着,我们将通过仿真实验和实际应用案例,研究神经网络PID控制系统在不同场景下的性能表现,并探讨其优点和可能存在的问题。
我们将对神经网络PID控制系统的未来发展进行展望,以期能为控制理论的发展和应用提供新的启示和参考。
二、神经网络PID控制系统的基本原理神经网络PID控制系统是一种结合了神经网络与传统PID控制算法的先进控制系统。
这种系统的基本原理在于利用神经网络的强大学习和自适应能力,优化和改进传统的PID控制算法,从而提高系统的控制精度和稳定性。
PID(比例-积分-微分)控制器是一种广泛使用的线性控制器,它通过计算误差的比例、积分和微分来调整系统的输出,以实现对目标值的精确追踪。
然而,传统的PID控制器在处理非线性、时变和不确定性的系统时,其性能可能会受到限制。
神经网络作为一种模拟人脑神经元网络工作的计算模型,具有很强的学习和适应能力。
通过训练,神经网络可以逼近任意的非线性函数,这使得它成为处理复杂、非线性系统问题的有力工具。
在神经网络PID控制系统中,神经网络被用来模拟和优化PID控制器的参数调整过程。
具体来说,神经网络的输入可以是系统的误差、误差的变化率等,输出则是PID控制器的比例、积分和微分系数。
通过训练神经网络,可以找到最优的PID参数组合,从而实现更好的控制效果。
基于BP神经网络PID整定原理和算法步骤

基于BP神经网络PID整定原理和算法步骤BP神经网络是一种常用的非线性拟合和模式识别方法,可以在一定程度上应用于PID整定中,提高调节器的自适应性。
下面将详细介绍基于BP神经网络的PID整定原理和算法步骤。
一、基本原理:BP神经网络是一种具有反馈连接的前向人工神经网络,通过训练样本的输入和输出数据,通过调整神经元之间的连接权重来模拟输入和输出之间的映射关系。
在PID整定中,可以将PID控制器的参数作为网络的输入,将控制效果指标作为网络的输出,通过训练网络来获取最优的PID参数。
二、算法步骤:1.确定训练数据集:选择一组适当的PID参数和相应的控制效果指标作为训练数据集,包括输入和输出数据。
2.构建BP神经网络模型:确定输入层、隐藏层和输出层的神经元数量,并随机初始化神经元之间的连接权重。
3.设置训练参数:设置学习速率、误差收敛条件和训练迭代次数等训练参数。
4.前向传播计算输出:将训练数据集的输入作为网络的输入,通过前向传播计算得到网络的输出。
5.反向传播更新权重:根据输出与期望输出之间的误差,利用误差反向传播算法来调整网络的连接权重,使误差逐渐减小。
6.判断是否达到收敛条件:判断网络的训练误差是否满足收敛条件,如果满足则跳转到第8步,否则继续迭代。
7.更新训练参数:根据训练误差的变化情况,动态调整学习速率等训练参数。
8.输出最优PID参数:将BP神经网络训练得到的最优权重作为PID 控制器的参数。
9.测试PID控制器:将最优PID参数应用于实际控制系统中,观察控制效果并进行评估。
10.调整PID参数:根据实际控制效果,对PID参数进行微调,以进一步优化控制性能。
三、应用注意事项:1.训练数据集的选择应尽量全面、充分,覆盖各种不同工况和负载情况。
2.隐藏层神经元数量的选择应根据实际情况进行合理调整,避免过拟合或欠拟合现象。
3.学习速率和训练迭代次数的设置应根据系统复杂度和训练误差的变化情况进行调整。
神经网络PID控制
[
]
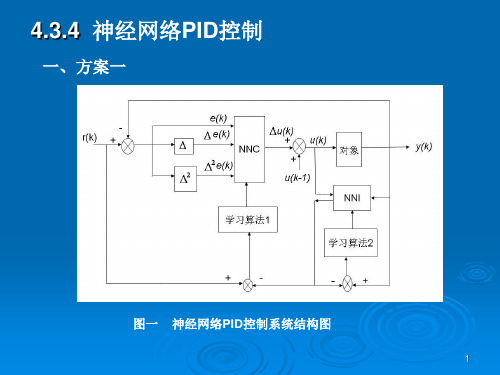
(10) 7. 采样得 (k + 1)、r(k + 1)。(仿真计算时由对象 y 。(仿真计算时由对象 y 数学模型计算 (k + 1))
12
NNC的权值进行修正。 8. 用 11)式及 10)式对 ( ( 的权值进行修正。 ∂Jc ∂Jc ∂y(k + 1) ∂u(k) ∆ki (k) = −λ = −λ ∂ki (k) ∂y(k + 1) ∂u(k) ∂ki (k) ˆ ∂y(k + 1) xi (k) = λ[r(k + 1) − y(k + 1)] ∂u(k) 0 < λ < 1 , i = 1,2,3 (11)
4.3.4 神经网络 神经网络PID控制 控制
一、方案一
图一
神经网络PID控制系统结构图 控制系统结构图 神经网络
1
x1(k) = e(k)
x2 (k) = ∆e(k) = e(k) − e(k −1)
x3 (k) = ∆2e(k) = e(k) − 2e(k − 1) + e(k − 2)
e(k) = r(k) − y(k)
13
9. 用下列各式对 的权值进行修正。 NNI的权值进行修正 的权值进行修正。
ˆ ∆ωi(3) (k) = η[ y(k + 1) − y(k + 1)]Oi(2) (k) +α∆ωi(3) (k −1)
( ˆ ∆ωij2) (k) = η[ y(k + 1) − y(k + 1)]ωi(3) (k) f ′ neti(2) (k) O(j1) (k) ( +α∆ωij2) (k −1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于神经网络PID控制算法在多缸电液伺服系统同步控制中的仿真研究丁曙光,刘勇合肥工业大学,合肥,230009摘要:本文介绍了神经网络控制原理,提出了神经网络PID算法,通过选定三层神经网络作为调节函数,经过Simulink仿真确定了神经网络PID控制器的参数,设计了神经网络PID控制器。
推导出多缸液压同步控制系统在各种工况下的传递函数,并把该控制器应用到多缸液压同步控制系统中。
经过仿真研究表明该控制器控制效果良好,能满足多缸液压同步的控制要求。
关键词:多缸同步;PID算法;仿真;神经网络Study on the simulation and appllication of hydraulic servo system of straihtening machine based onImmune Neural network PID control alorithmDING Shu-guang, GUI Gui-sheng,ZHAI HuaHefei University of Technology, Hefei 23009Abstract:The principle of immune feedback and immune-neural network PID algorithm was respectively.An immune-neural network PID controller was designed by which an adaline neural network was selected as antibody stay function and parameters of the immune-neural network PID controller were determined by simulation.The transfer function of the hydraulic servo system of crankshaft straightenin on were introduced in different working conditions.The immune-neural network PID controller was applied to hydraulic system of crankshaft straightenin.The simulation and equipment were done,and results show that its control effectiveness is better and can meet the needs of he hydraulic servo-system of crankshaft straightening hydraulic press.Key words:straightening machine; Immune control arithmetic; simulation;neural network0引言精密校直液压机(精校机)液压伺服系统是精校机的执行环节,高精度液压位置伺服控制是精校机的关键技术之一,它保证了液压伺服控制系统的控制精度、稳定性和快速性,是完成校直工艺的必要条件。
因此,精校机液压伺服控制系统的研究,为精校机产品的设计和制造提供了理论依据,对校直技术和成套设备的开发具有重大的意义[1]。
精校机液压位置伺服系统是一个复杂的系统,具有如下特点:精确模型难建立,要求位置控制精度高、超调量小、响应快、参数易变且难以确定[1]。
因此该系统的控制有较大的难度。
传统的PID控制虽然简单易行,但参数调整困难,具有明显的滞后特性,PID 控制很难一直保证系统的控制精度,Smith预估补偿国家重大科技专项资助(项目编号:2009ZX04004-021)安徽省自然科学基金资助(项目编号:090414155)和安徽省科技攻关项目资助(项目编号:06012019A)制方法从理论上为解决时滞系统的控制问题提供了一种有效的方法,但是Smith预估器控制的鲁棒性差,系统性能过分依赖补偿模型的准确性,限制了它在实际过程中的应用[1~5]。
近年来,人们开始将生物系统的许多有益特性应用于各种控制中[1~5],取得了一定成果。
自然免疫系统使生物体的一个高度进化、复杂的功能系统,它能自适应地识别和排除侵入肌体的抗原性异物,并且具有学习、记忆和自适应调节功能,以维护肌体内环境的稳定。
自然免疫系统非常复杂,但其抵御抗原(antigen)的自适应能力十分显著。
生物信息的这种智能特性启发人们利用它来解决一些工程难题,这就引起多种免疫方法的出现。
人工免疫系统就是借鉴自然免疫系统自适应、自组织的特性而发展起来的一种智能计算技术。
该算法在大量的干扰和不确定环境中都具很强的鲁棒性和自适应性,在控制、优化、模式识别、分类等领域有了初步的研究成果。
为了提高精校机液压位置伺服系统控制的精度和鲁棒性,本文基于免疫系统的反馈原理,并和神经网络相结合,提出了免疫神经网络PID的控制算法,将其应用到精校机液压位置伺服系统中,仿真和实验结果表明应用了免疫神经网络PID控制器的液压伺服系统在不同的负载和不同的环境中仍然能取得较为满意的控制效果,满足精校机的滑块位置控制要求。
1精校机液压位置伺服系统YH40-160曲轴校直机的液压位置系统由比例伺服阀、液压缸、位移传感器、滑块等组成,通过D/A 转换器采用闭环控制。
系统构成如图1所示其主要参数见下表1:表1 YH40-160型曲轴校直机主要参数名称参数公称力/kN 1600最大液压力/MPa 25滑块行程/mm 350滑块下平面距工作台上平面的距离/mm 470油缸直径/mm 280油缸杆径/mm 260泵排量/ml 63滑块及活塞杆质量/kg 338最大上模质量/kg 35工作台尺寸/mm 左右7600 前后525滑块速度/mm/s 快下20~100 工作0~25 回程20~100利用表一可以推导出YH40-160曲轴校直机的的传递函数[1]。
实际分析可知ωr很小远远小于ωh,所以在负载为惯性负载和外力负载和负载为惯性力负载+弹性负载+外负载力两种工况下系统的数学模型都可看成一个积分环节串接一个二阶环节组成。
负载为惯性负载和外力负载是的传递函数为[1]:22()2(1)vh hKW SSS Sξωω=⨯++(1)理论上可以根据稳定性要求选择稳态速度误差系数Kv就可以得到比较理想的静动态特性。
但本系统为一个Ⅰ型系统由于穿越频率较低,影响了系统的快速性,且系统参数在不同的工况、不同的环境下是有较大的变化,所以仅仅靠静态选择系统的误差系数Kv、利用传统的PID控制要实现高的静动态性能是很困难的,需要设计高性能的控制器来实现之。
2免疫反馈控制原理[5~6]当外来物侵入机体时,免疫系统就会起作用。
免疫系统启动免役机制进行免疫应答。
免疫系统具有大量的称为淋巴的免疫细胞,主要包括两类:T细胞和B细胞。
B细胞的主要功能是产生抗体,执行获得性免役功能;而T细胞分为辅助T细胞Th、抑制T 细胞Ts。
免疫调节的过程为当外界抗原进入生物体内,被抗原呈递细胞消化后会产生细胞介素激活免疫反应,当抗原呈递细胞(APC)把抗原呈给T细胞时,通常首先激活辅助性T细胞(Th),活化并释放淋巴因子,进而激活B细胞产生抗体。
APC递呈细胞的抗原还能缓慢激活抑制T细胞(Ts)。
活化的Ts细胞反过来对Th细胞或B细胞发挥抑制作用。
图2为免疫系统反馈原理图。
3免疫神经网络PID控制器设计传统的PID控制器由比例、积分和微分环节构成,经过离散处理的传统PID控制算法为抑制抗原APC抗原加工Ts细胞Th细胞B细胞抗体激活消灭图2 免疫系统反馈原理图S I 图1 精校机液压系统)())1(11()(11k e Z T ZT K k u D I P ---+-+= (2)在免疫应答反馈调节过程中,人体内最终的抗体数量由激活的B 细胞数量决定,而B 细胞的激活数量又受到Th 和Ts 细胞的共同约束一个来自起促进作用的Th 细胞,另一个来自起抑制作用的Ts 细胞,第k 代B 细胞浓度可表示为)()()(k S k S k U s h -= (3)以抗原数量作为偏差e(k),刺激总量U(k)作为控制输入量u(k))()(1k e K k U h = (4) )())(()(2k e k u K k U S ∆=φ (5))()))((1()(k e k u K k u ∆-=ηφ (6)式中))((,*,21k u K K K K ∆==φη为与抗体量变速度相关的一个非线性函数,即抗体抑制调节函数。
基于免疫反馈原理的免疫控制器是一个与偏差呈非线性关系的P 控制器,将PID 控制算法(2)与(6)结合构造的免疫PID 控制器为:))1(11()(11---+-+=ZT ZT K k u D I P)))((1()(k u K k e ∆-⨯ηφ (7)设计免疫PID 控制器的一个关键是构造出合适的抗体抑制调节函数,本文采用单层Adaline 网络来构造抗体抑制调节函数——非线性函数))((k u ∆φ,其结构图如图3。
以u 和u ∆作为网路的输入,网路的输出为))((k u ∆φ。
网路的阈值函数为Sigmoid 函数,通过最小二乘(LMS )学习来逼近Adaline 网络的权值,网路的权值逼近公式为:)()()()1(k X k e k W k W μ+=+ (8)式中X(k)为神经网路的输入变量,W(k)为神经网 络的第k 次修正权值,e(k)为Y Y s 与的差值,μ为步长系数。
⎥⎦⎤⎢⎣⎡∆=u u X (9) ⎥⎦⎤⎢⎣⎡=21W W W (10)把该抗体抑制调节函数代入到免疫PID 控制器中就得到了免疫神经网络PID 控制器,整个系统的方框图见图4。
4免疫神经PID 算法仿真研究被控对象的传递函数选负载为惯性负载和外力负载时的传递函数即[1]:)12()(22+⨯+=S SS KS W hhvωξω (11)把表1所列的参数代入相关的公式可以得到系统的,7.829=h ωKv =100。
但随着工作环境和负载的不同,系统的阻尼比ζ的变化比较大,本系统为从0.15到0.35,因而增加了控制的难度。
利用Matlab 中的Simulink [7]对曲轴校直机进行建模和对设计的免疫神经网络控制器进行仿真研究并与传统的PID 控制器进行比较。
首先利用扩充临界比例度法对传统PID 的参数进行整定,得到各个如下参数:K P 为2.614,K I 为2.614,K P 为0.00377, K D 为0.0011,而免疫神经网络PID 的η选为0.5,u 为0.4,K 为1,仿真结果见图5和图6。
