神经网络自适应PID控制
神经网络PID控制
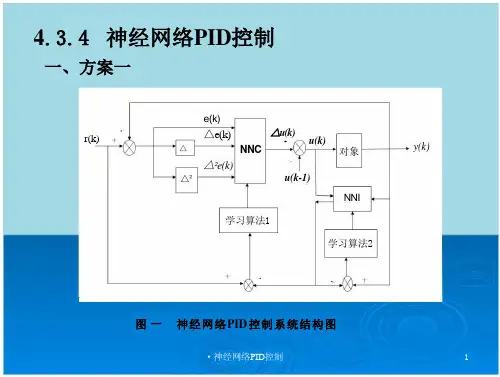
NNI
十
十
x₁(k)=e(k)x₂(k)=△e(k)=e(k)-e(k-1)x₃(k)=△²e(k)=e(k)-2e (k-1)+e(k-2)e(k)=r(k)-y(k)NNC 的输出为：△u(k)=k₁x₁(k)+k₂x₂(k)+k₃x₃(k)式中，}i=1,2,3 为权系数，△u(k) 为输入信号的加权和。由此可见，NNC 具有增量D 控制的结构
i=1,2,…,Q-1
BP网络的输入层节点的输为
网络的隐含层输入、输为
·神经网络PID控制 20
o(k)=1
(13)
(14)
式中o 为输出层权系数 阈值，
网络的输出层的输入输出为
·神经网络PID控制 21
图二 神经网络PID控制系统结构图
·神经网络PID控制 17
二、方案二
被控对象
u
个
经典PID控制算式为u(k)=u(k-1)+Kp[e(k)-e(k-1)]+K,e(k)+K,[e(k)-2e(k-1) + e(k-2)1
7.由(20)式，计算修正输出层敝系数。(k);8.由(21)式，计算修正隐含层敝系数。)(k);9.置k=k+1, 返回到“3”,直到性能指标J 满足要求。
·神经网络PID控制 26
系数a(k)是慢时变的，a(k)=1.2(1-0.8e -01k),神经网络结构为4—5—3,输入层的个神经元分别为模型翰入r(k)、 输 出(k)、误 差(k)和常量。学习速率=0.25,动量系数=0.05,加权系数初始值取随[=0.50.5]上的随机数。当输入信号为幅值是的正弦信号(t)sin(2πt)时，取采样时间为.001s,仿真结果如图所示。·神经网络PID控制 27
基于神经网络的自适应控制技术研究
基于神经网络的自适应控制技术研究神经网络作为一种模拟人脑神经元网络的计算模型，在多个领域得到了广泛的应用。
其中，自适应控制技术是神经网络研究的重要方向之一。
使用神经网络进行自适应控制，可以有效地解决各种非线性、时变和模型不确定的动态系统控制问题。
一、神经网络的基本原理神经网络模仿人类大脑组织，由若干个神经元构成。
每个神经元接受若干个输入信号，并将它们加权求和后传递到激活函数中进行处理，最终得到输出信号。
多个神经元可以组成网络，进行更加复杂的信息处理和控制。
神经网络的学习过程是通过对输入和输出数据的训练实现的。
通常采用的训练方法是反向传播算法。
该算法基于一种误差反向传播的思想，通过计算每个神经元的误差，根据误差大小对神经元的权重进行更新和调整，不断减小网络的误差，达到有效的学习效果。
二、自适应控制技术自适应控制技术是一种针对动态系统进行控制的技术。
动态系统具有非线性、时变性、模型不确定等特性，传统的线性控制方法往往难以达到理想的效果。
自适应控制技术基于神经网络模型，可以进行模型自适应、参数自适应和信号处理等多种操作，以适应各种复杂的动态系统。
常见的自适应控制方法有基于模型参考自适应控制、基于模型自适应控制、基于直接自适应控制等。
其中，基于模型参考自适应控制是一种应用广泛的方法。
该方法将实际输出与期望参考模型的输出进行比较，通过误差反馈，计算调整控制器参数的信号，最终实现对动态系统的控制。
三、神经网络自适应控制技术的研究进展神经网络自适应控制技术在航空、机械、电力、化工等行业中得到了广泛的应用。
在航空领域，神经网络自适应控制技术可以应用于飞机自动驾驶、导航、起降控制等方面。
在机械领域，神经网络自适应控制技术可以应用于机械臂、机器人控制、数控机床等领域。
在电力、化工领域，神经网络自适应控制技术可以应用于发电机组调节、化工装置控制等领域。
目前，神经网络自适应控制技术的研究主要集中在以下几个方面：1.神经网络自适应PID控制技术PID控制是一种基于比例、积分、微分三个控制器参数的控制方法。
(完整word版)基于BP神经网络的自整定PID控制仿真
基于BP神经网络的自整定PID控制仿真一、实验目的1.熟悉神经网络的特征、结构及学习算法。
2.通过实验掌握神经网络自整定PID的工作原理。
3.了解神经网络的结构对控制效果的影响。
4. 掌握用Matlab实现神经网络控制系统仿真的方法。
二、实验设备及条件1.计算机系统2.Matlab仿真软件三、实验原理在工业控制中，PID控制是工业控制中最常用的方法。
这是因为PID控制器结构简单，实现简单，控制效果良好，已得到广泛应用。
但是，PID具有一定的局限性：被控制对象参数随时间变化时，控制器的参数难以自动调整以适应外界环境的变化。
为了使控制器具有较好的自适应性，实现控制器参数的自动调整，可以采用神经网络控制的方法。
利用神经网络的自学习这一特性，并结合传统的PID控制理论，构造神经网络PID控制器，实现控制器参数的自动调整。
基于BP神经网络的PID控制器结构如图4所示。
控制器由两部分组成：一是常规PID控制器，用以直接对对象进行闭环控制，且3个参数在线整定；二是神经网络NN，根据系统的运行状态，学习调整权系数，从而调整PID参数，达到某种性能指标的最优化。
图4中神经网络采用结构为4-5-3型的BP网络。
BP网络是一种单向传播的多层前向网络。
输入节点对应系统的运行状态量，如系统的偏差与偏差变化率，必要时要进行归一化处理。
输入变量的个数取决于被控系统的复杂程度，输出节点对应的是PID的3个可调参数。
由于输出不能为负，所以输出层活化函数取2()(1)()(1)1(1)a k y k y k u k y k -=+-+-非负的Sigmoid 函数，隐含层取正负对称的Sigmoid 函数。
本系统选取的BP 网络结构如图5所示。
网络的学习过程由正向和反向传播两部分组成。
如果输出层不能得到期望输出，那么转入反向传播过程，通过修改各层神经元的权值，使得误差信号最小。
输出层节点分别对应3个可调参数K p 、K i 、K d 。
单神经元自适应PID
单神经元自适应PID一、单神经元神经网络与PID 结合的基础根据前面的推文“神经网络基础”中所介绍的，神经元是多输入单输出的，训练的目的确定权值，从而当给予输入时，能给出理想的输出。
对于PID 控制来讲，以增量式PID 为例，公式如下()()()[]()()()()[]212**1*-+--++--=∆k E k E k E kd k E ki k E k E kp k U输入是()k E 、()1-k E 和()2-k E ，输出是增量()k U ∆，对于PID 来讲，最重要的任务是确定系数。
两者相比较，只要将大量的()k E 、()1-k E 和()2-k E 作为输入，()k U ∆作为输出，确定权值的过程就是确定PID 系数的过程。
二、控制算法单神经元自适应PID 的整体结构如下图以智能车为例，上述参数解释为，()k r 为控制器输入的参考值，K 是神经元比例系数，()k u ∆是增量，()k u 是输出PWM ，()k y 是反馈值，偏差()()()k y k r k e -=。
（1）输入()()()11--=k e k e k x ()()k e k x =2()()()()2123-+--=k e k e k e k x（2）权值根据前面讲的，学习规则有两类有导师学习和无导师学习，其中无导师的Hebb 学习规则，又叫无监督Hebb 学习规则，其公式为()()()()()()k y k y k w k w k w k w i j ij ij ij ij η=∆∆+=+1η是设定的学习速率，()k y j 、()k y i 分别是k 时刻i 神经元与j 神经元的输出。
结合Delta 规则，得到有监督的Hebb 学习规则，其公式为()()()()()()()()[]k y k d k y k y k w k w k w k w j j i j ij ij ij ij -=∆∆+=+η1其中，()k d j 是期望输出，()()k y k d j j -在这里即为()()k e k x =2，。
单神经元自适应PID控制算法
单神经元自适应PID 控制算法一、单神经元PID 算法思想神经元网络是智能控制的一个重要分支，神经元网络是以大脑生理研究成果为基础，模拟大脑的某些机理与机制，由人工建立的以有向图为拓扑结构的网络，它通过对连续或断续的输入做状态响应而进行信息处理；神经元网络是本质性的并行结构，并且可以用硬件实现，它在处理对实时性要求很高的自动控制问题显示出很大的优越性；神经元网络是本质性的非线性系统，多层神经元网络具有逼近任意函数的能力，它给非线性系统的描述带来了统一的模型；神经元网络具有很强的信息综合能力，它能同时处理大量不同类型的输入信息，能很好地解决输入信息之间的冗余问题，能恰当地协调互相矛盾的输入信息，可以处理那些难以用模型或规则描述的系统信息。
神经元网络在复杂系统的控制方面具有明显的优势，神经元网络控制和辨识的研究已经成为智能控制研究的主流。
单神经元自适应PID 控制算法在总体上优于传统的PID 控制算法，它有利于控制系统控制品质的提高，受环境的影响较小，具有较强的控制鲁棒性，是一种很有发展前景的控制器。
二、单神经元自适应PID 算法模型单神经元作为构成神经网络的基本单位，具有自学习和自适应能力，且结构简单而易于计算。
传统的PID 则具有结构简单、调整方便和参数整定与工程指标联系紧密等特点。
将二者结合，可以在一定程度上解决传统PID 调节器不易在线实时整定参数，难以对一些复杂过程和参数时变、非线性、强耦合系统进行有效控制的不足。
2.1单神经元模型对人脑神经元进行抽象简化后得到一种称为McCulloch-Pitts 模型的人工神经元，如图2-1所示。
对于第i 个神经元，12N x x x 、、……、是神经元接收到的信息，12i i iN ωωω、、……、为连接强度，称之为权。
利用某种运算把输入信号的作用结合起来，给它们的总效果，称之为“净输入”，用i net 来表示。
根据不同的运算方式，净输入的表达方式有多种类型，其中最简单的一种是线性加权求和，即式 （2-1）。
神经PID控制
u 3 ( k ) = k d [e ( k ) e ( k 1)] = k d e ( k ) u 3 (k ) (k
与误差 e(k)的微分成比例,因,采样控制,
与误差的一阶差分成比例:
e(k ) = e(k ) e(k 1)
在 e(k ) ≠ 0 时起作用,可提高系统的稳定性,只有比例加微分一起控制才能奏效, 增加控制系统的阻尼比,在保证系统有一定的相对稳定性的情况下,容许采用较大的增 益,减小稳态误差. 微分作用不足之处是放大了噪声信号. 当对象与扰动是确定性时,有多种设计 PID 控制器的方法,得到的三个系数是常数.
1
神经PID控制 控制结构见下图,有两个神经网络: 神经 控制 NNI——系统在线辨识器;NNC——自适应PID控制器. 工作原理是 由NNI对被控对象在线辨识的基础上,通过对NNC的权系进行实时 调整,使系统具有自适应性,达到有效控制.
PID 控制器
r e
u
NNC
对象
y
学习算法
NNI
y
学习算法 -
r e
u
NNC
对象
y
学习算法
NNI
y
学习算法 -
e2
-
e1
图 4-4-1 神经 PID 控制框图
3
隐层第 i 节点的输出:
o i ( k ) = f [ x i ( k )]
xi (k ) =
∑
j=0
N
1
w ij I j ( k ), j = 1, 2 , , N ,
I 0 (k ) = 1
1 ex f ( x) = 1 + ex
u ( k ) = ci ( k ) ,代入上式,有 v i ( k )
基于神经网络的PID控制算法研究
基于神经网络的PID控制算法研究近年来，随着机器学习和人工智能技术的不断发展，神经网络在控制领域的应用也逐渐得到了广泛关注。
其中，基于神经网络的PID控制算法作为一种新型的控制方法，已经被证明具有极高的控制精度和适应性。
由于传统的PID控制算法存在着超调、稳态误差等问题，因此在实际工程中往往需要进行各种手动调参。
而基于神经网络的PID控制算法则可以通过学习数据来自适应地优化控制参数，从而在不同工况下都能够实现优秀的控制效果。
同时，神经网络还可以实现非线性控制和逆模型控制等高级控制策略，更加符合实际应用的需求。
基于神经网络的PID控制算法的基本思路是，将神经网络与PID控制器结合起来，构建一个新的混合型学习控制器。
具体而言，首先需要建立一个基于神经网络的模型来描述被控对象的动态特性，然后利用该模型对PID控制器进行参数的自适应优化，最终实现目标系统的控制。
一般来讲，神经网络PID控制算法的实现过程包括以下几个步骤：首先，需要选择合适的神经网络模型和控制器结构。
然后，利用样本数据对神经网络进行训练，得到一个有效的模型。
接着，将训练好的神经网络模型与PID控制器进行耦合，形成一个混合型控制器。
最后，通过仿真或者实际测试来验证控制器的性能。
在具体实现神经网络PID控制算法时，需要注意以下几个关键问题：一是神经网络的选择和搭建，不同的应用需要选择不同的网络结构和训练算法；二是神经网络模型的准确性，神经网络需要能够准确地描述被控对象的动态特性；三是控制器的参数优化，需要避免过度学习和过拟合等问题。
目前，神经网络PID控制算法已经成功应用于许多领域，例如机械控制、电力系统控制、化工过程控制等。
实际应用结果显示，基于神经网络的PID控制算法相比传统PID控制算法，在控制精度、抗干扰能力、稳定性等方面都具有显著的优势，是一种极具应用前景的控制策略。
总的来说，基于神经网络的PID控制算法是一种结合了神经网络与PID控制器的混合型学习控制策略，具有优秀的控制精度和适应性。
神经网络自适应PID控制
0 < η (k ) ≤ −2
∑∑ w
j =1i =1
s
3
e j (k )
ij ( k )
2 s 3 1 ∑ ∑ w (k ) q ( k ) j =1 i =1 ij
1 PIDNNC的设计及实现
s 3 e j (k ) q (k ) ≥ 0 ，则 2）如果 ∑∑ j =1i =1 wij ( k ) s 3
s
(
)
(
)
1 PIDNNC的设计及实现
关键步骤2： 关键步骤 ：
∂e j (k )
3 ∂e j (k ) ∆e j ( k ) = ∑ ∑ ∆wil (k ) ∂wil (k ) l =1 i =1
s
∂u (k ) ∂e j (k )
基于神经网络的自适应PID控制
1 PIDNNC的设计及实现 2 PIDNNC的初始权值的选取 3 PIDNNC在倒立摆镇定控制中的应用
基于BP神经网络的PID控制器的设计
基于BP神经网络的PID控制器的设计简介：PID控制器是一种常用的控制方法，可以使控制系统快速、稳定地对目标进行调节。
然而，传统的PID控制器需要依赖经验的设置参数，很难适用于非线性复杂的系统。
为了改善这一问题，本文提出了一种基于BP神经网络的PID控制器的设计方法。
一、神经网络介绍BP神经网络是一种常用的人工神经网络，通过反向传播算法进行学习和适应。
它可以用来建模非线性关系、解决分类和回归问题等。
BP神经网络由输入层、隐藏层和输出层构成，通过调整权重和偏置项，使得网络的输出接近于期望输出。
二、PID控制器的基本原理PID控制器是由比例（P）、积分（I）和微分（D）三个部分组成的，它们分别对应了系统的比例性能、整定性能和微分性能。
PID控制器的输出是由目标值与实际值之间的误差来决定的。
比例作用是根据误差的大小进行调节，积分作用是根据误差的积分值进行调节，微分作用是根据误差的变化率进行调节。
三、BP神经网络的PID控制器设计1.建立神经网络模型：确定输入层节点数、隐藏层节点数和输出层节点数。
2.确定权重和偏置项的初始值：可以使用随机数进行初始化。
3.设置训练样本集：训练样本集包括输入和输出的数据，可以根据实际情况进行设置。
4.确定学习率和训练次数：学习率决定了网络的更新速度，训练次数决定了网络的学习程度。
5.神经网络训练：使用BP算法对神经网络进行训练，通过反向传播算法调整权重和偏置项。
6.测试神经网络性能：使用测试数据对神经网络进行测试，评估其性能是否满足要求。
7.参数调整：根据测试结果对PID控制器的参数进行调整，使得神经网络对系统的控制更加精确。
四、实验结果分析通过对比传统的PID控制器和基于BP神经网络的PID控制器，可以发现基于BP神经网络的PID控制器具有更好的系统控制性能。
因为BP神经网络能够自适应地调整参数，适应非线性复杂系统的控制要求。
总结：基于BP神经网络的PID控制器是一种有效的控制方法，可以提高系统控制的精度和稳定性。
基于神经网络的自适应PID控制策略研究
基于神经网络的自适应PID控制策略研究近年来，神经网络技术逐渐成为控制领域中的热点研究方向之一。
在控制领域中，PID控制器是最常用的一种控制器，但是，在复杂的非线性系统中，PID控制器可能会失效，因此需要一种更为智能化的自适应控制策略。
本文将着重研究基于神经网络的自适应PID控制策略的原理和应用。
一、神经网络控制简介神经网络控制是一种使用神经网络技术实现控制的控制方法。
神经网络具有自学习和自适应能力，能够适应未知的非线性因素，因此能够有效地提高控制精度。
在神经网络控制中，通常使用BP神经网络进行训练，将网络的输入与输出之间的关系建模，进而得到控制器。
二、PID控制器PID控制器是最常用的一种控制器，它由比例项、积分项和微分项组成。
其中，比例项控制系统的静态误差，积分项控制系统的稳态误差，微分项控制系统的动态响应。
经过调整PID参数，可以实现对系统的稳态和动态性能的优化。
三、传统PID控制器的缺点通过传统PID控制器的参数调整，可以得到较好的控制效果。
但是，在非线性系统控制中，PID控制器的参数调整会变得更加困难，可能会导致系统不稳定或控制精度不高。
这是因为传统PID控制器中的参数是固定的，无法根据系统的变化进行自适应调整。
因此，需要一种更为灵活、智能的自适应控制方式。
四、基于神经网络的自适应PID控制策略与传统PID控制器不同，基于神经网络的自适应PID控制器能够在实时控制过程中不断调整控制器参数，以应对不同的情况。
它能够根据系统的输入和输出实时调整控制器的权值，从而实现对非线性系统的自适应控制。
基于神经网络的自适应PID控制策略的实现方法，一般是将系统的输入和输出作为训练数据，通过训练得到神经网络的权值。
在控制器实时控制过程中，根据系统输出实时调整神经网络的权值，从而实现自适应控制。
五、应用实例基于神经网络的自适应PID控制策略在实际应用中，可以针对不同的场景进行多样化应用。
下面以一个灯光控制系统为例来进行说明。
单神经元自适应PID控制 Hebb学习规则 matlab仿真 增量式PID 控制规律
实验一、单神经元自适应PID 控制一、实验目的1、熟悉单神经元PID 控制器的原理。
2、通过实验进一步掌握有监督的Hebb 学习规则及其算法仿真。
二、实验内容利用单神经元实现自适应PID 控制器，对如下二阶对象进行控制，在MATLAB 环境中进行仿真。
被控对象为：y(k)=0.368y(k-1)+0.26y(k-2)+0.1u(k-1)+0.632u(k-2) 三、实验原理线性神经网络是最简单的一种神经元结构，它不同于感知器，其函数是一线性函数，因此神经元的输出可以是任意值。
我们可以用它实现增量PID 控制器的功能，误差为神经元的输入，权系数为PID 控制系数，由于神经网络可以用在线学习对权系数进行实时修改，所以使得PID 控制具有了自适应功能。
PID 控制器的增量公式为一个３输入的线性神经元的计算公式为k 为神经元的比例系数，w i 为神经元权系数，x i 为神经元输入，u 为神经元的输出。
神经元的学习方法可以采用Hebb 学习规则。
有监督的Hebb 学习算法规范法处理后为3131111222333()()()()(1)()()(1)()()()()(1)()()()()(1)()()()()i i ii i i i i p d k k k u k u k k k x k k k u k e k x k k k u k e k x k k k u k e k x k ωωωωωωηωωηωωη=='==-++=++=++=+∑∑ 四、实验步骤1、编写程序实现单神经元的自适应PID 控制器，输入信号为单位阶跃信号。
单神经元控制的各参考参数为0.12,0.40,0.35,0.40p i d k ηηη====2、修改输入信号为()0.5(sin 4)r t sign t π=，进行上述试验。
3、改变被控制对象为如下几种情况，进行上述试验。
模型1：y(k)=0.368y(k-1)+0.264y(k-2)+u(k-1)+0.632u(k-2))2()(211---+-⨯+-+=∆k k k d k k P K i k e e e k e e k e k u )(332211x w x w x w k u ++=∆模型2：y(k)=0.368y(k-1)+0.264y(k-2)+gu(k-1)+0.632u(k-2)g=1+0.1*sin(0.01k)五、问题讨论神经网络学习算法的收敛速度与自适应控制效果的关系，收敛过程与学习规则中学习系数选取的关系。
基于BP神经网络的自适应PID控制器设计
基于BP神经网络的自适应PID控制器设计自适应PID控制器是一种基于BP神经网络的控制器设计方法，它结合了传统的PID控制器与神经网络的优势，可以适应系统参数变化、非线性和模型误差的情况。
本文将详细介绍基于BP神经网络的自适应PID控制器的设计原理和实现步骤。
1.简介PID控制器是一种经典的控制方法，通过计算误差的比例、积分和微分部分，调节输出控制量来实现对系统的控制。
然而，传统的PID控制器无法处理非线性和参数变化的系统，容易产生较大的误差。
而BP神经网络则具有非线性映射和自适应学习的能力，可以对非线性系统进行建模和控制。
2.BP神经网络的建模BP神经网络是一种前馈神经网络，具有输入层、隐含层和输出层。
输入层接收系统的输入量，输出层输出控制量，隐含层则通过一系列的神经元进行信息传递和处理。
BP神经网络通过训练集的样本进行学习，调整网络的权值和偏置，使得网络的输出与期望输出尽可能一致。
3.PID控制器的设计PID控制器由比例、积分和微分三个部分组成。
比例部分通过调节误差的大小来控制输出，积分部分可以控制持续的误差，微分部分则可以控制误差的变化率，提高系统的响应速度。
PID控制器的参数可以根据系统的特性进行调整。
4.自适应PID控制器的设计a.构建BP神经网络模型，通过训练集对模型进行学习，得到网络的权值和偏置。
b.使用PID控制器的比例、积分和微分部分计算出控制量，并将控制量作为输入量输入到BP神经网络中。
c.根据神经网络的输出，计算系统的输出，将其与期望输出进行比较，得到误差。
d.根据误差的大小，调整PID控制器的参数。
e.重复步骤b-d，直到系统达到期望输出。
5.应用实例自适应PID控制器可以应用于各种系统的控制中，如温度控制、位置控制等。
以温度控制为例，系统输入为温度传感器的读数，输出为控制器输出的控制量。
通过采集训练集数据和期望温度值，利用BP神经网络对系统进行建模和学习，然后根据PID控制器的参数计算出控制量，进而控制温度的变化。
基于深度神经网络的自适应PID控制
基于深度神经网络的自适应PID控制自适应 PID 控制是现代控制理论中的一种重要方法，它通过不断地对实际控制系统的反馈信息进行分析，来实现对系统参数的自适应优化，从而达到更优的控制效果。
在传统的控制方法中，PID 控制器是最常见的一种控制器，它通过改变比例、积分、微分三个参数来控制系统的输出行为。
虽然 PID 控制的思想简单而直观，但它往往需要通过人工调整控制器参数才能达到最佳的控制效果，这使得传统的PID 控制方法在复杂的工业控制系统中应用受到了很大的限制。
近年来，随着深度学习技术的快速发展，越来越多的控制问题开始通过深度神经网络来解决。
深度神经网络通过多层的非线性映射来实现复杂的数据处理和表达，具有非常强的模型适应力和自适应能力，并且能够从大量的数据中学习到系统的隐含规律，从而提高控制性能。
基于深度神经网络的自适应 PID 控制是一个典型的应用场景。
它通过将深度神经网络嵌入到PID 控制器中，实现对系统参数的自适应学习，从而优化控制效果。
具体实现上，基于深度神经网络的自适应PID 控制可以分为以下两个步骤：首先，通过采集真实系统的数据，训练一个深度神经网络，用来对系统的动态特性进行建模和预测。
其次，在 PID 控制器中将这个深度神经网络作为预估器，根据预测误差来自适应调整 PID 控制器的参数，从而达到更优的控制效果。
在实际应用中，基于深度神经网络的自适应 PID 控制已经得到了广泛的应用。
例如在工业自动化领域，它可以通过对温度、压力等参数的自适应调整来实现对化工过程的控制；在机器人控制中，它可以实现对机械臂的精确控制和路径规划；在无人驾驶汽车中，它可以通过对车速、转向等参数的自适应调整来实现对车辆的自动驾驶。
总之，基于深度神经网络的自适应 PID 控制是现代控制理论中的一种重要方法，它能够实现对复杂工业系统的自适应优化。
随着深度学习技术的发展，我们相信基于深度神经网络的自适应 PID 控制将会在更多的领域得到应用，并取得更加突出的成果。
基于RBF网络的自整定PID控制
1 PID控制原理
• PID控制系统框图如图1所示。
常规PID控制系统原理框图 图1 常规 控制系统原理框图
1 PID控制原理
• PID控制器是一种线性控制器，它根据给定 值与实际值的偏差构成控制量。常规PID控 制离散算法为：
1 PID控制原理
• 对于实际的工业生产过程来说，往往具有 非线性、时变不确定性等，应用常规的PID 控制便不能达到理想的控制效果;而且PID控 制器由于参数整定困难，在实际应用中往 往参数整定不良、性能欠佳，对于运行的 工况适应性很差。这样，人们就一直在寻 求PID控制器参数的自动整定技术，以便适 应复杂的工况和高指标的控制要求。
3 RBF神经网络PID整定原理
• 增量式PIபைடு நூலகம்控制算法
• PID三项输入为
3 RBF神经网络PID整定原理
• 神经网络整定指标为
• 参数调整使用梯度下降法
4 仿真实例——
基于RBF神经网络辨识的单神经元PID模型参考自适应控制
• 被控对象为：
• 采样时间为1ms，参考模型指令信号为： 1ms
4 仿真实例——
基于RBF神经网络辨识的单神经元PID模型参考自适应控制
• 建立3-6-1的RBF神经网络
图4参考模型辨识结果 参考模型辨识结果
4 仿真实例——
基于RBF神经网络辨识的单神经元PID模型参考自适应控制
图5 Jacobian信息辨识结果 信息辨识结果
4 仿真实例——
基于RBF神经网络辨识的单神经元PID模型参考自适应控制
2 RBF神经网络模型
• RBF网络结构如图2所示。
图2 RBF网络结构图 网络结构图
2 RBF神经网络模型
高速运动机器人关节神经网络PID自适应控制研究
制。
１ 机器人实验平台
机 器 人 实 验 系统 主 要 包括剧烈的Ｉ 。可是 目 前对机器人的控制，均是
忽 略 了关 节传 递 函数 的 这种 时变 性 ，将 其 等 效 为
微分系数ｋ ） ，作为样本数 据。在此基础上 ，利用神经 网络技 术推导了机器人的运动状态参数 与相应 Ｐ Ｉ Ｏ 参数值之间 的关系模型 ，最终 利用神经网络模 型构建最优的Ｐ Ｉ Ｄ 控 制器 ，以实现机 器人的 高速运动控制 。实验表 明 ，所设计的神经网络最优Ｐ Ｉ Ｄ 控制器 ，响应速度快 ，且基本无 超调 ，跟踪误差为 ±０ ． １ ｍｍ，可满足 实际作业 的需要。 关键词 ：机器人控制 ；建模 ；神经 网络 ；ＰＩ Ｄ 中图分类号 ：Ｔ Ｐ ２ ９ ２ 文献标识码 ：Ａ 文章编号 ：１ ０ ０ ９ —０ １ ３ ４ （ ２ ０ １ ３ ） Ｉ １ （ 上） 一０ ０ １ ８ －０ ３
节 角 位置 ０ ｉ 、 角速 度 与 角加 速度 ）与Ｐ Ｉ Ｄ参数 （ 即 比例 系数 ｋ 。 、积 分 系 数ｋ 、微 分 系数 ｋ ） ，作 为
训 练 样 本 数 据 。在 此基 础 上 ，利 用神 经 网络 建 模
技 术推 导机 器 人运 动状 态参 量 与Ｐ Ｉ Ｄ参数 之 间 的关
非 常 多 的研 究 工 作 。 文献 ［ ３ ， ４ ］ 介 绍 了机 器人 的神
经 网络 自适 应控 制 方法 ；Ｔ ａ ｙ ｅ ｂ ｉ ｄ 等研 究一 种 机 器 人关 节 的 自适 应迭 代 学 习算 法 ；ｗｅ ｎ ７ １ 踟 等设 计 了模 糊 自适 应控 制 算法 ，将其 用 于 机器 人 Ｐ Ｄ控 制 器 的 参 数 整 定 。 从 目前 已 有 的 运 动 控 制 算 法 来
基于BP神经网络的PID控制系统设计
基于BP神经网络的PID控制系统设计摘要本文主要研究一个基于神经网络的自适应PID控制系统的设计方法，利用BP神经网络对被控对象进行在线辨识和控制。
基于BP神经网络学习算法设计出两个神经网络模型：一个利用神经网络（NNM）对非线性映射的逼近能力，对被控对象进行辨识，另一个构成具有PID结构的控制器（NNC）。
通过神经网络NNM的在线学习和修正，产生对被控对象输出的预测作用，然后由网络NNC实施控制作用，从而实现对辨识对象的PID控制。
在利用神经网络对系统进行辨识时，选用白噪声信号作为系统的输入信号，以提高系统的辨识精度；另外，为了得到神经网络控制器的初始化权值，本文在自整定过程中采用常规PID控制器整定方法之一的稳定边界法。
在设计过程中运用MATLAB语言工具箱进行编程，并通过SIMULINK动态仿真工具对一阶非线性对象进行了仿真。
仿真结果表明了利用神经网络对系统进行辨识的有效性，并用经辨识所得到的输出值取代系统的实际输出值，利用神经网络NNC对系统进行控制，获得了满意的控制效果。
关键词：神经网络，BP学习算法，自适应，参数优化，辨识1 综述PID调节器从问世至今已历经了半个多世纪，在这几十年中，人们为它的发展和推广做出了巨大的努力，使之成为工业过程控制中主要的和可靠的技术工具。
近几十年来，现代控制理论迅速发展，出现了许多先进的控制算法，但到目前为止，即使在微处理技术迅速发展的今天，过程控制中大部分控制规律都未能离开PID，这充分说明PID控制仍具有很强的生命力。
过程工业控制中实际应用最多的仍是常规的PID控制算法，这是因为PID控制具有结构简单、容易实现、控制效果好和鲁棒性强等特点，且PID算法原理简明，参数物理意义明确，理论分析体系完整，为广大控制工程师所熟悉。
但在生产现场往往由于参数整定不好而使PID控制器控制效果欠佳，整定的好坏不但会影响到控制质量，而且还会影响到控制器的性能。
PID控制中一个至关重要的问题，就是控制器三参数(比例系数、积分时间、微分时间)的整定。
自适应 PID 控制器的设计及应用
自适应 PID 控制器的设计及应用在工业生产和自动控制领域中，PID 控制器是一种常用的控制算法。
PID 循环控制器通过比较系统实际输出值和理想输出值之间的差异，并通过调节控制器的输出来达到最终的控制目标。
然而，PID 控制器对于非线性系统和负载变化敏感性较高，需要手动调整参数，调参过程耗时长，因此PID 控制器的应用受到了一定的限制。
自适应 PID 控制器则是一种应对上述问题的解决方案，它采用自适应控制算法，并结合经验模型、神经网络等方法，自动地调整 PID 控制器的参数，从而适应复杂的工业生产和自动控制环境。
接下来我们将探讨自适应 PID 控制器的设计及应用。
自适应 PID 控制器的概念自适应控制理论是 20 世纪上半叶发展起来的一种创新类型控制系统，在自动控制和工业生产领域得到了广泛应用。
自适应控制是一种控制系统，通过及时测量和分析控制对象的响应，结合动态模型和智能算法，实现系统自身结构调整和参数优化的过程。
自适应 PID 控制器是基于 PID 算法的自适应控制系统的一个重要代表。
自适应PID 控制器的基本思想是，根据控制器的响应和控制对象的状态，自动调节 PID 控制器的参数，从而达到最优控制策略。
传统 PID 控制器仅仅考虑了系统误差，而忽略了系统参数变化和环境因素对控制效果的影响，自适应 PID 控制器则是基于这一观察提出的。
自适应 PID 控制器通过监控系统的响应和状态，实时调整 PID 控制器的三个参数，即 P（比例系数）、I（积分系数）和 D（微分系数）系数，以使控制系统更加精确、稳定和动态响应更好。
自适应 PID 控制器的设计自适应 PID 控制器的设计过程可以分为三个步骤：系统建模、参数调整和算法选择。
系统建模：在进行自适应 PID 控制器设计之前，首先需要对控制对象进行建模和测试。
模型建立的主要目的是得到系统的数学模型，从而帮助我们选择合适的自适应控制算法。
参数调整：自适应 PID 控制器有三个参数—— P、I 和 D，我们需要通过实验和模型验证确定这些参数的最优值。
基于BP神经网络的PID参数自适应整定
基于BP 神经网络的PID 参数自适应整定曾正1，蔡容容2，詹立新21 武汉大学电气工程学院，430072 2 武汉大学动力与机械学院，430072 联系方式：zengerzheng@摘 要：针对简单单入单出（SISO ）系统中PID 控制的参数整定问题进行了仿真研究，利用BP 神经网络进行PID 参数自适应整定。
首先，得到了问题的传递函数模型，并建立了对应的离散化传递函数模型作为仿真研究的对象，并对未校正系统进行了相关的理论分析。
然后，利用BP 神经网络算法在线进行PID 参数自适应整定。
同时，为了形成参照，给出了运用模拟退火算法离线整定PID 参数的仿真过程。
建立了3层BP 网络结构，以δ规则为学习规则，控制器算法为有监督的Hebb 算法，教师信号为给定与被控对象的输出间的偏差信号。
最后，针对系统在多工况下的复杂情况，从静态稳定和动态稳定的角度，对系统稳定性进行了仿真分析。
仿真结果表明，所设计的基于BP 神经网络参数自适应PID 控制系统，控制品质高、鲁棒性强。
为了支持更加复杂情况下的仿真，还搭建GUI 仿真界面。
关键字：PID 控制；参数整定；BP 神经网络；稳定分析；GUI ；1 问题背景分析 1.1 准备知识1.1.1 控制系统的性能指标当系统的时间响应()y t 中的瞬态分量较大而不能忽视时，称系统处于动态或过渡过程中，这时系统的特性称为动态特性。
动态特性指标通常根据系统的阶跃响应曲线定义。
设系统的阶跃响应曲线如图1所示，图中()lim ()x y y t →∞∞=称为稳态值。
动态性能指标主要有以下几种[1]。
图1 系统的阶跃响应曲线（1）上升时间r t ：阶跃响应曲线从零第一次上升到稳态值所需的时间为上升时间。
若阶跃曲线不超过稳态值（称为过阻尼系统），则定义阶跃响应曲线从稳态值的10%上升到90%所对应的时间为上升时间。
（2）最大超调p σ：设阶跃响应曲线的最大值为()p y t ，则对大超调p σ为()()100%()p p y t y y σ-∞=⨯∞ (1)p σ大，称系统阻尼小。
发动机神经网络自适应PID转速控制
一
定进展 ， 但 影 响发 动机 性 能 的参 数 相 当 多 ． 在 建模
卵 为歧 管压力 的函数 ， 可表示 为 ：
叼 ＝ ０ ． ９ ５ ２ — ０ ． ０ ７ ５ ／ ｐ （ ３ ）
时不 可能 面 面俱 到 （ 常会 忽 略一些 不重 要 的参数 ， 如 进 气歧 管截 面 积 随 温度 的 变 化 、发 动 机 的磨 损 情况 等） ，常造 成 发动机 模 型不精 确 ，且相 对可靠 性 比较
Ｊ ａ ｎ ． ２ ０ １ ４
发 动机神经 网络 自适应 Ｐ ｌ Ｄ转速控制
吴 笑伟 ， 史雷鸣
（ 河 南 交通 职 ３ ， ｋ 技术学院 汽车学院 ， 郑州 ４ ５ ０ ０ ０ ５ ）
摘要 ： 为 提 高 发 动 机 怠 速 控 制 的准 确 性 ， 解决 非线 性 、 复杂 的 系统 控 制 问题 ， 详 细 介 绍 发动 机 模 型 建 立 方 法 、 转 速 神 经 控 制 的 结 构
式中： 可表 示 为两个 并行 的等 嫡物理 过程 。
１ ． １ ２ 发动机曲轴系统动力学子模型 根 据 能量 守恒 定律
差。 对 发动机 转速 神经 控制 的结 构和 神经 网络 的形式 进 行研 究 ， 将 神 经 网络 同 Ｐ Ｉ Ｄ控 制相 结 合 。 很 好 地解 决 了发 动机转 速 与燃 油控制 问题 ， 可 以使发 动机 在 最
和 神 经 网络 的 形 式 ， 并将神经网络同 Ｐ Ｉ Ｄ 控 制很 好 的结 合 起 来 ， 以有 效 解 决 发 动 机 转 速控 制 问题 。
关键词 ： 发 动机 ； 神 经 网 络 自适 应 Ｐ Ｉ Ｄ； 设计 ； 转 速 控制 ； 神 经 网 络
中 图分 类 号 ： Ｕ ４ ６ ７ ． ２
AQM中基于神经网络自适应的PID控制器
—
６一１设 ＝ ［ ， ， ］ 网络 的输 入 向量 ； ． ， 为 ，
ＲＦ Ｂ 网络的径向基 向量 日 ＝［ 。ｈ ， ｈｒ． ｈ ，：…， 其中
ｈ 为高斯基 函数 ， ， 且
ｈ ： ｐ一 ｉ （ ｊ
）
Ｊ ２， ， ． ． ：１ … ６
，
图 １ 控制 系统 结 构 图
第２ ９卷
第 ３期
吉 首 大学 学 报 （ 自然 科 学 版 ）
Ｊｕ ａ ｏ Ｊ ｈ ｕ Ｕ ｉ ｒ ｔ Ｎ ｔｒ ｃｅ ｃ ｄｔ ｎ ｏ ｒ ｌ ｆ ｉ ｏ ｎｖ ｓ ｙ（ ａ ， Ｓ ｉ ｅＥ ｉｏ ） ｎ ｓ ｅｉ ｕｄ ｎ ｉ
Ｖ０ ．２ Ｎｏ 】 ９ ．３ Ｍａ ｙ．２ Ｏ Ｏ８
２０ ０ ８年 ５月
文章 编号 ：０７—２ ８ （０ ８０ ０ ８ —０ １０ ９ ５ ２０ ）３— ０ ８ ３
Ａ Ｍ 中基 于神 经 网 络 自适 应 的 ＰＤ控 制 器 Ｑ Ｉ
李 春 来 罗 晓 曙 ，
（． １湖南理工学院物理 与电子信息系 ， 湖南 长沙
摘
４４０ ；． 西师范大学物理与信息工程学院 ， １０６ ２广 广西 桂林
制器 ．
关 键词 ： 塞 控 制 ；Ｉ 拥 ＰＤ控 制 ； 经 网络 ； 识 神 辨 中 图分 类号 ：Ｐ９ ．７ Ｔ３ ３０ 文献标识码 ： Ａ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 s 3 e j (k ) 1 s 3 1 2 q (k )η 2 (k ) q(k )η (k ) + ∑ ∑ ∆V (k ) = ∑ ∑ wij (k ) 2 j =1 i =1 wij (k ) j =1 i =1
s
∂y j ( k ) ∂u ( k )
取符号函数（+1, -1）
输出层
wi = 1 (i = 1,2,3)
1 PIDNNC的设计及实现
定理2.1 定理2.1 闭环系统稳定的充分条件是，在采样周期k时隐 含层的所有学习速率都应取相同的值 η (k )，且满足下式：
s 3 e j (k ) q ( k ) < 0 ，则 1）如果 ∑∑ w (k ) j =1i =1 ij
j =1
s
s
隐 含 层
a 2 (k ) =
∑ w2 j (k )e j (k )
j =1
s s j =1 j =1
a3 (k ) = ∑ w3 j (k )e j (k ) − ∑ w3 j (k − 1)e j (k − 1)
输出层节点
u (k ) = ∑ wi (k )ai (k )
i =1
3
1 PIDNNC的设计及实现
K* feedbak plus
Demu
lqr_Scope_theta2
lqr_Scope_x_dot
lqr_Scope_theta1_dot
lqy_Scope_u
lqr_Scope_theta2_dot
2 PIDNNC的初始权值的选取
Q = 90 * diag (80,0.4,10,2.8,0.2,0.4)
1 PIDNNC的设计及实现
证明方法： 证明方法： 直接Lyapunov方法
1 s 2 V (k ) = ∑ e j (k ) 2 j =1
∆V (k ) ≤ 0
关键步骤1： 关键步骤 ：
∆V (k ) = V (k + 1) − V (k )
1 2 = ∑ ∆e j (k ) e j (k ) + ∆e j (k ) 2 j =1
∂u (k ) = ∂W (k ) ∂Wil (k ) il
3 p ( k )e 2 ( k ) l ∆e j ( k ) = ∑ ∑ η il (k ) l =1 i =1 wij ( k )
s
3 ∑ 1 q ( k )η ( k ) ∆e j ( k ) = wij ( k ) i =1
K = [32.1522 129.3426 − 234.6127 28.1289 1.9087 − 33.4221]
R = 5.5
2 PIDNNC的初始权值的选取
e1 e2 e3 a1 w21 w22 w31 w32 w
23
w33
a 2 w2 w3 a3
u
PD
w31 (0) = k x T = 5625 .78 ɺ
s
(
)
(
)
1 PIDNNC的设计及实现
关键步骤2： 关键步骤 ：
∂e j (k )
3 ∂e j (k ) ∆e j ( k ) = ∑ ∑ ∆wil (k ) ∂wil (k ) l =1 i =1
s
∂u (k ) ∂e j (k )
w32 (0) = kθɺ T = 381.74
1
w21 (0) = k x = 32 .1522
w 22 ( 0 ) = kθ1 = 129 .3426
w23 (0) = kθ 2 = −234.6127
w33 (0) = kθɺ T = −6684.42
2
3 PIDNNC在倒立摆镇定控制中 的应用
0 < η (k ) ≤ −2
∑∑ w
j =1i =1
s
3
e j (k )
ij ( k )
2 s 3 1 ∑ ∑ w (k ) q ( k ) j =1 i =1 ij
1 PIDNNC的设计及实现
s 3 e j (k ) q (k ) ≥ 0 ，则 2）如果 ∑∑ j =1i =1 wij ( k ) s 3
1 PIDNNC的设计及实现
→确定网络输入层节点的数目
→确定隐含层节点 →网络隐含层权值的初始值 →运行系统，在每个k采样周期内
——读取系统输出变量，并计算所有变量的误差值 ——计算网络隐含层输出 ——计算控制量 ——根据定理2.1确定学习速率，并根据权值调整律更新权值 ——输出控制量
2 PIDNNC的初始权值的选取
1. 获取模型(倒立摆)方程 2. 选择不同的Q、r值，使用LQR算法获得反馈矩阵K 3. 在simulink环境中运行闭环控制系统，察看控制性能 4. 选择最优的K，并赋值网络隐含层权值
y(n)=Cx(n)+Du(n) x(n+1)=Ax(n)+Bu(n) Discrete State-Space lqr_Scope_theta1 lqr_Scope_x
−2
∑∑ w
j =1i =1
e j (k )
ij ( k ) 2
s 3 1 ∑ ∑ w (k ) j =1 i =1 ij
≤ η (k ) ≤ 0
q ( k )
其中，
s s e (k ) sgn ∆y j (k ) e 2 (k ) ∑ j q(k ) = ∑ j ∆u (k ) j =1 j =1
PIDNNC R(k) E(k) e1 e2 es u(k) 被控对象 Y(k)
闭环系统结构
总误差函数
J j (k ) =
1 1 e j (k ) 2 = r j (k ) − y j (k ) 2 2 2
(
)
(
)
梯度下降法 调整原则 弹性原理
1 PIDNNC的设计及实现
隐含层
∆y j ( k ) wij (k + 1) = wij (k ) + η ij (k )e j (k ) ∑ e j (k ) sgn ∆u ( k ) j =1
3 PIDNNC在倒立摆镇定控制中 的应用
LQR控制器 0.1 位移(米 米)
0
神经网络控制器
0
10
20 时间（秒）
30
40
3 PIDNNC在倒立摆镇定控制中 的应用
0.2 LQR控制器
位移(米 米)
0 神经网络控制器
-0.2
0
10
时间（秒）
20
30
智能控制期末考核作业
《智能控制技术的现状及发展趋势》 要求调研10-20篇参考文献（其中英文3~5篇），通 过分析和整理文献内容，以小论文的形式提交调研报告； 主要从文献调研情况(20%)、论文内容(50%)、论文的 结构(15%)，文字表达(15%)方面进行评分。 模板请见“智能控制技术的现状及发展趋势 .doc” 4~8页 16周周三第四讲交,东1210
∑ w1 j (k )e j (k )
j =1
s
1 − z −1
u
es
ws3
s w (k )e (k ) (1 − z −1 ) a3 ( k ) = ∑ 3 j j j =1
激活函数：f = 1
多变量PID
1 PIDNNC的设计及实现
a1 (k ) = ∑ w1 j (k )e j (k ) + a1 (k − 1)
基于神经网络的自适应PID控制
1 PIDNNC的设计及实现 2 PIDNNC的初始权值的选取 3 PIDNNC在倒立摆镇定控制中的应用
1 PIDNNC的设计及实现
z-1 e1 e2 w11 w21 n1 ws1 n2 n3 f -z-1 输入层 隐含层 输出层 a1 f a2 f a3 f
a1 ( k ) =