基于神经网络的PID控制
神经网络PID控制
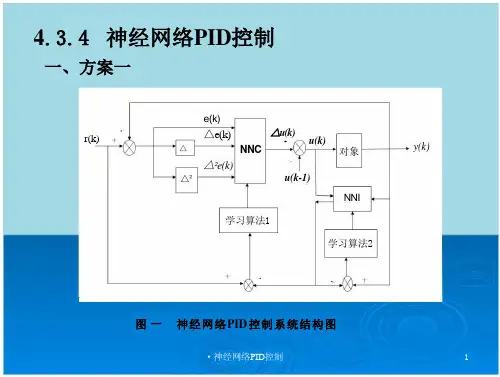
NNI
十
十
x₁(k)=e(k)x₂(k)=△e(k)=e(k)-e(k-1)x₃(k)=△²e(k)=e(k)-2e (k-1)+e(k-2)e(k)=r(k)-y(k)NNC 的输出为：△u(k)=k₁x₁(k)+k₂x₂(k)+k₃x₃(k)式中，}i=1,2,3 为权系数，△u(k) 为输入信号的加权和。由此可见，NNC 具有增量D 控制的结构
i=1,2,…,Q-1
BP网络的输入层节点的输为
网络的隐含层输入、输为
·神经网络PID控制 20
o(k)=1
(13)
(14)
式中o 为输出层权系数 阈值，
网络的输出层的输入输出为
·神经网络PID控制 21
图二 神经网络PID控制系统结构图
·神经网络PID控制 17
二、方案二
被控对象
u
个
经典PID控制算式为u(k)=u(k-1)+Kp[e(k)-e(k-1)]+K,e(k)+K,[e(k)-2e(k-1) + e(k-2)1
7.由(20)式，计算修正输出层敝系数。(k);8.由(21)式，计算修正隐含层敝系数。)(k);9.置k=k+1, 返回到“3”,直到性能指标J 满足要求。
·神经网络PID控制 26
系数a(k)是慢时变的，a(k)=1.2(1-0.8e -01k),神经网络结构为4—5—3,输入层的个神经元分别为模型翰入r(k)、 输 出(k)、误 差(k)和常量。学习速率=0.25,动量系数=0.05,加权系数初始值取随[=0.50.5]上的随机数。当输入信号为幅值是的正弦信号(t)sin(2πt)时，取采样时间为.001s,仿真结果如图所示。·神经网络PID控制 27
基于BP神经网络的PID控制系统设计
基于BP神经网络的PID控制系统设计一、引言PID（Proportional-Integral-Derivative）控制器是一种常用的自动控制器，其通过测量系统的输出偏差，根据比例、积分和微分三个因素来控制系统的输出。
然而，传统的PID控制器难以适应复杂、非线性和时变的系统，对于这类系统的控制，神经网络已经被证明是一种有效的方法。
本文将介绍基于BP神经网络的PID控制系统设计。
二、BP神经网络简介BP神经网络（Backpropagation Neural Network）是一种常用的前向反馈型人工神经网络，其通过反向传播算法来训练网络参数，从而实现对输入数据的学习和预测。
BP神经网络拥有多层神经元，每个神经元都与下一层神经元相连，并通过权重和阈值来传递和处理输入信息。
三、PID控制器简介PID控制器由比例（Proportional）、积分（Integral）和微分（Derivative）三个部分组成，其控制输出的公式为：u(t) = Kp * e(t) + Ki * ∑e(t)dt + Kd * de(t)/dt其中，u(t)为控制器的输出，Kp、Ki、Kd为控制器的三个参数，e(t)为系统的输出偏差，∑e(t)dt为偏差的积分项，de(t)/dt为偏差的微分项。
1.数据采集和预处理：首先需要采集系统的输入和输出数据，并对其进行预处理，包括数据归一化和滤波处理等。
2.神经网络设计和训练：根据系统的输入和输出数据，设计BP神经网络的结构，并使用反向传播算法来训练网络参数。
在训练过程中，根据系统的输出偏差来调整比例、积分和微分三个参数。
3.PID控制器实现：根据训练得到的神经网络参数，实现PID控制器的功能。
在每个控制周期内，根据系统的输出偏差来计算PID控制器的输出，将其作为控制信号发送给被控制系统。
4.参数调优和性能评估：根据控制系统的实际情况，对PID控制器的参数进行调优，以提高系统的控制性能。
基于BP神经网络的PID控制器设计
基于BP神经网络的PID控制器设计PID控制器是一种常用的控制器，可以通过根据系统的误差、历史误差和误差的变化率来计算控制信号，从而实现对系统的控制。
传统的PID控制器可以通过调节PID参数来实现对系统动态特性的控制，但是参数调节过程往往需要经验和反复试验，而且很难实现对非线性系统的精确控制。
近年来，基于BP神经网络的PID控制器设计方法得到了广泛的关注。
BP神经网络是一种常用的人工神经网络模型，可以通过训练得到输入与输出之间的映射关系。
在PID控制器设计中，可以将误差、历史误差和误差的变化率作为BP神经网络的输入，将控制信号作为输出，通过训练神经网络来实现对控制信号的合理生成。
1.数据预处理：首先需要采集系统的输入输出数据，包括系统的误差、历史误差和误差的变化率以及相应的控制信号。
对这些数据进行归一化处理，以便神经网络能够更好地学习和训练。
2.网络结构设计：根据系统的特性和要求，设计BP神经网络的输入层、隐藏层和输出层的神经元数量。
通常情况下，隐藏层的神经元数量可以根据经验设置为输入层和输出层神经元数量的平均值。
3.训练网络：采用反向传播算法对神经网络进行训练，以获得输入和输出之间的映射关系。
在训练过程中，需要设置学习率和动量系数，并且根据训练误差的变化情况来确定训练的终止条件。
4.参数调整：将训练得到的神经网络与PID控制器相结合，根据神经网络的输出和系统的误差、历史误差和误差的变化率来计算控制信号，并通过对PID参数的调整来实现对系统的控制。
1.适应能力强：BP神经网络能够通过训练来学习系统的动态特性，从而实现对非线性系统的精确控制。
2.自适应性高：BP神经网络能够根据实时的系统状态来实时调整控制信号，从而实现对系统动态特性的自适应控制。
3.参数调节方便：通过BP神经网络的训练过程，可以直接得到系统的输入和输出之间的映射关系，从而减少了传统PID控制器中参数调节的工作量。
4.系统稳定性好：基于BP神经网络的PID控制器能够根据系统状态及时调整控制信号，从而提高了系统的稳定性和鲁棒性。
基于神经网络的模糊PID控制器设计与实现
基于神经网络的模糊PID控制器设计与实现随着科技的不断发展，控制技术在工业自动化中的应用越来越广泛。
PID控制器因其简单易懂、易实现的特点而被广泛使用，但是传统的PID控制器在某些场合下会出现失效的情况。
为了解决这一问题，研究者们开始着手开发基于神经网络的模糊PID控制器。
本文将介绍基于神经网络的模糊PID控制器的设计与实现。
一、控制器介绍基于神经网络的模糊PID控制器是一种新型的控制器，它将模糊控制的优点与神经网络的处理能力相结合，形成了一种高效的自适应控制器。
该控制器利用神经网络的学习算法实现自适应参数的调节，将模糊控制中的模糊规则与神经网络的处理能力相结合，形成一种新的控制方法。
该控制器的核心思想是利用神经网络对系统进行建模，通过学习算法自适应地调节系统参数，从而实现对系统的控制。
其中，模糊控制器用于对输出进行模糊处理，神经网络用于对输入和输出进行处理，从而实现对系统的控制。
二、控制器设计基于神经网络的模糊PID控制器的设计需要以下几个步骤：1.系统建模系统建模是设计基于神经网络的模糊PID控制器的第一步。
系统建模的目的是构建系统的数学模型，以便于后续的设计过程。
在建模过程中，需要考虑系统的类型、运动方程、非线性因素等因素。
2.控制器设计控制器的设计是基于神经网络的模糊PID控制器设计的核心。
控制器的设计包括神经网络的结构设计、神经网络权值的选择、模糊控制的设计等。
3.参数调节参数调节是控制器设计的重要环节。
由于系统的运动方程等因素的影响，不同系统的参数可能不同。
因此，在实际应用中需要根据实际情况对控制器进行参数调节。
三、控制器实现基于神经网络的模糊PID控制器的实现需要以下步骤：1.数据采集数据采集是基于神经网络的模糊PID控制器实现的第一步。
数据采集的目的是获取系统的输入输出，以便为神经网络提供数据。
2.神经网络训练神经网络训练是实现控制器的关键步骤。
在训练过程中，通过对神经网络进行学习，让它逐渐对系统的输入输出进行建模。
基于BP神经网络的PID控制系统设计
基于BP神经网络的PID控制系统设计一、引言PID控制系统是目前工业控制中广泛应用的一种基本控制方法，它通过测量控制系统的偏差来调节系统的输出，以实现对控制对象的稳定控制。
然而，传统的PID控制器需要事先对系统建模，并进行参数调整，工作效果受到控制对象模型的准确性和外部干扰的影响。
而BP神经网络具有非线性映射、自适应性强、鲁棒性好等优点，可以有效地克服传统PID控制器的缺点。
因此，基于BP神经网络的PID控制系统设计成为当前研究的热点之一二、基于BP神经网络的PID控制系统设计理论1.PID控制器设计原理PID控制器是由比例环节（Proportional）、积分环节（Integral）和微分环节（Derivative）组成的控制器，其输出信号可以表示为：u(t) = Kp*e(t) + Ki*∫e(t)dt + Kd*(de(t)/dt)，其中e(t)为控制系统的输入偏差，t为时间，Kp、Ki和Kd分别为比例系数、积分系数和微分系数。
2.BP神经网络理论BP神经网络是一种前馈型神经网络，通过反向传播算法对输入信号进行学习和训练，从而得到最优的网络结构和参数。
BP神经网络由输入层、隐层和输出层组成，其中每个神经元与上、下相邻层之间的神经元互相连接，并具有非线性的激活函数。
3.基于BP神经网络的PID控制系统设计理论基于BP神经网络的PID控制系统设计的核心思想是将BP神经网络作为PID控制器的自适应调节器，根据控制对象的输入信号和输出信号之间的误差进行训练和学习，通过调整BP神经网络的权重和阈值来实现PID 控制器的参数调节，从而提高控制系统的稳定性和鲁棒性。
三、基于BP神经网络的PID控制系统设计步骤1.系统建模首先，需要对待控制对象进行建模，获取其数学模型。
对于一些复杂的非线性系统，可以采用黑箱建模的方法，利用系统的输入和输出数据进行数据拟合，获取系统的数学模型。
2.BP神经网络训练将系统的数学模型作为BP神经网络的训练集，通过反向传播算法对BP神经网络进行训练，得到最优的网络结构和参数。
(完整word版)基于BP神经网络的自整定PID控制仿真
基于BP神经网络的自整定PID控制仿真一、实验目的1.熟悉神经网络的特征、结构及学习算法。
2.通过实验掌握神经网络自整定PID的工作原理。
3.了解神经网络的结构对控制效果的影响。
4. 掌握用Matlab实现神经网络控制系统仿真的方法。
二、实验设备及条件1.计算机系统2.Matlab仿真软件三、实验原理在工业控制中，PID控制是工业控制中最常用的方法。
这是因为PID控制器结构简单，实现简单，控制效果良好，已得到广泛应用。
但是，PID具有一定的局限性：被控制对象参数随时间变化时，控制器的参数难以自动调整以适应外界环境的变化。
为了使控制器具有较好的自适应性，实现控制器参数的自动调整，可以采用神经网络控制的方法。
利用神经网络的自学习这一特性，并结合传统的PID控制理论，构造神经网络PID控制器，实现控制器参数的自动调整。
基于BP神经网络的PID控制器结构如图4所示。
控制器由两部分组成：一是常规PID控制器，用以直接对对象进行闭环控制，且3个参数在线整定；二是神经网络NN，根据系统的运行状态，学习调整权系数，从而调整PID参数，达到某种性能指标的最优化。
图4中神经网络采用结构为4-5-3型的BP网络。
BP网络是一种单向传播的多层前向网络。
输入节点对应系统的运行状态量，如系统的偏差与偏差变化率，必要时要进行归一化处理。
输入变量的个数取决于被控系统的复杂程度，输出节点对应的是PID的3个可调参数。
由于输出不能为负，所以输出层活化函数取2()(1)()(1)1(1)a k y k y k u k y k -=+-+-非负的Sigmoid 函数，隐含层取正负对称的Sigmoid 函数。
本系统选取的BP 网络结构如图5所示。
网络的学习过程由正向和反向传播两部分组成。
如果输出层不能得到期望输出，那么转入反向传播过程，通过修改各层神经元的权值，使得误差信号最小。
输出层节点分别对应3个可调参数K p 、K i 、K d 。
基于BP神经网络PID整定原理和算法步骤
基于BP神经网络PID整定原理和算法步骤BP神经网络是一种常用的非线性拟合和模式识别方法，可以在一定程度上应用于PID整定中，提高调节器的自适应性。
下面将详细介绍基于BP神经网络的PID整定原理和算法步骤。
一、基本原理：BP神经网络是一种具有反馈连接的前向人工神经网络，通过训练样本的输入和输出数据，通过调整神经元之间的连接权重来模拟输入和输出之间的映射关系。
在PID整定中，可以将PID控制器的参数作为网络的输入，将控制效果指标作为网络的输出，通过训练网络来获取最优的PID参数。
二、算法步骤：1.确定训练数据集：选择一组适当的PID参数和相应的控制效果指标作为训练数据集，包括输入和输出数据。
2.构建BP神经网络模型：确定输入层、隐藏层和输出层的神经元数量，并随机初始化神经元之间的连接权重。
3.设置训练参数：设置学习速率、误差收敛条件和训练迭代次数等训练参数。
4.前向传播计算输出：将训练数据集的输入作为网络的输入，通过前向传播计算得到网络的输出。
5.反向传播更新权重：根据输出与期望输出之间的误差，利用误差反向传播算法来调整网络的连接权重，使误差逐渐减小。
6.判断是否达到收敛条件：判断网络的训练误差是否满足收敛条件，如果满足则跳转到第8步，否则继续迭代。
7.更新训练参数：根据训练误差的变化情况，动态调整学习速率等训练参数。
8.输出最优PID参数：将BP神经网络训练得到的最优权重作为PID 控制器的参数。
9.测试PID控制器：将最优PID参数应用于实际控制系统中，观察控制效果并进行评估。
10.调整PID参数：根据实际控制效果，对PID参数进行微调，以进一步优化控制性能。
三、应用注意事项：1.训练数据集的选择应尽量全面、充分，覆盖各种不同工况和负载情况。
2.隐藏层神经元数量的选择应根据实际情况进行合理调整，避免过拟合或欠拟合现象。
3.学习速率和训练迭代次数的设置应根据系统复杂度和训练误差的变化情况进行调整。
基于BP_神经网络的PID_控制算法参数优化
- 22 -高 新 技 术从本质上来看，PID 控制算法就是对比例、积分和比例微分间的关系进行控制的一种算法。
PID 控制调节器具有适应性强、鲁棒性良好的特征，因此被广泛应用于工业控制领域。
但是，随着科学技术、控制理论发展，在工业生产中被控对象逐渐向复杂化和抽象化的趋势发展，并呈现滞后性、时变性和非线性的特征，这使传统PID 控制器难以精准调控这种较复杂的控制系统。
为了解决该问题，研究人员将控制理论与其他先进的算法相结合，形成全新的控制理论，包括神经网络控制、遗传算法以及模糊控制等。
对神经网络算法来说，由于其具有较高的鲁棒性和容错性，因此适用于复杂的非线性控制系统中，并且具有广阔的应用前景和较大的发展潜力。
1 BP 神经网络结构及算法BP 神经网络将网络视为一个连续域，在这个网络中，输入层和输出层都是任意时刻、任意数目的样本值，网络输出层值与输入层值间也可以具有任意关系，这个学习过程就称为BP 神经网络学习过程。
作为一种被广泛应用的神经网络模型，BP 神经网络由输入层、输出层和隐含层组成：1） 输入层。
从第i 个输入向量中产生相应的输出值。
2） 输出层。
在输出值的作用下将其转换为输入数据。
3） 隐含层。
在输出值的作用下对数据进行隐含处理，将处理后的结果反馈给输入层，3个输入层构成1个BP 神经网络。
当输入数据在时间域内经过多次的误差传播时，最后被一个误差源作为输出信号，即经过输入单元和输出组的中间信息。
如果该误差源的误差小于输出单元和输出组中各单元间的误差，那么这些单元在计算输出时就会有很大的变化；如果超过了期望值，那么这一单元被认为是输入量存在误差（也就是输入信号存在误差），将不再使用该单元；如果仍然超过期望值，那么输出量又会存在误差[1]。
通过分析输入与输出量间的关系可以得出BP 网络中各个隐藏层上节点数与该输出量间的关系。
BP 神经网络的拓扑结构如图1所示。
为了对BP 神经网络进行运算和优化，该文设定了中间层的加权和结点临界，以便将全部采样的真实输出量与预期的输出量的偏差控制在一个很低的区间，并且通过调节这个区间来保证它的稳定性。
基于RBF神经网络整定的PID控制器设计及仿真_毕业设计(论文)
华北电力大学毕业设计(论文)题目基于RBF神经网络整定的PID控制器设计及仿真基于RBF神经网络整定的PID控制器设计及仿真摘要目前，因为PID控制具有简单的控制结构，可通过调节比例积分和微分取得基本满意的控制性能，在实际应用中又较易于整定，所以广泛应用于过程控制和运动控制中，尤其在可建立精确模型的确定性控制系统中应用比较多。
然而随着现代工业过程的日益复杂，对控制要求的逐步增高（如稳定性、准确性、快速性等），经典控制理论面临着严重的挑战。
对工业控制领域中非线性系统，采用传统PID 控制不能获得满意的控制效果。
采用基于梯度下降算法优化RBF神经网络，它将神经网络和PID控制技术融为一体，既具有常规PID控制器结构简单、物理意义明确的优点，同时又具有神经网络自学习、自适应的功能。
因此，本文通过对RBF神经网络的结构和计算方法的学习，设计一个基于RBF神经网络整定的PID控制器，构建其模型，进而编写M语言程序。
运用MATLAB软件对所设计的RBF神经网络整定的PID控制算法进行仿真研究。
然后再进一步通过仿真实验数据，研究本控制系统的稳定性，鲁棒性，抗干扰能力等。
关键词：PID；RBF神经网络；参数整定SETTING OF THE PID CONTROLLER BASED ON RBF NEURAL NETWORK DESIGN AND SIMULATIONAbstractAt present, because the PID control has a simple control structure, through adjusting the proportional integral and differential gain basic satisfactory control performance, and is relatively easy to setting in practical application, so widely used in process control and motion control, especially in the accurate model can be built more deterministic control system application. With the increasingly complex of the modern industrial process, however, increased step by step to control requirements (e.g., stability, accuracy and quickness, etc.), classical control theory is faced with severe challenges. Non-linear systems in industrial control field, using the traditional PID control can not obtain satisfactory control effect. Optimized RBF neural network based on gradient descent algorithm, it will be integrated neural network and PID control technology, with a conventional PID controller has simple structure, physical meaning is clear advantages, at the same time with neural network self-learning, adaptive function. Therefore, this article through to the RBF neural network structure and the calculation method of learning, to design a setting of the PID controller based on RBF neural network, constructs its model, and then write M language program. Using the MATLAB software to design the RBF neural network setting of PID control algorithm simulation research. Data and then further through simulation experiment, the control system stability, robustness, anti-interference ability, etc.Keywords: PID; RBF neural network; Parameter setting目录摘要 (Ⅰ)Abstract (Ⅱ)1 绪论 (1)1.1 课题研究背景及意义 (1)1.2神经网络的发展历史 (3)2 神经网络 (6)2.1神经网络的基本概念和特点 (6)2.2人工神经网络构成的基本原理 (7)2.3神经网络的结构 (8)2.3.1前馈网络 (8)2.3.2 反馈网络 (8)2.4神经网络的学习方式 (9)2.4.1监督学习(有教师学习) (9)2.4.2非监督学习(无教师学习) (9)2.4.3再励学习(强化学习) (9)2.5 RBF神经网络 (10)2.5.1 RBF神经网络的发展简史 (10)2.5.2 RBF的数学模型 (10)2.5.3被控对象Jacobian信息的辨识算法 (11)2.5.4 RBF神经网络的学习算法 (12)2.6 本章小结 (14)3 PID控制器 (14)3.1 PID控制器简介 (14)3.2 经典PID控制原理 (14)3.3 现有PID控制器参数整定方法 (16)3.4 PID控制的局限 (17)3.5本章小结 (17)4 基于RBF神经网络整定的PID控制器设计 (17)4.1 RBF神经网络的PID整定原理 (17)4.2 神经网络PID控制器的设计 (18)4.3 本章小结 (19)5 仿真分析 (19)5.1 系统的稳定性分析 (19)5.2 系统抗干扰能力分析 (21)5.3 系统鲁棒性分析 (22)5.4 本章小结 (24)结论 (25)参考文献 (26)致谢 (27)附录仿真程序 (28)1 绪论1.1 课题研究背景及意义PID控制器（按比例、积分和微分进行控制的调节器）是最早发展起来的应用经典控制理论的控制策略之一，是工业过程控制中应用最广泛，历史最悠久，生命力最强的控制方式，在目前的工业生产中，90％以上的控制器为PID控制器。
基于神经网络的PID控制算法研究
基于神经网络的PID控制算法研究近年来，随着机器学习和人工智能技术的不断发展，神经网络在控制领域的应用也逐渐得到了广泛关注。
其中，基于神经网络的PID控制算法作为一种新型的控制方法，已经被证明具有极高的控制精度和适应性。
由于传统的PID控制算法存在着超调、稳态误差等问题，因此在实际工程中往往需要进行各种手动调参。
而基于神经网络的PID控制算法则可以通过学习数据来自适应地优化控制参数，从而在不同工况下都能够实现优秀的控制效果。
同时，神经网络还可以实现非线性控制和逆模型控制等高级控制策略，更加符合实际应用的需求。
基于神经网络的PID控制算法的基本思路是，将神经网络与PID控制器结合起来，构建一个新的混合型学习控制器。
具体而言，首先需要建立一个基于神经网络的模型来描述被控对象的动态特性，然后利用该模型对PID控制器进行参数的自适应优化，最终实现目标系统的控制。
一般来讲，神经网络PID控制算法的实现过程包括以下几个步骤：首先，需要选择合适的神经网络模型和控制器结构。
然后，利用样本数据对神经网络进行训练，得到一个有效的模型。
接着，将训练好的神经网络模型与PID控制器进行耦合，形成一个混合型控制器。
最后，通过仿真或者实际测试来验证控制器的性能。
在具体实现神经网络PID控制算法时，需要注意以下几个关键问题：一是神经网络的选择和搭建，不同的应用需要选择不同的网络结构和训练算法；二是神经网络模型的准确性，神经网络需要能够准确地描述被控对象的动态特性；三是控制器的参数优化，需要避免过度学习和过拟合等问题。
目前，神经网络PID控制算法已经成功应用于许多领域，例如机械控制、电力系统控制、化工过程控制等。
实际应用结果显示，基于神经网络的PID控制算法相比传统PID控制算法，在控制精度、抗干扰能力、稳定性等方面都具有显著的优势，是一种极具应用前景的控制策略。
总的来说，基于神经网络的PID控制算法是一种结合了神经网络与PID控制器的混合型学习控制策略，具有优秀的控制精度和适应性。
基于BP神经网络的PID控制器的设计
基于BP神经网络的PID控制器的设计简介：PID控制器是一种常用的控制方法，可以使控制系统快速、稳定地对目标进行调节。
然而，传统的PID控制器需要依赖经验的设置参数，很难适用于非线性复杂的系统。
为了改善这一问题，本文提出了一种基于BP神经网络的PID控制器的设计方法。
一、神经网络介绍BP神经网络是一种常用的人工神经网络，通过反向传播算法进行学习和适应。
它可以用来建模非线性关系、解决分类和回归问题等。
BP神经网络由输入层、隐藏层和输出层构成，通过调整权重和偏置项，使得网络的输出接近于期望输出。
二、PID控制器的基本原理PID控制器是由比例（P）、积分（I）和微分（D）三个部分组成的，它们分别对应了系统的比例性能、整定性能和微分性能。
PID控制器的输出是由目标值与实际值之间的误差来决定的。
比例作用是根据误差的大小进行调节，积分作用是根据误差的积分值进行调节，微分作用是根据误差的变化率进行调节。
三、BP神经网络的PID控制器设计1.建立神经网络模型：确定输入层节点数、隐藏层节点数和输出层节点数。
2.确定权重和偏置项的初始值：可以使用随机数进行初始化。
3.设置训练样本集：训练样本集包括输入和输出的数据，可以根据实际情况进行设置。
4.确定学习率和训练次数：学习率决定了网络的更新速度，训练次数决定了网络的学习程度。
5.神经网络训练：使用BP算法对神经网络进行训练，通过反向传播算法调整权重和偏置项。
6.测试神经网络性能：使用测试数据对神经网络进行测试，评估其性能是否满足要求。
7.参数调整：根据测试结果对PID控制器的参数进行调整，使得神经网络对系统的控制更加精确。
四、实验结果分析通过对比传统的PID控制器和基于BP神经网络的PID控制器，可以发现基于BP神经网络的PID控制器具有更好的系统控制性能。
因为BP神经网络能够自适应地调整参数，适应非线性复杂系统的控制要求。
总结：基于BP神经网络的PID控制器是一种有效的控制方法，可以提高系统控制的精度和稳定性。
基于BP神经网络PID整定原理和算法步骤
基于BP神经网络PID整定原理和算法步骤PID（比例、积分、微分）控制是一种常用的控制算法，用于调节系统的输出使其接近期望值。
BP（Back Propagation）神经网络是一种具有强大机器学习能力的神经网络模型。
基于BP神经网络的PID整定方法结合了PID控制算法和神经网络的优点，通过神经网络的学习能力优化PID 参数的选择，提高了控制系统的鲁棒性和适应性。
以下是基于BP神经网络的PID整定原理和算法步骤：一、原理：1.神经网络模型：建立一个具有输入层、隐藏层和输出层的BP神经网络模型，其中输入层接收系统的输入信号，输出层输出控制信号的PID 参数，隐藏层的神经元通过学习调整连接权重以优化参数选择。
2.参数训练：基于反向传播算法，通过输入输出样本对神经网络进行训练，使其学习输入输出之间的映射关系。
训练过程是一个迭代过程，通过不断调整连接权重和偏置，使神经网络的输出结果逼近期望值。
3.PID原理：PID控制算法根据系统当前误差，通过比例、积分和微分项生成控制信号。
调节PID参数可以改变控制信号的响应特性，使其更好地适应控制对象的动态特性。
二、算法步骤：1.数据采集：收集系统的输入输出数据，用于训练神经网络模型。
2.数据预处理：对采集到的数据进行预处理，包括去除噪声、归一化等处理，以提高神经网络的训练效果。
3.网络构建：根据需要构建BP神经网络模型，包括输入层、隐藏层和输出层。
隐藏层的神经元数量和层数可以根据实际情况进行选择。
4.神经网络训练：将预处理后的数据输入到神经网络中，利用反向传播算法对神经网络进行训练。
根据实际需求设置训练的轮数和学习率等参数。
5.训练结果评估：通过评估神经网络的训练结果，包括误差曲线、训练时间等指标，来判断训练是否达到预期效果。
6.PID参数优化：根据神经网络的输出结果调整PID的比例、积分和微分参数。
可以通过试错法或者自适应控制方法对参数进行调整。
7.控制性能评估：利用调整后的PID参数进行控制，通过评估系统的性能指标，例如超调量、调整时间等，来判断PID参数的选择是否合理。
基于神经网络 PID 的温度控制系统
PID 控制器广泛应用于各种工业控制过程中，对于具有线性特性的确定被控对象，调试整定好PID 控制器的参数后，即可投入生产，控制器具有结构简单、稳定性好、可靠性高等优点。
但是在温度控制过程中，PID 控制效果有时并不理想。
例如，当外部环境发生变化时，或者有外部干扰时，其参数将会发生改变。
而一般的PID 参数是根据以往的控制经验总结出来的，一组PID 控制参数只能对特定条件下的温度控制比较理想。
为了克服常规PID 控制的不足，提高其适应能力，本文提出了基于神经网络的PID 控制器。
传统PID 控制对于复杂控制对象，由于受外部环境不断变化的影响，其控制效果往往不够理想。
为了能够达到控制精度的要求，需要不断的根据受控对象模型参数的变化来调整PID 控制参数。
通过仿真可以看出基于单神经元的PID 控制器的控制效果要优于传统的PID 控制系统，具有较好的抗干扰性和鲁棒性。
其主要缺点是快速性较差。
由于编程算法的灵活性，我们可以通过在编写S-函数过程中，在输入和输出存在较大偏差时，直接给受控对象一个较大的控制信号，当偏差减小至某一点时，再使其进入单神经元PID 控制阶段。
这样可以解决其快速性较差的缺点。
还可以看出多层网的近似PID 控制即使控制对象结构发生较大变化，其控制效果仍能很快趋于稳定。
这也充分说明了基于多层网的神经网络具有非线性映射能力和自适应能力，并且具有逼近任意函数的能力。
其主要缺点是学习速度较慢，这可以通过采用各种改进的BP 算法(如引入动量项、变步长法、线性化快速算法等)来提高其收敛速度，改善其控制性能。
温度控制系统具有大滞后、强耦合、慢时变及非线性等特征的复杂系统。
在温度控制系统中，被控制对象存在着参数的不确定性和纯滞后等特性，难于建立其精确的数学模型，本文通过对受控对象（温度控制箱）温度控制系统的数字仿真和实时仿真研究，比较了传统PID 控制与神经网络PID 控制各自不同的控制特性，分析了传统PID 控制器和神经网络PID 控制器的优缺点。
基于神经网络的自适应PID控制策略研究
基于神经网络的自适应PID控制策略研究近年来，神经网络技术逐渐成为控制领域中的热点研究方向之一。
在控制领域中，PID控制器是最常用的一种控制器，但是，在复杂的非线性系统中，PID控制器可能会失效，因此需要一种更为智能化的自适应控制策略。
本文将着重研究基于神经网络的自适应PID控制策略的原理和应用。
一、神经网络控制简介神经网络控制是一种使用神经网络技术实现控制的控制方法。
神经网络具有自学习和自适应能力，能够适应未知的非线性因素，因此能够有效地提高控制精度。
在神经网络控制中，通常使用BP神经网络进行训练，将网络的输入与输出之间的关系建模，进而得到控制器。
二、PID控制器PID控制器是最常用的一种控制器，它由比例项、积分项和微分项组成。
其中，比例项控制系统的静态误差，积分项控制系统的稳态误差，微分项控制系统的动态响应。
经过调整PID参数，可以实现对系统的稳态和动态性能的优化。
三、传统PID控制器的缺点通过传统PID控制器的参数调整，可以得到较好的控制效果。
但是，在非线性系统控制中，PID控制器的参数调整会变得更加困难，可能会导致系统不稳定或控制精度不高。
这是因为传统PID控制器中的参数是固定的，无法根据系统的变化进行自适应调整。
因此，需要一种更为灵活、智能的自适应控制方式。
四、基于神经网络的自适应PID控制策略与传统PID控制器不同，基于神经网络的自适应PID控制器能够在实时控制过程中不断调整控制器参数，以应对不同的情况。
它能够根据系统的输入和输出实时调整控制器的权值，从而实现对非线性系统的自适应控制。
基于神经网络的自适应PID控制策略的实现方法，一般是将系统的输入和输出作为训练数据，通过训练得到神经网络的权值。
在控制器实时控制过程中，根据系统输出实时调整神经网络的权值，从而实现自适应控制。
五、应用实例基于神经网络的自适应PID控制策略在实际应用中，可以针对不同的场景进行多样化应用。
下面以一个灯光控制系统为例来进行说明。
基于BP神经网络的自适应PID控制器设计
基于BP神经网络的自适应PID控制器设计自适应PID控制器是一种基于BP神经网络的控制器设计方法，它结合了传统的PID控制器与神经网络的优势，可以适应系统参数变化、非线性和模型误差的情况。
本文将详细介绍基于BP神经网络的自适应PID控制器的设计原理和实现步骤。
1.简介PID控制器是一种经典的控制方法，通过计算误差的比例、积分和微分部分，调节输出控制量来实现对系统的控制。
然而，传统的PID控制器无法处理非线性和参数变化的系统，容易产生较大的误差。
而BP神经网络则具有非线性映射和自适应学习的能力，可以对非线性系统进行建模和控制。
2.BP神经网络的建模BP神经网络是一种前馈神经网络，具有输入层、隐含层和输出层。
输入层接收系统的输入量，输出层输出控制量，隐含层则通过一系列的神经元进行信息传递和处理。
BP神经网络通过训练集的样本进行学习，调整网络的权值和偏置，使得网络的输出与期望输出尽可能一致。
3.PID控制器的设计PID控制器由比例、积分和微分三个部分组成。
比例部分通过调节误差的大小来控制输出，积分部分可以控制持续的误差，微分部分则可以控制误差的变化率，提高系统的响应速度。
PID控制器的参数可以根据系统的特性进行调整。
4.自适应PID控制器的设计a.构建BP神经网络模型，通过训练集对模型进行学习，得到网络的权值和偏置。
b.使用PID控制器的比例、积分和微分部分计算出控制量，并将控制量作为输入量输入到BP神经网络中。
c.根据神经网络的输出，计算系统的输出，将其与期望输出进行比较，得到误差。
d.根据误差的大小，调整PID控制器的参数。
e.重复步骤b-d，直到系统达到期望输出。
5.应用实例自适应PID控制器可以应用于各种系统的控制中，如温度控制、位置控制等。
以温度控制为例，系统输入为温度传感器的读数，输出为控制器输出的控制量。
通过采集训练集数据和期望温度值，利用BP神经网络对系统进行建模和学习，然后根据PID控制器的参数计算出控制量，进而控制温度的变化。
基于深度神经网络的自适应PID控制
基于深度神经网络的自适应PID控制自适应 PID 控制是现代控制理论中的一种重要方法，它通过不断地对实际控制系统的反馈信息进行分析，来实现对系统参数的自适应优化，从而达到更优的控制效果。
在传统的控制方法中，PID 控制器是最常见的一种控制器，它通过改变比例、积分、微分三个参数来控制系统的输出行为。
虽然 PID 控制的思想简单而直观，但它往往需要通过人工调整控制器参数才能达到最佳的控制效果，这使得传统的PID 控制方法在复杂的工业控制系统中应用受到了很大的限制。
近年来，随着深度学习技术的快速发展，越来越多的控制问题开始通过深度神经网络来解决。
深度神经网络通过多层的非线性映射来实现复杂的数据处理和表达，具有非常强的模型适应力和自适应能力，并且能够从大量的数据中学习到系统的隐含规律，从而提高控制性能。
基于深度神经网络的自适应 PID 控制是一个典型的应用场景。
它通过将深度神经网络嵌入到PID 控制器中，实现对系统参数的自适应学习，从而优化控制效果。
具体实现上，基于深度神经网络的自适应PID 控制可以分为以下两个步骤：首先，通过采集真实系统的数据，训练一个深度神经网络，用来对系统的动态特性进行建模和预测。
其次，在 PID 控制器中将这个深度神经网络作为预估器，根据预测误差来自适应调整 PID 控制器的参数，从而达到更优的控制效果。
在实际应用中，基于深度神经网络的自适应 PID 控制已经得到了广泛的应用。
例如在工业自动化领域，它可以通过对温度、压力等参数的自适应调整来实现对化工过程的控制；在机器人控制中，它可以实现对机械臂的精确控制和路径规划；在无人驾驶汽车中，它可以通过对车速、转向等参数的自适应调整来实现对车辆的自动驾驶。
总之，基于深度神经网络的自适应 PID 控制是现代控制理论中的一种重要方法，它能够实现对复杂工业系统的自适应优化。
随着深度学习技术的发展，我们相信基于深度神经网络的自适应 PID 控制将会在更多的领域得到应用，并取得更加突出的成果。
基于BP算法的神经网络PID控制器设计及仿真
se s s G 5.01101)(−+=()(1)[(1)]()[()2(1)(2)]/p I D Iu k u k K e k K e k K e k e k e k T T =−+−++−−+−神经网络PID 控制器的设计及仿真一、传统PID 控制数字PID 控制算法分位置式和增量式两种，工程上常用的增量式PID 控制算法，其控制算式为：式中，pK 为比例系数，I K =p K /T T为积分系数，/D D K T T =为微分系数，T 为采样周期，IT 为积分时间，DT 为微分时间，()e k 为t kT =时刻的误差。
上述PID 控制算法易于用微机软件实现，PID 控制系统框图如图示。
现有一被控对象为：根据“稳定边界法”即临界比例度法，来整定调节器的参数，带入“稳定边界法整定参数计算表”得到，当采取P 调节时，KP=16，；当采取PI 调节时，KP=14.545，i T =1.7；当采取PID 调节时，KP=18.824，i T =1，d T =0.25。
通过Simulink 进行如下图所示的仿真：仿真结果如下图所示：二、基于BP算法的PID控制基于BP神经网络的PID控制系统结构如下图所示，控制器由两个部分组成：①经典的PID控制器：直接对被控对象进行闭环控制，并且KP,KI,KD三个参数为在线P,I,D整定；②神经网络NN：根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化。
即使神经网络的输出层神经元的输出状态对应于PID控制器的三个可调参数KP,KI,KD，通过神经网络的自学习、调整权系数，从而使其稳定P,I,D状态对应于某种最优控制规律下的PID控制器参数。
在这里设计的BP网络采用结构简单的三层BP神经网络，其结构如下图所示，有m个输入节点、Q个隐含层节点、3个输出节点。
输入节点对应所选的系统运行状态量，如系统不同时刻的输入量和输出量等，必要时要进行归一化K K K。
基于BP神经网络的PID控制系统设计汇总
基于BP神经网络的PID控制系统设计摘要本文主要研究一个基于神经网络的自适应PID控制系统的设计方法，利用BP神经网络对被控对象进行在线辨识和控制。
基于BP神经网络学习算法设计出两个神经网络模型：一个利用神经网络（NNM）对非线性映射的逼近能力，对被控对象进行辨识，另一个构成具有PID结构的控制器（NNC）。
通过神经网络NNM的在线学习和修正，产生对被控对象输出的预测作用，然后由网络NNC实施控制作用，从而实现对辨识对象的PID控制。
在利用神经网络对系统进行辨识时，选用白噪声信号作为系统的输入信号，以提高系统的辨识精度；另外，为了得到神经网络控制器的初始化权值，本文在自整定过程中采用常规PID控制器整定方法之一的稳定边界法。
在设计过程中运用MATLAB语言工具箱进行编程，并通过SIMULINK动态仿真工具对一阶非线性对象进行了仿真。
仿真结果表明了利用神经网络对系统进行辨识的有效性，并用经辨识所得到的输出值取代系统的实际输出值，利用神经网络NNC对系统进行控制，获得了满意的控制效果。
关键词：神经网络，BP学习算法，自适应，参数优化，辨识1 综述PID调节器从问世至今已历经了半个多世纪，在这几十年中，人们为它的发展和推广做出了巨大的努力，使之成为工业过程控制中主要的和可靠的技术工具。
近几十年来，现代控制理论迅速发展，出现了许多先进的控制算法，但到目前为止，即使在微处理技术迅速发展的今天，过程控制中大部分控制规律都未能离开PID，这充分说明PID控制仍具有很强的生命力。
过程工业控制中实际应用最多的仍是常规的PID控制算法，这是因为PID控制具有结构简单、容易实现、控制效果好和鲁棒性强等特点，且PID算法原理简明，参数物理意义明确，理论分析体系完整，为广大控制工程师所熟悉。
但在生产现场往往由于参数整定不好而使PID控制器控制效果欠佳，整定的好坏不但会影响到控制质量，而且还会影响到控制器的性能。
PID控制中一个至关重要的问题，就是控制器三参数(比例系数、积分时间、微分时间)的整定。
基于BP神经网络PID整定原理和算法步骤_精品
基于BP神经网络PID整定原理和算法步骤_精品1.基本原理PID控制器是一种经典的闭环控制算法，由比例项、积分项和微分项组成。
BP神经网络是一种具有自适应性的模型，可以根据输入和输出之间的关系来自动调整权重和偏置。
2.算法步骤2.1样本数据的采集在PID控制系统中，需要采集一些样本数据来训练神经网络。
可以通过试验或仿真的方式，对控制系统进行加扰动或变动目标值的操作，得到系统的输入与输出数据。
2.2数据的预处理对采集到的数据进行预处理，主要包括去除噪声、标准化等操作，使得数据更加准确和可靠。
2.3神经网络的构建根据PID控制器的结构，构建对应的BP神经网络模型。
一般来说，BP神经网络由输入层、隐含层和输出层组成。
输入层接收系统的输入数据，隐含层进行特征提取和非线性变换，输出层得到控制系统的输出。
2.4神经网络的训练将预处理后的样本数据输入到神经网络中进行训练。
训练过程中，通过调整网络的权重和偏置，使得网络的输出与期望的输出之间的误差最小化。
2.5PID参数的优化在神经网络训练完成后，可以得到最优的网络结构和权重。
根据神经网络的输出，可以得到相应的PID参数。
一般来说，比例项的参数可直接取输出层的权重，积分项和微分项的参数则可以根据网络的偏置来计算。
2.6控制系统的实时调整将优化得到的PID参数应用到实际的控制系统中。
在控制过程中，根据系统的实时反馈信号，可以通过PID控制器进行实时的调整，使得系统的响应特性达到最佳。
总结：基于BP神经网络的PID整定，通过训练神经网络来寻找最佳的PID 参数，以达到控制系统的最优响应特性。
该方法可以应用于各种复杂的控制系统中，具有很好的适应性和鲁棒性。
但需要注意的是，BP神经网络的训练过程需要较长的时间和大量的样本数据，因此在实际应用中需要进行一定的优化和加速。
基于BP神经网络的PID控制器设计
基于BP神经网络的PID控制器设计1.引言在工业控制系统中，PID（比例、积分、微分）控制器被广泛应用于各种自动控制任务。
然而，传统的PID控制器在处理非线性、时变以及多输入多输出（MIMO）系统时存在一些固有的局限性。
为了克服这些问题，本文提出了基于BP神经网络的PID控制器设计方法。
2.BP神经网络BP神经网络是一种前向反馈的人工神经网络，具有强大的非线性建模能力和自适应性能。
它由输入层、隐藏层和输出层组成，每个神经元与前一层的所有神经元和后一层的所有神经元连接。
BP神经网络通过反向传播算法来训练权重和偏置，实现输入与输出之间的映射关系。
3.PID控制器PID控制器由比例项、积分项和微分项组成，具有良好的稳定性和抗干扰能力。
比例项根据控制误差与参考值的比例进行调整，积分项根据控制误差与时间的积分进行调整，微分项根据控制误差的变化率进行调整。
4.BP神经网络与PID控制器结合将BP神经网络与PID控制器相结合，可以克服传统PID控制器在处理非线性、时变和MIMO系统时的局限性。
具体而言，可以使用BP神经网络来精确建模控制对象的非线性行为，并将其应用于PID控制器中，实现自适应调节。
在实际应用中，可以按照以下步骤进行基于BP神经网络的PID控制器设计：（1）收集系统输入输出数据，并进行预处理，例如归一化处理。
（2）使用BP神经网络对控制对象进行建模。
选择适当的网络结构、激活函数和误差函数，并使用反向传播算法进行网络训练。
（3）设计PID控制器，确定比例项、积分项和微分项的权重。
（4）将BP神经网络的输出作为PID控制器的输入，进行控制操作。
根据控制误差和调节参数，调整PID控制器的输出。
（5）反复迭代并调整BP神经网络和PID控制器的参数，使系统能够快速、准确地响应控制需求。
5.实验验证为了验证基于BP神经网络的PID控制器的有效性，可以选择一个具有非线性、时变特性的控制对象进行实验。
在实验中，可以使用MATLAB或其他神经网络工具箱来实现BP神经网络，并结合传统PID控制器进行控制。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基于神经网络的PID控制课程名称：智能控制任课教师：学生姓名：学号：年月日摘要：本文基于BP神经网络的PID控制方法设计控制器，通过BP神经网络与PID的控制相结合的神经网络控制基本原理和设计来自适应的功能调节PID的的三个参数，并根据被控对象的近似数学模型来输出输入与输出并分析BP神经网络学习速率η，隐层节点数的选择原则及PID参数对控制效果的影响。
计算机的仿真结果表示，基于BP神经网络的PID控制较常规的PID控制具有更好的自适应性，能取得良好的的控制结果。
关键字：BP算法神经网络 PID控制Abstract：In this paper, based on BP neural network PID control method designed controller, through the BP neural network PID control with a combination of neural network control basic principles and design features adaptively adjusting the PID of the three parameters, and based on the controlled object approximate mathematical model to analyze the output and the input and output BP n eural network learning rate η, hidden layer nodes and PID parameter selection principle effect of the control . Computer simulation results indicated that based on BP neural network PID control compared with conventional PID control has better adaptability , can achieve good control results . Keyword:BP algorithms neural networks PID control1引言PID控制是最早发展起来的应用经典控制理论的控制策略之一，由于算法简单，鲁棒性好和可靠性高，被广泛应用于工业过程并取得了良好的控制效果。
随着工业的发展，对象的复杂程度不断加深，尤其对于大滞后、时变的、非线性的复杂系统，常规PID控制显得无能为力。
因此常规PID控制的应用受到很大的限制和挑战。
神经网络在控制系统中的应用提高了整个系统的信息系统处理能力和适应能力，提高了系统的智能水平。
此外，神经网络具有逼近任意连续有界非线性函数的能力，对于非线性系统和不确定性系统，无疑是一种解决问题的有效途径。
本文将常规PID控制与神经网络控制相结合，发挥各自的优势，形成所谓的智能PID控制。
采用BP神经网络方法设计的控制系统具有更快的速度（实时性）、更强的适应性和更好的鲁棒性。
2 基于BP神经网络的PID控制PID控制要取得较好的控制结果，必须通过调整好比例、积分和微分三种控制作用，形成控制量中既要相互配合又相互制约的关系。
神经网络所具有的任意非线性表达能力，可以通过对系统性能的学习来实现最佳组合的PID控制。
采用BP网络，可以建立参数Kp、Ki、Kd自学习的PID控制器。
基于BP神经网络的PID控制系统结构由常规的PID控制器和神经网络两个部分构成。
2.1常规的PID控制器PID控制器由比例（P）、积分（I）、微分（D）3个部分组成，直接对被控对象进行闭环控制，并且三个参数 Kp、Ki、Kd为在线调整方式。
2.2 神经网络根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化，使输出层神经元的输出状态对应于PID 控制器的三个可调参数Kp 、Ki 、Kd 通过神经网络的自学习、加权系数调整，使神经网络输出对应于某种最优控制规律下的PID 控制器的参数。
2.3 基于BP 算法的三层前向网络的PID 控制方案本文用来控制对象的神经网络模型采用3层BP 网络，其结构如图2.3所示图2.3.1 控制对象的神经网络模型经典增量式数字PID 的控制算法为()()()()()()()()()p i d u k u k 1k error k error k 1k error k k (error k 2error k 1error k 2)=-+--++--+-式中，k p ,k i ,k d 分别为比例、积分、微分系数。
网络输入层的输入为O j (1)=x(j) j=1,2,...M （1）式中，输入变量的个数M 取决于被控系统的复杂程度。
网络隐含层的输入、输出为net i (2)(k)= 0M j =∑w ij (2) O j (1), （2）O i (2)(k)=f(net i (2)(k)) (i=1,...Q)， （3）式中，w ij (2)-隐含层加权系数；上角标（1）、（2）、（3）分别代表输入层、隐含层和输出层。
隐层神经元的活化函数取正负对称的Sigmoid 函数 f(x)=tanh(x)= x xx x e e e e---+ （4） net i (3)(k)= 0Q i =∑w ij (3) O i (2)(k), （5）O l (3)(k)=g(net l 3(k)) (l=1,2,3) （6）O 1(3)(k)=k p （7）O 2(3)(k)=k i （8）O 3(3)(k)=k d （9）输出层输出节点分别对应三个可调参数kp ，ki ，kd 。
由于kp ，ki ，kd 不能为负值，所以输出层神经元的激励函数取非负的Sigmoid 函数： g(x)= 12(1+tanh(x))= x x x e e e -+。
（10） 取性能指标函数为 E(k)=12(rin(k)-yout(k))2 （11） 按照最速下降法修正网络的加权系数，即按E(k)对加权系数的负梯度方向搜索调整，并附加一使搜索快速收敛全局绩效的惯性项 Δw li (3)(k)=-η(3)()liE k w ∂∂+αΔw li (3)(k-1) （12） 式中，η为学习速率；α为惯性系数。
(3)()li E k w ∂∂=(3)(3)(3)(3)(3)()()()()()()()()()()l l l l liO k net k E k y k u k y k u k O k net k w k ∂∂∂∂∂••••∂∂∂∂∂ （13） (3)(3)()()l li net k w k ∂∂=(2)()i O k （14） 由于()()y k u k ∂∂未知，所以近似用符号函数sgn （()()y k u k ∂∂）取代，由此带来计算不精确的影响可以通过调整学习速率η来补偿由上面公式，可求得(3)1()()u k O k ∂∂=e(k)-e(k-1) （15） (3)2()()u k O k ∂∂=e(k) （16） (3)3()()u k O k ∂∂=e(k)-2e(k-1)+e(k-2) （17） 上述分析可得网络输出层权的学习算法为Δw li (3)(k)=αΔw li (3)(k-1)+ηδl (3)O i (2)(k) （18）δl (3)=error(k)sgn(()()y k u k ∂∂)(3)()()l u k O k ∂∂g ’(net l (3)(k)) (l=1,2,3) （19） 同理可得隐含层加权系数的学习算法Δw ij (2)(k)=αΔw ij (2)(k-1)+ηδi (2)O j (1)(k) （20）δl (2)=f ’(net i (2)(k)) 31l =∑δl (3) w li (3)(k) (i=1,2,...Q) （21）g ’(·)=g(x)(1-g(x)),f ’(·)=(1-f 2(x))/2 （22）因此，基于BP 神经网络的PID 控制算法可归纳为：图2.3.2 基于BP 网络的PID 控制器结构（1） 确定BP 网络的结构，给出各层加权系数的初值，选定学习速率η和惯性系数α，此时K=1；采样得到人r(k)和y(k)，计算该时刻误差e(k)=r(k)-y(k);（2） 计算神经网络各层神经元的输入、输出，输出为PID 控制器的三个可调参数Kp 、Ki 、Kd ；根据增量式数字PID 控制算法计算PID 控制器的输出u(k)；进行神经网络学习，在线调整加权系数w ij (1)和w li (2)(k)，实现PID 控制参数的自适应调整；（3） 置k=k+1，返回到（1）；3 仿真分析 设被控对象的近似数学模型为：02()(1)(1)()1(1)a k y k u k y k y k -+-=+-，式中 a 0(k)是慢时变的，a 0(k)=1+0.15sin(k π/25)。
学习速率η=0.3和惯性系数α=0.5。
1、输入信号为正弦信号r(k)=sin(2πk/100)时得出仿真图如图3.1.1所示：图3.1.1 输出信号y(k)跟踪输入信号r(k)的响应曲线图3.1.2 控制信号u(k)的变化曲线3.1.3 PID三个参数的变化曲线3.1.4 误差曲线图2、输入信号为方波信号r(k)=sign(sin(2*pi*k/100))时得到仿真曲线如图3.2.1所示：图3.2.1 输出信号跟踪输入信号的响应曲线图图3.2.2 跟踪误差动态曲线图3.2.3 控制信号u(k)的变化曲线图3.2.4 三个参数的变化曲线分析BP神经网络学习速率η、隐层节点数的选择原则及对控制效果的影响从仿真中来观察发现改变学习速率会对控制效果发生改变，PID的三个参数也会随之发生改变，在一般情况下，倾向于选取较小的学习速率以保证系统的稳定性。
学习速率的选取范围在0.01~0.8之间。
从原理上看，隐含层节点数多，则可以有更多的输入点可供输入，即只要有足够多的隐含层和稳节点，就可实现更复杂的映射关系，但是通过改动模型的实现程序来看，怎样根据特定的问题来具体确定网络的结构尚无很好的方法，依旧需要凭经验和试凑。
所以隐含层的节点数可以影响控制效果，但是如何变的更好的控制效果，任然多和准来判定。
PID参数对控制效果的影响神经网络，根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化，使输出层神经元的输出对应于PID控制器的三个可调参数。
对于控制系统的稳定性而言，在系统稳定的前提下，加大比例参数Kp可以减少稳态误差，但不能消除稳态误差，主要还是影响系统的控制速率；而积分参数Ki 有助于提高系统的控制精度，所以对系统控制的稳态性能更大点；微分控制环节的加入微分参数Kd，可以在误差出现或变化瞬间，按偏差变化的趋势进行控制，起到一个早期的修正作用。