托勒密定理
托勒密定理推导过程_概述及解释说明

托勒密定理推导过程概述及解释说明1. 引言1.1 概述在几何学中,托勒密定理是一个重要的数学原理,它描述了一个四边形各边长度和对角线之间的关系。
该定理由古希腊数学家托勒密在《大地与天》一书中首次提出,并给出了其推导过程。
托勒密定理被广泛应用于数学、工程和物理等领域,对于解决相关问题具有重要意义。
1.2 文章结构本文将对托勒密定理的推导过程进行概述与解释说明。
文章分为五个部分:引言、托勒密定理推导过程、实例分析、托勒密定理的重要性与应用领域以及结论与总结。
在引言部分中,将介绍托勒密定理以及本文主要内容。
1.3 目的本文旨在通过梳理和解释托勒密定理的推导过程,增进读者对该数学原理的认识与理解。
同时,通过对实例问题的分析和相应领域的应用探讨,展示托勒密定理在现实世界中的实际价值。
最后,通过总结和展望未来研究方向,促进对于托勒密定理及其应用的深入研究和探索。
2. 托勒密定理推导过程:2.1 托勒密定理介绍托勒密定理,也被称为正交四边形定理,是平面几何中的一个重要定理。
它描述了一个在一个凸四边形内切于其边的圆上的一组关系。
托勒密定理可以用来计算非直角四边形的各种性质,比如角度、对角线长度以及相对边长等。
2.2 推导步骤解释推导托勒密定理时,我们假设有一个任意形状的凸四边形ABCD,并在该四边形内切一个圆O。
我们要证明以下关系成立:AB ×CD + BC ×AD = AC ×BD首先,在凸四边形ABCD中,通过连结AC和BD,得到两条对角线。
接下来,我们观察圆O与这两条对角线之间的关系。
假设∠AOC = α和∠BOC = β,根据圆心角和弧度之间的关系可知∠ADC = 180°- α和∠BDC = 180°- β。
同样地,我们有∠ADB = α和∠BCD = β。
根据三角函数中余弦定理可得:cos(∠ADC) = cos(180°- α) = -cosαcos(∠BDC) = cos(180°- β) = -cosβcos(∠ADB) = cosαcos(∠BCD) = cosβ由于在同一个圆上,AC和BD可以视为弦,角度对应的余弦值相同。
平面几何3--托勒密定理

厦门一中2010数学竞赛讲座—平面几何
平面几何定理3——托勒密定理
托勒密定理:圆内接四边形的两组对边乘积之和等于两对角线的乘积。
推论1 (三弦定理)若A 是圆上任意一点,AB ,AC ,AD 是圆上顺次的三条弦,则: sin sin sin .AC BAD AB CAD AD CAB ⋅∠=⋅∠+⋅∠
推论2 (四角定理)四边形ABCD 内接于圆O ,则
sin sin sin sin sin sin .ADC BAD ABD BDC ADB DBC ∠⋅∠=∠⋅∠+∠⋅∠,
四边形中的托勒密定理(托勒密不等式):设ABCD 为任意凸四边形,则 AB CD BC AD AC BD ⋅+⋅≥⋅,当且仅当A 、B 、C 、D 四点共圆时取等.
练习: 如图,△ABC 与△A 'B 'C '的三边分别为a 、b 、 c 与a '、b '、c ',且∠B =∠B ',∠A +∠A '=180°. 试证:aa '=bb '+cc '. (1)
(2)
图8A
C
A'B'
c b c'b'
练习 例2.(面积问题)如图
练习
例3(边长问题)如图
例4.(解代数问题)
练习
例5..(定理证明)
练习
练习
1
2.
3.
4.
5.。
托勒密定理五边形证明-概述说明以及解释

托勒密定理五边形证明-概述说明以及解释1.引言1.1 概述托勒密定理是几何学中一个非常重要的定理,它描述了一个特殊的五边形的性质。
这个定理的命名来自于古希腊数学家托勒密,他在其著作《大地与天球的数学基础》中首次提出了这个定理。
托勒密定理主要研究的是一个凸五边形,也就是一个有五个顶点的多边形,且其中的四个顶点都位于一个圆上。
这个定理给出了这个五边形的一条非常重要的性质,即其两对对角线的乘积之和等于两条对边的乘积之和。
具体而言,如果我们设这个五边形的顶点依次为A、B、C、D、E,那么托勒密定理可以表示为AC ×BD + AD ×BC = AB ×CD。
托勒密定理的证明过程非常有趣且具有一定的难度。
它通常使用几何、代数和三角等方法相结合,通过引入辅助线、利用相似三角形关系以及运用勾股定理等工具,从而逐步推导出定理的正确性。
托勒密定理的应用非常广泛。
一方面,在几何学中,托勒密定理是解决五边形相关问题的基础,通过利用这个定理,我们可以推导出许多与五边形有关的性质和公式。
另一方面,托勒密定理在实际应用中也具有一定的价值,如在工程测量中可以用于计算不易直接测量的距离或角度等。
对于托勒密定理的进一步研究也是一个有意义的课题。
目前,已经有许多学者在托勒密定理的基础上进行了延伸和拓展,提出了一些新的数学定理和性质。
同时,随着计算机技术的发展,我们可以利用计算机辅助证明的方法来进一步探索托勒密定理及其相关的数学问题。
综上所述,托勒密定理是几何学中一项重要的成果,它描述了一个特殊五边形的性质。
在本文中,我们将会介绍托勒密定理的定义、性质以及它的证明过程,并探讨其在几何学和实际应用中的意义。
同时,我们还将展望托勒密定理的进一步研究方向,以期能够为数学领域的发展做出更多的贡献。
1.2文章结构文章结构部分的内容可以包括以下内容:文章结构:本文分为引言、正文和结论三个部分。
引言部分主要概述了本文的内容和目的。
赣县中学高中数学竞赛平面几何第9九讲托定理勒密
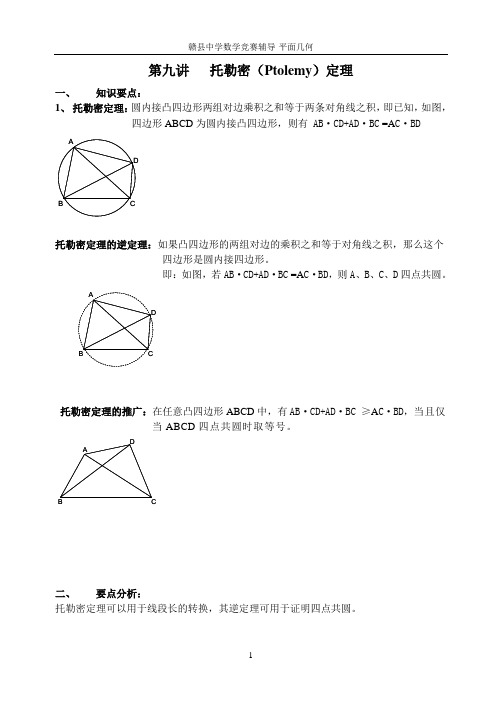
第九讲托勒密(Ptolemy)定理一、知识要点:1、托勒密定理:圆内接凸四边形两组对边乘积之和等于两条对角线之积,即已知,如图,四边形ABCD为圆内接凸四边形,则有 AB·CD+AD·BC =A C·BD ADB C托勒密定理的逆定理:如果凸四边形的两组对边的乘积之和等于对角线之积,那么这个四边形是圆内接四边形。
即:如图,若AB·CD+AD·BC =A C·BD,则A、B、C、D四点共圆。
ADB C托勒密定理的推广:在任意凸四边形ABCD中,有AB·CD+AD·BC ≥A C·BD,当且仅当ABCD四点共圆时取等号。
DAB C二、要点分析:托勒密定理可以用于线段长的转换,其逆定理可用于证明四点共圆。
三、 例题讲解:例1、设ABCD 为圆内接正方形,P 为弧DC 上的一点,求证:PA(PA+PC)=PB(PB+PD) PD CA B例2、如图,设P 、Q 为平行四边形ABCD 的边AB 、AD 上的两点,APQ ∆的外接圆交对角线AC 于R ,求证:A P ·AB+AQ ·AD=AR ·RCDA B CQP R例3、已知ABC ∆中,C B ∠=∠2,求证:AC 2=AB 2+AB ·BCAB C例4、如图所示,已知两同心圆O,四边形ABCD 内接于内圆,AB 、BC 、CD 、DA 的延长线交外圆于A 1、B 1、C 1、D 1,若外圆的半径是内圆的半径的2倍,求证:四边形A 1B 1C 1D 1的周长≥四边形ABCD 的周长的2倍,并确定等号成立的条件。
D 1例5、已知ABC ∆中,AB>AC,A ∠的一个外角平分线交ABC ∆的外接圆于点E,过E 作EF ⊥AB,垂足为F (如图),求证:2AF=AB-ACABC EF第九讲 托勒密(Ptolemy )定理练习1、 如图,已知圆内接正五边形ABCDE,若P 为弧AB 上一点,求证:PA+PD+PB=PE+PC AB C D EP2、 ABCD 为圆内接四边形,DC=BC ,对角线DB 与AC 交于E,若CE :EA=1:3,AB+AD=m,求BD 的长。
平面几何的几个重要定理——托勒密定理

托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).即:ABCD AB CD AD BC AC BD ⋅+⋅≥⋅定理:在四边形中,有:ABCD 并且当且仅当四边形内接于圆时,等式成立;()A B C D E B A E C A D A B E A C DA B B E A B E A C D A B C D A C B E A C C D A B A E B A C E A D A B C A E D A C A D B CE DA DBC A C E DA C A D ABCD A D B C A C BE E D A B C D A D B C A C B D E B D A B C D ∠=∠∠=∠∆∆∴=⇒⋅=⋅=∠=∠∴∆∆∴=⇒⋅=⋅∴⋅+⋅=⋅+∴⋅+⋅≥⋅证:在四边形内取点,使,则:和相似又且和相似且等号当且仅当在上时成立,即当且仅当、、、四点共圆时成立;一、直接应用托勒密定理例1 如图2,P 是正△ABC 外接圆的劣弧上任一点(不与B 、C 重合), 求证:PA=PB +PC .分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA ·BC=PB ·AC +PC ·AB ,∵AB=BC=AC . ∴PA=PB+PC .二、完善图形 借助托勒密定理例2 证明“勾股定理”:在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2 证明:如图,作以Rt △ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形.由托勒密定理,有 AC ·BD=AB ·CD +AD ·BC . ①又∵ABCD 是矩形,∴AB=CD ,AD=BC ,AC=BD . ②把②代人①,得AC 2=AB 2+BC 2.例3 如图,在△ABC 中,∠A 的平分 线交外接∠圆于D ,连结BD ,求证:AD ·BC=BD(AB +AC).证明:连结CD ,依托勒密定理,有AD ·BC =AB ·CD +AC ·BD .∵∠1=∠2,∴ BD=CD .故 AD ·BC=AB ·BD +AC ·BD=BD(AB +AC).三、构造图形 借助托勒密定理例4 若a 、b 、x 、y 是实数,且a 2+b 2=1,x 2+y 2=1.求证:ax +by ≤1.证明:如图作直径AB=1的圆,在AB 两边任作Rt △ACB 和Rt △ADB ,使AC =a ,BC=b ,BD =x ,AD =y .由勾股定理知a 、b 、x 、y 是满足题设条件的.据托勒密定理,有AC ·BD +BC ·AD=AB ·CD .∵CD ≤AB =1,∴ax +by ≤1.四、巧变原式 妙构图形,借助托勒密定理例5 已知a、b 、c 是△ABC 的三边,且a 2=b(b +c),求证:∠A=2∠B .分析:将a 2=b(b +c)变形为a ·a=b ·b +bc ,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b ,两对角线为a ,一底边为c .证明:如图 ,作△ABC 的外接圆,以 A 为圆心,BC 为半径作弧交圆于D ,连结BD 、DC 、DA .∵AD=BC , AC D BDC =∴∠ABD=∠BAC. 又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.依托勒密定理,有BC ·AD=AB ·CD +BD ·AC . ①而已知a 2=b(b+c),即a ·a=b ·c +b 2. ②∴∠BAC=2∠ABC .五、巧变形 妙引线 借肋托勒密定理例6 在△ABC 中,已知∠A ∶∠B ∶∠C=1∶2∶4,分析:将结论变形为AC ·BC +AB ·BC=AB ·AC ,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图,作△ABC 的外接圆,作弦BD=BC ,边结AD 、CD .在圆内接四边形ADBC 中,由托勒密定理,有AC ·BD +BC ·AD=AB ·CD易证AB=AD ,CD=AC ,∴AC ·BC +BC ·AB=AB ·AC ,1.已知△ABC 中,∠B=2∠C 。
平面几何3--托勒密定理及应用

平面几何(3)----托勒密定理及应用托勒密定理:圆内接四边形的两组对边乘积之和等于两对角线的乘积推论1(三弦定理) 如果A 是圆上任意一点,AB ,AC ,AD 是该圆上顺次的三条弦,则sin sin sin AC BAD AB CAD AD CAB ⋅∠=⋅∠+⋅∠推论2(四角定理) 四边形ABCD 内接于O ,则sin sin sin sin sin sin ADC BAD ABD BDC ADB DBC ∠⋅∠=∠⋅∠+∠⋅∠直线上的托勒密定理(或欧拉定理) 若A ,B ,C ,D 为一直线上依次排序的四点,则AB CD BC AD AC BD ⋅+⋅=⋅四边形中的托勒密定理:设ABCD 为任意凸四边形,则,AB CD BC AD AC BD ⋅+⋅≥⋅当且仅当A ,B ,C ,D 四点共圆时取等号托勒密定理的逆定理: 在凸四边形ABCD 中,若AB CD BC AD AC BD ⋅+⋅=⋅,则A ,B ,C ,D 四点共圆例1:在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若角A ,B ,C 的大小成等比数列,且22b a ac -=,则角B 的弧度数等于多少?例2:凸四边形ABCD 中,60,90o o ABC BAD BCD ∠=∠=∠=,AB=2,CD=1,对角线AC ,BD 交于点O ,如图,求sin AOB ∠例3:如图,在锐角ABC 的BC 边上有两点E ,F ,满足,BAE CAF ∠=∠作FM AB ⊥于M ,FN AC ⊥于N ,延长AE 交ABC 的外接圆于点D ,证明:四边形AMDN 与ABC 的面积相等.例4:如图,在ABC 中,60o A ∠=,,AB AC >点O 是外心,两条高BE ,CF 交于H 点,点M ,N 分别在线段BH ,HF 上,且满足BM=CN ,求MH NH OH+的值例5:若有四个圆都与第五个圆内切,第一个与第二个圆的外公切线长用12l 表示,其他前四个圆中的两两的外公切线也用同样的方法来标记,且前四个圆以顺时针的顺序排列,试证明依次以12233441,,,l l l l 为边长,以1324,l l 为对角线所构成的凸四边的四个顶点共圆.例6:经过XOY ∠的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P,Q ,求证:11OP OQ+为定值例7:圆内接六边形ABCDEF 的对角线共点的充要条件是1AB CD EF BC DE FA ⋅⋅=。
初中托勒密定理

初中托勒密定理初中托勒密定理托勒密定理是初中数学中的一个重要定理,它是由古希腊数学家托勒密发现的,因此得名。
该定理是关于四边形的一个定理,它表明,如果一个四边形的两条对角线相交于一点,那么这个四边形的两组对边乘积之和相等。
具体来说,设四边形ABCD的对角线AC和BD相交于点O,那么有以下公式:AB × CD + BC × AD = AC × BD其中,AB、BC、CD、AD分别表示四边形ABCD的四条边的长度,AC和BD分别表示四边形ABCD的两条对角线的长度。
托勒密定理的证明可以通过几何方法和代数方法来完成。
其中,几何方法是通过构造一些辅助线来证明该定理的,而代数方法则是通过将四边形的顶点坐标表示成复数来证明该定理的。
托勒密定理在初中数学中的应用非常广泛,它可以用来解决各种几何问题,例如求解四边形的面积、判断四边形是否为正方形等。
此外,托勒密定理还可以用来证明勾股定理和正弦定理等其他重要定理。
总之,托勒密定理是初中数学中的一个重要定理,它不仅具有理论意义,而且在实际应用中也有着广泛的应用。
因此,学生们应该认真学习和掌握该定理,以便在以后的学习和工作中能够灵活运用。
排版格式:初中托勒密定理托勒密定理是初中数学中的一个重要定理,它是由古希腊数学家托勒密发现的,因此得名。
该定理是关于四边形的一个定理,它表明,如果一个四边形的两条对角线相交于一点,那么这个四边形的两组对边乘积之和相等。
具体来说,设四边形ABCD的对角线AC和BD相交于点O,那么有以下公式:AB × CD + BC × AD = AC × BD其中,AB、BC、CD、AD分别表示四边形ABCD的四条边的长度,AC和BD分别表示四边形ABCD的两条对角线的长度。
托勒密定理的证明可以通过几何方法和代数方法来完成。
其中,几何方法是通过构造一些辅助线来证明该定理的,而代数方法则是通过将四边形的顶点坐标表示成复数来证明该定理的。
托勒密定理不等式

托勒密定理不等式托勒密定理不等式托勒密定理是欧几里得几何中的一个重要定理,也是三角学、解析几何和复数学中的基本定理之一。
它通常用于计算四边形的对角线长度,以及确定圆周上两个点之间的距离。
在本文中,我们将探讨托勒密定理的不等式形式。
一、托勒密定理先来回顾一下托勒密定理的内容。
托勒密定理指出,如果一个四边形ABCD中,对边AB和CD相交于点E,则有:AE × BD + CE × AD = AC × BD或者:AD × BC + AB × CD = AC × BD其中AC表示对角线AC的长度,BD表示对角线BD的长度。
这个定理可以通过欧氏几何证明,也可以用解析几何或复数学证明。
它在计算四边形对角线长度时非常有用。
二、托勒密不等式除了上述恒等式外,还有一个与之相关的不等式形式。
这个不等式被称为“托勒密不等式”,它表达了四边形内部任意两条线段乘积之和大于或等于对角线乘积。
具体地说,设ABCD是一个四边形,对角线AC和BD相交于点E。
则有:AE × CE + BE × DE ≥ AC × BD或者:AD × BC + AB × CD ≥ AC × BD这个不等式的证明可以用多种方法,其中一种比较简单的方法是利用向量的内积和余弦定理。
三、托勒密不等式的应用托勒密不等式在几何学和数学中有着广泛的应用。
下面我们来看几个例子。
1. 四边形内部任意两点之间的距离假设我们要求四边形ABCD内部任意两点P和Q之间的距离,如图所示:根据托勒密定理,我们可以得到:AC² = AD² + CD²BD² = AB² + AD²BC² = AB² + CD²将上述三个式子带入托勒密不等式中,得到:AP · CP + BQ · DQ≥ AC · BD这个不等式表明,如果P和Q分别在四边形ABCD的两条对角线上,则它们之间的距离最短。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
托勒密定理Last revision on 21 December 2020
托
勒密定理
【定理内容】
圆内接四边形中,两条对角线的乘积等于两组对边乘积之和. 即:若四边形ABCD 内接于圆,
则有BD AC BC AD CD AB ⋅=⋅+⋅. [评]等价叙述:四边形的两组对边之积的和
等于两对角线
之积的充要条件是四顶点共圆。
【证法欣赏】
证明:如图,过C 作CP 交BD 于P ,使21∠=∠,
∵43∠=∠,∴ACD ∆∽BCP ∆, ∴
BP
AD
BC AC =
,即AD BC BP AC ⋅=⋅ ① 又DCP ACB ∠=∠,65∠=∠,∴ACB ∆∽DCP ∆,
∴
DP
AB
DC AC =
,即DC AB DP AC ⋅=⋅ ② ∴①+②得:DC AB AD BC DP BP AC ⋅+⋅=+⋅)( 即BD AC BC AD CD AB ⋅=⋅+⋅ 【定理推广】 托勒密定理的推广:
在四边形ABCD 中,有BD AC BC AD CD AB ⋅≥⋅+⋅;当且仅当四边形ABCD 内接于圆时,等式成立。
[证] 在四边形ABCD 内取点E ,使CAD BAE ∠=∠,ACD ABE ∠=∠
则ABE ∆∽ACD ∆ ∴
AD
AE
CD BE AC AB ==, ∴BE AC CD AB ⋅=⋅; ∵
AD
AE
AC AB =,且EAD BAC ∠=∠ C
D
A
B
E B
C
D
∴ABC ∆∽AED ∆ ∴
AD
ED
AC BC =
,即ED AC BC AD ⋅=⋅; ∴)(ED BE AC BC AD CD AB +⋅=⋅+⋅ ∴BD AC BC AD CD AB ⋅≥⋅+⋅ 当且仅当E 在BD 上时“=”成立,
即四点共圆时成立;、、、当且仅当D C B A
【定理推广】 托勒密定理的推论:
等腰梯形一条对角线的平方等于一腰的平方加上两底之积. 即:若四边形ABCD 是等腰梯形,且BC AD //, 则BC AD AB AC ⋅+=22.
分析:因为等腰梯形必内接于圆,符合托勒密定理的条件,其对角线相等,两腰相等,结论显然成立。
【定理应用】
【例1】 如图,P 是正ABC ∆外接圆的劣弧BC 上任一点(不与B 、C 重合),
求证:PC PB PA +=. 证明:由托勒密定理得: ∵CA BC AB == ∴PC PB PA +=.
[注]此例证法甚多,如“截长”、“补短”等,详情参看《初中
数学一
题多解欣赏》.
【定理应用】
【例2】 证明“勾股定理”:
已知:在ABC Rt ∆中,︒=∠90B , 求证:222BC AB AC +=。
证明:如图,以ABC Rt ∆的斜边AC 为对角
B
C
线作矩形ABCD ,则ABCD 是圆内接四边形. 由托勒密定理,得
BC AD CD AB BD AC ⋅+⋅=⋅ ① ∵ABCD 是矩形,
∴CD AB =,BC AD =,BD AC = ② 把②代人①,得:222BC AB AC +=.
【定理应用】
【例3】 如图,在ABC ∆中,A ∠的平分线交外接圆于D ,连结BD ,
求证:)(AC AB BD BC AD +=⋅. 证明:连结CD ,由托勒密定理,得
BD AC CD AB BC AD ⋅+⋅=⋅. ∵CAD BAD ∠=∠,∴CD BD =. 故)(AC AB BD BC AD +=⋅.
【定理应用】
【例4】 若a 、b 、x 、y 是实数,且122=+b a ,122=+y x .
求证:1≤+by ax .
证明:如图,作直径1=AB 的圆,在AB 两侧任作ACB Rt ∆和ADB Rt ∆, 使a AC =,b BC =,x BD =,y AD =. 由勾股定理知a 、b 、x 、y 是满足题设条件的. 据托勒密定理,有CD AB BC AD BD AC ⋅=⋅+⋅. ∵1=≤AB CD ,
∴1≤⋅=⋅+⋅CD AB BC AD BD AC ,即1≤+by ax .
【定理应用】
【例5】 已知a 、b 、c 是ABC ∆的三边,且)(2c b b a +=,
求证:B A ∠=∠2.
证明:∵)(2c b b a +=,∴c b b b a a ⋅+⋅=⋅, 由托勒密定理,构造圆内接四边形。
如图 ,作ABC ∆的外接圆,以A 为圆心,BC 为半径作弧交圆于D ,连结
BD 、CD 、AD .
∵BC AD =,∴BAC ABD ∠=∠,则21∠=∠, ∴b AC BD ==
由托勒密定理得:AC BD CD AB AD BC ⋅+⋅=⋅ 即b b DC c a a ⋅+⋅=⋅①
又∵)(2c b b a +=,∴c b b b a a ⋅+⋅=⋅, ② 比较①②得b BD CD ==,则213∠=∠=∠, ∴ABC BAC ∠=∠2
【定理应用】
【例6】 在ABC ∆中,已知4:2:1::=∠∠∠C B A ,求证:
BC
AC AB 1
11=
+. 证明:如图,作ABC ∆的外接圆,作弦BC BD =,连结AD 、CD . ∵4:2:1::=∠∠∠C B A ,
∴CDA CBA CAD ∠=∠=∠,CAB ADB ABD ∠=∠=∠3 ∴AD AB =,AC CD =,
在圆内接四边形ADBC 中,由托勒密定理,得: ∴AC AB AB BC BC AC ⋅=⋅+⋅, 则
BC
AC AB 1
11=
+. 【定理应用】
【例7】 由ABC ∆外接圆的弧BC 上一点P 分别向边BC 、AC 与AB 作垂线PK 、PL 和
PN ,求证:
PM
AB
PL AC PK BC +=. 证:连接PA 、PB 、PC ,
四边形ABPC ,由托勒密定理得: 即
PM CP PM
AB
PL BP PL AC PK AP PK BC ⋅⋅+⋅⋅=⋅⋅ ①
∵LAP KBP ∠=∠, ∴KBP Rt ∆∽LAP Rt ∆ ∴
PA
PB
PL PK =
,∴PL BP PK AP ⋅=⋅② 同理可得PM CP PL BP ⋅=⋅③ ②③代人①得:PM
AB
PL AC PK BC +
=. 【练习】
[1] 已知ABC ∆中,C B ∠=∠2。
求证:)(2BC AB AB AC +=. [2] 已知正七边形721A A A 。
求证:
4
131211
11A A A A A A +=. (第21届全苏数学竞赛)
[提示]1. 过A 作BC 的平行线交△ABC 的外接圆于D ,连结BD 。
则CD=DA=AB ,AC=BD 。
由托勒密定理,AC ·BD=AD ·BC+CD ·AB 。
2.。
