各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆)
四个重要定理(梅涅劳斯,塞瓦,托勒密,西姆松)
四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC的三边BC、CA、AB或其延长线上有点P、Q、R，则P、Q、R共线的充要条件是 。
塞瓦(Ceva)定理（塞瓦点）△ABC的三边BC、CA、AB上有点P、Q、R，则AP、BQ、CR共点的充要条件是。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)定理（西姆松线）从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题：1． 设AD是△ABC的边BC上的中线，直线CF交AD于F。
求证：。
【分析】CEF截△ABD→（梅氏定理）【评注】也可以添加辅助线证明：过A、B、D之一作CF的平行线。
2． 过△ABC的重心G的直线分别交AB、AC于E、F，交CB于D。
求证：。
【分析】连结并延长AG交BC于M，则M为BC的中点。
DEG截△ABM→（梅氏定理）DGF截△ACM→（梅氏定理）∴===1【评注】梅氏定理3． D、E、F分别在△ABC的BC、CA、AB边上，，AD、BE、CF交成△LMN。
求S△LMN。
【分析】【评注】梅氏定理4． 以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证：AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5． 已知△ABC中，∠B=2∠C。
求证：AC2=AB2+AB·BC。
【分析】过A作BC的平行线交△ABC的外接圆于D，连结BD。
则CD=DA=AB，AC=BD。
由托勒密定理，AC·BD=AD·BC+CD·AB。
【评注】托勒密定理6． 已知正七边形A1A2A3A4A5A6A7。
求证：。
（第21届全苏数学竞赛）【分析】【评注】托勒密定理7． △ABC的BC边上的高AD的延长线交外接圆于P，作PE⊥AB于E，延长ED交AC延长线于F。
求证：BC·EF=BF·CE+BE·CF。
各种圆定理总结
各种圆定理总结各种圆定理总结圆定理，是指在圆内、圆外、圆周、圆弧、切线等圆的各个部分之间成立的一系列定理。
这些定理在几何中有广泛的应用，在解决一些复杂问题的时候也是十分常用的。
下面将会对一些重要的圆定理进行总结。
1. 垂直平分线定理在一个平面内，若过一点P作圆的两条切线，两条切线相交于点A，则AP为该点P到圆心的一条垂直平分线。
证明：如图1所示，过点P作两条切线AC、BD于圆心O处相交于点A。
连线PO，则有：∠APO = 1/2∠ACO =1/2∠BDO，但∠APO = ∠BPO（PA、PB是切线），所以∠BPO = 1/2∠BDO，由此可得PO⊥AB，即AP为AB的垂直平分线。
2. 弦长定理在圆上，从同一点出发的两条弦所夹角的大小相等，则它们所夹的弧所对应的弦的长度相等。
证明：如图2所示，从同一点A出发，过B、C作圆的两条弦，∠BAC = ∠BCA。
过AB的中点M作交于圆上的一条垂线，过AC的中点N作交于圆上的一条垂线。
由于BM = MA、CN = NA，∠AMB = ∠CNA，知∆AMB ≌ ∆CNA，从而MB = NC。
因此，AB = 2MB，AC = 2NC，即AB = AC。
3. 切割定理若有一条割线切圆于点A，圆心为O，割线与圆心的连线交割线于点B，则AO是AB的中线。
证明：如图3所示，AX为圆抛物线，圆心是O，AP为圆的半径，AP⊥OX。
设BO = x，则AB = 2x，PB = x，OP = r。
则有AP^2=AO^2-OP^2=(2x)^2-r^2，又有BP^2=AB^2-AP^2，代入AB=2x、AP=x，可得BP=x。
根据勾股定理，得到OP^2+BP^2=r^2+x^2，代入OP=r、BP=x，可得AO^2=4x^2。
所以AO=2x=AB/2，即AO是AB的中线。
4. 余切定理圆的半径r和圆周上一条弦所夹角的余切值相等，则弦的长度等于半径的两倍乘以余切值的倒数。
证明：如图4所示，有一条弦AB，圆心为O，角AOB = θ，半径为r。
几何中的著名定理大全
1． Steiner-lehmus 定理：设三角形的两个角的平分线相等，则这两个角的对边必相等。
2． Euler 公式： ⊿ABC 的外接圆半径和内切圆半径分别为R 和r ，则⊿ABC 的外心O 与内心I 的距离为)2(r R R d -=.3．Euler 定理：设⊿ABC 的外心为O ，垂心为H ，重心为G ，则O,H,G 在一条直线上，外心与重心的距离等于垂心与重心距离的一半。
4． 九点圆（Euler 圆Feuerbach 圆）定理：在⊿ABC 中，三边的中点，从三顶点向三边做垂线所得垂足，三个顶点与垂心连线的中点，这九个点共圆。
4.已知非等腰锐角三角形ABC 的外心、内心和垂心分别是O 、I 、H ，060=∠A ，若三角形ABC 的三条高线分别是AD 、BE 、CF ，则三角形OIH 的外接圆半径与三角形DEF 的外接圆半径之比为 .5． Euler 定理2：四边形ABCD 两对角线AC,BD 的中点分别是M,N,则22222224MN BD AC DA CD BC AB ++=+++6.Carnot 定理：设G 为⊿ABC 的重心，P 为⊿ABC 所在平面上任意一点，则)(313322222222222c b a PG PG GC GB GA PC PB PA +++=+++=++，其中后一等式为Leibnitz 公式。
6． 张角公式：已知⊿ABC 之BC 边上一点D ，设∠BAD=α，∠DAC=β，则. AB AC AD βαβαsin sin )sin(+=+7． Newton 定理：设⊙O 的外切四边形ABCD 的对角线AC,BD 的中点分别为E,F,则E,O,F 共线。
8． Newton 线定理：任意四边形的两条对角线的中点，两组对边延长线交点所构成的线段的中点，这三点在一条直线上。
10．Ptolemy 定理：圆内接四边形ABCD 的两组对边乘积的和等于他对角线的乘积。
BD AC BC AD CD AB ⋅=⋅+⋅11.Morley 定理：⊿ABC 的各角的三等分线交点做成⊿DEF,则⊿DEF 是正三角形.12.Stewart 定理：⊿ABC 的边BC 上任取一点D,若BD=u,DC=v,AD=t,则uv a v c u b t -+=222. 13.Ceva 定理：在⊿ABC 内任取一点P,直线AP,BP,CP 分别与边BC,CA,AB 相交于D,E,F,则1=⋅⋅FBAF EA CE DC BD ,其中点P 称为⊿ABC 的西瓦点. Ceva -1定理：在⊿ABC 的边BC,CA,AB 上分别取点D,E,F,如果 1=⋅⋅FBAF EA CE DC BD ,那么直线AD,BE,CF 相交于一点. 14.Menelaus 定理：一直线与⊿ABC 的三边BC,CA,AB 或延长线分别交于X,Y ,Z,则1=⋅⋅YACY XC BX ZB AZ ,其中直线XYZ 称为⊿ABC 的Menelaus 线. Menelaus -1定理：X,Y,Z 分别是⊿ABC 的三边BC,CA,AB 上或其延长线上的三点,如果1=⋅⋅YA CY XC BX ZB AZ ,那么X,Y,Z 三点共线. 15.Desargues 定理：在⊿ABC 和⊿A ’B ’C ’中若AA ’,BB ’,CC ’相交于一点S,则BC 与B ’C ’,CA 与C ’A ’,AB 与A ’B ’的交点D,E,F 三点共线.16.Pascal 定理：设圆内接六边形ABCDEF 的对边的延长线相交于三点X,Y ,Z,则这三点在一条直线上.17.Pappus 定理：有相异两直线l,m,若在l 上依次有A,E,C 三点,在m 上依次有D,B,F 三点,且AB 和DE 的交点为P;BC 和EF 的交点为Q;CD 和FA 的交点为R,则P,Q,R 三点共线.18.Simson 定理：从一点向三角形的各边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上.此直线称为此点关于三角形的.Simson 线.19.清宫定理：设P,Q,为三角形ABC 外接圆上异于A,B,C 的两点,P 点关于三边BC,CA,AB 的对称点分别为U,V ,W,若QU,QV ,QW 和边BC,CA,AB 或其延长线的交点分别为D,E,F,则D,E,F 三点在同一直线上.20.欧拉Euler 关于垂足三角形的面积公式:P 是⊿ABC 所在平面上任意一点,过P 向⊿ABC 的三边做垂线,垂足分别是A 1,B 1,C 1,若OP=d,则ABC C B A S R d R S 2221114-=,其中O 是⊿ABC 的外心,R 为其半径.21.Opiel 奥倍儿定理：通过三角形ABC 的顶点A,B,C 引三条互相平行的直线,设他们和三角形ABC 的外接圆的交点分别为A1,B1,C1,在三角形ABC 的外接圆周上取一点P,设PA1,PB1,PC1与三角形的三边BC,CA,AB 或其延长线的交点分别为D,E,F,则D,E,F22.Steiner （斯坦纳）定理：设三角形A 1C为P,则P关于三角形ABC的西姆松线通过线段PH中点.23 Steiner（斯坦纳）定理2：若P为三角形ABC内任意一点,作PD垂直于BC,交BC于D,PE垂直于CA,交CA于E,PF垂直于AB,交AB于F,则AF2+BD2+CE2=AE2+CD2+BF2.24.Weitzenbock外森皮克不等式：⊿ABC的三边分别为a,b,c,面积为S,则22c24.b+≥S3a+25.Finsler-Hadwiger定理：⊿ABC的三边分别为a,b,c,面积为S,则22)22224--a---+≥S3+b-)(ac)(c(abbc26.Monge(蒙日)定理：三个圆每两个的根轴或平行或交于一点。
竞赛常用定理--数学
几何篇梅涅劳斯定理：当直线交三角形ABC三边所在直线BC、AC、A于点D、E、F时，（AF/FB）×（BD/DC）×（CE/EA）=1以及逆定理：在三角形ABC三边所在直线上有三点D、E、F，且（AF/FB）×（BD/DC）×（CE/EA）=1，那么D、E、F三点共线。
角元形式梅捏劳斯定理：（sin∠BAD/sin∠DAC）×(sin∠ACF/sin∠FCB)×(sin∠CBE/sin∠EBA)=1塞瓦定理：指在△ABC内任取一点O，直线AO、BO、CO分别交对边于D、E、F，则(BD/DC)×(CE/EA)×(AF/FB)=1。
角元塞瓦定理：AD,BE,CF交于一点的充分必要条件是：(sin∠BAD/sin∠DAC)*(sin∠ACF/sin∠FCB)*(sin∠CBE/sin∠EBA)=1逆定理：在△ABC的边BC，CA，AB上分别取点D，E，F，如果(AF/FB)(BD/DC)(CE/EA)=1那么直线AD，BE，CF相交于同一点。
”正弦定理：在△ABC中，角A、B、C所对的边长分别为a、b、c，三角形外接圆的半径为R。
则有：a/sinA=b/sinB=c/sinC=2R余弦定理：，在△ABC中，余弦定理可表示为：c²=a²+b²-2ab cosCa²=b²+c²-2bc cosAb²=a²+c²-2ac cosB托勒密定理：指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
三弦定理：由圆上一点引出三条弦,中间一弦与最大角正弦的积等于其余每条弦与不相邻角正弦的积之和。
用图表述；圆上一点A,引出三条弦AB(左)、AC(右)、及中间弦AD,BC与AD交于P,根据《三弦定理》,有以下关系, ABsin∠CAP +ACsin∠BAP= ADsin∠BAC。
四个重要定理(梅涅劳斯_塞瓦_托勒密_西姆松)
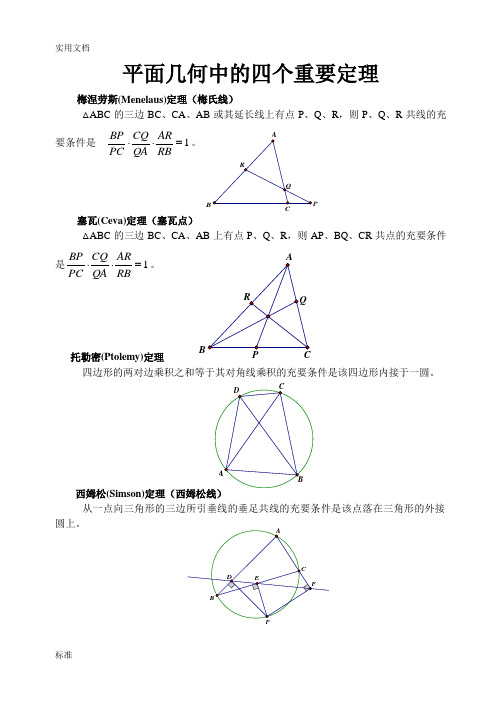
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ，则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理（塞瓦点）△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ，则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题：1、设AD 是△ABC 的边BC 上的中线，直线CF 交AD 于F 。
求证：FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅（梅氏定理） 【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ，交CB 于D 。
求证：1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ，则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅（梅氏定理）DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅（梅氏定理）∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上，λ===EACEFB AF DC BD ，AD 、BE 、CF 交成△LMN 。
求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证：AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中，∠B=2∠C 。
各种圆定理总结
费尔巴赫定理费尔巴赫定理三角形的与内切圆内切，而与旁切圆外切。
此定理由德国数学家费尔巴赫（K·W·Feuerbach，1800—1834）于1822年提出。
费尔巴赫定理的证明在不等边△ABC中,设O,H,I,Q,Ia分别表示△ABC的外心，垂心，内心，九点圆心和∠A所对的旁切圆圆心.s,R,r,ra分别表示△ABC的半周长，外接圆半径，内切圆半径和∠A 所对的旁切圆半径,BC=a,CA=b,AB=c.易得∠HAO=|B-C|,∠HAI=∠OAI=|B-C|/2;AH=2R*cosA,AO=R,A I=√[(s-a)bc/s],AIa=√[sbc/(s-a)]在△AHI中，由余弦定理可求得:HI^2=4R^2+4Rr+3r^2-s^2;在△AHO中，由余弦定理可求得:HO^2=9R^2+8Rr+2r^2-2s^2;在△AIO中，由余弦定理可求得:OI^2=R(R-2r).∵九点圆心在线段HO的中点,∴在△HIO中，由中线公式可求得.4IQ^2=2(4R^2+4Rr+3r^2-s^2)+2(R^2-2Rr)-(9R^2+8Rr+2r^2-2s^2)=(R-2r)^2故IQ=(R-2r)/2.又△ABC的九点圆半径为R/2,所以九点圆与内切圆的圆心距为d=R/2-r=(R-2r)/2=IQ.因此三角形的九点圆与内切圆内切。
在△AHIa中，由余弦定理可求得:IaH^2=4R^2+4Rr+r^2-s^2+2(ra)^2;在△AOIa中，由余弦定理可求得:IaO^2=R(R+2ra).在△HIaO中，由中线公式可求得.4IaQ^2=2(4R^2+4Rr+r^2-s^2+2ra^2)+2(R^2+2Rra)-(9R^2+8Rr+2r^2-2s^2)=(R+2ra) ^2故IaQ=(R+2ra)/2.九点圆与∠A的旁切圆的圆心距为d=R/2+ra=(R+2ra)/2=IaQ.故三角形的九点圆与∠A的旁切圆外切。
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ，则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理（塞瓦点）△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ，则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题：1、设AD 是△ABC 的边BC 上的中线，直线CF 交AD 于F 。
求证：FBAF2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅（梅氏定理） 【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ，交CB 于D 。
求证：1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ，则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅（梅氏定理）DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅（梅氏定理）∴FA CF EA BE +=MD AG )DC DB (GM ⋅+⋅=MDGM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上，λ===EACEFB AF DC BD ，AD 、BE 、CF 交成△LMN。
求S △LMN 。
【分析】【评注】梅氏定理BD4、以△ABC 各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证：AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中，∠B=2∠C 。
与圆有关的20个定理
与圆有关的20个定理圆是几何学中非常重要的一个图形，其形状和性质在数学和实际生活中有广泛的应用。
以下是与圆有关的20个定理的集合，包括圆的基本性质、圆与其他几何图形的关系和圆上的特殊点和线。
1. 定理1：周长公式圆的周长公式是C = 2πr，其中C表示圆的周长，r表示圆的半径，π是一个常数，大约为3.14。
这个公式可以使用圆的直径d而不是半径r来表达：C = πd。
2. 定理2：面积公式圆的面积公式是A = πr²，其中A表示圆的面积，r表示圆的半径。
与周长公式一样，也可以使用圆的直径来表达圆的面积：A = (π/4)d²。
3. 定理3：圆周的弧度弧度是一种测量角度的单位，它是定义为一个圆弧所对应的圆心角的度数除以360度的比例。
例如，如果一个圆弧所对应的圆心角是90度，则该圆弧的弧度是1/4。
4. 定理4：内切圆内切圆是一个圆，恰好与给定的多边形的内部相切，且每个边都是它的切线。
内切圆的半径称为内切圆半径，且由公式r = A/P得出，其中A是多边形的面积，P是多边形的周长。
5. 定理5：外接圆外接圆是一个圆，它恰好与给定的多边形的每个顶点相切。
外接圆的半径称为外接圆半径且可以由a²+b²=c²公式或者P=2πr公式来计算。
6. 定理6：圆柱体的侧面积一个圆柱体的侧面积是由公式A=2πrh得出的，其中r是圆柱体的半径，h是圆柱体的高。
7. 定理7：球的表面积球的表面积是由公式A=4πr²得出的，其中r是球的半径。
8. 定理8：圆锥的侧面积一个圆锥的侧面积是由公式A=πrl得出的，其中r是圆锥的底面半径，l是圆锥的斜线长度。
9. 定理9：勾股定理勾股定理是一个直角三角形的定理，它表明a²+b²=c²，其中a和b是直角三角形的两个直角边，c是斜边。
10. 定理10：圆的切线对于给定的一个圆，一个切线是从圆外的一点切到圆上的一点。
圆的所有定理公式大全
圆的所有定理公式大全圆是几何学中一个重要的基本图形，它具有许多特殊的性质和定理。
在这篇文章中，我们将介绍一些圆的定理和公式，帮助读者更好地理解圆的性质和应用。
1. 圆的基本性质：- 圆是一个平面上所有到圆心距离相等的点的集合。
- 圆心到圆上任意一点的距离称为半径（r）。
- 圆的直径（d）是通过圆心的一条线段，它等于半径的两倍。
2. 圆的周长和面积：- 圆的周长（C）等于圆的直径（d）乘以π（圆周率）。
C = πd 或C = 2πr- 圆的面积（A）等于半径（r）的平方乘以π（圆周率）。
A = πr²3. 弧长和扇形面积：- 弧长（L）是圆的一部分的弧长。
它等于弧度（θ）乘以半径（r）。
L = θr （其中θ 的单位为弧度）- 扇形面积（A）等于角度（θ）比上360度再乘以圆的面积。
A = (θ/360)πr² （其中θ 的单位为角度）4. 圆的相交性质：- 弦：圆上连接两个点的线段称为弦。
如果一个弦通过圆心，它称为直径。
- 弦切角：如果两个弦的端点相连成一个角，则这个角叫做弦切角。
- 切线：与圆相切且与半径垂直的线段称为切线。
切线与半径的交点称为切点。
- 切线切割定理：一个切点与切点外的任意一点相连，此线段与切线的交点与切点相连的线段平方等于此直线与切线相交的两条弦构成的弧的两个弧度之积。
5. 圆的角度定理：- 圆心角：以圆心为顶点的角叫做圆心角。
圆心角的度数等于所对弧所对应的圆周角度数。
- 直径角：直径所对的角称为直径角，它的度数为 180 度。
- 弧角定理：圆上的两条弦所对的圆心角等于它们所对弧所对应的圆周角的一半。
6. 圆的判定定理：- 定理 1：如果一个点到圆心的距离等于圆的半径，那么这个点在圆上。
- 定理 2：如果一个点在圆上，那么它到圆心的距离等于圆的半径。
7. 圆的位置关系：- 外切圆：与一个三角形的三边都相切的圆，叫做该三角形的外切圆。
- 内切圆：与一个三角形的三条边都相切于一个点的圆，叫做该三角形的内切圆。
平面几何的26个定理
高一数学竞赛班二试讲义第1讲 平面几何中的26个定理班级 姓名一、知识点金1. 梅涅劳斯定理：若直线l 不经过ABC ∆的顶点，并且与ABC ∆的三边,,BC CA AB 或它们的延长线分别交于,,P Q R ，则1BP CQ AR PC QA RB⋅⋅= 注：梅涅劳斯定理的逆定理也成立（用同一法证明）2. 塞瓦定理： 设,,P Q R 分别是ABC ∆的三边,,BC CA AB 或它们的延长线上的点，若,,AP BQ CR 三线共点，则1BP CQ AR PC QA RB⋅⋅= 注：塞瓦定理的逆定理也成立3. 托勒密定理：在四边形ABCD 中，有AB CD BC AD AC BD ⋅+⋅≥⋅，并且当且仅当四边形ABCD 内接于圆时，等式成立。
AB AE AC ADBC ED AC AD==⇒又4. 西姆松定理：若从ABC ∆外接圆上一点P 作,,BC AB CA 的垂线，垂足分别为,,D E F ，则,,D E F 三点共线。
西姆松定理的逆定理：从一点P 作,,BC AB CA 的垂线，垂足分别为,,D E F 。
若,,D E F 三点共线，则点P 在ABC ∆的外接圆上。
5． 蝴蝶定理：圆O 中的弦PQ 的中点M ，过点M 任作两弦AB ，CD ，弦AD 与BC 分别交PQ 于X ，Y ，则M 为XY 之中点。
证明：过圆心O 作AD 与BC 的垂线，垂足为S 、T ，，OY ，OM ，SM ，MT 。
∴AM/CM=AD/BC∵AS=1/2AD，BT=1/2BC ∴AM/CM=AS/CT又∵∠A=∠C ∴△AMS∽△CMT∴∠MSX=∠MTY∴∠OMX+∠OSX=180°∴O，S ，X ，M同理，O ，T ，∴∠MTY=∠MOY，∠MSX=∠MOX∴∠MOX=∠MOY ， ∵OM⊥PQ ∴XM=YM注：把圆换成椭圆、抛物线、双曲线蝴蝶定理也成立6． 坎迪定理：设AB 是已知圆的弦，M 是AB 上一点，弦,CD EF 过点M ，连结,CF ED ，分别交AB 于,L N ，则1111LM MN AM MB-=-。
各种圆定理总结包括托勒密定理塞瓦定理西姆松定理梅涅劳斯定理圆幂定理和四点共圆
托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出一般几何教科书中的“定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。
证明一、（以下是推论的证明，托勒密定理可视作特殊情况。
）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、C D、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到：(a? b)(c? d) + (a? d)(b? c) = (a? c)(b?d) ，两边取，运用得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。
四点不限于同一。
平面上，托勒密不等式是三角不等式的形式。
二、设ABCD是。
在BC上，∠BAC = ∠BDC，而在AB上，∠ADB = ∠ACB。
在AC上取一点K，使得∠ABK = ∠CBD；因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD，所以∠CBK = ∠ABD。
关于圆的所有定理
关于圆的所有定理1．圆是以圆心为对称中心的中心对称图形；围绕圆心旋转任意一个角度α,都能够与原来的重合．2.顶点在圆心的角叫做圆心角．圆心到弦的距离叫做弦心距．圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理）切线长定理（从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角）垂径定理（垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧）圆周角定理弦切角定理（定义弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半. (弦切角就是切线与弦所夹的角））3．在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等．4．在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等．5．把整个圆周等分成360份,每一份弧是1°的弧．圆心角的度数和它所对的弧的度数相等．6.圆是中心对称图形,即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合,这一性质不难理解．圆和其他中心对称图形不同,它还具有旋转不变性,即围绕圆心旋转任意一个角度,都能够与原来的图形重合．7.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧8.（1）平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧（2）弦的垂直平分线经过圆心,并且平分弦所对的两条弧（3）平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧9.圆的两条平行弦所夹的弧相等10.(1)一条弧所对的圆周角等于它所对的圆心角的一半.(2)同弧或等弧所对的圆周角相等；同圆或等圆中,相等的圆周角所对的弧也相等.(3)半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径.(4)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.11.(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.(2)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(3)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(4)弦的垂直平分线经过圆心,并且平分弦所对的两条弦.(5)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.(6)圆的两条平行弦所夹的弧度数相等.12.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴．垂直于弦的直径平分这条弦,并且平分弦所对的两条弧．13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧.14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.15.在同圆或等圆中,相等的弦所对的弧相等,所对的圆心角相等,所对的弦的弦心距也相等.16.同一个弧有无数个相对的圆周角.17.弧的比等于弧所对的圆心角的比.18.圆的内接四边形的对角互补或相等.19.不在同一条直线上的三个点能确定一个圆.20.直径是圆中最长的弦.21.一条弦把一个圆分成一个优弧和一个劣弧.。
圆的十八个定理
圆的十八个定理圆的十八个定理包括：1.圆心角定理：在同圆或等圆中，相等的圆心角所对弧相等，所对的弦相等，所对的弦的弦心距相等。
2.圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。
3.垂径定理：垂直弦的直径平分该弦，并且平分这条弦所对的两条弧。
4.切线之判定定理：经过半径的外端并且垂直于该半径的直线是圆的切线。
5.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这一点与圆心的连线平分这两条切线的夹角。
6.公切线长定理：如果两圆有两条外公切线或两条内公切线，那么这两条外公切线长相等，两条内公切线长也相等。
如果他们相交，那么交点一定在两圆的连心线上。
7.相交弦定理：圆内两条弦相交，被交点分成的两条线段长的乘积相等。
8.切割线定理：从圆外一点向圆引一条切线和一条割线，则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。
9.割线长定理：从圆外一点向圆引两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。
10.切线的性质定理：圆的切线垂直于经过切点的半径。
11.弦切角定理：弦切角等于它所夹的弧对的圆周角。
12.定理：相交两圆的连心线垂直平分两圆的公共弦。
13.把圆分成n(n≥3)个等分：依次连结各分点所得的多边形是这个圆的内接正n边形；经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。
14.任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆。
15.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形。
16.圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。
17.两圆的半径分别为R、r，圆心距为d：两圆外离d>R+r；两圆外切d=R+r；两圆相交R-r<dr)；两圆内切d=R-r(R>r)；两圆内含d<R-r(R>r)。
18.圆锥曲线：圆是一种特殊的圆锥曲线，它是由一个固定点（焦点）和一个固定直线（准线）上的所有点的轨迹组成的。
各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆).
托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出一般几何教科书中的“托勒密定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。
证明一、（以下是推论的证明，托勒密定理可视作特殊情况。
）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式：(a − b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ，两边取模，运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。
四点不限于同一平面。
平面上，托勒密不等式是三角不等式的反演形式。
二、设ABCD是圆内接四边形。
在弦BC上，圆周角∠BAC = ∠BDC，而在AB上，∠ADB = ∠ACB。
在AC上取一点K，使得∠ABK = ∠CBD；因为∠ABK + ∠CBK =∠ABC = ∠CBD + ∠ABD，所以∠CBK = ∠ABD。
圆（圆幂定理、根轴，托勒密定理、帕斯卡定理、牛顿定理Ⅰ、Ⅱ）
圆（圆幂定理、根轴，托勒密定理、帕斯卡定理、牛顿定理
Ⅰ、Ⅱ）
一、圆幂定理、根轴
1. 圆幂定理：
圆幂定理为以下三个定理的统称，即
相交弦定理（Ⅰ:AP·PB=CP·PD）
割线定理（Ⅱ：PA·PB=PC·PD）
切割线定理（Ⅲ：PA2=PC·PD）
2. 根轴：
到两圆幂相等的点的集合为一条垂直于两圆圆心连线的直线
且：若两圆相交则根轴为公共弦所在直线
若两圆相切则根轴为公切线
同心圆无根轴
二、几条重要的定理
1. 托勒密定理
凸四边形 ABCD 中有
AC · BD ≥ AB · CD + AD · BC
等号当且仅当四边形 ABCD 是圆内接四边形时成立
2. 帕斯卡定理
圆内接六边形三组对边所在直线交点共线
3. 牛顿定理Ⅰ
圆外切四边形的对角线交点和以切点为顶点的四边形对角线交点重
合
4. 牛顿定理Ⅱ
圆外切四边形两条对角线中点和该圆圆心，三点共线
本文素材来源网络！知识分享，若有不当，多加指正！。
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)
P 、Q R ,则P 、Q R 共线的充要条件是聖CQ ARj 。
PC QA RBBP CQ AR PC QA RB _ °平面几何中的四个重要定理梅涅劳斯（Menelaus ）定理（梅氏线）△ABC 的三边BC CA AB 或其延长线上有点塞瓦（Ceva ）定理（塞瓦点）△ABC 的三边 BC CA AB 上有点 P 、Q R ,贝U AP 、BQ CR 共点的充要条件是 托勒密（Ptolemy ）定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松（Simson ）定理（西姆松线）从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接 圆上。
例题:PA 1设AD是MBC的边BC上的中线，直线CF交AD于F。
求证：AE 2AFED。
AE DC RF【分析】CEF截△ARCH — .— .— =1 （梅氏定理）ED CR FA【评注】也可以添加辅助线证明：过A、R、D之一作CF的平行线。
2、过△ARC的重心G的直线分别交AB AC于E、F,交CR于D。
RE CF=1。
求证：EA FADEG截A ARM H REEAAGGMMDDR（梅氏定理）DGF截△ACM H =1 (梅氏定理)FA GM DCRE CF=GM (DR DC)=GM2MDEA FA AG MD 2GM MD【评注】梅氏定理3、D E、F分别在A ARC的RC CA AR边上,RD AFDC FRCEEAAD RE、CF交成△ LMN 求S A LM N O【分析】【评注】梅氏定理4、以A ARC各边为底边向外作相似的等腰A RCE A CAF A ARG 求证：AE、RF、CG相交【分析】连结并延长AG交RC于M,则M为RC的中点。
FLEM N【评注】塞瓦定理5、已知△ABC 中，/ B=2/ G 求证：AC^AB+ABBCo【分析】过A 作BC 的平行线交△ABC 的外接圆于D,连结BD 贝 U CD=DA=AB AC=BD由托勒密定理，AC BD=ADBC+CDAB【评注】托勒密定理求证：1 1 1A !A 2=A !A 3 A !A 4。
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ，则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理（塞瓦点）△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ，则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题：1、设AD 是△ABC 的边BC 上的中线，直线CF 交AD 于F 。
求证：FBAF2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅（梅氏定理） 【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ，交CB 于D 。
求证：1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ，则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅（梅氏定理）DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅（梅氏定理）∴FA CF EA BE +=MD AG )DC DB (GM ⋅+⋅=MDGM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上，λ===EACEFB AF DC BD ，AD 、BE 、CF 交成△LMN。
求S △LMN 。
【分析】【评注】梅氏定理BD4、以△ABC 各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证：AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中，∠B=2∠C 。
数学定理整理
梅涅劳斯定理梅涅劳斯定理（简称梅氏定理）：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AD/D B)×(B E/E C)×(C F/FA)=1。
或：设X、Y、Z分别在△ABC 的BC、CA、AB所在直线上，则X、Y、Z共线的充要条件是(AD/D B)×(B E/EC)×(C F/FA)=1。
在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
于是L、M、N三点共线的充要条件是λμν=1。
如图：若E，F，D三点共线，则(sin∠ACF/sin∠FCB)(sin∠BAD/sin∠DAC)(sin∠CBA/sin∠AB E)=1即图中的蓝角正弦值之积等于红角正弦值之积该形式的梅涅劳斯定理也很实用第二角元形式的梅涅劳斯定理在平面上任取一点O，且EDF 共线，则（sin∠A O F/sin∠FOB)(sin∠B O D/sin∠D O C)(sin∠C O A/sin∠A O E)=1。
(O不与点A、B、C重合)塞瓦定理在△ABC内任取一点O，直线AO、BO、CO分别交对边于D、E、F，则(BD/DC)*(CE/EA)*(AF/FB)=11.塞瓦定理角元形式AD,BE,CF交于一点的充分必要条件是：(sin∠BAD/sin∠DAC)*(sin∠ACF/sin∠FCB)*(sin∠CBE/ sin∠EBA)=1由正弦定理及三角形面积公式易证2.如图，对于圆周上顺次6点A，B，C，D，E，F，直线AD，BE，CF交于一点的充分必要条件是：(AB/BC)*(CD/DE)*(EF/FA)=1由塞瓦定理的角元形式，正弦定理及圆弦长与所对圆周角关系易证。
罗斯定理设有一个三角形，而、与分别是三角形的三条边、和上的点。
如果设、、，以及、、，那么右图中红色的小三角形的面积占三角形面积的比例就是：这个三角形是由线段、和围出来的，或者可以看成将三角形沿着、、剪裁而剩下的三角形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质.定理的提出一般几何教科书中的托勒密定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。
证明一、(以下是推论的证明，托勒密定理可视作特殊情况。
)在任意四边形ABCD 中，作△ ABE使/ BAE= / CAD / ABE= / ACD因为△ ABE ACD所以BE/CD=AB/AC, 即BE-AC=AB CD (1)而/ BAC= / DAE ,，/ ACB= / ADE所以△ ABC AED 相似.BC/ED=AC/AD 即ED- AC=BC AD (2)⑴+⑵，得AC(BE+ED)=AB CD+AD BC又因为BE+EI> BD(仅在四边形ABCD是某圆的内接四边形时，等号成立，即托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式：(a -b)(c - d) + (a - d)(b - c) = (a - c)(b - d)，两边取模，运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。
四点不限于同一平面。
平面上，托勒密不等式是三角不等式的反演形式。
二、设ABCD是圆内接四边形。
在弦BC上，圆周角/ BAC = / BDC，而在AB上，/ ADB = / ACB。
在AC 上取一点K，使得/ ABK = / CBD ; 因为/ ABK + / CBK = / ABC = / CBD + / ABD，所以/ CBK = / ABD。
因此△ ABK 与厶DBC 相似，同理也有△ ABD ~ △ KBC 。
因此 AK/AB = CD/BD ，且 CK/BC = DA/BD ;因此 AK- BD = A BCD ，且 CK- BD =BC- DA ; 两式相加，得 (AK+CK) - BD = AB-CD + BC- DA ; 但 AK+ CK = AC ，因此 AC - BD = AB-CD + BC- DA 。
证毕。
三、托勒密定理：圆内接四边形中，两条对角线的乘积(两对角线所包矩形的面积 )等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和 )•已知：圆内接四边形 ABCD ，求证： AC- BD = AB- CD + AD- BC •证明：如图 1 ,过 C 作 CP 交 BD 于 P ,使/ 1= / 2 ,又/ 3= / 4 ,•••△ ACD BCP .得 AC : BC=AD : BP ,AC - BP=AD BC ①。
又/ ACB= / DCP , / 5= / 6 , •△ ACB DCP .得 AC : CD=AB : DP , AC ・DP=AB ・ CD ②。
① + ②得 AC(BP + DP)=AB ・ CD + AD- BC .即 AC- B D=AB- CD + AD - BC .推论1. 任意凸四边形 ABCD ，必有 AC- BDC AB- CD+AD BC ，当且仅当 ABCD 四点共圆时取 等号。
2. 托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆、推广托勒密不等式：四边形的任两组对边乘积不小于另外一组对边的乘积，取等号当且仅当 共圆或共线。
简单的证明：复数恒等式： (a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d) ，两边取模,得不等式 AC- BDC |(a -b)(c-d)|+|(b-c)(a-d)|=AB 注意:1.等号成立的条件是 (a-b)(c-d)与(a-d)(b-c)的辐角相等，这与 价。
2. 四点不限于同一平面。
欧拉定理：在一条线段上AD 上，顺次标有 B 、C 两点，贝U AD- BC+AB CD=AC BDC D+BC ADA 、B 、C 、D 四点共圆等塞瓦定理简介塞瓦(Giovanni Ceva , 1648〜1734 )意大利水利工程师，数学家。
塞瓦定理载于塞瓦于678年发表的《直线论》一书，也有书中说塞瓦定理是塞瓦重新发现。
具体内容•/ BD/DC=S △ ABD/S △ ACD=S △ BOD/S △ COD=(S △ ABD-S △ BOD)/(S △ ACD-S D)=S△ AOB/S △ AOC ③同理 CE/EA=S △ BOC/ S △ AOB ④ AF/FB=S △ AOC/S △ BOC ⑤ ③X ④ X ⑤得 BD/DC*CE/EA*AF/FB=1利用塞瓦定理证明三角形三条高线必交于一点 ：设三边AB 、BC 、AC 的垂足分别为 D 、E 、F , 根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA ) /[(CD*ctgB )*ctgB)/(AE*ctgC)]*[(BF*ctgC)/[(BF*ctgA)]=1，所以三条高 CD 、AE 、BF 交于一点。
可用塞瓦定理证明的其他定理 ；三角形三条中线交于一点(重心)：如图5 D , E 分别为BC , AC 中点 所以BD=DCAE=EC 所以 BD/DC=1 CE/EA=1且因为AF=BF 所以AF/FB 必等于1所以AF=FB 所以三角形三条中线交于一点塞瓦定理在厶ABC 内任取一点 0 ,直线AO 、BO 、CO 分别交对边于 证法简介(I)本题可利用梅涅劳斯定理证明：•••△ ADC 被直线BOE 所截，••• (CB/BD)*(DO/OA)*(AE/EC)=1 而由△ ABD 被直线COF 所截 ②乜:即得：(D)D 、E 、F ，贝U (BD/DC)*(CE/EA)*(AF/FB)=1①(BC/CD)*(DO/OA)*(AF/FB)=1②(BD/DC)*(CE/EA)*(AF/FB)=1也可以利用面积关系证明△ CO]*[(AE此外，可用定比分点来定义塞瓦定理：在厶ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是入=BL/L C、卩=CM/MA、v =AN/NB。
于是AL、BM、CN三线交于一点的充要条件是入yv。
1 (注意与梅涅劳斯定理相区分，那里是入yv-1)塞瓦定理推论1. 设E是厶ABD内任意一点，AE、BE、DE分别交对边于C、G、F，贝U (BD/BC)*(CE/ AE)*(GA/DG)=1因为(BC/CD)*(DG/GA)*(AF/FB)=1 ,(塞瓦定理)所以(BD/CD)*(CE/AE)*(AF/FB)=K(K为未知参数)且(BD/BC)*(CE/AE)*(GA/DG)=K ( K为未知参数)又由梅涅劳斯定理得：(BD/CD)*(CE/AE)*(AF/FB)=1所以(BD/BC)*(CE/AE)*(GA/DG)=12. 塞瓦定理角元形式AD,BE,CF 交于一点的充分必要条件是：(sin / BAD/sin / DAC)*(sin / ACF/sin / FCB)*(sin / CBE/sin / EBA)=1由正弦定理及三角形面积公式易证3. 如图，对于圆周上顺次6点A,B,C,D,E,F ，直线AD,BE,CF 交于一点的充分必要条件是：(AB/BC)*(CD/DE)*(EF/FA)=1由塞瓦定理的角元形式，正弦定理及圆弦长与所对圆周角关系易证。
4. 还能利用塞瓦定理证三角形三条高交于一点设三边AB、BC、AC的垂足分别为D、E、F ,根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA ) /[(CD*ctgB ) ]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/[(AE*ctgB)]=1 ，所以三条高CD、AE、BF父于一点。
梅涅劳斯定理图5梅涅劳斯定理证明梅涅劳斯(Menelaus )定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出：如果一条直线与△ ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB) X(BD/DC)X (C E/EA)=1 。
或：设X、Y、Z分别在△ ABC的BC、CA、AB所在直线上，则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=证明一：过点A作AG // BC交DF的延长线于G,贝U AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG 。
三式相乘得：(AF/FB) X (BD/DC)X (CE/EA)=(AG/BD)X (BD/DC)X (DC/AG)=1证明二：过点C 作CP // DF 交AB 于P，贝U BD/DC=FB/PF , CE/EA=PF/AF所以有AF/FB X BD/DC X CE/EA=AF/F X FB/PF X PF/AF=1它的逆定理也成立：若有三点F、D、E分别在△ ABC的边AB、BC、CA或其延长线上，且满足(AF/FB) X (BD/DC)X (CE/EA)=1 ，贝U F、D、E三点共线。
利用这个逆定理，可以判断三点共线。
梅涅劳斯(Menelaus)定理证明三：过ABC三点向三边引垂线AA'BB'CC',所以AD : DB=AA' : BB' , BE : EC=BB' : CC' , CF : FA=CC' : AA'所以(AF/FB) X (BD/DC)X (CE/EA)=1证明四: 连接BF 。
(AD : DB ) (BE : EC ) • ( CF:FA) =(S △ ADF : S △ BDF ) • ( S △ BEF : S △ CEF ) S △ BAF )=(S △ ADF : S △ BDF ) - ( S △ BDF : S △ CDF )-(S △ CDF : S △ ADF ) =1 此外，用定比分点定义该定理可使其容易理解和记忆: 在厶ABC 的三边 BC 、CA 、 AB 或其延长线上分别取 又分比是 入=BL/LC 、3 =CM/MA 、v 第一角元形式的梅涅劳斯定理=AN/NB 。
于是 L 、M 、N 三点共线的充要条件是 入uv 如图：若 E , F , （sin / ACF/sin / FCB ）（sin / 即图中的蓝角正弦值之积等于红角正弦值之积 BAD/sin / DAC)(sin / CBA/sin / ABE)=1 该形式的梅涅劳斯定理也很实用 第二角元形式的梅涅劳斯定理 在平面上任取一点 in / COA/sin / AOE)=1 O ，且 EDF 共线，则（sin / AOF/sin / FOB ）（sin / 。