南京大学2005级数学系数学分析2期末(AB卷合一)
2005-2006(2)期末考试试卷(A)(高等数学)

2、计算积分值 u(s,t) (s,t) xdx ydy 。
(1,0) x2 y2
第 1 页(共 1 页)
zdxdydz ,其中 由曲面 z x2 y2 及平面 z 4 所围成的闭区域。
5、(1) 求变力 F (2x 3y x 2 y, x 2 y xy 2) 将圆周 L : x2 y2 2 上的质点沿顺时针方
向移动一周所做的功。(6 分)
(2) 利 用 高 斯 公 式 计 算 (x 2 y)dydz (3y z)dzdx (3x 2z)dxdy , 其 中 是 由 x 0, y 0, z 0 及 x y z 1在第一卦限所围成的立体的表面外侧。(6 分) 123
。
5、设 L 为连接(3, 0) 和(0,3) 两点的直线段,则 (x y)ds =
。
L
6、lim sin(xy) =
。
x y3
x
7、函数 u x2 y2 z2 在点 (1,1,1) 处沿方向 l 的方向导数是
度
。(其中l 的方向角为60o , 45o , 6
设
f
(x,
y)
( x 2
y2 ) sin
x2
1
y2
0
x2 y2 0 x2 y2 0
,试讨论在点(0, 0) 处:
1、 f (x, y) 是否连续? 2、 f (x, y) 的偏导数是否存在? 3、 f (x, y) 是否可微?
五、证明题(5 分×2=10 分)
1、证明曲线积分 xdx ydy 与路径无关,其中 L 为不通过原点的任一曲线。
一、填空题(2 分 7=14 分)
1、以 a {2, 1,1} 和b {1, 2, 3} 为边的平行四边形的面积等于
2005年数学一数学二考研真题与答案

2005年数学一试题分析、详解和评注一、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)(1)曲线122+=x x y 的斜渐近线方程为 .4121-=x y【分析】 本题属基本题型,直接用斜渐近线方程公式进行计算即可.【详解】 因为a=212lim )(lim 22=+=∞→∞→x x x x x f x x ,[]41)12(2lim)(lim -=+-=-=∞→∞→x x ax x f b x x ,于是所求斜渐近线方程为.4121-=x y 【评注】 如何求垂直渐近线、水平渐近线和斜渐近线,是基本要求,应熟练掌握。
这里应注意两点:1)当存在水平渐近线时,不需要再求斜渐近线;2)若当∞→x 时,极限xx f a x )(lim∞→=不存在,则应进一步讨论+∞→x 或-∞→x 的情形,即在右或左侧是否存在斜渐近线。
完全类似例题见《数学复习指南》(理工类)P.192【例7.32】(2) 微分方程x x y y x ln 2=+'满足91)1(-=y 的解为.91ln 31x x x y -=. 【分析】直接套用一阶线性微分方程)()(x Q y x P y =+'的通解公式:⎰+⎰⎰=-])([)()(C dx e x Q e y dxx P dx x P ,再由初始条件确定任意常数即可. 【详解】 原方程等价为x y xy ln 2=+', 于是通解为 ⎰⎰+⋅=+⎰⋅⎰=-]ln [1]ln [2222C xdx x xC dx ex ey dxx dxx =2191ln 31x C x x x +-, 由91)1(-=y 得C=0,故所求解为.91ln 31x x x y -=【评注】 本题虽属基本题型,但在用相关公式时应注意先化为标准型. 另外,本题也可如下求解:原方程可化为x x xy y x ln 222=+',即 x x y x ln ][22=',两边积分得C x x x xdx x y x +-==⎰332291ln 31ln , 再代入初始条件即可得所求解为.91ln 31x x x y -=完全类似公式见《数学复习指南》(理工类)P.154(3)设函数181261),,(222z y x z y x u +++=,单位向量}1,1,1{31=n ,则)3,2,1(nu∂∂=33. 【分析】 函数u(x,y,z)沿单位向量γβαcos ,cos ,{cos =n}的方向导数为:γβαcos cos cos zu y u x u n u ∂∂+∂∂+∂∂=∂∂ 因此,本题直接用上述公式即可.【详解】 因为3x x u =∂∂,6y y u =∂∂,9zz u =∂∂,于是所求方向导数为)3,2,1(nu ∂∂=.33313131313131=⋅+⋅+⋅ 【评注】 本题若n=},,{l n m 非单位向量,则应先将其单位化,从而得方向余弦为:,cos 222ln m m ++=α,cos 222ln m n ++=β222cos ln m l ++=α.完全类似例题见《数学复习指南》(理工类)P.330【例12.30】(4)设Ω是由锥面22y x z +=与半球面222y x R z --=围成的空间区域,∑是Ω的整个边界的外侧,则⎰⎰∑=++zdxdy ydzdx xdydz 3)221(2R -π. 【分析】本题∑是封闭曲面且取外侧,自然想到用高斯公式转化为三重积分,再用球面(或柱面)坐标进行计算即可.【详解】⎰⎰∑=++zdxdy ydzdx xdydz ⎰⎰⎰Ωdxdydz 3=.)221(2sin 3320402R d d d R⎰⎰⎰-=πππθϕϕρρ .【评注】 本题属基本题型,不论是用球面坐标还是用柱面坐标进行计算,均应特别注意计算的准确性,主要考查基本的计算能力.完全类似例题见《数学复习指南》(理工类)P.325【例12.22】(5)设321,,ααα均为3维列向量,记矩阵),,(321ααα=A ,)93,42,(321321321ααααααααα++++++=B , 如果1=A ,那么=B 2 .【分析】 将B 写成用A 右乘另一矩阵的形式,再用方阵相乘的行列式性质进行计算即可.【详解】 由题设,有)93,42,(321321321ααααααααα++++++=B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡941321111),,(321ααα, 于是有 .221941321111=⨯=⋅=A B【评注】 本题相当于矩阵B 的列向量组可由矩阵A 的列向量组线性表示,关键是将其转化为用矩阵乘积形式表示。
数学分析(二):多元微积分_南京大学中国大学mooc课后章节答案期末考试题库2023年

数学分析(二):多元微积分_南京大学中国大学mooc课后章节答案期末考试题库2023年1.在3维欧氏空间中,向量 (1, 2, 1) 与 (4, 3, -5)之间的标准内积等于参考答案:52.空间曲线【图片】的长度为参考答案:5/33.【图片】与【图片】之间的内积等于参考答案:204.下列结论中, 正确的是参考答案:如果 f 是从平面到面的可微映射且其 Jacobi 矩阵的范数有界, 则 f 为Lipschitz 映射.5.【图片】在 (1,1) 处分别关于x, y 的偏导数为参考答案:2cos1, cos16.下列二元函数中, 不是凸函数的是参考答案:xy7.下列函数中, 不是有界变差函数的是参考答案:(在 0 处规定补充函数值为零)8.下列结论中,错误的是参考答案:平面上的零测集一定是可求面积集.9.设 A 是平面上的子集, 其特征函数是在 A 中定义为 1, 在 A 外定义为 0 的函数.则特征函数的间断点为参考答案:A 的边界点.10.下列集合中, 不是零测集的为参考答案:平面上的正方形区域 [0, 1]x[0, 1].11.将所有3行4列的实矩阵放在一起,构成的向量空间的维数等于参考答案:1212.下列结论中, 错误的是参考答案:函数 sin x 是 [-1, 1] 上的压缩映射13.下列结论中,正确的是参考答案:如果函数在某一点可微,则在这一点的偏导数都存在.14.下列问题中,不属于第二型曲线积分的是参考答案:已知物体的密度求其质量.15.在3维欧氏空间中,向量 (1, 2, 1) 叉乘 (4, 3, 5) 等于参考答案:(7, -1, -5)16.考虑平面上的环形区域【图片】, 其边界由两个圆周组成,半径小的称为内圆, 半径大的称为外圆. 则边界的诱导定向为参考答案:内圆顺时针, 外圆逆时针.17.向量场【图片】沿空间曲线【图片】从点 (1,0,1) 到 (0,1,0) 的积分等于参考答案:118.在4维欧氏空间中, 对称的二次型的全体构成了一个向量空间, 它的维数等于参考答案:1019.在4维欧氏空间中, 反对称的二次型的全体构成了一个向量空间, 它的维数等于参考答案:620.方程【图片】在(x,y)=(0,1) 附近确定了隐函数 y = f(x), 则 y'(0) 等于参考答案:-1/221.下列实数集的子集中, 是开集的为参考答案:(0, 1)。
05级高数(A-2)期末试卷

2005级《高等数学A-2》期末试卷一、 单项选择题(将答案写在括号内,每题4分,共 48分)1.微分方程20y y y '''-+=的一个解是( ).(A) 2y x = (B) x y e = (C) sin y x = (D) x y e -=2.微分方程 x e x y y y 228644+=+'-'' 的一个特解应具形式 ( ).(a,b,c,d 为常数)(A) x ce bx ax 22++ (B) x e dx c bx ax 222+++(C) x x c x e be ax 222++ (D) x e cx bx ax 222)(++3. 若0),(00=y x f x ,0),(00=y x f y ,则在点),(00y x 处,函数),(y x f ( ).)A (连续. )B (取得极值. )C (可能取得极值. )D (全微分0d =z .4.设()f u 可微,⎰⎰≤++=222x 22d )()(t y y x f t F σ,则()F t '=( ).(A) ()tf t π (B) 22()tf t π (C) 22()tf t (D) 2()tf t π5.设曲面06333=-+++xyz z y x ,则在点)1,2,1(-处的切平面方程为( ).)A ( 018511=-++z y x )B ( 018511=-+-z y x)C ( 018511=--+z y x )D ( 018511=+++z y x6.)(d d 12222==⎰⎰≤++y x e I y x y x . (A))1(-e π (B)e π (C)1-e π (D)e π27. 函数),(y x f 在点),(00y x 处连续,且两个偏导数),(),,(0000y x f y x f y x存在是),(y x f 在该点可微的( ).)A ( 充分条件,但不是必要条件. )B (必要条件,但不是充分条件.)C ( 充分必要条件. )D (既不是充分条件,又不是必要条件.8. 已知)0,0(,)1,1(为函数22442),(y xy x y x y x f ---+=的两个驻点,则(). )A ()0,0(f 是极大值. )B ()0,0(f 是极小值.)C ()1,1(f 是极小值. )D ()1,1(f 是极大值.9. 周期为2的函数)(x f ,它在一个周期上的表达式为x x f =)(11 <≤-x ,设它的傅里叶级数的和函数为)(x S ,则=)23(S ( ). (A) 0 (B) 1 (C) 21 (D) 21- 10.设∑是平面4=++z y x 被圆柱面122=+y x 截出的有限部分,则曲面积分=⎰⎰∑S y d ( ). (A)34 (B)π34 (C)0 (D) π11.下列级数收敛的是( ).∑∞=1!)(n n n n n e A ∑∞=1!2)(n n n n n B ∑∞=1!2)(n n n n n C ∑∞=1!)(n nn n D . 12. 设幂级数∑∞=-1)2(n n n x a 在2-=x 时收敛,则该级数在5=x 处( ).)(A 发散 )(B 条件收敛 )(C 绝对收敛 )(D 不能判定其敛散性.二、 填空题(将答案填在横线上,每题4分,共24分)1.=-+=)1,(,arcsin )1(),(x f yx y x y x f x 则设 2. ⎰⎰=∑S x I d 2= .(其中∑是2222R z y x =++) 3.分表达式为化为球坐标下的三次积z z y x y x y x x d d d 22222221010⎰⎰⎰--+-4.=+⎰⎰≤+y x x y y x y x d d )sin sin (1225.设z yx z y x f 1)(),,(=,则=)1,1,1(df 6.=++⎰⎰⎰≤++1222222d d d )(z y x z y x z y x三、(6分)求幂级数∑∞=--111)1(n n n x n的收敛半径、收敛域及和函数. 四、(5分)计算I=y x z x x z z y z y y x ⎰⎰∑-+-+-d d )33(d d )3(d d )2(,其中:0,0,0x y z ∑===及1=++z y x 所围立体表面的外侧.五、(5分) 设,)(22ba z y e u ax ++=而b a x b z x a y ,,cos ,sin ==为常数,求.d d x u 六、(6分)设L 为x y x =+22从点)0,1(A 到点)0,0(O 的上半圆弧,求曲线积分⎰-++-L x x y y e x y y e d )1cos (d )1sin ( .七、(6分)设)(x f 有连续的二阶导数且满足[]0d )(d )(ln ='+'-⎰y x f x xy x f x c 其中c 为xoy 面上第一象限内任一简单闭曲线,且,0)1()1(='=f f 求)(x f。
2004-2005 学年第二学期大学数学分析试题及答案

一:填空(20 分)
1、函数 f (x) = e x 的带有拉格朗日型余项的麦克劳林公式为
。
2、设 f(x)为区间 I 上的可导函数,则 f 为 I 上的凸函数的充要条件为 f (x)
f (x1) + f (x1)(x2 − x1)
n+1
,
n
=
(4
1,2,
分)
n
所以当 x (0,2) 时,
f (x) = x = 4 (−1)n+1 sin nx = 4 sin x − 1 sin 2x + 1 sin 3x + (6 分)
n
2 2 2 2 3 2
5、因 an
=
n(n
1 + 1)(n
+
2)
=
1 2
1
n(n
+
1)
−
(n
由罗尔定理存在 (,1) (0,1) 使得 F ( ) = 0 ,即 f ( ) = − f ( ) (4 分)
23
n
,当 x = −1时
二:判断(16 分)
1、实轴上的任一有界点集 S 至少有一个聚点。( )
2、设 H = { ( 1 , 1 ) n+2 n
n = 1, 2, } ,则 H 能覆盖区间 (0,1)。( )
3、黎曼函数
f
(x)
=
1 , q
x = p , p, q互素, q p q
在 区 间 [0 , 1] 上 可 积 , 且
连续及连续函数的局部保号性,存在 x0 的某领域 (x0 − , x0 + ) (当 x0 = a 或
04级2004-2005学年第二学期高等数学A类期末考试安排概要
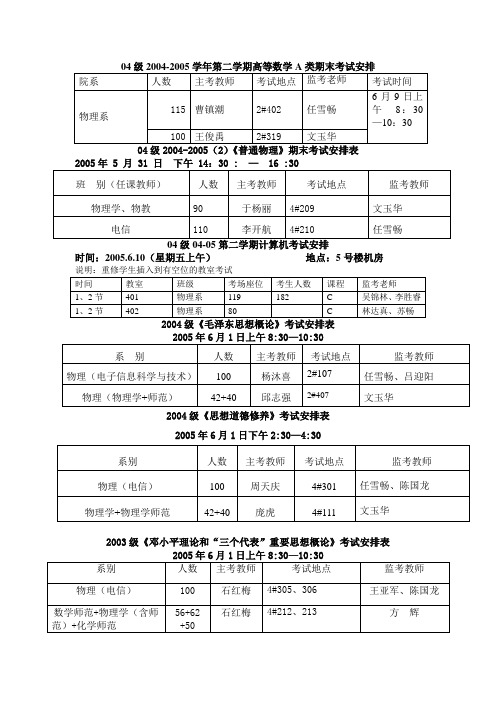
系别
人数
主考教师
考试地点
监考教师
物理(电信)
100
周天庆
4#301
任雪畅、陈国龙
物理学+物理学师范
42+40
庞虎
4#111
文玉华
2003级《邓小平理论和“三个代表”重要思想概论》考试安排表
2005年6月1日上午8:30—10:30
系别
人数
主考教师
考试地点
监考教师
03072
模拟电子线路
100
6月3下午
吴晓芳
郭生士
4#209
(07)物理
03
03071
电子线路
61
6月3上午
侯芳
方辉
2#209
(07)物理
03
03078
心理学
40
6月6日下午
4#418
(07)物理
02
02071,02072,02078
近代物理实验笔试
150
6月1晚
沈桂平
黄文达、陈谋智、高玉琳
博二201、202
半导体集成电路
30
6月1上午
李开航
陈小红
嘉四108
(07)物理
02
02072
单片机原理与应用
90
6月6下午
郑振耀
王冬、蔡淑惠
南二105南二106
(07)物理
02
02072
信号与系统
90
6月8下午
王冬
孙惠军、董继杨
南二101南二102
(07)物理
02
02072
微波原理
90
2005年考研数学二真题答案解析

1..【分析】 本题属基本题型,幂指函数的求导(或微分)问题可化为指数函数求导或取对数后转化为隐函数求导.【详解】 方法一: x x y )sin 1(+==)sin 1ln(x x e +,于是]sin 1cos )sin 1[ln()sin 1ln(x xx x e y x x +⋅++⋅='+,从而π=x dy=.)(dx dx y ππ-='方法二: 两边取对数,)sin 1ln(ln x x y +=,对x 求导,得x xx x y ysin 1cos )sin 1ln(1+++=', 于是]sin 1cos )sin 1[ln()sin 1(x xx x x y x +⋅++⋅+=',故π=x dy=.)(dx dx y ππ-='【评注】 幂指函数的求导问题,既不能单纯作为指数函数对待,也不能单纯作为幂函数,而直接运用相应的求导公式.2..【分析】 本题属基本题型,直接用斜渐近线方程公式进行计算即可.【详解】 因为a=,1)1(lim )(lim23=+=+∞→+∞→x x x x x f x x[]23)1(lim)(lim 2323=-+=-=+∞→+∞→xxx ax x f b x x ,于是所求斜渐近线方程为.23+=x y 【评注】 如何求垂直渐近线、水平渐近线和斜渐近线,是基本要求,应熟练掌握。
这里应注意两点:1)当存在水平渐近线时,不需要再求斜渐近线;2)若当∞→x 时,极限x x f a x )(lim∞→=不存在,则应进一步讨论+∞→x 或-∞→x 的情形,即在右或左侧是否存在斜渐近线,本题定义域为x>0,所以只考虑+∞→x 的情形. 3..【分析】 作三角代换求积分即可. 【详解】 令t x sin =,则=--⎰1221)2(x xxdx⎰-202cos )sin 2(cos sin πdt t t tt=.4)arctan(cos cos 1cos 20202πππ=-=+-⎰t tt d【评注】 本题为广义积分,但仍可以与普通积分一样对待作变量代换等. 4...【分析】直接套用一阶线性微分方程)()(x Q y x P y =+'的通解公式:⎰+⎰⎰=-])([)()(C dx e x Q e y dxx P dx x P ,再由初始条件确定任意常数即可. 【详解】 原方程等价为x y x y ln 2=+',于是通解为⎰⎰+⋅=+⎰⋅⎰=-]ln [1]ln [2222C xdx x x C dx ex ey dxx dxx=2191ln 31x C x x x +-, 由91)1(-=y 得C=0,故所求解为.91ln 31x x x y -=【评注】 本题虽属基本题型,但在用相关公式时应注意先化为标准型. 另外,本题也可如下求解:原方程可化为x x xy y x ln 222=+',即 x x y x ln ][22=',两边积分得Cx x x xdx x y x +-==⎰332291ln 31ln ,再代入初始条件即可得所求解为.91ln 31x x x y -=5…【分析】 题设相当于已知1)()(lim0=→x x x αβ,由此确定k 即可.【详解】 由题设,200cos arcsin 1lim )()(limkx xx x x x x x -+=→→αβ=)cos arcsin 1(cos 1arcsin lim20x x x kx x x x x ++-+→=k 21143cos 1arcsin lim 20==-+→k x x x x x ,得.43=k 【评注】 无穷小量比较问题是历年考查较多的部分,本质上,这类问题均转化为极限的计算.6…【分析】 将B 写成用A 右乘另一矩阵的形式,再用方阵相乘的行列式性质进行计算即可.【详解】 由题设,有)93,42,(321321321ααααααααα++++++=B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡941321111),,(321ααα, 于是有.221941321111=⨯=⋅=A B【评注】 本题相当于矩阵B 的列向量组可由矩阵A 的列向量组线性表示,关键是将其转化为用矩阵乘积形式表示。
20052006学年第一学期离散数学期末考试试卷A卷终稿.doc

南昌大学 2005~2006学年第一学期期末考试试卷试卷编号: 12062 ( A )卷课程名称: 离散数学 适用班级: 计算机2004级1-6班 姓名: 学号: 班级: 专业: 学院: 信息工程学院 系别: 计算机系 考试日期: 2006年1月9日题号一 二三四总分累分人 签 名12 3 4 5 6 1 2题分 20 24 5 5 6 6 8 10 6 10 100 得分考生注意事项:1、本试卷共 7页,请查看试卷中是否有缺页或破损。
如有立即举手报告以便更换。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
一、 填空题(每小题2分,共20分)得分 评阅人1、设Q 表示今天我们踢足球,P 表示今天下午我们有时间,则命题“今天我们踢足球,仅当下午我们有时间。
”可符号化为 .2、设集合A ={∅,{a }},则A 的幂集P (A )= .3、已知序偶< x -2,18> = < 9,2x -y >,则x = ,y = .4、设集合A ={1,2,3,4 }, B ={6,8,12}, A 到B 的关系R =},,2,{B y A x x y y x ∈∈=><,那么 R -1= .5、设X ={a ,b ,c },R 是X 上的二元关系,其关系矩阵为M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001001101,那么R 的 关系图为:.6、集合A 上的关系R 是反自反的,当且仅当其关系矩阵中 , 其关系图中 .7、设A ={a ,b },B ={0,1,2},那么可定义 种不同的A 到B 的单射函数。
8、设集合A ={1, 2, 3},B ={a , b },C ={x , y , z },B A f →:,C A g →:的函数,且有},3,,2,,1{><><><=b b a f ,},3,,2,,1{><><><=z y x g ,则f 是 函数,g 是 函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京大学2005级数学系数学分析(二)期末测试
说明:前四道大题共100分,最后一题为附加题。
考试时间共120分钟。
未特别标明A 、B 卷的题目为公用题。
一、叙述题(20分)
1. 设:n m f → 为多元向量值函数,0n x ∈ .叙述f 在0x 可微的定义.
(10分)
2. (A 卷)叙述正项级数Cauchy 判别法(也叫根值判别法)的条件及结论,并举一
个不能用Cauchy 判别法判别收敛性的例子.
(10分)
(B 卷)叙述正项级数d ’Alembert 判别法(也叫比值判别法)的条件及结论,并举一个不能用d ’Alembert 判别法判别收敛性的例子.
(10分)
二、判断题(20分):判断下列级数的敛散性并说明理由.
(A 卷)1.1cos n n ∞
=∑
(5分)
2.2
1
1sin
n n
∞
=∑
(5分)
3.2
2
1(ln )
n n n ∞
=∑
(5分)
4.1(1)ln 12n
n n ∞
=⎡⎤
-+⎢⎥⎣⎦
∑
(5分)
(B 卷)1.2
1sin n n ∞=∑
(5分)
2.1
n ∞
=-∑ (5分) 3.2
1ln n n n
∞
=∑
(5分)
4.1(1)ln 12n
n n ∞
=⎡⎤
-+⎢⎥⎣⎦
∑
(5分)
三、计算题(20分)
1. 方程2232327x y z xy z +++-=在(1,2,1)-附近决定了隐函数(,)z z x y =.
求
2
(1,2)z x y
∂-∂∂的值. (10分)
2. (A 卷)求函数333(,,)f x y z x y z =++在约束条件0x y z ++=,22212x y z ++=下
的极值.
(10分)
(B 卷)求函数333(,,)f x y z x y z =++在约束条件2x y z ++=,22212x y z ++=下的极值.
(10分)
四、证明题(40分)
1. (A 卷)设级数1
n n n a ∞
=⋅∑收敛.证明:级数1
n n a ∞
=∑也收敛.(提示:Abel 判别法)(10
分)
(B 卷)
设级数1
n n a ∞
=∑收敛.证明:级数1
n n a ∞
=∑也收敛.(提示:Abel 判别法)(10分)
2. (A 卷)
设(0,1)λ∈为固定的实数,:n
f →
为可微的多元函数,且2
1n
j j
f
x λ=⎛⎫
∂≤
⎪ ⎪
∂⎝⎭
∑.证明: i 、
()(),,n
f x f y x y x y λ-≤-∀∈
;
ii 、 当1n =时,存在唯一的x ∈ ,使得()f x x =.
(10分)
(B 卷)
设(0,1)λ∈为固定的实数,12(,,,):n
n
n f f f f =→ 为可微映射,
且2
,1n i i j j
f x λ=⎛⎫
∂≤ ⎪ ⎪∂⎝⎭
∑.证明:
i 、
()(),,n
f x f y x y x y λ-≤-∀∈
;
ii 、 存在唯一的n x ∈ ,使得()f x x =.
(10分)
3. 设1α>,0n a >,记1
n
n i
i S a
==∑,1,2,.n = .证明级数1
n n n
a S α
∞
=∑
总是收敛的.
(提示:可利用积分判别的思想.)
(10分) 4. 设()ij A a =为n 阶实正定对称方阵,(1,2,,)i b i n = 为实数.考虑n
上的函数
12,1
1
(,,,)n
n
n ij
i j i i
i j i f x x x a
x x b x
===
-
∑∑ .证明:
(i) f 在n 上有唯一的最小值点; (ii)
f 的最小值为,1
1
4
n
ij
i j i j a b b =-
∑,这里ij
a 是A 的逆矩阵在ij 位置的元素.
(10分)
五、附加题(10分)
(A 卷)设:n n f → 为可微的一一映射,f 的Jacobi 矩阵非退化,并且f 的逆映射f -1
连续.证明:f -1也是可微的.
(B 卷)设:n f → 为可微的多元函数,且(0,,0)0f = . 证明:存在任意可微次的多元函数:(1,2,,)n i g i n →= ,使得
1212121
(,,,)(,,,),(,,,)n
n
n i
i n n i f x x x x
g x x x x x x ==
⋅∀∈∑
.。
