干涉波前干涉2011
分波前干涉实验的现代应用及原理

分波前干涉实验的现代应用及原理分波前干涉实验,也称做前沿干涉实验,是一种利用前沿波来测量次级波的一种实验方法,这种实验涉及到波和光的原理,是物理学中研究有关声、光和电磁波传播行为的实验。
该实验不需要复杂的仪器,却能实现对声、光和电磁波的多种测试。
1、分波前现象的基本原理分波前现象是一种对非开放系统中的波能传播行为的实验方法,它是对多次复式干涉现象及相关现象的总结性阐释。
实验的基本原理是:一个定位的平行波束通过一组聚焦波束来形成一个复式的干涉现象,经过复式操作后,可以形成多次复式的干涉现象,然后导出强度的极大值和极小值。
这种现象比起两波束干涉现象来说更具有说服力,实验结果也更准确,所得的结果同时也比较稳定。
2、分波前干涉实验的现代应用(1)声学分波前干涉实验声学分波前干涉实验是利用多次复式干涉现象,测量声波能量的实验方法。
它可以用来测量声场和其他空间声学尺度参数,还可以用于测量声场的分布和噪声源的定位。
(2)光学分波前干涉实验光学分波前干涉实验是利用多次复式干涉现象,测量光波能量的实验方法。
它可以用来测量光场幅值的大小、折射率的改变等参数,也可以用于测量光的分布和定位光源等。
(3)电磁学分波前干涉实验电磁学分波前干涉实验是利用多次复式干涉现象,测量电磁波能量的实验方法。
它可以用来测量电磁波的电场和磁场的大小,以及其他参数的改变等。
三、总结分波前干涉实验是一种利用前沿波来测量次级波的一种实验方法,是物理学中研究有关声、光和电磁波传播行为的实验,它是对多次复式干涉现象及相关现象的总结性阐释,实验的基本原理是:一个定位的平行波束通过一组聚焦波束来形成一个复式的干涉现象,经过复式操作后,可以形成多次复式的干涉现象。
它可以用来测量声、光和电磁波能量的大小、改变等参数,同时也可以用于测量声、光和电磁波的分布和定位噪声源等。
分波前干涉实验的现代应用及原理

分波前干涉实验的现代应用及原理分波前干涉实验是一种经典的光学实验,它利用光的干涉现象来研究光的性质和波动特性。
这种实验在现代科学研究中有着广泛的应用,特别是在光学成像、光学通信和光学计算等领域。
分波前干涉实验的原理是基于光的干涉现象。
当两束光波相遇时,它们会发生干涉现象,即互相叠加形成干涉图样。
在分波前干涉实验中,首先将一束光通过一个波片分成两束光,这两束光分别经过不同的光学元件,再通过一个透镜汇聚到同一点上。
由于光程差的存在,光波在汇聚点上会发生干涉现象,形成干涉图样。
分波前干涉实验的现代应用之一是在光学成像中的应用。
在传统的成像系统中,由于衍射效应的存在,图像的分辨率有一定的限制。
而利用分波前干涉实验可以通过调整光波的相位和幅度,改善图像的分辨率。
通过在成像系统中引入干涉原理,可以实现超分辨成像,从而获得更清晰、更精细的图像。
另一个现代应用是在光学通信中的应用。
光通信是一种高速、大容量的通信方式,而光的干涉现象可以用来调制和解调光信号。
通过在光通信系统中引入分波前干涉实验,可以提高光信号的传输效率和稳定性。
利用干涉原理,可以实现更高的信号传输速率和更低的误码率,从而提升光通信系统的性能。
分波前干涉实验还在光学计算中得到了广泛应用。
光学计算是一种利用光的干涉现象来进行计算和处理信息的方法。
通过在光学计算系统中引入分波前干涉实验,可以实现光学逻辑门和光学储存器等光学计算元件的设计和制造。
这种基于干涉原理的光学计算方法具有高速、低功耗和大容量的优势,可以应用于光学计算机和光学存储器等领域。
分波前干涉实验在现代科学研究中有着广泛的应用。
它在光学成像、光学通信和光学计算等领域发挥着重要作用。
通过利用光的干涉现象,可以提高图像的分辨率、改善光信号的传输效率和稳定性,以及实现光学计算和信息处理。
随着科学技术的不断发展,分波前干涉实验将在更多的领域得到应用,并为人类带来更多的科学发现和技术突破。
波的干涉实验研究波的干涉现象

波的干涉实验研究波的干涉现象波的干涉是波动现象中一种非常有趣和重要的现象。
通过干涉实验,我们可以更好地理解波的性质和行为,同时也可以应用于科学、工程和技术领域。
本文将对波的干涉实验以及干涉现象进行深入探讨。
波动是一种能量的传递方式,而波的干涉是指两个或多个波在相同的介质中相遇时产生的相互影响。
干涉实验的核心是通过将波源和探测器安排在特定位置,观察干涉图案并进行分析。
最常见的干涉实验是光的干涉实验,例如杨氏双缝干涉实验。
在杨氏双缝干涉实验中,将一束光通过一个狭缝,然后经过两个相距较远的并行狭缝。
当光通过两个狭缝时,形成两个相干的光源,并在屏幕上形成干涉图案。
干涉图案包括了明暗相间的条纹,称为干涉条纹。
这些干涉条纹是由于光波的波峰和波谷相互叠加形成的。
干涉条纹的形态和间距是与波长、狭缝间距以及观察位置之间的关系密切相关的。
当光源中的波长不变时,狭缝间距越大,干涉条纹之间的间距越大。
观察者距离狭缝越远,间距也越大。
这些规律显示了干涉现象的一些基本特征。
除了光的干涉实验,声波的干涉实验也是非常常见的。
例如,我们可以通过两个孔洞对声音进行干涉实验,类似于杨氏双缝干涉实验。
通过调整孔洞之间的距离和观察者的位置,我们可以观察到声音的干涉条纹。
这些实验不仅帮助我们理解声波的干涉现象,还可以应用于声学工程和音响技术的设计。
干涉实验不仅在光和声波中有应用,还可以应用于其他波动系统,如水波、电磁波等。
这些实验为我们提供了探索波动现象的机会,有助于深入理解波的特性和行为。
通过干涉实验,我们可以研究波的相位差、相长干涉、相消干涉等现象,从而揭示波的干涉的奥秘。
总之,波的干涉实验是研究波的干涉现象的重要手段。
通过观察干涉图案,我们可以了解波的性质和行为规律。
干涉实验不仅限于光和声波,还可以应用于其他波动系统中。
波的干涉现象在科学、工程和技术领域具有广泛的应用,可以帮助我们解决实际问题并推动相关领域的发展。
分波前干涉
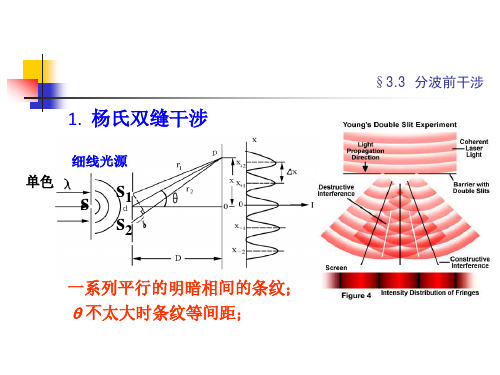
§3.3 分波前干涉
(1)条纹(中心)的位置
δ
= ϕ2
− ϕ1
−
2π λ
(r2
− r1)
2 I1I2 cosδ
现已有 亮纹:
ϕ 2- ϕ 1=0 δ = ±2kπ (k = 0,1,2,)
(相长干涉) 或波程差 ∆L = r2 − r1 = ±kλ
在θ 较小的情况下
∆L ≈ d sinθ ≈ d tanθ = d x = ±kλ
D
∴ x = ±k Dλ
k = ∆L/λ 称为干涉的级次。
d
∴ x = ±k Dλ
d 亮纹中心的位置和级次:
k = 0, x0 = 0称0级中央亮纹
Dλ
k = 1, x±1 = ± d 称 ± 1级亮纹
k
=
2,
x±2
=
±
2Dλ
d
称 ±, 干涉条纹的级次也越大.
2 I1I2 cosδ
§3.3 分波前干涉
(2) 条纹间距 相邻两亮纹(或暗纹)之间的距离都是
∆x = Dλ
d
♦可以测光波的波长 ♦对非单色光源, 有色散现象:
白光入射时,0级亮纹为白色 (可用来定0级位置);
其余级亮纹 构成彩带, 第二级亮纹就会出现重叠(为什么?)
§3.3 分波前干涉 红光入射的杨氏双缝干涉照片 白光入射的杨氏双缝干涉照片
§3.3 分波前干涉
§3.3 分波前干涉
暗纹:(相消干涉)
∆L ≈ d sinθ ≈ d tanθ
= d x = ±(2k −1) λ (k = 1,2,3,)
D
2
暗纹中心的位置和级次:
→ x = ±(2k − 1) Dλ
分波前干涉实验的现代应用及原理

分波前干涉实验的现代应用及原理分波前干涉实验是一种光学实验,它在现代科学研究中有着广泛的应用。
分波前干涉实验通过将光波分成两条或多条不同的路径,然后再将它们重新合并,利用不同路径上的光波相位差来观察干涉现象,从而研究光的性质和光与物质的相互作用。
分波前干涉实验的原理基于光的波动性质。
光是一种电磁波,它可以通过传播的方式将能量传递出去。
当光波遇到障碍物或介质边界时,会发生折射、反射、散射等现象,这些现象都会导致光波的传播路径发生变化。
分波前干涉实验利用光波的干涉现象来研究光的传播路径和相位变化。
在分波前干涉实验中,首先需要将光波分成两条或多条不同的路径。
这可以通过使用光学元件如分光镜、反射镜、透镜等来实现。
分波前干涉实验中常用的元件是分光镜,它可以将入射的光波分成两条不同的路径。
然后,光波在不同的路径上传播,经过一系列的反射、折射、透射等过程,最后再将两条路径上的光波重新合并。
在光波重新合并的过程中,光波的相位差会产生干涉现象。
相位差是指两条光波在某一点的相位差异,它可以由光波的传播路径长度差、折射率差等因素引起。
当两条光波的相位差满足一定条件时,它们将发生干涉现象。
干涉现象可以表现为明暗条纹或彩色条纹的形式,这取决于光波的相位差和干涉条件。
分波前干涉实验在现代科学研究中有着广泛的应用。
首先,它可以用来研究光的波动性质。
通过观察干涉现象,可以确定光波的波长、频率、相速度等特性。
其次,分波前干涉实验可以用来测量光学元件的性能。
例如,通过测量光波的相位差,可以计算出光学元件的折射率、厚度等参数。
此外,分波前干涉实验还可以用来研究光与物质的相互作用。
例如,在光学材料的研究中,可以通过分波前干涉实验来分析光波在材料中的传播和反射特性,从而研究材料的光学性质。
除了光学领域,分波前干涉实验还在其他领域中得到应用。
例如,在粒子物理学中,分波前干涉实验可以用来研究粒子的波动性质和相互作用。
在声学领域,分波前干涉实验可以用来研究声波的传播和干涉现象。
高中物理干涉的原理及应用

高中物理干涉的原理及应用1. 干涉的基本概念干涉是指两个或多个波在空间中相遇,产生叠加效应的现象。
在高中物理中,我们主要研究光波的干涉现象。
干涉是光的波动性的重要证据之一,对于理解光的性质和现象具有重要意义。
2. 干涉的原理干涉现象是由波的叠加原理所引起的。
当两个或多个波相遇时,它们会叠加而形成新的波。
这种叠加可能是增强的,也可能是相互抵消的,具体情况取决于波的相位差。
3. 干涉的类型3.1. 光的干涉光的干涉现象可以分为两类:分波干涉和波前干涉。
分波干涉是指光源经过一个狭缝后所发出的光波,再次经过另一个狭缝后,形成干涉图样。
波前干涉是指来自单一光源的光波通过不同路径传播后,再次相遇产生的干涉图样。
### 3.2. 声波的干涉声波的干涉现象与光的干涉类似,同样分为分波干涉和波前干涉。
声波的干涉实验可以用声源、共振腔、声屏障等实验装置来实现。
4. 干涉的应用干涉在生活和科学研究中有广泛的应用,下面列举几个典型的例子: ### 4.1. 干涉测距干涉测距是利用干涉现象进行长度测量的一种方法。
通过使用干涉仪测量入射波与反射波之间的相位差,可以计算出被测距离。
### 4.2. 多光束干涉多光束干涉是指由多个波源产生的干涉现象。
在多光束干涉实验中,可以观察到彩色的干涉条纹,这在光学原理的研究中具有重要意义。
### 4.3. 光学薄膜光学薄膜的干涉效应被广泛应用于光学元件的设计和制造。
通过在光学元件的表面上涂覆一层薄膜,可以改变光的反射和透射特性,从而实现对光的精确控制。
### 4.4. 色散干涉色散干涉是指由于折射率对波长的依赖而产生的干涉现象。
例如,彩虹就是色散干涉的结果,当太阳光经过水滴折射和反射后,形成了七彩的光谱。
5. 干涉的实验装置干涉的实验装置有多种,以下是几个常见的: ### 5.1. 杨氏双缝干涉实验杨氏双缝干涉实验是经典的光的干涉实验,通过使用两个狭缝和一个屏幕,我们可以观察到干涉条纹,从而研究光的干涉现象。
14-6 分波前干涉
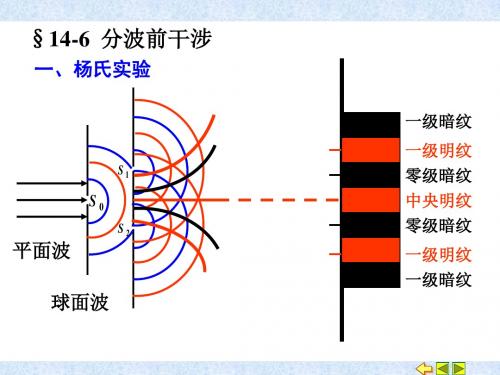
(2) 若入射光的波长为600nm,求相邻两明纹间的距离.
解 (1) x k d d k, k 0 , 1 , 2 ,
x14 x4x1d dk4k1
dd' k 4x1k4150n0m(2)
xd3.0mm
d
例 2: 在杨氏实验中双缝的间距为0.20 mm,光屏与 狭缝的距离为50 cm, 测得光屏上相邻亮条纹的间距 为1.5 mm。求光波的波长。
x
例: 讨论双缝干涉装置
的一缝后插入透明 媒质,屏幕上条纹的 移动问题.
解: (1) 讨论S2后面插入折
射率为n, 厚度 为l 的透
s1
r 10 20 1
d
s2
r
n
2
l
D
θ
x
50
0
明媒质
真空中:
xk
D d
kλ
D d D x
k 0 x 0 0 中央明纹
插入媒质: δ[(r2l)nl]r1
这表示干涉条纹整体向下平移了10mm。
例4 折射率为1.5的玻璃片插入杨氏实验 的一束光路中,光屏上原来第5级亮条纹所 在的位置变为中央亮条纹,试求插入的玻 璃片的厚度。已知光波波长为6×10-7m。
求玻璃片的厚 度为多少?
hr1S1r Nhomakorabear2
θ d
S2 D
第5级亮条 纹位置变成 中央亮条纹
P
P0
最后得到玻璃片的厚度为
h5561076106m
n1 1.51
答:插入的玻璃片的厚度为6×10-6m。
其他分波阵面干涉装置
劳埃镜 费涅耳双棱镜 费涅耳双面镜
1、洛埃镜
光栏
E
分波前干涉PPT课件

半波损失
*当光从折射率小的光疏介质,正入射或掠入射于折射率 大的光密介质时,则反射光有半波损失。
*当光从折射率大的光密介质,正入射于折射率小的光疏介质 时,反射光没有半波损失。
*折射光没有相位突变
没有半波损失
有
半 波
n
1
反射波 n1 n2
n
2
反射波
损 失
n2
折射波
n
1
折射波 n1 n2
五、干涉条纹的可见度与光源的宽度和单色性
例:在杨氏实验装置中,采用加有蓝绿色滤光片的白光 光源,其波长范围为x=100nm,平均波长为490nm.试 估算从第几级开始,条纹变得无法分辨?
解 设该蓝绿光的波长范围为l1~l2,则按题意有
l2 l1 l 100nm,
1 2
(l2
l1 )
l
490nm
对应于l1l,杨氏干涉条纹中第k级明纹的位置分别为
原子发射的光,其波列长度是有限的 ,光谱线都有一定宽度,不是严格的 I0/2 单色光钠光灯发出的黄色光不是单色 光。氦-氖激光器发出的光也不是严 格的单色光。
l
l
Δλ
波列越长,谱线宽度越窄, 光的单色性越好。
Δλ
谱线宽度
相干光
先对光波做一描述:
光波是矢量 E 和 H 在空间的传播。
E
实验证明光波中参与与物
4.思考:
(1)要条纹变宽,可采取什么措施? x=Dld
(2)用白光照射双缝, 在 S1和 S2 用一滤光片,则结果将 如何?在 S1和 S2 分别用不同滤光片,则结果又如何? (3)用单色光照射双缝, 在S1或 S2 前放一透明介质片 (如云母),则结果将如何?
此时中央 明纹下移
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两者的对应关系,不是相等关系。 在运算操作中体现其作用
辐角取负数,使得相位的落后表现为辐角的增加。
两种典型的波及其复数形式:
平面简谐波
U
(rr,
t)
=
A
cos(ωt
-
r k
⋅
rr
-
ϕ0
)
U% (rr, t) = Aeikr⋅rr ⋅ e-iωt 设 ϕ0 = 0
U% *(P) = A(P)e-iϕ(P)
• 作业: – 147页 1题、2题、 3 题、4题 – 148页 5题、6题
第二节 波 前
x
波前概念:
U%波
1 波前的传统概念:
跑在最前面的波面称为波前。
z
2 广义波前概念:
y
U% (x, y)
在研究定态光波时,波面是否跑在前面不重要。
决定光波在某个平面上(x, y)被接收效果的,是该
z = 0 面上的球面波波前函数。
x
发散球面波:
U% (P) = a1 exp(ikr) r
Q
R
U%3
z
r = (x−x0)2 +(y−y0)2 +(z−z0)2
x0 = y0 = 0 z0 = −R z = 0
U% 3 ( x,
y)
=
a1 r
exp(ikr)
r = x2 + y2 + R2
平面或球面波前函数及其共轭波前
O
r
y
r
P x' ρ
O' y'
z
ρ = x '2 + y '2
x
r
O
r = z2 + ρ2
y
z
r = z2 + ρ 2 = z(1+ ρ 2 − ...)
2z2
U (x ', y ') =
a
exp[ik (z + ρ 2 )]
z(1 + ρ 2 / 2 z 2 )
2z
平面波前 U (x ', y ') = a exp(ikz) z
P x'
ρ
O' y'
U (x ',
y ')
=
z(1 +
a
ρ2
/ 2z2)
exp[ik ( z
+
ρ2
)] 2z
傍轴条件:(振幅为常数的条件)
ρ2
z2
<< 1
或 z2 >> ρ 2
远场条件:(位相为常数的条件)
1 k ρ2 <<π 或
2z
z >> ρ 2 λ
复振幅近似为:
U ( x ', y ') = a exp(ikr ) z
U (x ', y ') = a exp(ikz) r
两者都满足时:
U (x ', y ') = a exp(ikz) z
傍轴条件和远场条件,那个更严格?
傍轴条件 远场条件
ρρ << 1
zz ρρ << 1 zλ
可见,当λ< z 时,远场条件更严格。 当λ> z 时,傍轴条件更严格。
在光学中,一般是远场条件蕴含傍轴条件
= Aexp[ik(x cosα + y cos β + z cosγ )]
平面波复振幅的特点:
1)振幅为常数,与场点位置无关。 2)相位分布是场点位置的线性函数。(线性相因子)
* 线性相因子系数Ù平面波传播方向
kx2
+ ky2
+ kz2
=k
=
2π λ
球面波的复振幅及其特点
(1) 发散球面波 复振幅表达式为:
一般矢量波有三个自由度。 电磁场有两个垂直于传播方向的自由度。是横波。
波线
在波的几何描述中,有如下概念: 球面波 波面
波面:等相面。 波线:能量传播的路径。 在各向同性媒质中,波面与波线正交; 在各向异性媒质中,波面与波线一般不正交;
按照等相面的形状,可分为: 球面波:波面是球面。几何光学中的同心光束。 平面波:波面是平面。几何光学中的平行光束。
(1)一列平面波,其传播方向平行于(xz)平面,且
与z轴夹角r为θ。写出在 z = 0 面上的波前函数。
对于波矢 k1
x
k1x = k1 sinθ
k1
θ
k1y = 0
U%1
z
k1z = k1 cosθ
U%1(x, y) = Aexp(ik1xsinθ)
平面或球面波前函数及其共轭波前
(2)分析与 U1 共轭的是怎样的一列波。
r r0’ r0
z
P x' ρ
O' y'
r0
'
=
z
+
x2 + y2 2z
−...
r0
=
z
+
x '2 + y '2 2z
− ...
r0
=
z
+
x '2 + y '2 2z
− ...
r0
'
=
z
+
x2 + y2 2z
−...
Q
x
O
y
r r0’ r0
z
r = z2 + (x - x ') 2 + ( y - y ') 2
A (P): 振幅的空间分布
ϕ (P): 位相的空间分布 时间项:ωt [ω为圆频率]
与时间无关 与场点坐标无关
体现了定态波振幅稳定,频率单一的特点。
波函数的复数表示
为了运算和理论分析上的方便,将简谐波函数的 实数形式变换为复数形式.
两者的对应关系:
U ( P , t ) = A( P ) cos(ω t - ϕ ( P ))
傍轴距离: z1 = 50 ρ ≅ 70 cm 远场距离: z2 = 50ρ 2 / λ = 50cm
轴外物点满足傍轴条件与远场条件时的复振幅
r = z2 + (x - x') 2 + (y - y') 2
Q
x
r0 = z2 + x ' 2 + y ' 2
O
y
r0 ' = z 2 + x 2 + y 2
对于场点:P(x, y, z)
设点源坐标为: Q(x0, y0 , z0 )
z P(x, y, z)
k r
球面波复振幅表达式为:
U% (P) = a1 exp(ikr) r
Q(x0, y0 , z0 )
o
y
x
r = (x − x0)2 + (y − y0)2 + (z − z0)2
• 例题: 已知相位分布
中,e-iωt 是独立的。
振幅的空间分布A (P) 和相位的空间分布 ϕ (P)
是关注的重点。
引入复振幅的概念,用来统一表示光波的空间分布特点:
U% (P) = A(P)eiϕ(P)
分析定态波场,就是分析复振幅分布。
平面波的复振幅及其特点
平U% (面rr)波=复A振ex幅p(i表kr 达⋅ rr)式为: = Aexp[i(kx x + ky y + kz z)]
面上的光场分布 U% (x, y)
在现代波动光学中,波前指与接收平面直接打交道的
光场分布: U% (x, y) (也称波前函数)
在此概念下,波前不一定就是等相面; 不再关心等相面是何种形貌。
波前分析是现代波动光学的主要内容
波前的描述与识别 波前的叠加与干涉 波前的变换与分解 波前的记录与再现
平面或球面波前函数及其共轭波前
例题5 设单色点光源发射的光波波长λ~ 0.5um, 横向观测范围的线度ρ~ 1mm,估算傍轴距离和远场距离。
取50倍作为<<1 的条件。
傍轴距离: ρ ρ = 1 / 5 0
zz 远场距离: ρ ρ = 1 / 5 0
zλ
z1 = 50 ρ ≅ 7mm
z2 = 50ρ 2 / λ = 100m
例题6 某点声源发射的声波波长λ~ 1m, 横向观测范围的线度ρ~ 10m,估算傍轴距离和远场距离。
定态波和脉冲波时间划分是相对的。
光波周期: T ≈ 1 0 -14 s
普通光源微观粒子一次持续发光时间: τ ≈ 1 0 -8 s
波列内含有周期数:1 0 6
视为定态波。
对于一次持续发光时间为: 1 0 -12 s
就认为是脉冲波。
当前脉冲波在实验室中可达到: 4 .5 × 1 0 -15 s
定态光波的标量表示
r = z + x '2 + y '2 + x2 + y2 − xx '+ yy ' + ...
2z
2z
z
=
r0
+
x2 + y2 2z
−
xx '+ z
U% (x, y) = A exp(-i2π fx)
分析与该波前函数相联系的波的类型和特征。
据题意: kx = −2π f ky = 0 Z = 0 U% (rr) = Aexp[i(kxx + ky y + kz z)]
