初三数学综合试卷
初三数学试卷题及答案

#### 一、选择题(每题4分,共20分)1. 下列数中,是正数的是()A. -3B. 0C. 1.5D. -1.2答案:C2. 下列代数式中,正确的是()A. a + b = b + aB. a - b = b - aC. ab = baD. a ÷ b = b ÷ a答案:A3. 在直角坐标系中,点A(2,3)关于x轴的对称点是()A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,6)答案:A4. 一个长方形的长是6cm,宽是4cm,它的对角线长是()A. 8cmB. 10cmC. 12cmD. 14cm答案:B5. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x^2 + 1D. y = 2x^2 - 3答案:B#### 二、填空题(每题5分,共25分)6. 若a = -3,则a^2的值是______。
答案:97. 分数3/4与-1/2的和是______。
答案:1/48. 在等腰三角形ABC中,底边BC的长度为6cm,腰AB和AC的长度相等,则AB 和AC的长度是______。
答案:6cm9. 如果x + 2 = 5,那么x的值是______。
答案:310. 下列等式正确的是______。
答案:a + b = b + a#### 三、解答题(每题10分,共30分)11. 解方程:3x - 5 = 2x + 1。
解答:3x - 5 = 2x + 13x - 2x = 1 + 5x = 6答案:x = 612. 计算下列三角形的面积:底边长为8cm,高为6cm。
解答:三角形面积公式:S = (底边长× 高) / 2S = (8cm × 6cm) / 2S = 48cm² / 2S = 24cm²答案:24cm²13. 已知函数y = 2x - 3,当x = 4时,求y的值。
初三数学综合试卷 5
初三数学综合试卷 52012.1(考试时间:120分钟 满分:150分)一、选择题(每题3分,共24分) 1.与2是同类二次根式的是A . 4B . 6C .12D . 8 2.在Rt △ABC 中,∠C=90°,AC=3,A cos =43,则AB 长为A .7B . 4C .5D .33.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:选 手 甲 乙 丙 丁 平均数(环) 9.2 9.2 9.2 9.2 方差(环2)0.0350.0150.0250.027则这四人中成绩发挥最稳定的是A .甲B .乙C .丙D .丁4.不论k 取何值,关于x 的方程x 2-kx -4=0的根的情况是 A .有两个不相等的实数根 B .有两个相等实数根 C .方程只有一个实数根 D .没有实数根 5.如图,⊙O 的半径5cm ,弦AB 垂直于直径CD ,垂足为M ,若OM ∶OD=3∶5,则AB 长为 A .4cm B .6cm C .8cm D .10cm 6.二次函数解析式为y=-(x+1)2-2,则它的顶点坐标为A .(1,2)B .(-1,2)C . (1,-2)D .(-1,-2)7.下列函数中,y 随x 的增大而减小的是A .y=2x+1B .xy 3-=(0x >) C .y=-x 2 D .122+-=x x y (1<x )8.如图所示的抛物线是二次函数y=ax 2+bx+c(a≠0)的图像,则下列结论:①abc>0;② b+2a=0;③抛物线与x 轴的另一个交点为(4,0); ④a+c>b ⑤3a+c <0 其中正确的结论有A .5个B .4个C .3个D .2个二、填空题:(每题3分,计30分)9.若式子1-a 有意义,则字母a 的取值范围是________________. 10.数据-3,2,1,0,4,这组数据的极差为__________.11.某厂八月份生产某种机器100台,计划十月份生产该种机器280台.设九、十月份每月的平均增长率为x ,根据题意列出的方程是_________________.12.已知⊙1O 与⊙2O 的半径分别为5和2,12O O =3,则⊙1O 与⊙2O 的位置关系是________.13.在△ABC 中,(2sinA -1)2+1cos 2B -=0,则△ABC 的形状为________.14.若一个正多边形的每一个外角都是36°,则这个正多边形的边数为__________. 15.一个圆柱的侧面展开图是相邻边长分别为4和6的矩形,则该圆柱的底面圆的半径是____.16.如图,在⊙O 中,∠OAC=24˚,弦CD ∥OA ,∠CDO =__________˚17.如图,在Rt △ABC 中,∠ABC=90˚,点E 在AB 上,AB=8,以BE 为直径的⊙O 与AC相切于点D ,若AD=4,则△ABC 的面积为_________.18.如图,在矩形ABCD 中,CD=1,点C 沿抛物线y=x 2-6x+10滑动,在滑动过程中CD ∥x 轴,AB 在CD的下方,则点D 在运动的过程中所形成的图形的解析式为 .三、解答题:19.(本题8分)计算:12+(-21)-2+(π-2012)0-3tan30˚20.(本题8分)先化简,再求值 12112-⎪⎪⎪⎭⎫⎝⎛+-÷+x xx x x ,其中x=12+ 21.(本题8分)某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩。
初三数学试卷综合题及答案

一、选择题(每题5分,共50分)1. 已知等差数列{an}的前n项和为Sn,且a1=3,S10=120,则该数列的公差d为:A. 1B. 2C. 3D. 4答案:B解析:由等差数列前n项和公式得:S10 = n/2 (a1 + a10) = 10/2 (3 + a10) = 120解得:a10 = 24又因为a10 = a1 + 9d,代入a1=3,得:24 = 3 + 9d解得:d = 22. 在直角坐标系中,点A(2,3)关于直线y=x的对称点为B,则点B的坐标为:A.(3,2)B.(2,3)C.(-3,-2)D.(-2,-3)答案:A解析:直线y=x是第一象限和第三象限的对角线,点A(2,3)关于该直线的对称点B的坐标为(3,2)。
3. 若函数f(x) = 2x + 1的图像向右平移a个单位,向上平移b个单位,则新函数g(x)的解析式为:A. g(x) = 2x + 1 - a + bB. g(x) = 2x + 1 + a + bC. g(x) = 2x - 1 + a + bD. g(x) = 2x - 1 - a - b答案:B解析:函数图像向右平移a个单位,相当于将x的值减去a;向上平移b个单位,相当于将y的值加上b。
因此,新函数g(x)的解析式为g(x) = 2x + 1 + a + b。
4. 在△ABC中,∠A=45°,∠B=60°,则∠C的大小为:A. 45°B. 60°C. 75°D. 90°答案:C解析:三角形内角和为180°,所以∠C = 180° - ∠A - ∠B = 180° - 45° - 60° = 75°。
5. 若等比数列{an}的首项为2,公比为q,且S5=32,则q的值为:A. 2B. 4C. 8D. 16答案:B解析:由等比数列前n项和公式得:S5 = a1 (1 - q^5) / (1 - q) = 32代入a1=2,得:2 (1 - q^5) / (1 - q) = 32化简得:1 - q^5 = 16(1 - q)解得:q = 4二、填空题(每题10分,共40分)6. 若等差数列{an}的公差为d,且a1=5,a10=25,则该数列的第15项an为______。
初三中考必考的数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √9B. πC. √-1D. √42. 若a > b,那么下列不等式中正确的是()A. a + 2 > b + 2B. a - 2 < b - 2C. 2a > 2bD. 2a < 2b3. 下列函数中,定义域为实数集R的是()A. y = √xB. y = x^2C. y = 1/xD. y = |x|4. 在直角坐标系中,点A(-2,3)关于原点的对称点是()A. (2,-3)B. (-2,-3)C. (-2,3)D. (2,3)5. 若一个等腰三角形的底边长为6cm,腰长为8cm,则该三角形的周长是()A. 22cmB. 24cmC. 26cmD. 28cm6. 已知一次函数y = kx + b的图象经过点(2,3)和(-1,1),则该函数的解析式为()A. y = 2x - 1B. y = -2x + 1C. y = 2x + 1D. y = -2x - 17. 下列图形中,不是轴对称图形的是()A. 矩形B. 正方形C. 菱形D. 梯形8. 在三角形ABC中,若∠A = 60°,∠B = 45°,则∠C的度数是()A. 45°B. 60°C. 75°D. 90°9. 若一个数x满足不等式x - 3 < 2x + 1,则x的取值范围是()A. x > -4B. x < -4C. x ≥ -4D. x ≤ -410. 下列等式中,正确的是()A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C. (a + b)^2 = a^2 - 2ab + b^2D. (a - b)^2 = a^2 + 2ab - b^2二、填空题(每题3分,共30分)11. 若m = 2,则方程2m - 3 = 0的解是______。
数学初三考试试卷及答案

一、选择题(每题3分,共30分)1. 已知函数f(x) = 2x + 3,那么f(-1)的值为:A. -1B. 1C. 2D. 52. 下列各组数中,成等差数列的是:A. 1, 2, 4, 8B. 1, 3, 5, 7C. 2, 4, 6, 8D. 3, 6, 9, 123. 下列各式中,正确的是:A. (a + b)² = a² + b²B. (a - b)² = a² - b²C. (a + b)² = a² + 2ab + b²D. (a - b)² = a² - 2ab + b²4. 若m、n是方程x² - mx + n = 0的两根,则下列各式中正确的是:A. m + n = mB. m + n = -mC. mn = mD. mn = -m5. 已知等腰三角形ABC中,AB = AC,且∠BAC = 60°,那么∠B的度数为:A. 30°B. 45°C. 60°D. 90°6. 下列函数中,y = 2x - 1的图像是一条直线的是:A. y = x²B. y = √xC. y = 2x - 1D. y = x³7. 已知a、b、c是等差数列的三个相邻项,且a + b + c = 12,则b的值为:A. 4B. 6C. 8D. 108. 在△ABC中,∠A = 45°,∠B = 60°,则△ABC是:A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形9. 已知x + y = 5,xy = 6,则x² + y²的值为:A. 19B. 20C. 21D. 2210. 已知函数f(x) = ax² + bx + c(a ≠ 0),若f(1) = 2,f(-1) = 4,则下列各式中正确的是:A. a = 1,b = 1,c = 1B. a = 1,b = 2,c = 1C. a = 2,b = 1,c = 1D. a = 2,b = 2,c = 1二、填空题(每题5分,共25分)11. 已知等差数列{an}中,a1 = 3,d = 2,则an = ________。
楚雄市新街中学初三数学综合训练试卷及答案
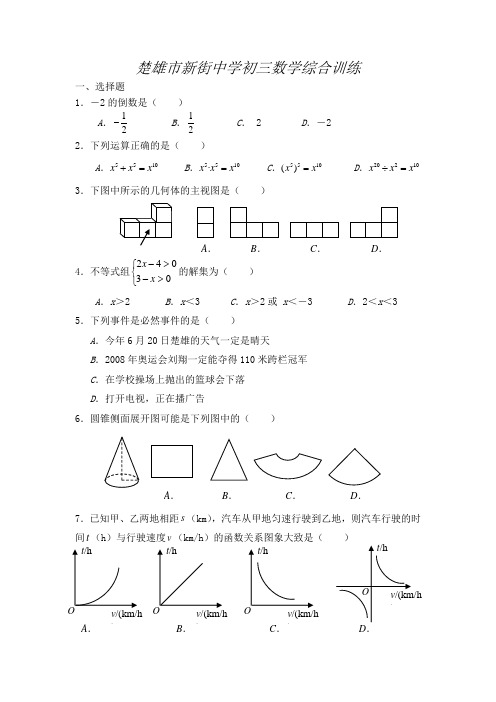
楚雄市新街中学初三数学综合训练一、选择题1.-2的倒数是( )A .12-B .12C . 2D .-22.下列运算正确的是( )A .5510x x x +=B .5510·x x x = C .5510()x x = D .20210x x x ÷= 3.下图中所示的几何体的主视图是( )4.不等式组⎩⎨⎧>->-03042x x 的解集为( )A .x >2B .x <3C .x >2或 x <-3D .2<x <3 5.下列事件是必然事件的是( )A .今年6月20日楚雄的天气一定是晴天B .2008年奥运会刘翔一定能夺得110米跨栏冠军C .在学校操场上抛出的篮球会下落D .打开电视,正在播广告6.圆锥侧面展开图可能是下列图中的( )7.已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )A .B .C .D .A .B .C .D .)))A .B .C .8.如图,小明从点O 出发,先向西走40米,再向南走30米到达点M ,如果点M 的位置用(-40,-30)表示,那么(10,20)表示的位置是( )A .点AB .点BC .点CD .点D 二、填空题9.分解因式:21x -= . 10.如图,直线a b ,被直线c 所截,若a b ∥,160∠=°,则2∠= °.11.楚雄鄂加老虎山电站年发电量约为156亿千瓦时,用科学记数法表示156亿千瓦时= 千瓦时. 12.函数13y x =-中,自变量x 的取值范围是 . 13.为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2,则图2中“乒乓球”部分占 (填百分数).14.下面是一个简单的数值运算程序,当输入x 的值为2时,输出的数值是 .15.如图,点P 在AOB ∠的平分线上,若使AOP BOP △≌△,则需添加的一个条件是 .(只写一个即可,不添加辅助线)1 2c ab图1图2ABP O输入x(2)⨯-4+输出三、解答题16.先化简,再求值:223(2)()()a b ab b b a b a b --÷-+-,其中112a b ==-,.17.解分式方程:233x x=-.18.AB 是⊙O 的直径,PA 切⊙O 于A ,OP 交⊙O 于C ,连BC .若30P ∠=,求B ∠的度数.19.如图,E F ,是平行四边形ABCD 的对角线AC 上的点,CE AF =. 请你猜想:BE 与DF 有怎样的位置..关系和数量..关系?并对你的猜想加以证明. 猜想: 证明:20.如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:(1)作出关于直线AB 的轴对称图形; (2)将你画出的部分连同原图形绕点O 逆时针旋转90°;(3)发挥你的想象,给得到的图案适当涂上阴影,让它变得更加美丽.APAO ABCDE F21.根据“十一五”规划,双柏—元谋的高速工路即将动工.工程需要测量某一条河的宽度.如图,一测量员在河岸边的A 处测得对岸岸边的一根标杆B 在它的正北方向,测量员从A 点开始沿岸边向正东方向前进100米到达点C 处,测得68=∠ACB .求所测之处河AB 的宽度. (o o o sin68≈0.93,cos68≈0.37,tan68≈2.48)22.一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.(1)从箱子中任意摸出一个球是白球的概率是多少?(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.23.某产品每件成本10元,试销阶段每件产品的销售价x (元)与产品的日销量y若日销量y (件)是销售价x (元)的一次函数.(1)求出日销量y (件)与销售价x (元)的函数关系式;(2)要使每日的销售利润最大,每件产品的销售价应定位多少元?此时每日的销售利润是多少? 24.(本小题(1)~(3)问共12分;第(4)问为附加题,共5分,附加题得分可以记入总分,若记入总分后超过120分,则按120分记)如图,抛物线2y 23=--x x 与x 轴交A 、B(A 点在B 点左侧),直线l 与抛物线交于A 、C 其中C 点的横坐标为2. (1)求A 、B 两点的坐标;(2)求直线AC 的函数表达式;(3)P 是线段AC 上的一个动点,过P 点作y 平行线交抛物线于E 点,求线段PE (4)点G 抛物线上的动点,在x 轴上是否存在点使A 、C 、F 、G 四边形?如果存在,求出所有满足条件的F 如果不存在,请说明理由.第24题学校 班级 考号 姓名__________________________◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆楚雄市新街中学初三年级数学综合训练(答题卡)9. . 10. . 11. . 12. .13. . 14. . 15. . 三、解答题16. 先化简,再求值: 17. 解分式方程:233x x=-. 223(2)()()a b ab b b a b a b --÷-+-, 解:其中112a b ==-,解:18.解:19. 猜想:证明:APABCDE F20.解: 21.解:22.解:(1)(2)23.解:(1)(2) 24.解:AOB楚雄市新街中学初三数学综合训练(参考答案)一、选择题(本大题共8个小题,每小题3分,满分24分)1.A 2.B 3. D 4.D 5.C 6.D 7.C 8.B 二、填空题(本大题共7个小题,每小题3分,满分21分)9.(x +1)(x -1) 10.60 11.1.56×10912.x ≠3 13.10% 14.0 15.OA=OB 或∠OAP=∠OBP 或∠OPA=∠OPB 三、解答题(本大题共9个小题,满分75分) 16.(本小题7分)解:解:原式22222()aab b a b =---- 将112a b ==-,代入上式得22222a ab b a b =---+ 原式12(1)2=-⨯⨯-2ab =- 1=17.(本小题7分)解:去分母,得23(3)x x =-去括号,移项,合并,得9x =检验,得9x=是原方程的根.18.(本小题8分)PA 切⊙O 于A AB ,是⊙O 的直径,∴90PAO∠=.30P ∠=,∴60AOP ∠=.∴1302BAOP ∠=∠=.19.(本小题8分) 猜想:BE DF ∥,BE DF =证明:证法一:如图19- 1四边形ABCD 是平行四边形. BC AD ∴= 12∠=∠ 又CE AF =BCE DAF ∴△≌△ BE DF ∴= 34∠=∠ BE DF ∴∥证法二:如图19-2连结BD ,交AC 于点O ,连结DE ,BF .四边形ABCD 是平行四边形 BO OD ∴=,AO CO = 又AF CE =ABCDEF图19-2O ABCDEF 图19-123 4 1白1白2红白1白2红红白2白1第二次摸出 的球第一次摸出 的球开始AE CF∴=EO FO∴=∴四边形BEDF是平行四边形BE DF∴∥20.(本小题9分)如图.三步各计3分,共9分.21.(本小题9分)解:解:在BACRt∆中,68=∠ACB,∴24848.210068tan=⨯≈⋅=ACAB(米)答:所测之处河的宽度AB约为248米22.(本题8分)解:(1)从箱子中任意摸出一个球是白球的概率是23P=(2)记两个白球分别为白1与白2,画树状图如右所示:从树状图可看出:事件发生的所有可能的结果总数为6,两次摸出球的都是白球的结果总数为2,因此其概率2163P==.23.(本题满分8分)解:(1)y=-x+40;(2)w=y(x-10)=(-x+40)(x-10)当销售价定为25元/件时日销售利润最大,为225元. 24.(本小题(1)~(3)问共12分;第(4)问为附加题,共5分,附加题得分可以记入总分,若记入总分后超过120分,则按120分记)解:(1)令y=0,2230--=x x,解得11x=-或23x=∵ A点在B点左侧∴ A(-1,0) B(3,0).(2)将C点的横坐标x=2代入223y x x=--得y=-3,∴C(2,-3)设直线AC的函数解析式为y=kx+b∴-0-12-3-1解得,+==⎧⎧⎨⎨+==⎩⎩k b kk b b∴直线AC的函数解析式是y=-x-1(3)设P点的横坐标为x(-1≤x≤2)则P、E的坐标分别为:P(x,-x-1), E2(,23)x x x--∵P点在E点的上方,PE=22(1)(23)2x x x x x-----=-++=49)21(2+--x∴当12x=时,PE的最大值=94;(4)存在4个这样的点F,分别是1F(1,0)、2F(-3,0)、3F(74+,0)、4F(74-,0),理由略。
初三数学试卷试题及答案

初三数学试卷试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 2B. πC. 0.5D. √4答案:B2. 如果一个三角形的两边长分别为3和4,那么第三边的长x满足的条件是:A. x > 1B. 1 < x < 7C. x = 7D. 7 < x < 10答案:B3. 一个数的平方根是它本身的数是:A. 0B. 1C. -1D. 0或1答案:D4. 下列哪个选项不是单项式?A. 3xB. 5x^2C. 2xyD. x/y答案:D5. 一个圆的直径是10cm,那么它的面积是:A. 25π cm²B. 50π cm²C. 100π cm²D. 200π cm²答案:B6. 函数y=2x+3的图像不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:B7. 一个数的相反数是它本身,这个数是:A. 0B. 1C. -1D. 0或1答案:A8. 一个等腰三角形的两边长分别为5和8,那么第三边的长是:A. 5B. 8C. 13D. 不能确定答案:B9. 一个数的绝对值是它本身,这个数是:A. 正数B. 负数C. 非负数D. 非正数答案:C10. 函数y=x^2的图像是:A. 直线B. 抛物线C. 双曲线D. 圆答案:B二、填空题(每题3分,共30分)1. 圆的周长公式是______。
答案:C=2πr2. 一个数的立方根是它本身的数是______。
答案:0,1,-13. 一个等边三角形的内角和是______度。
答案:1804. 函数y=3x-2与x轴的交点坐标是______。
答案:(2/3, 0)5. 如果一个数的平方是25,那么这个数是______。
答案:±56. 一个数的倒数是它本身,这个数是______。
答案:±17. 一个直角三角形的两条直角边长分别为3和4,那么斜边长是______。
09.2024石景山初三二模数学试卷答案

石景山区2024年初三综合练习数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可。
2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
3.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
第一部分选择题一、选择题(共16分,每题2分)题号12345678答案ACBADBAC第二部分非选择题二、填空题(共16分,每题2分)9.1x 10.23y x ()11.31x y,12.6 13.214.1015.1.816.24006000;三、解答题(共68分,第17-18题,每题5分,第19-20题,每题6分,第21-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分)17.解:原式6113…………………………4分 .…………………………5分18.解:原不等式组为3452924x x xx,①.②解不等式①,得3x .…………………………2分解不等式②,得1x .…………………………4分∴原不等式组的解集为31x .…………………………5分19.(1)证明:∵90AD BC BCD ∥,°,∴90ADC °.∵AB AC ,AE 平分BAC ,∴90AEC °.∴四边形AECD 是矩形.…………………………3分(2)解:∵90130BCD °,°,∴260 °.∵AB AC ,∴ABC △是等边三角形.∴2BC AC AB .在Rt ADC △中,cos 12CD AC ,∴CD .在Rt BCD △中,BD .…………………………6分20.解:设引进新设备前工程队每天改造道路x 米.根据题意,得……………1分21075021022120x x %.…………………………3分解这个方程,得30x .…………………………4分经检验,30x 是所列方程的解,并且符合实际问题的意义.……………5分答:引进新设备前工程队每天改造道路30米.…………………………6分21.(1)证明:依题意,得226491m m ()()2236364m m 40 .∴此方程有两个不相等的实数根.…………………………2分(2)解:∵x,12x x ,∴123131x m x m ,.∵2123x x ,∴312313m m ().∴2m .…………………………5分AB CDE2122.解:(1)∵一次函数0y k x b k ()的图象由函数2y x 的图象平移得到,∴2k .∵一次函数0y k x b k ()的图象经过点13A (,),∴23b .∴1b .∴该函数的解析式为21y x .…………………………2分∵函数21y x 的图象与过点03(,)且平行于x 轴的直线交于点B ,∴点B 的纵坐标为3.令3y ,得2x .∴点B 的坐标为23(-,).…………………………3分(2)13n ≤≤.…………………………5分23.解:(1)m 的值为90,n 的值为92;…………………………2分(2)七年级;…………………………4分(3)50.…………………………5分24.(1)证明:连接OB ,如图1.∵PA PB ,是O ⊙的切线,OA OB ,是O ⊙的半径,∴PA PB ,90OAP OBP °.∴90D C °,1290 °.∵OB OC ,∴2C .∴1D .∴PD PB .又∵PA PB ,∴PD PA .…………………………3分图1(2)解:连接OB ,AB ,如图2.在Rt PAE △中,1sin 3PA E PE ,设3PA x PE x ,.则PD PB PA x,AE .在Rt OBE △中,1sin 3OB E OE,13 .解得1x .∴2AD,CD∵AC 是O ⊙的直径,∴90CBA °.∵90CBA CAD °,C C ,∴CBA △∽CAD △.∴BC ACAC DC.∴BC …………………………6分25.解:(1)如图;………2分(2)答案不唯一,如5.5,66.0;………4分(3)>.………5分26.解:(1)由题意,抛物线的对称轴为22bx b.∵点24M m N n (,),(,)在抛物线22y x bx c 上,且m n ,∴42b b .∴3b .…………………………2分(2)∵点24M m N n (,),(,),0T x p (,)在抛物线22y x bx c 上,∴44m b c ,168n b c ,2002p x bx c .∵m p ,∴0p m .即2002440x bx c b c ()().002220x x b ()().∵001x ,∴020x .∴0220x b .022x b .∴221b ≥.∴32b ≥.∵p n ,∴0p n .即20021680x bx c b c ()().004420x x b ()().∵001x ,∴040x .∴0420x b .024x b .∴240b ≤.∴2b ≤.综上所述,b 的取值范围是322b ≤≤.…………………………6分27.(1)15;…………………………1分(2)①解:∵四边形ABCD 是正方形,∴90ABC °,BA BC .∵点F 与点C 关于直线BE 对称,∴BF BC ,90MHF °.∴BF BA .设1 .在BFC △中,BF BC ,可得1809024522().在BFA △中,BF BA ,可得18019022BFA.∴3290454522BFA()().……………3分②数量关系:2222MB MD AB .证明:过点A 作AN AM 交BM 于点N ,连接BD ,如图2.在Rt FHM △中,345 ,可得45HMF .∴45ANM AMN ,135ANB .∴AM AN .∵四边形ABCD 是正方形,∴90BAD °,AD AB ,BD .∴45 .∴AMD △≌ANB △.∴135AMD ANB .∴90BMD AMD AMN .在Rt BMD △中,由勾股定理,得222MB MD BD ,即2222MB MD AB .…………………………7分28.解:(1)①2;…………………………1分②322t ≤;…………………………3分(2)2b≤或2b ≤.…………………………7分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学综合试卷 姓名________
一填空题: 1. -32的倒数是__________; x 的绝对值等于 3-,则x=_______.
2. 12的平方根是_________; 正八边形的每个内角为______. -2cos45 °_________;
3. 我国现有总人口129533万人,如果以亿为单位,并保留两位小数可以约是________亿人.
4. -20-(-1)-1=_________; 分解因式x 2-y 2
+3y-3x=___________________.
5. 如果x m =4,x n
=8(m,n 为自然数),那么x =
6. 梯形的面积是12cm 2
,底边上的高线长是4cm,则该梯形的中位线长是 .
7.
如图,已知D 、E 分别是△ABC 中边AB 、BC 的中点,
则DE ∶AC= S △D E B ∶S △A D C = .
8. 如图一圆弧形桥拱,拱形的半径为10m,拱的跨 度为16m, 则其拱高等于
9. 相交两圆的公共弦长为6,两圆的半径是方程x 2
-(3 +5)x+15 =0 的两根,则两
圆的圆心距等于
10. 若样本x 1-2,x 2-2,…x n -2的平均数为10,方差为2,则对于样本x 1+3,x 2+3,…x n +3的平均数为_____,标准差为
________. 11. 如果函数y=k 2
22-+k k x
的图象是双曲线,且在第二,四象限内,那么k 的值是 .
12. 圆锥的底面圆周长是40 πcm,锥角等于120 °,则它的侧面 开图的面积为 .
13. 如果两圆的圆心都在x 轴上,⊙O 的圆心坐标为(7,0),半径为1,⊙O 2的圆心坐标为
(x,0),半径为2,当2<x<4时,两圆位置关系是 . 14. 已知点P (n,2n)是第一象限的点,下面四个命题⑴点P 关于y 轴对称的点P 1的坐标
是(n,-2n)⑵点p 到原点O 的距离是 n ⑶直线y=-nx+2n 不经过第三象限⑷对于
函数y= ,当x<0时y 随x 的增大而减小;其中真命题有_________ (填上所有真命题的序号) 15. 已知⊙O 的直径为10 ,弦AB=8cm ,那么AB 的弦心距为_______,与AB 距离为1cm 的平行弦CD 的长为
__________.
16. 观察下列规律:1+2+1=22 1+2+3+2+1=32 1+2+3+4+3+2+1=16=42 1+2+3+4+5+4+3+2+1=25=52 计
算:1+2+3+…+1999+2000+1999+…+3+2+1=_________________.(用科学记数法表示) 二选择题
1.若k>1,则关于x 的方程2x 2-(4k+1)x+2k 2-1=0的根的情况----------------------------------------------------( ) (A)有一正根和一负根 (B)有两个正根 (C)有两个负根 (D)没有实数根
2.下列命题正确的有----------------------------------------------------------------------------------------------------------( )
⑴既为轴对称图形,又为中心对称图形的四边形为正方形⑵以一条对角线所在直线为对称轴的平行四边形为菱形⑶频数是指一组数据中,落在各个小组内得数据⑷频率分布表中,个小组的频数之和等于样本容量⑸两圆相切,又二条公切线⑹圆周角相等,则所对两弧相等 (A)2 (B)3 (C)4 (D)5 三计算或解方程 1.3
21- -3× +(23-)°-(sin30°)2
- 2. x 2+)8(+x x =12-8x
A
B C E A B D
121
+n m -32235x n
060
1tg -
四 如图,点B 、E 、F ,、C 在同一条直线上,AF 、DE 相交于点O,OE=OF ,BE=CF , ∠B=∠C, 求证AB=DC
五. 二次函数y=x 2-mx+m-2 (1)试证明此函数图象与x 轴有交点(2)当函数图象顶点到x 轴距离为
25时,求函数解析式.
六. 一个批发与零售兼营的商店,凡一次购买铅笔301支(包含301支)可以按批发价付款,购买300支(含300支),
只能按零售价付款,现有学生小王来购买铅笔,如果给学校初三年级学生每人买一支,则只能按零售价付款,需用(m 2-1)元(m 为正整数且m 2-1>100),如果多买60支,则可以按批发价付款,同样需用(m 2-1)元(1)设这个学校初三年级共有x 名学生,则x 的取值范围____________;铅笔零售价应为________________批发价每支应为_________元(用x,m 的代数式表示).⑵若按批发价购15支比按零售价每购15支少付款1元,试求这个学校初三年级共有多少名学生,并确定m 的值.。
七.如图⊙O 1,⊙O 2内切于点P ,⊙O 2的弦BE 与⊙O 1相切于点C ,PB 交⊙O1于D ,PC 的延长线交⊙O 2于点A ,连结AB,CD,PE 。
⑴求证①∠BP A=∠EP A ②
BD
BC
AC AB ⑵如图若⊙O 1的切线BE 经过⊙O 2的圆心,⊙O 1、⊙O 2半径分别为r 、R ,其中R ≥r ,求证PC ·AC 时定值。
八.如图直角坐标系中,O 是坐标原点,A 点坐标为(-3,0),B(m,-5
6
)OA 为直径的⊙M 上一点,且tg
∠AOB =
2
1
,BH 垂直于x 轴,垂足为H
, ⑴的坐标 ⑵求图象经过ABO 三点的二次函数解析式 ⑶设C 点为⑵中二 图象的顶点,问经过BC 两点的直线是否与⊙M 相切。
说明理由。
F
O B A C
M E
H x
A
B E B
E A
F O
C D
B E。
