2012年数学建模大赛A题解题思路
2012年全国大学生数学建模竞赛A题国一

摘要
在问题一中,首先根据 T 检验、方差显著性检验和 Wilcoxon 秩和检验对两组评酒 员给葡萄酒的评价结果的差异的显著性检验。在大多数评酒员评分可靠的假设下,分别 利用评分方差比较模型,说明第二组结果可靠。在此基础上引入了评酒员“失误度”概 念来衡量每位评酒员与所有评酒员总体评价的差异, 对各组失误度求和得到第二组结果 更可靠。为了进一步优化评酒员评分,利用根据失误度对评酒员排序,跨组选取失误度 最小的 10 位评酒员组成新的评分组,其平均值认为比第二组更可靠,作为整个文章中 评价葡萄酒质量的标准指标。 在问题二中,由于红、白葡萄的理化指标有较大差异,分开考虑红白两种葡萄酒: 对于红葡萄酒,对应问题一得出的葡萄酒质量指标,从三个角度,即外观分析(又分为 由大分子因子决定的澄清度和基于 LAB 色彩模型的色调考虑到指标间存在的竞争关系 采用非线性回归分析和逐步回归分析) 、香气分析(Fisher 线性判别分析)和口感分析 (主成分分析和因子分析) ,后进行异常点检验,逐一剔除异常点来求解酿酒葡萄的量 化指标。对于白葡萄酒的三个指标采用 Fisher 判别分析求解。最后将三个方面得分加权 平均得到酿酒葡萄量化的总分,进行聚类分析,根据聚类分析结果将红葡萄和白葡萄各 分为四级。 在问题三中,为研究酿酒葡萄与葡萄酒的理化指标之间的联系,将葡萄酒的理化指 标用酿酒葡萄的理化指标来表示。根据指标间的相关性,剔除部分相关性不强的指标, 选择部分相关性较好的酿酒葡萄的指标作为自变量, 对不同的葡萄酒指标分别进行多元 线性回归、逐步回归和回归检验。根据指标本身的特点及 AIC 信息统计量,剔除不显著 的自变量,而达到用尽量少的葡萄的理化指标来表示葡萄酒的理化指标的目的。在求解 过程中,建立典型相关分析模型来分析红葡萄酒色泽指标间的关系,利用主成分分析将 白葡萄的多个指标综合为少数几个主成分,再进行回归分析。模型求解结果显示,葡萄 酒的每个指标都能用部分葡萄的指标来线性表示,且具有较好的拟合效果。 在问题四中,为了分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,结合问 题一、二、三的结果以及理化指标和芳香物质的化学意义,综合评估各个广义上的理化 指标(附件二和附件三) ,针对红葡萄酒和白葡萄酒的区别分别在酿酒葡萄和葡萄酒的 理化指标中选取对葡萄酒质量影响较大的指标, 通过线性回归分析将理化指标和葡萄酒 质量进行拟合,从而得出酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响。为进一步 论证结果,首先,对模型进行残差分析以及拟合情况分析;其次,用分组样本检验方法, 将白葡萄酒的 28 个样本数据分成两组,采用用一组进行拟合,另一组进行结果回带分 析的方式,进一步论证用葡萄和葡萄酒的理化指标来评价葡萄酒的质量的可靠性。通过 论证分析得出结论:葡萄和葡萄酒的理化指标可以用来评价葡萄酒的质量,但也有其不 足之处,如当从葡萄酒食用性方便角度考虑,用评酒员评价方法就更直接。 关键词:葡萄酒质量 识别聚类 失误度 非线性回归 逐步回归 Fisher 判别分析 主成 分分析 因子分析 显著性检验 残差分析 异常点检测
2012研究生数学建模A题

2.运用信噪比的取值探讨基因识别方法。
关键词:Voss映射Z-curve映射MATLAB软件SPSS软件快速傅里叶变换
一、问题的重述
DNA是生物遗传信息的载体,DNA分子是一种长链聚合物,DNA序列由腺嘌呤(Adenine, A),鸟嘌呤(Guanine, G),胞嘧啶(Cytosine, C),胸腺嘧啶(Thymine,T)这四种核苷酸(nucleotide)符号按一定的顺序连接而成。其中带有遗传讯息的DNA片段称为基因(Genes)。其他的DNA序列片段,有些直接以自身构造发挥作用,有些则参与调控遗传讯息的表现。如何利用DNA这些重要的信息帮助人们在农业、工业等行业领域内实现新的突破是我们面临的一个新的实际课题。我们就当前国内外的研究现状与成果的相关情况,建立数学模型分析研究下面的问题:
问题一:
(1)基于Voss映射,探求功率谱和信噪比的计算方法。
(2)基于Z-curve映射,求解频谱与信噪比并对Z-curve映射和Voss映射下的频谱和信噪比进行比较。
(3)基于实数映射,求解功率谱与信噪比的计算方法。
问题二:
对8个人类和92个鼠类的基因序列进行分析,找到每类基因研究其阈值的确定方法和阈值结果,并对所得到的结果进行评价。
: ; : ;
: ; : 。
这样产生的四个数字序列又称为DNA序列的指示序列,并通过利用MATLAB软件对Voss映射进行编程分析(见附件1),得到功率谱和信噪比的快速计算方法。
(2)根据附件1中的Z-curve映射来探求频谱与信噪比的快速计算方法。通过运行程序得到Z-curve映射下频谱和信噪比的值,然后采用100个组进行对比分析,发现在Voss映射和Z-curve映射下得到的信噪比之间呈现一定的倍数比例关系。
2012年数学建模A题解题思路

2012年数学建模A题解题思路1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?要分析两组评酒员的评价结果是否有显著性差异,可以使用统计方法进行分析。
一种常用的方法是使用t检验来比较两组平均值的差异,确定是否有统计学意义上的差异。
首先,对于每个评酒员,计算他们对每种葡萄酒的评分的平均值。
然后,对于每组评酒员,计算他们对每种葡萄酒的平均评分的平均值。
接下来,使用t检验来比较两组评酒员对每种葡萄酒的平均评分的平均值是否有显著性差异。
如果t检验的结果显示两组评酒员对某种葡萄酒的评分存在显著性差异,那么可以认为这种葡萄酒的评分更可信的那组评酒员的结果更可信。
1. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
要根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级,可以使用聚类分析或者判别分析等方法。
聚类分析可以根据酿酒葡萄的理化指标和葡萄酒的质量将它们分为几个不同的类别。
这样可以根据每个类别的平均质量评分来进行分级。
判别分析可以建立一个数学模型,根据酿酒葡萄的理化指标预测葡萄酒的质量等级。
这样可以根据酿酒葡萄的理化指标将其进行分级。
1. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
要分析酿酒葡萄与葡萄酒的理化指标之间的联系,可以使用相关性分析来确定它们之间的相关性。
首先,计算每个理化指标与葡萄酒质量评分之间的相关性系数。
可以使用皮尔逊相关系数或者斯皮尔曼相关系数等方法。
相关性分析的结果可以告诉我们哪些理化指标与葡萄酒质量评分有显著相关性,从而可以了解酿酒葡萄的哪些理化指标对葡萄酒的质量有重要影响。
1. 分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?要分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,可以使用回归分析等方法。
回归分析可以建立一个数学模型,根据酿酒葡萄和葡萄酒的理化指标来预测葡萄酒的质量评分。
这样可以分析每个理化指标对葡萄酒质量的影响程度,并确定哪些指标对葡萄酒的质量影响最为重要。
2012年全国大学生数学建模A题--葡萄酒质量的评价分析

葡萄酒质量的评价分析摘要本文主要讨论了葡萄酒和葡萄的理化指标与葡萄酒质量的关系。
通过品酒员对样品酒的外观,香气,口感的评分数据与所酿葡萄酒的理化指标和对酿酒葡萄的化学分析来确定葡萄酒质量好坏以及它们之间的关系。
根据附录中所给的两组品酒员分别对红葡萄酒和白葡萄酒进行品尝后的评分数据和各种理化指标进行了严谨的分析之后,继而运用适当的数学软件结合数学模型进行大量的拟合数据分析。
在葡萄酒品尝评分表中,由于品酒员对葡萄酒的要求、口感及其他各方面的主观条件存在一定的差异,因此,我们对品酒员给出的评分数据进行了客观的分析,降低品酒员主观造成的误差,客观的反映了样品酒之间的真实差异,同时将酿酒葡萄进行了等级划分。
并通过所给的理化指标数据和芳香物质含量更加准确的描述了酿酒葡萄、葡萄酒、葡萄酒质量之间的联系。
对于问题一,题目中要求我们判断两组品酒员的评价结果有无显著性差异,哪一组结果更可信。
由于题中数据量很大,且杂乱无章,很难直接看出,因此我们将数据在统计图中进行表示,观察了数据的稳定情况,为了更好的表达数据的稳定情况,我们采用了求每组数据方差的方法,通过比较,得出两组品酒员的评价结果存在显著性差异,且第二组品酒员所给的评分更为可信。
对于问题二,题目要求根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级,由问题一所得结果可知,第二组评分更为可信,故直接采用第二组数据进行分析。
将该数据进行数学期望处理,得到了十位评委对每种样品酒的平均打分,我们根据帕克评分系统的标准[1]将样品酒进行了分级。
对于问题三,我们使用了EXCEL中拟合数据分析的功能来探究酿酒葡萄与葡萄酒的各项理化指标之间的联系。
经过对得到的散点图不断的尝试各种函数图像,最终我们找到了最适合它们之间关系的也就是散点落在函数图象外最少的数学函数图像,从而得到该图像的数学表达式。
由于图表中显示酿酒葡萄与葡萄酒对应的各项指标存在多项式函数关系,所以我们得出结论,酿酒葡萄与葡萄酒各项理化指标存在着多项式函数的联系。
2012高教社杯全国大学生数学建模竞赛全国一等奖A题

2011高教社杯全国大学生数学建模竞赛城市表层土壤重金属污染分析摘要本文主要研究重金属对城市表层土壤污染的问题,我们根据题目所给定的一些数据和信息分析并建立了扩散传播模型、权重分配模型、对比模型和转换模型解决问题。
首先,我们利用Matlab 软件拟出该城区地势图(图1),根据所给数据绘出该地区的三维地势及采样点在其上的综合空间分布图。
之后将8种重金属的浓度等高线投影到该地区三维地形图曲面上,接着分别计算8种重金属在五个区域的平均值,立体图和平面图(图1附件)相结合便可得出8种重金属元素在该城区的空间分布。
其次,在确定该城区内不同区域重金属的污染程度时,我们运用两种方法进行解答。
先假设各重金属毒性及其它性质相同,运用公式ijij P C P ='求出各区域各金属相对于背景平均值的比值作为金属污染程度,再运用1ji ij j C C ==∑求出各区域重金属污染程度,并将各区进行比较。
之后,我们加上各重金属的毒性,对各重金属求出权数,再结合国标重金属污染等级和已知的各组数据来确定金属的污染程度。
由上述两种方法的对比,更准确地得出重金属对各区的影响程度。
即: 工业区>交通区>生活区>公园绿地区>山区 并根据第一个模型的数据来说明重金属污染的主要原因。
再次,对重金属污染物的传播特征进行了分析,判断出重金属污染物主要是通过大气、土壤和水流进行传播。
在分析之中,我们得出这三种状态的传播并不是孤立存在的,而是可以相互影响和叠加的,因此,我们分别建立三个传播模型,再对这三个传播模型进行了时间和空间上的拟合,得出重金属浓度最高的区域图,并结合各重金属的分布图(图6)来确定各污染源的位置。
最后,本题中只给出了重金属对土壤的污染,对于研究城市地质环境的演变模式,还需要搜集一些信息(图7)。
根据每种因素对地质环境的影响程度进行由定性到定量的转化。
建立同一地质时期地质环境中各因素的正影响和负影响的权重分配模型,再对这些权重进行验算和修正。
2012数学建模A题前三问解题思路和具体过程
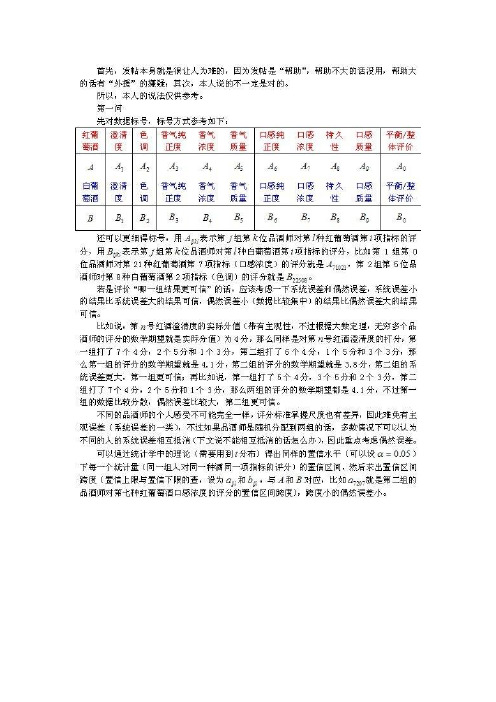
模型的建立与求解4.1 两组评酒员评价结果显著性差异的检验及可信度的鉴定(问题一)4.1.1 两组评酒员评价结果的显著性差的模型建立(1)思路一:将附件1中每个评酒员对葡萄酒的评价结果的数据导入matlab中,先对第一组中的数据按样品编号进行排序,得到正确顺序下各指标的打分情况数据,其matlab算法如程序1所示。
然后求出每一个品酒员对每一种样品的各个指标打出的分数的和,得到一个的矩阵。
使用同样的编程方法,我们获得第二组排序后各指标的分数和,得到一个的矩阵。
为方便排版起见我们将所获得的两组数据用Excel进行了处理。
(详见程序2后的附表1,其中的一部分结果如表1所示选取附表1中的前五行)。
表1:两组部分指标的分数和第一组各指标和第二组各指标和第一组各指标和第二组各指标和第一组各指标和第二组各指标和第一组各指标和第二组各指标和第一组各指标和第二组各指标和将得到的两组数据进行标准化处理,得到0-1型标准矩阵,进而对两个标准矩阵进行t检验和F检验,得到了最终的检测结果。
两种检验均表现为具有显著性差异。
(2)思路二:利用matlab读取附件1中的数据,再将读取到的数据利用matlab按照酒样品的编号及评酒员的编号进行排序,对每个评酒员对每个样品的评分进行求均值及方差(),首先由于总体样本的均值未知,故对其进行正态总体均值的比较t检验,最后得到h=0,即接受原假设,证明两组评酒员的评价结果没有显著性差异,进而对两组数据正态总体的方差进行F检验,得出h=1,证明两组评酒员的评价结果有显著性差异。
综上两种思路得出两组评酒员的评价结果是有显著性差异的问题一:T检验问题二:聚类分析主成分分析判别分析问题三:非线性拟合 F检验显著性问题四:线性拟合。
2012全国数学建模竞赛A题解答

我们参赛选择的题号是(从 A/B/C/D 中选择一项填写) : 我们的参赛报名号为(如果赛区设置报名号的话) : 所属学校(请填写完整的全名) : 参赛队员 (打印并签名) :1. 2. 3. 指导教师或指导教师组负责人 (打印并签名): 日期: 2012 沈阳航空航天大学 张 阳
A
袁亚军 邹 超 王诗云 年 9 月 10 日
5.1 评价结果的非参数显著性检验模型的建立
由于模型假设中样本酒的抽取过程是随机的,且葡萄酒种类是相当大的,有大数定 律知红葡萄酒的实际评定分数将近似服从正态分布。同时,两评酒组对各种样本酒做出 的打分为样本的估计值,应该是相互无影响的,在一定程度上具有一定的独立性。由于 是对同一个正态分布做出的估计,因此总体对应样本分布的平均值和方差都相等。
, na ) , ( j 1, 2, , na ) , ( j 1, 2,
nb
aijk bijk Maij Dbij Daij
Mbij
Ai Bi sigma a sigma a
pij
, np )
Pij
wij Wij spij
, NP )
, nw )
红葡萄酒第 i 个样本第 j 个一级理化指标值 (i 1, 2, 红葡萄酒第 i 个样本第 j 个二级理化指标值 (i 1, 2, 葡萄第 i 个样本第 j 个芳香物质指标值 (i 1, 2, 红葡萄酒第 i 个样本第 j 个芳香物质指标值 (i 1, 2,
2
A题
葡萄酒的评价
摘 要
本文针对葡萄酒应用非参数秩和检验方法、BP 神经网络方法、回归分析、主成分 分析等方法对了葡萄酒的评分问题进行了分析。 结合本题目需要解决的四个问题,我们分别建立了四个数学模型。分别简述如下: 模型一、两独立总体的 KruskalandWallis 非参数秩和检验模型 通过矩法正态分布检验,得到了评酒组评分总体不符合正态分布,否定了双独立样 本的 T 检验用于两评价组的显著性检验;两独立总体的 KruskalandWallis 非参数秩和检 验得到了两评价组的评价结果具有很高的相关性,并进行方差分析得到了两评价组可信 度近似,两评价组的评价结果无显著性差异且均可信。 模型二、基于 BP 神经网络的酿酒葡萄评价模型 应用主成分分析法对附录 2 中的数据进行筛选,得到 9 个主成分,应用其对神经网 络进行训练,从而建立了基于BP神经网络的酿酒葡萄评价模型,该模型体现了酿酒葡 萄理化指标和葡萄评分之间的关系。对其进行求解得到酿酒葡萄的一组评价分数。经检 验该组评价分数的平均误差小于 8% ,表明该模型的评价能力与评酒员很接近,从而说 明了模型的有效性。 根据模型计算的数值结果再应用五级制评价标准得到了酿酒葡萄的 分级。 模型三、以逐步回归分析为基础的线性回归模型 为了寻找葡萄酒的理化指标与酿酒葡萄的理化指标之间的关系,我们首先建立了多 元线性回归分析模型和多元二次回归分析模型,对模型进行分析发现酿酒葡萄的理化指 标之间的线性相关性,但二阶相关性偏低,模型结果误差较大,参数的可信区间无法求 解。 为了克服上述模型的不足我们在此基础上对模型进行改进, 采用逐步回归分析方法, 找到了酿酒葡萄的无线性或近似线性关系的理化指标,建立了由酿酒葡萄理化指标到葡 萄酒的回归分析模型,说明了理化指标相互转化的关系,经检验平均绝对误差为小于 1.5,从而说明了线性回归模型的有效性。 模型四、综合的 BP 神经网络的葡萄酒评级模型 基于模型二的建立,进一步建立了由葡萄的酒理化指标到葡萄酒质量的BP神经网 络模型,我们将两个模型进行加权求和,得到了综合的BP神经网络模型,经检验平均 误差小于 5% ,最大误差也小于 7% ,具有相当高的精度。
2012全国数学建模A题分析

2012全国数学建模竞赛A题详细分析1.问题重述在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏阵列件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。
不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响。
因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题。
对下列三个问题,分别给出小屋外表面光伏电池的铺设方案,使小屋的全年太阳能光伏发电总量尽可能大,而单位发电量的费用尽可能小,并计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh计算)及投资的回收年限。
在同一表面采用两种或两种以上类型的光伏阵列件时,同一型号的电池板可串联,而不同型号的电池板不可串联。
在不同表面上,即使是相同型号的电池也不能进行串、并联连接。
应注意分组连接方式及逆变器的选配。
问题1:请根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏阵列件,对小屋(见附件2)的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量。
问题2:电池板的朝向与倾角均会影响到光伏电池的工作效率,请选择架空方式安装光伏电池,重新考虑问题1。
问题3:根据附件7给出的小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果。
2.问题的分析2.1 问题一的分析问题一中要求根据山西省大同市的气象数据,选定光伏阵列件对小屋的部分外表面以贴附安装方式进行铺设,使小屋的全年太阳能光伏发电总量尽可能大,而单位发电量的费用尽可能小,最后给出铺设方案,包括电池组件分组数量和容量,以及相应的逆变器的容量和数量。
首先,附表中提供的大同地区的光照数据并未直接告知每个面获得的光照总量,需要根据光散射和直射的关系,建立光照模型,确定每个面的总的光照强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
首先纠正一下对于数学建模的看法,数学建模重要的是一种数学思想,即使是没有牢固的数学根底,一样可以在建模的赛场上大放异彩。
下面先把试题读一下,个人认为的重点词汇已经标出出来。
(不要盲目听从任何人所谓的专家建议)
A题葡萄酒的评价
确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒
员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡
萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒
葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某
一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的
和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:
1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?
2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?
附件1:葡萄酒品尝评分表(含4个表格)
附件2:葡萄和葡萄酒的理化指标(含2个表格)
附件3:葡萄和葡萄酒的芳香物质(含4个表格)
解题思路:
1、众所周知,对于同一事物的评价,如果大家的意见越一致,那么评
价的可信度就越高。
所以对于问题1的解题思路也就清晰明了了。
我们可以通过离散度(所谓离散程度,即观测变量各个取值之间的
差异程度。
它是用以衡量风险大小的指标。
)这一概念来对每一组评
酒员作出的评估作出风险分析。
显而易见的是若风险评估的值越高,这组评酒员的评价就存在问题了。
若风险评估值大小相当,这说明
这两组评酒员是没有明显差异的。
2、题目中要求对葡萄作出评级。
看起来似乎没有思路,那么我们可以
动一下我们的小脑筋。
既然对于评级我们没有参考标准,那么我们
可以参考评酒员的评价。
即使用逆向思维,从评酒员的评分发出,
那么大体上葡萄的分级基本上就能确定下来,根据确定先来的葡萄
分级进行逆推,就可以得出结论。
3、对于这个问题,最直观也是最基本的思路就是看两者之间的趋势。
(作出两者的趋势图)。
通过对趋势图的直接观察,两者之间的大体
关系即可确定,然后根据曲线拟合的方法可得出两者间的函数关系。
4、对于问题4的这中学术中称之为白痴型问题,大家肯定一眼就能得
出结论,那就是肯定能用理化指标来评价葡萄酒的质量。
但这里有
个前提,就是先分析葡萄和葡萄酒理化指标之间的关系,显然这是
解题的关键。
对于这种大量数据的问题,只要通过计算机实现,基
本上不要考虑认为分析,因为在浪费大量时间的前提下基本上不会
得出结论。
言归正传,谈一下解题的关键点或者是捷径,可以通过
附件一种的数据来作出评价。
至于具体的方法,因为只是初步的讲
解还未作出具体判断。
估计会在后续的评论中作出判断。
谢谢大家,小马过河预祝大家考出理想成绩。
