制程分析统计
产品制程问题的分析方法

QC七大手法
240 210 180 150
j ¤ _ ¤ 13.04V
¡ ¥ ^ ¡ u ]
120 90 60 30 0 13.10 13.12 13.13 13.15 13.17 13.19 13.20 13.22 13.24 13.25 13.27 13.29 13.30
O.C.V
QC七大手法
也称点检表或查核表用作记录作业现场或某项活动进行的状况为统计分析和追溯提供原始数据和第一手资料它是其它六大及时了解工作进展情况和机器的工作状况及时发现工作的问题
制程问题的分析方法
山西胜达 2014-8-1
课程目录
问题的发掘和把握 问题汇报的方法 发掘问题 解决问题的步骤 改善问题 QC七大手法 8D报告
91
93
100 100
60 40 4 Ñ Á Æ Î 14 ä Æ û Ë 20 0
ä Í ú Ç
Á ² Ë É
° É Û Ñ
± ²È °Ö ¼Ù ÀÆ Û
80
QC七大手法
特性要因图定义:也叫鱼骨图,用来对一个现象或结果 进行原因深入细致的分析,通常用来找原因及因素,最 好同层别法结合起来使用。 特性要因图用途: 特性要因图不止在发掘原因,还可据此整理问题,找出 问题的重点, 并依循原因找出解决问题的方法: 1)改善分析用; 2)制定标准用。
QC七大手法
Å Ð Á ¼ Í ý Ê Ý ¾ í ±
» ² Ï º ñ ¸ à À Í Ð » ² Ï º ñ ¸ ý Ê ¿ Á » ² Ï º ñ ¸ È ±Ê  (%) Û À ý » È ±Ê  (%)
ä Í ú Ç Á ² Ë É ° É Û Ñ Ï ¶ Ñ Á Û Î ¾ È Ñ Á Æ Î ä Æ û Ë
制程能力分析概述

制程能力分析概述导言制程能力分析是一种用于评估和监控生产过程的质量控制方法。
它可以帮助企业了解其生产过程的稳定性和可靠性,并提供改进过程的指导。
本文将对制程能力分析进行概述,介绍其基本原理、方法和应用,并探讨其在质量管理中的重要性。
什么是制程能力分析?制程能力分析是一种统计技术,用于评估和监控生产过程的稳定性和变异性。
它通过收集样本数据并进行统计分析,帮助企业监测过程的性能,并确定其是否满足预定的质量要求。
制程能力分析通常涉及计算过程的能力指标,如过程能力指数(Cp)、过程能力指数修正版(Cpk)等。
制程能力分析的基本原理制程能力分析的基本原理是基于正态分布假设和过程稳定性假设。
它假设生产过程符合正态分布,且过程的变异性是常数的。
基于这些假设,制程能力分析使用统计工具来评估过程的能力,以及过程的中心性和变异性。
制程能力分析的基本步骤制程能力分析的基本步骤通常包括以下几个方面:1.数据收集:收集生产过程的样本数据。
样本数据应该代表整个生产过程,并且在收集过程中应注意数据的准确性和可靠性。
2.过程稳定性分析:通过绘制控制图、计算过程的平均数和标准差等统计方法来评估过程的稳定性。
过程应该在统计控制下,并且无特殊因素的影响。
3.过程能力指数计算:通过计算过程的能力指数(如Cp和Cpk)来评估过程的能力。
能力指数可以告诉我们过程的“容量”,即过程是否能够在规定的公差范围内生产出合格产品。
4.制程改进:根据制程能力分析的结果,进行必要的改进措施。
这可能包括调整生产参数、改进工艺流程、优化设备等,以提高生产过程的能力。
5.监控和持续改进:制程能力分析不仅是一次性的评估,而且应该是一个持续的过程。
企业应该建立起监控和评估制程能力的系统,并持续改进过程。
制程能力分析的应用制程能力分析在质量管理中有广泛的应用。
它可以帮助企业提前发现生产过程中的问题,并及时采取措施进行纠正。
以下是一些制程能力分析的应用场景:1.检验新产品:在生产新产品之前,进行制程能力分析可以评估生产过程的稳定性和变异性,判断是否满足产品质量要求。
FQ-TS-SPC-005制程控制统计分析程序
制程统计分析控制程序制程统计分析控制程序1 目的为了解和改善过程,通过对过程能力的分析/评估使其有量化资料,为设计、制造过程的改进,选择材料,操作人员及作业方法,提供依据和参考。
2 范围本程序适用于富庆有限公司顾客要求和需做统计过程控制(PP K、CPK、CmK 、PPM)的所有产品。
3 引用文件《文件和资料控制程序》《开发设计管理程序》《过程控制程序》《失效模式及后果分析程序》《质量管理体系程序》《控制计划管理程序》《质量记录控制程序》《生产件批准程序》4 术语和定义SPC:指统计过程控制。
CpK:稳定过程的能力指数。
它是一项有关过程的指数,计算时需同时考虑过程数的趋势及该趋势接近于规格界限的程度。
PpK:初期过程的能力指数。
它是一项类似于CPK的指数,但计算时是以新产品的初期过程性能研究所得的数据为基础。
Ca:过程准确度。
指从生产过程中所获得的资料,其实际平均值与规格中心值之间偏差的程度。
Cp:过程精密度。
指从生产过程中全数抽样或随机抽样(一般样本在50个以上)所计算出来的样本标准差(σ×),以推定实际群体的标准差(σ)用3个标准差(3σ)与规格容许差比较。
PPM:质量水准,即每百万个零件不合格数。
指一种根据实际的缺陷材料来反映过程能力的一种方法。
PPM数据常用来优先制定纠正措施。
Cmk:设备能力指数:是反映机械设备在受控条件下,当其人/料/法不变时的生产能力大小。
5 职责品质部负责统计过程控制的监督、管理工作。
制程统计分析控制程序工程部门、生产部门、品质部门负责统计过程控制的数据搜集和分析。
6 工作流程和内容制程统计分析控制程序制程统计分析控制程序制程统计分析控制程序7 附件附件一: PPM、Cp、Cpk、Pp、Ppk过程能力计算及评价方法附件二:控制图的判定方法附件三:抽样检验作业指导书附件四:机械和工装设备能力计算作业规范附件一:PPM、Cp、Cpk、Pp、Ppk过程能力计算及评价方法1.质量水准PPM的过程能力计算及评值方法:当产品和/或过程特性的数据为计数值时,制造过程能力的计算及等级评价方法如下:(1)计算公式:不良品数PPM = × 1000000检验总数(2)等级评价及处理方法:制程统计分析控制程序2.稳定过程的能力指数Cp、Cpk计算及评价方法:(1)计算公式:A)Ca = (x-U) / (T / 2)×100%注: U = 规格中心值T = 公差 = SU - SL = 规格上限值–规格下限值σ= 产品和/或过程特性之数据分配的群体标准差的估计值x = 产品和/或过程特性之数据分配的平均值B)Cp = T / 6σ(当产品和/或过程特性为双边规格时)或CPU(上稳定过程的能力指数)= (SU-x)/ 3σ(当产品和/或过程特性为单边规格时)CPL(下稳定过程的能力指数)= (x-SL)/ 3σ(当产品和/或过程特性为单边规格时)Z1 = 3Cp(1+Ca)……根据Z1数值查常(正)态分配表得P1%;Z2 = 3Cp(1-Ca)……根据Z2数值查常(正)态分配表得P2%不合格率P% = P1% + P2%注:σ = R / d2( R 为全距之平均值,d2为系数,与抽样的样本大小n有关,当n = 4时,d2=2.059;当n = 5时,d2= 2.3267)C)Cpk = (1-∣Ca∣)× Cp当Ca = 0时,Cpk = Cp。
制程能力分析报告

制程能力分析报告1. 引言制程能力分析是对某一制造过程的稳定性和一致性进行评估的重要工具。
通过分析制程能力,我们可以了解到制造过程是否符合规定的要求,以及是否有必要进行改进。
本报告将针对某一制造过程的制程能力进行分析,并给出相应的结论和建议。
2. 数据收集在制程能力分析前,我们首先需要收集相关的数据。
这些数据可以是该制造过程的样本数据,也可以是历史数据。
为了保证分析结果的有效性,我们需要收集足够的样本数据。
在本次分析中,我们采集了100个样本数据,每个样本包含了关键的制造参数。
3. 数据分析在进行制程能力分析前,我们需要对数据进行一些基本的统计分析,以获取有关制程能力的指标。
以下是一些常用的制程能力指标:平均值 (Mean)平均值是样本数据的总和除以样本数量。
它代表了制程的中心位置。
通过计算平均值,我们可以了解到制程的整体水平。
标准差 (Standard Deviation)标准差是对数据的离散程度的度量。
它告诉我们数据点的分布情况,越小表示数据越集中,越大表示数据越分散。
通过计算标准差,我们可以评估制程的稳定性。
Cp指数和Cpk指数Cp指数和Cpk指数是制程能力的两个重要指标。
Cp指数衡量了制程能力的上限,而Cpk指数衡量了制程能力的上下限。
通过计算这两个指标,我们可以判断制程是否满足规定的要求。
4. 制程能力分析结果根据对收集的数据进行的分析,我们得到了以下的制程能力分析结果:•平均值:X•标准差:S•Cp指数:Cp•Cpk指数:Cpk5. 结论和建议根据制程能力分析的结果,我们得出以下结论和建议:•结论1:制程的平均值为X,说明制程的中心位置符合要求。
•结论2:制程的标准差为S,说明制程的稳定性较好。
•结论3:Cp指数为Cp,说明制程的上限能够满足要求。
•结论4:Cpk指数为Cpk,说明制程的上下限能够满足要求。
基于以上结论,我们可以得出以下的建议:1.继续保持制程的稳定性和一致性,以确保产品的质量。
制程不良统计、分析
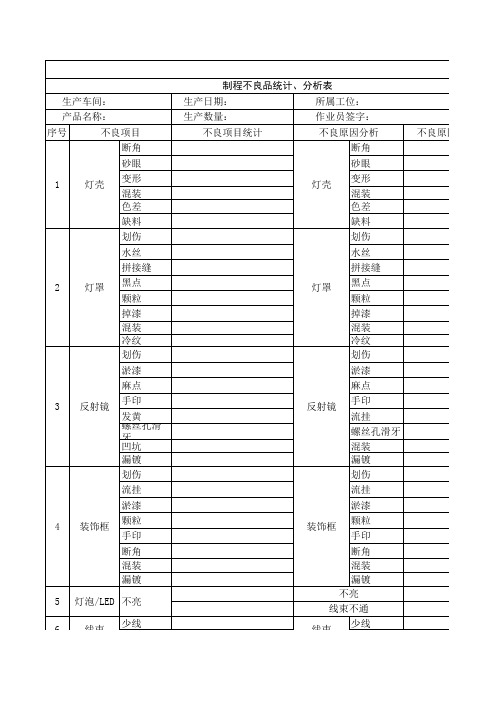
不良原因分析统计
”字标识;
改的上报品管部。
不良原因分析统计6Biblioteka 线束装反线束
装反
调节螺丝自身铆接漏气
调节螺丝与灯壳配合处漏气
后盖与灯壳配合处漏气
7
灯具气密
灯具漏气
线束与灯壳配合处漏气 线束里面线塞漏气 灯壳胶水漏气 灯壳砂眼
8
灯具调光
调光不良
银碗转不动
注:“不良项目”由生产班组所属工位人员进行统计,以“正”字标识; “不良原因”由品保部检验员和车间班组长共同分析原因,由检验员完成填写,同样以“正”字标识; 此表单由品管部检验员收集,并于每月3日前,将超过4%的不良品或者认为需要进行质量整改的上报品管部。
制程不良品统计、分析表 生产车间: 产品名称: 序号 不良项目 断角 砂眼 1 灯壳 变形 混装 色差 缺料 划伤 水丝 拼接缝 2 灯罩 黑点 颗粒 掉漆 混装 冷纹 划伤 淤漆 麻点 3 反射镜 手印 发黄 螺丝孔滑牙 凹坑 漏镀 划伤 流挂 淤漆 4 装饰框 颗粒 手印 断角 混装 漏镀 5 6 灯泡/LED 不亮 线束 少线 装饰框 反射镜 灯罩 灯壳 生产日期: 生产数量: 不良项目统计 所属工位: 作业员签字: 不良原因分析 断角 砂眼 变形 混装 色差 缺料 划伤 水丝 拼接缝 黑点 颗粒 掉漆 混装 冷纹 划伤 淤漆 麻点 手印 流挂 螺丝孔滑牙 混装 漏镀 划伤 流挂 淤漆 颗粒 手印 断角 混装 漏镀 不亮 线束不通 少线 线束
spc制程能力分析

SPC 概述Statistical Process ControlSPC Introduction统计性统计管理(SPC = Statistical Process Control)란 ?Statistical ...•统计性方法是用Sampling的Data Monitoring 、分析Process 变动时使用。
Process ...•反复性的事情或者阶段(SIPOC : Supplier → Input → Process → Output → Customer)Control ...• Process正在变化的事实早期警报。
警报是指最终Output出来之前纠正问题,能够具有充分的时间(管理图 : 随着时间工程散布的变化)SPC –对某个 Process掌握品质规格和工程能力状态, 利用统计性资料和分析技法, 在所愿的状态下一直能管理下去的技法。
2SPC 的发展历史SPC 的特征:控制过程,防患于未然。
重点在于预防•電視機彩色密度投机•美國:無不合規格產品出廠,注意力在符合規格•日本: 0.3% 超出產品規格,致力於命中目標製程- 產品-顧客產品(Output)Measurement製程(過程)(Process)展開特性 特徵顧客滿意ManMachine Material Method Environmental4M1E製程,程序影響工作結果之所有原因的集合,亦即為達成工作 結果之製造過程中所有活動的集合管制,控制確保達到要求標準,必要時採取矯正行動何謂製程管制 (程序控制)工作 結果原材料 方法 環境機器 人員原因 手段特性 目的SPC 即。
.自製程中蒐集資料,加以統計分析,並從分析中發覺異常原因,採取改正行動,使製程恢復正常,保持穩定,並持續不斷提昇製程能力的方法。
SPC 即。
.製程 資料異常 穩定製程 製程能力好能力的製程 製程改善製程解析及管制收集資料 統計分析 採取措施 製程能力分析持續改善SPC 的目的維持正常的製程 (在统计的控制之下)事先做好應該做的 (標準,系統) – ex :检测,機台操作程序製程異常發生能偵測出,並除去之,防止其再發能力要足 (有能力的程序)能力指標提昇能力–持續改善 (廣義)SPC 管理Tool的优点•Process由于偶然原因(White Noise = Common Cause Variation)和异常原因(Black Noise = Special Cause Variation)受影响一直变化。
QC七大手法及SPC制程统计方法

20世纪40年代,享有品质管理之父美誉的美国电气工程师Joseph Juran 引入了Pareto理论。正是Juran决 定将这一80/20比值称为“柏拉法则”(The Pareto Principle),将柏拉法则运用于业务度量有助于从“有 用多数”(useful many,即其它80%)中分离出“重要少数”(vital few,具有最重要影响的20%)。柏拉 图通过标示频率阐明柏拉法则——频率出现越高的内容对结果影响越大。柏拉图是品质管理七大基础手段之 一。图中横轴显示自变量,因变量由条形高度表示。表示累积相对频率的点对点图可附加至该条形图上。由 于统计变量值按相对频率顺序排列,图表可清晰显示哪些因素具有最大影响力,以及关注哪些方面可能会产 生最大利益。
噪音高
无专人保养
训练不足 设备老化
技术不高
人员流动率高 人员疲劳
作业条件不全 某作业流程不当
法
交期不稳 文件不足
料
品质欠佳 售后服务不好
不良 率高
二.QC(Quality Control)七大手法之查检 表
6
1.定义
一种为了便于收集数据,而使用简单记号填写并予以统计整理,以便于作进一步分析或作为核对,检查之 用而设计的表格或图表。
•中心偏左的直方图
下限
•中心偏右的直方图
中心值
上限
直方图偏向规格的下限, 并伸展至规格下限左侧。 表示已产生部分超出规格 下限要求的不良品。
10
制程能力知识分析讲解

4.制程能力指数Cpk
Cpk是综合Ca和Cp两者之指数,其计算公式:
Ca=( X-μ)/ ( T / 2 )
Cp=规格容许差/ 3σ
=规格公差/ 6σ=( T/ 2 ) /3σ
Cpk=( 1-| Ca | )×Cp
由上述可知:
1.当Ca=0,Cpk=Cp
2.单边规格时,Cpk=Cp
二、制程能力分析在什么时候实施是正确的?
12.5%<|Ca|25%
如有必要时,尽可能改进为A级。
25%<|Ca |50%
作业员可能看错规格不按SOP操作或检讨规格及作业标准。
50%<|Ca|
应采取紧急措施,全面检讨有可能影响之因素,必要时得停止生产。
*对策方法是以制造单位为主、技术/品管单位为辅。
2.制程精确度Cp (Capability ofprecision)
制程能力指数cpkcpk是综合cacp两者之指数其计算公式cp由上述可知单边规格时cpkcp二制程能力分析在什么时候实施是正确的正如前面所提到制程能力的评估必须要在制程稳定后才能实施也就是xr管制图已显示制程在稳定的统计管制状态下非机遇原因已经被发现经过分析与矫正以及防止再发而且继续保持在统计管制状态因此回忆过去我们所做的可以发现到一些问题
经过分析与矫正,以及防止再发),而且继续保持在统
计管制状态下。
要多少个样本数才能显示出制程的稳定性?理论
要求最好有25个以上的样组,才具代表性。请大家注
意!这里所提到的25个以上的样组数是针对管制图而言,并不是指Cpk。
所以只要能了解制程的稳定性,即使n=2 ~ 5
也能计算Cpk,但是唯一前提是必须先用计量值管制图,来持续观察制程稳定(必要时采取矫正行动)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形成错误子集的情 况
• 在子集里,偶然原因引 起的变动和异常原因引 起的变动同时存在. • 不注意不稳定的工程, 子集间的差距不好区别.
如果形成合理的子集….
• Graph> Time Series Plot
Fill-up
11
子集内的变动小,而 子集间的变动比较大。
Fill-up
面傈樊
10
9
Index
计算工程能力时注意事项
— 工序能力的测定只在以下条件下有意义.
– 连续性数据 (对离散形数据时没有意义的.)
• 速度,重量,大小.
– 工程处在管理状态时,即完全消除了异常原因的状态。
– 数据散布:正态分布(或近似)
3. 合理的子集
•工程能力决定于系统的变动,系统的变动是由以下多种原因 引起的
– set-up 流程 –制品即工程的状态 – 维护过程 • 层别的原理 – 在同一条件下将收集的数据组成一个子集,这样可以掌握系统或 设 备变动的本质。 • 子集构成原则 – 使子集内的变动变小 – 使子集间的变动变大
Long-term Process Data for Co2
15 14 UCL=14.18
Individual Value
13 X =12.64 12 LCL=11.10
11 10 9 0 50 100 150
Hale Waihona Puke Observation Number
利用minitab的工程能力分析
• 打开 process capability.mpj 文件. • Stat> Quality Tools> Capability Analysis(Normal)
通过合理的子集的建立,能够如实地掌握工程的固有能力。
组合标准偏差和全体标准偏差
组合标准偏差
• minitab 的基本选择. • 将子集内的变动平均之 后求出来。 • 在合理的子集下,为了 最佳的短期工程能力的 计算而使用. 全体标准偏差 • 以全体数据的变动中求出 来. • 估计实际能力时,用全体 标准偏差. • 在minitab中,为了显示 以全体标准偏差为基准的 工程能力,使用Pp 或Ppk 等符号。
30
40
50
60
70
25
35
45
55
65
75
85
Pp PPU PPL Ppk Cpm
0.93 0.97 0.90 0.90 *
Targ USL LSL k n
* 70.0000 20.0000 0.0376 50.0000
Mean Mean+3s Mean-3s s
44.0600 70.7996 17.3204 8.9132
例) 合理的子集的使用
• 使用Time Series Plot标记数据
3.5
output
2.5
1.5 index
10
20
30
• 比较子集内变动导致的标准偏差和全标准偏差.
变动的构成因素与合理的子集
Dem onstation of Rational Subgroups Shift is the Grouping Variable
工序能力因素
• 决定工程能力的要素有 :
–工程的平均和规格的中心 一致的程度. –散布大小 • 把工程平均管理成总是与规格 中心一致是相当困难的。所以 长期上默认为它从规格中心移 动 1.5 程度。
短期
时间1 时间2 时间3 时间4
长期
长期•短期 工序能力
1.5
LSL
USL
LSL
USL
6 st
%>USL Exp Obs %<LSL Exp Obs
0.00 0.00 0.00 2.00
PPM>USL Exp Obs PPM<LSL Exp Obs
0 0 0 20000
Cp CPU CPL Cpk Cpm
0.98 0.41 1.55 0.41 *
Targ USL LSL k n
* 70.0000 20.0000 0.5816 50.0000
合理子集的用法和意义
使用
• 以各工程变数的条件别形成
意义
• 如果组合标准偏差和全体 标准偏差之间有差异,就 数据的子集 说明工程平均或工程标准 –设备的开关 偏差随着时间变化 – 机器,产品,操作者别 – 预防保全方法别 • 子集的组合标准偏差是在 • 请对各子集执行工程能力分 最佳状态下估算的. 析。
通过分析点的排列类 型,可以很容易找到 10 20 工程改善的根据。
30
40
50
Process Capability Analysis for à À · æü® Fill-up
Process Data USL 11.000 Target * LSL Mean Sample N StDev (ST) StDev (LT) 9.000 9.699 50 0.100928 0.702044
Potential (ST) Capability Cp CPU CPL Cpk Cpm 3.30 4.30 2.31 2.31 *
Overall (LT) Capability Pp PPU PPL Ppk 0.47 0.62 0.33 0.33
• 在形成了合理的子集的前提下,我们可以 得到如下解释.
输入有数据的栏 输入子集的大小 或显示子集的栏 输入规格
Process Capability Analysis for Fill-up
Process Data USL 11.000 Target *
LSL Mean Sample N StDev (ST) StDev (LT) 9.000 9.699 50 0.100928 0.702044
从制造工程的观点上
Y f x1 , x2 ,...xn
Y 的变动由 x 1 , x 2 , , x n 引起。 各 x i 的变动原因及其形态都互不相同。 x i 中一部分变动周期短,一部分变动周期长,即从长远角度 上看工程具有多种多样的变动类型。
品质的变动原因
• 偶然原因 ( 一般原因 ) – 生产条件严格管理的状态下发生的是不可避免的不可 避免的原因.
ex) 作业者的熟练度差异,作业环境的差异等。
• 异常原因 ( 特殊原因 ) –不良资材的使用,制造设备的异常,操作者疏忽等等。
• 注意
– 工序能力分析是在工程的稳定状态,即没有由异常原因 引起的状态下执行。且使用在偶然原因的效果分析。
合理地形成子集的 情况
• 在子集中只有偶然原因 产生的变动 • 由异常原因产生的变动 是以子集间的差异显示 出来的. • 利用组合标准偏差将工 程设定为最佳状况的时 候,可以估计潜在工程 能力.
3 .5
Output
2 .5
1.5
H our
0 1 2 3 4 5 6 7 8 9 10 111213 14 1516 17 18192 02 1 22 3 0 1 2 3 4 5 6 7 2
总变动
=
由平均值移动造 成的变动
+
子集内的变动
4. 工程能力分析
Long-term Process Data for Co2
LSL
USL
ST LT
长期和短期的标 准偏差的差距变大
Potential (ST) Capability Cp CPU CPL Cpk Cpm 3.30 4.30 2.31 2.31 *
• 6 工序 : Cpk = 1.5
• 3 工序 : Cpk = 0.5
考虑到工程平均变动的工程能力指数
Cp = 2.0 Cpk = 1.5
Cp = 2.0
Cpk = 2.0
-6 LSL
0 1.5 Nominal
+6 USL
C pk
USL - 工程平均 = ( 5 目标值 + 6s )- ( 目标值 + 1. s ) = = 1.5 3s 3s
工程能力
• 下面两个图中哪一个具有较好的工程能力 ?
Process Capability Analysis for yield
Lower Spec Upper Spec
Lower Spec
为什么?
Upper Spec
Process Capability Analysis for yield
10
20
工程能力分析
1. 2. 3. 4. 5. 6. 何谓工程能力 短期与长期工程能力 合理的子集 工程能力分析 变动要因的诊断 工序能力分析步骤
1. 何谓工程能力(Process) ?
• 工程能力是生产工程能生产出 多么均一的品质的制品的工程 固有的能力。 • 所有品质特性具有目标值(Tar -get Value),与目标值的偏 差越小品质越优秀。
短期标准偏差是0.100928. 长期标准偏差是0.702044. 这个工程的潜在工序能力是3.30.
即如果最大限度地改进可能达到3.30。 此工程的当前能力是0.33.
这个工程的不良率现在是191636PPM.
5. 变动因素的诊断
• 工程能力分析是为了识别潜在的变动要因而使用。 • 通过变动因素的消除,能够改善工程. • 通过形成合理的子集,改善工程。
了解工序能力...
–可以计算出工程不良率. –可以建立改善目标. –提供与其他设备相比较的标准.
为了生产高品质 产品的工序设计
使工程平均与目标值一致 尽可能减少标准偏差
工程能力的向上
品质与损失
LSL 损失 良品 LSL 损失 良品 目标值 新的概念 目标值 USL USL 传统概念
只要品质特性值与目标值不一致,不管是 什么样的形式,损失是肯定发生的。
