深度优先搜索
深度优先搜索和广度优先搜索
二、 重排九宫问题游戏
在一个 3 乘 3 的九宫中有 1-8 的 8 个数及一个空格随机摆放在其中的格子里。如下面 左图所示。现在要求实现这样的问题：将该九宫调整为如下图右图所示的形式。调整规则是： 每次只能将与空格（上，下或左，右）相临的一个数字平移到空格中。试编程实现。
|2|8 |3|
|1|2|3|
from = f; to = t; distance = d; skip = false; } } class Depth { final int MAX = 100; // This array holds the flight information. FlightInfo flights[] = new FlightInfo[MAX]; int numFlights = 0; // number of entries in flight array Stack btStack = new Stack(); // backtrack stack public static void main(String args[]) {
下面是用深度优先搜索求解的程序:
// Find connections using a depth-first search. import java.util.*; import java.io.*; // Flight information. class FlightInfo {
String from; String to; int distance; boolean skip; // used in backtracking FlightInfo(String f, String t, int d) {
int dist; FlightInfo f; // See if at destination. dist = match(from, to); if(dist != 0) {
深度优先搜索和广度优先搜索
深度优先搜索和广度优先搜索一、深度优先搜索和广度优先搜索的深入讨论(一)深度优先搜索的特点是无论问题的内容和性质以及求解要求如何不同，它们的程序结构都是相同的，即都是深度优先算法(一)和深度优先算法(二)中描述的算法结构，不相同的仅仅是存储结点数据结构和产生规则以及输出要求。
(2)深度优先搜索法有递归以及非递归两种设计方法。
一般的，当搜索深度较小、问题递归方式比较明显时，用递归方法设计好，它可以使得程序结构更简捷易懂。
当搜索深度较大时，当数据量较大时，由于系统堆栈容量的限制，递归容易产生溢出，用非递归方法设计比较好。
(3)深度优先搜索方法有广义和狭义两种理解。
广义的理解是，只要最新产生的结点(即深度最大的结点)先进行扩展的方法，就称为深度优先搜索方法。
在这种理解情况下，深度优先搜索算法有全部保留和不全部保留产生的结点的两种情况。
而狭义的理解是，仅仅只保留全部产生结点的算法。
本书取前一种广义的理解。
不保留全部结点的算法属于一般的回溯算法范畴。
保留全部结点的算法，实际上是在数据库中产生一个结点之间的搜索树，因此也属于图搜索算法的范畴。
(4)不保留全部结点的深度优先搜索法，由于把扩展望的结点从数据库中弹出删除，这样，一般在数据库中存储的结点数就是深度值，因此它占用的空间较少，所以，当搜索树的结点较多，用其他方法易产生内存溢出时，深度优先搜索不失为一种有效的算法。
(5)从输出结果可看出，深度优先搜索找到的第一个解并不一定是最优解.如果要求出最优解的话，一种方法将是后面要介绍的动态规划法，另一种方法是修改原算法：把原输出过程的地方改为记录过程，即记录达到当前目标的路径和相应的路程值，并与前面已记录的值进行比较，保留其中最优的，等全部搜索完成后，才把保留的最优解输出。
二、广度优先搜索法的显著特点是：(1)在产生新的子结点时，深度越小的结点越先得到扩展，即先产生它的子结点。
为使算法便于实现，存放结点的数据库一般用队列的结构。
dfs通用步骤-概述说明以及解释
dfs通用步骤-概述说明以及解释1.引言1.1 概述DFS（深度优先搜索）是一种常用的图遍历算法，它通过深度优先的策略来遍历图中的所有节点。
在DFS中，从起始节点开始，一直向下访问直到无法继续为止，然后返回到上一个未完成的节点，继续访问它的下一个未被访问的邻居节点。
这个过程不断重复，直到图中所有的节点都被访问为止。
DFS算法的核心思想是沿着一条路径尽可能深入地搜索，直到无法继续为止。
在搜索过程中，DFS会使用一个栈来保存待访问的节点，以及记录已经访问过的节点。
当访问一个节点时，将其标记为已访问，并将其所有未访问的邻居节点加入到栈中。
然后从栈中取出下一个节点进行访问，重复这个过程直到栈为空。
优点是DFS算法实现起来比较简单，而且在解决一些问题时具有较好的效果。
同时，DFS算法可以用来解决一些经典的问题，比如寻找图中的连通分量、判断图中是否存在环、图的拓扑排序等。
然而，DFS算法也存在一些缺点。
首先，DFS算法不保证找到最优解，有可能陷入局部最优解而无法找到全局最优解。
另外，如果图非常庞大且存在大量的无效节点，DFS可能会陷入无限循环或者无法找到解。
综上所述，DFS是一种常用的图遍历算法，可以用来解决一些问题，但需要注意其局限性和缺点。
在实际应用中，我们需要根据具体问题的特点来选择合适的搜索策略。
在下一部分中，我们将详细介绍DFS算法的通用步骤和要点，以便读者更好地理解和应用该算法。
1.2 文章结构文章结构部分的内容如下所示：文章结构：在本文中，将按照以下顺序介绍DFS（深度优先搜索）通用步骤。
首先，引言部分将概述DFS的基本概念和应用场景。
其次，正文部分将详细解释DFS通用步骤的两个要点。
最后，结论部分将总结本文的主要内容并展望未来DFS的发展趋势。
通过这样的结构安排，读者可以清晰地了解到DFS算法的基本原理和它在实际问题中的应用。
接下来，让我们开始正文的介绍。
1.3 目的目的部分的内容可以包括对DFS（Depth First Search，深度优先搜索）的应用和重要性进行介绍。
深度优先搜索和广度优先搜索
深度优先搜索和⼴度优先搜索 深度优先搜索和⼴度优先搜索都是图的遍历算法。
⼀、深度优先搜索（Depth First Search） 1、介绍 深度优先搜索（DFS），顾名思义，在进⾏遍历或者说搜索的时候，选择⼀个没有被搜过的结点（⼀般选择顶点），按照深度优先，⼀直往该结点的后续路径结点进⾏访问，直到该路径的最后⼀个结点，然后再从未被访问的邻结点进⾏深度优先搜索，重复以上过程，直⾄所有点都被访问，遍历结束。
⼀般步骤：（1）访问顶点v；（2）依次从v的未被访问的邻接点出发，对图进⾏深度优先遍历；直⾄图中和v有路径相通的顶点都被访问；（3）若此时图中尚有顶点未被访问，则从⼀个未被访问的顶点出发，重新进⾏深度优先遍历，直到图中所有顶点均被访问过为⽌。
可以看出，深度优先算法使⽤递归即可实现。
2、⽆向图的深度优先搜索 下⾯以⽆向图为例，进⾏深度优先搜索遍历： 遍历过程： 所以遍历结果是：A→C→B→D→F→G→E。
3、有向图的深度优先搜索 下⾯以有向图为例，进⾏深度优先遍历： 遍历过程： 所以遍历结果为：A→B→C→E→D→F→G。
⼆、⼴度优先搜索（Breadth First Search） 1、介绍 ⼴度优先搜索（BFS）是图的另⼀种遍历⽅式，与DFS相对，是以⼴度优先进⾏搜索。
简⾔之就是先访问图的顶点，然后⼴度优先访问其邻接点，然后再依次进⾏被访问点的邻接点，⼀层⼀层访问，直⾄访问完所有点，遍历结束。
2、⽆向图的⼴度优先搜索 下⾯是⽆向图的⼴度优先搜索过程： 所以遍历结果为：A→C→D→F→B→G→E。
3、有向图的⼴度优先搜索 下⾯是有向图的⼴度优先搜索过程： 所以遍历结果为：A→B→C→E→F→D→G。
三、两者实现⽅式对⽐ 深度优先搜索⽤栈（stack）来实现，整个过程可以想象成⼀个倒⽴的树形：把根节点压⼊栈中。
每次从栈中弹出⼀个元素，搜索所有在它下⼀级的元素，把这些元素压⼊栈中。
并把这个元素记为它下⼀级元素的前驱。
深度优先搜索算法详解及代码实现
深度优先搜索算法详解及代码实现深度优先搜索（Depth-First Search，DFS）是一种常见的图遍历算法，用于遍历或搜索图或树的所有节点。
它的核心思想是从起始节点开始，沿着一条路径尽可能深入地访问其他节点，直到无法继续深入为止，然后回退到上一个节点，继续搜索未访问过的节点，直到所有节点都被访问为止。
一、算法原理深度优先搜索算法是通过递归或使用栈（Stack）的数据结构来实现的。
下面是深度优先搜索算法的详细步骤：1. 选择起始节点，并标记该节点为已访问。
2. 从起始节点出发，依次访问与当前节点相邻且未被访问的节点。
3. 若当前节点有未被访问的邻居节点，则选择其中一个节点，将其标记为已访问，并将当前节点入栈。
4. 重复步骤2和3，直到当前节点没有未被访问的邻居节点。
5. 若当前节点没有未被访问的邻居节点，则从栈中弹出一个节点作为当前节点。
6. 重复步骤2至5，直到栈为空。
深度优先搜索算法会不断地深入到图或树的某一分支直到底部，然后再回退到上层节点继续搜索其他分支。
因此，它的搜索路径类似于一条深入的迷宫路径，直到没有其他路径可走后，再原路返回。
二、代码实现以下是使用递归方式实现深度优先搜索算法的代码：```pythondef dfs(graph, start, visited):visited.add(start)print(start, end=" ")for neighbor in graph[start]:if neighbor not in visited:dfs(graph, neighbor, visited)# 示例数据graph = {'A': ['B', 'C'],'B': ['A', 'D', 'E'],'C': ['A', 'F'],'D': ['B'],'E': ['B', 'F'],'F': ['C', 'E']}start_node = 'A'visited = set()dfs(graph, start_node, visited)```上述代码首先定义了一个用于实现深度优先搜索的辅助函数`dfs`。
深度优先算法
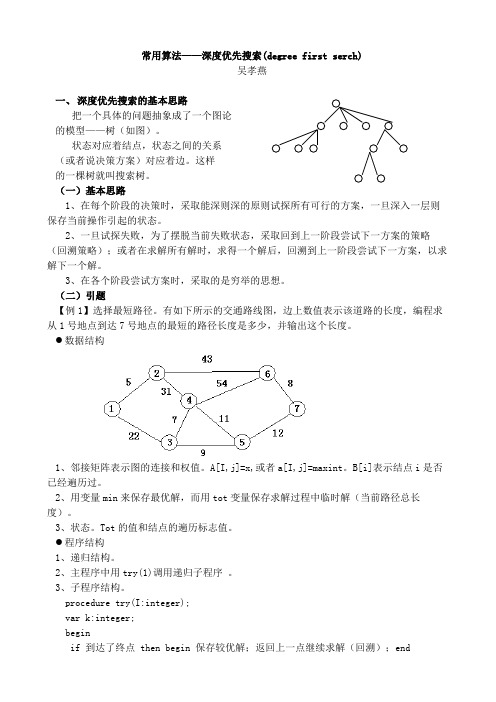
常用算法——深度优先搜索(degree first serch)吴孝燕一、深度优先搜索的基本思路把一个具体的问题抽象成了一个图论的模型——树（如图）。
状态对应着结点，状态之间的关系（或者说决策方案）对应着边。
这样的一棵树就叫搜索树。
（一）基本思路1、在每个阶段的决策时，采取能深则深的原则试探所有可行的方案，一旦深入一层则保存当前操作引起的状态。
2、一旦试探失败，为了摆脱当前失败状态，采取回到上一阶段尝试下一方案的策略（回溯策略）；或者在求解所有解时，求得一个解后，回溯到上一阶段尝试下一方案，以求解下一个解。
3、在各个阶段尝试方案时，采取的是穷举的思想。
（二）引题【例1】选择最短路径。
有如下所示的交通路线图，边上数值表示该道路的长度，编程求从1号地点到达7号地点的最短的路径长度是多少，并输出这个长度。
●数据结构1、邻接矩阵表示图的连接和权值。
A[I,j]=x,或者a[I,j]=maxint。
B[i]表示结点i是否已经遍历过。
2、用变量min来保存最优解，而用tot变量保存求解过程中临时解（当前路径总长度）。
3、状态。
Tot的值和结点的遍历标志值。
●程序结构1、递归结构。
2、主程序中用try(1)调用递归子程序。
3、子程序结构。
procedure try(I:integer);var k:integer;beginif 到达了终点 then begin 保存较优解；返回上一点继续求解（回溯）；endelsebegin穷举从I出发当前可以直接到达的点k；if I到k点有直接联边并且 k点没有遍历过 thenthen begin把A[I,K]累加入路径长度tot;k标记为已遍历；try(k); 现场恢复；end;end;●子程序procedure try(i:integer);var k:integer;beginif i=n then begin if tot<min then min:=tot;exit;endelsebeginfor k:=1 to n doif (b[k]=0) and (i<>k) and (a[i,k]<32700) thenbeginb[k]:=1;tot:=tot+a[i,k];try(k);b[k]:=0;tot:=tot-a[i,k]; end;end;end;●主程序数据输入readln(fi,n);for i:=1 to n dobeginfor j:=1 to n do read(fi,a[i,j]);readln(fi);end;close(fi);●主程序预处理和调用子程序tot:=0;min:=maxint;b[1]:=1;try(1);writeln('tot=',min);（三）递归程序结构框架Procedure try(i:integer);Var k:integer;BeginIf 所有阶段都已求解 thenBegin比较最优解并保存；回溯；endelsebeginfor k:=i 深度可能决策范围；do begin穷举当前阶段所有可能的决策（方案、结点）kif k方案可行 then begin记录状态变化；try(i+1);状态恢复（回溯）； endend;end;End;二、深度优先搜索的应用例1:有A，B，C，D，E 5本书，要分给张、王、刘、赵、钱5位同学，每人只选一本。
信息学竞赛中的深度优先搜索算法
信息学竞赛中的深度优先搜索算法深度优先搜索（Depth First Search, DFS）是一种经典的图遍历算法，在信息学竞赛中被广泛应用。
本文将介绍深度优先搜索算法的原理、应用场景以及相关的技巧与注意事项。
一、算法原理深度优先搜索通过递归或者栈的方式实现，主要思想是从图的一个节点开始，尽可能地沿着一条路径向下深入，直到无法继续深入，然后回溯到上一个节点，再选择其他未访问的节点进行探索，直到遍历完所有节点为止。
二、应用场景深度优先搜索算法在信息学竞赛中有广泛的应用，例如以下场景：1. 图的遍历：通过深度优先搜索可以遍历图中的所有节点，用于解决与图相关的问题，如寻找连通分量、判断是否存在路径等。
2. 剪枝搜索：在某些问题中，深度优先搜索可以用于剪枝搜索，即在搜索的过程中根据当前状态进行一定的剪枝操作，提高求解效率。
3. 拓扑排序：深度优先搜索还可以用于拓扑排序，即对有向无环图进行排序，用于解决任务调度、依赖关系等问题。
4. 迷宫求解：对于迷宫类的问题，深度优先搜索可以用于求解最短路径或者所有路径等。
三、算法实现技巧在实际应用深度优先搜索算法时，可以采用以下的一些技巧和优化，以提高算法效率：1. 记忆化搜索：通过记录已经计算过的状态或者路径，避免重复计算，提高搜索的效率。
2. 剪枝策略：通过某些条件判断，提前终止当前路径的搜索，从而避免无效的搜索过程。
3. 双向搜索：在某些情况下，可以同时从起点和终点进行深度优先搜索，当两者在某个节点相遇时，即可确定最短路径等。
四、注意事项在应用深度优先搜索算法时，需要注意以下几点：1. 图的表示：需要根据实际问题选择合适的图的表示方法，如邻接矩阵、邻接表等。
2. 访问标记：需要使用合适的方式标记已经访问过的节点，避免无限循环或者重复访问造成的错误。
3. 递归调用：在使用递归实现深度优先搜索时，需要注意递归的结束条件和过程中变量的传递。
4. 时间复杂度：深度优先搜索算法的时间复杂度一般为O(V+E)，其中V为节点数，E为边数。
深度优先搜索的基本原理
深度优先搜索的基本原理深度优先搜索是一种常用的搜索算法，它的主要思想是沿着搜索空间中的可能路径以深度优先的方式搜索整个空间，而不是广度优先的方式。
深度优先搜索可以用来解决多种种类的问题，包括最短路径，最大收益，最小化损失等等。
本文将对深度优先搜索的原理及应用进行简要介绍。
一、深度优先搜索原理深度优先搜索（Depth-FirstSearch，DFS）是一种搜索算法，它受到树的结构性质的启发，在给定的搜索空间中以深度优先的方式搜索整个空间，而不是广度优先的方式，也就是说，从一个节点出发之后，探索它的所有可能的路径，直到找到目标状态为止。
深度优先搜索的步骤分为以下几步：1.首先，在搜索空间中选择一个节点作为起点，并把它标记为处理过；2.然后，搜索深度优先，如果当前节点有直接相连的节点，则把它也标记为处理过，并选择一个未标记节点作为当前节点，重复上述步骤；3.最后，如果找到了目标状态，则结束搜索，否则，回退到尚未访问过的节点，重新开始搜索。
二、深度优先搜索的应用深度优先搜索可以应用于多种类的问题，其中最常用的是给定搜索空间中最短路径的搜索。
比如导航问题，给定搜索空间，从出发点到目标点，深度优先搜索可以帮助我们在最短的时间里找到最短路径。
深度优先搜索也可以应用于最大收益的搜索，比如深度优先搜索可以应用于棋盘游戏的最佳路径搜索，它可以帮助我们找到棋盘游戏中最大收益的路径。
另外，深度优先搜索也可以用来搜索最小化损失的路径。
三、深度优先搜索的优势1.深度优先搜索可以快速地找到最短路径，它可以帮助我们节省问题解决中的很多时间；2.深度优先搜索也可以应用于最大收益的搜索，比如棋盘游戏等；3.它不需要记录太多的搜索状态，从而提高搜索的效率；4.深度优先搜索不需要考虑太多的约束条件，并且也并不需要在搜索空间中记录太多的信息，使得搜索问题更加易于理解。
四、深度优先搜索的不足1.深度优先搜索只能从当前节点出发，很容易陷入死胡同，因此，有时候可能会导致搜索的中断或无法从死胡同出发，直至搜索完全空间；2.它只能找到单条最优路径，而不能找到整个搜索空间中的最优路径；3.深度优先搜索的空间复杂度较高，因此它的执行效率较低，在处理高维空间的问题时，它的效率就更低了。
算法描述的三种方法
算法描述的三种方法
1. 深度优先搜索算法：
通过递归的方式遍历图或树的每个节点，先访问当前节点，然后依次递归访问当前节点的每个邻接节点。
该算法使用栈来记录遍历的节点顺序。
示例：
对于以下图结构，初始节点为A：
A ->
B -> D
| |
V V
C E
通过深度优先搜索算法的结果为：A -> B -> D -> E -> C
2. 广度优先搜索算法：
通过迭代的方式遍历图或树的每个节点，先访问当前节点的所有邻接节点，然后将邻接节点加入队列尾部，依次访问队列中的节点。
该算法使用队列来记录遍历的节点顺序。
示例：
对于以下图结构，初始节点为A：
A ->
B -> D
| |
V V
C E
通过广度优先搜索算法的结果为：A -> B -> C -> D -> E
3. 贪心算法：
在每一步选择中，贪心算法选择当前状态下最优的选择，不考虑未来的后果。
贪心算法通常用于求解最优解问题，但并不
能保证一定能得到全局最优解。
示例：
如果要在一组物品中选择总重量不超过背包容量的物品，可以用贪心算法选择具有最高价值重量比的物品放入背包，直到背包无法再放入物品为止。
但是这种选择方式并不一定能得到真正的最优解。
c++ 深搜 dfs 教学设计
C++深搜(DFS)教学设计一、概述深度优先搜索（DFS）是一种常用的图算法，可用于解决许多实际问题，如路径搜索、图的连通性、拓扑排序等。
在C++编程语言中，深度优先搜索算法被广泛应用，因此对于学习C++编程的学生来说，掌握DFS算法是至关重要的。
二、教学目标1. 理解深度优先搜索算法的原理和基本概念2. 能够编写C++程序实现深度优先搜索算法3. 掌握DFS算法在实际问题中的应用和解决方法三、教学内容1. 深度优先搜索算法的基本原理- 深度优先搜索是一种通过递归或者栈结构来实现的算法- 深度优先搜索适用于解决图的连通性、路径搜索等问题2. C++中深度优先搜索算法的实现- 采用递归方式实现DFS算法- 采用栈结构实现DFS算法3. 深度优先搜索算法在实际问题中的应用- 图的连通性判断- 图的遍历和路径搜索- 拓扑排序等4. 代码演示和实例分析- 通过具体的案例对DFS算法进行演示和分析- 展示如何在C++中实现DFS算法，并解决实际问题四、教学方法1. 理论讲解结合实例分析：通过教师讲解和实例分析，让学生理解DFS算法的基本原理和实现方式。
2. 代码演示和实践操作：通过实际代码演示和让学生动手编写代码，加深学生对DFS算法的理解和掌握程度。
3. 课堂练习和作业布置：布置相关的课堂练习和作业，让学生独立完成DFS算法的实现和应用。
五、教学步骤1. 教师讲解深度优先搜索算法的基本原理和C++实现方式2. 通过具体案例演示DFS算法的应用和实现3. 让学生进行课堂练习和实践操作，编写DFS算法相关的代码4. 教师进行作业布置，让学生独立完成关于DFS算法的编程作业5. 教师对学生作业进行批改和指导，巩固学生对DFS算法的理解和运用六、教学评估1. 课堂讨论和提问：通过课堂讨论和提问，检测学生对DFS算法的理解程度2. 作业和实践操作：通过学生的作业和实践操作情况，评估学生对DFS算法的掌握情况3. 实际应用能力评估：通过实际案例的分析和解决，考察学生对DFS 算法在实际问题中的应用能力七、教学资源1. 教学课件：包括DFS算法的基本原理、C++实现等方面的内容2. 相关书籍和资料：提供给学生相关的C++编程和算法书籍或资料3. 网络资源和代码示例：引导学生利用网络资源和代码示例，加强对DFS算法的学习和理解八、教学反思通过对DFS算法的教学设计和实施，学生可以较好地掌握C++编程语言中深度优先搜索算法的实现和应用。
深度优先搜索算法利用深度优先搜索解决迷宫问题
深度优先搜索算法利用深度优先搜索解决迷宫问题深度优先搜索算法（Depth-First Search, DFS）是一种常用的图遍历算法，它通过优先遍历图中的深层节点来搜索目标节点。
在解决迷宫问题时，深度优先搜索算法可以帮助我们找到从起点到终点的路径。
一、深度优先搜索算法的实现原理深度优先搜索算法的实现原理相当简单直观。
它遵循以下步骤：1. 选择一个起始节点，并标记为已访问。
2. 递归地访问其相邻节点，若相邻节点未被访问，则标记为已访问，并继续访问其相邻节点。
3. 重复步骤2直到无法继续递归访问，则返回上一级节点，查找其他未被访问的相邻节点。
4. 重复步骤2和3，直到找到目标节点或者已经遍历所有节点。
二、利用深度优先搜索算法解决迷宫问题迷宫问题是一个经典的寻找路径问题，在一个二维的迷宫中，我们需要找到从起点到终点的路径。
利用深度优先搜索算法可以很好地解决这个问题。
以下是一种可能的解决方案：```1. 定义一个二维数组作为迷宫地图，其中0代表通路，1代表墙壁。
2. 定义一个和迷宫地图大小相同的二维数组visited，用于记录节点是否已经被访问过。
3. 定义一个存储路径的栈path，用于记录从起点到终点的路径。
4. 定义一个递归函数dfs，参数为当前节点的坐标(x, y)。
5. 在dfs函数中，首先判断当前节点是否为终点，如果是则返回True，表示找到了一条路径。
6. 然后判断当前节点是否越界或者已经访问过，如果是则返回False，表示该路径不可行。
7. 否则，将当前节点标记为已访问，并将其坐标添加到path路径中。
8. 依次递归访问当前节点的上、下、左、右四个相邻节点，如果其中任意一个节点返回True，则返回True。
9. 如果所有相邻节点都返回False，则将当前节点从path路径中删除，并返回False。
10. 最后，在主函数中调用dfs函数，并判断是否找到了一条路径。
```三、示例代码```pythondef dfs(x, y):if maze[x][y] == 1 or visited[x][y] == 1:return Falseif (x, y) == (end_x, end_y):return Truevisited[x][y] = 1path.append((x, y))if dfs(x+1, y) or dfs(x-1, y) or dfs(x, y+1) or dfs(x, y-1): return Truepath.pop()return Falseif __name__ == '__main__':maze = [[0, 1, 1, 0, 0],[0, 0, 0, 1, 0],[1, 1, 0, 0, 0],[1, 1, 1, 1, 0],[0, 0, 0, 1, 0]]visited = [[0] * 5 for _ in range(5)]path = []start_x, start_y = 0, 0end_x, end_y = 4, 4if dfs(start_x, start_y):print("Found path:")for x, y in path:print(f"({x}, {y}) ", end="")print(f"\nStart: ({start_x}, {start_y}), End: ({end_x}, {end_y})") else:print("No path found.")```四、总结深度优先搜索算法是一种有效解决迷宫问题的算法。
深度优先搜索
深度优先搜索所谓 " 深度 " 是对产生问题的状态结点而言的， " 深度优先 " 是一种控制结点扩展的策略，这种策略是优先扩展深度大的结点，把状态向纵深发展。
深度优先搜索也叫做 DFS法 (Depth First Search) 。
深度优先搜索的递归实现过程：procedure dfs(i);for j:=1 to r doif if 子结点子结点mr 符合条件 then产生的子结点mr 是目标结点 then输出mr 入栈；else dfs(i+1);栈顶元素出栈（即删去mr）;endif;endfor;[ 例 1] 骑士游历 :设有一个 n*m 的棋盘，在棋盘上任一点有一个中国象棋马.马走的规则为 :1.马走日字2.马只能向右走。
当 N,M 输入之后 , 找出一条从左下角到右上角的路径。
例如:输入N=4,M=4，输出 : 路径的格式 :(1,1)->(2,3)->(4,4)，若不存在路径,则输出"no"算法分析：我们以 4×4的棋盘为例进行分析，用树形结构表示马走的所有过程，求从起点到终点的路径 , 实际上就是从根结点开始深度优先搜索这棵树。
马从（1，1）开始，按深度优先搜索法，走一步到达（2，3），判断是否到达终点，若没有，则继续往前走，再走一步到达（4，4），然后判断是否到达终点，若到达则退出，搜索过程结束。
为了减少搜索次数，在马走的过程中，判断下一步所走的位置是否在棋盘上，如果不在棋盘上，则另选一条路径再走。
程序如下：constdx:array[1..4]of integer=(2,2,1,1);dy:array[1..4]of integer=(1,-1,2,-2);typemap=recordx,y:integer;end;vari,n,m:integer;a:array[0..50]of map;procedure dfs(i:integer);var j,k:integer;beginfor j:=1 to 4 doif(a[i-1].x+dx[j]>0)and(a[i-1].x+dx[j]<=n)and(a[i-1].y+dy[j]>0)and(a[i-1].y+dy[j]<=n) then{判断是否在棋盘上} begina[i].x:=a[i-1].x+dx[j];a[i].y:=a[i-1].y+dy[j];{入栈}if (a[i].x=n)and(a[i].y=m)thenbeginwrite('(',1,',',1,')');for k:=2 to i do write('->(',a[k].x,',',a[k].y,')');halt;{输出结果并退出程序 }end;dfs(i+1);{搜索下一步 }a[i].x:=0;a[i].y:=0;{出栈 }end;end;begina[1].x:=1;a[1].y:=1;readln(n,m);dfs(2);writeln('no');end.从上面的例子我们可以看出，深度优先搜索算法有两个特点：1、己产生的结点按深度排序，深度大的结点先得到扩展，即先产生它的子结点。
深度优先搜索和广度优先搜索的区别
深度优先搜索和⼴度优先搜索的区别1、深度优先算法占内存少但速度较慢，⼴度优先算法占内存多但速度较快，在距离和深度成正⽐的情况下能较快地求出最优解。
2、深度优先与⼴度优先的控制结构和产⽣系统很相似，唯⼀的区别在于对扩展节点选取上。
由于其保留了所有的前继节点，所以在产⽣后继节点时可以去掉⼀部分重复的节点，从⽽提⾼了搜索效率。
3、这两种算法每次都扩展⼀个节点的所有⼦节点，⽽不同的是，深度优先下⼀次扩展的是本次扩展出来的⼦节点中的⼀个，⽽⼴度优先扩展的则是本次扩展的节点的兄弟点。
在具体实现上为了提⾼效率,所以采⽤了不同的数据结构。
4、深度优先搜索的基本思想：任意选择图G的⼀个顶点v0作为根，通过相继地添加边来形成在顶点v0开始的路，其中每条新边都与路上的最后⼀个顶点以及不在路上的⼀个顶点相关联。
继续尽可能多地添加边到这条路。
若这条路经过图G的所有顶点，则这条路即为G的⼀棵⽣成树；若这条路没有经过G的所有顶点，不妨设形成这条路的顶点顺序v0,v1,......,vn。
则返回到路⾥的次最后顶点v(n-1).若有可能，则形成在顶点v(n-1)开始的经过的还没有放过的顶点的路；否则，返回到路⾥的顶点v(n-2)。
然后再试。
重复这个过程，在所访问过的最后⼀个顶点开始，在路上次返回的顶点，只要有可能就形成新的路，知道不能添加更多的边为⽌。
5、⼴度优先搜索的基本思想：从图的顶点中任意第选择⼀个根，然后添加与这个顶点相关联的所有边，在这个阶段添加的新顶点成为⽣成树⾥1层上的顶点，任意地排序它们。
下⼀步，按照顺序访问1层上的每⼀个顶点，只要不产⽣回路，就添加与这个顶点相关联的每个边。
这样就产⽣了树⾥2的上的顶点。
遵循同样的原则继续下去，经有限步骤就产⽣了⽣成树。
深度优先搜索和广度优先搜索
深度优先搜索和广度优先搜索深度优先搜索（DFS）和广度优先搜索（BFS）是图论中常用的两种搜索算法。
它们是解决许多与图相关的问题的重要工具。
本文将着重介绍深度优先搜索和广度优先搜索的原理、应用场景以及优缺点。
一、深度优先搜索（DFS）深度优先搜索是一种先序遍历二叉树的思想。
从图的一个顶点出发，递归地访问与该顶点相邻的顶点，直到无法再继续前进为止，然后回溯到前一个顶点，继续访问其未被访问的邻接顶点，直到遍历完整个图。
深度优先搜索的基本思想可用以下步骤总结：1. 选择一个初始顶点；2. 访问该顶点，并标记为已访问；3. 递归访问该顶点的邻接顶点，直到所有邻接顶点均被访问过。
深度优先搜索的应用场景较为广泛。
在寻找连通分量、解决迷宫问题、查找拓扑排序等问题中，深度优先搜索都能够发挥重要作用。
它的主要优点是容易实现，缺点是可能进入无限循环。
二、广度优先搜索（BFS）广度优先搜索是一种逐层访问的思想。
从图的一个顶点出发，先访问该顶点，然后依次访问与该顶点邻接且未被访问的顶点，直到遍历完整个图。
广度优先搜索的基本思想可用以下步骤总结：1. 选择一个初始顶点；2. 访问该顶点，并标记为已访问；3. 将该顶点的所有邻接顶点加入一个队列；4. 从队列中依次取出一个顶点，并访问该顶点的邻接顶点，标记为已访问；5. 重复步骤4，直到队列为空。
广度优先搜索的应用场景也非常广泛。
在求最短路径、社交网络分析、网络爬虫等方面都可以使用广度优先搜索算法。
它的主要优点是可以找到最短路径，缺点是需要使用队列数据结构。
三、DFS与BFS的比较深度优先搜索和广度优先搜索各自有着不同的优缺点，适用于不同的场景。
深度优先搜索的优点是在空间复杂度较低的情况下找到解，但可能陷入无限循环，搜索路径不一定是最短的。
广度优先搜索能找到最短路径，但需要保存所有搜索过的节点，空间复杂度较高。
需要根据实际问题选择合适的搜索算法，例如在求最短路径问题中，广度优先搜索更加合适；而在解决连通分量问题时，深度优先搜索更为适用。
深度优先搜索算法
深度优先搜索算法深度优先搜索算法是一种经典的算法，它在计算机科学领域中被广泛应用。
深度优先搜索算法通过沿着一个分支尽可能的往下搜索，直到搜索到所有分支的末端后，返回上一层节点，再继续往下搜索其它分支。
在搜索过程中，深度优先搜索算法采用递归的方式进行，它的工作原理与树的先序遍历算法相似。
本文将介绍深度优先搜索算法的基本原理、应用场景、实现方式及其优缺点等内容。
一、深度优先搜索算法的基本原理深度优先搜索算法是一种基于贪心法的搜索算法，它的目标是在搜索过程中尽可能的向下搜索，直到遇到死路或者找到了目标节点。
当搜索到一个节点时，首先将该节点标记为已访问。
然后从它的相邻节点中选择一个未被访问过的节点继续搜索。
如果没有未被访问过的节点，就返回到前一个节点，从该节点的其它相邻节点开始继续搜索。
这样不断地递归下去，直到搜索到目标节点或者搜索完所有的节点。
深度优先搜索算法的实现方式通常是通过递归函数的方式进行。
假设我们要搜索一棵树，从根节点开始进行深度优先搜索。
可以采用以下的伪代码：```function depthFirstSearch(node)://标记节点为已访问node.visited = true//递归搜索该节点的相邻节点for each adjacentNode in node.adjacentNodes:if adjacentNode.visited == false:depthFirstSearch(adjacentNode)```这段代码表示了深度优先搜索算法的基本思想。
在搜索过程中，首先将当前节点标记为已访问，然后递归搜索该节点的相邻节点。
如果相邻节点未被访问过，就以该节点为起点继续深度优先搜索。
通过递归函数不断往下搜索，最终遍历完整棵树。
二、深度优先搜索算法的应用场景深度优先搜索算法在计算机科学领域中有很多应用，例如图论、路径查找、迷宫和游戏等领域。
下面介绍一些具体的应用场景。
1.图论深度优先搜索算法被广泛应用于图论中。
深度优先算法与广度优先算法
深度优先算法与⼴度优先算法深度优先搜索和⼴度优先搜索，都是图形搜索算法，它两相似，⼜却不同，在应⽤上也被⽤到不同的地⽅。
这⾥拿⼀起讨论，⽅便⽐较。
⼀、深度优先搜索深度优先搜索属于图算法的⼀种，是⼀个针对图和树的遍历算法，英⽂缩写为DFS即Depth First Search。
深度优先搜索是图论中的经典算法，利⽤深度优先搜索算法可以产⽣⽬标图的相应拓扑排序表，利⽤拓扑排序表可以⽅便的解决很多相关的图论问题，如最⼤路径问题等等。
⼀般⽤堆数据结构来辅助实现DFS算法。
其过程简要来说是对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌，⽽且每个节点只能访问⼀次。
基本步奏（1）对于下⾯的树⽽⾔，DFS⽅法⾸先从根节点1开始，其搜索节点顺序是1,2,3,4,5,6,7,8（假定左分枝和右分枝中优先选择左分枝）。
（2）从stack中访问栈顶的点；（3）找出与此点邻接的且尚未遍历的点，进⾏标记，然后放⼊stack中，依次进⾏；（4）如果此点没有尚未遍历的邻接点，则将此点从stack中弹出，再按照（3）依次进⾏；（5）直到遍历完整个树，stack⾥的元素都将弹出，最后栈为空，DFS遍历完成。
⼆、⼴度优先搜索⼴度优先搜索（也称宽度优先搜索，缩写BFS，以下采⽤⼴度来描述）是连通图的⼀种遍历算法这⼀算法也是很多重要的图的算法的原型。
Dijkstra单源最短路径算法和Prim最⼩⽣成树算法都采⽤了和宽度优先搜索类似的思想。
其别名⼜叫BFS，属于⼀种盲⽬搜寻法，⽬的是系统地展开并检查图中的所有节点，以找寻结果。
换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为⽌。
基本过程，BFS是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。
如果所有节点均被访问，则算法中⽌。
⼀般⽤队列数据结构来辅助实现BFS算法。
基本步奏（1）给出⼀连通图，如图，初始化全是⽩⾊（未访问）；（2）搜索起点V1（灰⾊）；（3）已搜索V1（⿊⾊），即将搜索V2，V3，V4（标灰）；（4）对V2，V3，V4重复以上操作；（5）直到终点V7被染灰，终⽌；（6）最短路径为V1，V4，V7.作者：安然若知链接：https:///p/bff70b786bb6来源：简书简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。
DFS深度优先搜索（附例题）
DFS深度优先搜索（附例题）深度优先搜索，简称DFS，算是应⽤最⼴泛的搜索算法，属于图算法的⼀种,dfs按照深度优先的⽅式搜索，通俗说就是“⼀条路⾛到⿊”，dfs 是⼀种穷举，实质是将所有的可⾏⽅案列举出来，不断去试探，知道找到问题的解，其过程是对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌，且每个顶点只能访问⼀次。
dfs⼀般借助递归来实现例题：⾛迷宫#include <iostream>#include <string.h>using namespace std;int m,n;int sx,sy,ex,ey;//起点终点坐标int mp[20][20];//记录地图int cnt=0;//结果个数int ax[10]={0,0,-1,1};//x的四个⾛向int ay[10]={1,-1,0,0};//y的四个⾛向int vis[20][20];//记录是否来过int dfs(int x,int y){if((x>=0)&&(y>=0)&&(x<n)&&(y<m)&&(mp[x][y]==0)){//坐标合法性if(x==ex&&y==ey){//如果是终点cnt++;return0;}vis[x][y]=1;//将x，y设为已经来过if(vis[x][y]==1){//判断是否相邻顶点可⾛for(int i=0;i<4;i++){int tx=x+ax[i];int ty=y+ay[i];if((tx>=0)&&(ty>=0)&&(tx<n)&&(ty<m)&&(mp[tx][ty]==0)&&vis[tx][ty]==0)//相邻顶点可⾛条件dfs(tx,ty);//递归dfs此点}}vis[x][y]=0;return0;}}int main(){memset(vis,0,sizeof(vis));//将遍历数组全部置0cin>>n>>m;for(int i=0;i<n;i++){for(int j=0;j<m;j++){char c;cin>>c;if(c=='.'){//边输⼊边置mp的0或1，并设置起点坐标和终点坐标mp[i][j]=0;}else if(c=='S'){sx=i;sy=j;mp[i][j]=0;}else if(c=='T'){ex=i;ey=j;mp[i][j]=0;}elsemp[i][j]=1;//'#'为墙壁，⾛不通所以设为1}}dfs(sx,sy);//从起点开始遍历cout<<cnt<<endl;return0;}。
《深度优先搜索》课件
总结词
应用广泛，涉及图论和算法
要点二
详细描述
图的着色问题是一个经典的NP难问题，通过深度优先搜索 可以找到一种合适的颜色分配方案，使得相邻的顶点颜色 不同。在深度优先搜索过程中，我们可以使用回溯算法来 尝试不同的颜色分配方案，直到找到可行解或证明无解。
旅行商问题
总结词
组合优化问题，适合理解最短路径算法
详细描述
深度优先搜索、广度优先搜索和最佳优先搜索是常见的三种搜索算法。它们在处理问题的侧重点和适用场景上有 所不同。深度优先搜索更注重深度上的探索，而广度优先搜索则更注重广度上的探索。最佳优先搜索则是在启发 式搜索中常用的算法，它根据某种启发式信息来选择下一个要探索的节点。
02
深度优先搜索的基本原理
图的表示与遍历
图的表示
图是由节点和边组成的数据结构，可以用邻接矩阵或邻接表来表示。邻接矩阵是一种二 维矩阵，其中行和列都代表图中的节点，如果两个节点之间存在一条边，则矩阵中相应 的元素为1，否则为0。邻接表则是用链表来表示图中的边，每个节点包含一个链表，
链表中的元素是与该节点相邻的节点。
图的遍历
图的遍历是指按照某种顺序访问图中的所有节点。常见的图的遍历算法有深度优先搜索 （DFS）和广度优先搜索（BFS）。DFS是一种递归的算法，通过不断深入探索图的分 支，直到达到终点或无法再深入为止。BFS则是按照层次顺序访问图中的节点，从根节
05
深度优先搜索的案例分析
八皇后问题
总结词
经典问题，适合初学者理解深度优先搜索
详细描述
八皇后问题是一个经典的回溯算法问题，通过深度优先搜索 可以找出在8x8棋盘上放置8个皇后，使得它们互不攻击的方 案。在深度优先搜索过程中，我们可以使用递归和剪枝技巧 来减少搜索空间，提高搜索效率。
深度优先搜索原理与实践及代码示例
深度优先搜索原理与实践及代码示例深度优先搜索（Depth First Search，简称DFS）是一种用于遍历或搜索树或图的算法。
它通过从根节点开始，沿着树的深度遍历直到某个叶子节点，然后回溯到上一个节点，继续遍历下一个分支。
DFS通常使用递归实现，也可以使用栈来辅助实现。
一、DFS原理深度优先搜索基于“尽可能深入地搜索”的原则。
它从根节点出发，先访问子节点，再访问子节点的子节点，直到达到某个终止条件。
然后回溯到上一个节点，继续访问该节点的其他子节点，直到遍历完整个树或图。
二、DFS实践下面以一个简单的二叉树为例，演示DFS算法的实践过程。
假设有以下二叉树：```1/ \2 3/ \4 5```DFS的遍历顺序是：1 -> 2 -> 4 -> 5 -> 3。
以下是实现DFS遍历二叉树的示例代码：```pythonclass Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Nonedef dfs(node):if node is None:returnprint(node.data)dfs(node.left)dfs(node.right)# 创建二叉树node1 = Node(1)node2 = Node(2)node3 = Node(3)node4 = Node(4)node5 = Node(5)node1.left = node2node1.right = node3node2.left = node4node2.right = node5# DFS遍历二叉树dfs(node1)```运行上述代码，将输出：1 2 4 5 3。
可以看到，DFS按照深度优先的原则遍历二叉树节点。
三、DFS的应用深度优先搜索算法有广泛的应用，包括但不限于以下几个领域：1. 图的连通性判断：可以通过DFS遍历图的所有连通节点，判断图是否连通。
深度优先搜索
深度优先搜索(Depth-First-Search)引例:迷宫问题首先我们来想象一只老鼠，在一座不见天日的迷宫内，老鼠在入口处进去，要从出口出来。
那老鼠会怎么走？当然可以是这样的：老鼠如果遇到直路，就一直往前走，如果遇到分叉路口，就任意选择其中的一条继续往下走，如果遇到死胡同，就退回到最近的一个分叉路口，选择另一条道路再走下去，如果遇到了出口，老鼠的旅途就算成功结束了。
深度优先搜索的基本原则就是这样：按照某种条件往前试探搜索，如果前进中遭到失败（正如老鼠遇到死胡同）则退回头另选通路继续搜索，直到找到满足条件的目标为止。
递归程序设计然而要实现这样的算法，我们需要用到编程的一大利器---递归。
当一个函数直接或者间接的调用了自己本身的时候，则发生了递归。
讲一个更具体的例子：从前有座山，山里有座庙，庙里有个老和尚，老和尚在讲故事，讲什么呢？讲：从前有座山，山里有座庙，庙里有个老和尚，老和尚在讲故事，讲什么呢？讲：从前有座山，山里有座庙，庙里有个老和尚，老和尚在讲故事，讲什么呢？讲：…………。
好家伙，这样讲到世界末日还讲不玩，老和尚讲的故事实际上就是前面的故事情节，这样不断地调用程序本身，就形成了递归。
万一这个故事中的某一个老和尚看这个故事不顺眼，就把他要讲的故事换成：“你有完没完啊！”，这样，整个故事也就嘎然而止了。
我们编程就要注意这一点，在适当的时候，就必须要有一个这样的和尚挺身而出，把整个故事给停下来，或者说他不再往深一层次搜索，要不，我们的递归就会因计算机栈空间大小的限制而溢出，称为stack overflow。
递归的经典实例：int factorial(int n){if (n == 0) //基线条件(base case){return 1;}else{return n * factorial(n - 1); //将问题规模逐渐缩小，或者说转化为更小更简单的子问题 }}再来看另外一个例子---放苹果 (POJ1664)：把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？ 5，1，1和1，5，1 是同一种分法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当前方向入栈 x = xx，y = yy //前进一步 在地图上将 x，y 坐标标记为走过的路 判断结束 循环结束
下面贴出完整代码，比较长，做好心理准备。
public class DFS { //辅助方法：打印地图
if (map[yy][xx]==2) { d[step] = dir; System.out.println("找到出口"); break;
} if (map[yy][xx]!=0) {
//撞墙了或遇到走过的路 continue; } else { //记录当前方向 d[step] = dir; dir = 0; map[y][x] = 3; //堵回头路 x = xx; y = yy; step++; } } while (true); //下面为结果输出 System.out.println("一共走了" + step + "步!");
终于要说到代码实现了，深度优先搜索的原理不难理解，但要用代码实现，也有点小难度， 下面对各个难点进行说明：
1， 地图（迷宫）的表示 一般可以使用整形二维数组描述地图，0 代表空地，1 代表墙，2 代表出口，3 代表走过的路。 有点浪费内存，但是易于理解。 2， 下一步选择（方向）的表示 一般使用连续的整形，如表示“上下左右”四个方向就可用 1，2，3，4 来代替 3， 记录每一步选择（毛线） 上一章说过，可以使用栈或者一维数组进行记录
公主送毛线自然不是要教夫君打毛衣，而是指导他：“把线头系于迷宫入口处，一路放线 团，一边进入到迷宫，杀掉牛头怪，再循着线团走出迷宫”。
果然，忒修斯按照公主的方法顺利走到了迷宫中央，经过一番搏斗杀死了牛头怪，并沿 着毛线退出了迷宫。按理说后续应该是个大团圆的结局：忒修斯回到王国迎娶公主，三两年 后国王病逝忒修斯继承王位，于是国王与王后过上了幸福的生活。
}
public static void main(String[] args) {
//初始化地图，数组中 1 代表墙，0 代表路，2 是出口，3 是走过的路
[][] map = {
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,0,0,0,0,0,0,2},
{1,0,1,0,1,0,1,1,1,1},
第一幅图是简单的迷宫，左下角是入口，右上角是出口，接下来为方便演示，我们按照“右 上左下”的优先级顺利来进行探索（即遇到岔路先选择走右面，不行选择上面，然后是左面， 下面）。
图中的线条相当于毛线，记录这每一步的选择
因为先走右边，很快就走到了右下角，右边不能再走了，下一个选择是上边。上到顶发现 右边、上边都不能再走了，选择左边，往前走发现到了死胡同，上下左都不能走，右边是走 过的也不能走，该怎么办呢？
今天来说说深度优先搜索，属于搜索回朔类的算法，相对比较有趣。 关于这个算法的最早传说出现在古希腊时代：
没落贵族的忒修斯（没落到被选为了祭品），爱上了残暴国王弥诺斯的女儿阿里阿德涅 公主，而未来的岳父却决定把可怜的忒修斯送到克里特岛喂牛头怪。
这个特里克岛可是国王的呕心沥血之作，岛上最著名的建筑就是地下迷宫，据说被扔进 去了谁都绕不出来，就算你运气好，找到正确的路，还有一头凶猛的牛头怪养在必经之路上， 送到岛上作为祭品的人从来没能活着回来。
不过古希腊的剧作家个个都是苦大仇深，不爱写大团圆的结尾，一般都要主人公死光光 或落下终身残疾才成。这个故事的详细结局可以自行搜索，反正可怜的算法大师、深度优先 搜索算法的缔造者阿里阿德涅公主最后跳入大海喂鲨鱼了。
这个故事大家在小时候肯定都或多或少的知道，现在我们作为一名算法爱好者，应该考 虑一个在原著中被忽略的很重要的细节：为什么一团毛线，就可以让忒修斯顺利的找到牛 头怪，并能成功返回迷宫出口呢？
第四幅图就不用多上了，按照“右上左下”的优先顺序，很快找到了出口。 练习时间：请使用深度优先搜索原理走完下面的迷宫
注意：每次在岔路口选择都必须按照原则进行（不一定非要是“右上左下”，也可以是“上 下左右”），不能人为的做出判断。
下面是我用画笔绘制的将行走过程模拟图
静态图片可能无法完全说明问题，强烈建议读者自己用画笔来画一画。 经过这个练习，你会发现，使用深度优先算法找到的一般并不是最短的路径，但它保证 可以找到一条路径（如果迷宫没有问题的话），如果你坚持要找最短的，后面的广度优先算 法会满足你的要求，这是后话。现在故事讲了、原理分析了、图也画了，该真刀真枪的上代 码了， 请见下回分解。
x = startX; y = startY; map[y][x] = d[0] + 10; for (int i = 0; i <= step; i++) {
if (d[i]==1) x++; if (d[i]==2) y--; if (d[i]==3) x--; if (d[i]==4) y++; map[y][x] = d[i]+10; } printArray(map); } }
变态的特里克岛，但现在是旅游胜地
按常理忒修斯也难逃厄运，但后来的故事印证了两个亘古不变的真理：1，女人是不可靠 的，女儿也不例外 2，穷小子要翻身，就得靠女人
在忒修斯出发前，小伙子费劲脑汁与阿里阿德涅公主又见了最后一面，在这次历史性的 会晤中，公主送给了穷小伙两件足以挽救其性命的礼物：一团毛线和一把据说唯一能杀死牛 头怪的剑。
请大家思考，吃午饭去了，回来再写。
接着讨论这个问题：“为什么一团毛线，就可以让忒修斯顺利的找到牛头怪，并能成功返回 迷宫出口呢？”
事实上，如果只有毛线是不可能的，至少无法保证忒修斯顺利找到牛头怪！
当你在迷宫中遇到讨厌的岔路时，毛线只能让你知道回去该走哪条路，却无法告诉前方 该如何选择。毛线只能保证忒修斯可以全身而退，却无法指引牛头怪的方向。
{1,0,1,0,1,0,1,0,0,1},
{1,1,1,1,1,0,1,1,0,1},
{1,0,0,0,0,0,0,1,0,1},
{1,1,1,1,1,1,0,1,0,1},
{1,1,1,1,1,1,0,1,0,1},
{0,0,0,0,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
输出结果：略，大家可以自己运行一下。
现在我写这些代码算比较轻松了，但回想 N 年前刚学习深度优先时，虽然理论上明白了， 但是代码死活也整合不到一块儿去，动不动就数组下标越界或者死循环，希望大家练习这部 分代码的时候一定要有耐心，再加上细心。
深度优先搜索的应用：第一种应用自然是走迷宫啦，上一章列出的代码是寻找一条有效 的路径，深度优先也可以穷举出迷宫中所有的路径。只需要在每次找到迷宫出口时，不要结 束程序，而继续回溯，就可以继续寻找其他走出迷宫的办法，直到变量 step 为 0，程序退出。 你可以记录每一种走法的路径长度（step），最后得到最优解。
private static void printArray(int m[][]) { int v = 0; for (int y=0;y<10;y++) { for (int x = 0;x<10; x++) { v = m[y][x]; if (v==0) System.out.print(" "); if (v==1) System.out.print("■■"); if (v==2) System.out.print("XX"); if (v==3) System.out.print(" "); if (v==11) System.out.print("->"); if (v==12) System.out.print("^^"); if (v==13) System.out.print("<-"); if (v==14) System.out.print("vv"); } System.out.println(); }
这当然不能怪毛线，作为一团没有任何智能的妇女用品，它只能做到这一步了。
那可怜的忒修斯在迷宫中面对每一处岔路，是如何选择正确方向的呢？很遗憾，在大多 数情况下，他并没能做出正确的选择，但也没有像前人一样迷失在迷宫中被饿死，而是最终 找到了牛头怪并铲除了它！人和人的差距为什么这么大捏？？因为在出发前，阿里阿德涅公 主在他耳边悄悄的说了一个口诀。
唯一的选择就是沿着毛线退回到上一个路口重新做出选择，先退到路口 A，刚才在路口 A 选择的方向是左边，下一个选择是下边，可下边是走过的不能走，只能继续后退。
退到路口 B，刚才在路口 B 选择的是上边，下一个选择是左边，不行，再下一个是下边， 也不行，继续后退。
退到路口 C，刚才在路口 C 选择的是右边，下一个选择是上边，可以走，ok，掉转方向， let's go。
int startX = 0, startY = 8; //迷宫的入口坐标
int x = startX ,y = startY;
int xx=0, yy=0;
//开始进入迷宫 do {
dir++; //试探下一个方向 if (dir>4) {
//回朔 if (step==0) {
System.out.println("地图没有出口！"); return; } dir = d[step-1]; //取出上一次的方向 //沿着反方向后退一步 if (dir==1) x--; if (dir==2) y++; if (dir==3) x++; if (dir==4) y--; step--; continue; } //按照方向前进一步 xx = x; yy = y; if (dir==1) xx++; if (dir==2) yy--; if (dir==3) xx--; if (dir==4) yy++;